MatematiÄin bir alt dalÄą olan fonksiyonel analizde, tam normlu vektÃķr uzayÄąlarÄąna Banach uzayÄą denir. TanÄąmÄą gereÄi, Banach uzayÄą, vektÃķr uzunluÄunun ve vektÃķrler arasÄąndaki mesafenin hesaplanmasÄąna vesile olan bir metriÄe sahip bir vektÃķr uzayÄądÄąr ve bu metrik uzayda herhangi bir Cauchy vektÃķr dizisinin her zaman uzayÄąn içinde kalan ve iyi tanÄąmlanmÄąÅ bir limiti olmasÄą anlamÄąnda tamdÄąr.
Banach uzaylarÄą, bu kavramÄą 1920-1922'de ve ile birlikte sistematik olarak inceleyen PolonyalÄą matematikçi Stefan Banach'Äąn adÄąnÄą taÅÄąr., Banach uzayÄą terimini ilk kullanan matematikçiydi. Banach uzaylarÄą, yirminci yÞzyÄąlÄąn baÅlarÄąnda Hilbert, ve tarafÄąndan fonksiyon uzaylarÄą Þzerine yapÄąlan çalÄąÅmalardan ortaya Ã§ÄąktÄą .
Banach uzaylarÄą, fonksiyonel analizde merkezi bir rol oynar. DiÄer analiz alanlarÄąnda incelenen uzaylar genellikle Banach uzaylarÄądÄąr.
TanÄąm
Tam olan bir Banach uzayÄą adÄą verilir.
Normlu uzay 




Norm tarafÄąndan Þretilen metrik



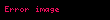

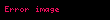





- " Her gerçel
için bir
sayÄąsÄą vardÄąr Ãķyle ki
"
ÃķzelliÄini saÄlarsa, bu diziye Cauchy dizisi adÄą verilir.
Norm tarafÄąndan Þretilen metriÄin tamlÄąÄÄą
Bir metrik uzayÄąnÄąn 










Sonuç olarak, 


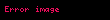
Ãrnekler
AÅaÄÄądaki uzaylarÄąn hepsi fonksiyonel analizin içinde çalÄąÅÄąlan birer Banach uzayÄądÄąr.
gerçel sayÄąlar cismi
ya da karmaÅÄąk sayÄąlar
cismi olmak Þzere Ãklid uzayÄą
,
- Daha genel olarak
ya da karmaÅÄąk sayÄąlar
cismi Þzerinde tanÄąmlÄą herhangi bir sonlu-boyutlu vektÃķr uzayÄą
- Bir Banach uzayÄąnÄąn herhangi kapalÄą bir altuzayÄą yine Banach uzayÄądÄąr. Mesela,
bir topolojik uzaysa ve
Banach uzayÄąysa,
'ten
'ye tanÄąmlanan ve hem sÞrekli hem de sÄąnÄąrlÄą olan fonksiyonlar uzayÄą
yine BanachtÄąr. Sonuç olarak, tÄąkÄąz bir
uzayÄą için,
Þzerinde tanÄąmlÄą sÞrekli fonksiyonlar uzayÄą
de Banach uzayÄądÄąr. AslÄąnda, vasÄątasÄąyla, her Banach uzayÄą
'nin kapalÄą bir alt uzayÄąna izomorftur.
- Hilbert uzaylarÄą
- Lebesgue uzaylarÄą:
,
,
,
, ,
- ,
,
- ,
uzayÄą,
uzayÄą,
- TÄąkÄąz Hausdorff uzayÄą Þzerindeki sÞrekli fonksiyonlar uzayÄą C(K)
- uzayÄą
AyrÄąca, matematiksel analizde uygulamalarÄą olan ve yoÄunlukla kullanÄąlan Åu uzaylar da Banach uzayÄądÄąr: , Bergman uzayÄą, , , , ,
Notlar
- ^ TesadÞf ki, Banach da buna karÅÄąlÄąk daha sonralarÄą terimini kullanmÄąÅtÄąr.
- ^ Bu cisim genelde,
ya da
olur. Belirli bir cisim kastedilmiyorsa, Almanca terim KÃķrper kaynaklÄą
kullanÄąlÄąr.
- ^ Burada belirli sÃķzÞnden kastedilen Åudur. EÄer
Þzerinde
normu yerine baÅka bir norm
alÄąnsaydÄą, o zaman
ile
aynÄą Banach uzayÄą olmazdÄą. Bu durum, normlar olsa bile deÄiÅmezdi. Yine de, bir vektÃķr uzayÄą Þzerinde tanÄąmlÄą denk normlar bir denklik baÄÄąntÄąsÄą oluÅtururlar.
- ^ Normlu bir
uzayÄą Þzerinde bir norm tarafÄąndan doÄurulan bir
metriÄi adÄą verilen ÃķzelliÄi saÄlar. Yani, her
için
vardÄąr. Bu Ãķzellik, ancak ve ancak yine bÞtÞn
için
gerçeklenirse olur. ÃbÞr taraftan, bir metrik uzayda saÄlanmasÄą, bu metrik uzayÄąn normlu bir uzay tarafÄąndan doÄurulduÄunu tek baÅÄąna gÃķstermez. Bunun olmasÄą için, yanÄą sÄąra bir de ÃķzelliÄi gerekir. Bu Ãķzellik, bir
fonksiyonu için
- Her
ve
için,
vardÄąr.
- Her
- ^ MetriÄi veya normu vurgulamak için
'de Cauchy,
-Cauchy veya
-Cauchy tanÄąmlarÄą da kullanÄąlÄąr.
Kaynakça
- ^ Bourbaki 1987, V.87
- ^ Narici & Beckenstein 2011, s. 93.
Referanslar
- Bourbaki, Nicolas (1987) [1981]. Topological Vector Spaces: Chapters 1â5. ÃlÃĐments de mathÃĐmatique. Eggleston, H.G.; Madan, S. tarafÄąndan çevrilmiÅtir. Berlin New York: Springer-Verlag. .
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press
wikipedia, wiki, viki, vikipedia, oku, kitap, kÞtÞphane, kÞtÞbhane, ara, ara bul, bul, herÅey, ne arasanÄąz burada,hikayeler, makale, kitaplar, ÃķÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tÞrk, tÞrkçe, turkce, nasÄąl yapÄąlÄąr, ne demek, nasÄąl, yapmak, yapÄąlÄąr, indir, Þcretsiz, Þcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mÞzik, ÅarkÄą, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematigin bir alt dali olan fonksiyonel analizde tam normlu vektor uzayilarina Banach uzayi denir Tanimi geregi Banach uzayi vektor uzunlugunun ve vektorler arasindaki mesafenin hesaplanmasina vesile olan bir metrige sahip bir vektor uzayidir ve bu metrik uzayda herhangi bir Cauchy vektor dizisinin her zaman uzayin icinde kalan ve iyi tanimlanmis bir limiti olmasi anlaminda tamdir Banach uzaylari bu kavrami 1920 1922 de ve ile birlikte sistematik olarak inceleyen Polonyali matematikci Stefan Banach in adini tasir Banach uzayi terimini ilk kullanan matematikciydi Banach uzaylari yirminci yuzyilin baslarinda Hilbert ve tarafindan fonksiyon uzaylari uzerine yapilan calismalardan ortaya cikti Banach uzaylari fonksiyonel analizde merkezi bir rol oynar Diger analiz alanlarinda incelenen uzaylar genellikle Banach uzaylaridir TanimTam olan bir Banach uzayi adi verilir Normlu uzay X displaystyle X ile gosterilsin X displaystyle X uzerinde tanimli norm displaystyle cdot ise Banach uzayinin gosterimi X displaystyle X cdot olur Ancak sadece bir tane Banach uzayindan bahsediliyorsa veya norma vurgu yapmaya gerek yoksa X displaystyle X cdot yerine sadece X displaystyle X bir Banach uzayidir da denir Norm tarafindan uretilen metrik X displaystyle X cdot normlu uzayi skaler bir cisim K displaystyle mathbb K uzerinde tanimlanmis bir X displaystyle X vektor uzayindan ve belirli bir norm fonksiyonu olan X R displaystyle cdot X to mathbb R ile tanimlanir Butun normlar gibi bu norm da bir metrik uzayi dogurur Bu metrige denir Eger bu metrik d displaystyle d ile gosterilirse o zaman su sekilde tanimlanir d x y y x x y displaystyle d x y y x x y Bu tanim altinda norm ozelliklerinden faydalanarak d displaystyle d nin gercekten bir metrik oldugu gosterilebilir Sonuc olarak X displaystyle X bir metrik uzayi olur ve X d displaystyle X d ile gosterilir X d displaystyle X d icinde bir xj j 1 displaystyle x j j 1 infty dizisi Her gercel e gt 0 displaystyle varepsilon gt 0 icin bir N Z displaystyle N in mathbb Z sayisi vardir oyle kid xn xm xn xm lt e m n N displaystyle d left x n x m right left x n x m right lt varepsilon quad forall m n geq N dd ozelligini saglarsa bu diziye Cauchy dizisi adi verilir Norm tarafindan uretilen metrigin tamligi Bir metrik uzayinin X d displaystyle X d deki her xj j 1 displaystyle x j j 1 infty Cauchy dizisinin limiti yine X displaystyle X teyse o zaman d displaystyle d ye X d displaystyle X d ye ise tam metrik uzay denir Burada limit kavrami X d displaystyle X d baglaminda limn xn x displaystyle lim n to infty x n x olarak yazilabilir Ayni zamanda xn x d xn x displaystyle left x n x right d left x n x right olacagi icin dizinin x displaystyle x degerine yakinsamasi daha once verilen limit ifadesine denk olarak R displaystyle mathbb R baglaminda limn xn x 0 displaystyle lim n to infty left x n x right 0 olarak yazilabilir Sonuc olarak X d displaystyle X d tam metrik uzaysa X displaystyle X cdot Banach uzayidir X displaystyle X cdot normlu uzayi eger Banach uzayiysa o zaman displaystyle cdot norm fonksiyonuna tam norm denir OrneklerAsagidaki uzaylarin hepsi fonksiyonel analizin icinde calisilan birer Banach uzayidir F displaystyle mathbb F gercel sayilar cismi R displaystyle mathbb R ya da karmasik sayilar C displaystyle mathbb C cismi olmak uzere Oklid uzayi Fn displaystyle mathbb F n Daha genel olarak R displaystyle mathbb R ya da karmasik sayilar C displaystyle mathbb C cismi uzerinde tanimli herhangi bir sonlu boyutlu vektor uzayi Bir Banach uzayinin herhangi kapali bir altuzayi yine Banach uzayidir Mesela X displaystyle X bir topolojik uzaysa ve Y displaystyle Y Banach uzayiysa X displaystyle X ten Y displaystyle Y ye tanimlanan ve hem surekli hem de sinirli olan fonksiyonlar uzayi B X Y displaystyle B X Y yine Banachtir Sonuc olarak tikiz bir K displaystyle K uzayi icin K displaystyle K uzerinde tanimli surekli fonksiyonlar uzayi C K Y displaystyle C K Y de Banach uzayidir Aslinda vasitasiyla her Banach uzayi C K R displaystyle C K mathbb R nin kapali bir alt uzayina izomorftur Hilbert uzaylari Lebesgue uzaylari âpn displaystyle ell p n â n displaystyle ell infty n âp displaystyle ell p â1 displaystyle ell 1 Lp displaystyle L p c0 displaystyle c 0 bv0 displaystyle operatorname bv 0 uzayi bs displaystyle operatorname bs uzayi Tikiz Hausdorff uzayi uzerindeki surekli fonksiyonlar uzayi C K uzayi AC a b displaystyle operatorname AC a b Ayrica matematiksel analizde uygulamalari olan ve yogunlukla kullanilan su uzaylar da Banach uzayidir Bergman uzayi Notlar Tesaduf ki Banach da buna karsilik daha sonralari terimini kullanmistir Bu cisim genelde C displaystyle mathbb C ya da R displaystyle mathbb R olur Belirli bir cisim kastedilmiyorsa Almanca terim Korper kaynakli K displaystyle mathbb K kullanilir Burada belirli sozunden kastedilen sudur Eger X displaystyle X uzerinde displaystyle cdot normu yerine baska bir norm displaystyle cdot prime alinsaydi o zaman X displaystyle X cdot ile X displaystyle left X cdot prime right ayni Banach uzayi olmazdi Bu durum normlar olsa bile degismezdi Yine de bir vektor uzayi uzerinde tanimli denk normlar bir denklik bagintisi olustururlar Normlu bir X displaystyle X uzayi uzerinde bir norm tarafindan dogurulan bir d displaystyle d metrigi adi verilen ozelligi saglar Yani her x y z X displaystyle x y z in X icin d x y d x z y z displaystyle d x y d x z y z vardir Bu ozellik ancak ve ancak yine butun x y X displaystyle x y in X icin d x y d x y 0 displaystyle d x y d x y 0 gerceklenirse olur Obur taraftan bir metrik uzayda saglanmasi bu metrik uzayin normlu bir uzay tarafindan doguruldugunu tek basina gostermez Bunun olmasi icin yani sira bir de ozelligi gerekir Bu ozellik bir f X R displaystyle f X mapsto mathbb R fonksiyonu icin Her x X displaystyle x in X ve s K displaystyle s in mathbb K icin f sx s f x displaystyle f sx s f x vardir olarak tanimlanir Metrigi veya normu vurgulamak icin X d displaystyle X d de Cauchy d displaystyle d Cauchy veya displaystyle cdot Cauchy tanimlari da kullanilir Kaynakca Bourbaki 1987 V 87 Narici amp Beckenstein 2011 s 93 ReferanslarBourbaki Nicolas 1987 1981 Topological Vector Spaces Chapters 1 5 Elements de mathematique Eggleston H G Madan S tarafindan cevrilmistir Berlin New York Springer Verlag ISBN 3 540 13627 4 Narici Lawrence Beckenstein Edward 2011 Topological Vector Spaces Pure and applied mathematics Second ed Boca Raton FL CRC Press ISBN 978 1584888666
 AzÉrbaycanca
AzÉrbaycanca ÐÐĩÐŧаŅŅŅКŅ
ÐÐĩÐŧаŅŅŅКŅ Dansk
Dansk Deutsch
Deutsch EspaÃąola
EspaÃąola Français
Français Indonesia
Indonesia Italiana
Italiana æĨæŽčŠ
æĨæŽčŠ ŌазаŌ
ŌазаŌ Lietuvos
Lietuvos Nederlands
Nederlands PortuguÊs
PortuguÊs Ð ŅŅŅКÐļÐđ
Ð ŅŅŅКÐļÐđ ā·ā·āķā·āķ―
ā·ā·āķā·āķ― āđāļāļāđāļāļĒ
āđāļāļāđāļāļĒ TÞrkçe
TÞrkçe ÐĢКŅаŅÐ―ŅŅКа
ÐĢКŅаŅÐ―ŅŅКа äļåäšš
äļåäšš United State
United State Afrikaans
Afrikaans