Termal akışkan dinamiği alanında, Nusselt sayısı (Nu), Wilhelm Nusselt'in adını taşıyan ve bir toplam ısı transferinin, kondüksiyon ısı transferine oranını ifade eden bir boyutsuz sayıdır. Toplam ısı transferi, kondüksiyon ve konveksiyonu içerir. Konveksiyon ise adveksiyon ve difüzyon bileşenlerinden oluşur. Kondüktif bileşen, konvektif koşullar altında ancak hareketsiz bir akışkan için varsayılarak ölçülür. Nusselt sayısı, akışkanın Rayleigh sayısı ile yakından ilişkilidir.:466
Nusselt sayısının bir büyüklüğündeki mertebesi, saf kondüksiyonla ısı transferini temsil ederken, bir ile 10 arasındaki değerler (İng. slug flow) veya laminer akışa özgüdür. Daha yüksek Nusselt sayıları daha aktif konveksiyon anlamına gelir ve türbülanslı akış genellikle 100-1000 aralığında bulunur.
Benzer şekilde, katı cisimler için ısı iletkenliğini ele alırken, Nusselt sayısının kütle transferi karşılığı Sherwood sayısıdır.
Tanım
Nusselt sayısı, bir sınır tabakası boyunca toplam ısı transferinin (kondüksiyon + konveksiyon) kondüksiyon ısı transferine oranıdır. Konveksiyon ve kondüksiyon ısı akışları, sınır tabakası yüzeyinin normaline paralel olup, ortalama akışkan akışına dik olarak gerçekleşir.
Burada h, akışın konvektif , L ve k akışkanın ısı iletkenliğini temsil eder.
- Karakteristik uzunluğun seçimi, sınır tabakasının büyüme veya kalınlık yönünde olmalıdır; karakteristik uzunluk örnekleri şunlardır: silindirin eksenine dik olarak (İng. cross flow) bir silindirin dış çapı, maruz kalan dikey bir plakanın uzunluğu veya bir kürenin çapı. Karmaşık geometriler için uzunluk, akışkan cismin hacminin yüzey alanına bölünmesiyle tanımlanabilir.
- Akışkanın ısı iletkenliği genellikle değerlendirilir ve mühendislik uygulamaları için bu, yığın (İng. bulk) akışkan sıcaklığı ile duvar yüzey sıcaklığının aritmetik ortalaması olarak hesaplanabilir.
Yukarıda verilen tanımın aksine, "ortalama Nusselt sayısı" olarak bilinen yerel Nusselt sayısı, uzunluğun yüzey sınırından ilgi noktasına olan mesafe olarak alınmasıyla tanımlanır.
"Olağan" ya da "ortalama" Nusselt sayısı, ilgi alanı boyunca bu ifadenin entegrasyonu ile elde edilir, örneğin:
Bağlam
Bir yüzey ile üzerinden akışkan akan bir akışkan arasında konvektif ısı transferini anlamak için konveksiyon sınır tabakalarının anlaşılması gereklidir. Akışkan serbest akım sıcaklığı ile yüzey sıcaklıkları farklı olduğunda bir termal sınır tabakası oluşur. Bu sıcaklık farkından kaynaklanan enerji değişimi nedeniyle bir sıcaklık profili ortaya çıkar.

Isı transfer oranı, kullanılarak şu şekilde ifade edilebilir:
,
burada h ve A ısı transfer yüzey alanıdır. Yüzeydeki ısı transferi iletim yoluyla gerçekleştiğinden, aynı miktar ısı iletkenliği k cinsinden şu şekilde ifade edilebilir:
.
Bu iki terim eşittir ve bu nedenle
.
Bu ifadeyi yeniden düzenleyerek,
.
Temsili bir uzunluk L ile çarptığımızda boyutsuz bir ifade elde ederiz:
.
Sağ taraf artık yüzeydeki sıcaklık gradyanının referans sıcaklık gradyanına oranını temsil ederken, sol taraf Biot modülüne benzer. Bu ifade, iletken termal direncin, akışkanın konvektif termal direncine oranı olan Nusselt sayısı, Nu olarak bilinir.
.
Türetme
Nusselt sayısı, (Fourier kanununun) boyutsuz bir analizi ile elde edilebilir çünkü bu sayı, yüzeydeki boyutsuz sıcaklık gradyanına eşittir:
, burada q , k sabit ısı iletkenliği ve T akışkan sıcaklığıdır.
Eğer: 

şuraya varırız:
sonra aşağıdaki tanımlamayı yapabiliriz:
bu nedenle denklem şu hale gelir:
Cismin yüzeyi üzerinde entegrasyon yaparak aşağıdaki sonucu elde edebiliriz:

burada 
Ampirik korelasyonlar
Genellikle doğal konveksiyon (zorlanmamış konveksiyon; İng. free convection) için, ortalama Nusselt sayısı Rayleigh sayısı ve Prandtl sayısının bir fonksiyonu olarak ifade edilir ve şu şekilde yazılır:
Zorlanmış konveksiyon durumunda ise, Nusselt sayısı genellikle Reynolds sayısı ve Prandtl sayısının bir fonksiyonu olarak ifade edilir:
Doğal konveksiyon
Dikey bir duvarda doğal konveksiyon
Churchill ve Chu'dan alıntılanmıştır:493:
Yatay plakadan doğal konveksiyon
Eğer karakteristik uzunluk şu şekilde tanımlanırsa
burada 

Daha soğuk bir ortamda sıcak bir cismin üst yüzeyi veya daha sıcak bir ortamda soğuk bir cismin alt yüzeyi için:493
Daha soğuk bir ortamda sıcak bir cismin alt yüzeyi veya daha sıcak bir ortamda soğuk bir cismin üst yüzeyi için:493
Alttan ısıtılan bir muhafazadan doğal konveksiyon
Bejan'dan alıntılanmıştır:
Bu denklem "yatay tabakanın yeterince geniş olduğu durumlarda, kısa dikey kenarların etkisinin minimal olması durumunda geçerlidir."
Bu, 1959'da Globe ve Dropkin tarafından ampirik olarak belirlenmiştir:"Testler, bakır üst ve alt kısımları olan ve yalıtımlı duvarlara sahip silindirik kaplarda yapılmıştır." Kullanılan kaplar yaklaşık 5 inç çapında ve 2 inç yüksekliğindeydi.
Laminer akışta düz plaka
Bir düz plaka üzerinde laminer akış için yerel Nusselt sayısı, plakanın kenarından aşağı yönde 
Bir düz plaka üzerinde laminer akış için ortalama Nusselt sayısı, plakanın kenarından aşağı yönde 
Konvektif akışta küre
Bazı uygulamalarda, örneğin hava içindeki küresel sıvı damlacıklarının buharlaşması gibi, şu korelasyon kullanılır:
Türbülanslı boru akışında zorlanmış konveksiyon
Gnielinski korelasyonu
Gnielinski'nin türbülanslı boru akışı için korelasyonu::{{{1}}}
Burada f, Darcy sürtünme faktörüdür ve veya Petukhov tarafından geliştirilen korelasyondan elde edilebilir::490
Gnielinski Korelasyonu şu durumlar için geçerlidir::490
Dittus–Boelter denklemi
W.H. McAdams tarafından tanıtılan Dittus–Boelter denklemi (türbülanslı akış için) Nusselt sayısını hesaplamak için bir (İng. explicit). Çözülmesi kolaydır ancak akışkan boyunca büyük sıcaklık farkları olduğunda daha az doğrudur. Dittus–Boelter denklemi pürüzsüz borular için uyarlanmıştır, bu nedenle pürüzlü borular (çoğu ticari uygulamada) için dikkatli kullanılmalıdır. Dittus–Boelter denklemi aşağıdaki gibidir:
Burada:
dairesel kanalın iç çapıdır
Prandtl sayısıdır
akışkan ısıtıldığında ve
akışkan soğutulduğunda kullanılır.:493
Dittus–Boelter denklemi şu durumlar için geçerlidir:514
Dittus–Boelter denklemi, kütlesel akışkan ile ısı transfer yüzeyi arasındaki sıcaklık farklarının minimal olduğu durumlarda iyi bir yaklaşımdır ve denklem karmaşıklığından ve yinelemeli çözümden kaçınır. Ortalama kütlesel akışkan sıcaklığı 20 °C (68 °F) olan suyu, viskozite 10,07×10-4 Pa.s ve ısı transfer yüzey sıcaklığı 40 °C (104 °F) olan bir durumda (viskozite 6,96×10-4 Pa.s, viskozite düzeltme faktörü 
Sieder–Tate korelasyonu
Sieder–Tate korelasyonu türbülanslı akış için bir (İng. implicit), çünkü sistemi doğrusal olmayan bir sınır değer problemi olarak analiz eder. Sieder–Tate sonucu, kütlesel akışkan ortalama sıcaklığı ile ısı transfer yüzey sıcaklığı arasındaki sıcaklık değişiminden dolayı viskozitedeki (
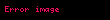
:493
Burada:
kütlesel akışkan sıcaklığındaki akışkan viskozitesidir
ısı transfer sınır yüzey sıcaklığındaki akışkan viskozitesidir
Sieder–Tate korelasyonu şu durumlar için geçerlidir:493
Tam gelişmiş laminer boru akışında zorlanmış konveksiyon
Tam gelişmiş iç laminer akışlı uzun borular için Nusselt sayıları sabit bir değere eğilim gösterir.
İç akış için:
Burada:
- Dh = Hidrolik çap
- kf = akışkanın ısı iletkenliği
- h = konvektif .
Dairesel borular için sabit sıcaklık ile konveksiyon
Incropera & DeWitt'e göre,:486-487
OEIS dizisi bu değeri şu şekilde verir: 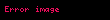
Dairesel borular için sabit ısı akısı ile konveksiyon
Sabit yüzey ısı akısı durumu için,:486-487
Ayrıca bakınız
- Sherwood sayısı (kütle transferi Nusselt sayısı)
- Reynolds sayısı
- Isı iletkenliği
Kaynakça
- ^ a b Çengel, Yunus A. (2002). Heat and Mass Transfer. 2nd. McGraw-Hill.
- ^ a b "The Nusselt Number". Whiting School of Engineering. 1 Nisan 2019 tarihinde kaynağından . Erişim tarihi: 3 Nisan 2019.
- ^ E. Sanvicente; ve diğerleri. (2012). "Transitional natural convection flow and heat transfer in an open channel". International Journal of Thermal Sciences. Cilt 63. ss. 87-104. doi:10.1016/j.ijthermalsci.2012.07.004.
- ^ a b c d e f g h i j k l m n ; DeWitt, David P. (2007). Fundamentals of Heat and Mass Transfer
![image]() . 6th. Hoboken: Wiley. ISBN .
. 6th. Hoboken: Wiley. ISBN . - ^ (2013). Convection Heat Transfer
![image]() (PDF). 4th. Wiley. ISBN .
(PDF). 4th. Wiley. ISBN . - ^ Globe, Samuel; Dropkin, David (1959). "Natural-Convection Heat Transfer in Liquids Confined by Two Horizontal Plates and Heated From Below". J. Heat Transfer. 81 (1). ss. 24-28. 25 Mart 2024 tarihinde kaynağından . Erişim tarihi: 7 Haziran 2024 – ASME Digital Collection vasıtasıyla.
- ^ McAllister, Sara; Chen, Jyh-Yuan; Fernández Pello, Carlos (2011). "Droplet Vaporization in Convective Flow". Fundamentals of combustion processes. Mechanical Engineering. New York: Springer. s. 159. doi:10.1007/978-1-4419-7943-8. ISBN . LCCN 2011925371.
- ^ Gnielinski, Volker (1975). "Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen". Forsch. Ing.-Wes. 41 (1). ss. 8-16. doi:10.1007/BF02559682.
- ^ (PDF). 3 Mart 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 23 Eylül 2009.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Termal akiskan dinamigi alaninda Nusselt sayisi Nu Wilhelm Nusselt in adini tasiyan ve bir toplam isi transferinin konduksiyon isi transferine oranini ifade eden bir boyutsuz sayidir Toplam isi transferi konduksiyon ve konveksiyonu icerir Konveksiyon ise adveksiyon ve difuzyon bilesenlerinden olusur Konduktif bilesen konvektif kosullar altinda ancak hareketsiz bir akiskan icin varsayilarak olculur Nusselt sayisi akiskanin Rayleigh sayisi ile yakindan iliskilidir 466 Nusselt sayisinin bir buyuklugundeki mertebesi saf konduksiyonla isi transferini temsil ederken bir ile 10 arasindaki degerler Ing slug flow veya laminer akisa ozgudur Daha yuksek Nusselt sayilari daha aktif konveksiyon anlamina gelir ve turbulansli akis genellikle 100 1000 araliginda bulunur Benzer sekilde kati cisimler icin isi iletkenligini ele alirken Nusselt sayisinin kutle transferi karsiligi Sherwood sayisidir TanimNusselt sayisi bir sinir tabakasi boyunca toplam isi transferinin konduksiyon konveksiyon konduksiyon isi transferine oranidir Konveksiyon ve konduksiyon isi akislari sinir tabakasi yuzeyinin normaline paralel olup ortalama akiskan akisina dik olarak gerceklesir NuL Toplam isi transferi Konduksiyon isi transferi hk L hLk displaystyle mathrm Nu L frac mbox Toplam isi transferi mbox Konduksiyon isi transferi frac h k L frac hL k Burada h akisin konvektif L ve k akiskanin isi iletkenligini temsil eder Karakteristik uzunlugun secimi sinir tabakasinin buyume veya kalinlik yonunde olmalidir karakteristik uzunluk ornekleri sunlardir silindirin eksenine dik olarak Ing cross flow bir silindirin dis capi maruz kalan dikey bir plakanin uzunlugu veya bir kurenin capi Karmasik geometriler icin uzunluk akiskan cismin hacminin yuzey alanina bolunmesiyle tanimlanabilir Akiskanin isi iletkenligi genellikle degerlendirilir ve muhendislik uygulamalari icin bu yigin Ing bulk akiskan sicakligi ile duvar yuzey sicakliginin aritmetik ortalamasi olarak hesaplanabilir Yukarida verilen tanimin aksine ortalama Nusselt sayisi olarak bilinen yerel Nusselt sayisi uzunlugun yuzey sinirindan ilgi noktasina olan mesafe olarak alinmasiyla tanimlanir Nux hxxk displaystyle mathrm Nu x frac h x x k Olagan ya da ortalama Nusselt sayisi ilgi alani boyunca bu ifadenin entegrasyonu ile elde edilir ornegin Nu 1L 0Lhx dx Lk h Lk displaystyle overline mathrm Nu frac frac 1 L int 0 L h x dx L k frac overline h L k BaglamBir yuzey ile uzerinden akiskan akan bir akiskan arasinda konvektif isi transferini anlamak icin konveksiyon sinir tabakalarinin anlasilmasi gereklidir Akiskan serbest akim sicakligi ile yuzey sicakliklari farkli oldugunda bir termal sinir tabakasi olusur Bu sicaklik farkindan kaynaklanan enerji degisimi nedeniyle bir sicaklik profili ortaya cikar Termal Sinir Tabakasi Isi transfer orani kullanilarak su sekilde ifade edilebilir Qy hA Ts T displaystyle Q y hA left T s T infty right burada h ve A isi transfer yuzey alanidir Yuzeydeki isi transferi iletim yoluyla gerceklestiginden ayni miktar isi iletkenligi k cinsinden su sekilde ifade edilebilir Qy kA y T Ts y 0 displaystyle Q y kA frac partial partial y left left T T s right right y 0 Bu iki terim esittir ve bu nedenle kA y T Ts y 0 hA Ts T displaystyle kA frac partial partial y left left T T s right right y 0 hA left T s T infty right Bu ifadeyi yeniden duzenleyerek hk Ts T y y 0 Ts T displaystyle frac h k frac left frac partial left T s T right partial y right y 0 left T s T infty right Temsili bir uzunluk L ile carptigimizda boyutsuz bir ifade elde ederiz hLk Ts T y y 0 Ts T L displaystyle frac hL k frac left frac partial left T s T right partial y right y 0 frac left T s T infty right L Sag taraf artik yuzeydeki sicaklik gradyaninin referans sicaklik gradyanina oranini temsil ederken sol taraf Biot modulune benzer Bu ifade iletken termal direncin akiskanin konvektif termal direncine orani olan Nusselt sayisi Nu olarak bilinir Nu hk L hLk displaystyle mathrm Nu frac h k L frac hL k TuretmeNusselt sayisi Fourier kanununun boyutsuz bir analizi ile elde edilebilir cunku bu sayi yuzeydeki boyutsuz sicaklik gradyanina esittir q kA T displaystyle q kA nabla T burada q k sabit isi iletkenligi ve T akiskan sicakligidir Eger L displaystyle nabla L nabla ve T T ThTh Tc displaystyle T frac T T h T h T c olursa suraya variriz T LkA Th Tc q hLk displaystyle nabla T frac L kA T h T c q frac hL k sonra asagidaki tanimlamayi yapabiliriz NuL hLk displaystyle mathrm Nu L frac hL k bu nedenle denklem su hale gelir NuL T displaystyle mathrm Nu L nabla T Cismin yuzeyi uzerinde entegrasyon yaparak asagidaki sonucu elde edebiliriz Nu 1S S NudS displaystyle overline mathrm Nu 1 over S int S mathrm Nu mathrm d S burada S SL2 displaystyle S frac S L 2 dir Ampirik korelasyonlarGenellikle dogal konveksiyon zorlanmamis konveksiyon Ing free convection icin ortalama Nusselt sayisi Rayleigh sayisi ve Prandtl sayisinin bir fonksiyonu olarak ifade edilir ve su sekilde yazilir Nu f Ra Pr displaystyle mathrm Nu f mathrm Ra mathrm Pr Zorlanmis konveksiyon durumunda ise Nusselt sayisi genellikle Reynolds sayisi ve Prandtl sayisinin bir fonksiyonu olarak ifade edilir Nu f Re Pr displaystyle mathrm Nu f mathrm Re mathrm Pr Dogal konveksiyon Dikey bir duvarda dogal konveksiyon Churchill ve Chu dan alintilanmistir 493 Nu L 0 68 0 663RaL1 4 1 0 492 Pr 9 16 4 9RaL 108 displaystyle overline mathrm Nu L 0 68 frac 0 663 mathrm Ra L 1 4 left 1 0 492 mathrm Pr 9 16 right 4 9 quad mathrm Ra L leq 10 8 Yatay plakadan dogal konveksiyon Eger karakteristik uzunluk su sekilde tanimlanirsa L AsP displaystyle L frac A s P burada As displaystyle mathrm A s plakanin yuzey alani ve P displaystyle P cevresidir Daha soguk bir ortamda sicak bir cismin ust yuzeyi veya daha sicak bir ortamda soguk bir cismin alt yuzeyi icin 493 Nu L 0 54RaL1 4104 RaL 107 displaystyle overline mathrm Nu L 0 54 mathrm Ra L 1 4 quad 10 4 leq mathrm Ra L leq 10 7 Nu L 0 15RaL1 3107 RaL 1011 displaystyle overline mathrm Nu L 0 15 mathrm Ra L 1 3 quad 10 7 leq mathrm Ra L leq 10 11 Daha soguk bir ortamda sicak bir cismin alt yuzeyi veya daha sicak bir ortamda soguk bir cismin ust yuzeyi icin 493 Nu L 0 52RaL1 5105 RaL 1010 displaystyle overline mathrm Nu L 0 52 mathrm Ra L 1 5 quad 10 5 leq mathrm Ra L leq 10 10 Alttan isitilan bir muhafazadan dogal konveksiyon Bejan dan alintilanmistir Nu L 0 069RaL1 3Pr0 0743 105 RaL 7 109 displaystyle overline mathrm Nu L 0 069 mathrm Ra L 1 3 Pr 0 074 quad 3 10 5 leq mathrm Ra L leq 7 10 9 Bu denklem yatay tabakanin yeterince genis oldugu durumlarda kisa dikey kenarlarin etkisinin minimal olmasi durumunda gecerlidir Bu 1959 da Globe ve Dropkin tarafindan ampirik olarak belirlenmistir Testler bakir ust ve alt kisimlari olan ve yalitimli duvarlara sahip silindirik kaplarda yapilmistir Kullanilan kaplar yaklasik 5 inc capinda ve 2 inc yuksekligindeydi Laminer akista duz plaka Bir duz plaka uzerinde laminer akis icin yerel Nusselt sayisi plakanin kenarindan asagi yonde x displaystyle x mesafesinde su sekilde verilir 490 Nux 0 332Rex1 2Pr1 3 Pr gt 0 6 displaystyle mathrm Nu x 0 332 mathrm Re x 1 2 mathrm Pr 1 3 mathrm Pr gt 0 6 Bir duz plaka uzerinde laminer akis icin ortalama Nusselt sayisi plakanin kenarindan asagi yonde x displaystyle x mesafesine kadar su sekilde verilir 490 Nu x 2 0 332Rex1 2Pr1 3 0 664Rex1 2Pr1 3 Pr gt 0 6 displaystyle overline mathrm Nu x 2 cdot 0 332 mathrm Re x 1 2 mathrm Pr 1 3 0 664 mathrm Re x 1 2 mathrm Pr 1 3 mathrm Pr gt 0 6 Konvektif akista kure Bazi uygulamalarda ornegin hava icindeki kuresel sivi damlaciklarinin buharlasmasi gibi su korelasyon kullanilir NuD 2 0 4ReD1 2Pr1 3 displaystyle mathrm Nu D 2 0 4 mathrm Re D 1 2 mathrm Pr 1 3 Turbulansli boru akisinda zorlanmis konveksiyon Gnielinski korelasyonu Gnielinski nin turbulansli boru akisi icin korelasyonu 1 NuD f 8 ReD 1000 Pr1 12 7 f 8 1 2 Pr2 3 1 displaystyle mathrm Nu D frac left f 8 right left mathrm Re D 1000 right mathrm Pr 1 12 7 f 8 1 2 left mathrm Pr 2 3 1 right Burada f Darcy surtunme faktorudur ve veya Petukhov tarafindan gelistirilen korelasyondan elde edilebilir 490 f 0 79ln ReD 1 64 2 displaystyle f left 0 79 ln left mathrm Re D right 1 64 right 2 Gnielinski Korelasyonu su durumlar icin gecerlidir 490 0 5 Pr 2000 displaystyle 0 5 leq mathrm Pr leq 2000 3000 ReD 5 106 displaystyle 3000 leq mathrm Re D leq 5 times 10 6 Dittus Boelter denklemi W H McAdams tarafindan tanitilan Dittus Boelter denklemi turbulansli akis icin Nusselt sayisini hesaplamak icin bir Ing explicit Cozulmesi kolaydir ancak akiskan boyunca buyuk sicaklik farklari oldugunda daha az dogrudur Dittus Boelter denklemi puruzsuz borular icin uyarlanmistir bu nedenle puruzlu borular cogu ticari uygulamada icin dikkatli kullanilmalidir Dittus Boelter denklemi asagidaki gibidir NuD 0 023ReD4 5Prn displaystyle mathrm Nu D 0 023 mathrm Re D 4 5 mathrm Pr n Burada D displaystyle D dairesel kanalin ic capidir Pr displaystyle mathrm Pr Prandtl sayisidir n 0 4 displaystyle n 0 4 akiskan isitildiginda ve n 0 3 displaystyle n 0 3 akiskan sogutuldugunda kullanilir 493 Dittus Boelter denklemi su durumlar icin gecerlidir 514 0 6 Pr 160 displaystyle 0 6 leq mathrm Pr leq 160 ReD 10 000 displaystyle mathrm Re D gtrsim 10 000 LD 10 displaystyle frac L D gtrsim 10 Dittus Boelter denklemi kutlesel akiskan ile isi transfer yuzeyi arasindaki sicaklik farklarinin minimal oldugu durumlarda iyi bir yaklasimdir ve denklem karmasikligindan ve yinelemeli cozumden kacinir Ortalama kutlesel akiskan sicakligi 20 C 68 F olan suyu viskozite 10 07 10 4 Pa s ve isi transfer yuzey sicakligi 40 C 104 F olan bir durumda viskozite 6 96 10 4 Pa s viskozite duzeltme faktoru m ms displaystyle mu mu s olarak 1 45 elde edilebilir Bu isi transfer yuzey sicakligi 100 C 212 F oldugunda viskozite 2 82 10 4 Pa s 3 57 ye cikarak Nusselt sayisi ve isi transfer katsayisi uzerinde onemli bir fark yaratir Sieder Tate korelasyonu Sieder Tate korelasyonu turbulansli akis icin bir Ing implicit cunku sistemi dogrusal olmayan bir sinir deger problemi olarak analiz eder Sieder Tate sonucu kutlesel akiskan ortalama sicakligi ile isi transfer yuzey sicakligi arasindaki sicaklik degisiminden dolayi viskozitedeki m displaystyle mu ve ms displaystyle mu s degisikligi dikkate aldigi icin daha dogru olabilir Sieder Tate korelasyonu normalde yinelemeli bir surecle cozulur cunku Nusselt sayisi degistikce viskozite faktoru de degisir NuD 0 027ReD4 5Pr1 3 mms 0 14 displaystyle mathrm Nu D 0 027 mathrm Re D 4 5 mathrm Pr 1 3 left frac mu mu s right 0 14 493 Burada m displaystyle mu kutlesel akiskan sicakligindaki akiskan viskozitesidir ms displaystyle mu s isi transfer sinir yuzey sicakligindaki akiskan viskozitesidir Sieder Tate korelasyonu su durumlar icin gecerlidir 493 0 7 Pr 16 700 displaystyle 0 7 leq mathrm Pr leq 16 700 ReD 10 000 displaystyle mathrm Re D geq 10 000 LD 10 displaystyle frac L D gtrsim 10 Tam gelismis laminer boru akisinda zorlanmis konveksiyon Tam gelismis ic laminer akisli uzun borular icin Nusselt sayilari sabit bir degere egilim gosterir Ic akis icin Nu hDhkf displaystyle mathrm Nu frac hD h k f Burada Dh Hidrolik cap kf akiskanin isi iletkenligi h konvektif Dairesel borular icin sabit sicaklik ile konveksiyon Incropera amp DeWitt e gore 486 487 NuD 3 66 displaystyle mathrm Nu D 3 66 OEIS dizisi bu degeri su sekilde verir NuD 3 6567934577632923619 displaystyle mathrm Nu D 3 6567934577632923619 Dairesel borular icin sabit isi akisi ile konveksiyon Sabit yuzey isi akisi durumu icin 486 487 NuD 4 36 displaystyle mathrm Nu D 4 36 Ayrica bakinizSherwood sayisi kutle transferi Nusselt sayisi Reynolds sayisi Isi iletkenligiKaynakca a b Cengel Yunus A 2002 Heat and Mass Transfer 2nd McGraw Hill a b The Nusselt Number Whiting School of Engineering 1 Nisan 2019 tarihinde kaynagindan Erisim tarihi 3 Nisan 2019 E Sanvicente ve digerleri 2012 Transitional natural convection flow and heat transfer in an open channel International Journal of Thermal Sciences Cilt 63 ss 87 104 doi 10 1016 j ijthermalsci 2012 07 004 a b c d e f g h i j k l m n DeWitt David P 2007 Fundamentals of Heat and Mass Transfer 6th Hoboken Wiley ISBN 978 0 471 45728 2 2013 Convection Heat Transfer PDF 4th Wiley ISBN 978 0 470 90037 6 Globe Samuel Dropkin David 1959 Natural Convection Heat Transfer in Liquids Confined by Two Horizontal Plates and Heated From Below J Heat Transfer 81 1 ss 24 28 25 Mart 2024 tarihinde kaynagindan Erisim tarihi 7 Haziran 2024 ASME Digital Collection vasitasiyla McAllister Sara Chen Jyh Yuan Fernandez Pello Carlos 2011 Droplet Vaporization in Convective Flow Fundamentals of combustion processes Mechanical Engineering New York Springer s 159 doi 10 1007 978 1 4419 7943 8 ISBN 978 1 4419 7942 1 LCCN 2011925371 Gnielinski Volker 1975 Neue Gleichungen fur den Warme und den Stoffubergang in turbulent durchstromten Rohren und Kanalen Forsch Ing Wes 41 1 ss 8 16 doi 10 1007 BF02559682 PDF 3 Mart 2016 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 23 Eylul 2009
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans