Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Qbit veya kuantum bit, iki durumlu bir cihazla gerçekleştirilen klasik ikili bitin kuantum bilgisayarlarındaki kuantum bilgisinin en küçük bilgi depolama birimidir. Bir kübit, iki durumlu (veya iki seviyeli) bir kuantum mekanik sistemidir ve kuantum mekaniğinin özelliklerini gösteren en basit kuantum sistemlerinden biridir. Örnekler arasında, iki seviye olarak yukarı spin ve aşağı spin alınabilecek elektronun spin'i; veya tek bir fotonun polarizasyonu yer alabilir, burada iki durum dikey polarizasyon ve yatay polarizasyon olarak kabul edilebilir. Klasik bir sistemde bir bit ya 1 durumda ya da 0 durumunda olmalıdır. Ancak, kuantum mekaniği qbiti her iki durumun da tutarlı bir süperpozisyonunda olabilecek şekilde izin verir. Bu özellik ise kuantum mekaniğinin ve kuantum hesaplamanın temel özelliklerinden biridir.
Bit ile Kübitin Karşılaştırılması
Klasik bilgisayarlarda bilgiyi temsil etmek için 0 veya 1 olarak ifade edilen ikili basamak kullanılır. Ne olursa olsun, bir bit her zaman ya 0 ya da 1 değerini almaktadır. Buna benzer olarak, bir elektrik anahtarı ise ya kapalı konumda ya da açık konumdadır. Bu sayfada bit ile ikili basamak aynı anlamda kullanılmaktadır.
Klasik bilgisayar teknolojisinde, işlenmiş bir bit, düşük DC voltajının iki seviyesinden biri şeklinde uygulanır ve bu iki mantık seviyesi arasındaki geçişte, elektrik voltajı anında bir seviyeden diğerine geçemediğinden dolayı, "yasak bölge" olarak adlandırılan bölge mümkün olduğunca hızlı bir şekilde geçilmelidir.
Bir kübit ile klasik bit arasında birkaç benzerlik vardır. Bir kübit ölçümünün iki olası sonucu vardır - genellikle bunlar klasik bitte olduğu gibi "0" ve "1" olarak kabul edilir, bir bit veya ikili basamak gibi. Ancak, bir bitin durumu sadece 0 veya 1 olabilirken, bir kübitin genel durumu, kuantum mekaniğine göre, her ikisinin kuantum süperpozisyonu şeklinde olabilir. Kaldı ki bir klasik bitin ölçümü o bitin durumunu bozmazken, bir kübitin ölçümü, hem kübitin eşevreliliğini hem de süperpozisyon durumunu geri döndürülemez şekilde bozacaktır. Bir kübitte bir bit tamamen kodlanabilir. Ancak, süper yoğun kodlama işlemleri kullanılarak daha fazla bilgi, örneğin iki bit, bir kübit içerisinde saklanabilir.
Kuantum mekaniği ilkelerine uyan, iki seviyeli herhangi bir sistemin kübit olarak kullanılması mümkündür. Örneğin elektronların spinleri, iki seviyeli sistemlerin bir örneğidir. Bir elektronun belirli bir yöndeki spinini belirlemek için bir ölçüm yapıldığını düşünelim. Sonuç olarak spinin ya ölçüm yapılan yönle aynı yönde olduğu ya da ters yönde olduğu bulunur. Bu iki ihtimal klasik bilgisayarlardaki bitlerin alabileceği iki değere (0 ve 1) karşılık gelir. Ancak bir elektronun belirli bir andaki spini sadece bu iki yönde değil başka herhangi bir yönde de olabilir. Dolayısıyla bir elektronun spini sadece 0 ve 1 durumlarını kodlamak için değil bu durumların herhangi bir lineer kombinasyonunu kodlamak için de kullanılabilir. Benzer biçimde atom çekirdeklerinin spin durumları da kübit olarak kullanılabilir.
Standart Gösterim
Kuantum mekaniğinde, bir kübitin genel kuantum durumu, iki ortonormal taban durumunun (veya taban vektörleri) doğrusal bir süperpozisyonu şeklinde temsil edilebilir. Bu vektörler genellikle şu şekilde gösterilir: 







Sonuç olarak, n kübitlik bir kuantum register n bitin 2n kombinasyonunun süperpozisyonu olarak bulunur.
Örneğin 3-kübitlik bir registerin durum vektörü aşağıdaki gibi olacaktır.









Kübit durumları

 ve
ve  tarafından veriliyor.
tarafından veriliyor.Bir saf kübit durumu bir temel durumun doğrusal gelmesidir. Bu anlamda kübit;
ve
nin bir olarak gösterilebilir:
Burada α ve β olasılık genliğidir ve genel olarak her ikisi de karmaşık sayıların içinde olabilir. Bu kübit standart baz içinde ölçülürse ise, olasılık 



Bu sağlar çünkü tek bir durumu veya diğer birini ölçmek gerekmektedir.
Bloch küresi
(diyagrama bakınız) bir tek kübit durumunun olasılığı için kullanılabilen gösterimdir. Bir küresel gösterimi klasik bit olabilen, bir yalnızca "Kuzey kutbu" veya "Güney kutbu", burada sırasıyla 


Kürenin yüzeyindeki iki-boyutlu uzayı saf kübit durumunun (State space) gösterimidir. Bu durum uzayının iki yerel serbestlik derecesi (fizik ve kimya) (Degrees of freedom) vardır. Bu ilk bakışta serbestlik dört derece olması gerektiğini görünebilir, karmaşık sayılar ile her ikisinin serbestlik derecesi α ve β dır. Ancak, serbestliğin bir derecesi 
Bu, bir içinde kübit koyma olasılığıdır, bir farklı saf durumun istatistiksel kombinasyonudur. Karışık durumlar Bloch kürenin içinde puan ile temsil edilebilir.
Operasyonlar olarak saf kübit durumları
Burada fiziksel operasyonların çeşitli türleri saf kübit durumları ile gerçekleştirilebilir.[]
- Bir bir kübit işlemi olabilir. Matematik dille, kübit bir uğrar. Birim dönüşüm kübit vektörün dönmesine karşılık Bloch küre içindedir.
- bir operasyondur ve bu bilginin içindedir kübit'in kapısı durumu hakkındadır. Ölçümün sonucu,
ile olasılığı ile
sonucunu veya
olasılık ile
sonucunu verir.
- Örneğin, eğer ölçüm sonuçları
ise ve α 1'e değişirse (yukarı faza) ve β 0'a değişirse kübit durumu ölçümü α ve β değerlerini değiştirir. Bir kübitin ölçümü durumu dolaşık ile diğer kuantum sistem dönüşümü, bir saf durum içine bir .
Dolaşıklık
Bir kübit ve bir klasikleşmiş bit arasındaki bir önemli ayırıcı özellik çoğul kübitler sergileyebilirler. Dolaşıklık bir özellik daha yüksek korelasyon ifade etmenizi sağlayan kübitlerin kümesi klasik sistemlerde mümkündür. İki dolaşık kübitlerin içindeki örneği:
Bu durum içinde, bir eş üst üstelik denilmektedir. Burada ölçümün eş olasılık 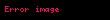


Bu iki dolaşmış kübitlerin biri Alice ve Bob verilen her birini, ayrı düşünülmektedir. Alice Qubit ölçümünü yapar, elde ettiği ile eş olasılık ya da 


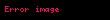

Dolaşıklık ayrıca birden çok durumları sağlar (örneğin Yukarıda belirtilen) bir seferde sadece tek bir değer olabilir. Klasik bit aksine, aynı anda hareket için. Dolaşıklık klasik bir bilgisayarda verimli yapılamaz herhangi bir kuantum hesaplama yapan zorunlu bir maddedir. Kuantum hesaplama ve iletişim başarıları gibi, birçok ve , bir dolanmanın bir olduğunu düşündürür, dolaşıklıkta kuantum hesaplamadan faydalanmak özeldir.
Kuantum kayıt
Birlikte alınan dolaşmış kübitlerin bir dizisi ile bir . Bir Kuantum bilgisayarının yazmacındaki kübitlerin manipüle edilerek hesaplamaları gerçekleştirmektir. Kübitlerin bir qbit'i sekiz topluluğudur. İlk olarak Aralık ayında Avusturya'daki Innsbruck Üniversitesi'nin Quantum Optik ve Kuantum Bilgi Enstitüsü'nde çalışan bir ekip tarafından gösterilmiştir.
Kübit çeşitlemeleri
Kübit'e benzer şekilde, 3 seviyeli bir kuantum sisteminde kuantum bilgileri ve birimidir. , bu klasik bilgi birimine benzer. Burada kullanıldığı şekliyle "qudit" bir d-düzeyinde kuantum sistemindeki bir kuantum bilgi birimini belirtmek için kullanılmaktadır.
Kübit depolama
31P nükleer spin " Solid-durum kuantum hafıza kullanarak", Nature dergisinin 23 Ekim 2008 sayısında yayınlanan başlıklı bir yazıda, Enerji Lawrence Berkeley ABD ile araştırmacıları dahil bilim, uluslararası bir ekip Lawrence Berkeley Ulusal Laboratuvarı (Berkeley Laboratuvarı); bir "bellek" kübit bir elektron kübit bir spin "işleme", içinde süper pozisyon durumu ilke göre nispeten uzun (1.75 saniye) ve tutarlı transferi bildirildi. Bu olay ilk nispeten tutarlı kuantum veri olarak kabul edilebilir depolama, kuantum bilgisayarı geliştirilmesine yönelik önemli bir adımdır. Benzer sistemlerin (yerine nötr vericilerden daha yüklü kullanılarak) son modifikasyonu dramatik bu kez oda sıcaklığından çok düşük sıcaklıklarda ve 39. dakikasında 3 saate kadar artırılmıştır.
Ayrıca bakınız
Kaynakça
- ^ . Evrim Ağacı. 20 Eylül 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Şubat 2023.
- ^ Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (İngilizce). Cambridge University Press. s. 13. ISBN .
- ^ "Kuantum Bilgisayar ve Blokzinciri Teknolojisi - Vikikitap: Özgür kütüphane". tr.wikibooks.org. 7 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Şubat 2023.
- ^ . Bilim Genc. 4 Mayıs 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Şubat 2023.
- ^ (İngilizce). 23 Kasım 2005 tarihinde kaynağından arşivlendi.
- ^ J. J. L. Morton (2008). "Solid-state quantum memory using the 31P nuclear spin". 455 (7216). ss. 1085-1088. Bibcode:2008Natur.455.1085M. doi:10.1038/nature07295.
- ^ Kamyar Saeedi (2013). "Room-Temperature Quantum Bit Storage Exceeding 39 Minutes Using Ionized Donors in Silicon-28". 342 (6160). ss. 830-833. doi:10.1126/science.1239584.
Dış bağlantılar
- Scientific American tarafından
- Qubit.org 13 Şubat 2005 tarihinde Wayback Machine sitesinde . kurucu ortağı, kuantum hesaplama öncülerinden David Deutsch tarafından eklenmiş bilgi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Ocak 2020 Bu maddenin iceriginin Turkcelestirilmesi veya Turkce dilbilgisi ve kurallari dogrultusunda duzeltilmesi gerekmektedir Bu maddedeki yazim ve noktalama yanlislari ya da anlatim bozukluklari giderilmelidir Yabanci sozcukler yerine Turkce karsiliklarinin kullanilmasi karakter hatalarinin duzeltilmesi dilbilgisi hatalarinin duzeltilmesi vs Duzenleme yapildiktan sonra bu sablon kaldirilmalidir Bu maddenin iceriginin Turkcelestirilmesi veya Turkce dilbilgisi ve kurallari dogrultusunda duzeltilmesi gerekmektedir Bu maddedeki yazim ve noktalama yanlislari ya da anlatim bozukluklari giderilmelidir Yabanci sozcukler yerine Turkce karsiliklarinin kullanilmasi karakter hatalarinin duzeltilmesi dilbilgisi hatalarinin duzeltilmesi vs Duzenleme yapildiktan sonra bu sablon kaldirilmalidir Qbit veya kuantum bit iki durumlu bir cihazla gerceklestirilen klasik ikili bitin kuantum bilgisayarlarindaki kuantum bilgisinin en kucuk bilgi depolama birimidir Bir kubit iki durumlu veya iki seviyeli bir kuantum mekanik sistemidir ve kuantum mekaniginin ozelliklerini gosteren en basit kuantum sistemlerinden biridir Ornekler arasinda iki seviye olarak yukari spin ve asagi spin alinabilecek elektronun spin i veya tek bir fotonun polarizasyonu yer alabilir burada iki durum dikey polarizasyon ve yatay polarizasyon olarak kabul edilebilir Klasik bir sistemde bir bit ya 1 durumda ya da 0 durumunda olmalidir Ancak kuantum mekanigi qbiti her iki durumun da tutarli bir superpozisyonunda olabilecek sekilde izin verir Bu ozellik ise kuantum mekaniginin ve kuantum hesaplamanin temel ozelliklerinden biridir Bit ile Kubitin KarsilastirilmasiKlasik bilgisayarlarda bilgiyi temsil etmek icin 0 veya 1 olarak ifade edilen ikili basamak kullanilir Ne olursa olsun bir bit her zaman ya 0 ya da 1 degerini almaktadir Buna benzer olarak bir elektrik anahtari ise ya kapali konumda ya da acik konumdadir Bu sayfada bit ile ikili basamak ayni anlamda kullanilmaktadir Klasik bilgisayar teknolojisinde islenmis bir bit dusuk DC voltajinin iki seviyesinden biri seklinde uygulanir ve bu iki mantik seviyesi arasindaki geciste elektrik voltaji aninda bir seviyeden digerine gecemediginden dolayi yasak bolge olarak adlandirilan bolge mumkun oldugunca hizli bir sekilde gecilmelidir Bir kubit ile klasik bit arasinda birkac benzerlik vardir Bir kubit olcumunun iki olasi sonucu vardir genellikle bunlar klasik bitte oldugu gibi 0 ve 1 olarak kabul edilir bir bit veya ikili basamak gibi Ancak bir bitin durumu sadece 0 veya 1 olabilirken bir kubitin genel durumu kuantum mekanigine gore her ikisinin kuantum superpozisyonu seklinde olabilir Kaldi ki bir klasik bitin olcumu o bitin durumunu bozmazken bir kubitin olcumu hem kubitin esevreliligini hem de superpozisyon durumunu geri dondurulemez sekilde bozacaktir Bir kubitte bir bit tamamen kodlanabilir Ancak super yogun kodlama islemleri kullanilarak daha fazla bilgi ornegin iki bit bir kubit icerisinde saklanabilir Kuantum mekanigi ilkelerine uyan iki seviyeli herhangi bir sistemin kubit olarak kullanilmasi mumkundur Ornegin elektronlarin spinleri iki seviyeli sistemlerin bir ornegidir Bir elektronun belirli bir yondeki spinini belirlemek icin bir olcum yapildigini dusunelim Sonuc olarak spinin ya olcum yapilan yonle ayni yonde oldugu ya da ters yonde oldugu bulunur Bu iki ihtimal klasik bilgisayarlardaki bitlerin alabilecegi iki degere 0 ve 1 karsilik gelir Ancak bir elektronun belirli bir andaki spini sadece bu iki yonde degil baska herhangi bir yonde de olabilir Dolayisiyla bir elektronun spini sadece 0 ve 1 durumlarini kodlamak icin degil bu durumlarin herhangi bir lineer kombinasyonunu kodlamak icin de kullanilabilir Benzer bicimde atom cekirdeklerinin spin durumlari da kubit olarak kullanilabilir Standart GosterimKuantum mekaniginde bir kubitin genel kuantum durumu iki ortonormal taban durumunun veya taban vektorleri dogrusal bir superpozisyonu seklinde temsil edilebilir Bu vektorler genellikle su sekilde gosterilir 0 10 displaystyle 0 rangle bigl begin smallmatrix 1 0 end smallmatrix bigr veya 1 01 displaystyle 1 rangle bigl begin smallmatrix 0 1 end smallmatrix bigr Bu vektorler genellikle konvensiyonel Dirac veya bra ket gosterimiyle yazilir Bu iki temel hesaplama durumlari geleneksel bicimde 0 displaystyle 0 rangle ve 1 displaystyle 1 rangle olarak yazilir Telaffuzu ket 0 ve ket 1 Birlikte hesaplama tabani olarak adlandirilan bu iki vektor kubitin iki boyutlu lineer vektor Hilbert uzayini olusturdugu soylenir Kubit taban durumlari ayrica tabanlarin durumlarinin carpimi seklinde de birlestirilebilir Birlikte alinan bir kubit kumesine kuantum register 24 Subat 2023 tarihinde Wayback Machine sitesinde denir Ornegin iki kubit asagidaki carpim taban durumlari tarafindan kapsanan dort boyutlu bir dogrusal vektor uzayinda temsil edilebilir 00 1000 displaystyle 00 rangle biggl begin smallmatrix 1 0 0 0 end smallmatrix biggr 01 0100 displaystyle 01 rangle biggl begin smallmatrix 0 1 0 0 end smallmatrix biggr 10 0010 displaystyle 10 rangle biggl begin smallmatrix 0 0 1 0 end smallmatrix biggr ve 11 0001 displaystyle 11 rangle biggl begin smallmatrix 0 0 0 1 end smallmatrix biggr Sonuc olarak n kubitlik bir kuantum register n bitin 2n kombinasyonunun superpozisyonu olarak bulunur Ornegin 3 kubitlik bir registerin durum vektoru asagidaki gibi olacaktir q2 displaystyle q 2 rangle a0 displaystyle a 0 000 displaystyle 000 rangle a1 displaystyle a 1 001 displaystyle 001 rangle a2 displaystyle a 2 010 displaystyle 010 rangle a3 displaystyle a 3 011 displaystyle 011 rangle a4 displaystyle a 4 100 displaystyle 100 rangle a5 displaystyle a 5 101 displaystyle 101 rangle a6 displaystyle a 6 110 displaystyle 110 rangle a7 displaystyle a 7 111 displaystyle 111 rangle Kubit durumlaribir kubitin gosterimi Olasilik genligi konu icinde a cos 82 displaystyle alpha cos left frac theta 2 right ve b eiϕsin 82 displaystyle beta e i phi sin left frac theta 2 right tarafindan veriliyor Bir saf kubit durumu bir temel durumun dogrusal gelmesidir Bu anlamda kubit 0 displaystyle 0 rangle ve 1 displaystyle 1 rangle nin bir olarak gosterilebilir ps a 0 b 1 displaystyle psi rangle alpha 0 rangle beta 1 rangle Burada a ve b olasilik genligidir ve genel olarak her ikisi de karmasik sayilarin icinde olabilir Bu kubit standart baz icinde olculurse ise olasilik a 2 displaystyle alpha 2 0 displaystyle 0 rangle dir ve cikisin olasiligi b 2 displaystyle beta 2 1 displaystyle 1 rangle dir Genliklerinin mutlak kareleri olasiliklara esit oldugundan a ve b denklemi ile kisitlanmasi gerektigi asagidadir a 2 b 2 1 displaystyle alpha 2 beta 2 1 Bu saglar cunku tek bir durumu veya diger birini olcmek gerekmektedir Bloch kuresi diyagrama bakiniz bir tek kubit durumunun olasiligi icin kullanilabilen gosterimdir Bir kuresel gosterimi klasik bit olabilen bir yalnizca Kuzey kutbu veya Guney kutbu burada sirasiyla 0 displaystyle 0 rangle ve 1 displaystyle 1 rangle lokasyonu icerisindedir Kure yuzeyinin geri kalani klasik bir bit ile aciklanamaz ama saf kubit durum yuzeyi uzerinde herhangi bir noktaya ile temsil edilebilir Ornegin saf kubit durumu 0 i 1 2 displaystyle 0 rangle i 1 rangle over sqrt 2 pozitif y ekseni uzerinde kurenin ekvatoruna yatik olur Kurenin yuzeyindeki iki boyutlu uzayi saf kubit durumunun State space gosterimidir Bu durum uzayinin iki yerel serbestlik derecesi fizik ve kimya Degrees of freedom vardir Bu ilk bakista serbestlik dort derece olmasi gerektigini gorunebilir karmasik sayilar ile her ikisinin serbestlik derecesi a ve b dir Ancak serbestligin bir derecesi a 2 b 2 1 displaystyle alpha 2 beta 2 1 kisitlamasi ile cikartilmistir Digeri keyfi secilebilen a nin gercek olmasi sadece iki serbestlik derecesinin ayrilmasi durumlarinin tum fiziksel gozlemlerinin sonucu degildir Bu bir icinde kubit koyma olasiligidir bir farkli saf durumun istatistiksel kombinasyonudur Karisik durumlar Bloch kurenin icinde puan ile temsil edilebilir Operasyonlar olarak saf kubit durumlari Burada fiziksel operasyonlarin cesitli turleri saf kubit durumlari ile gerceklestirilebilir kaynak belirtilmeli Bir bir kubit islemi olabilir Matematik dille kubit bir ugrar Birim donusum kubit vektorun donmesine karsilik Bloch kure icindedir bir operasyondur ve bu bilginin icindedir kubit in kapisi durumu hakkindadir Olcumun sonucu a 2 displaystyle alpha 2 ile olasiligi ile 0 displaystyle 0 rangle sonucunu veya b 2 displaystyle beta 2 olasilik ile 1 displaystyle 1 rangle sonucunu verir Ornegin eger olcum sonuclari 0 displaystyle 0 rangle ise ve a 1 e degisirse yukari faza ve b 0 a degisirse kubit durumu olcumu a ve b degerlerini degistirir Bir kubitin olcumu durumu dolasik ile diger kuantum sistem donusumu bir saf durum icine bir DolasiklikBir kubit ve bir klasiklesmis bit arasindaki bir onemli ayirici ozellik cogul kubitler sergileyebilirler Dolasiklik bir ozellik daha yuksek korelasyon ifade etmenizi saglayan kubitlerin kumesi klasik sistemlerde mumkundur Iki dolasik kubitlerin icindeki ornegi 12 00 11 displaystyle frac 1 sqrt 2 00 rangle 11 rangle Bu durum icinde bir es ust ustelik denilmektedir Burada olcumun es olasilik 00 displaystyle 00 rangle veya 11 displaystyle 11 rangle 1 2 2 1 2 displaystyle 1 sqrt 2 2 1 2 olusturmaktadir Bu iki dolasmis kubitlerin biri Alice ve Bob verilen her birini ayri dusunulmektedir Alice Qubit olcumunu yapar elde ettigi ile es olasilik ya da 0 displaystyle 0 rangle veya 1 displaystyle 1 rangle tir Cunku kubitlerin dolasikligi Bob simdi tam olarak Alice le ayni olcmeyi vermesi gerekir yani eger onun bir 0 displaystyle 0 rangle olcusu ile Bob un ayni olcmesi gerekir 00 displaystyle 00 rangle yalnizca burada durum Alice in kubit i bir 0 displaystyle 0 rangle dir Dolasiklik ayrica birden cok durumlari saglar ornegin Yukarida belirtilen bir seferde sadece tek bir deger olabilir Klasik bit aksine ayni anda hareket icin Dolasiklik klasik bir bilgisayarda verimli yapilamaz herhangi bir kuantum hesaplama yapan zorunlu bir maddedir Kuantum hesaplama ve iletisim basarilari gibi bircok ve bir dolanmanin bir oldugunu dusundurur dolasiklikta kuantum hesaplamadan faydalanmak ozeldir Kuantum kayit Birlikte alinan dolasmis kubitlerin bir dizisi ile bir Bir Kuantum bilgisayarinin yazmacindaki kubitlerin manipule edilerek hesaplamalari gerceklestirmektir Kubitlerin bir qbit i sekiz toplulugudur Ilk olarak Aralik ayinda Avusturya daki Innsbruck Universitesi nin Quantum Optik ve Kuantum Bilgi Enstitusu nde calisan bir ekip tarafindan gosterilmistir Kubit cesitlemeleriKubit e benzer sekilde 3 seviyeli bir kuantum sisteminde kuantum bilgileri ve birimidir bu klasik bilgi birimine benzer Burada kullanildigi sekliyle qudit bir d duzeyinde kuantum sistemindeki bir kuantum bilgi birimini belirtmek icin kullanilmaktadir Kubit depolama31P nukleer spin Solid durum kuantum hafiza kullanarak Nature dergisinin 23 Ekim 2008 sayisinda yayinlanan baslikli bir yazida Enerji Lawrence Berkeley ABD ile arastirmacilari dahil bilim uluslararasi bir ekip Lawrence Berkeley Ulusal Laboratuvari Berkeley Laboratuvari bir bellek kubit bir elektron kubit bir spin isleme icinde super pozisyon durumu ilke gore nispeten uzun 1 75 saniye ve tutarli transferi bildirildi Bu olay ilk nispeten tutarli kuantum veri olarak kabul edilebilir depolama kuantum bilgisayari gelistirilmesine yonelik onemli bir adimdir Benzer sistemlerin yerine notr vericilerden daha yuklu kullanilarak son modifikasyonu dramatik bu kez oda sicakligindan cok dusuk sicakliklarda ve 39 dakikasinda 3 saate kadar artirilmistir Ayrica bakinizKuantum bilgisayariKaynakca Evrim Agaci 20 Eylul 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Subat 2023 Nielsen Michael A Chuang Isaac L 2010 Quantum Computation and Quantum Information Ingilizce Cambridge University Press s 13 ISBN 978 1 107 00217 3 Kuantum Bilgisayar ve Blokzinciri Teknolojisi Vikikitap Ozgur kutuphane tr wikibooks org 7 Agustos 2020 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Subat 2023 Bilim Genc 4 Mayis 2019 tarihinde kaynagindan arsivlendi Erisim tarihi 21 Subat 2023 Ingilizce 23 Kasim 2005 tarihinde kaynagindan arsivlendi J J L Morton 2008 Solid state quantum memory using the 31P nuclear spin 455 7216 ss 1085 1088 Bibcode 2008Natur 455 1085M doi 10 1038 nature07295 Kamyar Saeedi 2013 Room Temperature Quantum Bit Storage Exceeding 39 Minutes Using Ionized Donors in Silicon 28 342 6160 ss 830 833 doi 10 1126 science 1239584 Dis baglantilarScientific American tarafindan Qubit org 13 Subat 2005 tarihinde Wayback Machine sitesinde kurucu ortagi kuantum hesaplama onculerinden David Deutsch tarafindan eklenmis bilgi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans