Matematikte simetri

Simetri yalnızca geometride değil, matematiğin diğer dallarında da ortaya çıkar. Simetri bir tür değişmezliktir: matematiksel bir nesnenin bir dizi işlem veya dönüşüm altında değişmeden kaldığı özelliktir.

Olağanüstü Lie grubunun kök sistemi E<sub id="mwCg">8</sub> . Lie gruplarının birçok simetrisi vardır.

Herhangi bir türden yapılandırılmış bir nesne (X) verildiğinde, simetri, yapıyı koruyan nesnenin kendi üzerine bir eşleştirilmesidir. Bu pek çok şekilde gerçekleşebilir; örneğin, X ek yapısı olmayan bir küme ise, bir simetri, kümeden kendisine doğru olan ve permütasyon gruplarına yol açan bir birebir haritasıdır. X nesnesi, kendi metrik yapısı veya başka herhangi bir metrik uzayıyla düzlemde bir noktalar kümesiyse, bir simetri, her nokta çifti arasındaki mesafeyi (yani bir izometri) koruyan kümenin kendisine ait bir birleşimidir.

Genel olarak, matematikteki her tür yapının kendine özgü bir simetrisi olacaktır ve bunların çoğu yukarıda belirtilen noktalarda listelenmiştir.

Geometride simetri

Temel geometride dikkate alınan simetri türleri, Simetri (geometri) ana makalesinde daha ayrıntılı olarak açıklanan , dönme simetrisi, ve içerir.

Analizde simetri

Çift ve tek işlevler

Çift işlevler

ƒ(x) = x², bir çift fonksiyon örneğidir.

F(x), gerçek bir değişkenin gerçek değerli bir fonksiyonu olsun, o zaman f, aşağıdaki denklem f alanındaki tüm x ve -x için geçerli olsa bile:

${\displaystyle f(x)=f(-x)}$

Geometrik olarak konuşursak, eşit bir fonksiyonun grafik yüzü y eksenine göre simetriktir, bu da grafiğinin y ekseni hakkında yansıdıktan sonra değişmeden kaldığı anlamına gelir. Çift işlevlerin örnekleri arasında |x|, x², x⁴, cos (x) ve cosh (x) gösterilebilir.

Tek fonksiyonlar

ƒ(x) = x³, tek bir fonksiyon örneğidir.

Yine, f(x), gerçek bir değişkenin gerçek değerli bir fonksiyonu olsun, aşağıdaki denklem f alanındaki tüm x ve -x için tutulursa, f tektir:

${\displaystyle -f(x)=f(-x)}$

Yani,

${\displaystyle f(x)+f(-x)=0\,.}$

Geometrik olarak, tek bir fonksiyonun grafiği, orijine göre dönme simetrisine sahiptir, bu da grafiğinin orijine göre 180 derece döndükten sonra değişmeden kaldığı anlamına gelir. Tek fonksiyonlara örnek olarak x, x³, sin (x), sinh (x) ve (x) verilebilir.

Entegrasyon

− A'dan + A'ya tek bir fonksiyonun integrali, A'nın sonlu olması ve fonksiyonun integrallenebilir olması koşuluyla (örneğin, − A ile A arasında dikey asimptot olmaması) sıfırdır.

− A'dan + A'ya kadar bir çift fonksiyonun integrali, A'nın sonlu olması ve fonksiyonun integrallenebilir olması koşuluyla (örneğin, − A ile A arasında dikey asimptot olmaması), 0'dan + A'ya integralin iki katıdır. Bu, A sonsuz olduğunda da geçerlidir, ancak yalnızca integral yakınsarsa.

Diziler

• Eşit bir işlevin Taylor serisi yalnızca eşit güçler içerir.
• Tek bir fonksiyonun Taylor serisi yalnızca tek sayı güçleri içerir.
• Periyodik çift fonksiyonun Fourier serisi yalnızca kosinüs terimlerini içerir.
• Periyodik bir tek fonksiyonun Fourier serisi yalnızca sinüs terimlerini içerir.

Doğrusal cebirde simetri

Matrislerde simetri

Doğrusal cebirde, simetrik bir matris, transpozisyonuna eşit olan bir kare matristir (yani, matris transpozisyonu altında değişmezdir). Resmi olarak, matris A simetriktir.

${\displaystyle A=A^{T}.}$

Tüm karşılık gelen konumlardaki girişlerin eşit olmasını gerektiren matris eşitliği tanımına göre, eşit matrisler aynı boyutlara sahip olmalıdır (farklı boyutlarda veya şekillerde matrisler eşit olamaz). Sonuç olarak, yalnızca kare matrisler simetrik olabilir.

Simetrik bir matrisin girdileri, ana köşegene göre simetriktir. Dolayısıyla, girişler A = (a_ij) olarak yazılırsa, tüm i ve j indisleri için a_ij = a_ji olur.

Örneğin, aşağıdaki 3 × 3 matris simetriktir:

${\displaystyle {\begin{bmatrix}1&7&3\\7&4&-5\\3&-5&6\end{bmatrix}}}$

Tüm köşegen dışı girişler sıfır olduğu için her kare köşegen matris simetriktir. Benzer şekilde, çarpık simetrik bir matrisin her köşegen öğesi sıfır olmalıdır, çünkü her biri kendi negatifidir.

Doğrusal cebirde, gerçek bir simetrik matris, gerçek bir iç çarpım uzayı üzerinde kendine eşlenik bir operatörü temsil eder. Karmaşık bir iç çarpım uzayı için karşılık gelen nesne, eşlenik devrikine eşit olan karmaşık değerli girdileri olan Hermitian bir matristir . Bu nedenle, karmaşık sayılar üzerindeki doğrusal cebirde, genellikle simetrik bir matrisin gerçek değerli girdilere sahip olanı ifade ettiği varsayılır. Simetrik matrisler, çeşitli uygulamalarda doğal olarak görünür ve tipik sayısal doğrusal cebir yazılımı, bunlar için özel düzenlemeler yapar.

Soyut cebirde simetri

Simetrik gruplar

Simetrik grup S_n (sonlu bir n sembol kümesinde), elemanları n sembollerinin tüm permütasyonları olan ve grup çalışması, sembol kümesinden kendisine bijektif fonksiyonlar olarak kabul edilen bu tür permütasyonların bileşimi olan gruptur. Bir dizi n sembolünün n! (n faktöriyel) olası permütasyonları olduğundan, simetrik grup S_n'nin dizisini (yani, elemanların sayısı) n! izler.

Simetrik polinomlar

Simetrik bir polinom, n değişkenli bir polinom P'dir (X₁, X₂,…, X_n), öyle ki eğer değişkenlerden herhangi biri değiştirilirse, biri aynı polinomu elde eder. Resmi olarak, eğer 1, 2, ..., n alt simgelerinin herhangi bir permütasyonu σ için, birinde P (X_σ(1), X_σ(2),…, X_σ(n)) = P(X ₁, X₂,…, X_n) varsa, P simetrik bir polinomdur. .

Simetrik polinomlar, bir değişkendeki bir polinomun kökleri ile katsayıları arasındaki ilişkinin incelenmesinde doğal olarak ortaya çıkar, çünkü katsayılar köklerdeki polinom ifadeleri ile verilebilir ve tüm kökler bu ortamda benzer bir rol oynar. Bu açıdan bakıldığında, temel simetrik polinomlar en temel simetrik polinomlardır. Bir teorem, herhangi bir simetrik polinomun, temel simetrik polinomlar cinsinden ifade edilebileceğini belirtir; bu, bir monik polinomun köklerindeki her simetrik polinom ifadesinin, alternatif olarak, polinom katsayılarında bir polinom ifadesi olarak verilebileceğini ima eder.

Örnekler

İki değişken X₁ ve X₂ için, biri aşağıdaki gibi simetrik polinomlara sahiptir:

• ${\displaystyle X_{1}^{3}+X_{2}^{3}-7}$
• ${\displaystyle 4X_{1}^{2}X_{2}^{2}+X_{1}^{3}X_{2}+X_{1}X_{2}^{3}+(X_{1}+X_{2})^{4}}$

ve X₁, X₂ ve X₃ değişkenlerinde simetrik bir polinom vardır:

• ${\displaystyle X_{1}X_{2}X_{3}-2X_{1}X_{2}-2X_{1}X_{3}-2X_{2}X_{3}\,}$

Simetrik tensörler

Matematikte simetrik bir tensör, vektör argümanlarının bir permütasyonu altında değişmeyen tensördür:

${\displaystyle T(v_{1},v_{2},\dots ,v_{r})=T(v_{\sigma 1},v_{\sigma 2},\dots ,v_{\sigma r})}$

{1,2, ..., r } sembollerinin her σ permütasyonu için. Alternatif olarak, r indeksleri ile bir miktar olarak koordinatlarda temsil edilen bir r^th sipariş simetrik tensörü tatmin eder

${\displaystyle T_{i_{1}i_{2}\dots i_{r}}=T_{i_{\sigma 1}i_{\sigma 2}\dots i_{\sigma r}}.}$

Sonlu boyutlu bir vektör uzayında r sınıfı simetrik tensörlerin uzayı, V üzerindeki r derece homojen polinomların uzayının çiftine doğal olarak izomorfiktir . Karakteristik sıfır alanlarının üzerinde, tüm simetrik tensörlerin derecelendirilmiş vektör uzayı, V üzerindeki simetrik cebir ile doğal olarak tanımlanabilir. Bununla ilgili bir kavram, antisimetrik tensör veya alternatif formdur . Simetrik tensörler, mühendislik, fizik ve matematikte yaygın olarak görülür.

Galois teorisi

Bir polinom verildiğinde, bazı köklerin çeşitli cebirsel denklemlerle birbirine bağlı olması olabilir. Örneğin, A ve B gibi iki kök için A² + 5B³ = 7 . Galois teorisinin ana fikri, kökler tarafından sağlanan herhangi bir cebirsel denklemin, kökler değiştirildikten sonra hala karşılanması özelliğine sahip köklerin bu permütasyonlarını (veya yeniden düzenlemelerini) dikkate almaktır. Önemli bir koşul, kendimizi katsayıları rasyonel sayılar olan cebirsel denklemlerle sınırlandırmamızdır. Bu nedenle, Galois teorisi cebirsel denklemlerin doğasında bulunan simetrileri inceler.

Cebirsel nesnelerin otomorfizmleri

Soyut cebirde, bir otomorfizm, matematiksel bir nesneden kendisine bir izomorfizmdir . Bir anlamda, nesnenin bir simetrisi ve tüm yapısını korurken nesneyi kendisine eşlemenin bir yoludur. Bir nesnenin tüm otomorfizmlerinin kümesi, otomorfizm grubu adı verilen bir grup oluşturur. Kabaca, nesnenin simetri grubudur .

Örnekler

• Küme teorisinde, bir X kümesinin elemanlarının rastgele bir permütasyonu bir otomorfizmdir. X'in otomorfizm grubu da X üzerinde simetrik grup olarak adlandırılır.
• Temel aritmetikte, eklenmiş bir grup olarak kabul edilen tam sayılar kümesi, Z, benzersiz bir önemsiz olmayan otomorfizme sahiptir: olumsuzlama. Bir halka olarak kabul edildiğinde, sadece önemsiz bir otomorfizmaya sahiptir. Genel olarak, olumsuzlama herhangi bir değişmeli grubun bir otomorfizmidir, ancak bir halka veya alan değildir.
• Bir grup otomorfizmi, bir gruptan kendisine bir grup izomorfizmidir . Gayri resmi olarak, yapı değişmeden kalacak şekilde grup elemanlarının bir permütasyonudur. Her G grubu için, görüntüsü içsel otomorfizmaların Inn (G) grubu ve çekirdeği G'nin merkezi olan doğal bir grup homomorfizmi G → Aut (G) vardır. Böylece, G bir merkeze sahipse, kendi otomorfizm grubuna gömülebilir.
• Doğrusal cebirde, bir vektör uzayı V'nin endomorfizmi, doğrusal bir operatör V → V'dir . Bir otomorfizm, V üzerinde ters çevrilebilir bir doğrusal operatördür. Vektör uzayı sonlu boyutlu olduğunda, V'nin otomorfizm grubu genel doğrusal grup GL (V) ile aynıdır.
• Bir alan otomorfizmi, bir cisimden kendisine bijektif halka homomorfizmidir . Rasyonel sayılar (Q) ve gerçek sayılar (R) durumunda, önemsiz alan otomorfizmaları yoktur. R'nin bazı alt alanları, tüm R'ye kadar uzanmayan, önemsiz olmayan alan otomorfizmlerine sahiptir (çünkü R'de karekök olan bir sayının özelliğini koruyamazlar). Karmaşık sayılarda, C, R'yi R'ye gönderen benzersiz bir nontrivial otomorfizm vardır: karmaşık konjugasyon, fakat sonsuz (sayılamayan) birçok "vahşi" otomorfizm vardır (seçim aksiyomunu varsayarak). Alan otomorfizmleri, alan uzantıları teorisi, özellikle Galois uzantıları için önemlidir. Bir Galois uzantısı L / K durumunda, K noktasal L sabitlemesinin tüm otomorfizmlerinin alt grubuna uzantının Galois grubu denir.

Temsil teorisinde simetri

Kuantum mekaniğinde simetri: bozonlar ve fermiyonlar

Kuantum mekaniğinde, bozonların permütasyon operatörleri altında simetrik temsilcileri vardır ve fermiyonların antisimetrik temsilcileri vardır.

Bu, fermiyonlar için Pauli dışlama ilkesini ifade eder. Aslında, tek değerli çok parçacıklı bir dalga fonksiyonuna sahip Pauli dışlama ilkesi, dalga fonksiyonunun antisimetrik olmasını gerektirmeye eşdeğerdir. Bir antisimetrik iki parçacık durumu, bir parçacığın durumda olduğu durumların toplamı olarak temsil edilir. ${\displaystyle \scriptstyle |x\rangle }$ ve diğer durumda ${\displaystyle \scriptstyle |y\rangle }$ :

${\displaystyle |\psi \rangle =\sum _{x,y}A(x,y)|x,y\rangle }$

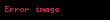
ve değişim altındaki antisimetri, A(x,y) = −A(y,x) . Bu Pauli dışlaması olan A(x,x) = 0 anlamına gelir. Herhangi bir temelde doğrudur, çünkü birimsel temel değişiklikleri antisimetrik matrisleri antisimetrik tutar, ancak kesin olarak konuşursak, A(x,y) miktarı bir matris değil, bir antisimetrik sıra-iki tensördür .

Tersine, diyagonal büyüklükler A(x,x) her temelde sıfırsa, o zaman dalga fonksiyonu bileşeni:

${\displaystyle A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )}$

zorunlu olarak antisimetriktir. Bunu kanıtlamak için matris öğesini düşünün:

${\displaystyle \langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))\,}$

Bu sıfırdır, çünkü iki parçacığın her ikisinin de süperpozisyon durumunda olma olasılığı sıfırdır. 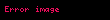${\displaystyle \scriptstyle |x\rangle +|y\rangle }$ . Ama bu eşittir

${\displaystyle \langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle \,}$

Sağ taraftaki ilk ve son terimler köşegen öğelerdir ve sıfırdır ve tüm toplam sıfıra eşittir. Dolayısıyla, dalga fonksiyonu matris öğeleri aşağıdakilere uyar:

${\displaystyle \langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0\,}$ .

veya

${\displaystyle A(x,y)=-A(y,x)\,}$

Küme teorisinde simetri

Simetrik ilişki

İlişki A'dan B'ye her durduğunda, B'den A'ya çok fazla duruyorsa, ilişkiye simetrik denir. Simetrinin antisimetrinin tam tersi olmadığı unutulmamalıdır.

Metrik uzaylarda simetri

Bir uzayın izometrileri

İzometri, metrik uzaylar arasında mesafeyi koruyan bir haritadır. Bir metrik boşluk veya kümenin elemanları arasındaki mesafeleri atamak için bir set ve şema göz önüne alındığında, bir izometri, öğeleri başka bir metrik alana eşleyen bir dönüşümdür, böylece yeni metrik alandaki öğeler arasındaki mesafe, orijinal metrik alandaki öğeler arasındaki mesafeye eşittir. İki boyutlu veya üç boyutlu bir alanda, iki geometrik şekil, bir izometri ile ilişkiliyse uyumludur: rijit cisim veya rijit cismin bileşke fonksiyonu ve bir yansıma ile ilişkilidir. Katı bir hareketle bir ilişkiye kadar, doğrudan bir izometri ile ilişkili ise eşittir.

İzometriler, geometride simetrinin çalışma tanımını birleştirmek ve fonksiyonlar, olasılık dağılımları, matrisler, diziler, grafikler vb. için kullanılmıştır.

Diferansiyel denklemlerin simetrileri

Diferansiyel denklemin simetrisi, diferansiyel denklemi değişmez bırakan bir dönüşümdür. Bu tür simetrilerin bilgisi diferansiyel denklemin çözülmesine yardımcı olabilir.

Diferansiyel denklem sisteminin bir çizgi simetrisi, diferansiyel denklem sisteminin sürekli bir simetrisidir. Bir çizgi simetrisi bilgisi, mesafenin azaltılması yoluyla sıradan bir diferansiyel denklemi basitleştirmek için kullanılabilir.

Sıradan diferansiyel denklemler için, uygun bir Lie simetrisi seti bilgisi, bir kişinin bir dizi ilk integrali açıkça hesaplamasına izin vererek, entegrasyon olmadan tam bir çözüm sağlar.

Simetriler, ilgili bir dizi adi diferansiyel denklem çözülerek bulunabilir. Bu denklemleri çözmek, genellikle orijinal diferansiyel denklemleri çözmekten çok daha kolaydır.

Olasılıkta simetri

Sonlu sayıda olası sonuç durumunda, permütasyonlara (yeniden etiketlemeler) göre simetri, ayrı bir tekdüze dağılımı ifade eder.

Olası sonuçların gerçek bir aralığı olması durumunda, eşit uzunluktaki alt aralıkların değişmesine göre simetri, sürekli bir tekdüze dağılıma karşılık gelir.

"Rastgele bir tamsayı almak" veya "rastgele bir gerçek sayı almak" gibi diğer durumlarda, yeniden etiketlemelere veya eşit uzunlukta alt aralıkların değiş tokuşuna göre hiçbir şekilde simetrik olasılık dağılımları yoktur. Diğer makul simetriler, belirli bir dağılımı seçmezler veya başka bir deyişle, maksimum simetri sağlayan benzersiz bir olasılık dağılımı yoktur.

Bir boyutta, olasılık dağılımını değiştirmeden bırakabilecek bir tür izometri vardır, yani bir noktadaki yansıma, örneğin sıfır.

Pozitif sonuçlara sahip rastgelelik için olası bir simetri, öncekinin logaritma için geçerli olmasıdır, yani sonuç ve karşılığının aynı dağılıma sahip olmasıdır. Bununla birlikte, bu simetri, herhangi bir belirli dağılımı benzersiz bir şekilde ayırmaz.

Bir düzlemdeki veya uzaydaki "rastgele bir nokta" için, bir başlangıç noktası seçilebilir ve sırasıyla dairesel veya küresel simetriye sahip bir olasılık dağılımı düşünülebilir.

Ayrıca bakınız

• Entegrasyonda simetri kullanımı
• Değişmezlik (matematik)

Kaynakça

1. ^ ^{a b c d} . Math Vault (İngilizce). 1 Ağustos 2019. 16 Ekim 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Aralık 2019. 
2. ^ . mathworld.wolfram.com (İngilizce). 19 Ekim 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Aralık 2019. 
3. ^ . plus.maths.org (İngilizce). 23 Haziran 2016. 2 Temmuz 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Aralık 2019. 
4. ^ ^{a b} . mathworld.wolfram.com (İngilizce). 7 Nisan 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Aralık 2019. 
5. ^ Jacobson (2009), p. 31.
6. ^ "§7.5.5 Automorphisms". Mathematical foundations of computational engineering. Felix Pahl translation. Springer. 2001. s. 376. ISBN . 11 Haziran 2020 tarihinde kaynağından . Erişim tarihi: 10 Aralık 2020. 
7. ^ Yale (May 1966). "Automorphisms of the Complex Numbers" (PDF). Mathematics Magazine. 39 (3): 135-141. doi:10.2307/2689301. 8 Kasım 2020 tarihinde kaynağından (PDF). Erişim tarihi: 10 Aralık 2020. 
8. ^ Petitjean (2007). "A definition of symmetry". Symmetry: Culture and Science. 18 (2–3): 99-119. 21 Nisan 2020 tarihinde kaynağından . Erişim tarihi: 10 Aralık 2020. 
9. ^ ^{a b} Applications of Lie Groups to Differential Equations. New York: Springer Verlag. 1986. ISBN . 

Bibliyografya

• Hermann Weyl, Simetri. 1952 orijinalinin yeniden basımı. Princeton Bilim Kütüphanesi. Princeton University Press, Princeton, NJ, 1989. viii + 168 s.ISBN 
• Mark Ronan, Simetri ve Canavar, Oxford University Press, 2006.ISBN  (Uzman olmayan okuyucu için kısa giriş)
• Marcus du Sautoy, Moonshine Bulmak: Bir Matematikçinin Simetri Yolculuğu, Dördüncü Emlak, 2009