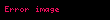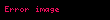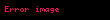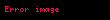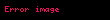Matematikte cebirin temel teoremi karma┼¤─▒k de─¤i┼¤kenli polinomlar─▒n k├Čklerinin varl─▒─¤─▒yla ilgili temel bir sonu├¦tur. D'Alembert-Gauss teoremi olarak da an─▒lmaktad─▒r.
Teoremin a├¦─▒k bir ifadesi ┼¤├Čyledir:
- Katsay─▒lar─▒ karma┼¤─▒k olan ve sabit olmayan tek de─¤i┼¤kenli her polinomun en az bir (karma┼¤─▒k) k├Čk├╝ vard─▒r.
Sonu├¦ olarak, katsay─▒lar─▒ tam say─▒, rasyonel say─▒ veya ger├¦el say─▒ olan ve sabit olmayan her polinomun en az bir karma┼¤─▒k k├Čk├╝ vard─▒r; ├¦├╝nk├╝ tam say─▒lar, rasyonel say─▒lar ve ger├¦el say─▒lar da asl─▒nda birer karma┼¤─▒k say─▒d─▒r. Bu sonu├¦ elde edildikten sonra, her polinomun karma┼¤─▒k say─▒lar cismi olan 'de ├¦arpanlar─▒na ayr─▒labilece─¤i g├Čr├╝lebilir; yani daha do─¤ru bir ┼¤ekilde dile getirilirse, her polinom derecesi kadar say─▒da do─¤rusal fonksiyonlar─▒n ├¦arp─▒m─▒ ┼¤eklinde yaz─▒labilir. Bu do─¤rusal fonksiyonlar─▒n ├╝niter olmas─▒ isteniyorsa bu ├¦arp─▒m─▒n ba┼¤─▒na bir karma┼¤─▒k say─▒ eklenir. Polinom bu son anlat─▒lan ┼¤ekilde ├¦arpanlar─▒na ayr─▒lmaya ├¦al─▒┼¤─▒l─▒rsa, b├Čyle bir ay─▒rma tek bir ┼¤ekilde yap─▒labilir. Matematiksel bir dille ┼¤u ifade edilmektedir: E─¤er ise ve
n dereceli bir polinomsa,
e┼¤itli─¤i yaz─▒labilir ve bu e┼¤itli─¤in bu ┼¤ekilde yaz─▒labilmesi sadece tek bir ┼¤ekilde yap─▒labilir. Bu ┼¤ekilde yaz─▒ld─▒ktan sonra, polinomun k├Čklerinin olaca─¤─▒ a├¦─▒kt─▒r. Burada polinomun k├Čklerinin birbirinden farkl─▒ olmak zorunda olmayaca─¤─▒na dikkat edilmelidir.
Cebirin temel teoremi, her ne kadar cebirin ve teoremin kan─▒tlanmas─▒ndan sonra ├╝retilmi┼¤ matemati─¤in b├╝y├╝k bir b├Čl├╝m├╝n├╝n geli┼¤tirilmesinde ├Čnemli bir yere sahipse de, isminin i├¦erdi─¤i cebir kelimesi teoremi dar bir alana sokmamal─▒d─▒r. Zira, bu teoremin tamamen cebirsel olan bir kan─▒t─▒ bile yok gibidir. Teoremin bu isimle an─▒lmas─▒n─▒n sebebi teoremin kan─▒tland─▒─¤─▒ d├Čnemde cebirin kendini "denklemler kuram─▒" yani polinomlar─▒n ├¦├Čz├╝m├╝yle u─¤ra┼¤an bir kuram olarak tan─▒mlamas─▒d─▒r. Ancak, kan─▒t─▒n yap─▒ld─▒─¤─▒ zamandan bu yana cebirin kapsam─▒na giren fikirler artm─▒┼¤sa da teoremin ismi de─¤i┼¤meden kalm─▒┼¤t─▒r.
Teorem, kendine matemati─¤in i├¦inde olduk├¦a geni┼¤ bir uygulama bulmu┼¤tur. ├¢rne─¤in, do─¤rusal cebirde indirgenmesinde ├Čnemli bir yere sahiptir. Yine analizde, rasyonel fonksiyonlar─▒n ayr─▒┼¤─▒m─▒nda ve daha bir├¦ok teoremin kan─▒t─▒nda kullan─▒lmaktad─▒r.
Teoremin dengi ifadeleri
Cebirin temel teoreminin birbirine denk olan de─¤i┼¤ik ifadeleri mevcuttur:
- Bunlardan ilki yukar─▒da da verilen ifadedir: ---Sabit olmayan ve katsay─▒lar─▒ karma┼¤─▒k olan her polinomun en az bir karma┼¤─▒k k├Čk├╝ vard─▒r.
├¢rne─¤in, 1+i karma┼¤─▒k say─▒s─▒ 
- C cismi cebirsel kapal─▒ bir cisimdir.
Bu sonu├¦, ayn─▒ zamanda bir polinomun b├Čl├╝nmesi ba─¤lam─▒nda da, yani karma┼¤─▒k katsay─▒l─▒ ├¦arpanlar─▒n─▒n ├¦arp─▒m─▒na e┼¤it olmas─▒ anlam─▒nda da ifade edilebilir:
- Karma┼¤─▒k de─¤i┼¤kenli her polinom b├Čl├╝nebilir; yani derecesi 1 olan ve karma┼¤─▒k katsay─▒lara sahip polinomlar─▒n ├¦arp─▒m─▒ ┼¤eklinde yaz─▒labilir.
Teorem, derecesi n olan ve karma┼¤─▒k katsay─▒l─▒ anXn┬Ā+...┬Ā+┬Āa1X┬Ā+┬Āa0 ┼¤eklindeki polinomlar─▒n an(X┬Ā-┬Ā╬▒1)...(X┬Ā-┬Ā╬▒n) halinde de yaz─▒labilece─¤ini i┼¤aret eder. Burada, 1'den k'ye kadar de─¤i┼¤en her ╬▒k polinomun bir k├Čk├╝d├╝r. Burada, farkl─▒ k'ler i├¦in ╬▒k'ler e┼¤it olabilir. Bu durumda, ╬▒k'ye katl─▒ k├Čk ad─▒ verilir.
Cebirin temel teoremi, katsay─▒lar─▒ ger├¦el say─▒ olan polinomlar ele al─▒nd─▒─¤─▒nda ┼¤u dengi ifadelere kar┼¤─▒l─▒k gelmektedir:
- Ger├¦el katsay─▒lara sahip, sabit olmayan her polinomun en az bir karma┼¤─▒k k├Čk├╝ vard─▒r.
- Ger├¦el katsay─▒l─▒ ya 1 derecelidir ya da ikinci dereceden diskriminant─▒ kesin negatif olan polinomlard─▒r (yani
ve
halinde yaz─▒labilen ve
ko┼¤ulunu sa─¤layan polinomlar).
- Sabit olmayan, ger├¦el katsay─▒lara sahip her polinom, derecesi 1 veya 2 olan polinomlar─▒n ├¦arp─▒m─▒ ┼¤eklinde yaz─▒labilir.
Teoremin tarihi
Peter Rothe (Petrus Roth), 1608'de yay─▒mlanan Arithmetica Philosophica adl─▒ kitab─▒nda ger├¦el katsay─▒lara sahip n'inci dereceden bir polinom denkleminin n tane ├¦├Čz├╝m├╝n├╝n olabilece─¤ini yazm─▒┼¤t─▒r. Albert Girard, 1629'da yay─▒mlanan L'invention nouvelle en l'Alg├©bre adl─▒ kitab─▒nda n'inci dereceden bir polinom denkleminin n tane ├¦├Čz├╝m├╝n├╝n oldu─¤unu yazm─▒┼¤t─▒r. Dahas─▒, bu ifadesinin "denklem eksikli olmad─▒k├¦a" ge├¦erli oldu─¤unu ifade etmi┼¤tir. Ancak, ne demek istedi─¤ini detayl─▒ bir ┼¤ekilde a├¦─▒klad─▒─¤─▒nda, asl─▒nda ifade etti─¤i ├Čnermenin her zaman ge├¦erli oldu─¤una inand─▒─¤─▒ ortaya ├¦─▒kmaktad─▒r. Mesela, x4 = 4x ŌłÆ 3 eksikli de─¤ildir; ancak yine de 4 k├Čk├╝ vard─▒r:1 (iki kere), ŌłÆ1 + iŌłÜ2 ve ŌłÆ1 ŌłÆ iŌłÜ2.

Yukar─▒daki dengi ifadelerde de ifade edildi─¤i gibi cebirin temel teoremini izleyen ifadelerden biri de sabit olmayan ve ger├¦el katsay─▒lara sahip bir polinomun derecesi bir veya 2 olan, ger├¦el katsay─▒l─▒ polinomlar─▒n ├¦arp─▒m─▒ ┼¤eklinde yaz─▒labilece─¤idir. Ancak, 1702'de Leibniz a'n─▒n reel oldu─¤u ve s─▒f─▒ra e┼¤it olmad─▒─¤─▒ x4 + a4 t├╝r├╝ndeki hi├¦bir polinomun bu ┼¤ekilde yaz─▒lamad─▒─¤─▒n─▒ s├Čylemi┼¤tir. Sonralar─▒, Bernoulli yine ayn─▒ ifadeyi bu sefer x4 ŌłÆ 4x3 + 2x2 + 4x + 4 polinomunu kastederek vermi┼¤tir. Ancak, 1742'de Euler'den bahsi ge├¦en polinomun
┼¤eklinde yaz─▒labildi─¤ini belirten bir mektup alm─▒┼¤t─▒r (Burada ╬▒, 4 + 2ŌłÜ7 say─▒s─▒n─▒n karek├Čk├╝d├╝r.). Euler, ayr─▒ca
oldu─¤undan da bahsetmi┼¤tir.
Teoremi ilk kan─▒tlama giri┼¤imi 1746'da d'Alembert taraf─▒ndan yap─▒lm─▒┼¤t─▒r; ancak kan─▒t─▒ eksikti. Kan─▒t─▒n sorunlar─▒ndan biri de Puiseux teoremi olarak da bilinen bir teoremi varsaymas─▒d─▒r ki bu teorem bu kan─▒t─▒n yap─▒lmaya tarihten 100 y─▒l sonra kan─▒tlanm─▒┼¤t─▒r. Dahas─▒, bu kan─▒t da cebirin temel teoremini varsayar. Teoremi kan─▒tlama giri┼¤imi euler taraf─▒ndan (1749'da), de Foncenex taraf─▒ndan (1759'da), Lagrange taraf─▒ndan (1795'te) yap─▒lm─▒┼¤t─▒r. Bu d├Črt giri┼¤imin hepsi de Girard'─▒n ifadesine dayanmaktad─▒r.
18'inci y├╝zy─▒l sonunda, k├Čklerin varl─▒─¤─▒n─▒ varsaymayan iki kan─▒t yay─▒nland─▒. Bunlardan biri James Wood taraf─▒ndan verilmi┼¤ti ve genel ├¦er├¦evede cebirsel bir kan─▒tt─▒; ancak zaman─▒nda pek de ├Čnemsenmedi. Wood'un verdi─¤i kan─▒t─▒n ayn─▒ zamanda cebirsel bir a├¦─▒─¤─▒ vard─▒. Di─¤er kan─▒t ise Gauss taraf─▒ndan 1799'da verilen kan─▒tt─▒ ve genel ├¦er├¦evede geometrik bir kan─▒tt─▒; ancak topolojik bir a├¦─▒─¤─▒ vard─▒. Bu a├¦─▒k, Alexander Ostrowski taraf─▒ndan 1920'de kapat─▒lm─▒┼¤t─▒r. Tamamen titizce haz─▒rlanm─▒┼¤ bir kan─▒t Argand taraf─▒ndan 1806'da verilmi┼¤tir ve ilk defa burada cebirin temel teoremi ger├¦el katsay─▒l─▒ polinomlardan de─¤il de karma┼¤─▒k katsay─▒l─▒ polinomlardan bahsederek ifade edilmi┼¤tir. Gauss, daha sonra biri 1816'da ve di─¤eri de ilk verdi─¤i kan─▒t─▒n de─¤i┼¤ik bir hali olmak ├╝zere 1849'da iki kan─▒t daha yay─▒mlam─▒┼¤t─▒r.
Teoremi ve kan─▒t─▒n─▒ i├¦eren ilk kitap Cauchy'nin Cours d'analyse de l'├ēcole Royale Polytechnique (1821) adl─▒ kitab─▒d─▒r. Argand'─▒n kan─▒t─▒n─▒ i├¦ermektedir; ancak Argand'a herhangi bir at─▒f yap─▒lmam─▒┼¤t─▒r.
Kan─▒tlar
Bu b├Čl├╝mde dahil edilen kan─▒tlar─▒n neredeyse hepsi bir ┼¤ekilde analizden en az─▒ndan ger├¦el ve karma┼¤─▒k fonksiyonlar─▒n s├╝reklili─¤ini kullanacak derecede faydalanmaktad─▒r. Baz─▒ kan─▒tlar t├╝revi ve hatta analitik fonksiyonlar─▒ kullanmaktad─▒r. Bu y├╝zden, asl─▒nda cebirin temel teoreminin ne temel ne de tamamen cebirsel bir ├Čzelli─¤i mevcuttur.
Teoremin baz─▒ kan─▒tlar─▒ sabit olmayan ve ger├¦el katsay─▒lara sahip polinomlar─▒n karma┼¤─▒k bir k├Čke sahip olaca─¤─▒n─▒ kan─▒tlamaktad─▒r. Ancak, bu t├╝r kan─▒tlar yine de teoremin en genel halini kan─▒tlamakta yeterlidir; ├¦├╝nk├╝ p(z) karma┼¤─▒k katsay─▒lara sahip sabit olmayan bir polinomsa
polinomunun sadece ger├¦el katsay─▒lar─▒ olacakt─▒r. Dahas─▒, z e─¤er q(z) 'yi s─▒f─▒r yapan bir say─▒ysa yani q(z) 'nin k├Čk├╝yse, o zaman ya z ya da z 'nin e┼¤leni─¤i p(z) 'nin k├Čk├╝ olacakt─▒r.
Teoremin cebirsel y├Čntemleri kullanmayan kan─▒tlar─▒n─▒n b├╝y├╝k bir k─▒sm─▒ b├╝y├╝me ├Čnsav─▒ da denilen ┼¤u ger├¦e─¤e dayanmaktad─▒r: bask─▒n katsay─▒s─▒ 1 olan n 'inci dereceden bir polinom |z| yeterince b├╝y├╝kken asl─▒nda zn gibi davran─▒r. Daha kesin bir ifade ise ┼¤├Čyle verilebilir: ├Čyle bir R say─▒s─▒ vard─▒r ki |z|┬Ā>┬ĀR iken ┼¤u e┼¤itsizlik sa─¤lan─▒r:
Karma┼¤─▒k analizdeki kan─▒tlar
Kan─▒t 1: |z|┬ĀŌēź┬Ār iken |p(z)|┬Ā>┬Ā|p(0)| olacak ┼¤ekilde orijin merkezli ve r yar─▒├¦apl─▒ bir kapal─▒ D diski alal─▒m. D t─▒k─▒z oldu─¤u i├¦in |p(z)| fonksiyonunun minimumum D ├╝zerinde vard─▒r ve dahas─▒ bu minimum D 'nin s─▒n─▒r ├╝zerinde de─¤ildir. Minimumun var oldu─¤u nokta z0 ise, o zaman minimum mutlak de─¤er ilkesi kullan─▒larak p(z0)┬Ā=┬Ā0 elde edilir. Ba┼¤ka bir deyi┼¤le, z0p(z) 'nin bir s─▒f─▒r─▒d─▒r.
Kan─▒t 2: Kan─▒t 1'in biraz daha de─¤i┼¤tirilmi┼¤ haliyle teorem yine kan─▒tlanabilir. Kan─▒t minimum mutlak de─¤er teoremi kullanmadan yap─▒labilir (bu t├╝r kan─▒tlar─▒n bir├¦o─¤u Cauchy integral teoremini veya sonu├¦lar─▒n─▒ kullan─▒r); ancak bu kez yap─▒lan ┼¤ey minimum mutlak de─¤er teoreminin polinomlar i├¦in basit ad─▒mlarla kan─▒tlanmas─▒d─▒r. Daha kesin bir ifadeyle, ├¦eli┼¤ki yoluyla kan─▒t yapmaya ├¦al─▒┼¤─▒rsak, 


Burada, 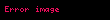
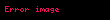










elde ederiz. r, 0'a yeteri kadar yak─▒n oldu─¤unda, ├╝stte |p(z)| i├¦in bulunan bu ├╝st s─▒n─▒r |a| 'dan kesinlikle daha k├╝├¦├╝k olacakt─▒r ve bu da z0 '─▒n tan─▒m─▒yla ├¦eli┼¤mektedir.
Kan─▒t 3: Bu ba─¤lamda elde edilen bir ba┼¤ka kan─▒t ise, D'nin d─▒┼¤─▒nda|p(z)|┬Ā>┬Ā|p(0)| oldu─¤unu g├Čzlemlenmesine ve bu y├╝zden |p(z)| 'nin karma┼¤─▒k d├╝zlemdeki minimumunun z0 ger├¦ekle┼¤mesine dayanmaktad─▒r. |p(z0)|┬Ā>┬Ā0 ise, o zaman 1/p karma┼¤─▒k d├╝zlemin t├╝m├╝nde s─▒n─▒rl─▒ bir holomorf fonksiyon olur. Karma┼¤─▒k d├╝zlemin t├╝m├╝nde s─▒n─▒rl─▒ olan holomorf bir fonksiyonun sabit olmas─▒ gerekti─¤ini belirten Liouville teoremi kullan─▒larak 1/p 'nin sabit oldu─¤u sonucuna ula┼¤─▒l─▒r. Bu y├╝zden p de sabit olur. Ama bu ├¦eli┼¤kidir ve bu y├╝zden p(z0)┬Ā=┬Ā0 olmal─▒d─▒r.
Kan─▒t 4: Bir di─¤er kan─▒t ise kullanmaktad─▒r. Pozitif bir R ger├¦el say─▒s─▒ se├¦elim ├Čyle ki p(z) 'nin k├Čklerinin mutlak de─¤erinin her biri bu R say─▒s─▒ndan k├╝├¦├╝k olsun. B├Čyle bir R say─▒s─▒ vard─▒r; ├¦├╝nk├╝ sabit olmayan ve derecesi n olan bir polinomun en fazla n tane s─▒f─▒r─▒ oldu─¤unu biliyoruz. r┬Ā>┬ĀR ko┼¤ulunu sa─¤layan her r i├¦in
say─▒s─▒n─▒ ele alal─▒m. Burada, c(r) 0 merkezli, r yar─▒├¦apl─▒ ve saatin tersi y├Čndeki ├¦emberdir. O zaman, kullan─▒larak bu say─▒n─▒n p(z) 'nin 0 merkezli ve r yar─▒├¦apl─▒ a├¦─▒k daire i├¦inde sahip oldu─¤u s─▒f─▒r say─▒s─▒ N'ye e┼¤it oldu─¤u elde edilir. r┬Ā>┬ĀR oldu─¤u i├¦in bu ayn─▒ zamanda p(z) 'nin toplam s─▒f─▒r say─▒s─▒na e┼¤ittir. Di─¤er taraftan, n/z 'nin c(r) boyunca al─▒nan integralinin 2ŽĆi 'ye b├Čl├╝nmesiyle n say─▒s─▒ elde edilir. Ama, o zaman bu iki say─▒ aras─▒ndaki fark ┼¤├Čyle olur:
Sa─¤daki integralin i├¦inde bulunan rasyonel ifadenin pay─▒n─▒ derecesi en fazla n┬ĀŌłÆ┬Ā1 iken, paydan─▒n derecesi ise n┬Ā+┬Ā1 dir. Bu sebeple, yukar─▒daki ifadedeki fark─▒ temsil eden say─▒, r sonsuza giderken 0'a yakla┼¤maktad─▒r. Ancak, bu say─▒ ayn─▒ zamanda N┬ĀŌłÆ┬Ān say─▒s─▒na e┼¤ittir. O zaman, N┬Ā=┬Ān olmal─▒d─▒r.
Kan─▒t 5: Bir ba┼¤ka kan─▒t ise do─¤rusal cebir ve Cauchy integral teoreminin birle┼¤tirilmesinden elde edilir. Derecesi n┬Ā>┬Ā0 olan her karma┼¤─▒k polinomun bir tane s─▒f─▒r─▒ oldu─¤unu g├Čstermek i├¦in nxn lik her karma┼¤─▒k matrisin karma┼¤─▒k bir ├Čzde─¤erinin oldu─¤unu g├Čstermek yeterlidir. ├ćeli┼¤ki y├Čntemiyle tart─▒┼¤al─▒m:
A, nxn lik karma┼¤─▒k bir kare matris olsun ve In de nxn lik birim matris olsun.
resolvent fonksiyonunu ele alal─▒m. R(z) karma┼¤─▒k d├╝zlemde tan─▒ml─▒ ve matrislerin vekt├Čr uzay─▒nda de─¤erler olan bir meromorf fonksiyondur. A 'n─▒n ├Čzde─¤erleri, kesinlikle R(z) 'nin kutuplar─▒d─▒r. Varsay─▒m─▒m─▒zdan dolay─▒ A 'n─▒n ├Čzde─¤eri olmad─▒─¤─▒ i├¦in, o zaman R(z) tam fonksiyon olur ve Cauchy integral teoremi sayesinde
elde ederiz. Di─¤er taraftan, R(z) 'yi geometrik seri olarak a├¦arsak
elde ederiz. Bu form├╝l, yar─▒├¦ap─▒ ||A|| (A'n─▒n operat├Čr normu) olan kapal─▒ diskin d─▒┼¤─▒nda ge├¦erlidir. Bu halde, r┬Ā>┬Ā||A|| alal─▒m. O zaman,
elde edilir. Burada sadece toplamdaki indeksin k┬Ā=┬Ā0 oldu─¤u durumda integralin de─¤eri 0 olmaz. Bu bir ├¦eli┼¤kidir. O y├╝zden, A'n─▒n ├Čzde─¤eri vard─▒r.
Notlar
- ^ Frans─▒zca vikipedideki "Th├®or├©me de d'Alembert-Gauss" maddesine bak─▒n─▒z
- ^ V. F. Bayart Th├®or├©me de D'Alembert-Gauss 5 Kas─▒m 2011 tarihinde Wayback Machine sitesinde . (Frans─▒zca dilinde)
- ^ Cebir III ders notlar─▒, Erhan G├╝zel taraf─▒ndan [1] 11 Kas─▒m 2010 tarihinde Wayback Machine sitesinde .
- ^ C. Antonini J.-F. Quint P. Borgnat J. B├®rard E. Lebeau E. Souche A. Chateau O. Teytaud R├®sultats li├®s ├Ā la compacit├®(T─▒k─▒zl─▒kla alakal─▒ sonu├¦lar) ba┼¤l─▒─¤─▒ndaki sonu├¦ k─▒sm─▒nda 4 May─▒s 2009 tarihinde Wayback Machine sitesinde . math├®matiques.net (Frans─▒zca dilinde)
- ^ Yaz─▒s─▒nda bu ifadeden demek istedi─¤i herhangi bir katsay─▒n─▒n 0 olmad─▒─¤─▒ durumdur
wikipedia, wiki, viki, vikipedia, oku, kitap, k├╝t├╝phane, k├╝t├╝bhane, ara, ara bul, bul, her┼¤ey, ne arasan─▒z burada,hikayeler, makale, kitaplar, ├Č─¤ren, wiki, bilgi, tarih, yukle, izle, telefon i├¦in, turk, t├╝rk, t├╝rk├¦e, turkce, nas─▒l yap─▒l─▒r, ne demek, nas─▒l, yapmak, yap─▒l─▒r, indir, ├╝cretsiz, ├╝cretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, m├╝zik, ┼¤ark─▒, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte cebirin temel teoremi karmasik degiskenli polinomlarin koklerinin varligiyla ilgili temel bir sonuctur D Alembert Gauss teoremi olarak da anilmaktadir Teoremin acik bir ifadesi soyledir Katsayilari karmasik olan ve sabit olmayan tek degiskenli her polinomun en az bir karmasik koku vardir Sonuc olarak katsayilari tam sayi rasyonel sayi veya gercel sayi olan ve sabit olmayan her polinomun en az bir karmasik koku vardir cunku tam sayilar rasyonel sayilar ve gercel sayilar da aslinda birer karmasik sayidir Bu sonuc elde edildikten sonra her polinomun karmasik sayilar cismi olan C displaystyle scriptstyle mathbb C de carpanlarina ayrilabilecegi gorulebilir yani daha dogru bir sekilde dile getirilirse her polinom derecesi kadar sayida dogrusal fonksiyonlarin carpimi seklinde yazilabilir Bu dogrusal fonksiyonlarin uniter olmasi isteniyorsa bu carpimin basina bir karmasik sayi eklenir Polinom bu son anlatilan sekilde carpanlarina ayrilmaya calisilirsa boyle bir ayirma tek bir sekilde yapilabilir Matematiksel bir dille su ifade edilmektedir Eger an 0 displaystyle a n neq 0 ise ve p z i 0naizi an zn an 1 zn 1 a2 z2 a1 z a0 displaystyle p z sum i 0 n a i z i a n cdot z n a n 1 cdot z n 1 cdots a 2 cdot z 2 a 1 cdot z a 0 n dereceli bir polinomsa p z an z an z a1 displaystyle p z a n z alpha n cdots z alpha 1 esitligi yazilabilir ve bu esitligin bu sekilde yazilabilmesi sadece tek bir sekilde yapilabilir Bu sekilde yazildiktan sonra polinomun koklerinin a1 an displaystyle alpha 1 cdots alpha n olacagi aciktir Burada polinomun koklerinin birbirinden farkli olmak zorunda olmayacagina dikkat edilmelidir Cebirin temel teoremi her ne kadar cebirin ve teoremin kanitlanmasindan sonra uretilmis matematigin buyuk bir bolumunun gelistirilmesinde onemli bir yere sahipse de isminin icerdigi cebir kelimesi teoremi dar bir alana sokmamalidir Zira bu teoremin tamamen cebirsel olan bir kaniti bile yok gibidir Teoremin bu isimle anilmasinin sebebi teoremin kanitlandigi donemde cebirin kendini denklemler kurami yani polinomlarin cozumuyle ugrasan bir kuram olarak tanimlamasidir Ancak kanitin yapildigi zamandan bu yana cebirin kapsamina giren fikirler artmissa da teoremin ismi degismeden kalmistir Teorem kendine matematigin icinde oldukca genis bir uygulama bulmustur Ornegin dogrusal cebirde indirgenmesinde onemli bir yere sahiptir Yine analizde rasyonel fonksiyonlarin ayrisiminda ve daha bircok teoremin kanitinda kullanilmaktadir Teoremin dengi ifadeleriCebirin temel teoreminin birbirine denk olan degisik ifadeleri mevcuttur Bunlardan ilki yukarida da verilen ifadedir Sabit olmayan ve katsayilari karmasik olan her polinomun en az bir karmasik koku vardir Ornegin 1 i karmasik sayisi X4 4 displaystyle X 4 4 polinomunun bir kokudur Bu halde teorem P X polinomunun bir kokunun varoldugunu ifade eder ancak bu kokun nasil bulunacagini aciklamaz Koklerin varligi ilgili bu ifade aslinda karmasik sayilar cisminin bir ozelligini de tanimlamaktadir Katsayilarini bir F cisminden alan tek degiskenli ve derecesi en az 1 olan her polinomun yine bu F cismi icinde bir koku varsa F cismine adi verilir Teorem bu yuzden su sekilde de ifade edilebilir Ccismi cebirsel kapali bir cisimdir Bu sonuc ayni zamanda bir polinomun bolunmesi baglaminda da yani karmasik katsayili carpanlarinin carpimina esit olmasi anlaminda da ifade edilebilir Karmasik degiskenli her polinom bolunebilir yani derecesi 1 olan ve karmasik katsayilara sahip polinomlarin carpimi seklinde yazilabilir Teorem derecesi n olan ve karmasik katsayili anXn a1X a0 seklindeki polinomlarin an X a1 X an halinde de yazilabilecegini isaret eder Burada 1 den k ye kadar degisen her ak polinomun bir kokudur Burada farkli k ler icin ak ler esit olabilir Bu durumda ak ye katli kok adi verilir Cebirin temel teoremi katsayilari gercel sayi olan polinomlar ele alindiginda su dengi ifadelere karsilik gelmektedir Gercel katsayilara sahip sabit olmayan her polinomun en az bir karmasik koku vardir Gercel katsayili ya 1 derecelidir ya da ikinci dereceden diskriminanti kesin negatif olan polinomlardir yani aX2 bX c displaystyle aX 2 bX c ve a 0 displaystyle a neq 0 halinde yazilabilen ve b2 4ac lt 0 displaystyle b 2 4ac lt 0 kosulunu saglayan polinomlar Sabit olmayan gercel katsayilara sahip her polinom derecesi 1 veya 2 olan polinomlarin carpimi seklinde yazilabilir Teoremin tarihiPeter Rothe Petrus Roth 1608 de yayimlanan Arithmetica Philosophica adli kitabinda gercel katsayilara sahip n inci dereceden bir polinom denkleminin n tane cozumunun olabilecegini yazmistir Albert Girard 1629 da yayimlanan L invention nouvelle en l Algebre adli kitabinda n inci dereceden bir polinom denkleminin n tane cozumunun oldugunu yazmistir Dahasi bu ifadesinin denklem eksikli olmadikca gecerli oldugunu ifade etmistir Ancak ne demek istedigini detayli bir sekilde acikladiginda aslinda ifade ettigi onermenin her zaman gecerli olduguna inandigi ortaya cikmaktadir Mesela x4 4x 3 eksikli degildir ancak yine de 4 koku vardir 1 iki kere 1 i 2 ve 1 i 2 Jean le Rond D Alembert teoremi kanitlama ihtiyaci hisseden ilk matematikciydi ve teoremi tamamen analitik amacla kanitlamaya calismisti ancak verdigi kanit eksikti Yukaridaki dengi ifadelerde de ifade edildigi gibi cebirin temel teoremini izleyen ifadelerden biri de sabit olmayan ve gercel katsayilara sahip bir polinomun derecesi bir veya 2 olan gercel katsayili polinomlarin carpimi seklinde yazilabilecegidir Ancak 1702 de Leibniz a nin reel oldugu ve sifira esit olmadigi x4 a4 turundeki hicbir polinomun bu sekilde yazilamadigini soylemistir Sonralari Bernoulli yine ayni ifadeyi bu sefer x4 4x3 2x2 4x 4 polinomunu kastederek vermistir Ancak 1742 de Euler den bahsi gecen polinomun x2 2 a x 1 7 a x2 2 a x 1 7 a displaystyle x 2 2 alpha x 1 sqrt 7 alpha x 2 2 alpha x 1 sqrt 7 alpha seklinde yazilabildigini belirten bir mektup almistir Burada a 4 2 7 sayisinin karekokudur Euler ayrica x4 a4 x2 a2 x a2 x2 a2 x a2 displaystyle x 4 a 4 x 2 a sqrt 2 cdot x a 2 x 2 a sqrt 2 cdot x a 2 oldugundan da bahsetmistir Teoremi ilk kanitlama girisimi 1746 da d Alembert tarafindan yapilmistir ancak kaniti eksikti Kanitin sorunlarindan biri de Puiseux teoremi olarak da bilinen bir teoremi varsaymasidir ki bu teorem bu kanitin yapilmaya tarihten 100 yil sonra kanitlanmistir Dahasi bu kanit da cebirin temel teoremini varsayar Teoremi kanitlama girisimi euler tarafindan 1749 da de Foncenex tarafindan 1759 da Lagrange tarafindan 1795 te yapilmistir Bu dort girisimin hepsi de Girard in ifadesine dayanmaktadir 18 inci yuzyil sonunda koklerin varligini varsaymayan iki kanit yayinlandi Bunlardan biri James Wood tarafindan verilmisti ve genel cercevede cebirsel bir kanitti ancak zamaninda pek de onemsenmedi Wood un verdigi kanitin ayni zamanda cebirsel bir acigi vardi Diger kanit ise Gauss tarafindan 1799 da verilen kanitti ve genel cercevede geometrik bir kanitti ancak topolojik bir acigi vardi Bu acik Alexander Ostrowski tarafindan 1920 de kapatilmistir Tamamen titizce hazirlanmis bir kanit Argand tarafindan 1806 da verilmistir ve ilk defa burada cebirin temel teoremi gercel katsayili polinomlardan degil de karmasik katsayili polinomlardan bahsederek ifade edilmistir Gauss daha sonra biri 1816 da ve digeri de ilk verdigi kanitin degisik bir hali olmak uzere 1849 da iki kanit daha yayimlamistir Teoremi ve kanitini iceren ilk kitap Cauchy nin Cours d analyse de l Ecole Royale Polytechnique 1821 adli kitabidir Argand in kanitini icermektedir ancak Argand a herhangi bir atif yapilmamistir KanitlarBu bolumde dahil edilen kanitlarin neredeyse hepsi bir sekilde analizden en azindan gercel ve karmasik fonksiyonlarin surekliligini kullanacak derecede faydalanmaktadir Bazi kanitlar turevi ve hatta analitik fonksiyonlari kullanmaktadir Bu yuzden aslinda cebirin temel teoreminin ne temel ne de tamamen cebirsel bir ozelligi mevcuttur Teoremin bazi kanitlari sabit olmayan ve gercel katsayilara sahip polinomlarin karmasik bir koke sahip olacagini kanitlamaktadir Ancak bu tur kanitlar yine de teoremin en genel halini kanitlamakta yeterlidir cunku p z karmasik katsayilara sahip sabit olmayan bir polinomsa q z p z p z displaystyle q z p z overline p overline z polinomunun sadece gercel katsayilari olacaktir Dahasi z eger q z yi sifir yapan bir sayiysa yani q z nin kokuyse o zaman ya z ya da z nin eslenigi p z nin koku olacaktir Teoremin cebirsel yontemleri kullanmayan kanitlarinin buyuk bir kismi buyume onsavi da denilen su gercege dayanmaktadir baskin katsayisi 1 olan n inci dereceden bir polinom z yeterince buyukken aslinda zn gibi davranir Daha kesin bir ifade ise soyle verilebilir oyle bir R sayisi vardir ki z gt R iken su esitsizlik saglanir 12 zn lt p z lt 32 zn displaystyle tfrac 1 2 z n lt p z lt tfrac 3 2 z n Karmasik analizdeki kanitlar Kanit 1 z r iken p z gt p 0 olacak sekilde orijin merkezli ve r yaricapli bir kapali D diski alalim D tikiz oldugu icin p z fonksiyonunun minimumum D uzerinde vardir ve dahasi bu minimum D nin sinir uzerinde degildir Minimumun var oldugu nokta z0 ise o zaman minimum mutlak deger ilkesi kullanilarak p z0 0 elde edilir Baska bir deyisle z0p z nin bir sifiridir Kanit 2 Kanit 1 in biraz daha degistirilmis haliyle teorem yine kanitlanabilir Kanit minimum mutlak deger teoremi kullanmadan yapilabilir bu tur kanitlarin bircogu Cauchy integral teoremini veya sonuclarini kullanir ancak bu kez yapilan sey minimum mutlak deger teoreminin polinomlar icin basit adimlarla kanitlanmasidir Daha kesin bir ifadeyle celiski yoluyla kanit yapmaya calisirsak a p z0 0 displaystyle a p z 0 neq 0 olsun O zaman p z displaystyle p z yi z z0 displaystyle z z 0 in kuvvetleri halinde acip su sekilde yazabiliriz p z a ck z z0 k ck 1 z z0 k 1 cn z z0 n displaystyle p z a c k z z 0 k c k 1 z z 0 k 1 ldots c n z z 0 n Burada cj displaystyle c j ler z p z z0 displaystyle z to p z z 0 polinomunun katsayilaridir ve k displaystyle k de sabit terimden sonra sifir olmayan ilk terimin indeksini temsil etmektedir Ama z0 displaystyle z 0 a yeteri kadar yakin z displaystyle z ler icin bu polinomun asimptotik olarak q z a ck z z0 k displaystyle q z a c k z z 0 k polinomuna benzer davrandigini gozlemleyebiliriz Baska bir deyisle p z q z z z0 k 1 displaystyle left frac p z q z z z 0 k 1 right ifadesi z0 displaystyle z 0 noktasinin belli bir komsulugunda pozitif bir M displaystyle M sabiti tarafindan sinirlandirilmistir Bu yuzden 80 arg a p arg ck k displaystyle theta 0 arg a pi arg c k k tanimlarsak ve z z0 rei80 displaystyle z z 0 re i theta 0 alirsak o zaman yeteri kadar kucuk pozitif r displaystyle r sayisi icin ucgen esitsizligini de kullanarak p z lt q z rk 1 p z q z rk 1 a 1 ckrkei arg a arg ck Mrk 1 a ck rk Mrk 1 displaystyle begin aligned p z amp lt q z r k 1 left frac p z q z r k 1 right 2em amp leq left a 1 c k r k e i arg a arg c k right Mr k 1 5em amp a c k r k Mr k 1 end aligned elde ederiz r 0 a yeteri kadar yakin oldugunda ustte p z icin bulunan bu ust sinir a dan kesinlikle daha kucuk olacaktir ve bu da z0 in tanimiyla celismektedir Kanit 3 Bu baglamda elde edilen bir baska kanit ise D nin disinda p z gt p 0 oldugunu gozlemlenmesine ve bu yuzden p z nin karmasik duzlemdeki minimumunun z0 gerceklesmesine dayanmaktadir p z0 gt 0 ise o zaman 1 p karmasik duzlemin tumunde sinirli bir holomorf fonksiyon olur Karmasik duzlemin tumunde sinirli olan holomorf bir fonksiyonun sabit olmasi gerektigini belirten Liouville teoremi kullanilarak 1 p nin sabit oldugu sonucuna ulasilir Bu yuzden p de sabit olur Ama bu celiskidir ve bu yuzden p z0 0 olmalidir Kanit 4 Bir diger kanit ise kullanmaktadir Pozitif bir R gercel sayisi secelim oyle ki p z nin koklerinin mutlak degerinin her biri bu R sayisindan kucuk olsun Boyle bir R sayisi vardir cunku sabit olmayan ve derecesi n olan bir polinomun en fazla n tane sifiri oldugunu biliyoruz r gt R kosulunu saglayan her r icin 12pi c r p z p z dz displaystyle frac 1 2 pi i int c r frac p z p z dz sayisini ele alalim Burada c r 0 merkezli r yaricapli ve saatin tersi yondeki cemberdir O zaman kullanilarak bu sayinin p z nin 0 merkezli ve r yaricapli acik daire icinde sahip oldugu sifir sayisi N ye esit oldugu elde edilir r gt R oldugu icin bu ayni zamanda p z nin toplam sifir sayisina esittir Diger taraftan n z nin c r boyunca alinan integralinin 2pi ye bolunmesiyle n sayisi elde edilir Ama o zaman bu iki sayi arasindaki fark soyle olur 12pi c r p z p z nz dz 12pi c r zp z np z zp z dz displaystyle frac 1 2 pi i int c r left frac p z p z frac n z right dz frac 1 2 pi i int c r frac zp z np z zp z dz Sagdaki integralin icinde bulunan rasyonel ifadenin payini derecesi en fazla n 1 iken paydanin derecesi ise n 1 dir Bu sebeple yukaridaki ifadedeki farki temsil eden sayi r sonsuza giderken 0 a yaklasmaktadir Ancak bu sayi ayni zamanda N n sayisina esittir O zaman N n olmalidir Kanit 5 Bir baska kanit ise dogrusal cebir ve Cauchy integral teoreminin birlestirilmesinden elde edilir Derecesi n gt 0 olan her karmasik polinomun bir tane sifiri oldugunu gostermek icin nxn lik her karmasik matrisin karmasik bir ozdegerinin oldugunu gostermek yeterlidir Celiski yontemiyle tartisalim A nxn lik karmasik bir kare matris olsun ve In de nxn lik birim matris olsun R z zIn A 1 displaystyle R z zI n A 1 resolvent fonksiyonunu ele alalim R z karmasik duzlemde tanimli ve matrislerin vektor uzayinda degerler olan bir meromorf fonksiyondur A nin ozdegerleri kesinlikle R z nin kutuplaridir Varsayimimizdan dolayi A nin ozdegeri olmadigi icin o zaman R z tam fonksiyon olur ve Cauchy integral teoremi sayesinde c r R z dz 0 displaystyle int c r R z dz 0 elde ederiz Diger taraftan R z yi geometrik seri olarak acarsak R z z 1 In z 1A 1 z 1 k 0 1zkAk displaystyle R z z 1 I n z 1 A 1 z 1 sum k 0 infty frac 1 z k A k cdot elde ederiz Bu formul yaricapi A A nin operator normu olan kapali diskin disinda gecerlidir Bu halde r gt A alalim O zaman c r R z dz k 0 c r dzzk 1Ak 2piIn displaystyle int c r R z dz sum k 0 infty int c r frac dz z k 1 A k 2 pi iI n elde edilir Burada sadece toplamdaki indeksin k 0 oldugu durumda integralin degeri 0 olmaz Bu bir celiskidir O yuzden A nin ozdegeri vardir Notlar Fransizca vikipedideki Theoreme de d Alembert Gauss maddesine bakiniz V F Bayart Theoreme de D Alembert Gauss 5 Kasim 2011 tarihinde Wayback Machine sitesinde Fransizca dilinde Cebir III ders notlari Erhan Guzel tarafindan 1 11 Kasim 2010 tarihinde Wayback Machine sitesinde C Antonini J F Quint P Borgnat J Berard E Lebeau E Souche A Chateau O Teytaud Resultats lies a la compacite Tikizlikla alakali sonuclar basligindaki sonuc kisminda 4 Mayis 2009 tarihinde Wayback Machine sitesinde mathematiques net Fransizca dilinde Yazisinda bu ifadeden demek istedigi herhangi bir katsayinin 0 olmadigi durumdur
 Azərbaycanca
Az╔Örbaycanca ąæąĄą╗ą░čĆčāčüą║č¢
ąæąĄą╗ą░čĆčāčüą║č¢ Dansk
Dansk Deutsch
Deutsch Espa├▒ola
Espa├▒ola Fran├¦ais
Fran├¦ais Indonesia
Indonesia Italiana
Italiana µŚźµ£¼Ķ¬×
µŚźµ£¼Ķ¬× ęÜą░ąĘą░ęø
ęÜą░ąĘą░ęø Lietuvos
Lietuvos Nederlands
Nederlands Português
Portugu├¬s ąĀčāčüčüą║ąĖą╣
ąĀčāčüčüą║ąĖą╣ ÓĘāÓĘÆÓČéÓĘäÓČĮ
ÓĘāÓĘÆÓČéÓĘäÓČĮ Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó
Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó T├╝rk├¦e
T├╝rk├¦e ąŻą║čĆą░茹Įčüčīą║ą░
ąŻą║čĆą░茹Įčüčīą║ą░ õĖŁÕ£ŗõ║║
õĖŁÕ£ŗõ║║ United State
United State Afrikaans
Afrikaans