Cisim, halka ve grup gibi soyut bir cebirsel yapıdır. Kabaca, elemanları arasında toplama, çıkarma, çarpma ve bölme (sıfıra bölme hariç) yapılabilen ve bu işlemlerde sayılardan alışık olduğumuz temel aritmetik kurallarının geçerli olduğu bir küme olarak tanımlanabilir.
Her cisim bir halkadır, fakat bunun tersi geçerli değildir. Mesela tam sayılar kümesi bir halka olduğu halde, içinde bölme yapılamadığı için cisim değildir. Değişmeli bölenler halkasına cisim denir.
Rasyonel sayılar ve gerçel sayılar , cisimlerin başlıca örneklerindendir. Ancak soyut cebirde toplama ve çarpma işlemlerinin tanımlı olduğu daha başka cisimler hayal etmek de mümkündür.
Tarihçe
Cisim kavramını ilk ortaya atan Richard Dedekind olmuştur. Dedekind, bu yapı için Almancada "cisim" ya da "vücut" anlamına gelen Körper kelimesini kullanmıştır.
Tanımı ve Temel Özellikleri
Cisim Aksiyomları


- Birleşme Özelliği Her
üçlüsü için
- Birim Elemanın Varlığı Öyle bir
mevcuttur ki her
için
- Her
için öyle bir
elemanı mevcuttur ki
- Değişme Özelliği Her
ikilisi için
özelliklerinin hepsi sağlanmalıdır. Cisimlerde, çarpma işlemi de benzer özellikleri sağlamaktadır:
- Birleşme Özelliği Her
üçlüsü için
- Birim Elemanın Varlığı Öyle bir
mevcuttur ki her
için
- Her
için öyle bir
elemanı mevcuttur ki
- Değişme Özelliği Her
ikilisi için
Dikkat edilmesi gereken husus, çarpmada 0'ın ters elemanının bulunmamasıdır. Çarpma ve toplama işlemleri ise, birbirleri ile
- Dağılma Özelliği Her
üçlüsü için
sayesinde bağlanır. Bu özelliklerin yanı sıra, tek elemandan oluşan trivial cismi cisim olarak saymak bazen problemlere yol açtığından,
- Trivial Olmama
varsayımı eklenir, çünkü 
Aksiyomlardan çıkan sonuçlar
Bu aksiyomlar sağlandığı anda bazı kurallar otomatikman kanıtlanır:
- Yutan Eleman Her
için
-
ise
- Eğer
ise veya
'dan farklı
'ler için
ise
- Çıkarma ve Bölme Verilen iki
için
ve
ise
özelliğini sağlayan bir ve sadece bir
mevcuttur. Bunlar,
ve
şeklinde gösterilir.
ve dolayısıyla
- Üs Alma Kısaca,
tane
yerine
gösterimi kullanılır. Bu gösterim, aşağıdaki özellikleri sağlar:
Örnekler
Temel Kavramlar
Altcisimler ve Cisim Uzatmaları
Bir cismin içinde daha küçük cisimlerin bulunduğu durumları incelemek çoğu zaman kullanışlıdır. Bu yüzden, 






Hiçbir altcismi bulunmayan cisimlere asal cisim denir. İki altcismin kesişimi de yine bir altcisim olduğundan, herhangi bir 





Mesela rasyonel sayıların kümesi 
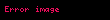
Karekteristik
Eğer bir 


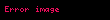

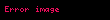
Karekteristiği 0 olan bir cismin içinde daima rasyonel sayılar 
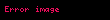
Homomorfizmalar ve İzomorfizmalar
İki cismin arasında bulunan benzerlikler, homomorfizma olarak adlandırılır. Resmen, bir 
Kısaca, 
Halkalar ile İlişkisi
Halkalardan Cisimlerin İnşası
Halkalar, cisimlerin daha genelleştirilmiş versiyonlarıdır. Halkalarda çarpma işleminin ters elemanlı ve değişmeli olması şartı aranmaz. Bunun bir sonucu olarak yukarıdaki özelliklerin birçoğu kaybolur, mesela bazı halkalarda 0'dan farklı iki sayının çarpımı 0 olabilir.
0'dan farklı iki sayının çarpımının asla 0 olmadığı halkalara tamlık bölgesi denir. Eleman sayısı sonlu olan tüm tamlık bölgeleri aynı zamanda bir cisimdir. Sonsuz elemanlı tamlık bölgelerini kullanarak da bir cisim elde etmek mümkündür. Sonsuz tamlık bölgelerine örnek olarak tam sayıların kümesi 
Kesir İnşası
Bir tamlık bölgesinden cisim elde etmenin bir yolu, ortaokulda gösterilen kesir kavramından esinlenmektir. 

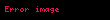
Öncelikle, iki ikilinin eşitlik şartlarını gevşetip, 
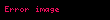

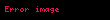
Çarpma işlemini akla gelen şekilde 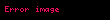
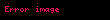
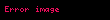

Toplama işlemini ise biraz daha karmaşık bir şekilde tanımlamak gerekir: 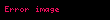
Bu işlemler ve bu eşitlik ilişkisi, nihayetinde bir cisim teşkil eder. Bu noktadan itibaren 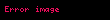
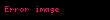


Tam sayılar 

Modüler Aritmetik
Tamlık bölgelerini kullanarak daha küçük cisimler elde etmenin bir yolu ise, bölüm halkalarını kullanmaktır. Şimdi 


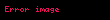


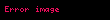

Bu yöntemi kullanarak 

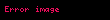

| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
Kaynakça
Ayrıca bakınız
 | Matematik ile ilgili bu madde seviyesindedir. Madde içeriğini genişleterek Vikipedi'ye katkı sağlayabilirsiniz. |
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cisim halka ve grup gibi soyut bir cebirsel yapidir Kabaca elemanlari arasinda toplama cikarma carpma ve bolme sifira bolme haric yapilabilen ve bu islemlerde sayilardan alisik oldugumuz temel aritmetik kurallarinin gecerli oldugu bir kume olarak tanimlanabilir Her cisim bir halkadir fakat bunun tersi gecerli degildir Mesela tam sayilar kumesi Z displaystyle mathbb Z bir halka oldugu halde icinde bolme yapilamadigi icin cisim degildir Degismeli bolenler halkasina cisim denir Rasyonel sayilar Q displaystyle mathbb Q ve gercel sayilar R displaystyle mathbb R cisimlerin baslica orneklerindendir Ancak soyut cebirde toplama ve carpma islemlerinin tanimli oldugu daha baska cisimler hayal etmek de mumkundur TarihceCisim kavramini ilk ortaya atan Richard Dedekind olmustur Dedekind bu yapi icin Almancada cisim ya da vucut anlamina gelen Korper kelimesini kullanmistir Tanimi ve Temel OzellikleriCisim Aksiyomlari K displaystyle mathbb K bos olmayan bir kume olsun Bu kumenin bir cisim olmasi icin elemanlari arasinda displaystyle ile gosterip ve toplama diye adlandiracagimiz ve displaystyle ile gosterip carpma diye adlandiracagimiz iki tane ikili islem tanimlanmis olmasi gereklidir Ayriyeten bu islemlerin bazi ozellikleri saglamasi gerekmektedir Toplama islemi icin Birlesme Ozelligi Her a b c K displaystyle a b c in mathbb K uclusu icin a b c a b c a b c displaystyle a b c a b c a b c Birim Elemanin Varligi Oyle bir 0 K displaystyle 0 in mathbb K mevcuttur ki her a K displaystyle a in mathbb K icin a 0 0 a a displaystyle a 0 0 a a Her a K displaystyle a in mathbb K icin oyle bir a K displaystyle a in mathbb K elemani mevcuttur ki a a a a 0 displaystyle a a a a 0 Degisme Ozelligi Her a b K displaystyle a b in mathbb K ikilisi icin a b b a displaystyle a b b a ozelliklerinin hepsi saglanmalidir Cisimlerde carpma islemi de benzer ozellikleri saglamaktadir Birlesme Ozelligi Her a b c K displaystyle a b c in mathbb K uclusu icin a b c a b c a b c displaystyle a b c a b c a b c Birim Elemanin Varligi Oyle bir 1 K displaystyle 1 in mathbb K mevcuttur ki her a K displaystyle a in mathbb K icin 1 a a 1 a displaystyle 1 a a 1 a Her a K 0 displaystyle a in mathbb K setminus 0 icin oyle bir a 1 K 0 displaystyle a 1 in mathbb K setminus 0 elemani mevcuttur ki a a 1 a 1 a 1 displaystyle a a 1 a 1 a 1 Degisme Ozelligi Her a b K displaystyle a b in mathbb K ikilisi icin a b b a displaystyle a b b a Dikkat edilmesi gereken husus carpmada 0 in ters elemaninin bulunmamasidir Carpma ve toplama islemleri ise birbirleri ile Dagilma Ozelligi Her a b c K displaystyle a b c in mathbb K uclusu icin a b c a b a c displaystyle a b c a b a c sayesinde baglanir Bu ozelliklerin yani sira tek elemandan olusan trivial cismi cisim olarak saymak bazen problemlere yol actigindan Trivial Olmama 0 1 displaystyle 0 neq 1 varsayimi eklenir cunku 0 1 displaystyle 0 1 oldugu durumda cisimdeki tum elemanlarin birbirine esit oldugu istisnai ve duzensiz bir yapi ortaya cikar Aksiyomlardan cikan sonuclar Bu aksiyomlar saglandigi anda bazi kurallar otomatikman kanitlanir Yutan Eleman Her x K displaystyle x in mathbb K icin 0 x 0 displaystyle 0 x 0 x y 0 displaystyle x y neq 0 ise x y 0 displaystyle x y neq 0 Eger x y x z displaystyle x y x z ise veya 0 displaystyle 0 dan farkli x displaystyle x ler icin xy xz displaystyle xy xz ise y z displaystyle y z Cikarma ve Bolme Verilen iki x y K displaystyle x y in mathbb K icin x r y displaystyle x r y ve x 0 displaystyle x neq 0 ise sx y displaystyle sx y ozelligini saglayan bir ve sadece bir r s K displaystyle r s in mathbb K mevcuttur Bunlar r y x displaystyle r y x ve s y x displaystyle s y x seklinde gosterilir 1 x x displaystyle 1 x x ve dolayisiyla y x x y displaystyle y x x y Us Alma Kisaca n displaystyle n tane x x x displaystyle x x x yerine xn displaystyle x n gosterimi kullanilir Bu gosterim asagidaki ozellikleri saglar x 1 n xn 1 x n displaystyle x 1 n x n 1 x n x y n xn yn displaystyle x y n x n y n xn xm xn m displaystyle x n x m x n m OrneklerTemel KavramlarAltcisimler ve Cisim Uzatmalari Bir cismin icinde daha kucuk cisimlerin bulundugu durumlari incelemek cogu zaman kullanislidir Bu yuzden K L displaystyle mathbb K subset mathbb L olsun ve hem K displaystyle mathbb K hem de L displaystyle mathbb L birer cisim olsun Bu durumda K displaystyle mathbb K ya L displaystyle mathbb L nin bir altcismi ve L displaystyle mathbb L ye de K displaystyle mathbb K nin bir uzantisi denir Cisim Teorisindeki bircok kuram cisim uzantilari kullanilarak kanitlandigindan altcisimler ve uzantilar vazgecilmezdir Hicbir altcismi bulunmayan cisimlere asal cisim denir Iki altcismin kesisimi de yine bir altcisim oldugundan herhangi bir L displaystyle mathbb L cisminin tum altcisimlerini kesistirince biricik bir asal cisim K displaystyle mathbb K elde edilir Dolayisiyla her L displaystyle mathbb L cisminin icinde bir ve yegane bir asal cisim K displaystyle mathbb K bulunur ve K displaystyle mathbb K L displaystyle mathbb L yi karakterize eder Mesela rasyonel sayilarin kumesi Q displaystyle mathbb Q bir asal cisimdir Bunun yaninda yukarida bahsedilen Fp displaystyle mathbb F p cisimleri de birer asal cisimdir Hatta bunlar disinda asal cisim bulunmamaktadir Karekteristik Eger bir L displaystyle mathbb L cisminin carpimsal birim elemani 1 displaystyle 1 in hicbir tam kati 0 displaystyle 0 a esit degilse yani hicbir zaman 1 1 1 0 displaystyle 1 1 1 0 olmuyorsa L displaystyle mathbb L nin karekteristiginin 0 oldugu soylenir Sayet belirli bir n icin n tane 1 1 1 0 displaystyle 1 1 1 0 oluyorsa bu ozelligi saglayan en kucuk n e o cismin karekteristigi denir Bir cismin karekteristigi daima ya 0 ya da bir asal sayi olur Karekteristigi 0 olan bir cismin icinde daima rasyonel sayilar Q displaystyle mathbb Q bir altcisim olarak bulunur Karekteristigi p olan cisimlerin icinde de Fp displaystyle mathbb F p cismi bulunur Bu cisimler asal cisim oldugundan bir cisim icinde bulunan asal cismi sadece o cismin karekteristigine bakarak bulmak mumkundur Homomorfizmalar ve Izomorfizmalar Iki cismin arasinda bulunan benzerlikler homomorfizma olarak adlandirilir Resmen bir ϕ K L displaystyle phi mathbb K mapsto mathbb L eslemesinin bir homomorfizma olmasi icin asagidaki ozellikleri saglamasi gerekir ϕ x y ϕ x ϕ y displaystyle phi x y phi x phi y ϕ xy ϕ x ϕ y displaystyle phi xy phi x phi y Kisaca ϕ displaystyle phi eslemesi toplama ve carpmaya saygi gostermelidir Halkalar ile IliskisiHalkalardan Cisimlerin Insasi Halkalar cisimlerin daha genellestirilmis versiyonlaridir Halkalarda carpma isleminin ters elemanli ve degismeli olmasi sarti aranmaz Bunun bir sonucu olarak yukaridaki ozelliklerin bircogu kaybolur mesela bazi halkalarda 0 dan farkli iki sayinin carpimi 0 olabilir 0 dan farkli iki sayinin carpiminin asla 0 olmadigi halkalara tamlik bolgesi denir Eleman sayisi sonlu olan tum tamlik bolgeleri ayni zamanda bir cisimdir Sonsuz elemanli tamlik bolgelerini kullanarak da bir cisim elde etmek mumkundur Sonsuz tamlik bolgelerine ornek olarak tam sayilarin kumesi Z displaystyle mathbb Z yi alalim Kesir Insasi Bir tamlik bolgesinden cisim elde etmenin bir yolu ortaokulda gosterilen kesir kavramindan esinlenmektir I displaystyle I bir tamlik bolgesi olsun O zaman I displaystyle I dan aldigimiz ikililerin kumesi olan I2 displaystyle I 2 den ikinci elemanin 0 oldugu ikilileri cikardiktan sonra bir cisim yapisi su sekilde tanimlanabilir Oncelikle iki ikilinin esitlik sartlarini gevsetip a1 b1 a2 b2 I2 displaystyle a 1 b 1 a 2 b 2 in I 2 ikililerini a1b2 b1a2 displaystyle a 1 b 2 b 1 a 2 ozelligi saglandigi surece esdeger kabul edilen bir tanimlanir b1 b2 0 textstyle b 1 b 2 neq 0 oldugu surece bu iliskinin bir oldugunu gostermek zor degildir Bu sekilde I2 displaystyle I 2 yi birbirine esdeger kabul ettigimiz altkumelere indirgemek mumkundur Carpma islemini akla gelen sekilde a1 b1 a2 b2 a1a2 b1b2 displaystyle a 1 b 1 a 2 b 2 a 1 a 2 b 1 b 2 olarak tanimlamak mumkundur Bu islemin birlesmeli degismeli birim elemanli ve ters elemanli oldugunu gormek de zor degildir Ayni zamanda bu iliski yukarida tanimlanan esdegerlik kuraliyla da celiskisizdir Bu tanim ve bu esitlik kaidesi altinda verilen bir a b displaystyle a b ikilisinin tersi b a displaystyle b a olur Bu sekilde insa ettigimiz yapi I displaystyle I da olmayan ters elemanlarla donatilir Toplama islemini ise biraz daha karmasik bir sekilde tanimlamak gerekir a1 b1 a2 b2 a1b2 b1a2 b1b2 displaystyle a 1 b 1 a 2 b 2 a 1 b 2 b 1 a 2 b 1 b 2 kuraliyla Toplama islemini ancak bu sekilde tanimlarsak yukarida saglanan esitlik iliskisi ile celiskisiz olur Yine bu tanimdaki toplamanin birlesmeli degismeli sifirli ve ters elemanli oldugu barizdir Bu islemler ve bu esitlik iliskisi nihayetinde bir cisim teskil eder Bu noktadan itibaren a b ab displaystyle a b frac a b olarak alistigimiz sekilde gosterilebilir Daha onemlisi a 1 displaystyle a 1 seklinde olan elemanlar ile I displaystyle I arasinda bir bijektif homomorfizma bulundugundan I displaystyle I nin bu olusturdugumuz yeni cismin bir parcasi oldugunu soylemek mumkundur Dolayisiyla bu yontem ile herhangi bir degismeli tamlik bolgesini kapsayan bir cisim elde etmek mumkundur Tam sayilar Z displaystyle mathbb Z uzerinde bu yapiyi kullanmak bize rasyonel sayilar cismi Q displaystyle mathbb Q yu verir Moduler Aritmetik Tamlik bolgelerini kullanarak daha kucuk cisimler elde etmenin bir yolu ise bolum halkalarini kullanmaktir Simdi I displaystyle I yine bir tamlik bolgesi olsun ve n I displaystyle n in I ise I displaystyle I nin bir elemani olsun Yeni bir halka elde etmek icin oncelikle bir esitlik iliskisi tanimlayalim x ymodn displaystyle x equiv y mod n diye gosterdigimiz iliski sadece ve sadece x y displaystyle x y n displaystyle n in bir kati ise gecerli olsun Bu esitlik iliskisi toplama ve carpma altinda da bozulmaz dolayisiyla yeni bir halka tanimlanmis olur ve bu halka I n displaystyle I n seklinde gosterilebilir Eger n displaystyle n bir asal eleman ise bu yeni urettigimiz halka ayni zamanda bir cisim yapisina sahip olur Bu yontemi kullanarak Z displaystyle mathbb Z den modulo 7 tam sayilarin cismini elde etmek mumkundur Bu sekilde Z displaystyle mathbb Z den elde edilen cisimler Fp displaystyle mathbb F p ile gosterilir Mesela F7 displaystyle mathbb F 7 de her sayinin gercekten bir carpimsal tersi vardir 0 1 2 3 4 5 60 0 0 0 0 0 0 01 0 1 2 3 4 5 62 0 2 4 6 1 3 53 0 3 6 2 5 1 44 0 4 1 5 2 6 35 0 5 3 1 6 4 26 0 6 5 4 3 2 1Kaynakca a b O Hagan Anthony 2013 The Oxford handbook of applied Bayesian analysis Oxford Oxford University Press ISBN 978 0198703174 Waerden Bartel L van der Artin Emil Noether Emmy 1993 Algebra 1 9 Aufl Berlin Gottingen Heidelberg Springer ISBN 978 3 540 56799 8 Ayrica bakinizGrup HalkaMatematik ile ilgili bu madde taslak seviyesindedir Madde icerigini genisleterek Vikipedi ye katki saglayabilirsiniz
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans