Eliptik Eğri Kriptolojisi (Elliptic Curve Cryptography), sonlu cisimler üzerindeki eliptik eğrilerin cebirsel topolojisine dayanan bir açık anahtar şifrelemesidir. Eliptik Eğri Kriptolojisi, diğer şifrelemeler göre daha küçük anahtar boyuna ihtiyaç duyar.

Eliptik Eğriler, anahtar anlasması, dijital imza, sözde rastlantısal üretici ve daha birçok alanda kullanılabilirler. Dolaylı olarak, anahtar anlasmasını simetrik bir şifreleme şemasıyla birleştirerek şifreleme için kullanılabilirler. Lenstra Eliptik Eğrileri gibi kriptografik uygulamaları olan eliptik eğrileri temel alan çarpanlarına ayırma algoritmalarında da kullanılırlar.
Mantık
Son zamanlardaki açık anahtar şifreleme algoritmaları iki ya da daha fazla çok büyük asal sayının çarpımının, çarpanlarına ayırılmasındaki zorluğuna dayanır. Eliptik eğri protokollerinde ise bu durum, eliptik eğrinin bilinen bir noktasına göre ayrık logaritmasını bulmanın imkânsız olduğunu varsaymaktadır. Buna “Eliptik Eğrinin Ayrık Logaritma Problemi” denir. Eliptik eğrinin güvenliği, nokta çarpımının hesaplanma hızına ve başlangıç noktası ile çarpım noktasına bakarak elde edilen noktanın hesaplanamamasına dayanmaktadır. Eliptik eğrinin boyutu aynı zamanda problemin zorluğunu da belirler.
Eliptik eğri kriptografisinin en büyük özelliği depolama ve iletme gereksinimlerini azaltarak daha küçük anahtar boyutuna sahip olmasıdır. Bir eliptik eğri grubu, büyük modülerli ve buna bağlı olarak büyük anahtar boyutlu RSA tabanlı sistem ile aynı güvenlik seviyesi sunabilir. Örneğin; Eliptik eğri ile 256-bitlik anahtar boyutunda elde edeceğimiz güvenliği RSA ‘de 3072-bitlik anahtar ile sağlanabilir.
Ulusal Standartlar ve Teknoloji Enstitüsü (İngilizce: National Institute of Standards and Technology, kısaca NIST), anahtar anlasması için eliptik eğri Diffie Hellman (ECDH) ve dijital imza için Eliptik Eğri Dijital İmza Algoritmasını (ECDSA), ABD Ulusal Güvenlik Ajansı (İngilizce: National Security Agency, kısaca NSA), kriptolojisinde önerilen algoritmalar arasına eliptik eğri kriptografisinin de girmesini onaylamıştır. NSA, çok gizli bilgileri korumak için 384-bitlik anahtar boyutunu tavsiye etmektedir. Ancak, Ağustos 2015'te, NSA, ECC'ye yönelik kuantum hesaplama saldırılarıyla ilgili endişeler nedeniyle Suite B'yi yeni bir şifre paketi ile değiştirmeyi planladığını duyurdu.
RSA patenti 2000'de dolmuş olsa da, ECC teknolojisinin belirli açılarını kapsayan patentler olabilir. Ancak ABD hükümeti eliptik eğri dijital imza standartının ve belirli kullanışlı ECC-tabanlı anahtar değişim yapılarının (ECDH dahil) bunlar ihlal edilmeden gerçeklenemeyeği yönünde tartışmalar mevcuttur, RSA Laboratuvarları ve Daniel J. Bernstein da dahil.
Tarihçe
Kriptografide eliptik eğrilerin kullanımı, 1985'te Neal Koblitz ve Victor S. Miller tarafından bağımsız olarak önerilmiştir. Eliptik eğri kriptografi algoritmaları, 2004'ten 2005'e kadar geniş kullanım alanına girmiştir.
Teori
Mevcut kriptografik amaçlar için, bir eliptik eğri, aşağıdaki denklemi sağlayan noktalardan oluşan (gerçek sayılardan ziyade) üzerinde bir düzlem eğrisidir. (Buradaki koordinatlar, 2 ve 3 hariç olmak üzere sabit bir sonlu cismin karakteristiğinden veya biraz daha karmaşık olan bir eğri denkleminden seçilir.)

Eliptik eğrinin grup işlemlerinin bulunduğu küme abelyen bir kümedir. Bu grubun yapısı, cebirsel çeşitliliğin altında yatan bölen grubundan geçmiştir.
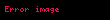
Kriptografik Şema
Birçok ayrık logaritma tabanlı protokol, 
- Eliptik Eğri Diffie-Hellman (ECDH) anahtar anlaşma şemasının Diffie-Hellman şemasına dayanmaktadır,
- Eliptik Eğri Entegre Şifreleme Şeması, Eliptik Eğri Artırılmış Şifreleme şeması olarak da bilinen veya sadece Eliptik Eğri Şifreleme Şeması,
- Eliptik Eğri Dijital İmza Algoritması (ECDSA), Dijital İmza Algoritmasına dayanmaktadır,
- Edwards-eğrisi Dijital İmza Algoritması (EdDSA), Schnorr imzasına dayanır ve eğrilerini kullanır,
- ECMQV anahtar anlaşma şeması, MQV anahtar anlaşma şemasına dayanmaktadır.
Ulusal Güvenlik Ajansı (NSA) 2005'te RSA konferansında dijital imza üretimi ve anahtar anlaşması için Eliptik Eğri Kriptolojisini özel olarak kullanan Suite B'yi duyurdu. SuitB, hem gizli hem de gizli olmayan ulusal güvenlik sistemlerini ve bilgilerini korumayı amaçlamıştır.
Yakın zamanda, Weil ve Tate çifti gibi çeşitli eliptik eğri gruplarında çift yönlü eşlemelere dayalı çok sayıda kriptografik ilke tanıtılmıştır. Bu ilkelere dayalı şemalar, eşleme tabanlı imzalar, işaretleme, anahtar anlaşması ve proxy şifrelemenin yanı sıra verimli kimlik tabanlı şifreleme de sağlar.
Yürütme
Alan Parametreler
Elipktik eğri kriptolojisini kullanmak için, tüm taraflar eliptik eğriyi tanımlayan alan parametreler adı verilen elemanlar üzerinde anlaşmalıdır. Cisim asıl durumda 











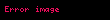


Eğer alan parametrelerinin guvenilir bir üretici tarafından oluşturulduğunun garantisi yoksa, bu parametreler kullanilmadan önce mutlaka doğrulanmalıdır.
Alan parametrelerinin oluşturulması genellikle her katılımcı tarafından yapılmaz çünkü bu durum zaman alan ve uygulaması zor olan bir eğri üzerindeki noktaların sayısını hesaplamayı gerektirir. Sonuç olarak, bazı yetkili standardizasyon kuruluşları yaygın cisim boyutları için eliptik eğri parametreleri yayınlamışlardır. Bu gibi alan parametreleri genellikle "standart eğriler" veya "adlandırılmış eğriler" olarak bilinir; Adlandırılmış bir eğri, bir ad veya standart belgelerde tanımlanan benzersiz nesne tanımlayıcısı tarafından referans edilebilir:
- NIST, Devlet İşlerinde Önerilen Eliptik Eğriler 20 Şubat 2018 tarihinde Wayback Machine sitesinde .
- , SEC 2: Önerilen Eliptik Eğri Alan Parametreleri 5 Nisan 2018 tarihinde Wayback Machine sitesinde .
- ECC Brainpool (RFC 5639),
SECG test vektörleri de mevcuttur. NIST birçok SECG eğrisini onayladı, dolayısıyla NIST ve SECG tarafından yayınlanan özellikler arasında örtüşme vardır. Eliptik Eğri alan parametreleri, değer veya ad ile belirtilebilir.
Eğer biri (yukarıda anlatılanlara rağmen) kendi alan parametrelerini oluşturmak isterse, altta yatan cismi seçmeli ve uygun sayıda noktaya sahip bir eğri bulmak için aşağıdaki stratejilerden birini kullanmalıdır:
- Rassal bir eğri seçin ve genel bir nokta sayma algoritması kullanın, örneğin Schoof'un algoritması veya Schoof – Elkies – Atkin algoritması,
- Nokta sayısını hesaplamayı kolaylaştıran bir eğri ailesi belirleyin veya
- Karmaşık çarpım tekniğini kullanarak puan sayısını belirleyin ve bu nokta sayısıyla bir eğri oluşturun.
Bazı eğri sınıfları zayıftır ve kesinlikle uzak durulmalıdır:
- Asal olmayan m ile tanımlanmış
üzerindeki eğri Weil descent atağına karşı zayıftır.
şeklindeki eğri, eğri üzerindeki noktaları
üzerindeki noktaları eşlediği bir atağa karşı zayıfdır.
Anahtar Boyu
ECDLP'yi çözmek için bilinen en hızlı algoritmaların 


Şimdiye kadar kırılmış en zorlu ECC şeması asıl durum için 112-bit anahtar ve iki bileşenli durum için 109 bitlik bir anahtara sahipti. Asıl durum için bu, Temmuz 2009'da 200'ün üzerinde PlayStation 3 oyun konsolunu kullanarak kırıldı ve sürekli olarak çalıştırılmasına rağmen ancak 3,5 ay içinde tamamlanabildi. İki bileşenli durumda ise, Nisan 2004'te 17 ayda 2600 bilgisayar kullanılarak kırıldı.
İzdüşümsel Koordinatlar
Toplama kuralının yakından incelendiğinde, iki noktayı toplamak için 









Hızlı İndirgeme (NIST Eğrileri)
İndirgeme modu p (toplama ve çarpma için gerekli), eğer p asalı sözde-Mersenne asalı ise (yani 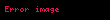


p sözde-Mersenne olmak üzere, 
Bernstein ve Lange'e göre, NIST FIPS 186-2'teki verimlilikle ilgili kararlar "sub-optimal". Diğer eğriler daha güvenli ve yeterince hızlı çalışıyor.
Uygulamalar
Eliptik eğriler şifreleme, dijital imzalar, sözde rastgele üreteçler ve diğer görevlere uyarlanabilir. Ayrıca, Lenstra eliptik eğri faktörizasyonu gibi kriptografi uygulamalarına sahip olan birkaç çarpanlarına ayırma algoritmasında da kullanılırlar.
NIST, 1999 yılında 15 eliptik eğri önerdi. Özellikle, FIPS 186-3'ün önerilen 10 sonlu cisim vardır:
- 92, 224, 256, 384 ve 521 bit boyutlarında asal p için
asıl 5 cisim. Asıl cisimlerin her biri için, bir eliptik eğri tavsiye edilir.
- 163, 233, 283, 409, and 571 bitlik m değeri için
İki bileşenli 5 cisim. İki bileşenli her biri için bir eliptik eğri ve bir Koblitz eğrisi seçildi.
NIST tavsiyesi, toplam 5 asıl eğri ve 10 iki bileşenli eğri içerir. Bu eğriler optimum güvenlik ve uygulama verimliliği için seçildi.
2013 yılında New York Times Çift Eliptik Eğri Deterministik Rastgele Bit Üretiminin(veya Dual_EC_DRBG), algoritmaya ve önerilen eliptik egriye kasti bir zayıflık ekleyen NSA'in etkisinden dolayı NIST ulusal standartlari icerisine dahil edildigini yazdi. Eylül 2013'te RSA Security 5 Nisan 2018 tarihinde Wayback Machine sitesinde ., müşterilerinin Dual_EC_DRBG'ye dayalı herhangi bir yazılımı kullanmaya devam etmelerini tavsiye eden bir karar yayınladı. Dual_EC_DRBG'nin "bir NSA gizli operasyonu" olarak ortaya çıkmasının ardından, şifreleme uzmanları, NIST'in eliptik eğrilerinin güvenliğiyle ilgili endişelerini dile getirerek, eliptik olmayan eğri gruplarına dayanan şifrelemeye geri dönüşü önerdiler.
Güvenlik
Yan Kanal Saldırıları
Diğer çoğu ayrık logaritma sistemlerinin aksine (karesini almak ve çarpmak için aynı yöntemi kullanmanın mümkün olduğu), eliptik eğride toplama işlemi çift(P=Q) ve genel toplam (P ≠ Q) bakımından kullanılan koordinat sistemine göre kayda değer ölçüde farklılık gösterir. Bu nedenle, yan kanal saldırılarının etkisini, örneğin "fixed pattern window" yöntemini kullanarak, ortadan kaldırmak önem kazanır (bu metot işlem süresini uzatmaz). Alternatif olarak, eliptik eğriler ailesinin çift ve toplama işlemlerinin aynı anda yapılabildiği özel bir türü olan Edward eğrisi de kullanılabilir. ECC sistemleri için bir başka endişe, özellikle akıllı kartlarda çalışırken, arıza saldırıları tehlikesidir.
Arka Kapı
Kriptografik uzmanlar Ulusal Güvenlik Ajansı'nın kleptografik bir arka kapıyı en az bir eliptik eğri tabanlı sözde rastgele üretecinin içine yerleştirdikleri endişesini dile getirdiler. Eski NSA çalışanı Edward Snowden tarafından sızdırılmış olan notlar, NSA'nın Dual_EC_DRBG standardında bir arka kapı koyduğunu gösteriyor. Olası arka kapıya ait bir analiz, algoritmanın gizli anahtarına sahip olan bir rakibin şifreleme anahtarlarını yalnızca 32 bayt şifreli metinle elde edebileceği sonucuna varmıştır.
Güvenli bir şekilde uygulanması kolay olan ve arka kapı şansını en aza indirgemek için tamamen kamuya açık bir şekilde tasarlanan eğrileri kataloglamak için SafeCurves projesi başlatıldı.
Kuantum Bilgisayar Atağı
Shor algoritması, olası bir kuantum bilgisayardaki ayrık logaritmaları hesaplayarak eliptik eğri kriptografisini kırmak için kullanılabilir. 256 bitlik bir modül (128 bit güvenlik seviyesi) ile bir eğriyi kırmak için yapılan son kuantum kaynak tahminleri 2330 qubit ve 126 milyar Toffoli kapısıdır. Buna karşılık, Shor algoritmasının RSA algoritmasını kırmak için kullandığı algoritma, 2048 bit RSA anahtarı için 4098 qubit ve 5.2 trilyon Toffoli geçit kapısı gerektirmektedir, bu da Eliptik Eğri Kriptolojisinin kuantum bilgisayarlar için RSA'dan daha kolay bir hedef olduğunu göstermektedir. Tüm bu rakamlar, şimdiye kadar yapılmış olan herhangi bir kuantum bilgisayarı fazlasıyla aşıyor ve bu derece güçlü bilgisayarların oluşturulmasının on yıl veya daha uzun bir süre olacağı tahmin ediliyor.
Ağustos 2015'te NSA, "uzak olmayan bir gelecekte" kuantum ataklarına dirençli yeni bir şifre paketine geçiş yapmayı planladığını duyurdu.“Ne yazık ki, eliptik eğri kullanımının büyümesi, kuantum hesaplaması üzerine yapılan araştırmada devam eden ilerlemenin gerçeğine karşı çarparak, kriptografik stratejimizin yeniden değerlendirilmesini gerekli kılmıştır.”
Patentler
En az bir Eliptik Eğri Kriptolojisi şema planı (ECMQV) ve bazı uygulama teknikleri patentlenmiştir.
Alternatif Temsiller
- Hessian eğrileri
- Edwards eğrileri
- Twisted eğrileri
- Twisted Hessian eğrileri
- Twisted Edwards eğrileri
- Doubling-oriented Doche–Icart–Kohel eğrileri
- Tripling-oriented Doche–Icart–Kohel eğrileri
- Jacobian eğrileri
- Montgomery eğrileri
Sonuç
ECC'nin diğer açık anahtar kripto sistemlerine göre daha geç geliştirilmesine karşın güvenilirliğinin test edilebilmesi için yeterli süre geçmiş ve ECC birçol atağa karşın ayakta kalabilmeyi başarmıştır. ECC'nin diğer popüler açık anahtar sistemlerine karşı aynı güvenlik seviyesinde hem anahtar boyutu hem de hız olarak büyük avantajı olmasına rağmen ECC'yi ilgilendiren patentlerin hala geçerli olması sebebiyle dezavantajı da vardır. Yine de özellikle yüksek hızın çok önemli olduğu kablosuz sistemler gibi çeşitli sistemlerde gittikçe daha sık kullanılmaktadır. Motorola, IBM, Sun Microsystems, Microsoft ve Hewlett-Packard gibi büyük teknoloji firmaları da ECC kullanan kripto sistemlere yatırım yapmaktadır.
- ^ [1] 12 Nisan 2018 tarihinde Wayback Machine sitesinde ."Information Assurance" 15 Ağustos 2015 tarihinde Wayback Machine sitesinde .. www.nsa.gov.
- ^ Lauter, Kristen. (PDF). 22 Ocak 2015 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 22 Ocak 2015.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Eliptik Egri Kriptolojisi Elliptic Curve Cryptography sonlu cisimler uzerindeki eliptik egrilerin cebirsel topolojisine dayanan bir acik anahtar sifrelemesidir Eliptik Egri Kriptolojisi diger sifrelemeler gore daha kucuk anahtar boyuna ihtiyac duyar Eliptik egriye P Q noktalarinin eklenmesi Eliptik Egriler anahtar anlasmasi dijital imza sozde rastlantisal uretici ve daha bircok alanda kullanilabilirler Dolayli olarak anahtar anlasmasini simetrik bir sifreleme semasiyla birlestirerek sifreleme icin kullanilabilirler Lenstra Eliptik Egrileri gibi kriptografik uygulamalari olan eliptik egrileri temel alan carpanlarina ayirma algoritmalarinda da kullanilirlar MantikSon zamanlardaki acik anahtar sifreleme algoritmalari iki ya da daha fazla cok buyuk asal sayinin carpiminin carpanlarina ayirilmasindaki zorluguna dayanir Eliptik egri protokollerinde ise bu durum eliptik egrinin bilinen bir noktasina gore ayrik logaritmasini bulmanin imkansiz oldugunu varsaymaktadir Buna Eliptik Egrinin Ayrik Logaritma Problemi denir Eliptik egrinin guvenligi nokta carpiminin hesaplanma hizina ve baslangic noktasi ile carpim noktasina bakarak elde edilen noktanin hesaplanamamasina dayanmaktadir Eliptik egrinin boyutu ayni zamanda problemin zorlugunu da belirler Eliptik egri kriptografisinin en buyuk ozelligi depolama ve iletme gereksinimlerini azaltarak daha kucuk anahtar boyutuna sahip olmasidir Bir eliptik egri grubu buyuk modulerli ve buna bagli olarak buyuk anahtar boyutlu RSA tabanli sistem ile ayni guvenlik seviyesi sunabilir Ornegin Eliptik egri ile 256 bitlik anahtar boyutunda elde edecegimiz guvenligi RSA de 3072 bitlik anahtar ile saglanabilir Ulusal Standartlar ve Teknoloji Enstitusu Ingilizce National Institute of Standards and Technology kisaca NIST anahtar anlasmasi icin eliptik egri Diffie Hellman ECDH ve dijital imza icin Eliptik Egri Dijital Imza Algoritmasini ECDSA ABD Ulusal Guvenlik Ajansi Ingilizce National Security Agency kisaca NSA kriptolojisinde onerilen algoritmalar arasina eliptik egri kriptografisinin de girmesini onaylamistir NSA cok gizli bilgileri korumak icin 384 bitlik anahtar boyutunu tavsiye etmektedir Ancak Agustos 2015 te NSA ECC ye yonelik kuantum hesaplama saldirilariyla ilgili endiseler nedeniyle Suite B yi yeni bir sifre paketi ile degistirmeyi planladigini duyurdu RSA patenti 2000 de dolmus olsa da ECC teknolojisinin belirli acilarini kapsayan patentler olabilir Ancak ABD hukumeti eliptik egri dijital imza standartinin ve belirli kullanisli ECC tabanli anahtar degisim yapilarinin ECDH dahil bunlar ihlal edilmeden gerceklenemeyegi yonunde tartismalar mevcuttur RSA Laboratuvarlari ve Daniel J Bernstein da dahil TarihceKriptografide eliptik egrilerin kullanimi 1985 te Neal Koblitz ve Victor S Miller tarafindan bagimsiz olarak onerilmistir Eliptik egri kriptografi algoritmalari 2004 ten 2005 e kadar genis kullanim alanina girmistir TeoriMevcut kriptografik amaclar icin bir eliptik egri asagidaki denklemi saglayan noktalardan olusan gercek sayilardan ziyade uzerinde bir duzlem egrisidir Buradaki koordinatlar 2 ve 3 haric olmak uzere sabit bir sonlu cismin karakteristiginden veya biraz daha karmasik olan bir egri denkleminden secilir y2 x3 ax b displaystyle y 2 x 3 ax b Eliptik egrinin grup islemlerinin bulundugu kume abelyen bir kumedir Bu grubun yapisi cebirsel cesitliligin altinda yatan bolen grubundan gecmistir Div0 E Pic0 E E displaystyle Div 0 E rightarrow Pic 0 E simeq E Kriptografik SemaBircok ayrik logaritma tabanli protokol Zp displaystyle displaystyle mathbb Z p times grubunun eliptik egri ile degistirilmesi sayesinde eliptik egrilere uyarlanabilmistir Eliptik Egri Diffie Hellman ECDH anahtar anlasma semasinin Diffie Hellman semasina dayanmaktadir Eliptik Egri Entegre Sifreleme Semasi Eliptik Egri Artirilmis Sifreleme semasi olarak da bilinen veya sadece Eliptik Egri Sifreleme Semasi Eliptik Egri Dijital Imza Algoritmasi ECDSA Dijital Imza Algoritmasina dayanmaktadir Edwards egrisi Dijital Imza Algoritmasi EdDSA Schnorr imzasina dayanir ve egrilerini kullanir ECMQV anahtar anlasma semasi MQV anahtar anlasma semasina dayanmaktadir Ulusal Guvenlik Ajansi NSA 2005 te RSA konferansinda dijital imza uretimi ve anahtar anlasmasi icin Eliptik Egri Kriptolojisini ozel olarak kullanan Suite B yi duyurdu SuitB hem gizli hem de gizli olmayan ulusal guvenlik sistemlerini ve bilgilerini korumayi amaclamistir Yakin zamanda Weil ve Tate cifti gibi cesitli eliptik egri gruplarinda cift yonlu eslemelere dayali cok sayida kriptografik ilke tanitilmistir Bu ilkelere dayali semalar esleme tabanli imzalar isaretleme anahtar anlasmasi ve proxy sifrelemenin yani sira verimli kimlik tabanli sifreleme de saglar YurutmeAlan Parametreler Elipktik egri kriptolojisini kullanmak icin tum taraflar eliptik egriyi tanimlayan alan parametreler adi verilen elemanlar uzerinde anlasmalidir Cisim asil durumda p displaystyle p sayisiyla iki bilesenli durumda ise m displaystyle m ve f displaystyle f cifti ile tanimlanir Eliptik egriler esitligi saglamak icin sabit a displaystyle a ve b displaystyle b sayilari ile tanimlanirlar Son olarak devirli alt grup ureteci olan G ile tanimlanir Kriptografik uygulamalar icin G nin mertebesi nG displaystyle nG infty denklemini saglayacak en kucuk n displaystyle n degeri genellikle asal bir sayidir n displaystyle n E Fp displaystyle displaystyle E mathbb F p alt grubunun buyuklugu oldugundan Lagrange Teoreminden 8 Nisan 2018 tarihinde Wayback Machine sitesinde h 1n E Fp displaystyle displaystyle h frac 1 n E mathbb F p sayisi tam sayidir Kriptografik uygulamalarda kofaktor olarak adlandirilan bu h displaystyle h sayisi kucuk h 4 displaystyle h leq 4 bir tam sayi olarak tercihen h 1 displaystyle h 1 secilmelidir Ozetle asil durum parametreleri p a b G n h displaystyle p a b G n h ve ikili durum parametleri ise m f a b G n h displaystyle m f a b G n h seklindedir Eger alan parametrelerinin guvenilir bir uretici tarafindan olusturuldugunun garantisi yoksa bu parametreler kullanilmadan once mutlaka dogrulanmalidir Alan parametrelerinin olusturulmasi genellikle her katilimci tarafindan yapilmaz cunku bu durum zaman alan ve uygulamasi zor olan bir egri uzerindeki noktalarin sayisini hesaplamayi gerektirir Sonuc olarak bazi yetkili standardizasyon kuruluslari yaygin cisim boyutlari icin eliptik egri parametreleri yayinlamislardir Bu gibi alan parametreleri genellikle standart egriler veya adlandirilmis egriler olarak bilinir Adlandirilmis bir egri bir ad veya standart belgelerde tanimlanan benzersiz nesne tanimlayicisi tarafindan referans edilebilir NIST Devlet Islerinde Onerilen Eliptik Egriler 20 Subat 2018 tarihinde Wayback Machine sitesinde SEC 2 Onerilen Eliptik Egri Alan Parametreleri 5 Nisan 2018 tarihinde Wayback Machine sitesinde ECC Brainpool RFC 5639 SECG test vektorleri de mevcuttur NIST bircok SECG egrisini onayladi dolayisiyla NIST ve SECG tarafindan yayinlanan ozellikler arasinda ortusme vardir Eliptik Egri alan parametreleri deger veya ad ile belirtilebilir Eger biri yukarida anlatilanlara ragmen kendi alan parametrelerini olusturmak isterse altta yatan cismi secmeli ve uygun sayida noktaya sahip bir egri bulmak icin asagidaki stratejilerden birini kullanmalidir Rassal bir egri secin ve genel bir nokta sayma algoritmasi kullanin ornegin Schoof un algoritmasi veya Schoof Elkies Atkin algoritmasi Nokta sayisini hesaplamayi kolaylastiran bir egri ailesi belirleyin veya Karmasik carpim teknigini kullanarak puan sayisini belirleyin ve bu nokta sayisiyla bir egri olusturun Bazi egri siniflari zayiftir ve kesinlikle uzak durulmalidir Asal olmayan m ile tanimlanmis F2m displaystyle displaystyle mathbb F 2 m uzerindeki egri Weil descent atagina karsi zayiftir E Fq q displaystyle displaystyle displaystyle E mathbb F q q seklindeki egri egri uzerindeki noktalari Fq displaystyle mathbb F q uzerindeki noktalari esledigi bir ataga karsi zayifdir Anahtar Boyu ECDLP yi cozmek icin bilinen en hizli algoritmalarin O n displaystyle O sqrt n adima ihtiyac duymasi nedeniyle cismin boyutunun guvenlik parametresinin kabaca iki kati olmasi gerekir Ornegin 128 bitlik bir guvenlik icin q 2256 displaystyle q approx 2 256 olacak sekilde Fq displaystyle displaystyle mathbb F q uzerinde bir egri secilmesi gerekir Bu 3072 bit acik anahtar ve 256 bit gizli anahtar gerektiren sonlu cisim kriptografisi Orn DSA ile ve yalnizca ozel anahtarin buyuk olmasi gereken 3072 bitlik carpanlarina ayirma kriptografisiyle Orn RSA karsilastirilabilir Ancak islemcinin gucu sinirli oldugunda sifrelemenin daha verimli olabilmesi icin anahtar boyutu kucultulebilir Simdiye kadar kirilmis en zorlu ECC semasi asil durum icin 112 bit anahtar ve iki bilesenli durum icin 109 bitlik bir anahtara sahipti Asil durum icin bu Temmuz 2009 da 200 un uzerinde PlayStation 3 oyun konsolunu kullanarak kirildi ve surekli olarak calistirilmasina ragmen ancak 3 5 ay icinde tamamlanabildi Iki bilesenli durumda ise Nisan 2004 te 17 ayda 2600 bilgisayar kullanilarak kirildi Izdusumsel Koordinatlar Toplama kuralinin yakindan incelendiginde iki noktayi toplamak icin Fq displaystyle displaystyle mathbb F q da sadece toplamin ve carpmanin degil ayni zamanda tersinin de gerekli oldugunu gostermektedir Ters islem verilen x Fq displaystyle x in displaystyle mathbb F q icin xy 1 displaystyle xy 1 olacak sekilde bir y Fq displaystyle y in displaystyle mathbb F q bulmak carpma isleminden birkac kat daha yavastir Neyse ki bir egri uzerindeki noktalar iki noktayi toplamak icin ters islem gerektirmeyen farkli koordinat sistemlerinde temsil edilebilir Bu tur birkac sistem onerisi Izdusumsel sistemde her nokta asagidaki iliskiyi kullanarak uc koordinat X Y Z displaystyle X Y Z ile temsil edilir x XZ y YZ displaystyle displaystyle x frac X Z displaystyle y frac Y Z Jacobian sisteminde bir nokta uc koordinat ile de temsil edilir X Y Z ama farkli bir iliski kullanilir x XZ2 y YZ3 displaystyle displaystyle x frac X Z 2 displaystyle y frac Y Z 3 Lopez Dahab sisteminde ise iliski x XZ y YZ2 displaystyle displaystyle x frac X Z displaystyle y frac Y Z 2 degistirilmis Jacobian sisteminde ayni iliskiler kullanilir ancak hesaplamalar icin dort koordinat X Y Z aZ4 displaystyle displaystyle X Y Z aZ 4 saklanir ve kullanilir ve Chudnovsky Jacobian sisteminde bes koordinat X Y Z Z2 Z3 displaystyle X Y Z Z 2 Z 3 kullanilir Burada farkli isimlendirme gelenekleri olabilecegine dikkat ediniz ornegin IEEE P1363 2000 standarti izdusumsel koordinatlar isimlendirmesini Jacobian koordinatlari icin kullanmaktadir Eger karisik koordinatlar kullanilirsa ek bir hizlandirma elde edilebilir Hizli Indirgeme NIST Egrileri Indirgeme modu p toplama ve carpma icin gerekli eger p asali sozde Mersenne asali ise yani p 2d displaystyle p approx 2 d ornegin p 2521 1 displaystyle p 2 521 1 veya p 2256 232 29 28 27 26 24 1 displaystyle p 2 256 2 32 2 9 2 8 2 7 2 6 2 4 1 cok daha hizli calistirilabilir Barrett indirgemesine gore 10 un katlari olcekli bir hizlanma elde edilebilir Buradaki hizlanma teorik olana gore daha kullanislidir ve sayilarin moduli si 2 nin uslerine yakin sayilara kiyasla ikilik tabanda bit duzeyinde operasyonlarla bilgisayarlarda daha verimli islenebilir p sozde Mersenne olmak uzere Fp displaystyle displaystyle mathbb F p uzerinde egriler NIST tarafindan onerilmektedir NIST egrilerinin bir diger avantaji ise Jacobian koordinatlarinda toplamayi gelistiren a 3 kullaniyor olmasidir Bernstein ve Lange e gore NIST FIPS 186 2 teki verimlilikle ilgili kararlar sub optimal Diger egriler daha guvenli ve yeterince hizli calisiyor UygulamalarEliptik egriler sifreleme dijital imzalar sozde rastgele uretecler ve diger gorevlere uyarlanabilir Ayrica Lenstra eliptik egri faktorizasyonu gibi kriptografi uygulamalarina sahip olan birkac carpanlarina ayirma algoritmasinda da kullanilirlar NIST 1999 yilinda 15 eliptik egri onerdi Ozellikle FIPS 186 3 un onerilen 10 sonlu cisim vardir 92 224 256 384 ve 521 bit boyutlarinda asal p icin Fp displaystyle displaystyle mathbb F p asil 5 cisim Asil cisimlerin her biri icin bir eliptik egri tavsiye edilir 163 233 283 409 and 571 bitlik m degeri icin F2m displaystyle displaystyle mathbb F 2 m Iki bilesenli 5 cisim Iki bilesenli her biri icin bir eliptik egri ve bir Koblitz egrisi secildi NIST tavsiyesi toplam 5 asil egri ve 10 iki bilesenli egri icerir Bu egriler optimum guvenlik ve uygulama verimliligi icin secildi 2013 yilinda New York Times Cift Eliptik Egri Deterministik Rastgele Bit Uretiminin veya Dual EC DRBG algoritmaya ve onerilen eliptik egriye kasti bir zayiflik ekleyen NSA in etkisinden dolayi NIST ulusal standartlari icerisine dahil edildigini yazdi Eylul 2013 te RSA Security 5 Nisan 2018 tarihinde Wayback Machine sitesinde musterilerinin Dual EC DRBG ye dayali herhangi bir yazilimi kullanmaya devam etmelerini tavsiye eden bir karar yayinladi Dual EC DRBG nin bir NSA gizli operasyonu olarak ortaya cikmasinin ardindan sifreleme uzmanlari NIST in eliptik egrilerinin guvenligiyle ilgili endiselerini dile getirerek eliptik olmayan egri gruplarina dayanan sifrelemeye geri donusu onerdiler GuvenlikYan Kanal Saldirilari Diger cogu ayrik logaritma sistemlerinin aksine karesini almak ve carpmak icin ayni yontemi kullanmanin mumkun oldugu eliptik egride toplama islemi cift P Q ve genel toplam P Q bakimindan kullanilan koordinat sistemine gore kayda deger olcude farklilik gosterir Bu nedenle yan kanal saldirilarinin etkisini ornegin fixed pattern window yontemini kullanarak ortadan kaldirmak onem kazanir bu metot islem suresini uzatmaz Alternatif olarak eliptik egriler ailesinin cift ve toplama islemlerinin ayni anda yapilabildigi ozel bir turu olan Edward egrisi de kullanilabilir ECC sistemleri icin bir baska endise ozellikle akilli kartlarda calisirken ariza saldirilari tehlikesidir Arka Kapi Kriptografik uzmanlar Ulusal Guvenlik Ajansi nin kleptografik bir arka kapiyi en az bir eliptik egri tabanli sozde rastgele uretecinin icine yerlestirdikleri endisesini dile getirdiler Eski NSA calisani Edward Snowden tarafindan sizdirilmis olan notlar NSA nin Dual EC DRBG standardinda bir arka kapi koydugunu gosteriyor Olasi arka kapiya ait bir analiz algoritmanin gizli anahtarina sahip olan bir rakibin sifreleme anahtarlarini yalnizca 32 bayt sifreli metinle elde edebilecegi sonucuna varmistir Guvenli bir sekilde uygulanmasi kolay olan ve arka kapi sansini en aza indirgemek icin tamamen kamuya acik bir sekilde tasarlanan egrileri kataloglamak icin SafeCurves projesi baslatildi Kuantum Bilgisayar Atagi Shor algoritmasi olasi bir kuantum bilgisayardaki ayrik logaritmalari hesaplayarak eliptik egri kriptografisini kirmak icin kullanilabilir 256 bitlik bir modul 128 bit guvenlik seviyesi ile bir egriyi kirmak icin yapilan son kuantum kaynak tahminleri 2330 qubit ve 126 milyar Toffoli kapisidir Buna karsilik Shor algoritmasinin RSA algoritmasini kirmak icin kullandigi algoritma 2048 bit RSA anahtari icin 4098 qubit ve 5 2 trilyon Toffoli gecit kapisi gerektirmektedir bu da Eliptik Egri Kriptolojisinin kuantum bilgisayarlar icin RSA dan daha kolay bir hedef oldugunu gostermektedir Tum bu rakamlar simdiye kadar yapilmis olan herhangi bir kuantum bilgisayari fazlasiyla asiyor ve bu derece guclu bilgisayarlarin olusturulmasinin on yil veya daha uzun bir sure olacagi tahmin ediliyor Agustos 2015 te NSA uzak olmayan bir gelecekte kuantum ataklarina direncli yeni bir sifre paketine gecis yapmayi planladigini duyurdu Ne yazik ki eliptik egri kullaniminin buyumesi kuantum hesaplamasi uzerine yapilan arastirmada devam eden ilerlemenin gercegine karsi carparak kriptografik stratejimizin yeniden degerlendirilmesini gerekli kilmistir PatentlerEn az bir Eliptik Egri Kriptolojisi sema plani ECMQV ve bazi uygulama teknikleri patentlenmistir Alternatif TemsillerHessian egrileri Edwards egrileri Twisted egrileri Twisted Hessian egrileri Twisted Edwards egrileri Doubling oriented Doche Icart Kohel egrileri Tripling oriented Doche Icart Kohel egrileri Jacobian egrileri Montgomery egrileriSonucECC nin diger acik anahtar kripto sistemlerine gore daha gec gelistirilmesine karsin guvenilirliginin test edilebilmesi icin yeterli sure gecmis ve ECC bircol ataga karsin ayakta kalabilmeyi basarmistir ECC nin diger populer acik anahtar sistemlerine karsi ayni guvenlik seviyesinde hem anahtar boyutu hem de hiz olarak buyuk avantaji olmasina ragmen ECC yi ilgilendiren patentlerin hala gecerli olmasi sebebiyle dezavantaji da vardir Yine de ozellikle yuksek hizin cok onemli oldugu kablosuz sistemler gibi cesitli sistemlerde gittikce daha sik kullanilmaktadir Motorola IBM Sun Microsystems Microsoft ve Hewlett Packard gibi buyuk teknoloji firmalari da ECC kullanan kripto sistemlere yatirim yapmaktadir 1 12 Nisan 2018 tarihinde Wayback Machine sitesinde Information Assurance 15 Agustos 2015 tarihinde Wayback Machine sitesinde www nsa gov Lauter Kristen PDF 22 Ocak 2015 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 22 Ocak 2015
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans


