Vektör uzayı veya Yöney uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesnelerin (vektörlerin) uzayına verilen isimdir. Daha resmî bir tanımla, bir vektör uzayı, iki elemanı arasında vektör toplamasının ve skaler denilen sayılarla çarpımın tanımlı olduğu ve bunların bazı aksiyomları sağladığı kümedir. Skalerler, rasyonal veya reel sayılar kümesinden gelebilir, ama herhangi bir cisim üzerinden bir vektör uzayı oluşturmak mümkündür. Vektör uzayları, skalerlerin geldiği cisime göre reel vektör uzayı, kompleks vektör uzayı veya genel bir cisim üzerinden K vektör uzayı şeklinde adlandırılır.
Vektör uzayları, geometride ve fizikte kullanılan ve bir yönü ve büyüklüğü olan Öklid Vektörlerininin bir genelleştirmesidir. Vektör uzayları Lineer Cebrin temelini oluşturur ve sadece yönü ve büyüklüğü olan vektörleri tasvir etmekle kalmayıp lineer denklem sistemlerinin çözümü, fonksiyon analizi, kuantum fiziği, bilgisayar bilimi, rölativite ve iktisat gibi bir sürü alanda kullanımlara sahiptir.
Bir vektör uzayı, boyut denilen bir nicelik ile karekterize edilir. Boyutu ve tanımlandığı cismi aynı olan iki vektör uzayı birbirine izomorftur. Boyutu bir doğal sayı olan vektör uzaylarına sonlu boyutlu denir. Sonsuz boyutlu vektör uzaylarının boyutu ise bir kardinaldir. Sonsuz boyutlu vektör uzayları özellikle fonksiyonal analizde çok kullanılır.
Toplama ve skaler çarpımı dışında yapılara sahip olan genişletilmiş vektör uzayları da mevcuttur. İki vektör arasında çarpımın tanımlı olduğu vektör uzaylarına cebir denir.
Tanımlar ve Özellikler
K bir cisim olsun. Boş olmayan bir V kümesi, bir K vektör uzayı ise V üzerinde iki işlemin tanımlı olması gerekir:
- Vektör toplaması işlemi, V kümesinin keyfî iki elemanı olan u ve v vektörlerini alır ve sonuç olarak yine V kümesinin bir elemanı olan u + v'yi verir.
- Skaler çarpımı işlemi, K cisminden herhangi bir λ elemanını, V kümesinden de herhangi bir v elemanını alır ve karşılığında yine V kümesinin bir elemanı olan λv elemanını verir.
K'nın elemanlarına skaler, V'nin elemanlarına ise vektör denir. Bu iki işlem, aynı zamanda birtakım aksiyomları sağlar:
| Aksiyom | İfadesi |
|---|---|
| Toplamanın Birleşme Özelliği | u + (v + w) = (u + v) + w |
| Toplamanın Değişme Özelliği | u + v = v + u |
| Toplamada Sıfır Elemanının Varlığı | V kümesinde bir adet 0 isimli eleman bulunur ve her eleman için 0 + v = v + 0 = v özelliği sağlanır |
| Toplamsal Varlığı | V kümesindeki her v elemanı için bir -v elemanı bulunur ve bu eleman için v + (-v) = (-v) + v = 0 özelliği sağlanır |
| Skaler Çarpımının Cisim Çarpımıyla Uyumu | λ(μv) = (λμ)v |
| Skaler Çarpımının Birim Elemanı | 1v = v |
| Skaler Çarpımının Vektör Toplaması üzerinde Dağılma Özelliği | λ(u + v) = λu + λv |
| Skaler Çarpımının Skaler Toplaması üzerinde Dağılma Özelliği | (λ + μ)v = λv + μv |
Eğer skalerler reel sayılardan geliyorsa buna bir reel vektör uzayı, kompleks sayılardan geliyorsa da kompleks vektör uzayı denir. Ancak skalerler herhangi bir cisimden gelmesi mümkündür. Bu aksiyomlar doğrudan aşağıdaki özelliklere sebep olur:
ise ya
ya da
Terimler
- Altuzay Eğer U, V'nin bir altkümesi ise ve U kendi içinde bir vektör uzayı ise U'ya V'nin bir altuzayı denir.
- Lineer Kombinasyon Birtakım
vektörleri ve
skalerleri için
toplamına, o vektörlerin bir lineer kombinasyonu denir.
- Lineer Bağımsızlık Eğer verilen birtakım
vektörleri arasından birisi, diğerlerinin lineer kombinasyonu olarak yazılabiliyorsa bu vektörlere lineer bağımlı denir. Eğer bu vektörlerin hiçbiri diğerleri cinsinden yazılamıyorsa bu vektörler kümesi lineer bağımsızdır. Lineer bağımsız vektörler lineer cebirde önemlidir, çünkü eğer bi vektörü birtakım lineer bağımsız vektörün lineer kombinasyonu olarak göstermek mümkünse, aynı zamanda bu gösterim biriciktir.
- Span
vektörlerinin span'i, bu vektörleri içeren tüm altuzayların kesişimine denir. Buna eşdeğer bir tanım ise, bu vektörlerin mümkün olan tüm lineer kombinasyonlarından oluşan vektör uzayına da
'nin span'i demektir. Bu,
şeklinde gösterilir.
- Üretici küme
vektörlerinin span'i, tüm vektör uzayı V'yi kapsıyorsa bu vektörler, V'nin üreticileridir.
- Baz
kümesi, hem lineer bağımsız, hem de bir üretici küme ise
'ye bir baz denir. Bir vektör uzayının bazı biricik değildir, ancak V için akla gelebilecek tüm baz kümelerin eleman sayısı eşittir.
- Boyut V bir vektör uzayı olsun. V için bulunabilen tüm baz kümelerinin eleman sayısı eşit olduğundan, bu sayıya vektör uzayının boyutu ismi verilir. Bir vektör uzayında birbirinden lineer bağımsız en fazla o vektör uzayının boyutu kadar vektör bulunabilir. Aynı şekilde, bir vektör uzayını üreten tüm kümelerin eleman sayısı en az o vektör uzayının boyutu kadardır. Dolayısıyla hem lineer bağımsız hem de üretici bir kümede tamı tamına boyut kadar vektör bulunur.
Örnekler
Bir düzlemde bulunan oklar
Kartezyen düzlemde bulunan oklar üzerinden bir reel vektör uzayı tanımlamak mümkündür. Vektör toplamı, iki oku uç uca yerleştirip, birinin başından diğerinin ucuna çizilmesiyle bulunur. Skaler çarpımı ise, bir vektörü alıp uzunluğunu skaler kadar gererek hesaplanır. Negatif bir sayıyla çarpım ise vektörün yön değiştirip uzunluğunun sayının mutlak değeriyle çarpıması vasıtasıyla tanımlanır. Bu tanımlar altında oklar bir reel vektör uzayı teşkil eder.
Bu vektör uzayının boyutu 2'dir. Aynı doğrultuda bulunmayan herhangi iki vektör ise bir baz teşkil eder. Bu uzayın alt uzayları ise; uzayın kendisi, orijinden geçen doğrular ve sadece orijin noktasından oluşan sıfır uzayıdır.
Sayı çiftleri
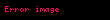
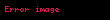
şeklinde, skaler çarpımı ise

şeklinde tanımlanabilir. Bu vektör uzayı yine 2 boyutludur. Burada lineer bağımlı iki vektör örneği vermek gerekirse 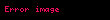


Sayı n-lileri
Daha genel olarak, herhangi bir 


Şimdi V bir n boyutlu 



wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Vektor uzayi veya Yoney uzayi matematikte olceklenebilir ve eklenebilir bir nesnelerin vektorlerin uzayina verilen isimdir Daha resmi bir tanimla bir vektor uzayi iki elemani arasinda vektor toplamasinin ve skaler denilen sayilarla carpimin tanimli oldugu ve bunlarin bazi aksiyomlari sagladigi kumedir Skalerler rasyonal veya reel sayilar kumesinden gelebilir ama herhangi bir cisim uzerinden bir vektor uzayi olusturmak mumkundur Vektor uzaylari skalerlerin geldigi cisime gore reel vektor uzayi kompleks vektor uzayi veya genel bir cisim uzerinden K vektor uzayi seklinde adlandirilir Vektor uzaylari geometride ve fizikte kullanilan ve bir yonu ve buyuklugu olan Oklid Vektorlerininin bir genellestirmesidir Vektor uzaylari Lineer Cebrin temelini olusturur ve sadece yonu ve buyuklugu olan vektorleri tasvir etmekle kalmayip lineer denklem sistemlerinin cozumu fonksiyon analizi kuantum fizigi bilgisayar bilimi rolativite ve iktisat gibi bir suru alanda kullanimlara sahiptir Bir vektor uzayi boyut denilen bir nicelik ile karekterize edilir Boyutu ve tanimlandigi cismi ayni olan iki vektor uzayi birbirine izomorftur Boyutu bir dogal sayi olan vektor uzaylarina sonlu boyutlu denir Sonsuz boyutlu vektor uzaylarinin boyutu ise bir kardinaldir Sonsuz boyutlu vektor uzaylari ozellikle fonksiyonal analizde cok kullanilir Toplama ve skaler carpimi disinda yapilara sahip olan genisletilmis vektor uzaylari da mevcuttur Iki vektor arasinda carpimin tanimli oldugu vektor uzaylarina cebir denir Tanimlar ve OzelliklerK bir cisim olsun Bos olmayan bir V kumesi bir K vektor uzayi ise V uzerinde iki islemin tanimli olmasi gerekir Vektor toplamasi islemi V kumesinin keyfi iki elemani olan u ve v vektorlerini alir ve sonuc olarak yine V kumesinin bir elemani olan u v yi verir Skaler carpimi islemi K cisminden herhangi bir l elemanini V kumesinden de herhangi bir v elemanini alir ve karsiliginda yine V kumesinin bir elemani olan lv elemanini verir K nin elemanlarina skaler V nin elemanlarina ise vektor denir Bu iki islem ayni zamanda birtakim aksiyomlari saglar Aksiyom IfadesiToplamanin Birlesme Ozelligi u v w u v wToplamanin Degisme Ozelligi u v v uToplamada Sifir Elemaninin Varligi V kumesinde bir adet 0 isimli eleman bulunur ve her eleman icin 0 v v 0 v ozelligi saglanirToplamsal Varligi V kumesindeki her v elemani icin bir v elemani bulunur ve bu eleman icin v v v v 0 ozelligi saglanirSkaler Carpiminin Cisim Carpimiyla Uyumu l mv lm vSkaler Carpiminin Birim Elemani 1v vSkaler Carpiminin Vektor Toplamasi uzerinde Dagilma Ozelligi l u v lu lvSkaler Carpiminin Skaler Toplamasi uzerinde Dagilma Ozelligi l m v lv mv Eger skalerler reel sayilardan geliyorsa buna bir reel vektor uzayi kompleks sayilardan geliyorsa da kompleks vektor uzayi denir Ancak skalerler herhangi bir cisimden gelmesi mumkundur Bu aksiyomlar dogrudan asagidaki ozelliklere sebep olur 0v 0 displaystyle 0 mathbf v mathbf 0 l0 0 displaystyle lambda mathbf 0 mathbf 0 1 v v displaystyle 1 mathbf v mathbf v lv 0 displaystyle lambda mathbf v mathbf 0 ise ya l 0 displaystyle lambda 0 ya da v 0 displaystyle mathbf v mathbf 0 TerimlerAltuzay Eger U V nin bir altkumesi ise ve U kendi icinde bir vektor uzayi ise U ya V nin bir altuzayi denir Lineer Kombinasyon Birtakim v1 v2 v3 displaystyle mathbf v 1 mathbf v 2 mathbf v 3 vektorleri ve l1 l2 l3 displaystyle mathbf lambda 1 mathbf lambda 2 mathbf lambda 3 skalerleri icin l1v1 l2v2 l3v3 displaystyle lambda 1 mathbf v 1 lambda 2 mathbf v 2 lambda 3 mathbf v 3 toplamina o vektorlerin bir lineer kombinasyonu denir Lineer Bagimsizlik Eger verilen birtakim v1 v2 v3 displaystyle mathbf v 1 mathbf v 2 mathbf v 3 vektorleri arasindan birisi digerlerinin lineer kombinasyonu olarak yazilabiliyorsa bu vektorlere lineer bagimli denir Eger bu vektorlerin hicbiri digerleri cinsinden yazilamiyorsa bu vektorler kumesi lineer bagimsizdir Lineer bagimsiz vektorler lineer cebirde onemlidir cunku eger bi vektoru birtakim lineer bagimsiz vektorun lineer kombinasyonu olarak gostermek mumkunse ayni zamanda bu gosterim biriciktir Span v1 v2 v3 displaystyle mathbf v 1 mathbf v 2 mathbf v 3 vektorlerinin span i bu vektorleri iceren tum altuzaylarin kesisimine denir Buna esdeger bir tanim ise bu vektorlerin mumkun olan tum lineer kombinasyonlarindan olusan vektor uzayina da v1 v2 v3 displaystyle mathbf v 1 mathbf v 2 mathbf v 3 nin span i demektir Bu v1 v2 v3 displaystyle langle mathbf v 1 mathbf v 2 mathbf v 3 rangle seklinde gosterilir Uretici kume v1 v2 v3 displaystyle mathbf v 1 mathbf v 2 mathbf v 3 vektorlerinin span i tum vektor uzayi V yi kapsiyorsa bu vektorler V nin ureticileridir Baz B v1 v2 v3 displaystyle mathcal B mathbf v 1 mathbf v 2 mathbf v 3 kumesi hem lineer bagimsiz hem de bir uretici kume ise B displaystyle mathcal B ye bir baz denir Bir vektor uzayinin bazi biricik degildir ancak V icin akla gelebilecek tum baz kumelerin eleman sayisi esittir Boyut V bir vektor uzayi olsun V icin bulunabilen tum baz kumelerinin eleman sayisi esit oldugundan bu sayiya vektor uzayinin boyutu ismi verilir Bir vektor uzayinda birbirinden lineer bagimsiz en fazla o vektor uzayinin boyutu kadar vektor bulunabilir Ayni sekilde bir vektor uzayini ureten tum kumelerin eleman sayisi en az o vektor uzayinin boyutu kadardir Dolayisiyla hem lineer bagimsiz hem de uretici bir kumede tami tamina boyut kadar vektor bulunur OrneklerBir duzlemde bulunan oklar Vektor Toplamasi v w siyah toplami v mavi ve w kirmizi Skaler Carpimi v ve 2w carpimlari Kartezyen duzlemde bulunan oklar uzerinden bir reel vektor uzayi tanimlamak mumkundur Vektor toplami iki oku uc uca yerlestirip birinin basindan digerinin ucuna cizilmesiyle bulunur Skaler carpimi ise bir vektoru alip uzunlugunu skaler kadar gererek hesaplanir Negatif bir sayiyla carpim ise vektorun yon degistirip uzunlugunun sayinin mutlak degeriyle carpimasi vasitasiyla tanimlanir Bu tanimlar altinda oklar bir reel vektor uzayi teskil eder Bu vektor uzayinin boyutu 2 dir Ayni dogrultuda bulunmayan herhangi iki vektor ise bir baz teskil eder Bu uzayin alt uzaylari ise uzayin kendisi orijinden gecen dogrular ve sadece orijin noktasindan olusan sifir uzayidir Sayi ciftleri R2 displaystyle mathbb R 2 den alinan sayi ciftleri uzerinde bir vektor uzayi yapisi tanimlamak mumkundur Iki ciftin toplami x1 y1 x2 y2 x1 x2 y1 y2 displaystyle x 1 y 1 x 2 y 2 x 1 x 2 y 1 y 2 seklinde skaler carpimi ise l x y lx ly displaystyle lambda x y lambda x lambda y seklinde tanimlanabilir Bu vektor uzayi yine 2 boyutludur Burada lineer bagimli iki vektor ornegi vermek gerekirse 1 2 displaystyle 1 2 ve 2 4 displaystyle 2 4 verilebilir Baz olarak da standart baz olarak adlandirilan B 1 0 0 1 displaystyle mathcal B 1 0 0 1 kumesi ornek verilebilir Sayi n lileri Daha genel olarak herhangi bir K displaystyle mathbb K cismi icin Kn displaystyle mathbb K n de bulunan tum n li sayi dizileri de yukarida tanimlanan sekilde n boyutlu bir K displaystyle mathbb K vektor uzayi teskil eder Simdi V bir n boyutlu K displaystyle mathbb K vektor uzayi olsun Eger B b1 b2 b3 bn displaystyle mathcal B b 1 b 2 b 3 b n bir baz kumesi ise V deki her elemani v l1b1 l2b2 lnbn displaystyle mathbf v lambda 1 b 1 lambda 2 b 2 lambda n b n seklinde yazmak mumkundur ve en onemlisi ise bunu saglayan l1 l2 l3 displaystyle mathbf lambda 1 mathbf lambda 2 mathbf lambda 3 katsayilari biriciktir Dolayisiyla V deki herhangi bir vektor l1 l2 l3 ln displaystyle mathbf lambda 1 mathbf lambda 2 mathbf lambda 3 lambda n seklinde temsil edilebilir Yani Kn displaystyle mathbb K n uzaylari akla gelebilecek tum soyut vektor uzaylarini somut bir sekilde temsil etmenin bir yoludur
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans