İntegral veya tümlev, toplama işleminin sürekli bir aralıkta alınan hâlidir. Türev ile birlikte kalkülüsün temelini oluşturan iki işlemden birisidir. Kalkülüsün temel teoremi sayesinde aynı zamanda türevin ters işlemidir.


Belirsiz integral, türev alma işleminin tersine tekabül eden işlemdir. Belirli integraller ise, belirsiz integraller kullanılarak hesaplanır. Kalkülüsün temel teoremi sayesinde bir fonksiyonun bir aralıkta belirli integralini hesaplamak için önce o fonksiyonun belirsiz integrali hesaplanır, sonra bu fonksiyonun iki uç noktasındaki değerleri çıkarılarak belirli integral elde edilir. Belirli integraller; alan, hacim ve bunların çok boyutlu karşılıklarını hesaplamak için gereklidir. Tek değişkenli fonksiyonlarda, belirli bir aralıkta alınan integral, o aralık boyunca fonksiyonun grafiğinin altında kalan alanı verir. İntegraller aynı zamanda diferansiyel denklemlerin çözümlerinde vazgeçilmezdir.
Tanım

İntegral, verilen bir f(x) fonksiyonunu türev kabul eden F(x) fonksiyonunun bulunması olarak yapılabilir. F(x) fonksiyonuna f(x) fonksiyonunun integrali veya ilkeli denir. İntegral, Latince toplam kelimesinin ("ſumma", "summa") baş harfi s'nin biraz evrim geçirmiş ∫ işareti ile gösterilir. Bu işaret Gottfried Wilhelm Leibniz tarafından tanımlanmıştır.
c bir sabiti gösterir ve integralin bir sabit farkı ile bulunabileceğine işaret eder.
Bir eksen takımında gösterilen f(x) göndermesinin altında kalan a < x < b aralığındaki alan, integral yardımıyla hesaplanabilir. Bu amaçla alan küçük dikdörtgenlere bölünerek, bunların alanı hesap edilip toplanır. Dikdörtgen sayısı arttıkça toplam eğri altındaki alan, alanın değerine yaklaşır ve integralin tam değeri bulunmuş olur. Bu toplama Riemann toplamı denir. İntegralin Riemann anlamındaki tanımı Riemann toplamındaki bölüntü sayısı olan n nin bir limit içerisinde sonsuza götürülmesiyle elde edilir.
Bu şekildeki integral belirli sınırlar arasında hesaplandığı için, belirli İntegral olarak isimlendirilir. Sınırlar göz önüne alınmadan hesaplanan integrale ise belirsiz integral denir. Bazı durumlarda f(x) göndermesinin integrali F(x) bulunamaz. Bu durumda belirli integral sayısal olarak hesaplanır.
Uzunluk, alan ve hacimlerin hesaplanmasında integral hesabın önemli yeri vardır. Birden fazla değişkene bağlı fonksiyonlarda integral kavramı genişletilebilir ve bu durumda katlı integraller ortaya çıkar.
Riemann'dan sonra soyut kümelerin de integrallenebilmesi amacıyla Lebesgue integrali geliştirilmiştir.
Köken


- Dilimize İngilizceden veya Fransızcadan geçmiş integral sözcüğü "bütüne ait olan" anlamına gelir ve İngilizceye intégral sözcüğünden; integralis (tüm yapmak, tümlemek) sözcüğünden; Latince integer (tüm, bütün, tam) sözcüğünden gelmiştir. Ayrıca integer sözcüğü tam sayı terimine karşılık olarak İngilizceye geçmiştir.
- Türkçede tümlev sözcüğü, Osmanlıca mütemmem ile tamamî sözcüklerinin ve İngilizcedeki integral sözcüğünün anlamını karşılamak için türetilmiştir.tümlev sözcüğü, "tümlenmiş şey" anlamına gelir. İsimden fiil yapan /-ev,-av/ yapım ekiyle kullanımda olan tümle[mek] fiilinden; isimden fiil yapan /-le[mek]/ yapım ekiyle muhtemelen Öz Türkçe *tüm (bknz. tümen) kökünden türetilmiştir.
- Osmanlıcada mütemmem sözcüğü kullanılmış (Arapçadaki *tm (tam) kökünden gelir) ancak Arapçada şu anda "olgun, evrimleşmiş, bütünleşmiş" anlamındaki tekâmül [1] 23 Şubat 2010 tarihinde Wayback Machine sitesinde arşivlendi. sözcüğü kullanılmaktadır (kâmil, mükemmel, küme ile aynı kökten: *kml).
İntegral alma yöntemleri
Değişken değiştirme
Değişken değiştirme, karmaşık problemleri basitleştirmek için kullanılan değişken değiştirme yöntemidir. Bu yöntemde ham (eski) değişken yerine yeni (daha basit) değişken kullanılır. Problem çözüldükten sonra yeni değişken ile elde edilen sonuç, eski değişkende yerine konur.
Basit örnek
Aşağıdaki 6.dereceden bir polinomu ilkel fonksiyon kullanarak çözmek neredeyse imkânsızdır. Bunun için değişken değiştirme yöntemini kullanalım:
Bu denklemde x3 = u değişken değişimini uygulanırsa aşağıdaki denklem elde edilir:
Böylece denklem ikinci dereceden denklem biçimine dönüştü. Bu denklemin kökleri;
Bu yeni değişkenin sonuçlarını, ham değişkende yerine koyalım:
Kısmi integral
Eğer integral 

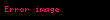
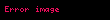
integralinde 
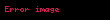
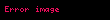
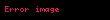

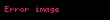
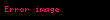
Sonuç olarak verilen integral 



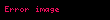
Örnek 1
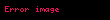
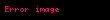

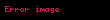
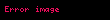
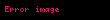
Burada belirsiz integralin keyfi sabiti 
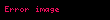
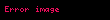

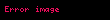
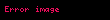
Örnek 2
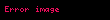


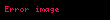
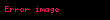
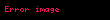

Bunu takiben,
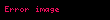
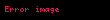
işlemleri yapılarak sonuç bulunur:
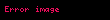
Ayrıca bakınız
- Temel göndermelerin integralleri için İntegral Tablosu
- Belirli integral
- Belirsiz integral
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Integral veya tumlev toplama isleminin surekli bir aralikta alinan halidir Turev ile birlikte kalkulusun temelini olusturan iki islemden birisidir Kalkulusun temel teoremi sayesinde ayni zamanda turevin ters islemidir f x in a dan b ye kadar olan integrali y f x fonksiyonunun a ile b arasindaki alanidir Alan hesabi olarak integralin uygulanmasi Belirsiz integral turev alma isleminin tersine tekabul eden islemdir Belirli integraller ise belirsiz integraller kullanilarak hesaplanir Kalkulusun temel teoremi sayesinde bir fonksiyonun bir aralikta belirli integralini hesaplamak icin once o fonksiyonun belirsiz integrali hesaplanir sonra bu fonksiyonun iki uc noktasindaki degerleri cikarilarak belirli integral elde edilir Belirli integraller alan hacim ve bunlarin cok boyutlu karsiliklarini hesaplamak icin gereklidir Tek degiskenli fonksiyonlarda belirli bir aralikta alinan integral o aralik boyunca fonksiyonun grafiginin altinda kalan alani verir Integraller ayni zamanda diferansiyel denklemlerin cozumlerinde vazgecilmezdir TanimGottfried Wilhelm Leibniz Integral verilen bir f x fonksiyonunu turev kabul eden F x fonksiyonunun bulunmasi olarak yapilabilir F x fonksiyonuna f x fonksiyonunun integrali veya ilkeli denir Integral Latince toplam kelimesinin ſumma summa bas harfi s nin biraz evrim gecirmis isareti ile gosterilir Bu isaret Gottfried Wilhelm Leibniz tarafindan tanimlanmistir F x f x c displaystyle F x int f x c c bir sabiti gosterir ve integralin bir sabit farki ile bulunabilecegine isaret eder Bir eksen takiminda gosterilen f x gondermesinin altinda kalan a lt x lt b araligindaki alan integral yardimiyla hesaplanabilir Bu amacla alan kucuk dikdortgenlere bolunerek bunlarin alani hesap edilip toplanir Dikdortgen sayisi arttikca toplam egri altindaki alan alanin degerine yaklasir ve integralin tam degeri bulunmus olur Bu toplama Riemann toplami denir Integralin Riemann anlamindaki tanimi Riemann toplamindaki boluntu sayisi olan n nin bir limit icerisinde sonsuza goturulmesiyle elde edilir S limDx 0 i 0n 1f xi Dxi abf x dx F b F a displaystyle S lim Delta x to 0 sum i 0 n 1 f x i Delta x i int a b f x dx F b F a Bu sekildeki integral belirli sinirlar arasinda hesaplandigi icin belirli Integral olarak isimlendirilir Sinirlar goz onune alinmadan hesaplanan integrale ise belirsiz integral denir Bazi durumlarda f x gondermesinin integrali F x bulunamaz Bu durumda belirli integral sayisal olarak hesaplanir Uzunluk alan ve hacimlerin hesaplanmasinda integral hesabin onemli yeri vardir Birden fazla degiskene bagli fonksiyonlarda integral kavrami genisletilebilir ve bu durumda katli integraller ortaya cikar Riemann dan sonra soyut kumelerin de integrallenebilmesi amaciyla Lebesgue integrali gelistirilmistir KokenSir Isaac NewtonBernhard RiemannDilimize Ingilizceden veya Fransizcadan gecmis integral sozcugu butune ait olan anlamina gelir ve Ingilizceye integral sozcugunden integralis tum yapmak tumlemek sozcugunden Latince integer tum butun tam sozcugunden gelmistir Ayrica integer sozcugu tam sayi terimine karsilik olarak Ingilizceye gecmistir Turkcede tumlev sozcugu Osmanlica mutemmem ile tamami sozcuklerinin ve Ingilizcedeki integral sozcugunun anlamini karsilamak icin turetilmistir tumlev sozcugu tumlenmis sey anlamina gelir Isimden fiil yapan ev av yapim ekiyle kullanimda olan tumle mek fiilinden isimden fiil yapan le mek yapim ekiyle muhtemelen Oz Turkce tum bknz tumen kokunden turetilmistir Osmanlicada mutemmem sozcugu kullanilmis Arapcadaki tm tam kokunden gelir ancak Arapcada su anda olgun evrimlesmis butunlesmis anlamindaki tekamul 1 23 Subat 2010 tarihinde Wayback Machine sitesinde arsivlendi sozcugu kullanilmaktadir kamil mukemmel kume ile ayni kokten kml Integral alma yontemleriDegisken degistirme Degisken degistirme karmasik problemleri basitlestirmek icin kullanilan degisken degistirme yontemidir Bu yontemde ham eski degisken yerine yeni daha basit degisken kullanilir Problem cozuldukten sonra yeni degisken ile elde edilen sonuc eski degiskende yerine konur Basit ornek Asagidaki 6 dereceden bir polinomu ilkel fonksiyon kullanarak cozmek neredeyse imkansizdir Bunun icin degisken degistirme yontemini kullanalim x6 9x3 8 0 displaystyle x 6 9x 3 8 0 Bu denklemde x3 u degisken degisimini uygulanirsa asagidaki denklem elde edilir u2 9u 8 0 displaystyle u 2 9u 8 0 Boylece denklem ikinci dereceden denklem bicimine donustu Bu denklemin kokleri u 1veu 8 dir displaystyle u 1 quad mbox ve quad u 8 dir Bu yeni degiskenin sonuclarini ham degiskende yerine koyalim x3 1vex3 8 x 1 1 3 1vex 8 1 3 2 displaystyle x 3 1 quad mbox ve quad x 3 8 quad Rightarrow qquad x 1 1 3 1 quad mbox ve quad x 8 1 3 2 Kismi integral Eger integral f x g x dx displaystyle int f x g x dx seklinde verilmis ve f x displaystyle f x veya g x displaystyle g x birbirleri cinsinden yazilamiyorsa kismi integrasyon yontemi uygulanir Bu indirgeme sirasiyla logaritma ters trigonometrik fonksiyonlar polinomlar trigonometrik fonksiyonlar ve son olarak ustel fonksiyonlara uygulanir Bazi egitmenler bu fonksiyonlarin bas harflerini LAPTU bir kolay hatirlama yontemi olarak kullanir f x g x dx displaystyle int f x g x dx integralinde f x displaystyle f x yukaridaki siralamada once geliyorsa f x u displaystyle f x u degisken degistirmesi yapilir ve geri kalan ifadeler ile g x dx dv displaystyle g x dx dv denklemi kurulur Bunu takiben u df x dx textstyle u df x over dx v G x textstyle v G x denliklerine ulasilir Burada G x displaystyle G x g x displaystyle g x in integrali alinmis halidir Sonuc olarak verilen integral I displaystyle I v displaystyle v ve u displaystyle u cinsinden yazilabilir I textstyle I uv vdu displaystyle uv int vdu Ornek 1 lnxdx displaystyle int lnxdx integrali degisken degistirme yontemiyle integrallenemez bu yuzden kismi integrasyon uygulamak gerekir Yukaridaki indirgeme sirasinda logaritma lnx displaystyle lnx onceliklidir dolayisiyla lnx u displaystyle lnx u dx dv displaystyle dx dv dxx du displaystyle frac dx x du x v displaystyle x v Burada belirsiz integralin keyfi sabiti c displaystyle c henuz eklenmemistir Bu sabit en son integralde eklenecektir Kismi integrasyon formulu uygulandiginda uv vdu displaystyle uv int vdu xlnx 1xxdx displaystyle xlnx int frac 1 x xdx halini alir Integraldeki x displaystyle x ler sadelesir Sonuc bulunur xlnx x displaystyle xlnx x c displaystyle c Ornek 2 xexdx displaystyle int xe x dx integrali icin de kismi integral uygulanmalidir Yukaridaki indirgeme onceligine gore polinom x displaystyle x ustel fonksiyondan ex displaystyle e x once gelir x u displaystyle x u ex dv displaystyle e x dv dx du displaystyle dx du ex v displaystyle e x v Bunu takiben uv vdu displaystyle uv int vdu xex exdx displaystyle xe x int e x dx islemleri yapilarak sonuc bulunur xex ex displaystyle xe x e x c displaystyle c Ayrica bakinizTemel gondermelerin integralleri icin Integral Tablosu Belirli integral Belirsiz integralKaynakca Douglas Harper Online Etymology Dictionary sozcuk 23 Subat 2007 tarihinde kaynagindan Erisim tarihi 5 Mayis 2010 Turk Dil Kurumu Bilim ve Sanat Terimleri Ana Sozlugu sozcuk olu kirik baglanti Mustafa Nihat Ozon Osmanlica Turkce Sozluk Inkilap ve Aka kitabevleri 4 basim Ocak 1965
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State