Matematik'te aritmetiğin temel teoremi, aynı zamanda benzersiz çarpanlara ayırma teoremi ve asal çarpanlara ayırma teoremi olarak da adlandırılır, şunu belirtir: 1'den büyük her tamsayı, benzersiz bir şekilde asal sayıların üslerinin çarpımı olarak gösterilebilir.

Örneğin,
Teorem bu örnekle ilgili iki şey söylüyor: birincisi, 1200 asal sayıların çarpımı olarak temsil edilebilir ve ikincisi, bu nasıl yapılırsa yapılsın her zaman tam olarak dört 2, bir 3 ve iki 5 olacaktır ve sonuç bunların dışında başka asal sayı içermeyecektir.
Çarpanların asal olması gereklidir: bileşik sayıları içeren çarpanlara ayırmalar benzersiz olmayabilir (örneğin, ).
Bu teorem (1'in asal sayı olarak kabul edilmemesinin ana nedenlerinden) biridir: eğer 1 asal olsaydı, asal sayılara ayırma benzersiz olmazdı; örneğin,
Teorem, bir alan üzerinde olarak adlandırılan ve , ve içeren diğer genelleştirilir. Ancak teorem için geçerli değildir. Benzersiz çarpanlara ayırmadaki bu başarısızlık, Fermat'ın Son Teoremi'nin ispatının zorluğunun nedenlerinden biridir. Cebirsel tamsayı halkalarında benzersiz çarpanlara ayırmanın örtülü kullanımı, Fermat'ın ifadesi ile .
Tarihçe
Temel teorem, Öklid'in Elementler'inin Kitap VII, 30, 31 ve 32. önermelerinden ve IX. Kitap, 14. önermesinden türetilebilir.
| “ | İki sayının çarpımı, bir sayı ile bir asal sayının çarpımına eşit ise, bu asal sayı başlangıçtaki iki sayıdan birinin çarpanıdır. | „ |
—Öklid, Elementler Kitap VII, Önerme 30 | ||
(Modern terminolojide: Eğer bir asal p ab çarpımını bölüyorsa, o zaman p ya ayı ya da byi ya da her ikisini de böler.) Önerme 30'a gönderme yapılır. olarak ve aritmetiğin temel teoreminin ispatında gereklidir.
| “ | Herhangi bir bileşik sayı bazı asal sayıların çarpımı ile ifade edilir. | „ |
—Öklid, Elementler Kitap VII, Önerme 31 | ||
(Modern terminolojide: birden büyük her tam sayı bir asal sayıya eşit olarak bölünür.) Önerme 31 doğrudan ile kanıtlanır.
| “ | Herhangi bir sayı ya asaldır ya da bir asal sayı ile tam olarak bölünür. | „ |
—Öklid, Elementler Kitap VII, Önerme 32 | ||
Önerme 32, önerme 31'den türetilmiştir ve çarpanlara ayırmanın mümkün olduğunu kanıtlamaktadır.
| “ | Bir sayı asal sayıların çarpımı olarak ifade edilen en küçük sayı ise herhangi başka bir sayının çarpımı olarak ifade edilmez. Başlangıçtaki çarpanları dışında başka asal ççarpanı yoktur. | „ |
—Öklid, Elementler Kitap IX, Önerme 14 | ||
(Modern terminolojide: birkaç asal sayının herhangi bir başka asal sayının katı değildir.) Kitap IX, önerme 14, Kitap VII, önerme 30'dan türetilmiştir ve çarpanlara ayırmanın benzersiz olduğunu kısmen kanıtlar. – André Weil. Aslında bu önermede üsler hepsi bire eşit olduğundan genel durum için hiçbir şey söylenmiyor.
Asal çarpanlara ayırmanın varlığına giden yolda ilk adımı Öklid atarken, son adımı ise attı ve aritmetiğin temel teoremini ilk kez belirtti.
Gauss' Disquisitiones Arithmeticae Madde 16'sı, modüler aritmetik kullanan erken modern bir ifade ve kanıttır.
Uygulamalar
Pozitif bir tam sayının kanonik gösterimi
Her pozitif tamsayı n > 1 asal kuvvetlerin çarpımı olarak tam olarak tek bir şekilde temsil edilebilir: 
Bu temsile n'nin kanonik temsili' of n, or the standard form denir.. Örneğin,
- 999 = 33×37,
- 1000 = 23×53,
- 1001 = 7×11×13.
p0 = 1 çarpanları, n değeri değiştirilmeden eklenebilir (örneğin, 1000 = 23×30×53). Aslında, herhangi bir pozitif tam sayı, tüm pozitif asal sayıların üzerine alınan bir olarak benzersiz bir şekilde temsil edilebilir;
burada sonlu sayıda ni pozitif tamsayılardır ve diğerleri sıfırdır.
Negatif üslere izin vermek, pozitif rasyonel sayılar için kanonik bir form sağlar.
Aritmetik işlemler
a ve b iki sayısının en büyük ortak bölen (OBEB) ve en küçük ortak kat (EKOK) çarpımının kanonik gösterimleri basitçe şu şekilde ifade edilebilir: a ve bnin kanonik temsilleri:



Bununla birlikte, özellikle büyük sayıların işlemleri, ürünlerin, EBOB'ların veya EKOK'ların hesaplanmasından çok daha zordur. Dolayısıyla bu formüllerin pratikte kullanımı sınırlıdır.
Aritmetik fonksiyonlar
Birçok aritmetik fonksiyon kanonik gösterim kullanılarak tanımlanır. Özellikle, ve çarpım fonksiyonlarının değerleri, asal sayıların kuvvetleri üzerindeki değerlerine göre belirlenir.
İspat
İspat, (Elementler VII, 30) kullanır: Eğer bir asal sayı iki tam sayının çarpımını bölüyorsa bölüyorsa, bu tam sayılardan en az birini bölmelidir.
Varlık
1'dan büyük her tam sayının ya asal ya da asal sayıların çarpımı olduğu gösterilmelidir. Birincisi, 2 asaldır. Daha sonra, yoluyla, bunun 1'dan büyük ve n'den küçük tüm sayılar için doğru olduğunu varsayalım. Eğer n asalsa kanıtlayacak başka bir şey yoktur. Aksi takdirde, a ve b tamsayıları vardır; burada n = a b ve 1 < a ≤ b < n. Tümevarım hipotezine göre, a = p1p2 ⋅⋅⋅ p' 'j ve b = q1q2 ⋅⋅⋅ qk asal sayıların çarpımlarıdır. Ama sonra n = a b = p1p2 ⋅⋅⋅ pj q1q2 ⋅⋅⋅ q' 'k asal sayıların çarpımıdır.
Benzersizlik
Teoremin tersine, iki farklı asal çarpanlara ayırmaya sahip bir tamsayı olduğunu varsayalım. n böyle bir en küçük tamsayı olsun ve her bir pi ve qi asal olduğu n = p1p2 ... pj = q1q2 ... qk yazalım. p1'nin q1q2 ... qk yi böldüğünü görürüz. Böylece by 'ne göre p1 bazı qi leri böler. Genelliği kaybetmeden, p1 q1 i böler diyelim. p1 ve q1 her ikisi de asal olduğundan, böylece p1 = q1 olur. n'yi çarpanlara ayırmamıza dönersek, p2 ... pj = q2 ... qk gerçekleşmesi için bu iki çarpanı sadeleştirebiliriz. Böylece elimizde kesin olarak n'den küçük iki asal tamsayı çarpan var ve bu da n'nin küçüklüğü ile çelişiyor.
Öklid'in tezi olmadan benzersizlik
Aritmetiğin temel teoremi, Öklid tezi kullanılmadan da kanıtlanabilir. Aşağıdaki kanıt, Öklid'in Öklid algoritması orijinal versiyonundan esinlenmiştir.



Böylece,

yazılabilir.
Her 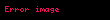























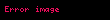
Böylece, tek bir farklı asal çarpanlara ayırmadan daha fazlasına sahip en küçük bir tam sayı olamaz. Her pozitif tamsayı ya benzersiz bir şekilde çarpanlara ayrılacak bir asal sayı ya da asal sayıları benzersiz bir şekilde çarpanlara ayıran bir bileşik ya da 
Genellemeler
Teoremin ilk genellemesi Gauss'un üzerine ikinci monografisinde (1832) bulunur. Bu makale, şimdi 'larının halka olarak adlandırılan tüm karmaşık sayı'lar a + bi kümesini tanıttı; burada a ve b tam sayılardır. Artık 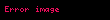
Benzer şekilde, 1844'te üzerinde çalışırken, 



Ancak benzersiz çarpanlara ayırmanın her zaman geçerli olmadığı da keşfedildi. Örnek olarak 
vardır.
Bunun gibi örnekler "asal" kavramının değişmesine neden oldu. 




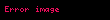


İndirgenemezler çarpanlara ayırmanın benzersiz olduğu yerlerde halkalara denir. Önemli örnekler, tamsayılar üzerindeki veya bir alan üzerindeki 'ları, 'ları ve 'larıdır.
1843 yılında kavramını ortaya attı, bu kavram Dedekind tarafından 1876'da, halkaların özel bir alt alanı olan modern teorisine geliştirildi. Burada idealler için çarpma tanımlanır ve bunların benzersiz çarpanlara ayrıldığı halkalara adı verilir.
bir versiyonu vardır, ancak benzersizliği sağlamak için bazı ek koşullar gerektirir.
Ayrıca bakınız
Notlar
- ^ a b Gauss (1986, Art. 16)
- ^ Gauss (1986, Art. 131)
- ^ Long (1972, s. 44)
- ^ Pettofrezzo & Byrkit (1970, s. 53)
- ^ Hardy & Wright (2008, Thm 2)
- ^ In a , the factorization into prime elements may be non unique, but one can recover a unique factorization if one factors into .
- ^ Weil (2007, s. 5) tarafından eleştirel olarak dikkat çekilen bir nokta: "Öklid'de bile, bir sayının çarpanlara ayrılmasının benzersizliği hakkında genel bir ifade bulamıyoruz. tam sayıların asal sayılara dönüştürülmesi; elbette bunun farkında olabilir, ancak sahip olduğu tek şey verilen herhangi bir asal sayının EKOK'u hakkında bir ifadedir (Eucl.IX.I4).
- ^ A. Goksel Agargun and E. Mehmet Özkan. "A Historical Survey of the Fundamental Theorem of Arithmetic" (PDF). Historia Mathematica: 209. 31 Mayıs 2023 tarihinde kaynağından (PDF). Erişim tarihi: 8 Ekim 2023.
One could say that Euclid takes the first step on the way to the existence of prime factorization, and al-Farisi takes the final step by actually proving the existence of a finite prime factorization in his first proposition.
- ^ Rashed, Roshdi (11 Eylül 2002). Encyclopedia of the History of Arabic Science (İngilizce). Routledge. s. 385. ISBN . 15 Ocak 2023 tarihinde kaynağından . Erişim tarihi: 8 Ekim 2023.
The famous physicist and mathematician Kamal al-Din al-Farisi compiled a paper in which he set out deliberately to prove the theorem of Ibn Qurra in an algebraic way. This forced him to an understanding of the first arithmetical functions and to a full preparation which led him to state for the first time the fundamental theorem of arithmetic.
- ^ Long (1972, s. 45)
- ^ Pettofrezzo & Byrkit (1970, s. 55)
- ^ Hardy & Wright (2008, § 1.2)
- ^ Dawson, John W. (2015), Why Prove it Again? Alternative Proofs in Mathematical Practice., Springer, s. 45, ISBN
- ^ Gauss, BQ, §§ 31–34
- ^ Hardy & Wright (2008, § 14.6)
Kaynakça
Disquisitiones Arithmeticae Latinceden İngilizce ve Almanca'ya çevrildi. Almanca baskısı sayı teorisi üzerine tüm makalelerini içerir: ikinci dereceden karşıtlığın tüm kanıtları, Gauss toplamının işaretinin belirlenmesi, iki ikinci dereceden karşılıklılık üzerine araştırmalar ve yayınlanmamış notlar.
- Gauss, Carl Friedrich (1986), Disquisitiones Arithemeticae (Second, corrected edition), Clarke, Arthur A. tarafından çevrildi, New York: , ISBN
- Gauss, Carl Friedrich (1965), Untersuchungen über hohere Arithmetik (Disquisitiones Arithemeticae & other papers on number theory) (Second edition) (Almanca), Maser, H. tarafından çevrildi, New York: Chelsea, ISBN
Gauss'un iki ikinci dereceden karşılıklılık üzerine yayınladığı iki monografinin bölümleri ardışık olarak numaralandırılmıştır: ilki §§ 1-23'ü ve ikincisi §§ 24-76'yı içerir. Bunlara atıfta bulunan dipnotlar "Gauss, BQ, § n" biçimindedir. Disquisitiones Arithmeticae'ye atıfta bulunan dipnotlar "Gauss, DA, Art. n" biçimindedir.
- Gauss, Carl Friedrich (1828), Theoria residuorum biquadraticorum, Commentatio prima, Göttingen: Comment. Soc. regiae sci, Göttingen 6
- Gauss, Carl Friedrich (1832), Theoria residuorum biquadraticorum, Commentatio secunda, Göttingen: Comment. Soc. regiae sci, Göttingen 7
Bunlar Gauss'un Werke, Cilt II, s.65–92 ve 93–148'inde; Almanca çeviriler Disquisitiones'ın Almanca baskısının s.511–533 ve 534–586 sayfalarındadır.
- Euclid (1956), The thirteen books of the Elements
![image]() , 2 (Books III-IX), Translated by (Second Edition Unabridged bas.), New York: Dover, ISBN
, 2 (Books III-IX), Translated by (Second Edition Unabridged bas.), New York: Dover, ISBN - Long, Calvin T. (1972), Elementary Introduction to Number Theory (2. bas.), Lexington: , LCCN 77-171950.
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 77-81766.
- Riesel, Hans (1994), Prime Numbers and Computer Methods for Factorization (second edition), Boston: Birkhäuser, ISBN
- Weil, André (2007) [1984], , Modern Birkhäuser Classics, Boston, MA: Birkhäuser, ISBN
External links
- Why isn’t the fundamental theorem of arithmetic obvious?
- GCD and the Fundamental Theorem of Arithmetic at .
- PlanetMath: Proof of fundamental theorem of arithmetic
- Fermat's Last Theorem Blog: Unique Factorization, a blog that covers the history of Fermat's Last Theorem from to the proof by Andrew Wiles.
- "Fundamental Theorem of Arithmetic" by Hector Zenil, , 2007.
- Grime, James, "1 and Prime Numbers", Numberphile, , 11 Aralık 2021 tarihinde kaynağından arşivlendi
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik te aritmetigin temel teoremi ayni zamanda benzersiz carpanlara ayirma teoremi ve asal carpanlara ayirma teoremi olarak da adlandirilir sunu belirtir 1 den buyuk her tamsayi benzersiz bir sekilde asal sayilarin uslerinin carpimi olarak gosterilebilir In Disquisitiones Arithmeticae 1801 Gauss benzersiz carpanlara ayirma teoremini kanitladi ve kanitlamak icin kullandi Ornegin 1200 24 31 52 2 2 2 2 3 5 5 5 2 5 2 3 2 2 displaystyle 1200 2 4 cdot 3 1 cdot 5 2 2 cdot 2 cdot 2 cdot 2 cdot 3 cdot 5 cdot 5 5 cdot 2 cdot 5 cdot 2 cdot 3 cdot 2 cdot 2 ldots Teorem bu ornekle ilgili iki sey soyluyor birincisi 1200 asal sayilarin carpimi olarak temsil edilebilir ve ikincisi bu nasil yapilirsa yapilsin her zaman tam olarak dort 2 bir 3 ve iki 5 olacaktir ve sonuc bunlarin disinda baska asal sayi icermeyecektir Carpanlarin asal olmasi gereklidir bilesik sayilari iceren carpanlara ayirmalar benzersiz olmayabilir ornegin 12 2 6 3 4 displaystyle 12 2 cdot 6 3 cdot 4 Bu teorem 1 in asal sayi olarak kabul edilmemesinin ana nedenlerinden biridir eger 1 asal olsaydi asal sayilara ayirma benzersiz olmazdi ornegin 2 2 1 2 1 1 displaystyle 2 2 cdot 1 2 cdot 1 cdot 1 ldots Teorem bir alan uzerinde olarak adlandirilan ve ve iceren diger genellestirilir Ancak teorem icin gecerli degildir Benzersiz carpanlara ayirmadaki bu basarisizlik Fermat in Son Teoremi nin ispatinin zorlugunun nedenlerinden biridir Cebirsel tamsayi halkalarinda benzersiz carpanlara ayirmanin ortulu kullanimi Fermat in ifadesi ile TarihceTemel teorem Oklid in Elementler inin Kitap VII 30 31 ve 32 onermelerinden ve IX Kitap 14 onermesinden turetilebilir Iki sayinin carpimi bir sayi ile bir asal sayinin carpimina esit ise bu asal sayi baslangictaki iki sayidan birinin carpanidir Oklid Elementler Kitap VII Onerme 30 Modern terminolojide Eger bir asal p ab carpimini boluyorsa o zaman p ya ayi ya da byi ya da her ikisini de boler Onerme 30 a gonderme yapilir olarak ve aritmetigin temel teoreminin ispatinda gereklidir Herhangi bir bilesik sayi bazi asal sayilarin carpimi ile ifade edilir Oklid Elementler Kitap VII Onerme 31 Modern terminolojide birden buyuk her tam sayi bir asal sayiya esit olarak bolunur Onerme 31 dogrudan ile kanitlanir Herhangi bir sayi ya asaldir ya da bir asal sayi ile tam olarak bolunur Oklid Elementler Kitap VII Onerme 32 Onerme 32 onerme 31 den turetilmistir ve carpanlara ayirmanin mumkun oldugunu kanitlamaktadir Bir sayi asal sayilarin carpimi olarak ifade edilen en kucuk sayi ise herhangi baska bir sayinin carpimi olarak ifade edilmez Baslangictaki carpanlari disinda baska asal ccarpani yoktur Oklid Elementler Kitap IX Onerme 14 Modern terminolojide birkac asal sayinin herhangi bir baska asal sayinin kati degildir Kitap IX onerme 14 Kitap VII onerme 30 dan turetilmistir ve carpanlara ayirmanin benzersiz oldugunu kismen kanitlar Andre Weil Aslinda bu onermede usler hepsi bire esit oldugundan genel durum icin hicbir sey soylenmiyor Asal carpanlara ayirmanin varligina giden yolda ilk adimi Oklid atarken son adimi ise atti ve aritmetigin temel teoremini ilk kez belirtti Gauss Disquisitiones Arithmeticae Madde 16 si moduler aritmetik kullanan erken modern bir ifade ve kanittir UygulamalarPozitif bir tam sayinin kanonik gosterimi Her pozitif tamsayi n gt 1 asal kuvvetlerin carpimi olarak tam olarak tek bir sekilde temsil edilebilir n p1n1p2n2 pknk i 1kpini displaystyle n p 1 n 1 p 2 n 2 cdots p k n k prod i 1 k p i n i burada p1 lt p2 lt lt pk asal sayilardir ve ni pozitif tam sayilardir Bu gosterim in 1 e esit oldugu kuraliyla genel olarak 1 dahil tum pozitif tam sayilara genisletilir bos carpim k 0 a karsilik gelir Bu temsile n nin kanonik temsili ofn or the standard form denir Ornegin 999 33 37 1000 23 53 1001 7 11 13 p0 1 carpanlari n degeri degistirilmeden eklenebilir ornegin 1000 23 30 53 Aslinda herhangi bir pozitif tam sayi tum pozitif asal sayilarin uzerine alinan bir olarak benzersiz bir sekilde temsil edilebilir n 2n13n25n37n4 i 1 pini displaystyle n 2 n 1 3 n 2 5 n 3 7 n 4 cdots prod i 1 infty p i n i burada sonlu sayida ni pozitif tamsayilardir ve digerleri sifirdir Negatif uslere izin vermek pozitif rasyonel sayilar icin kanonik bir form saglar Aritmetik islemler a ve b iki sayisinin en buyuk ortak bolen OBEB ve en kucuk ortak kat EKOK carpiminin kanonik gosterimleri basitce su sekilde ifade edilebilir a ve bnin kanonik temsilleri a b 2a1 b13a2 b25a3 b37a4 b4 piai bi displaystyle a cdot b 2 a 1 b 1 3 a 2 b 2 5 a 3 b 3 7 a 4 b 4 cdots prod p i a i b i EBOB a b 2min a1 b1 3min a2 b2 5min a3 b3 7min a4 b4 pimin ai bi displaystyle EBOB a b 2 min a 1 b 1 3 min a 2 b 2 5 min a 3 b 3 7 min a 4 b 4 cdots prod p i min a i b i EKOK a b 2max a1 b1 3max a2 b2 5max a3 b3 7max a4 b4 pimax ai bi displaystyle EKOK a b 2 max a 1 b 1 3 max a 2 b 2 5 max a 3 b 3 7 max a 4 b 4 cdots prod p i max a i b i Bununla birlikte ozellikle buyuk sayilarin islemleri urunlerin EBOB larin veya EKOK larin hesaplanmasindan cok daha zordur Dolayisiyla bu formullerin pratikte kullanimi sinirlidir Aritmetik fonksiyonlar Bircok aritmetik fonksiyon kanonik gosterim kullanilarak tanimlanir Ozellikle ve carpim fonksiyonlarinin degerleri asal sayilarin kuvvetleri uzerindeki degerlerine gore belirlenir IspatIspat Elementler VII 30 kullanir Eger bir asal sayi iki tam sayinin carpimini boluyorsa boluyorsa bu tam sayilardan en az birini bolmelidir Varlik 1 dan buyuk her tam sayinin ya asal ya da asal sayilarin carpimi oldugu gosterilmelidir Birincisi 2 asaldir Daha sonra yoluyla bunun 1 dan buyuk ve n den kucuk tum sayilar icin dogru oldugunu varsayalim Eger n asalsa kanitlayacak baska bir sey yoktur Aksi takdirde a ve b tamsayilari vardir burada n a b ve 1 lt a b lt n Tumevarim hipotezine gore a p1p2 p j veb q1q2 qkasal sayilarin carpimlaridir Ama sonran a b p1p2 pjq1q2 q k asal sayilarin carpimidir Benzersizlik Teoremin tersine iki farkli asal carpanlara ayirmaya sahip bir tamsayi oldugunu varsayalim n boyle bir en kucuk tamsayi olsun ve her bir pi ve qi asal oldugu n p1p2 pj q1q2 qk yazalim p1 nin q1q2 qk yi boldugunu goruruz Boylece by ne gore p1 bazi qi leri boler Genelligi kaybetmeden p1 q1 i boler diyelim p1 ve q1 her ikisi de asal oldugundan boylece p1 q1 olur n yi carpanlara ayirmamiza donersek p2 pj q2 qk gerceklesmesi icin bu iki carpani sadelestirebiliriz Boylece elimizde kesin olarak n den kucuk iki asal tamsayi carpan var ve bu da n nin kucuklugu ile celisiyor Oklid in tezi olmadan benzersizlik Aritmetigin temel teoremi Oklid tezi kullanilmadan da kanitlanabilir Asagidaki kanit Oklid in Oklid algoritmasi orijinal versiyonundan esinlenmistir s displaystyle s in asal sayilarin iki farkli carpimi olan en kucuk pozitif tamsayi oldugunu varsayalim Bu eger varsa s displaystyle s in 1 displaystyle 1 den buyuk bilesik sayi oldugu anlamina gelir Boylece s p1p2 pm q1q2 qn displaystyle begin aligned s amp p 1 p 2 cdots p m amp q 1 q 2 cdots q n end aligned yazilabilir Her pi displaystyle p i qj displaystyle q j den farkli olmalidir Aksi takdirde eger pi qj displaystyle p i q j dersek s displaystyle s den kucuk bazi pozitif t s pi s qj displaystyle t s p i s q j tamsayi carpanlari olacaktir Gerektiginde iki carpan degistirilerek p1 lt q1 displaystyle p 1 lt q 1 oldugu da varsayilabilir P p2 pm displaystyle P p 2 cdots p m ve Q q2 qn displaystyle Q q 2 cdots q n olarak ve s p1P q1Q displaystyle s p 1 P q 1 Q olarak ayrica p1 lt q1 displaystyle p 1 lt q 1 oldugundan Q lt P displaystyle Q lt P olarak secilir ve takiben s p1Q q1 p1 Q p1 P Q lt s displaystyle s p 1 Q q 1 p 1 Q p 1 P Q lt s elde edilir s displaystyle s den kucuk pozitif tamsayilarin benzersiz bir asal carpanlara ayirmaya sahip oldugu varsayildigindan p1 displaystyle p 1 q1 p1 displaystyle q 1 p 1 in ya da Q displaystyle Q nun carpanlari arasinda yer almalidir Q displaystyle Q s displaystyle s den kucuk oldugundan benzersiz asal carpanlara sahip olmalidir ve her icin qj displaystyle q j icin p1 displaystyle p 1 farkli oldugundan ikinci durum mumkun degildir Eger p1 displaystyle p 1 q1 p1 displaystyle q 1 p 1 in boleni ise q1 displaystyle q 1 in de boleni olacagindan p1 displaystyle p 1 ve q1 displaystyle q 1 farkli asal sayilar olacagindan ilk durum da mumkun degildir Boylece tek bir farkli asal carpanlara ayirmadan daha fazlasina sahip en kucuk bir tam sayi olamaz Her pozitif tamsayi ya benzersiz bir sekilde carpanlara ayrilacak bir asal sayi ya da asal sayilari benzersiz bir sekilde carpanlara ayiran bir bilesik ya da 1 displaystyle 1 tamsayisi durumunda herhangi bir asal carpani olmayan bir bilesik olmalidir GenellemelerTeoremin ilk genellemesi Gauss un uzerine ikinci monografisinde 1832 bulunur Bu makale simdi larinin halka olarak adlandirilan tum karmasik sayi lar a bi kumesini tanitti burada a ve b tam sayilardir Artik Z i displaystyle mathbb Z i ile gosterilmistir Bu halkanin sifirdan farkli 1 ve i dort birimine sahip oldugunu birim olmayan sayilarin asal sayilar ve bilesik sayilar olmak uzere iki sinifa ayrildigini ve bilesik sayilarrin asal sayilarin bir urunu olarak benzersiz carpanlara ayirmaya sahip oldugunu gosterdi Benzer sekilde 1844 te uzerinde calisirken Z w displaystyle mathbb Z omega halkasini tanitti burada w 1 32 textstyle omega frac 1 sqrt 3 2 w3 1 displaystyle omega 3 1 Bu halkasidir ve kendisi bunun alti birimi 1 w w2 displaystyle pm 1 pm omega pm omega 2 oldugunu ve benzersiz carpanlara ayirmaya sahip oldugunu kanitladi Ancak benzersiz carpanlara ayirmanin her zaman gecerli olmadigi da kesfedildi Ornek olarak Z 5 displaystyle mathbb Z sqrt 5 verilmistir Bu halkada 6 2 3 1 5 1 5 displaystyle 6 2 cdot 3 left 1 sqrt 5 right left 1 sqrt 5 right vardir Bunun gibi ornekler asal kavraminin degismesine neden oldu Z 5 displaystyle mathbb Z left sqrt 5 right de yukaridaki faktorlerden herhangi birinin bir carpim olarak temsil edilebilmesi durumunda kanitlanabilir ornegin 2 ab ise a veya bden biri bir birim olmalidir Bu asal in geleneksel tanimidir Bu faktorlerin hicbirinin Oklid tezine uymadigi da kanitlanabilir ornegin 2 carpimlari 6 yi bolmesine ragmen ne 1 5 ne de 1 5 i bolmez 2 Z 5 displaystyle mathbb Z left sqrt 5 right de olarak adlandirilir kendisine ve birim sayiya bolunebilir ancak asal degildir carpimi boluyorsa carpanlardan birini de bolmelidir Z 5 displaystyle mathbb Z left sqrt 5 right in belirtilmesi gereklidir cunku 2 asaldir ve Z displaystyle mathbb Z de indirgenemezdir Bu tanimlari kullanarak bir asal sayinin indirgenemez oldugu kanitlanabilir Oklid in klasik tezi Z displaystyle mathbb Z tamsayilar halkasinda her indirgenemez asaldir seklinde yeniden ifade edilebilir Bu ayni zamanda Z i displaystyle mathbb Z i ve Z w displaystyle mathbb Z omega icin de dogrudur ancak Z 5 displaystyle mathbb Z sqrt 5 icin gecerli degildir Indirgenemezler carpanlara ayirmanin benzersiz oldugu yerlerde halkalara denir Onemli ornekler tamsayilar uzerindeki veya bir alan uzerindeki lari lari ve laridir 1843 yilinda kavramini ortaya atti bu kavram Dedekind tarafindan 1876 da halkalarin ozel bir alt alani olan modern teorisine gelistirildi Burada idealler icin carpma tanimlanir ve bunlarin benzersiz carpanlara ayrildigi halkalara adi verilir bir versiyonu vardir ancak benzersizligi saglamak icin bazi ek kosullar gerektirir Ayrica bakinizAsal carpanlara ayirmaNotlar a b Gauss 1986 Art 16 Gauss 1986 Art 131 Long 1972 s 44 Pettofrezzo amp Byrkit 1970 s 53 Hardy amp Wright 2008 Thm 2 In a the factorization into prime elements may be non unique but one can recover a unique factorization if one factors into Weil 2007 s 5 tarafindan elestirel olarak dikkat cekilen bir nokta Oklid de bile bir sayinin carpanlara ayrilmasinin benzersizligi hakkinda genel bir ifade bulamiyoruz tam sayilarin asal sayilara donusturulmesi elbette bunun farkinda olabilir ancak sahip oldugu tek sey verilen herhangi bir asal sayinin EKOK u hakkinda bir ifadedir Eucl IX I4 A Goksel Agargun and E Mehmet Ozkan A Historical Survey of the Fundamental Theorem of Arithmetic PDF Historia Mathematica 209 31 Mayis 2023 tarihinde kaynagindan PDF Erisim tarihi 8 Ekim 2023 One could say that Euclid takes the first step on the way to the existence of prime factorization and al Farisi takes the final step by actually proving the existence of a finite prime factorization in his first proposition Rashed Roshdi 11 Eylul 2002 Encyclopedia of the History of Arabic Science Ingilizce Routledge s 385 ISBN 9781134977246 15 Ocak 2023 tarihinde kaynagindan Erisim tarihi 8 Ekim 2023 The famous physicist and mathematician Kamal al Din al Farisi compiled a paper in which he set out deliberately to prove the theorem of Ibn Qurra in an algebraic way This forced him to an understanding of the first arithmetical functions and to a full preparation which led him to state for the first time the fundamental theorem of arithmetic Long 1972 s 45 Pettofrezzo amp Byrkit 1970 s 55 Hardy amp Wright 2008 1 2 Dawson John W 2015 Why Prove it Again Alternative Proofs in Mathematical Practice Springer s 45 ISBN 9783319173689 Gauss BQ 31 34 Hardy amp Wright 2008 14 6 KaynakcaDisquisitiones Arithmeticae Latinceden Ingilizce ve Almanca ya cevrildi Almanca baskisi sayi teorisi uzerine tum makalelerini icerir ikinci dereceden karsitligin tum kanitlari Gauss toplaminin isaretinin belirlenmesi iki ikinci dereceden karsiliklilik uzerine arastirmalar ve yayinlanmamis notlar Gauss Carl Friedrich 1986 Disquisitiones Arithemeticae Second corrected edition Clarke Arthur A tarafindan cevrildi New York Springer ISBN 978 0 387 96254 2 Gauss Carl Friedrich 1965 Untersuchungen uber hohere Arithmetik Disquisitiones Arithemeticae amp other papers on number theory Second edition Almanca Maser H tarafindan cevrildi New York Chelsea ISBN 0 8284 0191 8 Gauss un iki ikinci dereceden karsiliklilik uzerine yayinladigi iki monografinin bolumleri ardisik olarak numaralandirilmistir ilki 1 23 u ve ikincisi 24 76 yi icerir Bunlara atifta bulunan dipnotlar Gauss BQ n bicimindedir Disquisitiones Arithmeticae ye atifta bulunan dipnotlar Gauss DA Art n bicimindedir Gauss Carl Friedrich 1828 Theoria residuorum biquadraticorum Commentatio prima Gottingen Comment Soc regiae sci Gottingen 6 Gauss Carl Friedrich 1832 Theoria residuorum biquadraticorum Commentatio secunda Gottingen Comment Soc regiae sci Gottingen 7 Bunlar Gauss un Werke Cilt II s 65 92 ve 93 148 inde Almanca ceviriler Disquisitiones in Almanca baskisinin s 511 533 ve 534 586 sayfalarindadir Euclid 1956 The thirteen books of the Elements 2 Books III IX Translated by Second Edition Unabridged bas New York Dover ISBN 978 0 486 60089 5 Long Calvin T 1972 Elementary Introduction to Number Theory 2 bas Lexington LCCN 77 171950 Pettofrezzo Anthony J Byrkit Donald R 1970 Elements of Number Theory Englewood Cliffs Prentice Hall LCCN 77 81766 Riesel Hans 1994 Prime Numbers and Computer Methods for Factorization second edition Boston Birkhauser ISBN 0 8176 3743 5 Weil Andre 2007 1984 Modern Birkhauser Classics Boston MA Birkhauser ISBN 978 0 817 64565 6 External linksWhy isn t the fundamental theorem of arithmetic obvious GCD and the Fundamental Theorem of Arithmetic at PlanetMath Proof of fundamental theorem of arithmetic Fermat s Last Theorem Blog Unique Factorization a blog that covers the history of Fermat s Last Theorem from to the proof by Andrew Wiles Fundamental Theorem of Arithmetic by Hector Zenil 2007 Grime James 1 and Prime Numbers Numberphile 11 Aralik 2021 tarihinde kaynagindan arsivlendi
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans





