Fizikte doğal birimler, evrensel fizik sabitleri kullanılarak elde edilen ölçü birimleridir. Örneğin temel yük (e), elektriksel yük ve ışık hızı (c), hız için kullanılan doğal birimlerdir. Herhangi bir evrensel fizik sabitini 1 birim olarak normalleştirmek için yalnızca evrensel kullanılır. Her ne kadar bu şekilde basitleştirme avantaj gibi görülüyor olsa bile, fizik yasalarının matematiksel ifadesinden elde edilen bu sabitlerin anlaşılması biraz zor olabilir.
Tanımlama
Doğal birimlerin tanımlarının kökeni yalnızca doğadan geldiğinden dolayı "doğaldır". Bunların büyüklükleri insan tarafından elde edilemez. Planck birimleri, her ne kadar doğal birimler sistemlerinden biri olsa bile, "doğal birimler" olarak adlandırılmasında bir kısıtlama yoktur. Planck birimleri, sınıflandırılan doğal birimlerdir. Fakat, bu birimler herhangi bir prototip nesne veya parçacığın bir özelliği olmaması için eşsiz olarak dikkate alınmışlardır, fakat vakumun bir özelliği olabilirler.
Diğer gibi doğal birimlerde de, uzunluk, kütle, zaman, sıcaklık, (elektrik akımı yerine) elektriksel yük kullanılır. Bazı fizikçiler sıcaklığı temek fiziksel nicelik olarak kabul etmiyor. Bunu serbest bir parçacığın birim derecedeki enerjisi olarak ifade ediyorlar. Çünkü enerji, kütle, uzunluk ve zamana bağlıdır. Hemen hemen tüm doğal birimler Boltzmann sabiti (kB=1) olarak normalleştirilebilir. Bu, örneğin sıcaklık birimini tanımlamanın basit bir yoldur.
SI'da elektriksel yük birimi amper iken (SI'dan türetilen birim) sisteminde elektriksel yük birimi coulombdur.
Gösterim ve kullanım
Doğal birimler, çoğunlukla 1 birim olarak normalleştirilir. Çoğu doğal birim sistemleri, c = 1 eşitliğini kullanır. Burada c, ışık hızıdır. Işık hızının yarı hızındaki bir v hızı için v = 12c ve c = 1 olur. Bu durumda v = 12 olur. v = 12 eşitliğinin anlamı "v hızı, örneğin Planck birimlerindeki değeri yarımdır" veya "v hızı, yarım Planck birim hızı kadardır".
c = 1, tüm birimlerde kullanılabilir. Örneğin E=mc², Planck birimlerinde E = m olarak yazılabilir. Bu denklemin anlamı; "Bir parçacığın Planck birimlerine göre enerjisi, parçacığın kütlesine eşittir."
Avantajlar ve dezavantajlar
Doğal birimler, SI ve diğer birim sistemleri ile karşılaştırıldıklarında, hem avantajları hem de dezavantajları vardır:
- Basitleştirilmiş denklemler: Sabitler 1'e normalleştirildiğinde, bu sabitleri bulunduran denklemler de çok sık ortaya çıkar ve bazen de anlaşılmaları basitleşir. Örneğin sabit kütleye sahip bir parçacık için E2 = p2c2 + m2c4 özel görelilik denkleminin çözümü biraz zordur. Fakat denklem doğal birimlere dönüştürülürse, E2 = p2 + m2 biçimini alır.
- Fiziksel anlamı: Doğal birimler sistemi (boyut analizinde) ortaya çıkar. Örneğin (Planck sabiti) kuantum mekaniğinde aksiyomun temel birimi olarak kabul edilir.
- Prototipleri yoktur: (Prototip), kilogram gibi bir birimi tanımlayan fiziksel, somut bir nesnedir. Prototipte herhangi bir zamanda her an bir eksiklik olabilir. Doğal birimlerin prototipinin olmaması bir avantajdır. (Bu avantajı, gibi doğal olmayan birim sistemlerinde paylaşır.)
- Büyük belirsizlik: a = 1010 eşitliğini Planck birimlerinde göz önüne alalım. Eğer a, bir uzunluk ifade ederse, denklem a = 1,6×10-25 metre olur (1 Planck uzunluğunun 1,616199(97)×10-35 metre olduğuna dikkat edin). Eğer a, bir kütle ifade ederse, denklem a = 220 kg olur (1 Planck kütlesinin 2,17651(13)×10-8 kg olduğuna dikkat edin. Bu yüzden, eğer a ifadesi tam olarak tanımlanmazsa, a = 1010 denklemi yanlış anlaşılmaya neden olabilir.
Normalleştirilecek sabitleri seçme
Fizik sabitlerinin çok oluşu, doğal birim sistemleri tasarlayıcıları tarafından, bu sabitlerden bazılarının normalleştirilmesi (1'e eşitlenmesi) gerektiği düşüncesini doğurdu. Yalnızca birkaç sabiti normalleştirmek yeterli değildir. Örneğin, protonun ve elektronun kütleleri normalleştirilemez. Eğer bir elektronun kütlesi 1 olarak normalleştirilirse, bir protonun kütlesi de ≈1836 olur. Çok basit bir örnek olarak, α≈1/137 de 1 olarak normalleştirilemez. Çünkü 1, . Diğer boyutsuz fiziksel sabitler ile ilgili iyi yapılı sabit de şöyledir:
Burada ke, Coulomb sabiti; e temel yük; ℏ, indirgenmiş Planck sabiti ve c, ışık hızıdır. Bu yüzden bu dört sabiti eşzamanlı olarak normalleştirmek mümkün değildir.
Elektromanyetizma birimleri
SI birimlerinde elektriksel yük birimi coulombtur. Bu farklı bir birimdir. Çünkü kütle, uzunluk, zaman gibi SI birimleri ile şöyle ifade edilebilir: [m]1/2 [L]3/2 [s]−1.
Elektromanyetizma için iki ana doğal birim sistemi vardır:
- (elektromanyetizma birimleri sisteminin rasyoneli olarak sınıflandırılır).
- (elektromanyetizma birimleri sisteminin irrasyoneli olarak sınıflandırılır).
Heaviside-Lorentz birimleri çok geneldir.Maxwell denklemleri genellikle, Lorentz-Heaviside birimlerinden ve Gauss birimlerinden daha basittir.
Bu iki birim sistemindeki e temel yük denklemi şöyledir:
(Lorentz–Heaviside),
(Gauss)
Burada; ħ, indirgenmiş Planck sabiti; c, ışık hızı ve α≈1/137, .
c = 1 olduğu doğal birimler sisteminde Lorentz-Heaviside birimleri, SI birimlerinden türetilebilir. Bunun için = μ0 = 1 olarak normalleştirilir. Gauss birimleri de SI'dan türetilebilir. Fakat, tüm elektriksel alanların 
Doğal birimler sistemleri
Planck birimleri
| Boyut | İfade | Değer (SI birimleri) | |
|---|---|---|---|
| Planck uzunluğu | Uzunluk (L) |  | 1.616 199(97) × 10−35m |
| Planck kütlesi | Kütle (M) |  | 2.176 51(13) × 10−8kg |
| Planck zamanı | Zaman (T) |  | 5.391 06(32) × 10−44s |
| Planck yükü | Elektriksel yük (Q) |  | 1.875 545 956(41) × 10−18C |
| Planck sıcaklığı | Sıcaklık (Θ) |  | 1.416 833(85) × 1032K |
Planck birimleri şöyle tanımlanır:
Burada c, bir vakumdaki ışık hızı; G, yerçekimi sabiti; 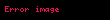
Planck birimleri doğal birimlerde bir sistemdir. Bunlar hiçbir fiziksel nesnenin, prototipin, hatta temel parçacığın bile özellikleri değildir. Yalnızca fizik yasalarının temel yapısını ifade ederler: c ve G, genel görelilikteki uzayzaman modelinin sabitleridir ve ℏ kuantum mekaniğinde enerjinin frekansa oranı veya dalga boyu ile eigen momentumunun çarpımıdır.
Özet tablosu
| Adı / Sembol | Planck ( ile | Rydberg | ) | ) | ||
|---|---|---|---|---|---|---|
Vakumdaki ışık hızı 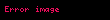 |  |  |  |  |  |  |
İndirgenmiş Planck sabiti |  |  |  |  |  |  |
Temel yük 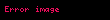 |  |  |  |  |  |  |
Manyetik akı kuantumu  |  |  |  |  |  |  |
Kuantum Hall etkisi  |  |  |  |  |  |  |
Kütleçekim sabiti  |  |  |  |  |  |  |
Boltzmann sabiti  |  |  |  |  |  |  |
 |  |  |  |  |  |  |
Burada:
Ayrıca bakınız
Kaynakça
- ^ http://books.google.com/books?id=12DKsFtFTgYC&pg=PA385 1 Ocak 2014 tarihinde Wayback Machine sitesinde . Thermodynamics and statistical mechanics, by Greiner, Neise, Stöcker
- ^ Dönüşümler için bakınız.
- ^ "Fundamental Physical Constants from NIST". 20 Şubat 2011 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — Planck length". 22 Kasım 2018 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ . 13 Eylül 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — Planck time". 1 Temmuz 2017 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — electric constant". 23 Nisan 2007 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — Planck constant over 2 pi". 11 Haziran 2017 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — speed of light in vacuum". 25 Haziran 2017 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
- ^ "CODATA — Planck temperature". 13 Mayıs 2016 tarihinde kaynağından . Erişim tarihi: 5 Kasım 2017.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte dogal birimler evrensel fizik sabitleri kullanilarak elde edilen olcu birimleridir Ornegin temel yuk e elektriksel yuk ve isik hizi c hiz icin kullanilan dogal birimlerdir Herhangi bir evrensel fizik sabitini 1 birim olarak normallestirmek icin yalnizca evrensel kullanilir Her ne kadar bu sekilde basitlestirme avantaj gibi goruluyor olsa bile fizik yasalarinin matematiksel ifadesinden elde edilen bu sabitlerin anlasilmasi biraz zor olabilir TanimlamaDogal birimlerin tanimlarinin kokeni yalnizca dogadan geldiginden dolayi dogaldir Bunlarin buyuklukleri insan tarafindan elde edilemez Planck birimleri her ne kadar dogal birimler sistemlerinden biri olsa bile dogal birimler olarak adlandirilmasinda bir kisitlama yoktur Planck birimleri siniflandirilan dogal birimlerdir Fakat bu birimler herhangi bir prototip nesne veya parcacigin bir ozelligi olmamasi icin essiz olarak dikkate alinmislardir fakat vakumun bir ozelligi olabilirler Diger gibi dogal birimlerde de uzunluk kutle zaman sicaklik elektrik akimi yerine elektriksel yuk kullanilir Bazi fizikciler sicakligi temek fiziksel nicelik olarak kabul etmiyor Bunu serbest bir parcacigin birim derecedeki enerjisi olarak ifade ediyorlar Cunku enerji kutle uzunluk ve zamana baglidir Hemen hemen tum dogal birimler Boltzmann sabiti kB 1 olarak normallestirilebilir Bu ornegin sicaklik birimini tanimlamanin basit bir yoldur SI da elektriksel yuk birimi amper iken SI dan turetilen birim sisteminde elektriksel yuk birimi coulombdur Gosterim ve kullanimDogal birimler cogunlukla 1 birim olarak normallestirilir Cogu dogal birim sistemleri c 1 esitligini kullanir Burada c isik hizidir Isik hizinin yari hizindaki bir v hizi icin v 1 2 c ve c 1 olur Bu durumda v 1 2 olur v 1 2 esitliginin anlami v hizi ornegin Planck birimlerindeki degeri yarimdir veya v hizi yarim Planck birim hizi kadardir c 1 tum birimlerde kullanilabilir Ornegin E mc Planck birimlerinde E m olarak yazilabilir Bu denklemin anlami Bir parcacigin Planck birimlerine gore enerjisi parcacigin kutlesine esittir Avantajlar ve dezavantajlar Dogal birimler SI ve diger birim sistemleri ile karsilastirildiklarinda hem avantajlari hem de dezavantajlari vardir Basitlestirilmis denklemler Sabitler 1 e normallestirildiginde bu sabitleri bulunduran denklemler de cok sik ortaya cikar ve bazen de anlasilmalari basitlesir Ornegin sabit kutleye sahip bir parcacik icin E2 p2c2 m2c4 ozel gorelilik denkleminin cozumu biraz zordur Fakat denklem dogal birimlere donusturulurse E2 p2 m2 bicimini alir Fiziksel anlami Dogal birimler sistemi boyut analizinde ortaya cikar Ornegin Planck sabiti kuantum mekaniginde aksiyomun temel birimi olarak kabul edilir Prototipleri yoktur Prototip kilogram gibi bir birimi tanimlayan fiziksel somut bir nesnedir Prototipte herhangi bir zamanda her an bir eksiklik olabilir Dogal birimlerin prototipinin olmamasi bir avantajdir Bu avantaji gibi dogal olmayan birim sistemlerinde paylasir Buyuk belirsizlik a 1010 esitligini Planck birimlerinde goz onune alalim Eger a bir uzunluk ifade ederse denklem a 1 6 10 25 metre olur 1 Planck uzunlugunun 1 616199 97 10 35 metre olduguna dikkat edin Eger a bir kutle ifade ederse denklem a 220 kg olur 1 Planck kutlesinin 2 17651 13 10 8 kg olduguna dikkat edin Bu yuzden eger a ifadesi tam olarak tanimlanmazsa a 1010 denklemi yanlis anlasilmaya neden olabilir Normallestirilecek sabitleri secmeFizik sabitlerinin cok olusu dogal birim sistemleri tasarlayicilari tarafindan bu sabitlerden bazilarinin normallestirilmesi 1 e esitlenmesi gerektigi dusuncesini dogurdu Yalnizca birkac sabiti normallestirmek yeterli degildir Ornegin protonun ve elektronun kutleleri normallestirilemez Eger bir elektronun kutlesi 1 olarak normallestirilirse bir protonun kutlesi de 1836 olur Cok basit bir ornek olarak a 1 137 de 1 olarak normallestirilemez Cunku 1 Diger boyutsuz fiziksel sabitler ile ilgili iyi yapili sabit de soyledir a kee2ℏc displaystyle alpha frac k mathrm e e 2 hbar c Burada ke Coulomb sabiti e temel yuk ℏ indirgenmis Planck sabiti ve c isik hizidir Bu yuzden bu dort sabiti eszamanli olarak normallestirmek mumkun degildir Elektromanyetizma birimleriSI birimlerinde elektriksel yuk birimi coulombtur Bu farkli bir birimdir Cunku kutle uzunluk zaman gibi SI birimleri ile soyle ifade edilebilir m 1 2 L 3 2 s 1 Elektromanyetizma icin iki ana dogal birim sistemi vardir elektromanyetizma birimleri sisteminin rasyoneli olarak siniflandirilir elektromanyetizma birimleri sisteminin irrasyoneli olarak siniflandirilir Heaviside Lorentz birimleri cok geneldir Maxwell denklemleri genellikle Lorentz Heaviside birimlerinden ve Gauss birimlerinden daha basittir Bu iki birim sistemindeki e temel yuk denklemi soyledir e 4paℏc displaystyle e sqrt 4 pi alpha hbar c Lorentz Heaviside e aℏc displaystyle e sqrt alpha hbar c Gauss Burada ħ indirgenmis Planck sabiti c isik hizi ve a 1 137 c 1 oldugu dogal birimler sisteminde Lorentz Heaviside birimleri SI birimlerinden turetilebilir Bunun icin m0 1 olarak normallestirilir Gauss birimleri de SI dan turetilebilir Fakat tum elektriksel alanlarin 4pϵ0 displaystyle sqrt 4 pi epsilon 0 bolunmesi tum manyetik alinganliklarin 4p ile carpilmasi gibi karmasik donusumler uygulanmalidir Dogal birimler sistemleriPlanck birimleri Tablo 1 Temel Planck birimleri Boyut Ifade Deger SI birimleri Planck uzunlugu Uzunluk L lP ℏGc3 displaystyle l text P sqrt frac hbar G c 3 1 616 199 97 10 35mPlanck kutlesi Kutle M mP ℏcG displaystyle m text P sqrt frac hbar c G 2 176 51 13 10 8kgPlanck zamani Zaman T tP lPc ℏmPc2 ℏGc5 displaystyle t text P frac l text P c frac hbar m text P c 2 sqrt frac hbar G c 5 5 391 06 32 10 44sPlanck yuku Elektriksel yuk Q qP 4pe0ℏc displaystyle q text P sqrt 4 pi varepsilon 0 hbar c 1 875 545 956 41 10 18CPlanck sicakligi Sicaklik 8 TP mPc2kB ℏc5GkB2 displaystyle T text P frac m text P c 2 k text B sqrt frac hbar c 5 Gk text B 2 1 416 833 85 1032K Planck birimleri soyle tanimlanir c G ℏ kB 1 displaystyle c G hbar k text B 1 Burada c bir vakumdaki isik hizi G yercekimi sabiti ℏ displaystyle hbar indirgenmis Planck sabiti ve kB Boltzmann sabitidir Planck birimleri dogal birimlerde bir sistemdir Bunlar hicbir fiziksel nesnenin prototipin hatta temel parcacigin bile ozellikleri degildir Yalnizca fizik yasalarinin temel yapisini ifade ederler c ve G genel gorelilikteki uzayzaman modelinin sabitleridir ve ℏ kuantum mekaniginde enerjinin frekansa orani veya dalga boyu ile eigen momentumunun carpimidir Ozet tablosuAdi Sembol Planck ile Rydberg Vakumdaki isik hizi c displaystyle c 1 displaystyle 1 1 displaystyle 1 1a displaystyle frac 1 alpha 2a displaystyle frac 2 alpha 1 displaystyle 1 1 displaystyle 1 Indirgenmis Planck sabiti ℏ h2p displaystyle hbar frac h 2 pi 1 displaystyle 1 1a displaystyle frac 1 alpha 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 Temel yuk e displaystyle e a displaystyle sqrt alpha 1 displaystyle 1 1 displaystyle 1 2 displaystyle sqrt 2 4pa displaystyle sqrt 4 pi alpha a displaystyle sqrt alpha Manyetik aki kuantumu KJ epℏ displaystyle K text J frac e pi hbar ap displaystyle frac sqrt alpha pi ap displaystyle frac alpha pi 1p displaystyle frac 1 pi 2p displaystyle frac sqrt 2 pi 4ap displaystyle sqrt frac 4 alpha pi ap displaystyle frac sqrt alpha pi Kuantum Hall etkisi RK 2pℏe2 displaystyle R text K frac 2 pi hbar e 2 2pa displaystyle frac 2 pi alpha 2pa displaystyle frac 2 pi alpha 2p displaystyle 2 pi p displaystyle pi 12a displaystyle frac 1 2 alpha 2pa displaystyle frac 2 pi alpha Kutlecekim sabiti G displaystyle G 1 displaystyle 1 1 displaystyle 1 aGa displaystyle frac alpha text G alpha 8aGa displaystyle frac 8 alpha text G alpha aGme2 displaystyle frac alpha text G m text e 2 aGme2 displaystyle frac alpha text G m text e 2 Boltzmann sabiti kB displaystyle k text B 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 1 displaystyle 1 me displaystyle m text e aG displaystyle sqrt alpha text G aGa displaystyle sqrt frac alpha text G alpha 1 displaystyle 1 12 displaystyle frac 1 2 511 keV displaystyle 511 text keV 511 keV displaystyle 511 text keV Burada a 7 2973525698 24 10 3 aG me mP 2 1 752 10 45 keV kiloelektronvoltAyrica bakinizBoyut analizi Temel birim Fizik sabitiKaynakca http books google com books id 12DKsFtFTgYC amp pg PA385 1 Ocak 2014 tarihinde Wayback Machine sitesinde Thermodynamics and statistical mechanics by Greiner Neise Stocker Donusumler icin bakiniz Fundamental Physical Constants from NIST 20 Subat 2011 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 CODATA Planck length 22 Kasim 2018 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 13 Eylul 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Kasim 2017 CODATA Planck time 1 Temmuz 2017 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 CODATA electric constant 23 Nisan 2007 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 CODATA Planck constant over 2 pi 11 Haziran 2017 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 CODATA speed of light in vacuum 25 Haziran 2017 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017 CODATA Planck temperature 13 Mayis 2016 tarihinde kaynagindan Erisim tarihi 5 Kasim 2017
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State