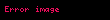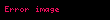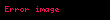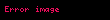Eliptik yörünge, Astronomi ve uzay mühendisliğinde, dışmerkezliği (basıklık) 0'dan büyük ancak 1'den küçük olan yörüngedir. Dışmerkezliği 0'a eşit olan yörünge daireseldir ve bu yörüngeye dairesel yörünge denir. Eliptik bir yörüngede her zaman negatiftir. Hohmann transfer yörüngesi, Molniya yörünge ve Tundra yörünge başlıca eliptik yörüngeler arasındadır.

Hız
Uzay mühendisliğince kabul edilen standart şartlar ve varsayımlar altında, eliptik yörüngede hareket halinde bulunan 0'dan büyük kütleli bir cismin yörüngesel hızı (
Burada,
standart kütleçekim değişkeni,
yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafe,
ise yarı-büyük eksen uzunluğudur.
Bu eşitlikten çıkartılacak iki önemli sonuç:
- Eliptik bir yörüngede yörüngesel hız dışmerkezliğe değil yarı-büyük eksenin (
) uzunluğuna bağlıdır.
- Hız ile alakalı bu eşitlik hiperbolik yörüngedeki gibidir. Aralarındaki fark hiperbolik yörüngede
'nın pozitif olmasıdır.
Enerji
Standart şartlar ve varsayımlar altında, eliptik yörüngede hareket eden bir cismin özgül yörüngesel enerjisi (
şeklinde ifade edilir.
Burada,
yörüngedeki cismin hızı,
yörüngedeki cisim ile merkezi cisim arasındaki radyal mesafe,
yarı-büyük eksenin uzunluğum
ise standart kütleçekim değişkenidir.
Sonuç:
- Özgül yörüngesel enerji dışmerkezlikten bağımsızdır ve sadece elipsin yarı-büyük ekseninden etkilenir.
Ayrıca bu noktada kullanarak;
- Özgül potansiyel enerjinin zaman-ortalamasının 2ε'ye eşit olduğu,
- r−1'nin zaman-ortalamasının a−1 olarak ifade edilebileceği ve
- Özgül kinetik enerjinin -ε'ye eşit olduğu bulunabilir.
Uçuş yolu açısı
şeklinde gösterilir. Burada,
açısal momentum,
yörüngedeki cismin yörüngesel hızı,
yörüngedeki cisim ile merkezi cisim arasındaki radyal mesafe,
de uçuş yolu açısıdır.
Hareket formülü
Bkz.
Ayrıca bakınız
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Eliptik yorunge Astronomi ve uzay muhendisliginde dismerkezligi basiklik 0 dan buyuk ancak 1 den kucuk olan yorungedir Dismerkezligi 0 a esit olan yorunge daireseldir ve bu yorungeye dairesel yorunge denir Eliptik bir yorungede her zaman negatiftir Hohmann transfer yorungesi Molniya yorunge ve Tundra yorunge baslica eliptik yorungeler arasindadir Birbirine yakin kutleye sahip iki cisim ortak kutlemerkezleri etrafinda eliptik yorungelerde hareket ederken goruluyor HizUzay muhendisligince kabul edilen standart sartlar ve varsayimlar altinda eliptik yorungede hareket halinde bulunan 0 dan buyuk kutleli bir cismin yorungesel hizi v displaystyle v asagidaki sekilde hesaplanabilir v m 2r 1a displaystyle v sqrt mu left 2 over r 1 over a right Burada m displaystyle mu standart kutlecekim degiskeni r displaystyle r yorungeyi cizen cisim ile merkezi kutle arasindaki radyal mesafe a displaystyle a ise yari buyuk eksen uzunlugudur Bu esitlikten cikartilacak iki onemli sonuc Eliptik bir yorungede yorungesel hiz dismerkezlige degil yari buyuk eksenin a displaystyle a uzunluguna baglidir Hiz ile alakali bu esitlik hiperbolik yorungedeki gibidir Aralarindaki fark hiperbolik yorungede 12a displaystyle 1 over 2a nin pozitif olmasidir EnerjiStandart sartlar ve varsayimlar altinda eliptik yorungede hareket eden bir cismin ozgul yorungesel enerjisi ϵ displaystyle epsilon 0 dan kucuktur ve bu yorunge icin enerji konservasyon esitligi v22 mr m2a ϵ lt 0 displaystyle v 2 over 2 mu over r mu over 2a epsilon lt 0 seklinde ifade edilir Burada v displaystyle v yorungedeki cismin hizi r displaystyle r yorungedeki cisim ile merkezi cisim arasindaki radyal mesafe a displaystyle a yari buyuk eksenin uzunlugum m displaystyle mu ise standart kutlecekim degiskenidir Sonuc Ozgul yorungesel enerji dismerkezlikten bagimsizdir ve sadece elipsin yari buyuk ekseninden etkilenir Ayrica bu noktada kullanarak Ozgul potansiyel enerjinin zaman ortalamasinin 2e ye esit oldugu r 1 nin zaman ortalamasinin a 1 olarak ifade edilebilecegi ve Ozgul kinetik enerjinin e ye esit oldugu bulunabilir Ucus yolu acisih rvcos ϕ displaystyle h rv cos phi seklinde gosterilir Burada h displaystyle h acisal momentum v displaystyle v yorungedeki cismin yorungesel hizi r displaystyle r yorungedeki cisim ile merkezi cisim arasindaki radyal mesafe ϕ displaystyle phi de ucus yolu acisidir Hareket formuluBkz Ayrica bakinizDairesel yorunge Yorungeler listesi Parabolik yorunge
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State