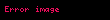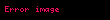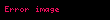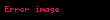Uzay mekaniğinde dışmerkezliği sıfıra eşit olan eliptik yörünge olarak özetlenebilecek dairesel yörünge, tanım olarak fizikte sabit eksen etrafında rotasyonun tipik bir örneğidir. Burada bahsedilen eksen, hareket düzlemine dik olarak kütle merkezlerinden geçen doğrudur.

Dairesel ivme
Kütleçekim tarafından yaratılan merkezcil ivme (hareket yönüne dik enine veya özekçil ivme), yörüngede aslında düz bir doğru boyunca ilerlemek isteyen cismin yönünü sürekli olarak aynı miktarda ve sürede değiştirerek kütle merkezi etrafında bir dairesel veya eliptik hareket etmesini sağlar. bulabilmek için aşağıdaki formül kullanılabilir.
Burada,
yörüngeyi çizen küçük cismin yörüngesel hızı,
çizilen dairenin yarıçapı
ise (radyan/saniye cinsinden) açısal frekansı ifade eder.
Hız
Uzay mühendisliğince kabul edilen standart şartlar ve varsayımlar altında, dairesel yörüngede hareket halinde bulunan 0'dan büyük kütleli bir cismin yörüngesel hızı (
Burada,
yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
ise standart kütleçekim değişkenidir. Bu değer evrensel kütleçekim sabiti
ile merkezi kütlenin
çarpımına eşittir.
Not: Bu eşitlikten çıkartılması gereken en önemli sonuç, dairesel yörüngede hareket eden bir cismin yörünge boyunca bulunduğu nokta veya konum her ne olursa olsun hızının daima aynı ve sabit kalacağı olmalıdır.
Yörüngesel periyot
Standart şartlar ve varsayımlar altında, dairesel yörüngede hareket eden bir cismin yörüngesel periyodu (
formülü ile hesaplanabilir. Burada,
yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
ise standart kütleçekim değişkenidir.
Enerji
Standart şartlar ve varsayımlar altında yörüngesel enerji (
formunu alacaktır. Burada,
cismin yörüngesel hızı,
yörüngeyi çizen cisim ile merkezi kütle arasındaki radyal mesafeye eşit olan yarıçap,
ise standart kütleçekim değişkenidir.
Burada limit 

burada zaman ortalamaları alınmadan dahi geçerlidir.
- Sistemin potansiyel enerjisi toplam enerjinin iki katına eşittir.
- Sistemin kinetik enerjisi toplam enerji çarpı (-1)'e eşittir.
Elbette bu durumda herhangi bir mesafeden kurtulma hızı, √2 çarpı dairesel yörüngede o mesafedeki hızıdır. Kinetik enerji ise bunun iki katıdır ve o yüzden sistemin toplam enerjisi sıfıra eşittir (kapalı sistem).
Hareket eşitliği
Standart şartlar ve varsayımlar altında kısaca
şeklinde ifade edilir. Burada,
yörüngedeki cisim ile merkezi kütle arasındaki radyal mesafe,
yörüngedeki cismin açısal momentumu (açısal devinirlik),
de standart kütleçekim değişkenidir.
Dairesel bir yörüngeye girmek için gereken delta-v
Belirli bir manevra yapabilmek için gereken delta-v, bir için gereken delta-v`den fazladır. Bu konuda ayrıntıli bilgi için göz atınız.
Ayrıca bakınız
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Uzay mekaniginde dismerkezligi sifira esit olan eliptik yorunge olarak ozetlenebilecek dairesel yorunge tanim olarak fizikte sabit eksen etrafinda rotasyonun tipik bir ornegidir Burada bahsedilen eksen hareket duzlemine dik olarak kutle merkezlerinden gecen dogrudur Farkli kutle ve yaricapa sahip iki cisim konum olarak uzaydaki bir boslukta bulunan ortak kutle merkezleri etrafinda dairesel yorungelerinde hareket ederken goruluyor Dairesel ivmeKutlecekim tarafindan yaratilan merkezcil ivme hareket yonune dik enine veya ozekcil ivme yorungede aslinda duz bir dogru boyunca ilerlemek isteyen cismin yonunu surekli olarak ayni miktarda ve surede degistirerek kutle merkezi etrafinda bir dairesel veya eliptik hareket etmesini saglar bulabilmek icin asagidaki formul kullanilabilir a v2rrr w2r displaystyle mathbf a frac v 2 r frac mathbf r r omega 2 mathbf r Burada v displaystyle v yorungeyi cizen kucuk cismin yorungesel hizi r displaystyle r cizilen dairenin yaricapi w displaystyle omega ise radyan saniye cinsinden acisal frekansi ifade eder HizUzay muhendisligince kabul edilen standart sartlar ve varsayimlar altinda dairesel yorungede hareket halinde bulunan 0 dan buyuk kutleli bir cismin yorungesel hizi vc displaystyle v c asagidaki sekilde hesaplanabilir vc mr displaystyle v c sqrt mu over r Burada r displaystyle r yorungeyi cizen cisim ile merkezi kutle arasindaki radyal mesafeye esit olan yaricap m GM displaystyle mu GM ise standart kutlecekim degiskenidir Bu deger evrensel kutlecekim sabiti G displaystyle G ile merkezi kutlenin M displaystyle M carpimina esittir Not Bu esitlikten cikartilmasi gereken en onemli sonuc dairesel yorungede hareket eden bir cismin yorunge boyunca bulundugu nokta veya konum her ne olursa olsun hizinin daima ayni ve sabit kalacagi olmalidir Yorungesel periyotStandart sartlar ve varsayimlar altinda dairesel yorungede hareket eden bir cismin yorungesel periyodu T displaystyle T T 2pr3m displaystyle T 2 pi sqrt r 3 over mu formulu ile hesaplanabilir Burada r displaystyle r yorungeyi cizen cisim ile merkezi kutle arasindaki radyal mesafeye esit olan yaricap m displaystyle mu ise standart kutlecekim degiskenidir EnerjiStandart sartlar ve varsayimlar altinda yorungesel enerji ϵ displaystyle epsilon kapali bir yorunge icin eksidir ve enerji korunum yasasi geregi yorungesel enerji v22 mr ϵ lt 0 displaystyle v 2 over 2 mu over r epsilon lt 0 formunu alacaktir Burada v displaystyle v cismin yorungesel hizi r displaystyle r yorungeyi cizen cisim ile merkezi kutle arasindaki radyal mesafeye esit olan yaricap m displaystyle mu ise standart kutlecekim degiskenidir Burada limit ϵ 0 displaystyle epsilon 0 dir ve bu cismin parabolik yorungeden v 2vc 2mr displaystyle v sqrt 2 v c sqrt 2 mu over r ile kacisini ifade eder burada zaman ortalamalari alinmadan dahi gecerlidir Sistemin potansiyel enerjisi toplam enerjinin iki katina esittir Sistemin kinetik enerjisi toplam enerji carpi 1 e esittir Elbette bu durumda herhangi bir mesafeden kurtulma hizi 2 carpi dairesel yorungede o mesafedeki hizidir Kinetik enerji ise bunun iki katidir ve o yuzden sistemin toplam enerjisi sifira esittir kapali sistem Hareket esitligiStandart sartlar ve varsayimlar altinda kisaca r h2m displaystyle r h 2 over mu seklinde ifade edilir Burada r displaystyle r yorungedeki cisim ile merkezi kutle arasindaki radyal mesafe h displaystyle h yorungedeki cismin acisal momentumu acisal devinirlik m displaystyle mu de standart kutlecekim degiskenidir Dairesel bir yorungeye girmek icin gereken delta vBelirli bir manevra yapabilmek icin gereken delta v bir icin gereken delta v den fazladir Bu konuda ayrintili bilgi icin goz atiniz Ayrica bakinizYorunge Eliptik yorunge Yorungeler listesi Iki cisim problemiKaynakca
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State