Elektriksel güç, elektrik enerjisinde elektrik devresi tarafından taşınan güç olarak tanımlanır. Gücün SI birimi watt'tır. Elektrikli cihazların birim zamanda harcadığı enerji miktarı olarak da bilinir. 1 saniyede 1 joule enerji harcayan elektrikli alet 1 watt gücündedir.
Güç | |
| Yaygın sembol(ler): | ℘ veya P |
| temel SI birimlerinden türetimi: | kg⋅m2⋅s−3 |
| SI nicelik boyutu: | wikidata |
| SI birimi: | watt (W) |
| Diğer niceliklerden türetimi: | |


Yeraltı iletimi için bakın.
Bir devrede elektrik akımı aktığında, mekaniksel veya enerjiye dönüştürülebilir. Aygıtlar elektrik enerjisini, ısı, ışık (ampuller), devinim (hareket) (elektrik motorları), ses (hoparlör) veya kimyasal dönüşümler gibi birçok kullanışlı biçime dönüştürür. Elektrik, kimyasal olarak pillere depolanabilir.
Tanım
Elektrik gücü, mekanik güç gibi, watt cinsinden ölçülen ve P harfiyle gösterilen iş yapma hızıdır. Watt terimi halk dilinde "watt cinsinden elektrik gücü" anlamında kullanılır. V değerinde bir elektrik potansiyeli (voltaj) farkından her t saniyede bir Q coulomb yükünden oluşan bir elektrik akımı I tarafından üretilen watt cinsinden elektrik gücü:
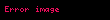
- W joule cinsinden iş,
- t saniye cinsinden zaman,
- Q coulomb cinsinden elektrik yükü,
- V volt cinsinden elektrik potansiyeli veya voltaj,
- I amper cinsinden elektrik akımıdır
yani,
- watt = volt çarpı amper.
Açıklama

Elektrik devrelerindeki elektrik bileşenlerinde oluşan elektrik potansiyel farkı (voltaj) boyunca elektrik yükleri hareket ettiğinde elektrik gücü diğer enerji türlerine dönüşür. Elektrik gücü açısından bakıldığında, bir elektrik devresindeki bileşenler iki kategoriye ayrılabilir:

Aktif cihazlar (güç kaynakları)
Elektrik akımı cihazdan alçak elektrik potansiyelinden yüksek elektrik potansiyeline doğru akmaya zorlanırsa, pozitif yükler negatif terminalden pozitif terminale doğru hareket eder, yükler üzerinde iş yapılır ve enerji, mekanik enerji veya kimyasal enerji gibi başka bir enerji türünden elektrik potansiyel enerjisine dönüştürülür. Bunun meydana geldiği cihazlara aktif cihazlar veya Elektrik jeneratörleri ve piller gibi güç kaynakları denir. Bazı cihazlar, içinden geçen voltaj ve akıma bağlı olarak kaynak veya yük olabilir. Örneğin, şarj edilebilir pil, bir devreye güç sağladığında kaynak görevi yapar ancak bir pil şarj cihazına bağlandığında ve yeniden şarj edilirken yük görevi yapar
Pasif cihazlar (yükler)
Geleneksel akım cihazdan yüksek potansiyelden (voltaj) düşük potansiyele doğru akarsa, pozitif yük pozitif (+) terminalden negatif (-) terminale doğru hareket ederse, cihaz üzerindeki yükler tarafından iş yapılır. Terminaller arasındaki gerilimden dolayı yüklerin potansiyel enerjisi cihazda kinetik enerjiye dönüştürülür. Bu cihazlara pasif bileşenler veya yükler denir; devreden elektrik gücünü 'tüketirler' ve bunu mekanik iş, ısı, ışık vb. gibi diğer enerji türlerine dönüştürürler. Örnekler arasında ampuller, elektrik motorları ve elektrikli ısıtıcılar gibi elektrikli cihazlar bulunur. Alternatif akım (AC) devrelerinde voltajın yönü periyodik olarak tersine döner, ancak akım her zaman yüksek potansiyelden düşük potansiyel tarafına doğru akar.

Pasif işaret kuralı
Elektrik gücü bir bileşenin içine veya dışına akabildiğinden, yönün pozitif güç akışını temsil ettiği bir kurala ihtiyaç vardır. Bir devrenin dışarı bir bileşenin içine akan elektrik gücü keyfi olarak pozitif bir işarete sahip olacak şekilde tanımlanırken, bir bileşenden bir devreye içeriye akan güç negatif bir işarete sahip olacak şekilde tanımlanır. Bu nedenle pasif bileşenler pozitif güç tüketimine sahipken, güç kaynakları negatif güç tüketimine sahiptir. Buna pasif işaret kuralı denir.
Direnç devreleri
Dirençli (Ohmik veya doğrusal) yükler durumunda, harcanan güç miktarı için alternatif ifadeler üretmek için güç formülü (P = I·V) ve Joule'ün birinci yasası (P = I^2·R), Ohm kanunuyla (V = I·R) birleştirilebilir:
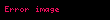
Harmoniksiz alternatif akım
Alternatif akım devrelerinde indüktans ve kapasitans gibi enerji depolama elemanları, enerji akış yönünün periyodik olarak tersine çevrilmesine neden olabilir.
AC dalga formunun tam bir döngüsü boyunca ortalaması alınan enerji akışının (güç) bir yönde net enerji aktarımıyla sonuçlanan kısmına, gerçek güç denir (aynı zamanda aktif güç olarak da adlandırılır).
Enerji akışının (güç), net enerji aktarımıyla sonuçlanmayan, bunun yerine depolanan enerji nedeniyle her döngüde kaynak ve yük arasında salınım yapan kısmının genliğine, reaktif gücün mutlak değeri denir.
Gerilim dalgasının RMS değeri ile akım dalgasının RMS değerinin çarpımına görünür güç denir.
Bir cihazın tükettiği watt cinsinden gerçek güç P, şu formülden hesaplanır:
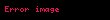
- Vp volt cinsinden tepe voltajı
- Ip amper cinsinden tepe akımı
- Vrms volt cinsinden voltajın karekök ortalaması
- Irms amper cinsinden akımın karekök ortalaması
- θ = θv − θi gerilim sinüs dalgasının akım sinüs dalgasına öncülük ettiği faz açısı veya eşdeğer olarak akım sinüs dalgasının gerilim sinüs dalgasını geride bıraktığı faz açısıdır

Gerçek güç, reaktif güç ve görünür güç arasındaki ilişki, büyüklüklerin vektörler halinde temsil edilmesiyle ifade edilebilir. Gerçek güç yatay bir vektörle, reaktif güç ise dikey bir vektörle temsil edilir. Görünen güç vektörü, gerçek ve reaktif güç vektörlerinin birleştirilmesiyle oluşturulan bir dik üçgenin hipotenüsüdür. Bu temsile genellikle güç üçgeni denir. Pisagor teoremini kullanarak gerçek, reaktif ve görünen güç arasındaki ilişki şu şekildedir: 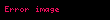
Gerçek ve reaktif güçler, akım ve voltajın her ikisi de sinüsoidler olduğunda ve aralarında bilinen bir θ faz açısı olduğunda doğrudan görünen güçten hesaplanabilir:
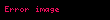
Gerçek gücün görünen güce oranı güç faktörü olarak adlandırılır ve her zaman -1 ile 1 arasında bir sayıdır. Akımların ve gerilimlerin sinüzoidal olmayan formlara sahip olduğu durumlarda, güç faktörü distorsiyonun etkilerini içerecek şekilde genelleştirilir.
Elektromanyetik alanlar
Elektrik enerjisi, elektrik ve manyetik alanların bir arada bulunduğu her yere akar ve aynı yerde dalgalanır. Bunu en basit örneği, önceki bölümdeki elektrik devresinde gösterilmiştir. Ancak genel durumda, basit P = IV denkleminin yerini daha karmaşık bir hesaplama alabilir.
Elektrik alan şiddet ve manyetik alan şiddet vektörlerinin çapraz çarpımının kapalı yüzey integrali, hacimden çıkan toplam anlık gücü (watt cinsinden) verir:
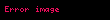
Sonuç skalerdir çünkü Poynting vektörünün yüzey integrali''dir.
Alternatif Akım
Alternatif akım devrelerinde bobin ve kapasitans gibi enerji depolayan elemanlar, enerji akışının yönüne ters, periyodik sonuç verebilirler. AC (Alternatif akım) dalga formunun tam bir çevrimindeki ortalama güç akışı, aktif güç (gerçek güç) olarak güç yönünde net enerji taşınmasına neden olur. Depolanan enerjiden dolayı güç akışının bu kısmı her bir çevrimde kaynağa geri döner. Bu durum reaktif güç olarak bilinir.

Yukarıdaki aktif güç ve güç üçgeni teoremi, sadece hem akımın hem de gerilimin tam sinüzoidal olduğunda geçerlidir. Bu yüzden akımın normal olarak bozuk olduğu alçak gerilim aktarma uygulamalarında çok az kullanılır.
Sinüsoidal Kaynakta Anlık Güç
Bir devrede bir elemanın anlık gücünü belli bir 
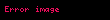
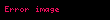
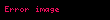
Gerilim ve akımın anlık değerlerini bildiğimize göre ifademizi açıp genişletebiliriz. Gerilim fazörünün açı değeri 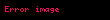
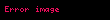
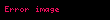
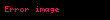
Yukarıdaki ifadede bulunan 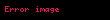
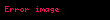
Bu trigonometrik dönüşümlerin ardından anlık güç formulasyonunu tekrar yazalım...
Anlık güç formülasyonunda bulunan 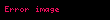
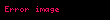
Bu trigonometrik eşitliğin sonrasında anlık güç aşağıdaki şekilde ifade edilebilir.
Son çıkan anlık güç ifadesinde bir şey dikkatimizi çekmektedir. Bu da 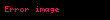
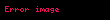
Sinüsoidal Kaynakta Anlık Güç
 |
Ayrıca bakınız
- (Elektrik üretimi)
- Enerji kaynakları
Kaynakça
- ^ a b Thomas, Roland E.; Rosa, Albert J.; Toussaint, Gregory J. (2016). The Analysis and Design of Linear Circuits (8 bas.). Wiley. ss. 812-813. ISBN .
- ^ Fraile Mora, Jesús (2012). Circuitos eléctricos (İspanyolca). Pearson. ss. 193-196. ISBN .
- ^ IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal, Nonsinusoidal, Balanced, or Unbalanced Conditions. IEEE. 2010. s. 4. doi:10.1109/IEEESTD.2010.5439063. ISBN .
- ^ Hayt, William H.; Buck, John A. (2012). Engineering Electromagnetics (8 bas.). McGraw-Hill. s. 385. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Elektriksel guc elektrik enerjisinde elektrik devresi tarafindan tasinan guc olarak tanimlanir Gucun SI birimi watt tir Elektrikli cihazlarin birim zamanda harcadigi enerji miktari olarak da bilinir 1 saniyede 1 joule enerji harcayan elektrikli alet 1 watt gucundedir GucYaygin sembol ler veya Ptemel SI birimlerinden turetimi kg m2 s 3SI nicelik boyutu wikidataSI birimi watt W Diger niceliklerden turetimi E t F v Voltaj U I t wElektrik enerjisi bunun gibi havai hatlar ve ayrica yer alti yuksek gerilim kablolari araciligiyla iletilir Elektrik gucu celik direkler vasitasiyla havai hatlar ile tasinir Yeralti iletimi icin bakin Bir devrede elektrik akimi aktiginda mekaniksel veya enerjiye donusturulebilir Aygitlar elektrik enerjisini isi isik ampuller devinim hareket elektrik motorlari ses hoparlor veya kimyasal donusumler gibi bircok kullanisli bicime donusturur Elektrik kimyasal olarak pillere depolanabilir TanimElektrik gucu mekanik guc gibi watt cinsinden olculen ve P harfiyle gosterilen is yapma hizidir Watt terimi halk dilinde watt cinsinden elektrik gucu anlaminda kullanilir V degerinde bir elektrik potansiyeli voltaj farkindan her t saniyede bir Q coulomb yukunden olusan bir elektrik akimi I tarafindan uretilen watt cinsinden elektrik gucu Birim zamanda yapilan is Wt WQQt VI displaystyle text Birim zamanda yapilan is wp frac W t frac W Q frac Q t VI burada W joule cinsinden is t saniye cinsinden zaman Q coulomb cinsinden elektrik yuku V volt cinsinden elektrik potansiyeli veya voltaj I amper cinsinden elektrik akimidir yani watt volt carpi amper AciklamaGuc kaynagini gosteren animasyon Elektrik devrelerindeki elektrik bilesenlerinde olusan elektrik potansiyel farki voltaj boyunca elektrik yukleri hareket ettiginde elektrik gucu diger enerji turlerine donusur Elektrik gucu acisindan bakildiginda bir elektrik devresindeki bilesenler iki kategoriye ayrilabilir Elektrik yukunu gosteren animasyonAktif cihazlar guc kaynaklari Elektrik akimi cihazdan alcak elektrik potansiyelinden yuksek elektrik potansiyeline dogru akmaya zorlanirsa pozitif yukler negatif terminalden pozitif terminale dogru hareket eder yukler uzerinde is yapilir ve enerji mekanik enerji veya kimyasal enerji gibi baska bir enerji turunden elektrik potansiyel enerjisine donusturulur Bunun meydana geldigi cihazlara aktif cihazlar veya Elektrik jeneratorleri ve piller gibi guc kaynaklari denir Bazi cihazlar icinden gecen voltaj ve akima bagli olarak kaynak veya yuk olabilir Ornegin sarj edilebilir pil bir devreye guc sagladiginda kaynak gorevi yapar ancak bir pil sarj cihazina baglandiginda ve yeniden sarj edilirken yuk gorevi yapar Pasif cihazlar yukler Geleneksel akim cihazdan yuksek potansiyelden voltaj dusuk potansiyele dogru akarsa pozitif yuk pozitif terminalden negatif terminale dogru hareket ederse cihaz uzerindeki yukler tarafindan is yapilir Terminaller arasindaki gerilimden dolayi yuklerin potansiyel enerjisi cihazda kinetik enerjiye donusturulur Bu cihazlara pasif bilesenler veya yukler denir devreden elektrik gucunu tuketirler ve bunu mekanik is isi isik vb gibi diger enerji turlerine donustururler Ornekler arasinda ampuller elektrik motorlari ve elektrikli isiticilar gibi elektrikli cihazlar bulunur Alternatif akim AC devrelerinde voltajin yonu periyodik olarak tersine doner ancak akim her zaman yuksek potansiyelden dusuk potansiyel tarafina dogru akar Gucun bir elektrik devresi araciligiyla aktarimiPasif isaret kurali Elektrik gucu bir bilesenin icine veya disina akabildiginden yonun pozitif guc akisini temsil ettigi bir kurala ihtiyac vardir Bir devrenin disari bir bilesenin icine akan elektrik gucu keyfi olarak pozitif bir isarete sahip olacak sekilde tanimlanirken bir bilesenden bir devreye iceriye akan guc negatif bir isarete sahip olacak sekilde tanimlanir Bu nedenle pasif bilesenler pozitif guc tuketimine sahipken guc kaynaklari negatif guc tuketimine sahiptir Buna pasif isaret kurali denir Direnc devreleri Direncli Ohmik veya dogrusal yukler durumunda harcanan guc miktari icin alternatif ifadeler uretmek icin guc formulu P I V ve Joule un birinci yasasi P I 2 R Ohm kanunuyla V I R birlestirilebilir IV I2R V2R displaystyle wp IV I 2 R frac V 2 R burada R elektrik direncidir Harmoniksiz alternatif akim Alternatif akim devrelerinde induktans ve kapasitans gibi enerji depolama elemanlari enerji akis yonunun periyodik olarak tersine cevrilmesine neden olabilir AC dalga formunun tam bir dongusu boyunca ortalamasi alinan enerji akisinin guc bir yonde net enerji aktarimiyla sonuclanan kismina gercek guc denir ayni zamanda aktif guc olarak da adlandirilir Enerji akisinin guc net enerji aktarimiyla sonuclanmayan bunun yerine depolanan enerji nedeniyle her dongude kaynak ve yuk arasinda salinim yapan kisminin genligine reaktif gucun mutlak degeri denir Gerilim dalgasinin RMS degeri ile akim dalgasinin RMS degerinin carpimina gorunur guc denir Bir cihazin tukettigi watt cinsinden gercek guc P su formulden hesaplanir 12VpIpcos 8 VrmsIrmscos 8 displaystyle wp 1 over 2 V p I p cos theta V rm rms I rm rms cos theta burada Vp volt cinsinden tepe voltaji Ip amper cinsinden tepe akimi Vrms volt cinsinden voltajin karekok ortalamasi Irms amper cinsinden akimin karekok ortalamasi 8 8v 8i gerilim sinus dalgasinin akim sinus dalgasina onculuk ettigi faz acisi veya esdeger olarak akim sinus dalgasinin gerilim sinus dalgasini geride biraktigi faz acisidirGuc ucgeni AC gucunun bilesenleri Gercek guc reaktif guc ve gorunur guc arasindaki iliski buyukluklerin vektorler halinde temsil edilmesiyle ifade edilebilir Gercek guc yatay bir vektorle reaktif guc ise dikey bir vektorle temsil edilir Gorunen guc vektoru gercek ve reaktif guc vektorlerinin birlestirilmesiyle olusturulan bir dik ucgenin hipotenusudur Bu temsile genellikle guc ucgeni denir Pisagor teoremini kullanarak gercek reaktif ve gorunen guc arasindaki iliski su sekildedir gorunur guc 2 gercek guc 2 reaktif guc 2 displaystyle text gorunur guc 2 text gercek guc 2 text reaktif guc 2 Gercek ve reaktif gucler akim ve voltajin her ikisi de sinusoidler oldugunda ve aralarinda bilinen bir 8 faz acisi oldugunda dogrudan gorunen gucten hesaplanabilir gercek guc gorunur guc cos 8 displaystyle text gercek guc text gorunur guc cos theta reaktif guc gorunur guc sin 8 displaystyle text reaktif guc text gorunur guc sin theta Gercek gucun gorunen guce orani guc faktoru olarak adlandirilir ve her zaman 1 ile 1 arasinda bir sayidir Akimlarin ve gerilimlerin sinuzoidal olmayan formlara sahip oldugu durumlarda guc faktoru distorsiyonun etkilerini icerecek sekilde genellestirilir Elektromanyetik alanlar Elektrik enerjisi elektrik ve manyetik alanlarin bir arada bulundugu her yere akar ve ayni yerde dalgalanir Bunu en basit ornegi onceki bolumdeki elektrik devresinde gosterilmistir Ancak genel durumda basit P IV denkleminin yerini daha karmasik bir hesaplama alabilir Elektrik alan siddet ve manyetik alan siddet vektorlerinin capraz carpiminin kapali yuzey integrali hacimden cikan toplam anlik gucu watt cinsinden verir alan E H dA displaystyle wp oint text alan mathbf E times mathbf H cdot d mathbf A Sonuc skalerdir cunku Poynting vektorunun yuzey integrali dir Alternatif Akim Alternatif akim devrelerinde bobin ve kapasitans gibi enerji depolayan elemanlar enerji akisinin yonune ters periyodik sonuc verebilirler AC Alternatif akim dalga formunun tam bir cevrimindeki ortalama guc akisi aktif guc gercek guc olarak guc yonunde net enerji tasinmasina neden olur Depolanan enerjiden dolayi guc akisinin bu kismi her bir cevrimde kaynaga geri doner Bu durum reaktif guc olarak bilinir Guc ucgeninde Yukaridaki aktif guc ve guc ucgeni teoremi sadece hem akimin hem de gerilimin tam sinuzoidal oldugunda gecerlidir Bu yuzden akimin normal olarak bozuk oldugu alcak gerilim aktarma uygulamalarinda cok az kullanilir Sinusoidal Kaynakta Anlik Guc Bir devrede bir elemanin anlik gucunu belli bir t displaystyle t aninda uclari arasindaki gerilim ve o anda uzerinden gecen akimin carpimiyla elde edebiliriz Gerilimi Volt displaystyle text Volt akimi da Amper displaystyle text Amper birimlerinden alirsak anlik gucun birimini Watt displaystyle text Watt olarak buluruz Anlik gucun genel ifadesini asagidaki gibi yazabiliriz p t v t i t displaystyle p t v t cdot i t dd Gerilim ve akimin anlik degerlerini bildigimize gore ifademizi acip genisletebiliriz Gerilim fazorunun aci degeri fv displaystyle varphi v akim fazorunun aci degeri ise fi displaystyle varphi i kabul edilecektir Akimi referans olarak alip akim fazina 0 displaystyle 0 dersek gerilim fazi fv fi displaystyle varphi v varphi i olur Bu genel bir yaklasimdir Buldugumuz anlik guc ifadesini hem kapasitif hem enduktif hem de resistif yukler icin kullanabiliriz Elimizde olmasi gereken bilgi faz farkinin degeridir Hesaplamamiza baslayalim v t vmax cos wt fv vmax cos wt fv fi displaystyle v t v max cdot cos omega t varphi v v max cdot cos omega t varphi v varphi i dd p vmax imaxcos wt fv fi cos wt displaystyle p v max cdot i max cos omega t varphi v varphi i cos omega t dd i t imax cos wt fi imax cos wt displaystyle i t i max cdot cos omega t varphi i i max cdot cos omega t dd Yukaridaki ifadede bulunan cos wt fv fi cos wt displaystyle cos omega t varphi v varphi i cos omega t carpimini cos a cos b displaystyle cos a cdot cos b carpimina benzetip trigonometrik donusum yaparsak asagidaki formulasyonu elde ederiz cos a cos b 12 cos a b cos a b displaystyle cos a cdot cos b frac 1 2 cos a b cos a b dd cos wt fv fi cos wt 12 cos fv fi cos 2wt fv fi displaystyle cos omega t varphi v varphi i cos omega t frac 1 2 cos varphi v varphi i cos 2 omega t varphi v varphi i dd Bu trigonometrik donusumlerin ardindan anlik guc formulasyonunu tekrar yazalim p vmax imax2cos fv fi vmax imax2cos 2wt fv fi displaystyle p frac v max cdot i max 2 cos varphi v varphi i frac v max cdot i max 2 cos 2 omega t varphi v varphi i dd Anlik guc formulasyonunda bulunan cos 2wt fv fi displaystyle cos 2 omega t varphi v varphi i ifadesini cos a b displaystyle cos a b trigonometrik donusumune gore acarsak anlik gucun asagidaki ifadesini elde ederiz cos a b cos a cos b sin a sin b displaystyle cos a b cos a cos b sin a sin b dd cos 2wt fv fi cos 2wt cos fv fi sin 2wt sin fv fi displaystyle cos 2 omega t varphi v varphi i cos 2 omega t cos varphi v varphi i sin 2 omega t sin varphi v varphi i dd Bu trigonometrik esitligin sonrasinda anlik guc asagidaki sekilde ifade edilebilir p vmax imax2cos fv fi vmax imax2cos 2wt cos fv fi vmax imax2sin 2wt sin fv fi displaystyle p frac v max cdot i max 2 cos varphi v varphi i frac v max cdot i max 2 cos 2 omega t cos varphi v varphi i frac v max cdot i max 2 sin 2 omega t sin varphi v varphi i dd p vmax imax2cos fv fi 1 cos 2wt vmax imax2sin fv fi sin 2wt displaystyle p frac v max cdot i max 2 cos varphi v varphi i 1 cos 2 omega t frac v max cdot i max 2 sin varphi v varphi i sin 2 omega t dd Son cikan anlik guc ifadesinde bir sey dikkatimizi cekmektedir Bu da fv fi displaystyle varphi v varphi i faz farkinin cos displaystyle cos ve sin displaystyle sin fonksiyonlarinin icinde gelmesidir Bundan sonra icinde cos fv fi displaystyle cos varphi v varphi i bulunan ifade Aktif Guc P sin fv fi displaystyle sin varphi v varphi i olan ifade Reaktif Guc Q olarak tanimlanacaktir Bu tanimdan sonra formulasyonu basitlestirirsek anlik guc asagidaki sekle donusur Sinusoidal Kaynakta Anlik Guc p P Pcos 2wt Qsin 2wt displaystyle p P P cos 2 omega t Q sin 2 omega t Ayrica bakinizElektrik uretimi Enerji kaynaklariKaynakca a b Thomas Roland E Rosa Albert J Toussaint Gregory J 2016 The Analysis and Design of Linear Circuits 8 bas Wiley ss 812 813 ISBN 978 1 119 23538 5 Fraile Mora Jesus 2012 Circuitos electricos Ispanyolca Pearson ss 193 196 ISBN 978 8 48 322795 4 IEEE Standard Definitions for the Measurement of Electric Power Quantities Under Sinusoidal Nonsinusoidal Balanced or Unbalanced Conditions IEEE 2010 s 4 doi 10 1109 IEEESTD 2010 5439063 ISBN 978 0 7381 6058 0 Hayt William H Buck John A 2012 Engineering Electromagnetics 8 bas McGraw Hill s 385 ISBN 978 0 07 338066 7
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State