Matematikte, hesaplanabilir sayılar, belirlenen herhangi bir doğruluk seviyesine ulaşacak şekilde sonlu ve sona eren bir algoritma ile hesaplanabilen reel sayıları ifade eder. Bu sayılar, yinelemeli sayılar, etkili sayılar ya da hesaplanabilir reel sayılarolarak da adlandırılır. Hesaplanabilir reel sayılar kavramı, o dönemde mevcut olan sezgisel hesaplanabilirlik kavramı üzerinden Emile Borel tarafından 1912'de ortaya konmuştur.

, Turing makineleri veya λ-hesaplama gibi formal algoritma temsilleri kullanılarak eşdeğer tanımlamalar yapılabilir. Hesaplanabilir sayılar, bir oluşturur ve matematikte pek çok durumda, ancak her durumda olmamak üzere, reel sayıların yerini alabilirler.
Turing makinesi örneği üzerinden yapılan gayri resmi tanımlama
Aşağıdaki metinde, Marvin Minsky sayıların hesaplanması konusunu, Alan Turing'in 1936 yılında tanımladığı sayılarla benzer bir yöntemle ifade etmektedir; yani, 0 ile 1 arasında "ondalık kesirler olarak yorumlanan sayı dizileri" şeklinde:
Hesaplanabilir bir sayı, başlangıçta n verilerek çalıştırıldığında, o sayının ninci basamağını kodlanmış olarak sonuçlandıran bir Turing makinesi bulunması halidir.
Tanımın temelini oluşturan kavramlar şöyledir: (1) Başta tanımlanmış bir n değerinin mevcudiyeti, (2) Her bir n değerinde, işlemin yalnızca belirli sayıda adımda gerçekleştirilmesi ve ardından makinenin istenilen sonucu üreterek faaliyetine son vermesidir.
(2) maddesinin bir başka versiyonu şu şekildedir: Makine, üzerindeki şeritte sıralı olarak bulunan tüm n sayısını yazdırır ve ninci sayıyı yazdıktan sonra işlemini durdurur - Bu durum, Minsky'nin gözlemlerini belirginleştirir: (3) Bir Turing makinesinin kullanılmasıyla, makinenin durum tablosunun şeklini alan sonlu bir tanımın, potansiyel olarak sonsuz bir ondalık sayı dizisini tanımlamak için nasıl kullanıldığıdır.
Fakat bu durum, sonucun önceden belirlenmiş herhangi bir doğruluk seviyesine uygun olması gerektiğini öngören modern tanımı kapsamaz. Başlangıçta sunulan gayri resmi tanım, (İng. table-maker's dilemma) olarak bilinen ve modern tanımın uğraşmadığı bir yuvarlama problemi ile karşı karşıyadır.
Tanım
Bir reel sayı a, eğer belirli bir hesaplanabilir fonksiyon 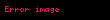
İki benzer ve denk tanım mevcuttur:
- Herhangi bir pozitif rasyonel
için,
koşulunu tatmin eden bir r rasyonel sayı elde edebilen hesaplanabilir bir fonksiyon vardır.
- Hesaplanabilir rasyonel sayılar dizisi
, a sayısına yakınsamakta ve her i için
eşitsizliğini sağlamaktadır.
Hesaplanabilir sayılar, hesaplanabilir aracılığıyla tanımlanabilen bir başka denk tanıma sahiptir. Bir hesaplanabilir Dedekind kesiti, bir rasyonel sayı 
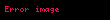
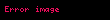

3 sayısının tanımlayan D adlı program tarafından sunulan bir örnekte, 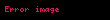
Bir reel sayının hesaplanabilir olması, ancak ve ancak ona tekabül eden hesaplanabilir bir Dedekind kesiti D'nin varlığı ile mümkündür. Her hesaplanabilir sayı için D fonksiyonu özgündür (tabii ki, farklı iki program aynı fonksiyonu temin edebilir).
Reel ve sanal parçaları hesaplanabilir olan bir karmaşık sayı, hesaplanabilir olarak tanımlanmaktadır.
Özellikler
Hesaplanabilir olarak sıralanamaz
Her bir Turing makinesi tanımına özgü bir tahsis edilmesi, hesaplanabilir sayılarla ilişkilendirilen doğal sayılar içerisinde bir 



Reel sayılar kümesinin olduğu bilinirken, hesaplanabilir sayılar kümesi klasik anlamda ve böylece reel sayıların büyük bir çoğunluğu hesaplanabilir nitelikte değildir. Bu durumda, herhangi bir hesaplanabilir sayı 


Alan özellikleri
Hesaplanabilir sayılarda gerçekleştirilen aritmetik işlemler, a ve b reel sayıları hesaplanabilir olduğunda, a + b, a - b, ab ve b sıfır olmadığı durumda a/b olacak şekilde, bu reel sayıların da hesaplanabilir olduğu şekilde kendileri hesaplanabilir niteliktedir. Bu operasyonlar gerçekte tek tip olarak hesaplanabilirdir; bir örneğe göre, (A, B, 

Hesaplanabilir reel sayıların bir alan oluşturduğu gerçeği, ilk defa tarafından 1954 yılında ispatlanmıştır.
Hesaplanabilir reel sayılar, bir hesaplanabilir alanın gerektirdiği etkin eşitlik tanımını karşılamadığı için, bir oluşturmamaktadır.
Sıralamanın hesaplanabilir olmaması
Hesaplanabilir sayılar arasındaki sıralama ilişkisi hesaplanabilir nitelikte değildir. A, 

Tam sıra ilişkisi hesaplanabilir olmamakla birlikte, birbirinden farklı sayı çiftlerine uygulanan kısıtlaması hesaplanabilir bir özellik göstermektedir. Bu bağlamda, 






Diğer özellikler
Hesaplanabilir reel sayılar, analiz disiplininde ele alınan reel sayıların tüm karakteristiklerini taşımazlar. Bir örnek olarak, hesaplanabilir reel sayılardan oluşturulan sınırlı ve artan bir dizinin en küçük üst sınırı, zorunlu olarak hesaplanabilir bir reel sayı olmayabilir. Bu tür bir diziye sahip olma özelliği, ilk olarak tarafından 1949'da tanıtılan bir olarak adlandırılır. Bu gibi karşıt örneklerin var oluşuna karşın, hesaplanabilir sayılar çerçevesinde kalkülüs ve reel analizin parçaları geliştirilebilir ve bu durum, alanının araştırılmasını teşvik eder.
Her hesaplanabilir sayı, aritmetiksel olarak tanımlanabilir niteliktedir, fakat bu ilişki karşılıklı olarak geçerli değildir. Aritmetiksel olarak tanımlanabilen ancak hesaplanamayan birçok reel sayı mevcuttur ki, bunlar arasında şunlar bulunmaktadır:
- Seçilen bir kodlama düzenine göre durma probleminin (veya diğer herhangi bir ) çözümünü içeren herhangi bir sayı.
-
, durma problemine olan bir tür reel sayıdır.
Bu örnekler, her bir için tanımlanabilir, ancak hesaplanamayan sayıların sonsuz bir setini aslında tanımlamaktadır. Bir reel sayının hesaplanabilir olması, sadece bu sayının temsil ettiği doğal sayıların kümesi (ikili formatta yazılıp bir özellik fonksiyonu olarak değerlendirildiğinde) hesaplanabilir olduğu durumlarda söz konusudur.
Hesaplanabilir reel sayılar kümesi (aynı zamanda hesaplanabilir reeller'n sonu olmayan her sayılabilir, alt kümesi de dahil olmak üzere) rasyonel sayılar kümesiyle .
Rakam dizileri ve Cantor ile Baire uzayları
Turing'in orijinal makalesi hesaplanabilir sayıları şu şekilde tanımlamıştır:
Bir reel sayı, rakam dizisi bir algoritma ya da Turing makinesi tarafından üretilebiliyorsa hesaplanabilirdir. Algoritma, bir tam sayı
girdisi alır ve reel sayının ondalık genişlemesinin
-inci rakamını çıktı olarak üretir.
(a'nın ondalık genişlemesi yalnızca ondalık noktasından sonraki rakamlara atıfta bulunur.)
Turing, bu tanımının yukarıda sunulan 



Reel sayıların belirli topolojik özellikleri göz önüne alınmadığında, 

Ondalık genişlemelerin bu karakteristiği, ondalık genişleme temelinde tanımlanan hesaplanabilir reel sayılar ile 


Hesaplanabilirlik teorisi veya ölçüm teorisi açısından, 


Öte yandan, 

Reel sayıların yerine kullanım
Hesaplanabilir sayılar, pratik uygulamalarda karşılaşılan belirli reel sayıları kapsar; bu sayılara tüm reel cebirsel sayılar, e, π ve pek çok transandantal sayı da dahildir. Hesaplanabilir reeller, hesaplamaya ya da yaklaşık değerlere ulaşmamız mümkün olan reel sayıları kapsamakla birlikte, tüm reel sayıların hesaplanabilir olduğu varsayımı, reel sayılar üzerine önemli ölçüde farklı çıkarımlarda bulunulmasına neden olur. Matematiğin tamamında tam reel sayılar kümesinin yerine hesaplanabilir sayıların kullanılabilirliği konusu doğal olarak gündeme gelir. Bu düşünce, oluşturmacı bir perspektiften ilgi çekicidir ve Errett Bishop ile Fred Richman tarafından Rus okulu olarak nitelendirilen oluşturmacı matematiğin bir dalı tarafından araştırılmıştır.
Hesaplanabilir sayılar temelinde analitik çalışmalar yapabilmek adına, belirli düzeylerde tedbirlerin alınması gerekliliği ortaya çıkmaktadır. Örnek vermek gerekirse, geleneksel bir dizi tanımı kullanıldığında, hesaplanabilir sayılar kümesinin, bir alma gibi temel bir işleme kapalı olmadığı görülür (bu durum, örneğinde olduğu gibi, ilgili bölüme müracaat edilebilir). Bu tür bir zorluğun üstesinden gelmek amacıyla, sadece hesaplanabilir bir bulunan dizilerin ele alınması önerilmektedir. Bu yaklaşımın matematikteki karşılığı, olarak isimlendirilen bir teori şeklinde kendini göstermektedir.
Reel sayıların kesin aritmetik temsilleri
Reel sayıları, yaklaşık değerler hesaplayan programlar olarak temsil eden bilgisayar yazılımları, "kesin aritmetik" adı altında ilk olarak 1985 yılında teklif edilmiştir. Çağdaş örnekler arasında CoRN kütüphanesi (Coq), ve RealLib paketi (C++) yer almaktadır. Bu alandaki ilişkili bir araştırma çizgisi, yeterli hassasiyette rasyonel veya kayan nokta sayılarıyla çalıştırılan bir programını temel almaktadır, paketi gibi.
Ayrıca bakınız
Notlar
- ^ van der Hoeven (2006).
- ^ P. Odifreddi, Classical Recursion Theory (1989), s.8. North-Holland, 0-444-87295-7
- ^ Turing (1936).
- ^ Minsky (1967).
- ^ Rice (1954).
- ^ Bridges & Richman (1987), s. 58.
- ^ Specker (1949).
- ^ Hirst (2007).
- ^ Zalta, Edward N., (Ed.) (2022), "Russian School of Constructive Mathematics", Constructive Mathematics, Metaphysics Research Lab, Stanford University
- ^ Boehm, Hans-J.; Cartwright, Robert; Riggle, Mark; O'Donnell, Michael J. (8 Ağustos 1986). "Exact real arithmetic: A case study in higher order programming" (PDF). Proceedings of the 1986 ACM conference on LISP and functional programming - LFP '86. ss. 162-173. doi:10.1145/319838.319860. ISBN . 24 Eylül 2020 tarihinde kaynağından (PDF).
- ^ O’Connor, Russell (2008). "Certified Exact Transcendental Real Number Computation in Coq". Theorem Proving in Higher Order Logics. Lecture Notes in Computer Science. 5170. ss. 246-261. arXiv:0805.2438 $2. doi:10.1007/978-3-540-71067-7_21. ISBN .
- ^ Lambov (2015).
- ^ Gowland, Paul; Lester, David (2001). "A Survey of Exact Arithmetic Implementations" (PDF). Computability and Complexity in Analysis. Lecture Notes in Computer Science (İngilizce). 2064. Springer. ss. 30-47. doi:10.1007/3-540-45335-0_3. ISBN . 24 Mart 2022 tarihinde kaynağından (PDF).
Kaynakça
- Bridges, Douglas; Richman, Fred (1987). Varieties of Constructive Mathematics. Cambridge University Press. ISBN .
- Hirst, Jeffry L. (2007). "Representations of reals in reverse mathematics". Bulletin of the Polish Academy of Sciences, Mathematics. 55 (4): 303-316. doi:10.4064/ba55-4-2.
- Lambov, Branimir (5 Nisan 2015). "RealLib". GitHub.
- Minsky, Marvin (1967). "9. The Computable Real Numbers". Computation: Finite and Infinite Machines. Prentice-Hall. ISBN . OCLC 0131655639.
- Rice, Henry Gordon (1954). "Recursive real numbers". Proceedings of the American Mathematical Society. 5 (5): 784-791. doi:10.1090/S0002-9939-1954-0063328-5. JSTOR 2031867.
- (1949). "Nicht konstruktiv beweisbare Sätze der Analysis" (PDF). Journal of Symbolic Logic. 14 (3): 145-158. doi:10.2307/2267043. JSTOR 2267043. 21 Temmuz 2018 tarihinde kaynağından (PDF).
- Turing, A. M. (1936). "On Computable Numbers, with an Application to the Entscheidungsproblem". Series 2. 42 (1) (1937 tarihinde yayınlandı): 230-65. doi:10.1112/plms/s2-42.1.230. Bilinmeyen parametre
|periyodik=görmezden gelindi ()
Turing, A. M. (1938). "On Computable Numbers, with an Application to the Entscheidungsproblem: A correction". Series 2. 43 (6) (1937 tarihinde yayınlandı): 544-6. doi:10.1112/plms/s2-43.6.544. Bilinmeyen parametre|periyodik=görmezden gelindi () Computable numbers (and Turing's a-machines) were introduced in this paper; the definition of computable numbers uses infinite decimal sequences. - van der Hoeven, Joris (2006). "Computations with effective real numbers". Theoretical Computer Science. 351 (1): 52-60. doi:10.1016/j.tcs.2005.09.060.
Ek okuma
- Aberth, Oliver (1968). "Analysis in the Computable Number Field". Journal of the Association for Computing Machinery. 15 (2): 276-299. doi:10.1145/321450.321460. Bu çalışma, hesaplanabilir sayılar alanında kalkülüsün evrimini detaylandırmaktadır.
- Bishop, Errett; Bridges, Douglas (1985). Constructive Analysis. Springer. ISBN .
- Stoltenberg-Hansen, V.; Tucker, J.V. (1999). "Computable Rings and Fields". Griffor, E.R. (Ed.). Handbook of Computability Theory. Elsevier. ss. 363-448. ISBN .
- Weihrauch, Klaus (2000). Computable analysis. Texts in Theoretical Computer Science. Springer. ISBN . §1.3.2, tekil gerçek sayıya yakınsayan aracılığıyla yapılan tanımı ele alır. Diğer gösterimler §4.1'de incelenmektedir.
- Weihrauch, Klaus (1995). A simple introduction to computable analysis. Fernuniv., Fachbereich Informatik.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte hesaplanabilir sayilar belirlenen herhangi bir dogruluk seviyesine ulasacak sekilde sonlu ve sona eren bir algoritma ile hesaplanabilen reel sayilari ifade eder Bu sayilar yinelemeli sayilar etkili sayilar ya da hesaplanabilir reel sayilarolarak da adlandirilir Hesaplanabilir reel sayilar kavrami o donemde mevcut olan sezgisel hesaplanabilirlik kavrami uzerinden Emile Borel tarafindan 1912 de ortaya konmustur p istenilen herhangi bir dogruluk derecesine kadar hesaplanabilirken neredeyse tum reel sayilar hesaplanabilir nitelikte degildir Turing makineleri veya l hesaplama gibi formal algoritma temsilleri kullanilarak esdeger tanimlamalar yapilabilir Hesaplanabilir sayilar bir olusturur ve matematikte pek cok durumda ancak her durumda olmamak uzere reel sayilarin yerini alabilirler Turing makinesi ornegi uzerinden yapilan gayri resmi tanimlamaAsagidaki metinde Marvin Minsky sayilarin hesaplanmasi konusunu Alan Turing in 1936 yilinda tanimladigi sayilarla benzer bir yontemle ifade etmektedir yani 0 ile 1 arasinda ondalik kesirler olarak yorumlanan sayi dizileri seklinde Hesaplanabilir bir sayi baslangicta n verilerek calistirildiginda o sayinin ninci basamagini kodlanmis olarak sonuclandiran bir Turing makinesi bulunmasi halidir Tanimin temelini olusturan kavramlar soyledir 1 Basta tanimlanmis bir n degerinin mevcudiyeti 2 Her bir n degerinde islemin yalnizca belirli sayida adimda gerceklestirilmesi ve ardindan makinenin istenilen sonucu ureterek faaliyetine son vermesidir 2 maddesinin bir baska versiyonu su sekildedir Makine uzerindeki seritte sirali olarak bulunan tum n sayisini yazdirir ve ninci sayiyi yazdiktan sonra islemini durdurur Bu durum Minsky nin gozlemlerini belirginlestirir 3 Bir Turing makinesinin kullanilmasiyla makinenin durum tablosunun seklini alan sonlu bir tanimin potansiyel olarak sonsuz bir ondalik sayi dizisini tanimlamak icin nasil kullanildigidir Fakat bu durum sonucun onceden belirlenmis herhangi bir dogruluk seviyesine uygun olmasi gerektigini ongoren modern tanimi kapsamaz Baslangicta sunulan gayri resmi tanim Ing table maker s dilemma olarak bilinen ve modern tanimin ugrasmadigi bir yuvarlama problemi ile karsi karsiyadir TanimBir reel sayi a eger belirli bir hesaplanabilir fonksiyon f N Z displaystyle f mathbb N to mathbb Z araciligiyla asagidaki yontemle yakinsanabiliyorsa hesaplanabilir olarak kabul edilir Pozitif her tam sayi n degeri icin fonksiyon a sayisinin asagidaki kosulu saglamasini garantileyen bir f n tam sayisini hesaplar f n 1n a f n 1n displaystyle f n 1 over n leq a leq f n 1 over n Iki benzer ve denk tanim mevcuttur Herhangi bir pozitif rasyonel e displaystyle varepsilon icin r a e displaystyle r a leq varepsilon kosulunu tatmin eden bir r rasyonel sayi elde edebilen hesaplanabilir bir fonksiyon vardir Hesaplanabilir rasyonel sayilar dizisi qi displaystyle q i a sayisina yakinsamakta ve her i icin qi qi 1 lt 2 i displaystyle q i q i 1 lt 2 i esitsizligini saglamaktadir Hesaplanabilir sayilar hesaplanabilir araciligiyla tanimlanabilen bir baska denk tanima sahiptir Bir hesaplanabilir Dedekind kesiti bir rasyonel sayi r displaystyle r girdisi saglandiginda D r true displaystyle D r mathrm true ya da D r false displaystyle D r mathrm false degerlerinden birini donduren hesaplanabilir bir fonksiyon D displaystyle D dir ve su sartlari karsilar rD r true displaystyle exists rD r mathrm true rD r false displaystyle exists rD r mathrm false D r true D s false r lt s displaystyle D r mathrm true wedge D s mathrm false Rightarrow r lt s D r true s gt r D s true displaystyle D r mathrm true Rightarrow exists s gt r D s mathrm true 3 sayisinin tanimlayan D adli program tarafindan sunulan bir ornekte q gt 0 displaystyle q gt 0 olmak uzere bu durum su sekilde ifade edilir p3 lt 3q3 D p q true displaystyle p 3 lt 3q 3 Rightarrow D p q mathrm true p3 gt 3q3 D p q false displaystyle p 3 gt 3q 3 Rightarrow D p q mathrm false Bir reel sayinin hesaplanabilir olmasi ancak ve ancak ona tekabul eden hesaplanabilir bir Dedekind kesiti D nin varligi ile mumkundur Her hesaplanabilir sayi icin D fonksiyonu ozgundur tabii ki farkli iki program ayni fonksiyonu temin edebilir Reel ve sanal parcalari hesaplanabilir olan bir karmasik sayi hesaplanabilir olarak tanimlanmaktadir OzelliklerHesaplanabilir olarak siralanamaz Her bir Turing makinesi tanimina ozgu bir tahsis edilmesi hesaplanabilir sayilarla iliskilendirilen dogal sayilar icerisinde bir S displaystyle S alt kumesi olusturur ve bu alt kumeden hesaplanabilir sayilara bir orten fonksiyonun varligini isaret eder Turing makinelerinin yalnizca sayilabilir miktarda oldugu bilinmekte olup bu durum hesaplanabilir sayilarin oldugunu ortaya koymaktadir Ne var ki bu Godel sayilarinin olusturdugu S displaystyle S kumesi nitelikte degildir ve buna bagli olarak bu kumeyle ilintili olarak tanimlanan S displaystyle S alt kumeleri de hesaplanabilir siralanabilir degildir Bu hesaplanabilir reel sayilari ureten Turing makinelerine denk gelen Godel sayilarini tespit edecek bir algoritmanin bulunmamasindan kaynaklanmaktadir Hesaplanabilir bir reel sayi uretmek icin bir Turing makinesinin bir tam fonksiyon hesaplamasi gerekmekte fakat bu durumun iliskili 0 kapsamindadir Bu nedenle dogal sayilardan hesaplanabilir reelleri temsil eden makinelerin olusturdugu S displaystyle S kumesine yonelik orten bir hesaplanabilir fonksiyon mevcut degildir ve bunlarin sayilamayacak kadar cok oldugunu olusturmaci bir bicimde ispatlamak icin kullanilamaz Reel sayilar kumesinin oldugu bilinirken hesaplanabilir sayilar kumesi klasik anlamda ve boylece reel sayilarin buyuk bir cogunlugu hesaplanabilir nitelikte degildir Bu durumda herhangi bir hesaplanabilir sayi x displaystyle x icin S displaystyle S icinde x displaystyle x e denk gelen minimal bir elementin varligini ongorur dolayisiyla bu haritanin bir bijeksiyon oldugu minimal elemanlardan olusan bir alt kumenin mevcut oldugu sonucuna varilir Bu bijeksiyonun ters cevrimi hesaplanabilir sayilarin dogal sayilara enjeksiyonunu saglar ve bunlarin sayilabilir oldugunu ispatlar Ancak hesaplanabilir reellerin kendileri sirali olsa dahi bu alt kume hesaplanabilir degildir Alan ozellikleri Hesaplanabilir sayilarda gerceklestirilen aritmetik islemler a ve b reel sayilari hesaplanabilir oldugunda a b a b ab ve b sifir olmadigi durumda a b olacak sekilde bu reel sayilarin da hesaplanabilir oldugu sekilde kendileri hesaplanabilir niteliktedir Bu operasyonlar gercekte tek tip olarak hesaplanabilirdir bir ornege gore A B ϵ displaystyle epsilon girdisine sahip bir Turing makinesi ayi yaklasik olarak betimleyen A Turing makinesinin tanimi byi yaklasik olarak betimleyen B Turing makinesinin tanimi ve r a bnin bir ϵ displaystyle epsilon yakinsamasi olarak cikti r uretebilir Hesaplanabilir reel sayilarin bir alan olusturdugu gercegi ilk defa tarafindan 1954 yilinda ispatlanmistir Hesaplanabilir reel sayilar bir hesaplanabilir alanin gerektirdigi etkin esitlik tanimini karsilamadigi icin bir olusturmamaktadir Siralamanin hesaplanabilir olmamasi Hesaplanabilir sayilar arasindaki siralama iliskisi hesaplanabilir nitelikte degildir A a displaystyle a sayisinin yaklasik degerini hesaplayan bir Turing makinesinin aciklamasi olsun Bu durumda girdi A oldugunda eger a gt 0 displaystyle a gt 0 ise EVET a 0 displaystyle a leq 0 ise HAYIR yanitini veren bir Turing makinesi mevcut degildir Bunun nedenini anlamak icin A ile tanimlanan makinenin ϵ displaystyle epsilon yaklasimlari olarak surekli olarak 0 degerini urettigini varsayin Makinenin a degerinin pozitif olacagini garanti altina alacak bir yaklasim uretmeden once ne kadar sure beklemesi gerektigi belirsizdir Sonuc olarak makine bir cikti saglamak amaciyla sayinin 0 olacagini tahmin etmek zorunda kalir ancak dizi sonradan 0 dan farkli bir deger alabilir Bu dusunce eger makine bir tam fonksiyon hesapliyorsa bazi dizilerde yanlis oldugunu gostermek icin kullanilabilir Hesaplanabilir gerceklerin olarak ifade edilmesi durumunda benzer bir sorun meydana gelir Esitlik iliskisi icin de benzer bir durum soz konusudur esitligi test etme islemi hesaplanabilir degildir Tam sira iliskisi hesaplanabilir olmamakla birlikte birbirinden farkli sayi ciftlerine uygulanan kisitlamasi hesaplanabilir bir ozellik gostermektedir Bu baglamda a b displaystyle a neq b kosulunu saglayan a displaystyle a ve b displaystyle b sayilarinin yaklasik degerlerini hesaplayan A ve B Turing makineleri icin girdi alabilen ve sonuc olarak bu sayilarin a lt b displaystyle a lt b ya da a gt b displaystyle a gt b iliskisine sahip olup olmadigini belirleyen bir program mevcuttur ϵ lt b a 2 displaystyle epsilon lt b a 2 olacak sekilde ϵ displaystyle epsilon yaklasimi kullanmak bu surec icin yeterli olup ϵ displaystyle epsilon degeri 0 a yaklastikca a displaystyle a ile b displaystyle b arasindaki iliskinin a lt b displaystyle a lt b veya a gt b displaystyle a gt b olduguna dair kesin bir karara varilabilir Diger ozellikler Hesaplanabilir reel sayilar analiz disiplininde ele alinan reel sayilarin tum karakteristiklerini tasimazlar Bir ornek olarak hesaplanabilir reel sayilardan olusturulan sinirli ve artan bir dizinin en kucuk ust siniri zorunlu olarak hesaplanabilir bir reel sayi olmayabilir Bu tur bir diziye sahip olma ozelligi ilk olarak tarafindan 1949 da tanitilan bir olarak adlandirilir Bu gibi karsit orneklerin var olusuna karsin hesaplanabilir sayilar cercevesinde kalkulus ve reel analizin parcalari gelistirilebilir ve bu durum alaninin arastirilmasini tesvik eder Her hesaplanabilir sayi aritmetiksel olarak tanimlanabilir niteliktedir fakat bu iliski karsilikli olarak gecerli degildir Aritmetiksel olarak tanimlanabilen ancak hesaplanamayan bircok reel sayi mevcuttur ki bunlar arasinda sunlar bulunmaktadir Secilen bir kodlama duzenine gore durma probleminin veya diger herhangi bir cozumunu iceren herhangi bir sayi W displaystyle Omega durma problemine olan bir tur reel sayidir Bu ornekler her bir icin tanimlanabilir ancak hesaplanamayan sayilarin sonsuz bir setini aslinda tanimlamaktadir Bir reel sayinin hesaplanabilir olmasi sadece bu sayinin temsil ettigi dogal sayilarin kumesi ikili formatta yazilip bir ozellik fonksiyonu olarak degerlendirildiginde hesaplanabilir oldugu durumlarda soz konusudur Hesaplanabilir reel sayilar kumesi ayni zamanda hesaplanabilir reeller n sonu olmayan her sayilabilir alt kumesi de dahil olmak uzere rasyonel sayilar kumesiyle Rakam dizileri ve Cantor ile Baire uzaylariTuring in orijinal makalesi hesaplanabilir sayilari su sekilde tanimlamistir Bir reel sayi rakam dizisi bir algoritma ya da Turing makinesi tarafindan uretilebiliyorsa hesaplanabilirdir Algoritma bir tam sayi n 1 displaystyle n geq 1 girdisi alir ve reel sayinin ondalik genislemesinin n displaystyle n inci rakamini cikti olarak uretir a nin ondalik genislemesi yalnizca ondalik noktasindan sonraki rakamlara atifta bulunur Turing bu taniminin yukarida sunulan ϵ displaystyle epsilon yaklasim tanimiyla esdeger oldugunu biliyordu Arguman soyle ilerler Eger bir sayi Turing baglaminda hesaplanabilirse o zaman ϵ displaystyle epsilon baglaminda da hesaplanabilir n gt log10 1 ϵ displaystyle n gt log 10 1 epsilon oldugunda a sayisinin ondalik genislemesinin ilk n rakami a icin bir ϵ displaystyle epsilon yaklasimi temin eder Tersini kanitlamak icin ϵ displaystyle epsilon ile hesaplanabilir bir reel sayi a alinir ve ondalik noktasindan sonra gelen ninci rakam kesin olana kadar giderek daha dogru yaklasimlar uretilir Bu islem her zaman a ile esit bir ondalik genisleme saglar ancak yanlis bir bicimde sonsuz bir 9 dizisiyle sonlanabilir ki bu durumda sonlu ve bu nedenle hesaplanabilir bir duzgun ondalik genislemesi olmalidir Reel sayilarin belirli topolojik ozellikleri goz onune alinmadiginda 0 1 displaystyle 0 1 icerisindeki reel sayilar yerine 2w displaystyle 2 omega elemanlariyla calismak siklikla daha avantajlidir 2w displaystyle 2 omega elemanlari ikili ondalik genislemelerle ozdeslestirilebilir ancak d1d2 dn0111 displaystyle d 1 d 2 ldots d n 0111 ldots ve d1d2 dn10 displaystyle d 1 d 2 ldots d n 10 ondalik genislemeleri ayni reel sayiyi temsil ettiginden 0 1 displaystyle 0 1 araligi yalnizca sonu tumuyle 1 lerle bitmeyen 2w displaystyle 2 omega alt kumesiyle bijektif ve alt kume topolojisi altinda homeomorfik bir bicimde ozdeslestirilebilir Ondalik genislemelerin bu karakteristigi ondalik genisleme temelinde tanimlanan hesaplanabilir reel sayilar ile ϵ displaystyle epsilon yaklasimi kavrami temelinde tanimlananlar arasinda etkin bir sekilde ayrim yapilmasinin mumkun olmadigini ortaya koymaktadir Hirst a hesaplanabilir sayisi icin ϵ displaystyle epsilon yaklasimlari ureten bir Turing makinesinin aciklamasini girdi olarak alan ve Turing in tanimi cercevesinde a sayisinin rakamlarini enumerate eden bir Turing makinesi ureten bir algoritmanin var olmadigini ispatlamistir Ayni sekilde bu durum hesaplanabilir reel sayilar uzerindeki aritmetik islemlerin ondalik sayilar eklenirken karsilasilan durumda oldugu gibi bu sayilarin ondalik temsilleri uzerinde etkin olmadigini da gostermektedir Tek bir rakam elde etmek icin mevcut konuma bir tasimanin olup olmadigini tespit etmek amaciyla saga dogru keyfi bir mesafe bakilmasi gerekebilir Bu duzensizlik cagdas hesaplanabilir sayi taniminin ondalik genislemeler yerine ϵ displaystyle epsilon yaklasimlarini tercih etmesinin temel sebeplerinden biridir Hesaplanabilirlik teorisi veya olcum teorisi acisindan 2w displaystyle 2 omega ve 0 1 displaystyle 0 1 yapilarinin ozdes oldugu kabul edilir Bu baglamda hesaplanabilirlik teorisyenleri genellikle 2w displaystyle 2 omega kumesinin elemanlarina reel sayilar olarak referans verirler Her ne kadar 2w displaystyle 2 omega tamamen baglantisiz bir uzay olsa da P10 displaystyle Pi 1 0 siniflari veya rastlantisallikla ilgili sorularin ele alinmasi 2w displaystyle 2 omega cercevesinde daha mumkundur Ote yandan ww displaystyle omega omega elemanlarina da zaman zaman reel sayilar denilmekte olup bu yapi R displaystyle mathbb R nin bir homeomorfik yansimasini icermesine ragmen yerel olarak kompakt olmaktan uzaktir ayni zamanda tamamen baglantisizdir Bu durum hesaplama ozellikleri acisindan belirgin farkliliklara neden olmaktadir Ornegin ϕ x n displaystyle phi x n niceliksiz ifadesiyle n w ϕ x n displaystyle forall n in omega phi x n kosulunu saglayan x R displaystyle x in mathbb R hesaplanabilir niteliktedir Buna karsin evrensel bir formulu saglayan tekil x ww displaystyle x in omega omega elemani icerisinde keyfi bir yukseklige sahip olabilir Reel sayilarin yerine kullanim Hesaplanabilir sayilar pratik uygulamalarda karsilasilan belirli reel sayilari kapsar bu sayilara tum reel cebirsel sayilar e p ve pek cok transandantal sayi da dahildir Hesaplanabilir reeller hesaplamaya ya da yaklasik degerlere ulasmamiz mumkun olan reel sayilari kapsamakla birlikte tum reel sayilarin hesaplanabilir oldugu varsayimi reel sayilar uzerine onemli olcude farkli cikarimlarda bulunulmasina neden olur Matematigin tamaminda tam reel sayilar kumesinin yerine hesaplanabilir sayilarin kullanilabilirligi konusu dogal olarak gundeme gelir Bu dusunce olusturmaci bir perspektiften ilgi cekicidir ve Errett Bishop ile Fred Richman tarafindan Rus okulu olarak nitelendirilen olusturmaci matematigin bir dali tarafindan arastirilmistir Hesaplanabilir sayilar temelinde analitik calismalar yapabilmek adina belirli duzeylerde tedbirlerin alinmasi gerekliligi ortaya cikmaktadir Ornek vermek gerekirse geleneksel bir dizi tanimi kullanildiginda hesaplanabilir sayilar kumesinin bir alma gibi temel bir isleme kapali olmadigi gorulur bu durum orneginde oldugu gibi ilgili bolume muracaat edilebilir Bu tur bir zorlugun ustesinden gelmek amaciyla sadece hesaplanabilir bir bulunan dizilerin ele alinmasi onerilmektedir Bu yaklasimin matematikteki karsiligi olarak isimlendirilen bir teori seklinde kendini gostermektedir Reel sayilarin kesin aritmetik temsilleri Reel sayilari yaklasik degerler hesaplayan programlar olarak temsil eden bilgisayar yazilimlari kesin aritmetik adi altinda ilk olarak 1985 yilinda teklif edilmistir Cagdas ornekler arasinda CoRN kutuphanesi Coq ve RealLib paketi C yer almaktadir Bu alandaki iliskili bir arastirma cizgisi yeterli hassasiyette rasyonel veya kayan nokta sayilariyla calistirilan bir programini temel almaktadir paketi gibi Ayrica bakinizCizilebilir sayiNotlar van der Hoeven 2006 P Odifreddi Classical Recursion Theory 1989 s 8 North Holland 0 444 87295 7 Turing 1936 Minsky 1967 Rice 1954 Bridges amp Richman 1987 s 58 Specker 1949 Hirst 2007 Zalta Edward N Ed 2022 Russian School of Constructive Mathematics Constructive Mathematics Metaphysics Research Lab Stanford University Boehm Hans J Cartwright Robert Riggle Mark O Donnell Michael J 8 Agustos 1986 Exact real arithmetic A case study in higher order programming PDF Proceedings of the 1986 ACM conference on LISP and functional programming LFP 86 ss 162 173 doi 10 1145 319838 319860 ISBN 0897912004 24 Eylul 2020 tarihinde kaynagindan PDF O Connor Russell 2008 Certified Exact Transcendental Real Number Computation in Coq Theorem Proving in Higher Order Logics Lecture Notes in Computer Science 5170 ss 246 261 arXiv 0805 2438 2 doi 10 1007 978 3 540 71067 7 21 ISBN 978 3 540 71065 3 Lambov 2015 Gowland Paul Lester David 2001 A Survey of Exact Arithmetic Implementations PDF Computability and Complexity in Analysis Lecture Notes in Computer Science Ingilizce 2064 Springer ss 30 47 doi 10 1007 3 540 45335 0 3 ISBN 978 3 540 42197 9 24 Mart 2022 tarihinde kaynagindan PDF KaynakcaBridges Douglas Richman Fred 1987 Varieties of Constructive Mathematics Cambridge University Press ISBN 978 0 521 31802 0 Hirst Jeffry L 2007 Representations of reals in reverse mathematics Bulletin of the Polish Academy of Sciences Mathematics 55 4 303 316 doi 10 4064 ba55 4 2 Lambov Branimir 5 Nisan 2015 RealLib GitHub Arsivlenmesi gereken baglantiya sahip kaynak sablonu iceren maddeler link Minsky Marvin 1967 9 The Computable Real Numbers Computation Finite and Infinite Machines Prentice Hall ISBN 0 13 165563 9 OCLC 0131655639 Rice Henry Gordon 1954 Recursive real numbers Proceedings of the American Mathematical Society 5 5 784 791 doi 10 1090 S0002 9939 1954 0063328 5 JSTOR 2031867 1949 Nicht konstruktiv beweisbare Satze der Analysis PDF Journal of Symbolic Logic 14 3 145 158 doi 10 2307 2267043 JSTOR 2267043 21 Temmuz 2018 tarihinde kaynagindan PDF Turing A M 1936 On Computable Numbers with an Application to the Entscheidungsproblem Series 2 42 1 1937 tarihinde yayinlandi 230 65 doi 10 1112 plms s2 42 1 230 Bilinmeyen parametre periyodik gormezden gelindi yardim Turing A M 1938 On Computable Numbers with an Application to the Entscheidungsproblem A correction Series 2 43 6 1937 tarihinde yayinlandi 544 6 doi 10 1112 plms s2 43 6 544 Bilinmeyen parametre periyodik gormezden gelindi yardim Computable numbers and Turing s a machines were introduced in this paper the definition of computable numbers uses infinite decimal sequences van der Hoeven Joris 2006 Computations with effective real numbers Theoretical Computer Science 351 1 52 60 doi 10 1016 j tcs 2005 09 060 Ek okumaAberth Oliver 1968 Analysis in the Computable Number Field Journal of the Association for Computing Machinery 15 2 276 299 doi 10 1145 321450 321460 Bu calisma hesaplanabilir sayilar alaninda kalkulusun evrimini detaylandirmaktadir Bishop Errett Bridges Douglas 1985 Constructive Analysis Springer ISBN 0 387 15066 8 Stoltenberg Hansen V Tucker J V 1999 Computable Rings and Fields Griffor E R Ed Handbook of Computability Theory Elsevier ss 363 448 ISBN 978 0 08 053304 9 Weihrauch Klaus 2000 Computable analysis Texts in Theoretical Computer Science Springer ISBN 3 540 66817 9 1 3 2 tekil gercek sayiya yakinsayan araciligiyla yapilan tanimi ele alir Diger gosterimler 4 1 de incelenmektedir Weihrauch Klaus 1995 A simple introduction to computable analysis Fernuniv Fachbereich Informatik
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans