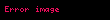Çizilebilir sayı terimi,geometri ve cebirde kullanılır ve bir reel sayı 'nin, belirli koşullar altında bir çizgi olarak çizilebilip çizilemeyeceğini ifade eder. Eğer birim uzunlukta herhangi çizgiyi kullanarak, sadece pergel ve cetvel yardımıyla ve belirli sayıda adımda, r uzunluğunda bir başka çizgi çizebilirse, bu durumda r sayısı çizilebilir bir sayıdır. Başka bir deyişle, r sayısını, sadece tam sayıları ve temel matematik işlemleri (toplama, çıkarma, çarpma, bölme) ile karekök alma işlemini kullanarak açık bir şekilde ifade edebiliyorsa, r sayısı çizilebilir kabul edilir.

Çizilebilir sayılar kavramı, geometri ve cebirde önemli bir yere sahiptir ve bu kavramla yakından ilgili olan çizilebilir noktalar, geometrik ve cebirsel yöntemlerle tanımlanabilir. Bir noktanın çizilebilir olarak kabul edilebilmesi için, önceden belirlenmiş birim uzunluktaki bir çizginin başlangıcından, pergel ve cetvel kullanarak ulaşılabilecek bir konumda olması gerekir. Bu, bir çizginin sonu, iki çizginin veya iki çemberin kesişme noktası gibi belirli bir noktaya işaret eder. Ayrıca, bir noktanın çizilebilir olması, bu noktanın Kartezyen koordinatlarının her ikisinin de çizilebilir sayılar olmasını gerektirir. Burada bir segmentin başlangıç ve bitiş noktaları, bir Kartezyen koordinat sisteminde sırasıyla (0, 0) ve (1, 0) olarak düşünülür. Çizilebilir sayılar ve noktalar, diğer yöntemlerle elde edilen sayı ve noktalardan farklılaştırılmak amacıyla bazen cetvel ve pergel sayıları ve cetvel ve pergel noktaları olarak adlandırılır. Bu tanımlamalar, geometri ve cebirdeki çeşitli problemlerin çözümünde temel oluşturur.
Çizilebilir sayıların oluşturduğu küme, bir alanı teşkil eder: Bu kümedeki elemanlara uygulanan dört temel aritmetik işlemin her biri, yine bir çizilebilir sayının elde edilmesini sağlar. Bu alan, rasyonel sayılar üzerine bir olarak işlev görür ve bu yapı, cebirsel sayılar alanının bir alt kümesi olarak kabul edilir. Rasyonel sayıların Euklidyen kapanışı olarak tanımlanan bu alan, rasyonel sayılardan türeyen ve pozitif elemanlarının tümünün kareköklerini barındıran en minimal alan genişlemesidir.
Çizilebilir sayıların cebirsel ve geometrik tanımlamalarının eşdeğerliğini ispatlama süreci, antik Yunan matematiğine ait birkaç ünlü problemin de içinde bulunduğu, pergel ve cetvel kullanılarak oluşturulan geometrik soruların, cebirsel bir çerçeveye dönüştürülmesine olanak tanır. Bu soruların cebirsel olarak ifade edilmesi, geometrik olarak formüle edilen ve yüzyıllarca çözüme direnç göstermiş aynı problemlerin, çizilebilir olmadıklarına dair ispatların ortaya konulmasını sağlamıştır.
Geometrik tanımlamalar
Geometrik olarak çizilebilir noktalar
Öklidyen düzlemde yer alan 







- Uç noktaları
kümesine dahil olan doğru parçasına, çizilebilir doğru parçası denir ve
- Merkezi
içerisinde yer alan ve bir
noktasından geçen (ya da alternatif bir ifadeyle, yarıçapı
kümesindeki iki ayrı nokta arasındaki mesafe olan) çembere, çizilebilir çember adı verilir.
Buna göre, 


- İki paralel olmayan çizilmiş doğru parçasının veya bu parçalar üzerinden çizilen doğruların noktaları,
- Bir çizilebilir çember ile çizilmiş bir doğru parçasının veya bu parça üzerinden çizilen bir doğrunun kesişim noktaları,
- İki ayrı çizilebilir çemberin kesişim noktaları.
Örneğin, çizilmiş 


Geometrik olarak çizilebilir sayılar
Geometrik formülasyona ilişkin başlangıç verisi, 




Çizilebilir bir sayının eşdeğer tanımları arasında, bir çizilebilir noktanın 

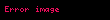










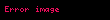


Cebirsel tanımlar
Cebirsel olarak çizilebilir reel sayılar
Cebirsel olarak çizilebilir reel sayılar, toplama, çıkarma, çarpma, çarpmaya göre ters işlem ve pozitif sayıların kareköklerinin kullanımıyla tam sayıların kombinasyonunu içeren formüller aracılığıyla ifade edilebilen reel sayıların bir alt kümesini temsil eder. Bu formüllerin yapısal karmaşıklığını artırarak daha da sadeleştirilebilir şekilde, söz konusu formüllerdeki tam sayılar yalnızca 0 ve 1 olarak kısıtlanabilir. Mesela, 2'nin karekökü çizilebilir olarak kabul edilir, zira bu, 

Benzer bir biçimde, cebirsel olarak çizilebilir karmaşık sayılar, pozitif sayılarla sınırlı olmayan ve rastgele karmaşık sayıları argüman olarak kabul edebilen, argümanının (ana karekökünü) hesaplayan genelleştirilmiş bir karekök işlemi kullanılarak ifade edilebilen karmaşık sayıların bir alt kümesini oluşturur. Bu kapsamda, gerçek ve sanal kısımları her ikisi de çizilebilir reel sayılar olan karmaşık sayılar da, aynı karmaşık sayılar sisteminin bir parçası olarak tanımlanabilir. Mesela, 


Bu iki çizilebilir karmaşık sayılar tanımı eşdeğerdir. Bir bakış açısından, eğer 




, burada
ve
olarak ifade edilir.
Cebirsel olarak çizilebilir noktalar
Cebirsel olarak çizilebilir noktalar, her iki reel Kartezyen koordinatı da cebirsel olarak çizilebilir reel sayılar olan noktalar olarak ifade edilebilir. Diğer bir deyişle, cebirsel olarak çizilebilir karmaşık sayılarla tanımlanan karmaşık düzlemdeki noktalar şeklinde de tanımlanabilirler. Cebirsel olarak çizilebilir karmaşık sayılarla ilgili iki tanım arasındaki eşdeğerlik dikkate alındığında, cebirsel olarak çizilebilir noktaların her iki tanımının da birbirine eşdeğer olduğu sonucuna varılır.
Cebirsel ve geometrik tanımların eşdeğerliği








 , kesişme teoremi temelinde yapılmıştır.
, kesişme teoremi temelinde yapılmıştır. , kesişme teoremi temelinde yapılmıştır.
, kesişme teoremi temelinde yapılmıştır. , geometrik ortalama teoremi temelinde yapılmıştır.
, geometrik ortalama teoremi temelinde yapılmıştır.Diğer bir perspektiften, geometrik nesnelerin bir kümesi, cebirsel olarak çizilebilir reel sayılar kullanılarak belirlenebilir: noktalar için koordinatlar, doğrular için eğim ve 
Cebirsel özellikler
Cebirsel olarak çizilebilir sayıların tanımı, ilgili sayıların toplamları, farkları, çarpımları ve çarpmaya bağlı tersleri gibi işlemleri kapsar; bu işlemler, soyut cebir içerisinde bir alanın tanımlanmasında kullanılan temel işlemlerle özdeştir. Bu bağlamda, ele alınan herhangi bir yöntemle tanımlanan konstrüktif sayılar bir alan yapısını oluşturur. Özellikle, çizilebilir reel sayılar, pozitif elemanlarının her birinin bir karekökünü barındıran, sıralanabilir bir alan olan bir Öklid alanını meydana getirir. Bu alanın ve alt alanlarının incelenmesi, bir sayının çizilebilir olabilmesi için zorunlu koşulları belirlememize olanak tanır. Bu koşullar, klasik geometrik yapı problemlerinde karşımıza çıkan ve çizilebilir olmayan belirli sayıların tespit edilmesinde kullanılabilir.
Çizilebilir sayıların genel alanı yerine, herhangi bir çizilebilir sayı 















Reel sayıların durumuna paralel olarak, bir karmaşık sayının çizilebilirliği, yalnızca o sayının, sonlu sayıda karmaşık kuadratik genişlemelerden oluşan bir alan kulesinin en üstünde yer alan bir alanda bulunması ile mümkündür. Daha açık bir tanımla, 










Trigonometrik sayılar
Trigonometrik sayılar, 


- İki sayısının kuvvetleri
- İki sayısının bir kuvvetine bir eklenmesiyle elde edilen asal sayılar olan Fermat asalları
- İki sayısının kuvvetlerinin ve birbirinden farklı Fermat asallarının herhangi bir sayıda kombinasyonunun çarpımları.
Buna göre, 


İmkansız çizimler
Antik Yunanlılar, çözümünü bulamadıkları bazı pergel ve cetvel çizimi problemlerinin sadece zorlu değil, çözümsüz olduğunu varsaymıştır. Ancak, birtakım sayıların çizilemezliği, bu tür yapıların mantıken gerçekleştirilemeyeceğini ortaya koymaktadır. Bununla birlikte, problem kendileri, sadece pergel ve cetvel kullanımıyla sınırlı kalmadan, bu sınırların ötesindeki yöntemlerle çözülebilir; Antik Yunanlılar bu tür çözümleri bilmekteydi. Bu yöntemlerden bir tanesinin, Arşimet'in yöntemiyle Açının Üçe Bölünmesi problemine getirdiği çözüm olduğu bilinmektedir.
Özellikle, çizilebilir sayılarla ilgili cebirsel ifadeleme, aşağıda belirtilen çizim problemlerinin gerçekleştirilemeyeceğinin ispatlanmasını sağlar:
- Delos problemi
- Birim karenin iki katına çıkarılması meselesi, ilk kare üzerine, kenarlarının uzunluğu
ve yüzölçümü
olan yeni bir kare konumlandırılarak halledilir. Eş anlamda, küpün hacmini iki katına çıkarma sorusu, hacmi
olan bir küp için kenar uzunluğunun
değerinde tesis edilmesini talep eder. Ancak, bu uzunluk, söz konusu uzunluğun olan
'nin,
üstünde üçüncü dereceden olması sebebiyle çizilebilir değildir. Yalnızca tek bir reel irrasyonel köke sahip olan bu kübik polinom, eğer bir kuadratik reel kök mevcut olsaydı, yoluyla ikinci bir reel kökün elde edilebileceği varsayımıyla, indirgenemez niteliktedir.[25]
- Bu probleme göre, verilen bir
açısından,
açısının inşa edilmesi gerekmektedir. Cebirsel olarak, açılar trigonometrik fonksiyonları, örneğin sinüsleri veya kosinüsleri ile temsil edilebilir, bu da verilen açı ile başlangıç segmenti arasında oluşturulan bir doğru segmentinin son noktasının Kartezyen koordinatlarını verir. Böylece, bir
açısı,
bir çizilebilir sayı olduğunda çizilebilir hale gelir ve açının üçe bölünmesi problemi,
inşa edilmesi olarak formüle edilebilir. Örneğin, eşkenar üçgenin
açısı pergel ve cetvel ile çizilebilir, burada
. Ancak, üçe bölünmüş açısı
çizilemez, çünkü
minimal polinomu
üzerinde 3 dereceli
olur. Bu belirli üçe bölme problemi örneğinin pergel ve cetvel ile çözülemediği için, genel problem de çözülemez.
- Daireyi kareyle çevreleme
- Alanı bir birim çember ile aynı olan
alanına sahip bir karenin kenar uzunluğu
, bir transandantal sayı olacaktır. Dolayısıyla, bu kare ve kenar uzunluğu çizilebilir değildir, çünkü
üzerinde cebirsel değildir.
- Merkezi orijinde olan düzenli bir
-genin köşeleri arasındaki açılar
olacaktır. Çokgen, bu açının kosinüsü bir trigonometrik sayı olduğunda çizilebilir. Bu bağlamda, örneğin, 15-geni çizebilirken, düzenli yedigen çizilemez, çünkü 7 asal sayıdır fakat bir Fermat asalı değildir. Yedigenin çizilemezliğinin daha doğrudan bir kanıtı için, düzenli yedigenin köşelerini
polinomunun karmaşık kökleri olarak temsil edin.
faktörünü çıkarıp,
ile bölerek ve
ile yer değiştirerek daha basit
polinomunu elde edersiniz; bu, üç reel kökü olan indirgenemez bir kübik polinomdur ve her bir kök, bir karmaşık sayı köşenin reel kısmının iki katıdır. Kökleri çizilebilir olmadığı için, yedigen de çizilebilir değildir.
- İki nokta ve bir dairesel ayna verildiğinde, verilen noktalardan biri diğerinin yansımasını çember üzerinde nerede görür? Geometrik olarak, her bir verilen noktadan yansıma noktasına giden çizgiler, çemberde eşit açılarla ve eşit uzunlukta kirişlerle kesişir. Ancak, bir yansıma noktasını pergel ve cetvel kullanarak çizmek imkansızdır. Özellikle, iki noktası
ve
içinde olan bir birim çember için, çözümün koordinatları indirgenemez derece-dört polinomunun
köklerini oluşturur. Derecesi iki sayısının kuvveti olmasına rağmen, bu polinomun derecesi üç ile bölünebilir, bu yüzden iteratif bir karesel genişletmeden gelmez ve Alhazen Problemi'nin pergel ve cetvelle bir çözümü yoktur.
Tarihçe
Çizilebilir sayılar kavramının doğuşu, küpün iki katına çıkarılması, bir açının üçe bölünmesi ve dairenin kareye çevrilmesi gibi üç imkansız pergel ve cetvel inşası ile yakından ilişkilidir. Geometrik inşalarda yalnızca pergel ve cetvel kullanımı kısıtlaması sık sık Plato'ya atfedilir, çünkü bu Plutarch'ta geçen bir bölümden kaynaklanır. Plutarch'a göre, Plato, küpün iki katına çıkarılması (Delos) problemini Knidoslu Ödoksus, Archytas ve Menaechmus'a vermiş ve onlar problemi mekanik yöntemler kullanarak çözmüşler, ancak Plato'dan kullanarak problemi çözmedikleri için bir azar işitmişlerdir. Ancak, bu atfın sorgulandığı bilinmektedir, kısmen, üçünün de çözüm bulduğu ancak bu çözümlerin pratik değerden yoksun olduğunu söyleyen başka bir hikâye versiyonunun varlığı nedeniyle (bu hikâye, Eratosthenes tarafından Askalonlu Eutokios'a atfedilir).Proclus, Rodoslu Eudemos'u alıntılayarak, iki cetvel ve pergel inşasını Oenopides'e (M.Ö. 450 civarı) atfetmiş ve bu, bazı yazarların Oenopides'in kısıtlamayı ortaya koyduğu hipotezini geliştirmelerine yol açmıştır. Pergel ve cetvelle yapılan kısıtlama, klasik inşaat problemlerinin çözülemezliği için esastır. Örneğin, açının üçe bölünmesi, antik Yunanlıların bildiği birçok yöntemle yapılabilir. 'in , Menaechmus'un veya Archimedes'in işaretli cetveli () inşası gibi yöntemler kullanılmıştır, aynı zamanda daha modern bir yaklaşım olan yöntemi de kullanılmıştır.
Klasik üç çizim probleminden biri olmamakla birlikte, cetvel ve pergel ile düzenli çokgenlerin çizimi problemi sıklıkla onlarla birlikte ele alınır. Yunanlılar, 




(1837) küpün iki katına çıkarılması ve bir açının üçe bölünmesi problemlerinin, yalnızca pergel ve cetvel kullanılarak çözülemeyeceğini cebirsel olarak kanıtladı. Aynı makalede, hangi düzenli çokgenlerin çizilebileceğini belirleyen problemin de çözümünü verdi: bir düzenli çokgenin çizilebilmesi ancak ve ancak kenar sayısının, bir ikinin kuvveti ile herhangi sayıda farklı Fermat asalının çarpımı olması durumudur (yani Gauss tarafından verilen yeterli koşullar aynı zamanda gerekli koşullardır). Dairenin kareye çevrilmesinin imkansızlığı üzerine bir kanıt girişimi, tarafından 1667 yılında Vera Circuli et Hyperbolae Quadratura (Dairenin ve Hiperbolün Gerçek Kareye Çevrilmesi) adlı eserinde verilmiştir. Kanıtı hatalı olsa da, bu makale, π'nin cebirsel özelliklerini kullanarak problemin çözümünü deneyen ilk çalışmadır. Dairenin kareye çevrilmesinin imkansızlığı, Ferdinand von Lindemann tarafından 1882 yılında, Charles Hermite'in çalışmalarını genişleterek ve π'nin bir transandantal sayı olduğunu kanıtlayarak kesin olarak ispatlanana kadar kanıtlanmadı. Heysem problemi'nin pergel ve cetvelle çözülemeyeceği, Elkin (1965)'in çalışmalarına kadar kanıtlanmadı.
Çizilebilir sayıların kendileri üzerine yapılan çalışma, René Descartes tarafından 1637 yılında yayımlanan kitabı Yöntem Üzerine Konuşmanın bir ek bölümü olan ile başlatılmıştır. Descartes, geometrik doğru parçalarına sayılar atayarak, İskenderiyeli Pappus tarafından öne sürülen antik bir cetvel ve pergel inşaat problemi çözümüyle felsefi yönteminin gücünü sergilemiştir.
Kaynakça
- ^ Sansan, Burcu (2019). "1.2". Cisim Genişlemeleri ve Origami Çizimleri (PDF) (Master's Thesis tez). Istanbul Technical University. 3 Mart 2024 tarihinde kaynağından (PDF). Erişim tarihi: 3 Mart 2024.
- ^ Kazarinoff (2003, ss. 10 & 15); Martin (1998), Corollary 2.16, p. 41.
- ^ a b c d Martin (1998).
- ^ a b Courant & Robbins (1996).
- ^ a b c d e f g Kazarinoff (2003).
- ^ Bu orta nokta inşası, Öklid'in Elementleri kitabının I. Kitap, 10. Önerme'sinde verilmiştir.
- ^ Herstein (1986). Uzunluk temelli tanımı uygulamak için, sıfır sayısının özel bir durum olarak çizilebilir sayılar arasına alınması zorunludur.
- ^ Moise (1974), s. 227; Martin (1998), Teorem 2.4, s. 33.
- ^ Roman (1995).
- ^ a b Lawrence & Zorzitto (2021), s. 440.
- ^ Toplama ve çarpma işlemleri için bkz. Kay (2021), Teorem 8.1.10, s. 187. Bölme işlemi için bkz. Kay (2021), Denklemler 8.8, s. 188 ve 9.2, s. 224. Karekök genişletmesi, trigonometrinin kullanılarak elde edilebilir; eşdeğer bir formül için bkz. Lawrence & Zorzitto (2021), s. 440.
- ^ Herstein (1986); Moise (1974); Fraleigh (1994); Courant & Robbins (1996).
- ^ Martin (1998); Courant & Robbins (1996).
- ^ Martin (1998), Theorem 2.7, p. 35.
- ^ Fraleigh (1994), s. 429.
- ^ Roman (1995), s. 59.
- ^ a b Neumann (1998).
- ^ Rotman (2006), s. 361.
- ^ Rotman (2006), s. 362.
- ^ Martin (1998), Theorem 2.10, p. 37.
- ^ Stewart (1989), s. 51.
- ^ Klein (1897), s. 3.
- ^ Bu alternatif çözümlerin açıklamaları, Knorr (1986) içeriğinin büyük bir kısmını oluşturur.
- ^ Klein (1897, s. 13); Fraleigh (1994, ss. 429–430)
- ^ Courant & Robbins (1996), Section III.3.1, "Doubling the cube", pp. 134–135.
- ^ Fraleigh (1994); Courant & Robbins (1996)
- ^ a b Fraleigh (1994).
- ^ Neumann (1998). Elkin (1965), farklı noktalar ve farklı bir polinom kullanarak aynı sonuca varır.
- ^ Plutarch, Quaestiones convivales , 718ef.
- ^ a b Knorr (1986).
- ^ Friedman (2018).
- ^ a b Klein (1897).
- ^ Martin (1998), s. 46.
- ^ Wantzel (1837).
- ^ Martin (1998), s. 44.
- ^ Elkin (1965); ayrıca problemin daha fazla tarihçesi ile bağımsız bir çözüm için bkz. Neumann (1998).
- ^ Boyer (2004).
Bibliografya
- Boyer, Carl B. (2004) [1956], History of Analytic Geometry, Dover, ISBN , MR 2108489
- ; (1996), "Chapter III: Geometrical constructions, the algebra of number fields", What is Mathematics? An elementary approach to ideas and methods (2.2 isbn = 0-19-510519-2 bas.), Oxford University Press, ss. 117-164
- Elkin, Jack M. (March 1965), "A deceptively easy problem", The Mathematics Teacher, 58 (3), ss. 194-199, doi:10.5951/MT.58.3.0194, JSTOR 27968003
- Fraleigh, John B., A First Course in Abstract Algebra (5.5yıl=1994 bas.), Addison Wesley, ISBN , MR 0225619
- Friedman, Michael (2018), A History of Folding in Mathematics: Mathematizing the Margins, Science Networks. Historical Studies, 59, Birkhäuser, doi:10.1007/978-3-319-72487-4, ISBN , MR 3793627
- (1986), Abstract Algebra, Macmillan, ISBN , MR 1011035
- Kay, Anthony (2021), Number Systems: A Path into Rigorous Mathematics, Taylor & Francis, ISBN
- (2003) [1970], Ruler and the Round: Classic Problems in Geometric Constructions, Dover, ISBN , MR 1963960
- Klein, Felix (1897), Famous Problems of Elementary Geometry, Beman, Wooster Woodruff; Smith, David Eugene tarafından çevrildi, Ginn & Co
- (1986), The Ancient Tradition of Geometric Problems, Dover Books on Mathematics, Courier Dover Publications, ISBN , MR 0884893
- Lawrence, John W.; Zorzitto, Frank A. (2021), Abstract Algebra: A Comprehensive Introduction, Cambridge Mathematical Textbooks, Cambridge University Press, ISBN
- Martin, George E. (1998), Geometric Constructions, Undergraduate Texts in Mathematics, Springer-Verlag, New York, doi:10.1007/978-1-4612-0629-3, ISBN , MR 1483895
- Moise, Edwin E. (1974), Elementary Geometry from an Advanced Standpoint (2.2yayıncı=Addison Wesley bas.), ISBN , MR 0344984
- (1998), "Reflections on reflection in a spherical mirror", American Mathematical Monthly, 105 (6), ss. 523-528, doi:10.2307/2589403, JSTOR 2589403, MR 1626185
- (1995), Field Theory, Springer-Verlag, ISBN , MR 1329733
- , A First Course in Abstract Algebra with Applications (3.3yıl=2006 bas.), Prentice Hall, ISBN
- , Galois Theory (2.2yıl=1989 bas.), Chapman and Hall, ISBN , MR 1036521
- (1837), "Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se résoudre avec la règle et le compas", Journal de Mathématiques Pures et Appliquées, 1 (2), ss. 366-372
Dış bağlantılar
| Wikimedia Commons'ta Çizilebilir sayı ile ilgili ortam dosyaları bulunmaktadır. |
- Eric W. Weisstein, Constructible Number (MathWorld)
- Constructible Numbers at
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cizilebilir sayi terimi geometri ve cebirde kullanilir ve bir reel sayi r displaystyle r nin belirli kosullar altinda bir cizgi olarak cizilebilip cizilemeyecegini ifade eder Eger birim uzunlukta herhangi cizgiyi kullanarak sadece pergel ve cetvel yardimiyla ve belirli sayida adimda r uzunlugunda bir baska cizgi cizebilirse bu durumda r sayisi cizilebilir bir sayidir Baska bir deyisle r sayisini sadece tam sayilari ve temel matematik islemleri toplama cikarma carpma bolme ile karekok alma islemini kullanarak acik bir sekilde ifade edebiliyorsa r sayisi cizilebilir kabul edilir Karekok 2 1 uzunlugunda iki dik kenari olan bir dik ucgenin hipotenusunun uzunluguna esittir ve bu nedenle bir cizilebilir sayidir Cizilebilir sayilar kavrami geometri ve cebirde onemli bir yere sahiptir ve bu kavramla yakindan ilgili olan cizilebilir noktalar geometrik ve cebirsel yontemlerle tanimlanabilir Bir noktanin cizilebilir olarak kabul edilebilmesi icin onceden belirlenmis birim uzunluktaki bir cizginin baslangicindan pergel ve cetvel kullanarak ulasilabilecek bir konumda olmasi gerekir Bu bir cizginin sonu iki cizginin veya iki cemberin kesisme noktasi gibi belirli bir noktaya isaret eder Ayrica bir noktanin cizilebilir olmasi bu noktanin Kartezyen koordinatlarinin her ikisinin de cizilebilir sayilar olmasini gerektirir Burada bir segmentin baslangic ve bitis noktalari bir Kartezyen koordinat sisteminde sirasiyla 0 0 ve 1 0 olarak dusunulur Cizilebilir sayilar ve noktalar diger yontemlerle elde edilen sayi ve noktalardan farklilastirilmak amaciyla bazen cetvel ve pergel sayilari ve cetvel ve pergel noktalari olarak adlandirilir Bu tanimlamalar geometri ve cebirdeki cesitli problemlerin cozumunde temel olusturur Cizilebilir sayilarin olusturdugu kume bir alani teskil eder Bu kumedeki elemanlara uygulanan dort temel aritmetik islemin her biri yine bir cizilebilir sayinin elde edilmesini saglar Bu alan rasyonel sayilar uzerine bir olarak islev gorur ve bu yapi cebirsel sayilar alaninin bir alt kumesi olarak kabul edilir Rasyonel sayilarin Euklidyen kapanisi olarak tanimlanan bu alan rasyonel sayilardan tureyen ve pozitif elemanlarinin tumunun karekoklerini barindiran en minimal alan genislemesidir Cizilebilir sayilarin cebirsel ve geometrik tanimlamalarinin esdegerligini ispatlama sureci antik Yunan matematigine ait birkac unlu problemin de icinde bulundugu pergel ve cetvel kullanilarak olusturulan geometrik sorularin cebirsel bir cerceveye donusturulmesine olanak tanir Bu sorularin cebirsel olarak ifade edilmesi geometrik olarak formule edilen ve yuzyillarca cozume direnc gostermis ayni problemlerin cizilebilir olmadiklarina dair ispatlarin ortaya konulmasini saglamistir Geometrik tanimlamalarGeometrik olarak cizilebilir noktalar Oklidyen duzlemde yer alan O displaystyle O ve A displaystyle A isimli iki ayri nokta verildiginde bu noktalari baslangic kabul ederek pergel ve cetvel ile cizilebilen noktalarin olusturdugu kume S displaystyle S olarak tanimlanmaktadir Bu baglamda S displaystyle S kumesine ait noktalar cizilebilir noktalar olarak isimlendirilir O displaystyle O ve A displaystyle A noktalari bu tanim cercevesinde S displaystyle S kumesinin dogal uyeleridir S displaystyle S kumesindeki diger elemanlari daha detayli bir sekilde tanimlamak amaciyla asagidaki iki tanim kullanilmaktadir Uc noktalari S displaystyle S kumesine dahil olan dogru parcasina cizilebilir dogru parcasi denir ve Merkezi S displaystyle S icerisinde yer alan ve bir S displaystyle S noktasindan gecen ya da alternatif bir ifadeyle yaricapi S displaystyle S kumesindeki iki ayri nokta arasindaki mesafe olan cembere cizilebilir cember adi verilir Buna gore O displaystyle O ve A displaystyle A haricindeki S displaystyle S noktalari asagidakileri icerir Iki paralel olmayan cizilmis dogru parcasinin veya bu parcalar uzerinden cizilen dogrularin noktalari Bir cizilebilir cember ile cizilmis bir dogru parcasinin veya bu parca uzerinden cizilen bir dogrunun kesisim noktalari Iki ayri cizilebilir cemberin kesisim noktalari Ornegin cizilmis OA displaystyle OA dogru parcasinin orta noktasi bir cizilebilir noktadir Bunun icin bir yontem OA displaystyle OA yaricapi ile iki cember cizmek ve bu iki cemberin kesisme noktalarindan gecen bir cizgi cizmektir O zaman OA displaystyle OA segmentinin orta noktasi bu cizilmis cizginin segmenti kestigi noktadir Geometrik olarak cizilebilir sayilar Geometrik formulasyona iliskin baslangic verisi O displaystyle O noktasinin orijin olarak 0 0 displaystyle 0 0 koordinatlari ile ve A displaystyle A noktasinin 1 0 displaystyle 1 0 koordinatlari ile iliskilendirildigi bir Kartezyen koordinat sisteminin tanimlanmasini saglar Artik S displaystyle S noktalari cizilebilir bir noktanin koordinati olarak tanimlanan bir cizilebilir sayinin geometri ile cebir arasinda bir bag kurulmasini mumkun kilar Cizilebilir bir sayinin esdeger tanimlari arasinda bir cizilebilir noktanin x displaystyle x koordinati olan x 0 displaystyle x 0 veya cizilebilir bir dogru parcasinin uzunlugu bulunmaktadir Bu esitligin bir yonunde eger bir cizilebilir noktanin koordinatlari x y displaystyle x y ise x 0 displaystyle x 0 noktasi x displaystyle x eksenine dik bir projeksiyon olarak cizilebilir ve orijinden bu noktaya kadar olan mesafe x displaystyle x uzunlugundadir Tersi durumda eger x displaystyle x bir cizilebilir dogru parcasinin uzunlugu ise x displaystyle x yaricapi ve O displaystyle O merkezi ile tanimlanan bir cemberin x displaystyle x ekseni ile kesisimi x 0 displaystyle x 0 noktasini saglar Bu esitlikten yola cikarak Kartezyen koordinatlari geometrik olarak cizilebilir sayilar olan her noktanin kendisinin de geometrik olarak cizilebilir bir nokta oldugu anlasilmaktadir Zira x displaystyle x ve y displaystyle y geometrik olarak cizilebilir sayilar oldugunda x y displaystyle x y noktasi koordinat eksenlerine dik x 0 displaystyle x 0 ve 0 y displaystyle 0 y noktalarindan gecen dogrularin kesisimi ile olusturulabilir Cebirsel tanimlarCebirsel olarak cizilebilir reel sayilar Cebirsel olarak cizilebilir reel sayilar toplama cikarma carpma carpmaya gore ters islem ve pozitif sayilarin karekoklerinin kullanimiyla tam sayilarin kombinasyonunu iceren formuller araciligiyla ifade edilebilen reel sayilarin bir alt kumesini temsil eder Bu formullerin yapisal karmasikligini artirarak daha da sadelestirilebilir sekilde soz konusu formullerdeki tam sayilar yalnizca 0 ve 1 olarak kisitlanabilir Mesela 2 nin karekoku cizilebilir olarak kabul edilir zira bu 2 displaystyle sqrt 2 veya 1 1 displaystyle sqrt 1 1 gibi formullerle ifade edilebilir Benzer bir bicimde cebirsel olarak cizilebilir karmasik sayilar pozitif sayilarla sinirli olmayan ve rastgele karmasik sayilari arguman olarak kabul edebilen argumaninin ana karekokunu hesaplayan genellestirilmis bir karekok islemi kullanilarak ifade edilebilen karmasik sayilarin bir alt kumesini olusturur Bu kapsamda gercek ve sanal kisimlari her ikisi de cizilebilir reel sayilar olan karmasik sayilar da ayni karmasik sayilar sisteminin bir parcasi olarak tanimlanabilir Mesela i displaystyle i karmasik sayisi icin 1 displaystyle sqrt 1 veya 0 1 displaystyle sqrt 0 1 gibi formuller gecerlidir ve bu sayinin gercek ve sanal kisimlari sirasiyla cizilebilir sayilar olan 0 ve 1 degerlerindedir Bu iki cizilebilir karmasik sayilar tanimi esdegerdir Bir bakis acisindan eger q x iy displaystyle q x iy formuluyle ifade edilen bir karmasik sayinin reel ve sanal bilesenleri x displaystyle x ve y displaystyle y cizilebilir reel sayilar kategorisinde ise bu bilesenlerin formulleri x y 1 displaystyle x y sqrt 1 genel formulu icerisine yerlestirilerek q displaystyle q karmasik sayisinin bir formulu turetilebilir Diger yandan cebirsel olarak cizilebilir bir karmasik sayi icin var olan herhangi bir formul soz konusu formuldeki her islemin reel ve sanal kisimlar uzerindeki islemlere donusturulmesi ile bu sayinin reel ve sanal parcalari icin formullere cevrilebilir Bu donusum icin asagidaki genisletmeler kullanilir a ib c id a c i b d displaystyle a ib pm c id a pm c i b pm d a ib c id ac bd i ad bc displaystyle a ib c id ac bd i ad bc 1a ib aa2 b2 i ba2 b2 displaystyle frac 1 a ib frac a a 2 b 2 i frac b a 2 b 2 a ib a r rs ibrs displaystyle sqrt a ib frac a r sqrt r s i frac b sqrt r s burada r a2 b2 displaystyle r sqrt a 2 b 2 ve s a r 2 b2 displaystyle s sqrt a r 2 b 2 olarak ifade edilir Cebirsel olarak cizilebilir noktalar Cebirsel olarak cizilebilir noktalar her iki reel Kartezyen koordinati da cebirsel olarak cizilebilir reel sayilar olan noktalar olarak ifade edilebilir Diger bir deyisle cebirsel olarak cizilebilir karmasik sayilarla tanimlanan karmasik duzlemdeki noktalar seklinde de tanimlanabilirler Cebirsel olarak cizilebilir karmasik sayilarla ilgili iki tanim arasindaki esdegerlik dikkate alindiginda cebirsel olarak cizilebilir noktalarin her iki taniminin da birbirine esdeger oldugu sonucuna varilir Cebirsel ve geometrik tanimlarin esdegerligia displaystyle a ve b displaystyle b degerleri geometrik yontemlerle olusturulan segmentlerin sifirdan farkli uzunluklarina karsilik geliyorsa temel pergel ve duz cizgi kullanimi ile a b displaystyle a b a b displaystyle a b ab displaystyle ab ve a b displaystyle a b uzunluklarinda yeni segmentlerin olusturulmasi mumkundur Bu islemlerin son ikisi kesisme teoremine dayali bir yontemle gerceklestirilebilir Bu araclara dayanarak gerceklestirilen biraz daha karmasik bir insa yontemi geometrik ortalama teoremini temel alir ve a displaystyle a uzunlugunda bir segment kullanilarak a displaystyle sqrt a uzunlugunda bir segmentin olusturulmasini saglar Bu teknikler bir sayinin formulunun ilgili sayinin geometrik insasina donusturulmesi suretiyle her cebirsel olarak cizilebilir sayinin geometrik olarak da cizilebilecegi sonucunu dogurmaktadir Bu gorseller cizilebilir sayilarin olusturulmasi icin pergel ve cetvel kullanilarak gerceklestirilen cizme islemlerini gostermektedir ab displaystyle ab kesisme teoremi temelinde yapilmistir ab displaystyle frac a b kesisme teoremi temelinde yapilmistir p displaystyle sqrt p geometrik ortalama teoremi temelinde yapilmistir Diger bir perspektiften geometrik nesnelerin bir kumesi cebirsel olarak cizilebilir reel sayilar kullanilarak belirlenebilir noktalar icin koordinatlar dogrular icin egim ve y displaystyle y kesisim cemberler icin ise merkez ve yaricap Bu degerlere dayanarak sadece aritmetik ve karekokler kullanilarak pergel ve duz cizgi ile yapilan bir cizimin tek bir adiminda dahil edilebilecek herhangi bir ek nesne icin formullerin gelistirilmesi mumkundur bu oldukca mesakkatli bir surectir Bu formullerden hareketle geometrik olarak cizilebilir her sayinin cebirsel olarak da cizilebilecegi sonucuna varilmaktadir Cebirsel ozelliklerCebirsel olarak cizilebilir sayilarin tanimi ilgili sayilarin toplamlari farklari carpimlari ve carpmaya bagli tersleri gibi islemleri kapsar bu islemler soyut cebir icerisinde bir alanin tanimlanmasinda kullanilan temel islemlerle ozdestir Bu baglamda ele alinan herhangi bir yontemle tanimlanan konstruktif sayilar bir alan yapisini olusturur Ozellikle cizilebilir reel sayilar pozitif elemanlarinin her birinin bir karekokunu barindiran siralanabilir bir alan olan bir Oklid alanini meydana getirir Bu alanin ve alt alanlarinin incelenmesi bir sayinin cizilebilir olabilmesi icin zorunlu kosullari belirlememize olanak tanir Bu kosullar klasik geometrik yapi problemlerinde karsimiza cikan ve cizilebilir olmayan belirli sayilarin tespit edilmesinde kullanilabilir Cizilebilir sayilarin genel alani yerine herhangi bir cizilebilir sayi g displaystyle gamma ile uretilen ve bu sayiya ozgu Q g displaystyle mathbb Q gamma alt alanini incelemek ve g displaystyle gamma nin cebirsel yapisini kullanarak soz konusu alani parcalara ayirmak daha faydalidir g displaystyle gamma cizilebilir bir reel sayi oldugunda bu sayinin cizilebilirligini mumkun kilan formulasyondaki degerlerin kullanilmasi her bir i displaystyle i icin Q a1 ai displaystyle mathbb Q alpha 1 dots a i nin Q a1 ai 1 displaystyle mathbb Q alpha 1 dots a i 1 ya kiyasla derecesi 2 olan bir genislemesi oldugu bir a1 an g displaystyle alpha 1 dots a n gamma reel sayi dizisinin olusturulmasina imkan tanir Alternatif bir terminoloji ile ifade edildiginde bir reel sayinin cizilebilir olmasi yalnizca bu sayinin Q displaystyle mathbb Q rasyonel alani ile baslayip g displaystyle gamma nin bulundugu Kn displaystyle K n ye kadar uzanan ve her 0 lt j n displaystyle 0 lt j leq n icin Kj Kj 1 2 displaystyle K j K j 1 2 olan sonlu bir kuadratik genisleme alan kulesinin zirvesindeki bir alanda yer almasi durumuna baglidir Bu ayrisma surecinden Q g Q displaystyle mathbb Q gamma mathbb Q alan genislemesinin derecesinin kuadratik genisleme asamalarinin sayisini gosteren r displaystyle r ile 2r displaystyle 2 r oldugu anlasilir Reel sayilarin durumuna paralel olarak bir karmasik sayinin cizilebilirligi yalnizca o sayinin sonlu sayida karmasik kuadratik genislemelerden olusan bir alan kulesinin en ustunde yer alan bir alanda bulunmasi ile mumkundur Daha acik bir tanimla g displaystyle gamma sayisinin cizilebilir olmasi Q F0 F1 Fn displaystyle mathbb Q F 0 subseteq F 1 subseteq dots subseteq F n seklinde bir alanlar dizisi var oldugunda g displaystyle gamma sayisinin Fn displaystyle F n icinde yer almasi ve her 0 lt j n displaystyle 0 lt j leq n icin Fj Fj 1 2 displaystyle F j F j 1 2 iliskisinin gecerli olmasi durumunda gerceklesir Bu tanimlama ile reel cizilebilir sayilara iliskin tanimlama arasindaki temel fark bu kapsamdaki alanlarin yalnizca reel sayilari kapsamak zorunda olmayisidir Dolayisiyla bir karmasik sayi g displaystyle gamma cizilebilirse bu durumda Q g Q displaystyle mathbb Q gamma mathbb Q ikinin bir kuvveti seklinde ifade edilir Ancak bu gerekli kosul tek basina yeterli olmayip derecesi ikinin bir kuvveti olan fakat kuadratik genislemeler dizisi ile ayristirilamayan alan genislemelerinin var oldugu durumlar da bulunmaktadir Q displaystyle mathbb Q uzerinden kuadratik genislemelerin kuleleri araciligiyla olusturulabilen alanlar Q displaystyle mathbb Q icin tekrarlanan kuadratik genislemeler olarak adlandirilir Reel ve karmasik cizilebilir sayilarin olusturdugu alanlar Q displaystyle mathbb Q uzerinden gerceklestirilen tum gercek veya karmasik tekrarlanan kuadratik genislemelerin birlesimlerinden meydana gelir Trigonometrik sayilarTrigonometrik sayilar p displaystyle pi nin rasyonel katlarinin sinus veya kosinus degerleri olarak tanimlanir Bu tur sayilar daima cebirsel niteliktedir ancak bu sayilarin her birinin cizilebilir olmasi zorunlu degildir Ozellikle 2p n displaystyle 2 pi n acisinin sinusu veya kosinusu sadece belirli n displaystyle n sayilari icin cizilebilir olma ozelligi gosterir Iki sayisinin kuvvetleri Iki sayisinin bir kuvvetine bir eklenmesiyle elde edilen asal sayilar olan Fermat asallari Iki sayisinin kuvvetlerinin ve birbirinden farkli Fermat asallarinin herhangi bir sayida kombinasyonunun carpimlari Buna gore cos p 15 displaystyle cos pi 15 15 sayisinin 3 ve 5 olmak uzere iki Fermat asalinin carpimi olmasi sebebiyle cizilebilir bir degere sahiptir Ancak cos p 9 displaystyle cos pi 9 farkli Fermat asallarinin bir carpimi olmadigi icin ve cos p 7 displaystyle cos pi 7 bir Fermat asali olmayan bir asal sayi oldugu icin cizilebilir sayilar arasinda yer almaz Imkansiz cizimlerBir kup ve onun iki katiBir aci ve onun uce bolunmesiEsit alanlara sahip daire ve kare Antik Yunanlilar cozumunu bulamadiklari bazi pergel ve cetvel cizimi problemlerinin sadece zorlu degil cozumsuz oldugunu varsaymistir Ancak birtakim sayilarin cizilemezligi bu tur yapilarin mantiken gerceklestirilemeyecegini ortaya koymaktadir Bununla birlikte problem kendileri sadece pergel ve cetvel kullanimiyla sinirli kalmadan bu sinirlarin otesindeki yontemlerle cozulebilir Antik Yunanlilar bu tur cozumleri bilmekteydi Bu yontemlerden bir tanesinin Arsimet in yontemiyle Acinin Uce Bolunmesi problemine getirdigi cozum oldugu bilinmektedir Ozellikle cizilebilir sayilarla ilgili cebirsel ifadeleme asagida belirtilen cizim problemlerinin gerceklestirilemeyeceginin ispatlanmasini saglar Delos problemi Birim karenin iki katina cikarilmasi meselesi ilk kare uzerine kenarlarinin uzunlugu 2 displaystyle sqrt 2 ve yuzolcumu 2 displaystyle 2 olan yeni bir kare konumlandirilarak halledilir Es anlamda kupun hacmini iki katina cikarma sorusu hacmi 2 displaystyle 2 olan bir kup icin kenar uzunlugunun 23 displaystyle sqrt 3 2 degerinde tesis edilmesini talep eder Ancak bu uzunluk soz konusu uzunlugun olan x3 2 displaystyle x 3 2 nin Q displaystyle mathbb Q ustunde ucuncu dereceden olmasi sebebiyle cizilebilir degildir Yalnizca tek bir reel irrasyonel koke sahip olan bu kubik polinom eger bir kuadratik reel kok mevcut olsaydi yoluyla ikinci bir reel kokun elde edilebilecegi varsayimiyla indirgenemez niteliktedir 25 Bu probleme gore verilen bir 8 displaystyle theta acisindan 8 3 displaystyle theta 3 acisinin insa edilmesi gerekmektedir Cebirsel olarak acilar trigonometrik fonksiyonlari ornegin sinusleri veya kosinusleri ile temsil edilebilir bu da verilen aci ile baslangic segmenti arasinda olusturulan bir dogru segmentinin son noktasinin Kartezyen koordinatlarini verir Boylece bir 8 displaystyle theta acisi x cos 8 displaystyle x cos theta bir cizilebilir sayi oldugunda cizilebilir hale gelir ve acinin uce bolunmesi problemi cos 13arccos x displaystyle cos tfrac 1 3 arccos x insa edilmesi olarak formule edilebilir Ornegin eskenar ucgenin 8 p 3 60 displaystyle theta pi 3 60 circ acisi pergel ve cetvel ile cizilebilir burada x cos 8 12 displaystyle x cos theta tfrac 1 2 Ancak uce bolunmus acisi 8 3 p 9 20 displaystyle theta 3 pi 9 20 circ cizilemez cunku cos p 9 displaystyle cos pi 9 minimal polinomu Q displaystyle mathbb Q uzerinde 3 dereceli 8x3 6x 1 displaystyle 8x 3 6x 1 olur Bu belirli uce bolme problemi orneginin pergel ve cetvel ile cozulemedigi icin genel problem de cozulemez Daireyi kareyle cevreleme Alani bir birim cember ile ayni olan p displaystyle pi alanina sahip bir karenin kenar uzunlugu p displaystyle sqrt pi bir transandantal sayi olacaktir Dolayisiyla bu kare ve kenar uzunlugu cizilebilir degildir cunku Q displaystyle mathbb Q uzerinde cebirsel degildir Merkezi orijinde olan duzenli bir n displaystyle n genin koseleri arasindaki acilar 2p n displaystyle 2 pi n olacaktir Cokgen bu acinin kosinusu bir trigonometrik sayi oldugunda cizilebilir Bu baglamda ornegin 15 geni cizebilirken duzenli yedigen cizilemez cunku 7 asal sayidir fakat bir Fermat asali degildir Yedigenin cizilemezliginin daha dogrudan bir kaniti icin duzenli yedigenin koselerini x7 1 displaystyle x 7 1 polinomunun karmasik kokleri olarak temsil edin x 1 displaystyle x 1 faktorunu cikarip x3 displaystyle x 3 ile bolerek ve y x 1 x displaystyle y x 1 x ile yer degistirerek daha basit y3 y2 2y 1 displaystyle y 3 y 2 2y 1 polinomunu elde edersiniz bu uc reel koku olan indirgenemez bir kubik polinomdur ve her bir kok bir karmasik sayi kosenin reel kisminin iki katidir Kokleri cizilebilir olmadigi icin yedigen de cizilebilir degildir Iki nokta ve bir dairesel ayna verildiginde verilen noktalardan biri digerinin yansimasini cember uzerinde nerede gorur Geometrik olarak her bir verilen noktadan yansima noktasina giden cizgiler cemberde esit acilarla ve esit uzunlukta kirislerle kesisir Ancak bir yansima noktasini pergel ve cetvel kullanarak cizmek imkansizdir Ozellikle iki noktasi 16 16 displaystyle tfrac 1 6 tfrac 1 6 ve 12 12 displaystyle tfrac 1 2 tfrac 1 2 icinde olan bir birim cember icin cozumun koordinatlari indirgenemez derece dort polinomunun x4 2x3 4x2 2x 1 displaystyle x 4 2x 3 4x 2 2x 1 koklerini olusturur Derecesi iki sayisinin kuvveti olmasina ragmen bu polinomun derecesi uc ile bolunebilir bu yuzden iteratif bir karesel genisletmeden gelmez ve Alhazen Problemi nin pergel ve cetvelle bir cozumu yoktur TarihceCizilebilir sayilar kavraminin dogusu kupun iki katina cikarilmasi bir acinin uce bolunmesi ve dairenin kareye cevrilmesi gibi uc imkansiz pergel ve cetvel insasi ile yakindan iliskilidir Geometrik insalarda yalnizca pergel ve cetvel kullanimi kisitlamasi sik sik Plato ya atfedilir cunku bu Plutarch ta gecen bir bolumden kaynaklanir Plutarch a gore Plato kupun iki katina cikarilmasi Delos problemini Knidoslu Odoksus Archytas ve Menaechmus a vermis ve onlar problemi mekanik yontemler kullanarak cozmusler ancak Plato dan kullanarak problemi cozmedikleri icin bir azar isitmislerdir Ancak bu atfin sorgulandigi bilinmektedir kismen ucunun de cozum buldugu ancak bu cozumlerin pratik degerden yoksun oldugunu soyleyen baska bir hikaye versiyonunun varligi nedeniyle bu hikaye Eratosthenes tarafindan Askalonlu Eutokios a atfedilir Proclus Rodoslu Eudemos u alintilayarak iki cetvel ve pergel insasini Oenopides e M O 450 civari atfetmis ve bu bazi yazarlarin Oenopides in kisitlamayi ortaya koydugu hipotezini gelistirmelerine yol acmistir Pergel ve cetvelle yapilan kisitlama klasik insaat problemlerinin cozulemezligi icin esastir Ornegin acinin uce bolunmesi antik Yunanlilarin bildigi bircok yontemle yapilabilir in Menaechmus un veya Archimedes in isaretli cetveli insasi gibi yontemler kullanilmistir ayni zamanda daha modern bir yaklasim olan yontemi de kullanilmistir Klasik uc cizim probleminden biri olmamakla birlikte cetvel ve pergel ile duzenli cokgenlerin cizimi problemi siklikla onlarla birlikte ele alinir Yunanlilar n 2h displaystyle n 2 h herhangi bir h 2 displaystyle h geq 2 tam sayisi icin 3 5 veya bu sayilarin herhangi iki veya ucunun carpimi ile duzenli n displaystyle n genler cizmeyi biliyordu ancak diger duzenli n displaystyle n genler onlara meydan okuyordu 1796 yilinda o zamanlar 18 yasinda bir ogrenci olan Carl Friedrich Gauss bir gazetede cetvel ve pergel ile duzenli bir 17 geni insa ettigini duyurdu Gauss un yaklasimi geometrikten ziyade cebirseldi aslinda poligonu gercekten insa etmemis ancak merkezi bir acinin kosinusunun bir cizilebilir sayi oldugunu gostermisti Arguman 1801 yilinda yayimlanan Disquisitiones Arithmeticae kitabinda genellestirilmis ve bir duzenli n displaystyle n genin insasi icin yeterli kosulu vermistir Gauss bu kosulun ayni zamanda gerekli oldugunu iddia etti ancak kanitlamadi ve ozellikle Felix Klein bu kanitin bir kismini ona atfetti de klasik uc problemden biri degildir ancak Ibnu l Heysem Alhazen adiyla anilmasina ragmen bir ortacag Islam matematikcisi olmasina karsin problem zaten ikinci yuzyildan Batlamyus un yer almaktadir 1837 kupun iki katina cikarilmasi ve bir acinin uce bolunmesi problemlerinin yalnizca pergel ve cetvel kullanilarak cozulemeyecegini cebirsel olarak kanitladi Ayni makalede hangi duzenli cokgenlerin cizilebilecegini belirleyen problemin de cozumunu verdi bir duzenli cokgenin cizilebilmesi ancak ve ancak kenar sayisinin bir ikinin kuvveti ile herhangi sayida farkli Fermat asalinin carpimi olmasi durumudur yani Gauss tarafindan verilen yeterli kosullar ayni zamanda gerekli kosullardir Dairenin kareye cevrilmesinin imkansizligi uzerine bir kanit girisimi tarafindan 1667 yilinda Vera Circuli et Hyperbolae Quadratura Dairenin ve Hiperbolun Gercek Kareye Cevrilmesi adli eserinde verilmistir Kaniti hatali olsa da bu makale p nin cebirsel ozelliklerini kullanarak problemin cozumunu deneyen ilk calismadir Dairenin kareye cevrilmesinin imkansizligi Ferdinand von Lindemann tarafindan 1882 yilinda Charles Hermite in calismalarini genisleterek ve p nin bir transandantal sayi oldugunu kanitlayarak kesin olarak ispatlanana kadar kanitlanmadi Heysem problemi nin pergel ve cetvelle cozulemeyecegi Elkin 1965 in calismalarina kadar kanitlanmadi Cizilebilir sayilarin kendileri uzerine yapilan calisma Rene Descartes tarafindan 1637 yilinda yayimlanan kitabi Yontem Uzerine Konusmanin bir ek bolumu olan ile baslatilmistir Descartes geometrik dogru parcalarina sayilar atayarak Iskenderiyeli Pappus tarafindan one surulen antik bir cetvel ve pergel insaat problemi cozumuyle felsefi yonteminin gucunu sergilemistir Kaynakca Sansan Burcu 2019 1 2 Cisim Genislemeleri ve Origami Cizimleri PDF Master s Thesis tez Istanbul Technical University 3 Mart 2024 tarihinde kaynagindan PDF Erisim tarihi 3 Mart 2024 Kazarinoff 2003 ss 10 amp 15 Martin 1998 Corollary 2 16 p 41 a b c d Martin 1998 a b Courant amp Robbins 1996 a b c d e f g Kazarinoff 2003 Bu orta nokta insasi Oklid in Elementleri kitabinin I Kitap 10 Onerme sinde verilmistir Herstein 1986 Uzunluk temelli tanimi uygulamak icin sifir sayisinin ozel bir durum olarak cizilebilir sayilar arasina alinmasi zorunludur Moise 1974 s 227 Martin 1998 Teorem 2 4 s 33 Roman 1995 a b Lawrence amp Zorzitto 2021 s 440 Toplama ve carpma islemleri icin bkz Kay 2021 Teorem 8 1 10 s 187 Bolme islemi icin bkz Kay 2021 Denklemler 8 8 s 188 ve 9 2 s 224 Karekok genisletmesi trigonometrinin kullanilarak elde edilebilir esdeger bir formul icin bkz Lawrence amp Zorzitto 2021 s 440 Herstein 1986 Moise 1974 Fraleigh 1994 Courant amp Robbins 1996 Martin 1998 Courant amp Robbins 1996 Martin 1998 Theorem 2 7 p 35 Fraleigh 1994 s 429 Roman 1995 s 59 a b Neumann 1998 Rotman 2006 s 361 Rotman 2006 s 362 Martin 1998 Theorem 2 10 p 37 Stewart 1989 s 51 Klein 1897 s 3 Bu alternatif cozumlerin aciklamalari Knorr 1986 iceriginin buyuk bir kismini olusturur Klein 1897 s 13 Fraleigh 1994 ss 429 430 Courant amp Robbins 1996 Section III 3 1 Doubling the cube pp 134 135 Fraleigh 1994 Courant amp Robbins 1996 a b Fraleigh 1994 Neumann 1998 Elkin 1965 farkli noktalar ve farkli bir polinom kullanarak ayni sonuca varir Plutarch Quaestiones convivales 718ef a b Knorr 1986 Friedman 2018 a b Klein 1897 Martin 1998 s 46 Wantzel 1837 Martin 1998 s 44 Elkin 1965 ayrica problemin daha fazla tarihcesi ile bagimsiz bir cozum icin bkz Neumann 1998 Boyer 2004 BibliografyaBoyer Carl B 2004 1956 History of Analytic Geometry Dover ISBN 978 0 486 43832 0 MR 2108489 1996 Chapter III Geometrical constructions the algebra of number fields What is Mathematics An elementary approach to ideas and methods 2 2 isbn 0 19 510519 2 bas Oxford University Press ss 117 164 KB1 bakim Dikey cizgi eksik link Elkin Jack M March 1965 A deceptively easy problem The Mathematics Teacher 58 3 ss 194 199 doi 10 5951 MT 58 3 0194 JSTOR 27968003 Fraleigh John B A First Course in Abstract Algebra 5 5yil 1994 bas Addison Wesley ISBN 978 0 201 53467 2 MR 0225619 Friedman Michael 2018 A History of Folding in Mathematics Mathematizing the Margins Science Networks Historical Studies 59 Birkhauser doi 10 1007 978 3 319 72487 4 ISBN 978 3 319 72486 7 MR 3793627 1986 Abstract Algebra Macmillan ISBN 0 02 353820 1 MR 1011035 Kay Anthony 2021 Number Systems A Path into Rigorous Mathematics Taylor amp Francis ISBN 978 0 367 18065 2 2003 1970 Ruler and the Round Classic Problems in Geometric Constructions Dover ISBN 0 486 42515 0 MR 1963960 Klein Felix 1897 Famous Problems of Elementary Geometry Beman Wooster Woodruff Smith David Eugene tarafindan cevrildi Ginn amp Co 1986 The Ancient Tradition of Geometric Problems Dover Books on Mathematics Courier Dover Publications ISBN 978 0 486 67532 9 MR 0884893 Lawrence John W Zorzitto Frank A 2021 Abstract Algebra A Comprehensive Introduction Cambridge Mathematical Textbooks Cambridge University Press ISBN 978 1 108 86551 7 Martin George E 1998 Geometric Constructions Undergraduate Texts in Mathematics Springer Verlag New York doi 10 1007 978 1 4612 0629 3 ISBN 0 387 98276 0 MR 1483895 Moise Edwin E 1974 Elementary Geometry from an Advanced Standpoint 2 2yayinci Addison Wesley bas ISBN 0 201 04793 4 MR 0344984 1998 Reflections on reflection in a spherical mirror American Mathematical Monthly 105 6 ss 523 528 doi 10 2307 2589403 JSTOR 2589403 MR 1626185 1995 Field Theory Springer Verlag ISBN 978 0 387 94408 1 MR 1329733 A First Course in Abstract Algebra with Applications 3 3yil 2006 bas Prentice Hall ISBN 978 0 13 186267 8 Galois Theory 2 2yil 1989 bas Chapman and Hall ISBN 978 0 412 34550 0 MR 1036521 1837 Recherches sur les moyens de reconnaitre si un Probleme de Geometrie peut se resoudre avec la regle et le compas Journal de Mathematiques Pures et Appliquees 1 2 ss 366 372 Dis baglantilarWikimedia Commons ta Cizilebilir sayi ile ilgili ortam dosyalari bulunmaktadir Eric W Weisstein Constructible Number MathWorld Constructible Numbers at
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State