Doğrusal olmayan optik ya da nonlineer optik, ışığın doğrusal olmayan sistem ve malzemelerdeki davranışı ile özelliklerini inceleyen optiğin bir alt dalıdır. Bu malzemelerde elektrik alan () ile polarizasyon yoğunluğu () arasındaki ilişki doğrusal değildir; bu durum daha çok yüksek genlikte (108 V/m seviyelerinde) ışık veren lazerlerde ve lityum niobat gibi kristal yapılarında görülür. Schwinger sınırından daha kuvvetli alanlarda vakum da doğrusallığını kaybeder. Süperpozisyon prensibi bu malzemeler için geçerli değildir.

Doğrusal olmayan optiğin prensipleri, birçok lazer ve elektro-optik aygıt tasarımında sıklıkla kullanılmaktadır. Bu optik dalı aynı zamanda fiber optikte ultra kısa darbe iletimi gibi alanlarda da önem taşımaktadır.
Temeller
Doğrusal olmayan polarizasyon

Doğrusal bir ortamda polarizasyon ile elektrik alanın ilişkisi şu şekilde ifade edilebilir:
Bu formülde 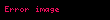

ya da
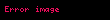
Doğrusal olmayan optikte dalga denklemi
Doğrusal olmayan ortamlardaki farklı frekans harmonikleri elektromanyetik dalga denkleminin modifikasyonu ile açıklanabilir. Sadeleşmemiş, zamana bağlı elektrik alan dalga denklemi Maxwell denklemleri aracılığı ile şu şekilde yazılabilir:
Bu denklemde 
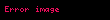
Bu formülde 



Başlıca doğrusal olmayan optik süreçler
Frekans karıştırma ve ikinci harmonik üretimi

Doğrusal olmayan kristal gibi ortamlarda elektromanyetik dalgalar enerji alışverişi ile farklı bir frekansa geçebilir. Bu süreçlerden biri ikinci harmonik üretimi ya da frekans ikilemesidir. Bu süreçte kristal ortamı asıl alanın iki katı frekansında (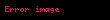
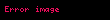
Bu durumda ikinci mertebeden polarizasyonda zamandan bağımsız bir DC polarizasyonu oluşur ve bu optik rektifikasyon olarak bilinir. Enerjinin korunumu ikinci harmonik üretiminde de geçerlidir; doğrusal olmayan etkileşim ile ikinci harmonikten asıl dalgaya enerji geçişi olabilir. Farklı frekanslarda dalgalar dağılım nedeniyle farklı hızlarda hareket eder. Bu nedenle asıl dalga ile harmoniklerin toplamının tam parlaklığı sağlayabilmesi için faz eşlenmesi (phase matching) koşullarının sağlanması gerekir: ikinci harmonik üretimi için bu koşul harmoniğin dalga vektörünün asıl dalganın dalga vektörünün iki katı olması olarak ifade edilebilir. Faz eşleme ile dalgaların yapıcı girişimi sağlanır.
Doğrusal olmayan malzemelerde farklı frekanslardaki birden fazla foton birbiri ile etkileşime geçip başka frekanslarda üst harmonikler oluşturabilir; bu frekans karıştırma olarak bilinir. Farklı 
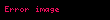
Bu alan için ikinci mertebeden polarizasyon (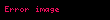
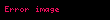

Elektro-optik etkiler

Elektro-optik etkiler DC ya da düşük frekanslı AC elektrik alanların doğrusal olmayan bazı kristal malzemelere uygulanması ile gözlemlenir. En bilinen iki elektro-optik etki, Pockels ve Kerr etkileridir. Bu iki etkide de elektrik alanın uygulanması ile ilgili maddenin kırılma indisinde değişim yaşanır. Bu nedenle Pockels ve Kerr etkileri optik iletişim için ışığın modülasyonunda sıklıkla kullanılmaktadır. Elektro-optik etkilerde kırılma indisinin değişimi, indisin sadece bu etkilere bağlı olduğu varsayılarak basitçe şu şekilde ifade edilebilir:
Burada 


- Pockels etkisi
Pockels etkisi doğrusal olan 



şeklinde ifade edilebilir. Bu formülde voltaj ve elektrik alan arasındaki ilişki basitçe 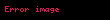


formülü ile belirtilir.
- Kerr etkisi
Ortamın izotropik olduğu durumlarda ise üçüncü mertebeden polarizasyona dayalı olan Kerr etkisi gözlemlenir; bu etki malzemenin tersleme simetrisi fark etmezsizin tüm doğrusal olmayan ortamlarda gözlemlenebilir. Bu etki, Pockels etkisine benzer bir şekilde ortamda çift kırılmaya ve dalgalarda faz farkına yol açar. Buna karşın etki elektrik alanın karesine bağlı olan 
olarak yazılabilir.
Diğer optik süreçler ve uygulamaları

Birçok fiber optik kablo tasarımlarında doğrusal olmayan optik süreçler rol oynamaktadır. Bu süreçlere Raman ile Brillouin saçılmaları ve öz faz modülasyonu (frequency-chirping) örnek gösterilebilir. Uyarılmış Raman etkisi ile fiber optikte dalgalar yükseltilebilir: bu Raman amplifikasyonu olarak bilinir. Bu optik süreçler aynı zamanda ultra kısa darbe lazerlerin tasarımında da kullanılmaktadır.
Doğrusal olmayan optik prensipleri kullanılarak optik aberasyon kusurları düzeltilebilmektedir; bu optik faz konjugasyonu (optical phase conjugation) olarak bilinir.
Ayrıca bakınız
Kaynakça
- ^ Paschotta, Rüdiger. (İngilizce). rp-photonics.com. 12 Ocak 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Haziran 2020.
- ^ a b c d Boyd, Robert (2008). Nonlinear Optics (İngilizce) (3. bas.). Academic Press. ISBN .
- ^ a b c d e Pedrotti, Frank L.; Pedrotti, Leno M.; Pedrotti, Leno S. (2007). Introduction to Optics (İngilizce) (3 bas.). Pearson. ss. 510-533. ISBN .
- ^ Paschotta, Rüdiger. (İngilizce). rp-photonics.com. 29 Nisan 2006 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Haziran 2020.
Dış bağlantılar
- Lazer fiziği ve teknolojisi ansiklopedisi 3 Haziran 2009 tarihinde Wayback Machine sitesinde . (İngilizce)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Dogrusal olmayan optik ya da nonlineer optik isigin dogrusal olmayan sistem ve malzemelerdeki davranisi ile ozelliklerini inceleyen optigin bir alt dalidir Bu malzemelerde elektrik alan E displaystyle E ile polarizasyon yogunlugu P displaystyle P arasindaki iliski dogrusal degildir bu durum daha cok yuksek genlikte 108 V m seviyelerinde isik veren lazerlerde ve lityum niobat gibi kristal yapilarinda gorulur Schwinger sinirindan daha kuvvetli alanlarda vakum da dogrusalligini kaybeder Superpozisyon prensibi bu malzemeler icin gecerli degildir KTP kristalinin yapisi Isiga tepkisi dogrusal olmayan bu kristal ikinci harmonik uretiminde kullanilir Dogrusal olmayan optigin prensipleri bircok lazer ve elektro optik aygit tasariminda siklikla kullanilmaktadir Bu optik dali ayni zamanda fiber optikte ultra kisa darbe iletimi gibi alanlarda da onem tasimaktadir TemellerDogrusal olmayan polarizasyon Ikinci mertebeden polarizasyona bagli bir optik surec ikinci harmonik uretimi Dogrusal bir ortamda polarizasyon ile elektrik alanin iliskisi su sekilde ifade edilebilir P e0xE displaystyle overrightarrow textbf P varepsilon 0 chi overrightarrow textbf E Bu formulde e0 displaystyle varepsilon 0 vakum gecirgenligine x displaystyle chi ise ortamin elektrik duyarliligini tekabul eder Ortamin tepkisinin lineer tepkiden sapmasinin az oldugu durumlarda Taylor serisi acilimi uygulanir P e0 x1E x2E2 x3E3 displaystyle textbf P varepsilon 0 left chi 1 textbf E chi 2 textbf E 2 chi 3 textbf E 3 cdots right ya da P P1 Dogrusal kisim P2 P3 Dogrusal olmayan kisim displaystyle textbf P underbrace textbf P 1 text Dogrusal kisim underbrace left textbf P 2 textbf P 3 cdots right text Dogrusal olmayan kisim P1 displaystyle textbf P 1 ortamin dogrusal polarizasyonunu ifade ederken diger terimler daha ust mertebeden polarizasyonlari ifade eder mertebe arttikca bu terimlerin elektrik duyarliligi ve dolayisiyla toplam polarizasyona etkisi azalir Bu nedenle bu terimlerin polarizasyonu etkileyebilmesi icin yuksek gucte ve uyumlu isik gerekir Yuksek mertebeden polarizasyonlarin tanimi bircok dogrusal olmayan optik surecin teorik temelini olusturur Dogrusal olmayan optikte dalga denklemi Dogrusal olmayan ortamlardaki farkli frekans harmonikleri elektromanyetik dalga denkleminin modifikasyonu ile aciklanabilir Sadelesmemis zamana bagli elektrik alan dalga denklemi Maxwell denklemleri araciligi ile su sekilde yazilabilir E m 2 t2D 0 displaystyle nabla times nabla times tilde textbf E mu frac partial 2 partial t 2 tilde textbf D 0 Bu denklemde D displaystyle D elektrik yer degistirme alanini belirtir ve elektrik alanla arasinda D e0E P displaystyle tilde textbf D varepsilon 0 tilde textbf E tilde textbf P iliskisi vardir Yuk kaynaginin olmadigi durumlarda vektor hesabi donusumleri ile denklem su sekilde ifade edilir 2E 1c2 2 t2E 1e0c2 2 t2P displaystyle nabla 2 tilde textbf E frac 1 c 2 frac partial 2 partial t 2 tilde textbf E frac 1 varepsilon 0 c 2 frac partial 2 partial t 2 tilde textbf P Bu formulde P displaystyle textbf P P1 displaystyle textbf P 1 ve PNL displaystyle textbf P NL olarak dogrusal ve dogrusal olmayan bilesenleri ile ifade edilebilir P1 displaystyle textbf P 1 in izotropik bir yalitkanlik sabiti oldugu varsayilirsa homojen olmayan bir dalga denklemi elde edilir 2E e 1 c2 2 t2E 1e0c2 2 t2P NL displaystyle nabla 2 tilde textbf E frac varepsilon 1 c 2 frac partial 2 partial t 2 tilde textbf E frac 1 varepsilon 0 c 2 frac partial 2 partial t 2 tilde textbf P NL Baslica dogrusal olmayan optik sureclerFrekans karistirma ve ikinci harmonik uretimi Bir elektronun elektrik alana anharmonik tepkisi salinim Mavi ok dogrusal tepkiyi yesil ok ikinci harmonik uretimini ve kirmizi ok da optik rektifikasyonu gosterir Dogrusal olmayan kristal gibi ortamlarda elektromanyetik dalgalar enerji alisverisi ile farkli bir frekansa gecebilir Bu sureclerden biri ikinci harmonik uretimi ya da frekans ikilemesidir Bu surecte kristal ortami asil alanin iki kati frekansinda 2w displaystyle 2 omega bir harmonik alan uretir Tersleme simetrisi olan izotropik ortamlarda ikinci harmonik alan bir etkide bulunmazken bu simetrinin olmadigi ortamlarda bu harmonik onem kazanir Bir E0coswt displaystyle E 0 cos omega t alaninin ikinci harmonigi ifadenin karesinin trigonometrik donusumu ile su sekilde yazilabilir P2 12e2x2E02 12e2x2E02cos2wt displaystyle P 2 frac 1 2 varepsilon 2 chi 2 E 0 2 frac 1 2 varepsilon 2 chi 2 E 0 2 cos2 omega t Bu durumda ikinci mertebeden polarizasyonda zamandan bagimsiz bir DC polarizasyonu olusur ve bu optik rektifikasyon olarak bilinir Enerjinin korunumu ikinci harmonik uretiminde de gecerlidir dogrusal olmayan etkilesim ile ikinci harmonikten asil dalgaya enerji gecisi olabilir Farkli frekanslarda dalgalar dagilim nedeniyle farkli hizlarda hareket eder Bu nedenle asil dalga ile harmoniklerin toplaminin tam parlakligi saglayabilmesi icin faz eslenmesi phase matching kosullarinin saglanmasi gerekir ikinci harmonik uretimi icin bu kosul harmonigin dalga vektorunun asil dalganin dalga vektorunun iki kati olmasi olarak ifade edilebilir Faz esleme ile dalgalarin yapici girisimi saglanir Dogrusal olmayan malzemelerde farkli frekanslardaki birden fazla foton birbiri ile etkilesime gecip baska frekanslarda ust harmonikler olusturabilir bu frekans karistirma olarak bilinir Farkli w1 displaystyle omega 1 ve w2 displaystyle omega 2 acisal frekanslarindaki es A genlikliginde bilesenlere sahip bir elektrik alan fazor acilimi ile su sekilde yazilabilir E A12 E01 eiw1t e iw1t E02 eiw2t e iw2t displaystyle E A frac 1 2 left E 01 e i omega 1 t e i omega 1 t E 02 e i omega 2 t e i omega 2 t right Bu alan icin ikinci mertebeden polarizasyon P e0xE2 displaystyle P varepsilon 0 chi E 2 alanin karesi ile dogru orantilidir ve 2w1 displaystyle 2 omega 1 2w2 displaystyle 2 omega 2 w1 w2 displaystyle omega 1 omega 2 ile w1 w2 displaystyle omega 1 omega 2 bilesenlerine sahiptir Elektro optik etkiler Bir Pockels hucresi ile polarizasyon modulasyonu Elektro optik etkiler DC ya da dusuk frekansli AC elektrik alanlarin dogrusal olmayan bazi kristal malzemelere uygulanmasi ile gozlemlenir En bilinen iki elektro optik etki Pockels ve Kerr etkileridir Bu iki etkide de elektrik alanin uygulanmasi ile ilgili maddenin kirilma indisinde degisim yasanir Bu nedenle Pockels ve Kerr etkileri optik iletisim icin isigin modulasyonunda siklikla kullanilmaktadir Elektro optik etkilerde kirilma indisinin degisimi indisin sadece bu etkilere bagli oldugu varsayilarak basitce su sekilde ifade edilebilir 1n2 1n02 rE RE2 displaystyle frac 1 n 2 frac 1 n 0 2 rE RE 2 Burada n displaystyle n etken kirilma indisi n0 displaystyle n 0 sabit indis ve r displaystyle r ile R displaystyle R ise malzemeye gore degisen elektro optik katsayilardir Pockels etkisi Pockels etkisi dogrusal olan r displaystyle r katsayisinin bir sonucudur ve tersleme simetrisi olmayan malzemelerde gorulur Malzemeye dogru akimin olusmasi ile cift kirilma gozlemlenebilir ya da kristalin anizotropisini belirten kristal ekseni degisir Her ne kadar etki ikinci mertebeden polarizasyona bagli olsa da indise dogrusal bir bicimde yansir Pockels etkisi gosteren tum kristaller ayni zamanda piezoelektriktir Pockels etkisi kristal eksenini degistirebildiginden dolayi faz geciktiric phase retarder olarak kullanilabilir L displaystyle L uzunlugundaki bir Pockels hucresinde V displaystyle V voltajinin l0 displaystyle lambda 0 dalga boylu bir dalgada yarattigi faz farki F 2pl0rn03V displaystyle Phi frac 2 pi lambda 0 rn 0 3 V seklinde ifade edilebilir Bu formulde voltaj ve elektrik alan arasindaki iliski basitce V EL displaystyle V EL seklinde yazilabilir Bu sistemde p displaystyle pi kadar bir faz farki yaratan maksimum yarisi genlik voltaji ise VHW l0 2rn03 displaystyle V HW lambda 0 left 2rn 0 3 right ile ifade edilebilir Bu hucrede iletilen isigin parlakligi ise I Imaxsin2 p2VVHW displaystyle I I max sin 2 left frac pi 2 frac V V HW right formulu ile belirtilir Kerr etkisi Ortamin izotropik oldugu durumlarda ise ucuncu mertebeden polarizasyona dayali olan Kerr etkisi gozlemlenir bu etki malzemenin tersleme simetrisi fark etmezsizin tum dogrusal olmayan ortamlarda gozlemlenebilir Bu etki Pockels etkisine benzer bir sekilde ortamda cift kirilmaya ve dalgalarda faz farkina yol acar Buna karsin etki elektrik alanin karesine bagli olan R displaystyle R katsayisina etki eder Kirilma indisi farki bu durumda dn R2n03E2 displaystyle delta n frac R 2 n 0 3 E 2 olarak yazilabilir Diger optik surecler ve uygulamalariDogrusal olmayan bir optik fiberde soliton simulasyonu Bircok fiber optik kablo tasarimlarinda dogrusal olmayan optik surecler rol oynamaktadir Bu sureclere Raman ile Brillouin sacilmalari ve oz faz modulasyonu frequency chirping ornek gosterilebilir Uyarilmis Raman etkisi ile fiber optikte dalgalar yukseltilebilir bu Raman amplifikasyonu olarak bilinir Bu optik surecler ayni zamanda ultra kisa darbe lazerlerin tasariminda da kullanilmaktadir Dogrusal olmayan optik prensipleri kullanilarak optik aberasyon kusurlari duzeltilebilmektedir bu optik faz konjugasyonu optical phase conjugation olarak bilinir Ayrica bakinizDogrusal olmayan Schrodinger denklemi Kuantum optigi Soliton SupersureklilikKaynakca Paschotta Rudiger Ingilizce rp photonics com 12 Ocak 2006 tarihinde kaynagindan arsivlendi Erisim tarihi 25 Haziran 2020 a b c d Boyd Robert 2008 Nonlinear Optics Ingilizce 3 bas Academic Press ISBN 978 0 12 369470 6 a b c d e Pedrotti Frank L Pedrotti Leno M Pedrotti Leno S 2007 Introduction to Optics Ingilizce 3 bas Pearson ss 510 533 ISBN 9780131499331 Paschotta Rudiger Ingilizce rp photonics com 29 Nisan 2006 tarihinde kaynagindan arsivlendi Erisim tarihi 24 Haziran 2020 Dis baglantilarLazer fizigi ve teknolojisi ansiklopedisi 3 Haziran 2009 tarihinde Wayback Machine sitesinde Ingilizce
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans