Yüzey, matematikte ve özellikle topolojide iki boyutlu çokkatlı. İki gerçel değişkenli ve gerçel değerli bir fonksiyonun üç boyutlu uzayda (R³) grafiği tipik yüzey örneğidir. Ayrıca Dünya yüzeyi, bir yumurtanın kabuğu, bir birer yüzeydir.
Bir yüzeyin iki boyutlu bir çokkatlı olması, öncelikle onun (belirli özellikleri sağlayan) bir topolojik uzay olması demektir. Bunun yanında yüzeyin verilen (herhangi) bir x noktası çevresinde öyle bir komşuluk bulunabilir ki, bu komşuluk 2 boyutlu uzayın bir parçasına benzer. Bu komşuluğa denir. Bu benzeme uyarınca, x çevresinde sağ-sol ve yukarı-aşağı kavramları iyi bir biçimde tanımlanabilir. Daha iyi bir deyişle, x'in çevresine bir koordinat sistemi döşenebilir. Böylece yüzey, bir düzlem parçası olmasa bile x çevresindeki noktalar bir düzlemdeymiş gibi koordinatlara sahip olur.
Dünya yüzeyi matematiksel olarak bir yüzeydir. Dünya'nın çizilen her haritası, yukarıdaki anlamda bir koordinat sistemi tarif eder. Bu sayede denizcilikte yön bulma kolaylaşır ve iki denizci aynı koordinat sisteminde konuşarak birbirleriyle anlaşabilir. Dünya yüzeyi için standart koordinat sistemi, enlem ve boylamlarla verilir. Örneğin, Dünya yüzeyinden gün dönümü çizgisi ve kutuplar silindiğinde kalan parçaya ( Doğu, Batı) ilâ ( Kuzey, Güney) koordinatları verilerek bu parça bir yamaya dönüştürülebilir. Gün dönümü çizgisi ya da kutupların silinmediği durumda bazı enlem-boylam çiftlerinin aynı noktayı tarif edeceklerine dikkat ediniz.
Topolojik bir yüzey, her zaman R³'te görülemeyebilir. Örneğin ya da R³'te ancak R4'e . Topolojinin temel teoremlerinden biri, bir yüzeyi gömebilmek için en fazla dört boyuta (R4) gerek olduğunu söyler.
Matematiksel tanım
İki boyutlu bir çokkatlıya yüzey denir. Daha ayrıntılı bir söyleyişle, ( olmayan topolojik) yüzey, aşağıdaki koşulları sağlayan bir topolojik uzaydır:
- Hausdorff'tur;
- Herhangi bir noktasının çevresinde öyle bir bulunabilir ki bu komşuluk R²'nin açık bir alt kümesine homeomorfiktir;
- (Kimi tanımlarda) özelliğini sağlar;
- (Kimi tanımlarda) .
Yukarıki tanımda ikinci koşulda R² yerine, üst yarı düzlemi (yani ikinci koordinatları negatif olmayan noktaların kümesi) temsil etmek üzere H² konduğunda, bu tanım, kenarı olan (kenarlı) topolojik bir yüzey tanımına dönüşür. Bu durumda ikinci koşulda homeomorfizma sözcüğünün anlamlı olabilmesi için H² üzerinde bir topoloji bulunması gerekir. Bu topoloji standart olarak R²'den .
Kenarı olan bir yüzeyin kenarı olmayandan farklı olarak şu tür noktaları da vardır: noktanın yeterince küçük her komşuluğu H²'de çapı yarı düzlemin en altında oturan bir yarım daireye homeomorfiktir. Noktanın R²'de açık bir bölgeye homeomorfik bir komşuluğu olması söz konusu değildir. Kenarlı yüzeylere birkaç örnek: düzlemde bir daire, kapalı bir eğriyle çevrelenmiş bir düzlem bölgesi, bir yarıküre (içi boş), açık bir dairesel parçası koparılmış bir simit (yüzeyi).
Bir yüzeyin içinde bir Möbius şeridi varsa (yüzeye gömülebiliyorsa) bu yüzeye denir. İçinde bir Möbius şeridi yoksa böyle bir yüzeye yön verilebilir denir. Yön verilemez yüzeylere birkaç örnek: Möbius şeridi, gerçel izdüşümsel düzlem, Klein şişesi. Bunlardan Möbius şeridi kenarı (bir çember) olan bir yüzeyken diğerleri kenarsız yüzeylerdir.
Yüzeylerin sınıflandırılması
Matematiğin temel uğraşlarından biri sınıflamadır. Tanımladığı bir nesne türünde, nesnelerin bazılarını bibirinden ayırt etmeden, olası tüm nesneleri listelemek sınıflamadaki amaçtır. Dolayısıyla yukarıda soyut tanımı verilen yüzeylerin tümünü listelemek, topolojinin ilgilendiği bir sorudur. Bunu yaparken iki homeomorfik yüzeyi bir tutar, bunların arasında ayrım gözetmez. Bu koşullar altında listeyi oluşturmaya çalışır. Örneğin bu listede (içi boş) bir küp ve bir küre birlikte görünmeyecektir; yalnızca biri listede yer alacaktır çünkü bu iki yüzey, R³'ten tetiklenen topolojileriyle birbirine homeomorfik yüzeylerdir.
Şu ve benzeri soruların yanıtlanması gerekir: Bir küreyle bir simit, Möbius şeridiyle daire, kenarı olan yüzeyle olmayan ve yön verilebilir olanla olmayan birbirine homeomorfik midir?
Yüzeylerin sınıflandırılması problemi ilk kez August Ferdinand Möbius tarafından çalışılmış ve R³'te yatan yön verilebilir yüzeyler için 1870 yılında sonuç ilan edilmiştir. Max Wilhelm Dehn ve P. Heegard 1907 yılında üçgenlenebilir yüzeyler için tüm sınıflandırmayı vermiştir. Her topolojik yüzeyin üçgenlenebilir olduğunu 1925 yılında Tibor Radó ispatlayarak sınıflandırmayı sona erdirmiştir (ispat için L. V. Ahlfors ve L. Sario'nun aşağıda listelenmiş kitabına bakınız).
Bu sınıflandırmaya göre, tıkız, yön verilebilir, kenarsız yüzeyler, şunlardan biri(ne homeomorfik) olmak zorundadır:

İlk şekil bir küredir (S²). İkincisi bir simit (T²). Üçüncü şekil çift bir yüzeyi (F²) anlatır. Listede sırasıyla 3, 4, 5, … delikli yüzeyler (sırasıyla F3, F4, F5, …) yer alacaktır. Dikkat edilirse, iki ayrı simitten birer daire oyulup kalan yüzeyler birbirlerine yapıştırılırsa, çıkan yüzey, iki delikli bir yüzey olacaktır. Üzerindeki topoloji, bu yapıştırma sırasında kullanılan özdeşleştirme aracılığıyla gelen bölüm topolojisidir. Bu işlem şöyle gösterilir:
F2 = T² # T²
Daireler oyarak yapıştırma işlemine denir. Üç delikli bir yüzey, çift delikli bir yüzeyle torusun bağlantılı toplamı olarak inşa edilebilir.
Bu sınıflandırmadan anlaşılıyor ki, tıkız, yön verilebilir, kenarsız yüzeyler delik sayılarıyla anlatılabilirler. Kürenin delik sayısına 0 diyoruz. Simidin delik sayısı 1'dir.
Tıkız, yön verilebilir, kenarsız S adlı bir yüzey için 2 - 2g sayısı yüzeyin Euler sayısına eşittir ve şöyle gösterilir:
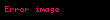
Yön verilemez yüzeyler için sınıflandırmaysa temelde aynı olmasına karşın, söz konusu yüzeylere daha az aşinayız. Tıkız, yön verilemez, kenarsız yüzeylerin en basiti gerçel izdüşümsel düzlemdir (RP²). Bu yüzey, bir Möbius şeridiyle bir dairenin kenarlarından birbirlerine yapıştırılmasıyla inşa edilir. Üzerindeki topoloji, bu yapıştırma aracılığıyla gelen bölüm topolojisidir. İki tane RP²'nin bağlantılı toplamına Klein şişesi (K²) denir:
K² = RP² # RP²
Bu işlem iki Möbius şeridinin kenarlarından birbirlerine yapıştırılmasından başka bir şey değildir.
Sınıflandırma şunu söyler: tıkız, yön verilemez, kenarsız yüzeyler aşağıdakilerden biri(ne homeomorfik) olmak zorundadır:
RP², K² = RP² # RP², (RP² # RP² # RP²), (RP² # RP² # RP² # RP²), 
Gösterilebilir ki bu listedeki yüzeylerin Euler sayıları 1'den başlar ve birer birer azalır:


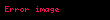
Dolayısıyla, (tıkız, kenarsız) bir yüzeyin Euler sayısını ve yön verilebilir olup olmadığını söylemek, yüzeyi anlatmaya yeter.
Kaynakça
- Hatcher, Allen (2002). Algebraic topology. Cambridge: Cambridge University Press.
- Munkres, James R. (2000). Topology (Second Edition). Prentice Hall. s. 537.
- Ahlfors, Lars V.; Sario, Leo (1960). Riemann surfaces. Princeton: Princeton University Press. s. 382.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Yuzey matematikte ve ozellikle topolojide iki boyutlu cokkatli Iki gercel degiskenli ve gercel degerli bir fonksiyonun uc boyutlu uzayda R grafigi tipik yuzey ornegidir Ayrica Dunya yuzeyi bir yumurtanin kabugu bir birer yuzeydir Bir yuzeyin iki boyutlu bir cokkatli olmasi oncelikle onun belirli ozellikleri saglayan bir topolojik uzay olmasi demektir Bunun yaninda yuzeyin verilen herhangi bir x noktasi cevresinde oyle bir komsuluk bulunabilir ki bu komsuluk 2 boyutlu uzayin bir parcasina benzer Bu komsuluga denir Bu benzeme uyarinca x cevresinde sag sol ve yukari asagi kavramlari iyi bir bicimde tanimlanabilir Daha iyi bir deyisle x in cevresine bir koordinat sistemi dosenebilir Boylece yuzey bir duzlem parcasi olmasa bile x cevresindeki noktalar bir duzlemdeymis gibi koordinatlara sahip olur Dunya yuzeyi matematiksel olarak bir yuzeydir Dunya nin cizilen her haritasi yukaridaki anlamda bir koordinat sistemi tarif eder Bu sayede denizcilikte yon bulma kolaylasir ve iki denizci ayni koordinat sisteminde konusarak birbirleriyle anlasabilir Dunya yuzeyi icin standart koordinat sistemi enlem ve boylamlarla verilir Ornegin Dunya yuzeyinden gun donumu cizgisi ve kutuplar silindiginde kalan parcaya 180 displaystyle 180 circ Dogu 180 displaystyle 180 circ Bati ila 90 displaystyle 90 circ Kuzey 90 displaystyle 90 circ Guney koordinatlari verilerek bu parca bir yamaya donusturulebilir Gun donumu cizgisi ya da kutuplarin silinmedigi durumda bazi enlem boylam ciftlerinin ayni noktayi tarif edeceklerine dikkat ediniz Topolojik bir yuzey her zaman R te gorulemeyebilir Ornegin ya da R te ancak R4 e Topolojinin temel teoremlerinden biri bir yuzeyi gomebilmek icin en fazla dort boyuta R4 gerek oldugunu soyler Matematiksel tanimIki boyutlu bir cokkatliya yuzey denir Daha ayrintili bir soyleyisle olmayan topolojik yuzey asagidaki kosullari saglayan bir topolojik uzaydir Hausdorff tur Herhangi bir noktasinin cevresinde oyle bir bulunabilir ki bu komsuluk R nin acik bir alt kumesine homeomorfiktir Kimi tanimlarda ozelligini saglar Kimi tanimlarda Yukariki tanimda ikinci kosulda R yerine ust yari duzlemi yani ikinci koordinatlari negatif olmayan noktalarin kumesi temsil etmek uzere H kondugunda bu tanim kenari olan kenarli topolojik bir yuzey tanimina donusur Bu durumda ikinci kosulda homeomorfizma sozcugunun anlamli olabilmesi icin H uzerinde bir topoloji bulunmasi gerekir Bu topoloji standart olarak R den Kenari olan bir yuzeyin kenari olmayandan farkli olarak su tur noktalari da vardir noktanin yeterince kucuk her komsulugu H de capi yari duzlemin en altinda oturan bir yarim daireye homeomorfiktir Noktanin R de acik bir bolgeye homeomorfik bir komsulugu olmasi soz konusu degildir Kenarli yuzeylere birkac ornek duzlemde bir daire kapali bir egriyle cevrelenmis bir duzlem bolgesi bir yarikure ici bos acik bir dairesel parcasi koparilmis bir simit yuzeyi Bir yuzeyin icinde bir Mobius seridi varsa yuzeye gomulebiliyorsa bu yuzeye denir Icinde bir Mobius seridi yoksa boyle bir yuzeye yon verilebilir denir Yon verilemez yuzeylere birkac ornek Mobius seridi gercel izdusumsel duzlem Klein sisesi Bunlardan Mobius seridi kenari bir cember olan bir yuzeyken digerleri kenarsiz yuzeylerdir Yuzeylerin siniflandirilmasiMatematigin temel ugraslarindan biri siniflamadir Tanimladigi bir nesne turunde nesnelerin bazilarini bibirinden ayirt etmeden olasi tum nesneleri listelemek siniflamadaki amactir Dolayisiyla yukarida soyut tanimi verilen yuzeylerin tumunu listelemek topolojinin ilgilendigi bir sorudur Bunu yaparken iki homeomorfik yuzeyi bir tutar bunlarin arasinda ayrim gozetmez Bu kosullar altinda listeyi olusturmaya calisir Ornegin bu listede ici bos bir kup ve bir kure birlikte gorunmeyecektir yalnizca biri listede yer alacaktir cunku bu iki yuzey R ten tetiklenen topolojileriyle birbirine homeomorfik yuzeylerdir Su ve benzeri sorularin yanitlanmasi gerekir Bir kureyle bir simit Mobius seridiyle daire kenari olan yuzeyle olmayan ve yon verilebilir olanla olmayan birbirine homeomorfik midir Yuzeylerin siniflandirilmasi problemi ilk kez August Ferdinand Mobius tarafindan calisilmis ve R te yatan yon verilebilir yuzeyler icin 1870 yilinda sonuc ilan edilmistir Max Wilhelm Dehn ve P Heegard 1907 yilinda ucgenlenebilir yuzeyler icin tum siniflandirmayi vermistir Her topolojik yuzeyin ucgenlenebilir oldugunu 1925 yilinda Tibor Rado ispatlayarak siniflandirmayi sona erdirmistir ispat icin L V Ahlfors ve L Sario nun asagida listelenmis kitabina bakiniz Bu siniflandirmaya gore tikiz yon verilebilir kenarsiz yuzeyler sunlardan biri ne homeomorfik olmak zorundadir Ilk sekil bir kuredir S Ikincisi bir simit T Ucuncu sekil cift bir yuzeyi F anlatir Listede sirasiyla 3 4 5 delikli yuzeyler sirasiyla F3 F4 F5 yer alacaktir Dikkat edilirse iki ayri simitten birer daire oyulup kalan yuzeyler birbirlerine yapistirilirsa cikan yuzey iki delikli bir yuzey olacaktir Uzerindeki topoloji bu yapistirma sirasinda kullanilan ozdeslestirme araciligiyla gelen bolum topolojisidir Bu islem soyle gosterilir F2 T T Daireler oyarak yapistirma islemine denir Uc delikli bir yuzey cift delikli bir yuzeyle torusun baglantili toplami olarak insa edilebilir Bu siniflandirmadan anlasiliyor ki tikiz yon verilebilir kenarsiz yuzeyler delik sayilariyla anlatilabilirler Kurenin delik sayisina 0 diyoruz Simidin delik sayisi 1 dir Tikiz yon verilebilir kenarsiz S adli bir yuzey icin 2 2g sayisi yuzeyin Euler sayisina esittir ve soyle gosterilir x S 2 2g displaystyle chi S 2 2g Yon verilemez yuzeyler icin siniflandirmaysa temelde ayni olmasina karsin soz konusu yuzeylere daha az asinayiz Tikiz yon verilemez kenarsiz yuzeylerin en basiti gercel izdusumsel duzlemdir RP Bu yuzey bir Mobius seridiyle bir dairenin kenarlarindan birbirlerine yapistirilmasiyla insa edilir Uzerindeki topoloji bu yapistirma araciligiyla gelen bolum topolojisidir Iki tane RP nin baglantili toplamina Klein sisesi K denir K RP RP Bu islem iki Mobius seridinin kenarlarindan birbirlerine yapistirilmasindan baska bir sey degildir Siniflandirma sunu soyler tikiz yon verilemez kenarsiz yuzeyler asagidakilerden biri ne homeomorfik olmak zorundadir RP K RP RP RP RP RP RP RP RP RP displaystyle cdots Gosterilebilir ki bu listedeki yuzeylerin Euler sayilari 1 den baslar ve birer birer azalir x RP2 1 displaystyle chi RP 2 1 x RP2 RP2 0 displaystyle chi RP 2 RP 2 0 x RP2 RP2 RP2 1 displaystyle chi RP 2 RP 2 RP 2 1 Dolayisiyla tikiz kenarsiz bir yuzeyin Euler sayisini ve yon verilebilir olup olmadigini soylemek yuzeyi anlatmaya yeter Kaynakca Hatcher Allen 2002 Algebraic topology Cambridge Cambridge University Press Munkres James R 2000 Topology Second Edition Prentice Hall s 537 Ahlfors Lars V Sario Leo 1960 Riemann surfaces Princeton Princeton University Press s 382
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State