Vektör kalkulus

Vektör hesabı (vektör analizi, yöney hesabı veya yöney analizi de denilir), iki veya daha çok boyutlu (bazı sonuçlar — çapraz çarpımı içeren sonuçlar — sadece üç boyuta uygulanabilir) vektörlerin çok değişkenli gerçel analiziyle uğraşan bir matematik dalıdır. Fizik ve mühendislikte epey faydalı olan formül takımlarından ve problem çözme tekniklerini kapsamaktadır. Vektör hesabı köklerini kuaterniyon analizinden almaktadır ve Amerikan mühendis ve bilim insanı J. Willard Gibbs ve İngiliz mühendis Oliver Heaviside tarafından formüle edilmiştir.

Vektör hesabı bir skaleri uzaydaki her noktaya bağlayan skaler alanlarla ve bir vektörü uzaydaki her noktaya bağlayan vektör alanı ile ilgilidir. Örneğin, bir yüzme havuzunun sıcaklığı bir skaler alandır: Her noktaya skaler sıcaklık değeri verilir. Aynı havuzdaki su akışı ise bir vektör alanıdır: Her noktaya bir hız vektörü verilir.

Vektör cebiri

Cebirsel (türevsel olmayan) vektör işlemlerine denir. Bu işlemler bir vektör uzayı için tanımlanır ve bir vektör alanının tamamına etki eder. Temel cebirsel işlemler şunlardır:

İşlem	Gösterim	Açıklama
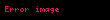	${\displaystyle \mathbf {v} _{1}+\mathbf {v} _{2}}$	İki vektör alanının toplamı olan bir vektör alanı verir.
Skaler çarpım	${\displaystyle a\mathbf {v} }$	Bir skaler alanı ile bir vektör alanının çarpımı olan bir vektör alanı verir.
Nokta çarpım	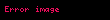${\displaystyle \mathbf {v} _{1}\cdot \mathbf {v} _{2}}$	İki vektör alanının çarpımı olan bir vektör alanı verir.
Çapraz çarpım	${\displaystyle \mathbf {v} _{1}\times \mathbf {v} _{2}}$	${\displaystyle \mathbb {R} ^{3}}$ uzayında iki vektör alanının çarpımı olan bir (sahte) vektör alanı verir.

Ayrıca aşağıdaki üçlü çarpımlar sıkça kullanılır:

İşlem	Gösterim	Açıklama
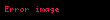	${\displaystyle \mathbf {v} _{1}\cdot \left(\mathbf {v} _{2}\times \mathbf {v} _{3}\right)}$	Çapraz çarpımın nokta çarpımı.
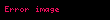	${\displaystyle \mathbf {v} _{1}\times \left(\mathbf {v} _{2}\times \mathbf {v} _{3}\right)}$	Çapraz çarpımın çapraz çarpımı.

Vektör işlemleri

Vektör hesabı genelde veya operatörü (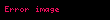${\displaystyle \nabla }$) ile ifade edilen skaler alanlarda veya vektör alanlarında tanımlı incelemektedir. Vektör hesabındaki en önemli 4 işlem ise şunlardır.

İşlem	Gösterim (notasyon)	Açıklama	Tanım/Görüntü kümesi
Gradyan	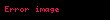${\displaystyle \operatorname {grad} (f)=\nabla f}$	Skaler alandaki değişimin oranını ve yönünü ölçer.	Skaler alanları vektör alanlarına gönderir.
(Rotasyonel)	${\displaystyle \operatorname {curl} (\mathbf {F} )=\nabla \times \mathbf {F} }$	Bir vektör alanındaki bir nokta etrafındaki dönme meyilini ölçer.	Vektör alanlarını vektör alanlarına gönderir.
Diverjans	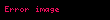${\displaystyle \operatorname {div} (\mathbf {F} )=\nabla \cdot \mathbf {F} }$	Bir vektör alanında verilmiş olan bir noktadaki bir kaynağın veya batığın büyüklüğünü ölçer.	Vektör alanlarını skaler alanlara gönderir.
Laplasyen	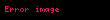${\displaystyle \Delta f=\nabla ^{2}f=\nabla \cdot \nabla f}$	Diverjans ve gradyan işlemlerinin bir bileşkesidir.	Skaler alanları skaler alanlara gönderir.

Jacobi adı verilen bir nicelik ise, fonksiyonların tanım ve değer kümesinin her ikisinin de çok değişkenli olduğu zaman, integral almada değişken değiştirme gibi fonksiyonların incelendiği alanlarda çok yararlıdır.

Teoremler

Benzer bir şekilde, bu operatörlere ilişkin, hesabın temel teoremini daha yüksek boyutlara genelleyen çeşitli önemli teoremler mevcuttur:

Teorem	İfadesi	Açıklama
Gradyan teoremi	${\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{L}\nabla \varphi \cdot d\mathbf {r} .}$	Bir gradyan (vektör) alanının çizgi integrali, skaler alanındaki eğrinin sonnoktalarının farkına eşittir.
Green teoremi	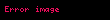${\displaystyle \int _{C}L\,dx+M\,dy=\iint _{D}\left({\frac {\partial M}{\partial x}}-{\frac {\partial L}{\partial y}}\right)\,dA}$	Bir vektör alanının skaler körlünün düzlemdeki bir bölgedeki integrali bu bölgeyi sınırlayan eğri üzerindeki vektör alanının çizgi integraline eşittir.
Stokes teoremi	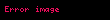${\displaystyle \int _{\Sigma }\nabla \times \mathbf {F} \cdot d\mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot d\mathbf {r} ,}$	Bir yüzey üzerindeki vektör alanının körlünün integrali, yüzeyi sınırlayan eğri üzerindeki vektör alanının çizgi integraline eşittir.
Diverjans teoremi	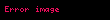${\displaystyle \iiint \limits _{V}\left(\nabla \cdot \mathbf {F} \right)dV=\iint \limits _{\partial V}\mathbf {F} \cdot d\mathbf {S} ,}$	Bir katı üzerindeki vektör alanının diverjansının integrali, katyı sınırlayan yüzeyinden geçen akımın integraline eşittir.

Vektör hesabının kullanımı koordinat sistemine "eli olma" kuralı getirilmesini gerektirebilir (Çapraz çarpıma bakınız.). Birçok analitik sonuç, genel bağlamda, vektör hesabının bir altkümesini oluşturduğu diferansiyel geometri ile daha kolay bir şekilde anlaşılabilir.

Ayrıca bakınız

• Vektör hesabı özdeşlikleri

Kaynakça

• Michael J. Crowe (1994), A History of Vector Analysis : The Evolution of the Idea of a Vectorial System, Dover Publications; Reprint edition,   (Summary^[])
• H. M. Schey (2005), Div Grad Curl and all that: An informal text on vector calculus, W. W. Norton & Company,  
• J.E. Marsden (1976), Vector Calculus, W. H. Freeman & Company,  
• Chen-To Tai (1995). Vektör analizinin tarihsel bir çalışması25 Eylül 2008 tarihinde Wayback Machine sitesinde .. Teknik Rapor RL 915, Radyasyon Laboratuvarı, University of Michigan.

Dış bağlantılar

• Vektör Hesabı:21 Temmuz 2011 tarihinde Wayback Machine sitesinde . Matematik ve Fizik öğrencilerinin kullanımı için bir ders kitabı, ('in derslerine dayanılmıştır) tarafından, 1902'de yayınlanmıştır.