Azərbaycanca
Беларускі
Dansk
Deutsch
Española
Français
Indonesia
Italiana
日本語
Қазақ
Lietuvos
Nederlands
Português
Русский
සිංහල
แบบไทย
Türkçe
Українська
中國人
United State
Afrikaans
Yörünge durum vektörleri veya durum vektörleri, gök mekaniği ve yörünge mekaniğinde, konum ve hız kartezyen vektörlerin zaman (devir) ile birlikte uzaydaki yörüngede bulunan bir cismin benzersiz şekildeki gidim izinin belirlenmesidir.
Yörünge durum vektörleri geleneksel konum-hız vektörleri, iki-satırlı öğe kümesi (TLE) ve vektör kovaryans matrisi (VCM) gibi birçok biçimde bulunur.
Referans düzlemi
Durum vektörleri, her zaman olmasa bile genellikle eylemsiz referans çerçevesinde olmak üzere bazı referans düzlemleri göz önüne alınarak tanımlanmaktadır. Dünya yakınında hareket etmekte olan cisimlerin durum vektörleri için en çok kullanılan referans düzlemlerinden birisi Dünya-merkezli eylemsizlik sistemidir. Bu düzlem aşağıdaki esaslara göre tanımlanmaktadır:
- Başlangıç olarak Dünya'nın kütle merkezi,
- Z ekseni Dünyanın dönme ekseniyle çakışık, kuzeye doğru pozitif yönlü,
- X/Y düzlemi Dünyanın ekvator düzlemiyle çakışık, +X ekseni ilkbahar ekinoksuna işaret eder ve Y ekseni sağ el setini tamamlar.
ECI referans çerçevesi, Dünya'nın ekseninin 26.000 yıllık yavaş devinimi nedeniyle tam anlamıyla eylemsiz değildir, bu nedenle Dünya'nın B1950 veya J2000 gibi standart bir astronomik dönemdeki yönelimi ile tanımlanan referans çerçeveleri de yaygın olarak kullanılmaktadır.
Çeşitli uygulama gereksinimlerini karşılamak için Güneş'i veya diğer gezegenleri veya uyduları merkez alanlar, Güneş Sistemi'nin çift merkezi ve toplam açısal momentumu (özellikle ICRF) tarafından tanımlananlar ve hatta bir uzay aracının kendi yörünge düzlemi ve açısal momentumu dahil olmak üzere birçok başka referans çerçevesi kullanılabilir.
Konum ve hız vektörleri
Konum vektörü 
seçilen referans çerçevesinde cismin konumunu tanımlarken, hız vektörü 
aynı zamanda aynı çerçevedeki cismin hızını tanımlar. Bu iki vektör ve geçerli oldukları zaman bir arada, Yörünge belirleme bölümünde ayrıntılı olarak açıklandığı gibi cismin yörüngesini benzersiz bir şekilde tanımlar. Temel mantık, Newton'un kütle çekim yasasının bir ivme vermesidir 
; eğer çarpım Yörüngenin merkezindeki yerçekimi sabiti ve çekici kütlenin 
'si biliniyorsa, konum ve hız bu ikinci dereceden diferansiyel denklem için başlangıç değerleridir. 
eşitliğinin tek bir çözümü vardır.
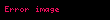
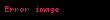
Cismin durum vektörlerinin yörüngesini belirlemesi için yörüngede olması gerekmez; sadece balistik olarak, yani sadece kendi eylemsizliği ve yerçekiminin etkileri altında hareket etmesi gerekir. Örneğin, yörünge altı bir yörüngede bulunan bir uzay aracı ya da füze olabilir. Sürükleme veya itme gibi diğer kuvvetler önemliyse, gelecekteki konum ve hızı belirlemek için entegrasyon gerçekleştirilirken bunlar yerçekimi kuvvetlerine vektörel olarak eklenmelidir.
Uzayda hareket eden herhangi bir nesne için hız vektörü yörüngeye teğettir. Eğer 
yörüngeye teğet olan birim vektörüyse, o halde; 
Türetme
Hız vektörü 
, konum vektöründen , zamana göre farklılaşma yoluyla türetilebilir: 
Bir nesnenin durum vektörü, klasik veya Kepler yörünge elemanlarını hesaplamak için kullanılabilir veya tam tersi de yapılabilir. Her bir gösterimin avantajları vardır. Elemanlar bir yörüngenin boyutu, şekli ve yönü hakkında daha açıklayıcıdır ve hareketinin sadece küçük sapmalarla problemi tarafından doğru bir şekilde modellenmesi koşuluyla, herhangi bir rastgele zamanda nesnenin durumunu hızlı ve kolay bir şekilde tahmin etmek için kullanılabilir.
Öte yandan, durum vektörü, ana cismin yerçekiminin yanı sıra üçüncü cisimlerden gelen sürükleme, itme ve yerçekimi bozulmaları gibi önemli, rastgele, zamanla değişen kuvvetleri hesaba katan sayısal bir entegrasyonda daha kullanışlıdır.
Belirli açısal momentum vektörünü aşağıdaki gibi hesaplamak için durum vektörleri ( ile ) kullanılabilir:
Alçak Dünya yörüngesindeki uydular bile Dünya'nın küresel olmayan şekli, güneş radyasyonu basıncı, Ay gelgiti ve atmosferik sürüklenmeden kaynaklanan önemli tedirginlikler yaşadığından, herhangi bir andaki durum vektöründen hesaplanan Kepleryen elemanlar yalnızca kısa bir süre için geçerliliğini korur ve geçerli bir nesne durumunu belirlemek için sık sık yeniden hesaplanması gerekir. Bu tür eleman kümeleri salınımlı elemanlar olarak bilinir çünkü gerçek yörünge ile sadece o anda çakışırlar.
Ayrıca bakınız
Kaynakça
- ^ a b Howard Curtis (10 Ocak 2005). Orbital Mechanics for Engineering Students (PDF). Embry-Riddle Aeronautical University Daytona Beach, Florida: Elsevier. ISBN . 10 Kasım 2020 tarihinde kaynağından (PDF). Erişim tarihi: 8 Ocak 2023.
- ^ Xu, Guochang; Xu, Yan (2016). "Coordinate and Time Systems" (PDF). GPS. ss. 17-36. doi:10.1007/978-3-662-50367-6_2. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Yorunge durum vektorleri veya durum vektorleri gok mekanigi ve yorunge mekaniginde konum ve hiz kartezyen vektorlerin zaman devir ile birlikte uzaydaki yorungede bulunan bir cismin benzersiz sekildeki gidim izinin belirlenmesidir Yorunge konum vektoru yorunge hiz vektoru diger yorunge elemanlari Yorunge durum vektorleri geleneksel konum hiz vektorleri iki satirli oge kumesi TLE ve vektor kovaryans matrisi VCM gibi bircok bicimde bulunur Referans duzlemiDurum vektorleri her zaman olmasa bile genellikle eylemsiz referans cercevesinde olmak uzere bazi referans duzlemleri goz onune alinarak tanimlanmaktadir Dunya yakininda hareket etmekte olan cisimlerin durum vektorleri icin en cok kullanilan referans duzlemlerinden birisi Dunya merkezli eylemsizlik sistemidir Bu duzlem asagidaki esaslara gore tanimlanmaktadir Baslangic olarak Dunya nin kutle merkezi Z ekseni Dunyanin donme ekseniyle cakisik kuzeye dogru pozitif yonlu X Y duzlemi Dunyanin ekvator duzlemiyle cakisik X ekseni ilkbahar ekinoksuna isaret eder ve Y ekseni sag el setini tamamlar ECI referans cercevesi Dunya nin ekseninin 26 000 yillik yavas devinimi nedeniyle tam anlamiyla eylemsiz degildir bu nedenle Dunya nin B1950 veya J2000 gibi standart bir astronomik donemdeki yonelimi ile tanimlanan referans cerceveleri de yaygin olarak kullanilmaktadir Cesitli uygulama gereksinimlerini karsilamak icin Gunes i veya diger gezegenleri veya uydulari merkez alanlar Gunes Sistemi nin cift merkezi ve toplam acisal momentumu ozellikle ICRF tarafindan tanimlananlar ve hatta bir uzay aracinin kendi yorunge duzlemi ve acisal momentumu dahil olmak uzere bircok baska referans cercevesi kullanilabilir Konum ve hiz vektorleriKonum vektoru r displaystyle mathbf r secilen referans cercevesinde cismin konumunu tanimlarken hiz vektoru v displaystyle mathbf v ayni zamanda ayni cercevedeki cismin hizini tanimlar Bu iki vektor ve gecerli olduklari zaman bir arada Yorunge belirleme bolumunde ayrintili olarak aciklandigi gibi cismin yorungesini benzersiz bir sekilde tanimlar Temel mantik Newton un kutle cekim yasasinin bir ivme vermesidir r GM r2 displaystyle ddot mathbf r GM r 2 eger carpim Yorungenin merkezindeki yercekimi sabiti ve cekici kutlenin GM displaystyle GM si biliniyorsa konum ve hiz bu ikinci dereceden diferansiyel denklem icin baslangic degerleridir r t displaystyle mathbf r t esitliginin tek bir cozumu vardir Cismin durum vektorlerinin yorungesini belirlemesi icin yorungede olmasi gerekmez sadece balistik olarak yani sadece kendi eylemsizligi ve yercekiminin etkileri altinda hareket etmesi gerekir Ornegin yorunge alti bir yorungede bulunan bir uzay araci ya da fuze olabilir Surukleme veya itme gibi diger kuvvetler onemliyse gelecekteki konum ve hizi belirlemek icin entegrasyon gerceklestirilirken bunlar yercekimi kuvvetlerine vektorel olarak eklenmelidir Uzayda hareket eden herhangi bir nesne icin hiz vektoru yorungeye tegettir Eger u t displaystyle hat mathbf u t yorungeye teget olan birim vektoruyse o halde v vu t displaystyle mathbf v v hat mathbf u t Turetme Hiz vektoru v displaystyle mathbf v konum vektorunden r displaystyle mathbf r zamana gore farklilasma yoluyla turetilebilir v drdt textstyle mathbf v frac d mathbf r dt Bir nesnenin durum vektoru klasik veya Kepler yorunge elemanlarini hesaplamak icin kullanilabilir veya tam tersi de yapilabilir Her bir gosterimin avantajlari vardir Elemanlar bir yorungenin boyutu sekli ve yonu hakkinda daha aciklayicidir ve hareketinin sadece kucuk sapmalarla problemi tarafindan dogru bir sekilde modellenmesi kosuluyla herhangi bir rastgele zamanda nesnenin durumunu hizli ve kolay bir sekilde tahmin etmek icin kullanilabilir Ote yandan durum vektoru ana cismin yercekiminin yani sira ucuncu cisimlerden gelen surukleme itme ve yercekimi bozulmalari gibi onemli rastgele zamanla degisen kuvvetleri hesaba katan sayisal bir entegrasyonda daha kullanislidir Belirli acisal momentum vektorunu asagidaki gibi hesaplamak icin durum vektorleri r displaystyle mathbf r ile v displaystyle mathbf v kullanilabilir h r v displaystyle mathbf h mathbf r times mathbf v Alcak Dunya yorungesindeki uydular bile Dunya nin kuresel olmayan sekli gunes radyasyonu basinci Ay gelgiti ve atmosferik suruklenmeden kaynaklanan onemli tedirginlikler yasadigindan herhangi bir andaki durum vektorunden hesaplanan Kepleryen elemanlar yalnizca kisa bir sure icin gecerliligini korur ve gecerli bir nesne durumunu belirlemek icin sik sik yeniden hesaplanmasi gerekir Bu tur eleman kumeleri salinimli elemanlar olarak bilinir cunku gercek yorunge ile sadece o anda cakisirlar Ayrica bakinizYorunge duzlemi Radyal enine normalKaynakca a b Howard Curtis 10 Ocak 2005 Orbital Mechanics for Engineering Students PDF Embry Riddle Aeronautical University Daytona Beach Florida Elsevier ISBN 0 7506 6169 0 10 Kasim 2020 tarihinde kaynagindan PDF Erisim tarihi 8 Ocak 2023 Xu Guochang Xu Yan 2016 Coordinate and Time Systems PDF GPS ss 17 36 doi 10 1007 978 3 662 50367 6 2 ISBN 978 3 662 50365 2