Bu maddenin içeriğinin Türkçeleştirilmesi veya doğrultusunda düzeltilmesi gerekmektedir. Bu maddedeki yazım ve noktalama yanlışları ya da anlatım bozuklukları giderilmelidir. (Yabancı sözcükler yerine Türkçe karşılıklarının kullanılması, karakter hatalarının düzeltilmesi, dilbilgisi hatalarının düzeltilmesi vs.) Düzenleme yapıldıktan sonra bu şablon kaldırılmalıdır. |
Yörünge mekaniği veya astrodinamik, roketler ve diğer uzay araçlarının hareketini ilgilendiren pratik problemlere balistik ve gök mekaniğinin uygulamasıdır. Bu nesnelerin hareketi genellikle Newton'un hareket kanunları ve Newton'un evrensel çekim yasası ile hesaplanır. Bu uzay görevi tasarımı ve denetimi altında olan bir çekirdek disiplindir. Gök mekaniği; daha genel olarak yıldız sistemleri, gezegenler, uydular ve kuyruklu yıldızlar gibi kütle çekimi etkisinde bulunan yörünge sistemleri için geçerlidir. Yörünge mekaniği; uzay araçlarının yörüngelerine ait yörünge manevraları, yörünge düzlemi değişiklikleri ve gezegenler arası transferler gibi kavramlara odaklanır ve itici manevralar sonuçlarını tahmin etmek için görev planlamacıları tarafından kullanılır. Genel görelilik teorisi, yörüngeleri hesaplamak için Newton yasalarından daha kesin bir teoridir ve doğru hesaplar yapmak ya da yüksek yerçekimini ihtiva eden durumlar söz konusu olunca bazen gereklidir (Güneşe yakın yörüngeler gibi).

Tarihçe
Yirminci yüzyılda uzay yolculuğunun yükselişine kadar, yörünge ve gök mekaniği arasında çok az fark vardı ve Sputnik döneminde bu alan uzay dinamiği olarak adlandırılırdı. (konumun zamana göre belirlenmesi) gibi kimi problemleri çözmek için kullanılan kimi sorunları çözmek için kullanılan bazı temel teknikler bu nedenle her iki alanda da aynıdır. Ayrıca bu alanların tarihi neredeyse tamamen paylaşılır.
Johannes Kepler, 1605 yılında yayınladığı kurallarıyla gezegen yörüngelerini başarı ile açıklayan ilk kişidir. Isaac Newton, 1687 yayınladığı Philosophiæ Naturalis Principia Mathematica kitabında gök hareketinin daha genel yasalarını açıklamıştır.
Pratik teknikleri
Baş kurallar
Aşağıdaki baş kurallar yine bu kurallarca tanımlanan klasik mekanik tarafından varsayılan durumlar için kullanışlıdır. Bu baş kurallar kimi yıldız (mesela Güneş) gibi küçük cisimlerin yörüngesini hesaplamak için kullanılabilir.
- Kepler'in gezegensel hareket yasaları:
- Yörüngeler eliptiktir ve bu elipsin bir odağında daha ağır olan nesne bulunur. Bu durumun özel bir örneği merkezinde bir gezegen olan dairesel bir yörüngedir (daire özel bir elipstir).
- Uydudan gezegene çizilen bir çizgi, yörüngesinin hangi kısmı ölçülürse ölçülsün; eşit zamanlarda eşit alanlar oluşturur.
- Bir uydunun yörünge döneminin karesi, gezegenin ortalama uzaklığın küpü ile doğru orantılıdır.
- Uydunun yörünge dönemi ve şekli, kuvvet uygulanmadan değişemez.
- Düşük yörüngede olan bir uydu daha yüksek bir yörüngede olan uyduda gezegenin yüzeyine göre, güçlü kütle çekiminden dolayı daha hızlı bir şekilde hareket eder.
- Uydunun yörüngede sadece bir noktasında bir itme tatbik edilir ise, yolundaki geri kalanı değişecek olsa da her bir takip eden yörüngede aynı noktaya geri döner.
- Bir dairesel yörünge için; uydunun hareketine ters yönde uygulanan itki yörüngeyi eliptik şekline getirir, uydu alçalır ve en düşük yörünge noktasına itki noktasından 180 derece uzakta ulaşır, sonra tekrar yükselişe geçer. Uydunun hareket yönünde uygulanan itme 180 derece uzakta atış noktası arasında bir apoaps ile elips yörünge oluşturur.
Yörünge mekaniği kuralları sonuçları bazen sezgilere aykırıdır. Örneğin iki uzay aracı, aynı dairesel yörüngede ve kenetlenme eğiliminde ise çok yakın olmadıkları sürece sürüklenen uzay aracı daha hızlı gitmek için basitçe motorlarını ateşleyemez. Bu; yörüngesinin şeklini değiştirir, irtifa kazanmasına sebep olur ve takip edilen araca göre yavaşlamasına ve dolayısıyla daha sonra hedefi kaçırmasına sebep olur. Kenetlenmeden önceki uzay randevusu normalde sonuçta tamamlamak için saatler hatta günler gerektiren birden fazla yörünge dönemlerde birden tam hesaplanan motor atışlarını alır. Yörünge mekaniğinin standart varsayımlarca hesaplanamayan derecelerde gerçekte var olan yörüngeler hesaplanan yörüngeler ile farklık gösterecektir. Örneğin, basit atmosferik sürüklenme fenomeni Dünya yörüngesindeki nesnelerin yörüngesini hesaplamayı zorlaştıran bir faktördür. Bu baş kuralları birbirine yakın kütleli iki cisim, ikili yıldız sistemi gibi, kullanmak yanlıştır. Gök mekaniği daha geniş durumlarda uygulanabilir daha genel kuralları kullanır. Matematiksel Newton yasaları kullanılarak elde edilebilen Kepler'in gezegensel hareket yasaları, sadece sigara yerçekimi kuvvetleri yokluğunda, iki gravitating cisimlerin hareketini tanımlayan kesinlikle tutun; onlar da parabolik ve hiperbolik yörüngeleri açıklar. Yıldızlı gibi büyük nesnelerin yakın klasik mekanik ve genel görelilik arasındaki farklar da önem kazanmaktadır.
Astrodinamiğin kuralları
Astrodinamiğin temel kuralları Newton'un evrensel çekim yasası ve Newton'un hareket kanunlarıdır ve bu kanunlar için temel matematiksel araç ise diferansiyel kalkülüstür.
Atmosfer dışındaki her yol veya yörünge geri dönüştürülebilirdir, yani, uzay-zaman fonksiyonunda zaman ters çevrilir. Hızlar ters çevrilir ve ivmeler(roket itişinden kaynaklananlar da dahil olmak üzere). Yani bir roket hızı yönü boyunca ateşlenirse, çevrilen durumda hıza aksi istikamette olur. Tabii ki roket ile sağlana itmelerde tamamen çevrim olmaz, her iki türlü de aynı delta-v kullanılır ve kütle oranı aynı olacak şekilde uygulanır.
Astrodinamiğin standart varsayımları dışarıdan herhangi bir cisim ile girişim içermez, kütle diğer cisimleri için ihmal edilebilirdir ve güneş rüzgarları, atmosferik sürüklenme, gibi kuvvetlerde ihmal edilebilir olarak varsayılır. Tabii ki daha isabetli hesaplar işleri daha da basitleştiren bu varsayımlar olmadan elde edilebilir, fakat o zaman daha karmaşık bir hale bürünür. Ayrıca daha fazla isabetli hesap yapmak o kadar da değerli farklılıklar oluşturmaz.
Yörüngedeki cisim sadece merkezdeki çekici bir cismin etkisinde olduğu düşünüldüğü zaman Keplerin gezegensel hareket kanunları Newton'un hareket yasalarından türetilebilir. Bir motor etkisi veya itici bir kuvvet olduğunda Newton'un yasaları geçerliliğini korur faka Keplerin yasaları artık geçerli değildir. İtici etki durduğu zaman oluşan yörünge farklı olacaktır fakat Keplerin yasaları ile tekrar açıklanabilir. Açıklayıcı bu üç yasa şöyledir:
- Bütün gezegenlerin yörüngeleri odaklarından birinde güneş olan bir elipstir.
- Gezegen ile güneşi birleştiren bir doğru eş zaman aralığında eşit alanlar tarar.
- Yörünge periyodunun kareleri (^2) yarı-büyük eksenin 3. kuvveti ile doğru orantılıdır.
Kaçış hızı
Kaçış hızı aşağıda görüldüğü üzere kolayca türetilebilir. Herhangi bir uzay aracının belirli bir enerjisi iki bileşenden, belirli potansiyel enerji ve belirli bir kinetik enerjiden oluşur. Kütlesi M olan bir gezegen ile ilişkili belirli potansiyel enerji aşağıdaki gibi verilir;

Bu arada bir cismin özel kinetik enerjisi aşağıdaki gibi ifade edilir:

Daha sonra enerji korunacağından,

Toplam ;

Merkezdeki cismin merkezi ile uzaydaki araç arasındaki mesafeye, 


Dünya'dan kaçış hızı 11 km/s civarıdır fakat bu hız Güneşin çekim kuvvetinden dolayı sonsuz bir mesafeye ulaşabilmek için yetersizdir. Mesafesi Güneş–Dünya arası mesafe kadar Güneşten uzak bir mesafeye, ama Dünya'ya yakın değil, kaçmak için 42 km/s civarında hız gerekir. Fakat Dünya'dan ateşlenen bir uzay aracı için ancak Dünya'nın yörüngesinde hareket ederken (nedeniyle tahrik sistemi) daha da ivme hepsinin aynı yöne taşıyor ise, Dünya'dan başlatılan uzay aracı için, Dünya'nın yörüngesel hız için "kısmını kredi", olacak.
Serbest yörüngeler için formüller
Yörüngeler konik kesitlerdir, yani açısı bilinen bir objenin mesafesi formüldeki kutupsal koordinatlara karşılık gelir, yani;
Burada μ ifadesi olarak ifade edilir ki bu da G.M yani kütle çekim sabiti çarpı kütledir, m1 and m2 buradaki kütleler sırası ile birinci ve ikinci cisimlerin kütleleridir ve h ifadesi de birinci nesnenin ikinciye göre verir. Ayrıca, "θ" parametresi gerçek anomali olarak, p semi-latus rectum olarak, "e" olarak ifade edilir be bu ifadelerin hepsi 6 bağımsız elde edilebilir.
Çembersel yörüngeler
Merkezi bir nesnenin yerçekiminin hakim olduğu tüm bağıl yörüngeler doğada elips şeklindedir. Bu durumların özel bir hali, sıfır dış merkezliliğe sahip bir elips olan çembersel bir yörüngedir. Kütlesi "M" olan bir objeden "r" uzaklığındaki çembersel yörüngeye sahip bir cismin "v" hızı şöyle bulunur
. burada 
- 6.673 84 × 10−11 m³/(kg·s²
Bu formülü doğru kullanmak için birimleri tutarlı olmalıdır; örneğin "M" kilogram ve "r" ifadesi de metreye eşit olmalıdır. Yani cevap saniyede metre olarak bulunmalıdır.
GM' ifadesi çoğunlukla standart kütle çekim parametresi olarak adlandırılır ki her gezegen veya güneş sistemindeki her uydu için farklıdır. Bir kez dairesel yörünge hızı bilinirse kaçış hızı yörünge hızının karekök 2 katı olarak bulunur
Eliptik yörüngeler
Eğer 0<e<1 ise serbest yörüngelerin denkleminin paydası θ gerçek anomalisi ile değişiklik gösterir, fakat pozitif olarak kalır ve asla sıfıra eşit olmaz. Buna mukabil, göreli konum vektörü periapsis en küçük bir büyüklük olacak, rp (ve aşağıdaki gibi verilen) şekilde sınırlı kalır
θ = 180 olduğu vakit r en yüksek değerine ulaşır. Bu noktaya ise apoapsis denir ve radyal koordinatları, ra, şu şekilde gösterilir
Aşağıda gösterilen 2a değeri periapsis ve apoapsis noktalarını birleştiren çizgi mesafesi bu iki nokta arasındaki mesafe olsun
Yukarıdaki denklemleri yerine koyduğumuz zaman
a elipsin semimajor eksendir. P'yi yalnız bırakıp sonucu konik kesit eğrisi formülünde yazınca şu sonuca ulaşılır,
Yörünge periyodu
Standart varsayımlar altında Yörünge periyodu (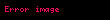
Burada:
,
uzunluğuna eşittir.
Sonuç:
- Yörünge periyodu yarıçapı uzunluğuna eşit olan bir çembersel yörünge için (
) değerine eşittir.
- Belirli bir yarı-büyük yörünge süresi, dış merkezliliğe bağlı değildir (Ayrıca bakınız: ).
Hız
Standart varsayımlar altında eliptik bir yörünge izleyen bir cisim için yörünge hızı (
Burada:
, ,
, yörüngedeki cisimlerin birbirleri arasındaki mesafeyi,
, uzunluğunu ifade eder.
Hiperbolik bir yörünge için hız denklemi ya + 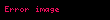
Enerji
Standart varsayımlar altında eliptik bir yörüngenin , (
Burada:
yörüngedeki cismin hızı,
merkezdeki cisim ile yörüngedeki cisim arasındaki mesafe,
,
.
Sonuçlar:
- Büyük ekseni verilen bir yörünge için belirli bir yörünge enerjisi dış merkezlilikten bağımsızdır
kullanarak şunları buluruz
- özgül potansiyel enerjinin zaman-ortalaması eşittir 2ε
- r−1 nın zaman-ortalaması a−1e eşittir
- spesifik kinetik enerjinin zaman-ortalaması -ε a eşittir.
Parabolik yörüngeler
Dış merkezlilik bire eşit ise yörünge denklemi şu şekilde olur
Burada:
merkezdeki cismin kütle merkezi ile yörüngedeki cismin arasındaki radyal mesafe,
yörüngedeki cismin ,
yörüngedeki cismin gerçek anomalisi,
ise .
Gerçek anomali, θ, 180° ye yaklaştıkça payda sıfıra yaklaşır ve bu nedenle "r" sıfıra yakınsar. Dolayısıyla, yörüngenin enerjisi ("e"=1) şu şekilde verilir:
Burada:
yörüngedeki cismin hızıdır.
Diğer bir deyişle, parabolik bir yolun her noktasında hız
olur.
Hiperbolik yörüngeler
Eğer e>1 ise yörünge formülü
hiperbolik bir yörüngenin geometrisini tanımlar. Sistem, iki simetrik eğrilerden oluşur; yörüngedeki cisim bunlardan birini kaplar. Diğeri boş bir matematiksel görüntüdür. Açıkça, yukarıdaki denklemin paydası cosθ = -1/e olduğu zaman sıfıra gider. Bu değeri gerçek anomali olarak ifade ederiz.
θ∞ = cos−1(-1/e)
Radyal mesafe sonsuza yaklaştığı için gerçek anomali θ∞ya yaklaşır. θ∞asimptotun gerçek anomalisi olarak bilinir. θ∞ ifadesinin 90 ile 180 derece arasında olduğu görülebilir. sin²θ+cos²θ=1 trigonometrik eşitliğinden şu denkleme de ulaşılabilir:
sinθ∞ = (e2-1)1/2/e
Enerji
Standart varsayımlar altında hiperbolik bir yörüngenin (
Burada:
yörüngedeki cisminin yörünge hızı,
merkezdeki cisim ile yörüngedeki cisim arasındaki radyal mesafe,
negatif ve,
.
Hiperbolik aşırı hız
Standart varsayımlar altında hiperbolik bir yörünge izleyen bir cisim hiperbolik aşırı hız (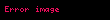
Burada:
ve,
yörünge'nin hiperbol'ünün negatif . Hiperbolik aşırı hız kavramı aşağıdaki ifade ile veya bir diye adıyla karakteristik enerji ile ilişkilidir.
Yörüngelerin hesaplanması
Kepler denklemi
Yörüngeleri hesaplamak için tarihsel denebilecek bir yaklaşımla 'ni kullanmaktır: :
Burada M ortalama ayrıklık, E ve 
Kepler'in bu formülü ile 

- Gerçek anomali
kullanılarak
hesaplamak
- Dış merkezlilik anomalisi
kullanılarak uçuş süresi
ni hesaplamak.
Belirli bir zamanda dış merkezlik anomalisini bulmak (problemin ters hali) daha zordur. Kepler denklemi 


Kepler denklemi bütün reel 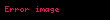

Bu denklemi çözünce şuna ulaşılır:
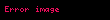
Alternatif olarak, Kepler Denklemi sayısal olarak çözülebilir. Bunun için ilk olarak bir 

Bu yaklaşımın ana zorluğu aşırı ekstrem eliptik yörüngeler için yakınsama aşırı zor ve uzun sürebilir. Paraboliğe yakın yörüngeler için dış merkezlilik 

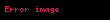
Konik yörüngeler
Basit prosedürler için, değişken elipsler için delta-v hesabı gibi, geleneksel yaklaşım oldukça etkilidir. Diğerleri, özellikle yakın dairesel ve hiperbolik yörüngeler için daha karmaşıktır.
Yamalı konik yaklaşımı
Hohmann transfer yörüngesi gezegenler arası yörüngeler için yetersizdir çünkü gezegenin kendi kütlesini ihmal eder. Bir gezegenin çevresinde gezegenin yerçekimi uzay aracının hareketini domine eder ve çoğu durumda Hohmann delta-v değerini aşırı abartır yani ateşleme zamanında oldukça yanılır. Delta-v'nin birinci dereceden bir yaklaşımını almak için nispeten basit bir yol olan 'Yamalı Konik Yaklaşım' kullanılır. Yörüngeden geçen ve egemen olan cisim belirlenir ve sadece bu cismin o yörünge bölgesine etkisi modellenir. Örneğin Mars ile Dünya arası bir yörünge için Dünya'nın kütlesi sadece kütle çekiminin etki alanı boyunca hesaplanır. Uzay aracı bu yörünge için yeterli kaçış hızı ile gezegenler arası uzaya fırlatılmalıdır. Daha sonra, Mars'ın etki alanına yaklaşana kadar sadece Güneşin etkisi göz önünde bulundurulmalıdır. Bu aşama sırasında transfer yörünge modeli hesaplar için uygundur. Son olarak, yörüngenin Mars'ın kütlesince etki eden kısmında sadece Mars'ın etkisi göze alınmalıdır. Uzay aracı Mars'a hiperbolik bir yörünge ile yaklaşmalıdır ve son retrograd (geri, geriye) yönlü ateşleme aracın hızını Mars tarafından yakalanacak kadar düşürmelidir.
'nin 
burada 


Bu basite indirgeme şekli kabaca gerekli yakıt miktarını ve uçuş zamanını hesaplamak için yeterlidir fakat genellikle uzay aracını varacağı noktaya rehberlik etmek için kullanmaya isabetsiz kalır. Yani, bunu yapmak için sayısal metot gerekir:
Evrensel değişken förmülasyonu
o 2-cisim sorununu çözmek için geleneksel yaklaşımlardaki hesaplama eksikliklerin giderilmesi, evrensel değişken formülasyonu sayesinde olmuştur. Çembersel, eliptik, parabolik ve hiperbolik yörünge durumlarında da işe yarar, diferansiyel denklemler de çözüme iyi derecede yakınsar. Ayrıca kökler teorisi ile birleşen problemler ile iyi bir şekilde genelleştirilebilir.
Karışıklıklar (perturbations)
Evrensel değişken formülasyonu parametrelerin varyasyonu tekniği ile iyi çalışır, fakat bu durum şu ana kadar geçerlidir, Kepler'in 6 yörünge elamanı yerine başka bir yörünge elemanları kümesi kullanılır: Uydunun ilk konumu ve hız vektörü 


Fakat, pertürbasyonlar yörünge öğelerinin zaman içinde değişmesine neden olur. Yani, pozisyon elemanını 

- Ekvatoral çıkıntılar node(?) ve yerlerinde çıkarıma neden olur.
- Kütle çekim alanında ek karışıklık oluşturur
- Ay ve Güneşin kütle çekim karışıklığı yörüngeleri değiştirir.
- Atmosferik sürüklenme ek bir itki kullanılmaz ise yarı-büyük ekseni düşürür.
Çok büyük zaman aralıklarından sonra (yörüngede milyonlarca turdan sonra), çok küçük karışıklar bile dominant hale gelebilir ve yörüngedeki davranış kaotik olabilir. öte taraftan karışıklıklar (perturbations), zeki astrodinamikçiler tarafında yörünge bakım görevleri için düzenlenebilir, örneğin , bakım veya onarımı veya düşük irtifada seçili hedefleri kapsayacak şekilde yerberi aşamaları.
Yörünge manevraları
Bir uzay uçuşunda yörünge manevrası, kullanılarak aracın yörüngesinin değiştirilmesi olayıdır. Örneğin Dünyadan çok uzakta Güneş etrafında bir yörüngeye sahip bir uzay aracı için yörünge manevrası derin-uzay manevrası (DUM) olarak adlandırılır.
Yörünge transferi
Transfer yörüngeleri genellikle eliptik olan ve bir yörüngeden diğer yörüngeye ulaşmak için kullanılan yörüngelerdir. Genellikle başında, sonunda ve bazen birkaç defada ortada bir ateşleme gerektirir.
- Hohmann transfer yörüngesi en düşük delta-v gerektirir.
- Bİr Hohmann transferden daha az enerji gerektirebilir fakat yörüngelerin oranı 11.94'e eşit veya büyük ise, ama Hohmann transferinin üzerinde bir sürede seyahat zamanı gerektirir.
- Daha hızlı transferler daha fazla delta-v pahasına hedef ve kaynak yörünge ile kesişen başka bir yörünge kullanabilir.
- Düşük itkili motor kullanmak ( gibi), ilk yörüngede en uygun transfer yörüngesi sürekli apogee hızın yönünde sokarak elde edilir son istenen dairesel yörüngeye supersynchronous... Fakat bu metot düşük itkiden dolayı daha fazla zaman alır.
Düzlemsel olmayan yörüngeler arasında transfer durumunda yörünge düzlemlerinin kesişim noktasında yapılmalıdır. (the "node").





Kütle çekimi yardımı ve Oberth efekti
olduğu durumlarda, uzay aracı gezegenin etkisi ile savrulur ve farklı bir yönde ve fraklı bir hızda gezegenin etkisinden ayrılır. Bu yardım daha fazla yakıt taşımaktan daha fazla kullanışlıdır. Bu yardım ile yapılan manevra uzak mesafeler için herhangi bir fiziksel çarpışma olmamasına rağmen elastik çarpışma gibi düşünülebilir. Newton'un 3. hareket kanunundan (etki aynı güçte tepki yaratır) dolayı bir uzay aracı tarafından elde edilen momentum gezegen tarafından kayıp edilmiş olmalı ya da tam tersi. Fakat, gezegen uzay aracına göre çok çok daha fazla kütleye sahip olduğundan aracın gezegenin yörüngesine etkisi ihmal edilebilir düzeydedir. kütle çekim yardımı operasyonunda düşünülebilir. Bu etki ateşleme sisteminin kullanımı bu yöntemle yüksek hızlarda daha iyi çalışır ve dolayısı ile değişimler gezegenin yörüngesine yakın iken daha etkilidir, yani bu durum delta-v'nin daha efektif kullanılmasıdır.
Gezegenler arası taşıma ağı ve belirsiz (fuzzy) yörüngeler
Şimdi rota aramak için bilgisayarları, Güneş sistemindeki gezegenlerin ve uyduların doğrusalsızlığından faydalanarak, kullanmak mümkün. Örneğin, Dünya'nın yükseklerinde olan ve geçen bir yörüngeden Mars'a yörünge grafiklemek mümkündür.[]. Ortaklaşa Gezegenler arası taşıma ağı olarak adlandırılan bu sistemde belirsiz hatta kaotik yörüngeler hiç yakıt kullanmadan Lagrange noktasına ulaşabilirler (yörünge tutarak n uygulamada bazı düzeltmeler gerektirir).
Onlarla en büyük sorun, son derece yavaş olmaları ve yıllarca sürebilmeleri. Ayrıca ateşleme pencereleri çok fazla uzakta olabilir.
Fakat yine de gibi projelerde görevlendirildiler. Bu uzay aracı (L1) Dünya-Güneş noktasına ulaştı ve çok az propilen kullanarak geri döndü.
Ayrıca bakınız
Kaynakça
- ^ William Thompson 1961
- ^ "Tesseral Harmonic". 30 Temmuz 2016 tarihinde kaynağından . Erişim tarihi: 20 Mayıs 2016.
- ^ Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. s. 317. ISBN . 16 Temmuz 2017 tarihinde kaynağından . Erişim tarihi: 20 Mayıs 2016.
- ^ Spitzer, Arnon (1997). Optimal Transfer Orbit Trajectory using Electric Propulsion. USPTO. 7 Nisan 2016 tarihinde kaynağından . Erişim tarihi: 20 Mayıs 2016.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddenin iceriginin Turkcelestirilmesi veya Turkce dilbilgisi ve kurallari dogrultusunda duzeltilmesi gerekmektedir Bu maddedeki yazim ve noktalama yanlislari ya da anlatim bozukluklari giderilmelidir Yabanci sozcukler yerine Turkce karsiliklarinin kullanilmasi karakter hatalarinin duzeltilmesi dilbilgisi hatalarinin duzeltilmesi vs Duzenleme yapildiktan sonra bu sablon kaldirilmalidir Yorunge mekanigi veya astrodinamik roketler ve diger uzay araclarinin hareketini ilgilendiren pratik problemlere balistik ve gok mekaniginin uygulamasidir Bu nesnelerin hareketi genellikle Newton un hareket kanunlari ve Newton un evrensel cekim yasasi ile hesaplanir Bu uzay gorevi tasarimi ve denetimi altinda olan bir cekirdek disiplindir Gok mekanigi daha genel olarak yildiz sistemleri gezegenler uydular ve kuyruklu yildizlar gibi kutle cekimi etkisinde bulunan yorunge sistemleri icin gecerlidir Yorunge mekanigi uzay araclarinin yorungelerine ait yorunge manevralari yorunge duzlemi degisiklikleri ve gezegenler arasi transferler gibi kavramlara odaklanir ve itici manevralar sonuclarini tahmin etmek icin gorev planlamacilari tarafindan kullanilir Genel gorelilik teorisi yorungeleri hesaplamak icin Newton yasalarindan daha kesin bir teoridir ve dogru hesaplar yapmak ya da yuksek yercekimini ihtiva eden durumlar soz konusu olunca bazen gereklidir Gunese yakin yorungeler gibi Yeryuzunun yorungesindeki bir uyduda ve ice dogru ivme vardir TarihceYirminci yuzyilda uzay yolculugunun yukselisine kadar yorunge ve gok mekanigi arasinda cok az fark vardi ve Sputnik doneminde bu alan uzay dinamigi olarak adlandirilirdi konumun zamana gore belirlenmesi gibi kimi problemleri cozmek icin kullanilan kimi sorunlari cozmek icin kullanilan bazi temel teknikler bu nedenle her iki alanda da aynidir Ayrica bu alanlarin tarihi neredeyse tamamen paylasilir Johannes Kepler 1605 yilinda yayinladigi kurallariyla gezegen yorungelerini basari ile aciklayan ilk kisidir Isaac Newton 1687 yayinladigi Philosophiae Naturalis Principia Mathematica kitabinda gok hareketinin daha genel yasalarini aciklamistir Pratik teknikleriBas kurallar Asagidaki bas kurallar yine bu kurallarca tanimlanan klasik mekanik tarafindan varsayilan durumlar icin kullanislidir Bu bas kurallar kimi yildiz mesela Gunes gibi kucuk cisimlerin yorungesini hesaplamak icin kullanilabilir Kepler in gezegensel hareket yasalari Yorungeler eliptiktir ve bu elipsin bir odaginda daha agir olan nesne bulunur Bu durumun ozel bir ornegi merkezinde bir gezegen olan dairesel bir yorungedir daire ozel bir elipstir Uydudan gezegene cizilen bir cizgi yorungesinin hangi kismi olculurse olculsun esit zamanlarda esit alanlar olusturur Bir uydunun yorunge doneminin karesi gezegenin ortalama uzakligin kupu ile dogru orantilidir Uydunun yorunge donemi ve sekli kuvvet uygulanmadan degisemez Dusuk yorungede olan bir uydu daha yuksek bir yorungede olan uyduda gezegenin yuzeyine gore guclu kutle cekiminden dolayi daha hizli bir sekilde hareket eder Uydunun yorungede sadece bir noktasinda bir itme tatbik edilir ise yolundaki geri kalani degisecek olsa da her bir takip eden yorungede ayni noktaya geri doner Bir dairesel yorunge icin uydunun hareketine ters yonde uygulanan itki yorungeyi eliptik sekline getirir uydu alcalir ve en dusuk yorunge noktasina itki noktasindan 180 derece uzakta ulasir sonra tekrar yukselise gecer Uydunun hareket yonunde uygulanan itme 180 derece uzakta atis noktasi arasinda bir apoaps ile elips yorunge olusturur Yorunge mekanigi kurallari sonuclari bazen sezgilere aykiridir Ornegin iki uzay araci ayni dairesel yorungede ve kenetlenme egiliminde ise cok yakin olmadiklari surece suruklenen uzay araci daha hizli gitmek icin basitce motorlarini atesleyemez Bu yorungesinin seklini degistirir irtifa kazanmasina sebep olur ve takip edilen araca gore yavaslamasina ve dolayisiyla daha sonra hedefi kacirmasina sebep olur Kenetlenmeden onceki uzay randevusu normalde sonucta tamamlamak icin saatler hatta gunler gerektiren birden fazla yorunge donemlerde birden tam hesaplanan motor atislarini alir Yorunge mekaniginin standart varsayimlarca hesaplanamayan derecelerde gercekte var olan yorungeler hesaplanan yorungeler ile farklik gosterecektir Ornegin basit atmosferik suruklenme fenomeni Dunya yorungesindeki nesnelerin yorungesini hesaplamayi zorlastiran bir faktordur Bu bas kurallari birbirine yakin kutleli iki cisim ikili yildiz sistemi gibi kullanmak yanlistir Gok mekanigi daha genis durumlarda uygulanabilir daha genel kurallari kullanir Matematiksel Newton yasalari kullanilarak elde edilebilen Kepler in gezegensel hareket yasalari sadece sigara yercekimi kuvvetleri yoklugunda iki gravitating cisimlerin hareketini tanimlayan kesinlikle tutun onlar da parabolik ve hiperbolik yorungeleri aciklar Yildizli gibi buyuk nesnelerin yakin klasik mekanik ve genel gorelilik arasindaki farklar da onem kazanmaktadir Astrodinamigin kurallariAstrodinamigin temel kurallari Newton un evrensel cekim yasasi ve Newton un hareket kanunlaridir ve bu kanunlar icin temel matematiksel arac ise diferansiyel kalkulustur Atmosfer disindaki her yol veya yorunge geri donusturulebilirdir yani uzay zaman fonksiyonunda zaman ters cevrilir Hizlar ters cevrilir ve ivmeler roket itisinden kaynaklananlar da dahil olmak uzere Yani bir roket hizi yonu boyunca ateslenirse cevrilen durumda hiza aksi istikamette olur Tabii ki roket ile saglana itmelerde tamamen cevrim olmaz her iki turlu de ayni delta v kullanilir ve kutle orani ayni olacak sekilde uygulanir Astrodinamigin standart varsayimlari disaridan herhangi bir cisim ile girisim icermez kutle diger cisimleri icin ihmal edilebilirdir ve gunes ruzgarlari atmosferik suruklenme gibi kuvvetlerde ihmal edilebilir olarak varsayilir Tabii ki daha isabetli hesaplar isleri daha da basitlestiren bu varsayimlar olmadan elde edilebilir fakat o zaman daha karmasik bir hale burunur Ayrica daha fazla isabetli hesap yapmak o kadar da degerli farkliliklar olusturmaz Yorungedeki cisim sadece merkezdeki cekici bir cismin etkisinde oldugu dusunuldugu zaman Keplerin gezegensel hareket kanunlari Newton un hareket yasalarindan turetilebilir Bir motor etkisi veya itici bir kuvvet oldugunda Newton un yasalari gecerliligini korur faka Keplerin yasalari artik gecerli degildir Itici etki durdugu zaman olusan yorunge farkli olacaktir fakat Keplerin yasalari ile tekrar aciklanabilir Aciklayici bu uc yasa soyledir Butun gezegenlerin yorungeleri odaklarindan birinde gunes olan bir elipstir Gezegen ile gunesi birlestiren bir dogru es zaman araliginda esit alanlar tarar Yorunge periyodunun kareleri 2 yari buyuk eksenin 3 kuvveti ile dogru orantilidir Kacis hiziKacis hizi asagida goruldugu uzere kolayca turetilebilir Herhangi bir uzay aracinin belirli bir enerjisi iki bilesenden belirli potansiyel enerji ve belirli bir kinetik enerjiden olusur Kutlesi M olan bir gezegen ile iliskili belirli potansiyel enerji asagidaki gibi verilir ϵp GMr displaystyle epsilon p frac GM r Bu arada bir cismin ozel kinetik enerjisi asagidaki gibi ifade edilir ϵk v22 displaystyle epsilon k frac v 2 2 Daha sonra enerji korunacagindan ϵ ϵk ϵp displaystyle epsilon epsilon k epsilon p Toplam ϵ v22 GMr displaystyle epsilon frac v 2 2 frac GM r Merkezdeki cismin merkezi ile uzaydaki arac arasindaki mesafeye r displaystyle r bagli degildir O halde nesne sonsuz r displaystyle r mesafesine sadece bu negatif olmazsa ulasabilir ki bu da gosterir ki v 2GMr displaystyle v geq sqrt frac 2GM r Dunya dan kacis hizi 11 km s civaridir fakat bu hiz Gunesin cekim kuvvetinden dolayi sonsuz bir mesafeye ulasabilmek icin yetersizdir Mesafesi Gunes Dunya arasi mesafe kadar Gunesten uzak bir mesafeye ama Dunya ya yakin degil kacmak icin 42 km s civarinda hiz gerekir Fakat Dunya dan ateslenen bir uzay araci icin ancak Dunya nin yorungesinde hareket ederken nedeniyle tahrik sistemi daha da ivme hepsinin ayni yone tasiyor ise Dunya dan baslatilan uzay araci icin Dunya nin yorungesel hiz icin kismini kredi olacak Serbest yorungeler icin formuller Yorungeler konik kesitlerdir yani acisi bilinen bir objenin mesafesi formuldeki kutupsal koordinatlara karsilik gelir yani r p1 ecos 8 displaystyle r frac p 1 e cos theta m G m1 m2 displaystyle mu G m 1 m 2 p h2 m displaystyle p h 2 mu Burada m ifadesi olarak ifade edilir ki bu da G M yani kutle cekim sabiti carpi kutledir m1 and m2 buradaki kutleler sirasi ile birinci ve ikinci cisimlerin kutleleridir ve h ifadesi de birinci nesnenin ikinciye gore verir Ayrica 8 parametresi gercek anomali olarak p semi latus rectum olarak e olarak ifade edilir be bu ifadelerin hepsi 6 bagimsiz elde edilebilir Cembersel yorungeler Merkezi bir nesnenin yercekiminin hakim oldugu tum bagil yorungeler dogada elips seklindedir Bu durumlarin ozel bir hali sifir dis merkezlilige sahip bir elips olan cembersel bir yorungedir Kutlesi M olan bir objeden r uzakligindaki cembersel yorungeye sahip bir cismin v hizi soyle bulunur v GMr displaystyle v sqrt frac GM r burada G displaystyle G kutle cekim sabitidir ki bu sabitte asagidaki degere esittir 6 673 84 10 11 m kg s Bu formulu dogru kullanmak icin birimleri tutarli olmalidir ornegin M kilogram ve r ifadesi de metreye esit olmalidir Yani cevap saniyede metre olarak bulunmalidir GM ifadesi cogunlukla standart kutle cekim parametresi olarak adlandirilir ki her gezegen veya gunes sistemindeki her uydu icin farklidir Bir kez dairesel yorunge hizi bilinirse kacis hizi yorunge hizinin karekok 2 kati olarak bulunur v 2GMr 2GMr displaystyle v sqrt 2 sqrt frac GM r sqrt frac 2GM r Eliptik yorungeler Eger 0 lt e lt 1 ise serbest yorungelerin denkleminin paydasi 8 gercek anomalisi ile degisiklik gosterir fakat pozitif olarak kalir ve asla sifira esit olmaz Buna mukabil goreli konum vektoru periapsis en kucuk bir buyukluk olacak rp ve asagidaki gibi verilen sekilde sinirli kalir rp p1 e displaystyle r p frac p 1 e 8 180 oldugu vakit r en yuksek degerine ulasir Bu noktaya ise apoapsis denir ve radyal koordinatlari ra su sekilde gosterilir 2a rp ra displaystyle 2a r p r a Asagida gosterilen 2a degeri periapsis ve apoapsis noktalarini birlestiren cizgi mesafesi bu iki nokta arasindaki mesafe olsun 2a rp ra displaystyle 2a r p r a Yukaridaki denklemleri yerine koydugumuz zaman a p1 e2 displaystyle a frac p 1 e 2 a elipsin semimajor eksendir P yi yalniz birakip sonucu konik kesit egrisi formulunde yazinca su sonuca ulasilir r a 1 e2 1 ecos 8 displaystyle r frac a 1 e 2 1 e cos theta Yorunge periyodu Standart varsayimlar altinda Yorunge periyodu T displaystyle T eliptik yorunge boyunca seyahat eden bir cisim icin su sekilde hesaplanabilir T 2pa3m displaystyle T 2 pi sqrt a 3 over mu Burada m displaystyle mu a displaystyle a uzunluguna esittir Sonuc Yorunge periyodu yaricapi uzunluguna esit olan bir cembersel yorunge icin a displaystyle a degerine esittir Belirli bir yari buyuk yorunge suresi dis merkezlilige bagli degildir Ayrica bakiniz Hiz Standart varsayimlar altinda eliptik bir yorunge izleyen bir cisim icin yorunge hizi v displaystyle v kullanilarak hesaplanir v m 2r 1a displaystyle v sqrt mu left 2 over r 1 over a right Burada m displaystyle mu r displaystyle r yorungedeki cisimlerin birbirleri arasindaki mesafeyi a displaystyle a uzunlugunu ifade eder Hiperbolik bir yorunge icin hiz denklemi ya 1a displaystyle 1 over a ifadesini ya da bu durumda a negatif oldugu varsayimi ile aynidir Enerji Standart varsayimlar altinda eliptik bir yorungenin ϵ displaystyle epsilon sifira esittir ve bu yorungede orbital enerji korunumu denklemi asagidaki sekilde olabilir v22 mr m2a ϵ lt 0 displaystyle v 2 over 2 mu over r mu over 2a epsilon lt 0 Burada v displaystyle v yorungedeki cismin hizi r displaystyle r merkezdeki cisim ile yorungedeki cisim arasindaki mesafe a displaystyle a m displaystyle mu Sonuclar Buyuk ekseni verilen bir yorunge icin belirli bir yorunge enerjisi dis merkezlilikten bagimsizdir kullanarak sunlari buluruz ozgul potansiyel enerjinin zaman ortalamasi esittir 2e r 1 nin zaman ortalamasi a 1e esittir spesifik kinetik enerjinin zaman ortalamasi e a esittir Parabolik yorungeler Dis merkezlilik bire esit ise yorunge denklemi su sekilde olur r h2m11 cos 8 displaystyle r h 2 over mu 1 over 1 cos theta Burada r displaystyle r merkezdeki cismin kutle merkezi ile yorungedeki cismin arasindaki radyal mesafe h displaystyle h yorungedeki cismin 8 displaystyle theta yorungedeki cismin gercek anomalisi m displaystyle mu ise Gercek anomali 8 180 ye yaklastikca payda sifira yaklasir ve bu nedenle r sifira yakinsar Dolayisiyla yorungenin enerjisi e 1 su sekilde verilir ϵ v22 mr 0 displaystyle epsilon v 2 over 2 mu over r 0 Burada v displaystyle v yorungedeki cismin hizidir Diger bir deyisle parabolik bir yolun her noktasinda hiz v 2mr displaystyle v sqrt 2 mu over r olur Hiperbolik yorungeler Eger e gt 1 ise yorunge formulu r h2m11 ecos 8 displaystyle r h 2 over mu 1 over 1 e cos theta hiperbolik bir yorungenin geometrisini tanimlar Sistem iki simetrik egrilerden olusur yorungedeki cisim bunlardan birini kaplar Digeri bos bir matematiksel goruntudur Acikca yukaridaki denklemin paydasi cos8 1 e oldugu zaman sifira gider Bu degeri gercek anomali olarak ifade ederiz 8 cos 1 1 e Radyal mesafe sonsuza yaklastigi icin gercek anomali 8 ya yaklasir 8 asimptotun gercek anomalisi olarak bilinir 8 ifadesinin 90 ile 180 derece arasinda oldugu gorulebilir sin 8 cos 8 1 trigonometrik esitliginden su denkleme de ulasilabilir sin8 e2 1 1 2 eEnerji Standart varsayimlar altinda hiperbolik bir yorungenin ϵ displaystyle epsilon sifirdan buyuktur ve bu formda bir yorunge icin soyledir ϵ v22 mr m 2a displaystyle epsilon v 2 over 2 mu over r mu over 2a Burada v displaystyle v yorungedeki cisminin yorunge hizi r displaystyle r merkezdeki cisim ile yorungedeki cisim arasindaki radyal mesafe a displaystyle a negatif ve m displaystyle mu Hiperbolik asiri hiz Standart varsayimlar altinda hiperbolik bir yorunge izleyen bir cisim hiperbolik asiri hiz v displaystyle v infty adi verilen yorunge hizina ulasir ve bu su sekilde hesaplanir v m a displaystyle v infty sqrt mu over a Burada m displaystyle mu ve a displaystyle a yorunge nin hiperbol unun negatif Hiperbolik asiri hiz kavrami asagidaki ifade ile veya bir diye adiyla karakteristik enerji ile iliskilidir 2ϵ C3 v 2 displaystyle 2 epsilon C 3 v infty 2 Yorungelerin hesaplanmasiKepler denklemi Yorungeleri hesaplamak icin tarihsel denebilecek bir yaklasimla ni kullanmaktir M E ϵ sin E displaystyle M E epsilon cdot sin E Burada M ortalama ayriklik E ve ϵ displaystyle displaystyle epsilon Kepler in bu formulu ile 8 displaystyle theta from finding the time of flight to reach an angle of 8 displaystyle theta from is broken into two steps Gercek anomali 8 displaystyle theta kullanilarak E displaystyle E hesaplamak Dis merkezlilik anomalisi E displaystyle E kullanilarak ucus suresi t displaystyle t ni hesaplamak Belirli bir zamanda dis merkezlik anomalisini bulmak problemin ters hali daha zordur Kepler denklemi E displaystyle E askindir yani E displaystyle E icin cebirsel bir cozum yoktur Kepler denklemi E displaystyle E icin analitik olarak ter cevirme ile bulunabilir Kepler denklemi butun reel ϵ displaystyle textstyle epsilon degerlerine gore cozumu soyledir E n 1 Mn3n lim8 0 dn 1d8n 1 88 sin 8 3n ϵ 1 n 1 Mnn lim8 0 dn 1d8n 1 88 ϵ sin 8 n ϵ 1 displaystyle E begin cases displaystyle sum n 1 infty frac M frac n 3 n lim theta to 0 left frac mathrm d n 1 mathrm d theta n 1 left frac theta sqrt 3 theta sin theta n right right amp epsilon 1 displaystyle sum n 1 infty frac M n n lim theta to 0 left frac mathrm d n 1 mathrm d theta n 1 left frac theta theta epsilon cdot sin theta n right right amp epsilon neq 1 end cases Bu denklemi cozunce suna ulasilir E x 160x3 11400x5 125200x7 4317248000x9 12137207200000x11 15143912713500800000x13 x 6M 13 ϵ 111 ϵM ϵ 1 ϵ 4M33 9ϵ2 ϵ 1 ϵ 7M55 225ϵ3 54ϵ2 ϵ 1 ϵ 10M77 11025ϵ4 4131ϵ3 243ϵ2 ϵ 1 ϵ 13M99 ϵ 1 displaystyle E begin cases displaystyle x frac 1 60 x 3 frac 1 1400 x 5 frac 1 25200 x 7 frac 43 17248000 x 9 frac 1213 7207200000 x 11 frac 151439 12713500800000 x 13 cdots x 6M frac 1 3 amp epsilon 1 displaystyle frac 1 1 epsilon M frac epsilon 1 epsilon 4 frac M 3 3 frac 9 epsilon 2 epsilon 1 epsilon 7 frac M 5 5 frac 225 epsilon 3 54 epsilon 2 epsilon 1 epsilon 10 frac M 7 7 frac 11025 epsilon 4 4131 epsilon 3 243 epsilon 2 epsilon 1 epsilon 13 frac M 9 9 cdots amp epsilon neq 1 end cases Alternatif olarak Kepler Denklemi sayisal olarak cozulebilir Bunun icin ilk olarak bir E displaystyle E degeri tahmin edilir ve ucus zamani icin kullanilir ardindan E displaystyle E degeri gerekli hassasiyete kadar istenen degere yakin bir ucus zamani elde etmek icin uyarlanir Genellikle Newton yontemi yakinsamayi nispeten hizli elde etmek icin kullanilir Bu yaklasimin ana zorlugu asiri ekstrem eliptik yorungeler icin yakinsama asiri zor ve uzun surebilir Parabolige yakin yorungeler icin dis merkezlilik ϵ displaystyle epsilon neredeyse bire esittir ve bu degeri e 1 displaystyle e 1 formulunde ortalama ayriklik icin kullaninca E sin E displaystyle E sin E kendimizi neredeyse birbirine esit iki degeri birbirinden cikarirken buluruz ev hesabin dogrulugu zarara ugrar Cembersel sekle yakin yorungeler icin ilk etapta periapsis bulmak zordur ve gercekten cembersel yorungeler hic periapsis olmaz Ayrica denklem eliptik bir yorunge varsayimi uzerinde elde edilmistir yani parabolik veya hiperbolik yorungeler icin de gecerli degildir Daha sonra Evrensel degisken bu sikintilar asagidaki gelismesine yol acti Konik yorungeler Basit prosedurler icin degisken elipsler icin delta v hesabi gibi geleneksel yaklasim oldukca etkilidir Digerleri ozellikle yakin dairesel ve hiperbolik yorungeler icin daha karmasiktir Yamali konik yaklasimi Hohmann transfer yorungesi gezegenler arasi yorungeler icin yetersizdir cunku gezegenin kendi kutlesini ihmal eder Bir gezegenin cevresinde gezegenin yercekimi uzay aracinin hareketini domine eder ve cogu durumda Hohmann delta v degerini asiri abartir yani atesleme zamaninda oldukca yanilir Delta v nin birinci dereceden bir yaklasimini almak icin nispeten basit bir yol olan Yamali Konik Yaklasim kullanilir Yorungeden gecen ve egemen olan cisim belirlenir ve sadece bu cismin o yorunge bolgesine etkisi modellenir Ornegin Mars ile Dunya arasi bir yorunge icin Dunya nin kutlesi sadece kutle cekiminin etki alani boyunca hesaplanir Uzay araci bu yorunge icin yeterli kacis hizi ile gezegenler arasi uzaya firlatilmalidir Daha sonra Mars in etki alanina yaklasana kadar sadece Gunesin etkisi goz onunde bulundurulmalidir Bu asama sirasinda transfer yorunge modeli hesaplar icin uygundur Son olarak yorungenin Mars in kutlesince etki eden kisminda sadece Mars in etkisi goze alinmalidir Uzay araci Mars a hiperbolik bir yorunge ile yaklasmalidir ve son retrograd geri geriye yonlu atesleme aracin hizini Mars tarafindan yakalanacak kadar dusurmelidir nin rSOI displaystyle r SOI yaricapi ile degisir rSOI ap mpms 2 5 displaystyle r SOI a p left frac m p m s right 2 5 burada ap displaystyle a p yorungenin Gunes e gore yari buyuk ekseni mp displaystyle m p ve ms displaystyle m s ise sirasiyla ve Gunesin kutleleridir Bu basite indirgeme sekli kabaca gerekli yakit miktarini ve ucus zamanini hesaplamak icin yeterlidir fakat genellikle uzay aracini varacagi noktaya rehberlik etmek icin kullanmaya isabetsiz kalir Yani bunu yapmak icin sayisal metot gerekir Evrensel degisken formulasyonu o 2 cisim sorununu cozmek icin geleneksel yaklasimlardaki hesaplama eksikliklerin giderilmesi evrensel degisken formulasyonu sayesinde olmustur Cembersel eliptik parabolik ve hiperbolik yorunge durumlarinda da ise yarar diferansiyel denklemler de cozume iyi derecede yakinsar Ayrica kokler teorisi ile birlesen problemler ile iyi bir sekilde genellestirilebilir Karisikliklar perturbations Evrensel degisken formulasyonu parametrelerin varyasyonu teknigi ile iyi calisir fakat bu durum su ana kadar gecerlidir Kepler in 6 yorunge elamani yerine baska bir yorunge elemanlari kumesi kullanilir Uydunun ilk konumu ve hiz vektoru x0 displaystyle x 0 and v0 displaystyle v 0 bilinen bir t 0 displaystyle t 0 doneminde Iki cisim iceren simulasyonda bu elemanlar evrensel degisken formulasyonunda kullanilarak uydunun konumunu ve ileri bir durumdaki hizini belirlemek icin yeterlidir Aksine uydunun yorungedeki herhangi bir anda konum ve hizini olcebiliriz ve daha sonra evrensel degisken teorsis yaklasimini kullanarak ilk konumunu ve epoch noktasindaki hizini hesaplayabiliriz Tamamen mukemmel bir iki cisimli sistemde yorunge elemanlari degismez bir hal alir tipki Kepler elemanlarinin olacagi gibi Fakat perturbasyonlar yorunge ogelerinin zaman icinde degismesine neden olur Yani pozisyon elemanini x0 t displaystyle x 0 t seklinde ve hiz elemanini v0 t displaystyle v 0 t seklinde zamana bagli olarak degistiklerini gostererek yazariz Duzensizliklerin etkisini hesaplamak icin teknigi bulma ifadelerden biri olur Ve bu gercek yorungeler basit modellerden kuresel bir dunyaya gore farkli etkileri sunlardir Ekvatoral cikintilar node ve yerlerinde cikarima neden olur Kutle cekim alaninda ek karisiklik olusturur Ay ve Gunesin kutle cekim karisikligi yorungeleri degistirir Atmosferik suruklenme ek bir itki kullanilmaz ise yari buyuk ekseni dusurur Cok buyuk zaman araliklarindan sonra yorungede milyonlarca turdan sonra cok kucuk karisiklar bile dominant hale gelebilir ve yorungedeki davranis kaotik olabilir ote taraftan karisikliklar perturbations zeki astrodinamikciler tarafinda yorunge bakim gorevleri icin duzenlenebilir ornegin bakim veya onarimi veya dusuk irtifada secili hedefleri kapsayacak sekilde yerberi asamalari Yorunge manevralariBir uzay ucusunda yorunge manevrasi kullanilarak aracin yorungesinin degistirilmesi olayidir Ornegin Dunyadan cok uzakta Gunes etrafinda bir yorungeye sahip bir uzay araci icin yorunge manevrasi derin uzay manevrasi DUM olarak adlandirilir Yorunge transferi Transfer yorungeleri genellikle eliptik olan ve bir yorungeden diger yorungeye ulasmak icin kullanilan yorungelerdir Genellikle basinda sonunda ve bazen birkac defada ortada bir atesleme gerektirir Hohmann transfer yorungesi en dusuk delta v gerektirir BIr Hohmann transferden daha az enerji gerektirebilir fakat yorungelerin orani 11 94 e esit veya buyuk ise ama Hohmann transferinin uzerinde bir surede seyahat zamani gerektirir Daha hizli transferler daha fazla delta v pahasina hedef ve kaynak yorunge ile kesisen baska bir yorunge kullanabilir Dusuk itkili motor kullanmak gibi ilk yorungede en uygun transfer yorungesi surekli apogee hizin yonunde sokarak elde edilir son istenen dairesel yorungeye supersynchronous Fakat bu metot dusuk itkiden dolayi daha fazla zaman alir Duzlemsel olmayan yorungeler arasinda transfer durumunda yorunge duzlemlerinin kesisim noktasinda yapilmalidir the node A from a low circular orbit to a higher circular orbitA from a low circular starting orbit dark blue to a higher circular orbit red Generic two impulse elliptical transfer between two circular orbitsA general transfer from a low circular orbit to a higher circular orbitAn optimal sequence for transferring a satellite from a supersynchronous to a geosynchronous orbit using electric propulsion Kutle cekimi yardimi ve Oberth efekti oldugu durumlarda uzay araci gezegenin etkisi ile savrulur ve farkli bir yonde ve frakli bir hizda gezegenin etkisinden ayrilir Bu yardim daha fazla yakit tasimaktan daha fazla kullanislidir Bu yardim ile yapilan manevra uzak mesafeler icin herhangi bir fiziksel carpisma olmamasina ragmen elastik carpisma gibi dusunulebilir Newton un 3 hareket kanunundan etki ayni gucte tepki yaratir dolayi bir uzay araci tarafindan elde edilen momentum gezegen tarafindan kayip edilmis olmali ya da tam tersi Fakat gezegen uzay aracina gore cok cok daha fazla kutleye sahip oldugundan aracin gezegenin yorungesine etkisi ihmal edilebilir duzeydedir kutle cekim yardimi operasyonunda dusunulebilir Bu etki atesleme sisteminin kullanimi bu yontemle yuksek hizlarda daha iyi calisir ve dolayisi ile degisimler gezegenin yorungesine yakin iken daha etkilidir yani bu durum delta v nin daha efektif kullanilmasidir Gezegenler arasi tasima agi ve belirsiz fuzzy yorungeler Simdi rota aramak icin bilgisayarlari Gunes sistemindeki gezegenlerin ve uydularin dogrusalsizligindan faydalanarak kullanmak mumkun Ornegin Dunya nin yukseklerinde olan ve gecen bir yorungeden Mars a yorunge grafiklemek mumkundur kaynak belirtilmeli Ortaklasa Gezegenler arasi tasima agi olarak adlandirilan bu sistemde belirsiz hatta kaotik yorungeler hic yakit kullanmadan Lagrange noktasina ulasabilirler yorunge tutarak n uygulamada bazi duzeltmeler gerektirir Onlarla en buyuk sorun son derece yavas olmalari ve yillarca surebilmeleri Ayrica atesleme pencereleri cok fazla uzakta olabilir Fakat yine de gibi projelerde gorevlendirildiler Bu uzay araci L1 Dunya Gunes noktasina ulasti ve cok az propilen kullanarak geri dondu Ayrica bakinizKepler Yorungesi Aerodinamik Astrofizik Gok mekanigi Kaos teorisi Lagrange noktasi Yorunge Roche limiti Havacilik MuhendisligiKaynakca William Thompson 1961 Tesseral Harmonic 30 Temmuz 2016 tarihinde kaynagindan Erisim tarihi 20 Mayis 2016 Vallado David Anthony 2001 Fundamentals of Astrodynamics and Applications Springer s 317 ISBN 0 7923 6903 3 16 Temmuz 2017 tarihinde kaynagindan Erisim tarihi 20 Mayis 2016 Spitzer Arnon 1997 Optimal Transfer Orbit Trajectory using Electric Propulsion USPTO 7 Nisan 2016 tarihinde kaynagindan Erisim tarihi 20 Mayis 2016
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State