Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi (eğer varsa), fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi . Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun (yani türevi alınan fonksiyonun) türevi denir.
Türev için birden fazla farklı gösterim vardır. En yaygın kullanılan ikisi Lagrange gösterimi olan türev işareti ve Leibniz gösterimidir. Fizikçiler arasında Newton gösterimi de yaygındır. Gottfried Wilhelm Leibniz'in adını taşıyan , iki diferansiyelin oranı olarak gösterilirken, türev işareti için (′) kullanılır. Daha yüksek mertebeden gösterimler tekrarlanan türeve işaret eder ve bunlar genellikle Leibniz gösteriminde diferansiyellere üst simgeler eklenerek, türev işaretinde ise işaret sayısı artırılarak gösterilir. Daha yüksek mertebeden türevlerin fizikte uygulamaları yaygındır. Örneğin, hareket eden bir cismin zamana göre konumunun birinci türevi cismin hızı iken, konumun zaman ilerledikçe nasıl değiştiğini gösteren ikinci türev cismin ivmesidir. Diğer deyişle, ivme, hızın zaman ilerledikçe nasıl değiştiğini gösteren ikinci türevdir.
Türevler, birden fazla gerçek değişken üzerinden tanımlı fonksiyonlar için de genelleştirilebilir. Bu genellemede, türev, grafiği (uygun bir çevirme veya döndürmeden sonra) orijinal fonksiyonun grafiğine en iyi doğrusal yaklaşım olan doğrusal bir dönüşüm olarak yeniden yorumlanır. Jacobi matrisi, bağımsız ve bağımlı değişkenlerin seçimiyle verilen bir baza göre bu doğrusal dönüşümü temsil eden matristir ve bağımsız değişkenlerin her birine göre kısmi türevler alarak hesaplanabilir. Birden fazla değişkenin gerçel değerli bir fonksiyonu için, Jacobi matrisi gradyan vektörüne indirgenir.
Tanım
Limit üzerinden tanım


tanım kümesindeki bir 

varsa; yani, limit bir gerçel sayıya eşitse, o zaman 



yazılır. Eğer limitin değeri 



olarak yazılır.
Limitin sonsuz olması veya var olmaması durumunda, 



Yukarıdaki limit 







ε-δ tanımı
Limit üzerinden verilen türev tanımı (ε-δ limit tanımı) üzerinden de yazılabilir. Eğer limit varsa ve 



Süreklilik ve türevlenebilme

Eğer bir 


- Eğer
pozitif bir sayı ise
ifadesi 0'a eşit olacaktır. Yani sağdan limit 0'a eşittir.
- Eğer
negatif bir sayı ise
sayısı (negatif kalarak)
'a yaklaştıkça
ifadesi
'a doğru gidecektir. Yani soldan limit yoktur.

Ancak bir fonksiyon tanım kümesindeki her noktada sürekli ise, bu özellik, fonksiyonun her yerde türevli olacağı anlamına gelmez. Mesela, mutlak değer fonksiyonu 0 noktasında süreklidir ama türevli değildir. Nedeni, 0'da türevi tanımlayan 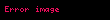


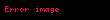
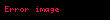

Uygulamada karşılaşılan türevlerin çoğunun her ya da türevi vardır.
Gösterim
Bir fonksiyonun türevini yazmanın yaygın bir yollarından biri, Gottfried Wilhelm Leibniz tarafından 1675 yılında tanımlanan ve türevi iki (mesela 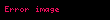

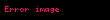



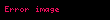
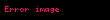




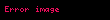

Türev için bir diğer yaygın gösterim, bir fonksiyonun hemen yanında kesme işaretine benzeyen türev işaretinin kullanılmasıdır; bu gösterim, aynı zamanda Joseph-Louis Lagrange'a atfen Lagrange gösterimi olaraka da bilinir. Birinci türev bu gösterimde 
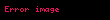
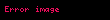

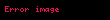
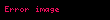
Newton gösteriminde veya nokta gösteriminde, zamana göre türevi temsil etmek için bir fonksiyon sembolünün üzerine bir nokta yerleştirilir. Eğer 


Başka bir gösterim ise diferansiyel operatörü sembolüyle gösteren D-gösterimidir. Bu gösterimde türevi gösterirken 





Türev alma kuralları
Temel fonksiyonlar için kurallar
Aşağıda en yaygın temel fonksiyonların türevleri için kurallar verilmiştir. Burada, 

Birleşik fonksiyonlar için kurallar
- Kuvvet fonksiyonlarının türevi ():
- Üstel fonksiyon, doğal logaritma ve genel tabanlı logaritmanın türevi
,
,
,
- Trigonometrik fonksiyonların türevi
- Ters trigonometrik fonksiyonların türevi
için
için
Basit işlemlerle elde edilmiş fonksiyonlar için türevler
Aşağıda, temel fonksiyonlardan basit aritmetik işlemler veya bileşke yoluyla elde edilmiş fonksiyonların türevini hesaplamak için bilinen en temel kurallardan bazıları verilmiştir. Bu amaçla 

- Sabit fonksiyon: eğer
sabitse, o zaman her
için
- :
(her
ve
fonksiyonu ve bütün
ve
gerçel sayıları için).
- Çarpma kuralı:
(her
ve
fonksiyonu için)
- Özel bir durum olarak, her
sayısı için
olur çünkü is
sayısı sabittir ve
olur.
- Özel bir durum olarak, her
- Bölme kuralı:
(her
ve
olan her
fonksiyonu için)
- Bileşke fonksiyonlar için Zincir kuralı : Eğer
ise, o zaman
Örnek


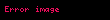


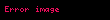

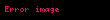
Yüksek mertebeden türevler
Daha yüksek mertebeden türevler, bir fonksiyonun tekrar tekrar türevlenmesinin sonucudur. 
nin birinci türevi fonksiyonun türevidir ve
ile gösterilir.
nin türevi ise
nin ikinci türevidir ve
ile gösterilir.
nin türevi ise
nin üçüncü türevidir ve
ile gösterilir.
Bu süreç tekrarlanarak, eğer türev varsa, fonksiyonun (n-1)inci türevi başlangıçta alınan fonksiyonun n'inci türevidir. Gösterim kısmında verilen bilgiye de dayanarak,
in türevi
nin n'inci türevidir ve
olarak gösterilir.
Ck fonksiyon
Arka arkaya 








C∞ fonksiyon
Tanım kümesindeki bütün noktalarda sonsuz kere türevli olan, yani, keyfi bir 






Diğer boyutlarda türev
Vektör değerli fonksiyonlar
Vektör değerli bir fonksiyon 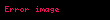


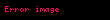

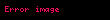
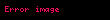
Kısmî türev
Kısmî türev, çok değişkenli bir fonksiyonun sadece ilgili değişkeni sabit değilken alınan türevdir. Bu tarz türevleri içeren denklemlere kısmî diferansiyel denklem denir.
Kısmî türevin tanımı

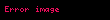
şeklinde tanımlanan n tane bağımsız değişkene bağlı z fonksiyonunun diğer değişkenler sabit tutularak herhangi bir değişkendeki 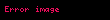
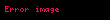

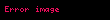
ifadesine 
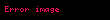

şeklinde gösterilir.



Örnek:

Yönlü türev
Eğer f bir Rn üzerinde gerçek değerli fonksiyon ise yönü içinde f in kısmî türevi içinde çeşitli ölçmeler ise (mesela f bir x ve y fonksiyonunun x yönü ve y yönü içinde f 'nin kısmî türevinde çeşitli ölçmeler ise) buna yönlü türev denir.
Bununla birlikte köşegen çizgi y = x boyunca gibi herhangi diğer yön içinde f in yönlü ölçü çeşitleri yoktur.
Burada yönlü türev ölçüsü kullanılıyor.
bir vektörse vnin yönü içinde fin yönlü türevinin x noktasında sınırıdır.
Bâzı durumlarda bu vektörün uzunluğunu değiştirme sonrası yön türevi hesaplamak veya tahmin etmek daha kolay olabilir. Genellikle bu bir birim vektör yönünde bir yönde türevinin hesaplanması içinde sorunu açmak için yapılır. Bunun nasıl çalıştığını görmek için bunu v = λu varsayalım.h = k/λ fark katsayısı içinde yerine konur.Aradaki fark katsayısı:
Bu u sırasıyla fin yönlü türevi için λ zaman içinde farklı katsayısıdır. Dahası sıfıra yönelen k olarak alınan limit olarak aynı h ve k için herhangi diğerinin çarpımıdır. Bunun için Dv(f) = λDu(f). Bu nedenle yeniden ölçeklendirme özelliği, yönlü türevler sık sık sadece birim vektörler için kabul edilir.
Eğer f'in tüm kısmî türevleri var ve x'de sürekli ve formülü ile v yönünde f içinde belirlenen yönlü türev ise
Bu tanımının bir sonucudur. Bu yönlü türev, aşağıda v içinde . Bu da
Dv + w(f) = Dv(f) + Dw(f).
demektir. Aynı tanım, ayrıca f olduğunda Rm içindeki değerleri ile bir fonksiyondur. Yukardaki tanım, vektörlerin her bir bileşeni için uygulanır. Bu durum içinde yönlü türev Rm içinde bir vektördür.
Toplam türev
Bir 

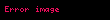




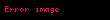
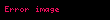

Benzer bir şekilde, tek değişkenli fonksiyonlar için tanımlana türevde de 

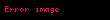


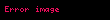

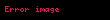
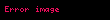
Toplam türev, eğer bir noktada varsa, o zaman yine aynı noktada bütün kısmi türevler ve yönlü türevler de vardır. Bu halde, bütün 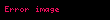

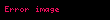


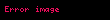



Ayrıca bakınız
Notlar
- ^ Nadiren de olsa bazı kitap ve tezlerde pürüzsüz fonksiyon kullanımı da vardır.
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte turev bir fonksiyonun tanimli oldugu herhangi bir noktada degisim yonunu veya hizini veren temel bir kavramdir Tek degiskenli bir fonksiyonun tanim kumesinin belli bir noktasinda turevi eger varsa fonksiyonun grafigine bu noktada karsilik gelen degerde cizilen egimidir Teget dogru tanim kumesinin bu noktasinda fonksiyonun en iyi Bu nedenle turev genellikle anlik degisim orani ya da daha acik bir ifadeyle bagimli degiskendeki anlik degisimin bagimsiz degiskendeki anlik degisime orani olarak tanimlanir Bir fonksiyonun turevini teorik olarak bulmaya turev alma denilir Eger bir fonksiyonun tanim kumesindeki her degerinde hesaplanan turev degerlerini veren baska bir fonksiyon varsa bu fonksiyona eldeki fonksiyonun yani turevi alinan fonksiyonun turevi denir Turev icin birden fazla farkli gosterim vardir En yaygin kullanilan ikisi Lagrange gosterimi olan turev isareti ve Leibniz gosterimidir Fizikciler arasinda Newton gosterimi de yaygindir Gottfried Wilhelm Leibniz in adini tasiyan iki diferansiyelin orani olarak gosterilirken turev isareti icin kullanilir Daha yuksek mertebeden gosterimler tekrarlanan tureve isaret eder ve bunlar genellikle Leibniz gosteriminde diferansiyellere ust simgeler eklenerek turev isaretinde ise isaret sayisi artirilarak gosterilir Daha yuksek mertebeden turevlerin fizikte uygulamalari yaygindir Ornegin hareket eden bir cismin zamana gore konumunun birinci turevi cismin hizi iken konumun zaman ilerledikce nasil degistigini gosteren ikinci turev cismin ivmesidir Diger deyisle ivme hizin zaman ilerledikce nasil degistigini gosteren ikinci turevdir Turevler birden fazla gercek degisken uzerinden tanimli fonksiyonlar icin de genellestirilebilir Bu genellemede turev grafigi uygun bir cevirme veya dondurmeden sonra orijinal fonksiyonun grafigine en iyi dogrusal yaklasim olan dogrusal bir donusum olarak yeniden yorumlanir Jacobi matrisi bagimsiz ve bagimli degiskenlerin secimiyle verilen bir baza gore bu dogrusal donusumu temsil eden matristir ve bagimsiz degiskenlerin her birine gore kismi turevler alarak hesaplanabilir Birden fazla degiskenin gercel degerli bir fonksiyonu icin Jacobi matrisi gradyan vektorune indirgenir TanimLimit uzerinden tanim Fonksiyonun grafigi siyah teget gecen dogrunun grafigi kirmizi renkte gosterilmistir Teget cizginin egimi fonksiyonun turevine esittir Turevin geometrik tarifi tanim kumesindeki bir a displaystyle a noktasindaki turevini hesaplamak icin tanim kumesinde bu a displaystyle a noktasini iceren bir acik aralik olmalidir Bu kosulda eger limh 0f a h f a h displaystyle lim h rightarrow 0 frac f a h f a h varsa yani limit bir gercel sayiya esitse o zaman f displaystyle f fonksiyonuna a displaystyle a noktasinda turevlenebilir ya da f displaystyle f nin a displaystyle a noktasinda turevi vardir denir O halde f a limh 0f a h f a h veya dfdx a limh 0f a h f a h displaystyle f a lim h rightarrow 0 frac f a h f a h quad text veya quad frac df dx a lim h rightarrow 0 frac f a h f a h yazilir Eger limitin degeri L displaystyle L ise o zaman L displaystyle L ye f displaystyle f nin a displaystyle a noktasindaki turevi denir ve kisa bir gosterimle f a L veya dfdx a L displaystyle f a L quad text veya quad frac df dx a L olarak yazilir Limitin sonsuz olmasi veya var olmamasi durumunda f displaystyle f ye a displaystyle a noktasinda turevlenemez f displaystyle f nin a noktasinda turevi yoktur ya da f displaystyle f a noktasinda turevli degildir denir Yukaridaki limit a displaystyle a civarinda dogrudur Baska bir deyisle h displaystyle h sayisi 0 displaystyle 0 civarinda 0 displaystyle 0 a yaklastikca a h displaystyle a h sayisi a displaystyle a civarinda a displaystyle a ya yaklasir Bu sebepten dolayi eger fonksiyonun tanimli oldugu uc noktalarda turev alma ihtiyaci varsa limit a h displaystyle a h degerinin tanli oldugu taraftan yani soldan limit ya da sagdan limit olarak alinmalidir e d tanimi Limit uzerinden verilen turev tanimi e d limit tanimi uzerinden de yazilabilir Eger limit varsa ve L displaystyle L ye esitse o zaman her e gt 0 displaystyle varepsilon gt 0 icin bir d gt 0 displaystyle delta gt 0 vardir oyle ki butun h lt d displaystyle h lt delta kosulunu saglayan ve sifira esit olmayan her h displaystyle h icin L f a h f a h lt e displaystyle left L frac f a h f a h right lt varepsilon saglanir Burada sol taraftaki dik cubuklarla gosterilen mutlak degerdir Sureklilik ve turevlenebilmeBu fonksiyonun isaretlenen noktada fonksiyon ayni noktada surekli olmadigi icin turevi yoktur Eger bir f displaystyle f fonksiyonu a displaystyle a noktasinda turevlenebilir ise o zaman a displaystyle a noktasinda noktada surekli olmak zorundadir Mesela bir nokta secelim ve bu noktada sicrama gosteren ele alalim Diger deyisle fonksiyon a noktasindan kucuk sayilar icin 0 degerini alacaktir geriye kalan noktalarda ise 1 degerini alacaktir Limitin tanimina bakildigi zaman Eger h displaystyle h pozitif bir sayi ise f a h f a h displaystyle frac f a h f a h ifadesi 0 a esit olacaktir Yani sagdan limit 0 a esittir Eger h displaystyle h negatif bir sayi ise h displaystyle h sayisi negatif kalarak 0 displaystyle 0 a yaklastikca f a h f a h displaystyle frac f a h f a h ifadesi displaystyle infty a dogru gidecektir Yani soldan limit yoktur Mutlak deger fonksiyonu sureklidir ama x 0 da turevli degildir Bu noktadaki teget dogrularin egimleri sagdan ve soldan yaklasimda ayni degere yaklasmazlar Ancak bir fonksiyon tanim kumesindeki her noktada surekli ise bu ozellik fonksiyonun her yerde turevli olacagi anlamina gelmez Mesela mutlak deger fonksiyonu 0 noktasinda sureklidir ama turevli degildir Nedeni 0 da turevi tanimlayan limh 0 0 h 0 h displaystyle lim h rightarrow 0 frac 0 h 0 h limitinin bulunamamasidir Ancak bu fonksiyon 0 displaystyle 0 haricindeki her noktada turevlidir Bir diger ornek olarak x3 displaystyle sqrt 3 x fonksiyonu verilebilir Bu fonksiyon 0 da turevli olmayip da baska her yerde turevli olan bir fonksiyondur Bu fonksiyonun 0 da turevlenebilir olmayisinin nedeni limh 00 h3 03h displaystyle lim h rightarrow 0 frac sqrt 3 0 h sqrt 3 0 h limitinin displaystyle infty yani sonsuz olmasidir Dolayisiyla mutlak deger fonksiyonunun grafigi 0 noktasinda kirikken x3 displaystyle sqrt 3 x fonksiyonunun grafigi 0 da da kirilmasizdir Uygulamada karsilasilan turevlerin cogunun her ya da turevi vardir GosterimBir fonksiyonun turevini yazmanin yaygin bir yollarindan biri Gottfried Wilhelm Leibniz tarafindan 1675 yilinda tanimlanan ve turevi iki mesela dy displaystyle dy ve dx displaystyle dx bolumu olarak gosteren Leibniz gosterimidir Bu kullanim bir fonksiyonu y f x displaystyle y f x olarak yazarken yani bagimli ve bagimsiz degiskenler arasinda fonksiyonel bir iliski gosterilmek istendiginde yaygin bir sekilde kullanilmaktadir Bu gosterimde birinci turev dydx displaystyle frac dy dx ile gosterilir ve y nin x e gore turevi seklinde okunur Bu bicimde yazilan turev gosterimi ayni zamanda bir turev operatorunun verilen bir fonksiyona uygulanmasi olarak da yorumlanabilir Diger deyisle dydx ddxf x displaystyle frac dy dx frac d dx f x yazilirsa bu ayni zamanda f x displaystyle f x uzerinde x e gore turev alma operatoru olan ddx displaystyle frac d dx in uygulanmasi olarak yorumlanabilir Daha yuksek turevler mesela y f x displaystyle y f x in n displaystyle n inci mertebeden turevi su gosterim kullanilarak ifade edilir dnydxn displaystyle frac d n y dx n Ornegin d2ydx2 ddx ddxf x displaystyle frac d 2 y dx 2 frac d dx Bigl frac d dx f x Bigr yazildiginda turevin turevinin alindigini gosterir ve bu tur gosterim uygulamada cok kullanisli hale gelir Bazi alternatiflerinin aksine Leibniz gosterimi paydada turevlendirme icin degiskenin acikca belirtilmesini icerir ve bu da birden fazla birbiriyle iliskili nicelikle calisirken belirsizligi ortadan kaldirir Bir bileske fonksiyonun turevi zincir kurali ile ifade edilir Eger u g x displaystyle u g x ve y f g x displaystyle y f g x ise o zaman dydx dydu dudx displaystyle frac dy dx frac dy du cdot frac du dx olur Turev icin bir diger yaygin gosterim bir fonksiyonun hemen yaninda kesme isaretine benzeyen turev isaretinin kullanilmasidir bu gosterim ayni zamanda Joseph Louis Lagrange a atfen Lagrange gosterimi olaraka da bilinir Birinci turev bu gosterimde f x displaystyle f prime x halinde yazilir ve f nin turevi olarak okunur Benzer sekilde ikinci ve ucuncu turevler su sekilde yazilabilir f x displaystyle f x ve f x displaystyle f x Bu noktadan sonraki daha yuksek mertebeden turevlerin sayisini belirtmek icin bazi yazarlar ust simge olarak Roma rakamlarini kullanirken digerleri sayiyi parantez icine koyar fiv displaystyle f mathrm iv veya f 4 displaystyle f 4 gibi Genel durumda ise f n displaystyle f n kullanilir Newton gosteriminde veya nokta gosteriminde zamana gore turevi temsil etmek icin bir fonksiyon sembolunun uzerine bir nokta yerlestirilir Eger y displaystyle y zamana bagli bir fonksiyonsa o zaman birinci ve ikinci mertebeden turevler sirasiyla y displaystyle dot y ve y displaystyle ddot y biciminde gosterilirler Bu gosterim yalnizca zaman veya yay uzunluguna gore turevler icin kullanilir Kullanimi fizik ve diferansiyel geometrideki diferansiyel denklemlerde de mevcuttur Ancak nokta gosterimi yuksek mertebeden turevler 4 veya daha fazla mertebeden icin yonetilemez hale gelir ve birden fazla bagimsiz degiskenle bas edemez Baska bir gosterim ise diferansiyel operatoru semboluyle gosteren D gosterimidir Bu gosterimde turevi gosterirken D displaystyle D operatoru kullanilir Mesela f x displaystyle f x in birinci turevi gosterilirken Df x displaystyle Df x yazilir Daha yuksek mertebeden turevler icin ust simge kullanilir Dnf x displaystyle D n f x Bu notasyona bazen Euler gosterimi denir ancak bu gosterim Euler tarafindan degil ilk defa kullanilmistir Bu notasyonun kismi tureve yonelik kullanimi da cok elverislidir Kismi turevi belirtmek icin turevlenen degisken bir alt simge ile gosterilir ornegin u f x y displaystyle u f x y fonksiyonu icin x displaystyle x e gore kismi turev Dxu displaystyle D x u veya Dxf x y displaystyle D x f x y olarak yazilabilir Daha yuksek kismi turevler ise ust simgeler veya coklu alt simgelerle gosterilebilir Ornegin yine u f x y displaystyle u f x y fonksiyonu icin Dxyf x y y xf x y textstyle D xy f x y frac partial partial y Bigl frac partial partial x f x y Bigr ve Dx2f x y x xf x y displaystyle textstyle D x 2 f x y frac partial partial x Bigl frac partial partial x f x y Bigr yazilabilir Turev alma kurallariTemel fonksiyonlar icin kurallar Asagida en yaygin temel fonksiyonlarin turevleri icin kurallar verilmistir Burada a displaystyle a gercek bir sayidir ve e displaystyle e dogal logaritmanin tabani ve yaklasik olarak 2 71828 dir Birlesik fonksiyonlar icin kurallar Kuvvet fonksiyonlarinin turevi ddxxa axa 1 displaystyle frac d dx x a ax a 1 Ustel fonksiyon dogal logaritma ve genel tabanli logaritmanin turevi ddxex ex displaystyle frac d dx e x e x ddxax axln a displaystyle frac d dx a x a x ln a a gt 0 displaystyle quad a gt 0 ddxln x 1x displaystyle frac d dx ln x frac 1 x x gt 0 displaystyle quad x gt 0 ddxloga x 1xln a displaystyle frac d dx log a x frac 1 x ln a x a gt 0 displaystyle quad x a gt 0 Trigonometrik fonksiyonlarin turevi ddxsin x cos x displaystyle frac d dx sin x cos x ddxcos x sin x displaystyle frac d dx cos x sin x ddxtan x sec2 x 1cos2 x 1 tan2 x displaystyle frac d dx tan x sec 2 x frac 1 cos 2 x 1 tan 2 x Ters trigonometrik fonksiyonlarin turevi ddxarcsin x 11 x2 displaystyle frac d dx arcsin x frac 1 sqrt 1 x 2 quad 1 lt x lt 1 displaystyle 1 lt x lt 1 icin ddxarccos x 11 x2 displaystyle frac d dx arccos x frac 1 sqrt 1 x 2 quad 1 lt x lt 1 displaystyle 1 lt x lt 1 icin ddxarctan x 11 x2 displaystyle frac d dx arctan x frac 1 1 x 2 Basit islemlerle elde edilmis fonksiyonlar icin turevler Asagida temel fonksiyonlardan basit aritmetik islemler veya bileske yoluyla elde edilmis fonksiyonlarin turevini hesaplamak icin bilinen en temel kurallardan bazilari verilmistir Bu amacla f displaystyle f ve g displaystyle g fonksiyon olsun Sabit fonksiyon eger f displaystyle f sabitse o zaman her x displaystyle x icin f x 0 displaystyle f x 0 af bg af bg displaystyle alpha f beta g alpha f beta g her f displaystyle f ve g displaystyle g fonksiyonu ve butun a displaystyle alpha ve b displaystyle beta gercel sayilari icin Carpma kurali fg f g fg displaystyle fg f g fg her f displaystyle f ve g displaystyle g fonksiyonu icin Ozel bir durum olarak her a displaystyle alpha sayisi icin af af displaystyle alpha f alpha f olur cunku is a displaystyle alpha sayisi sabittir ve a f 0 f 0 displaystyle alpha f 0 cdot f 0 olur dd Bolme kurali fg f g fg g2 displaystyle left frac f g right frac f g fg g 2 her f displaystyle f ve g 0 displaystyle g neq 0 olan her g displaystyle g fonksiyonu icin Bileske fonksiyonlar icin Zincir kurali Eger f x h g x displaystyle f x h g x ise o zaman f x h g x g x displaystyle f x h g x cdot g x Ornek f x x4 sin x2 ln x ex 7 displaystyle f x x 4 sin left x 2 right ln x e x 7 olsun O zaman f x 4x 4 1 d x2 dxcos x2 d ln x dxex ln x d ex dx 0 4x3 2xcos x2 1xex ln x ex displaystyle begin aligned f x amp 4x 4 1 frac d left x 2 right dx cos left x 2 right frac d left ln x right dx e x ln x frac d left e x right dx 0 amp 4x 3 2x cos left x 2 right frac 1 x e x ln x e x end aligned Burada ikinci terim zincir kurali kullanilarak ve ucuncu terim carpim kurali kullanilarak hesaplanmistir Ayrica x2 displaystyle x 2 x4 displaystyle x 4 sin x displaystyle sin x ln x displaystyle ln x ex displaystyle e x ve sabit 7 displaystyle 7 gibi temel fonksiyonlarin turevleri de kullanildi Yuksek mertebeden turevlerDaha yuksek mertebeden turevler bir fonksiyonun tekrar tekrar turevlenmesinin sonucudur f displaystyle f turevlenebilir bir fonksiyon ise f displaystyle f nin birinci turevi fonksiyonun turevidir ve f displaystyle f ile gosterilir f displaystyle f nin turevi ise f displaystyle f nin ikinci turevidir ve f displaystyle f ile gosterilir f displaystyle f nin turevi ise f displaystyle f nin ucuncu turevidir ve f displaystyle f ile gosterilir Bu surec tekrarlanarak eger turev varsa fonksiyonun n 1 inci turevi baslangicta alinan fonksiyonun n inci turevidir Gosterim kisminda verilen bilgiye de dayanarak f n 1 displaystyle f n 1 in turevi f displaystyle f nin n inci turevidir ve f n displaystyle f n olarak gosterilir Ck fonksiyon Arka arkaya k displaystyle k tane turevi hesaplanabilen fonksiyonlara k displaystyle k kere turevli ya da k kere turevlenebilir fonksiyonlar denilir Eger k displaystyle k inci turev ayni zamanda surekli ise o zaman bu fonksiyon Ck displaystyle C k sinifina aittir Daha matematiksel bir ifadeyle bir W displaystyle Omega kumesi uzerinde tanimli bir f displaystyle f fonksiyonu verilsin Eger bu fonksiyon k displaystyle k kere turevlenebilen ve k displaystyle k inci turevi surekli olan bir fonksiyon ise o zaman f Ck W displaystyle f in C k Omega yazilir ve fonksiyona k displaystyle k kere surekli turevlenebilir fonksiyon denir C fonksiyon Tanim kumesindeki butun noktalarda sonsuz kere turevli olan yani keyfi bir k displaystyle k pozitif bir tam sayisi icin k displaystyle k inci turevi var olan bir fonksiyona duzgun fonksiyon ya da sonsuz turevli fonksiyon denir Diger deyisle k displaystyle k kere turevlenme sayisinda herhangi bir sinir yoksa yani fonksiyon icin hesaplanabilen yuksek mertebeden herhangi bir turevinin turevi yine hesaplanabiliyorsa bu fonksiyona sonsuz kere turevli ya da duzgun fonksiyon denir Duzgun bir fonksiyonun turevlenebilirlik sinifini gostermek icin C displaystyle C infty gosterimi kullanilir Daha matematiksel bir ifadeyle bir W displaystyle Omega kumesi uzerinde tanimli bir f displaystyle f fonksiyonu verilsin Eger bu fonksiyon sonsuz turevlenebilir bir fonksiyon ise o zaman f C W displaystyle f in C infty Omega yazilir Diger boyutlarda turevVektor degerli fonksiyonlar Vektor degerli bir fonksiyon y displaystyle mathbf y gercel sayilar uzerindeki gercel bir degiskeni bir Rn displaystyle mathbb R n vektor uzayindaki vektorlere gonderir Bir vektor degerli fonksiyon koordinat fonksiyonlarina ayrilabilir yani y y1 t y2 t yn t displaystyle mathbf y y 1 t y 2 t dots y n t yazilabilir R2 displaystyle mathbb R 2 ve R3 displaystyle mathbb R 3 deki bu fonksiyonlarin guzel bir ornegidir Bu fonksiyonlarin koordinat fonksiyonlarinin here biri gercel degerli oldugu icin yukarida verilen turev tanimlari her biri icin gecerlidir O zaman y t displaystyle mathbf y t nin turevi y t displaystyle mathbf y t inin koordinate fonksiyonlarinin turevlerinden olusan bir vektor olur ki buna da tanjant ya da teget vektor denilir Kismi turev Kismi turev cok degiskenli bir fonksiyonun sadece ilgili degiskeni sabit degilken alinan turevdir Bu tarz turevleri iceren denklemlere kismi diferansiyel denklem denir Kismi turevin tanimi z Rn Rn R displaystyle z mathbb R n times mathbb R n to mathbb R z f x1 x2 xm xn displaystyle z f x 1 x 2 x m x n seklinde tanimlanan n tane bagimsiz degiskene bagli z fonksiyonunun diger degiskenler sabit tutularak herhangi bir degiskendeki Dxm displaystyle Delta x m degisimine karsilik fonksiyonun degisim hizi DzDxm f x1 x2 xm Dxm xn f x1 x2 xm xn Dxm displaystyle frac Delta z Delta x m frac f x 1 x 2 x m Delta x m x n f x 1 x 2 x m x n Delta x m Dxm h displaystyle Delta x m h z xm limh 0f x1 x2 xm h xn f x1 x2 xm xn h displaystyle frac partial z partial x m underset h to 0 mathop lim frac f x 1 x 2 x m h x n f x 1 x 2 x m x n h ifadesine z displaystyle z fonksiyonunun xm displaystyle x m degiskenine gore kismi turevi denir f xm fxm Dxmf z xm zxm displaystyle frac partial f partial x m f x m D x m f frac partial z partial x m z x m seklinde gosterilir z f x y displaystyle z f left x y right ise fx x y limh 0f x h y f x y h displaystyle f x left x y right underset h to 0 mathop lim frac f left x h y right f left x y right h fy x y limk 0f x y k f x y k displaystyle f y left x y right underset k to 0 mathop lim frac f left x y k right f left x y right k Ornek f x y x3 x2y y3fx x3 x x2y x y3 xfx 3x2 2xy 0fx 3x2 2xy displaystyle begin aligned amp f x y x 3 x 2 y y 3 amp f x left x 3 right x left x 2 y right x left y 3 right x amp f x 3 x 2 2xy 0 amp f x 3 x 2 2xy end aligned Yonlu turev Eger f bir Rn uzerinde gercek degerli fonksiyon ise yonu icinde f in kismi turevi icinde cesitli olcmeler ise mesela f bir x ve y fonksiyonunun x yonu ve y yonu icinde f nin kismi turevinde cesitli olcmeler ise buna yonlu turev denir Bununla birlikte kosegen cizgi y x boyunca gibi herhangi diger yon icinde f in yonlu olcu cesitleri yoktur Burada yonlu turev olcusu kullaniliyor v v1 vn displaystyle mathbf v v 1 ldots v n bir vektorse vnin yonu icinde fin yonlu turevinin x noktasinda siniridir Dvf x limh 0f x hv f x h displaystyle mathrm D mathbf v f mathbf x lim h rightarrow 0 frac f mathbf x h mathbf v f mathbf x h Bazi durumlarda bu vektorun uzunlugunu degistirme sonrasi yon turevi hesaplamak veya tahmin etmek daha kolay olabilir Genellikle bu bir birim vektor yonunde bir yonde turevinin hesaplanmasi icinde sorunu acmak icin yapilir Bunun nasil calistigini gormek icin bunu v lu varsayalim h k l fark katsayisi icinde yerine konur Aradaki fark katsayisi f x k l lu f x k l l f x ku f x k displaystyle frac f mathbf x k lambda lambda mathbf u f mathbf x k lambda lambda cdot frac f mathbf x k mathbf u f mathbf x k Bu u sirasiyla fin yonlu turevi icin l zaman icinde farkli katsayisidir Dahasi sifira yonelen k olarak alinan limit olarak ayni h ve k icin herhangi digerinin carpimidir Bunun icin Dv f lDu f Bu nedenle yeniden olceklendirme ozelligi yonlu turevler sik sik sadece birim vektorler icin kabul edilir Eger f in tum kismi turevleri var ve x de surekli ve formulu ile v yonunde f icinde belirlenen yonlu turev ise Dvf x j 1nvj f xj displaystyle mathrm D mathbf v f boldsymbol x sum j 1 n v j frac partial f partial x j Bu taniminin bir sonucudur Bu yonlu turev asagida v icinde Bu da Dv w f Dv f Dw f demektir Ayni tanim ayrica f oldugunda Rm icindeki degerleri ile bir fonksiyondur Yukardaki tanim vektorlerin her bir bileseni icin uygulanir Bu durum icinde yonlu turev Rm icinde bir vektordur Toplam turev Bir f displaystyle f fonksiyonu Rn displaystyle mathbb R n deki acik bir kumeden Rm displaystyle mathbb R m e tanimlanmis bir fonksiyonsa f displaystyle f nin secilen bir noktadaki ve yondeki yonlu turevi f displaystyle f nin yine ayni noktada ve ayni yonde en iyi dogrusal yaklasimidir Ancak n gt 1 displaystyle n gt 1 ise yonlu turev f displaystyle f nin davranisi hakkinda tam bir aciklama veremez Toplam turevi bu baglamda tam bir aciklama saglamaktadir Yani bir a displaystyle mathbf a vektorunden baslayan herhangi bir v displaystyle mathbf v vektoru icin asagidaki dogrusal yaklasim saglanir f a v f a f a v displaystyle f mathbf a mathbf v approx f mathbf a f mathbf a mathbf v Benzer bir sekilde tek degiskenli fonksiyonlar icin tanimlana turevde de f a displaystyle f mathbf a buradaki yaklasim hatasini olabildigince kucuk yapacak sekilde secilir f displaystyle f nin bir a displaystyle mathbf a noktasindaki toplam turevi f a Rn Rm displaystyle f mathbf a colon mathbb R n to mathbb R m limh 0 f a h f a f a h h 0 displaystyle lim mathbf h to 0 frac lVert f mathbf a mathbf h f mathbf a f mathbf a mathbf h rVert lVert mathbf h rVert 0 olacak sekilde biricik olarak tanimlanan dogrusal bir donusumdur Burada h displaystyle mathbf h Rn displaystyle mathbb R n icinde bir vektordur ancak f a h displaystyle f mathbf a mathbf h Rm displaystyle mathbb R m icinde bir vektordur Toplam turev eger bir noktada varsa o zaman yine ayni noktada butun kismi turevler ve yonlu turevler de vardir Bu halde butun v displaystyle mathbf v vektoru icin f displaystyle f nin v displaystyle mathbf v yonundeki yonlu turevi f a v displaystyle f mathbf a mathbf v olur Eger f displaystyle f koordinat fonksiyonlari cinsinden yani f f1 f2 fm displaystyle f f 1 f 2 dots f m olacak sekilde yazilirsa o zaman toplam turev kismi turevlerin matrisi olarak ifade edilebilir f a Jaca fi xj ij displaystyle f mathbf a operatorname Jac mathbf a left frac partial f i partial x j right ij Bu matrise f displaystyle f nin a displaystyle a noktasindaki Jacobi matrisi denir Ayrica bakinizIntegralNotlar Nadiren de olsa bazi kitap ve tezlerde puruzsuz fonksiyon kullanimi da vardir Kaynakca
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans