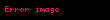Matematik alanında, toplam veya genel toplam olarak sonuçlanan, toplananlar ya da toplamalar diye adlandırılan bir sayı dizisinin eklenme sürecine toplam/toplama denir. Sayıların yanı sıra, fonksiyonlar, vektörler, matrisler, polinomlar ve genelde "+" işareti ile tanımlanmış işleme sahip diğer tüm matematiksel nesne türleri de toplanabilir.
Sonsuz diziler üzerinde gerçekleştirilen toplam işlemleri seriler olarak isimlendirilir. Bu tür toplamlar, limit kavramını barındırır ve bu makale kapsamında değerlendirilmemektedir.
Belirli bir diziye ilişkin toplam, ardışık toplama işlemleri ile tanımlanır. Örnek olarak, [1, 2, 4, 2] elemanlarının toplamı 1 + 2 + 4 + 2 şeklinde ifade edilir ve bu işlem sonucunda 9 değeri elde edilir; bir diğer deyişle 1 + 2 + 4 + 2 = 9. Toplama işleminin birleşme ve değişme özellikleri dolayısıyla, işlem sırasının değişmesinden bağımsız olarak sonuç değişmez ve parantez kullanımına gerek kalmaz. Tek bir eleman içeren bir dizinin toplamı, o elemanın kendisidir. Eleman barındırmayan boş bir dizinin toplamı ise, konvansiyonel olarak sıfır olarak kabul edilir.
Genellikle, bir dizinin elemanları, bu elemanların dizideki konumlarına bağlı olarak belirli bir düzen içinde bir fonksiyon olarak tanımlanmaktadır. Basit düzenlerde, uzun dizilerdeki toplamlar, birçok toplananın üç nokta ile yer değiştirmesi şeklinde ifade edilebilir. Örnek olarak, ilk yüz doğal sayının toplamı 1 + 2 + 3 + 4 + ⋯ + 99 + 100 biçiminde belirtilebilir. Diğer durumlarda, toplama işlemi Σ notasyonu ile ifade edilir; burada , büyütülmüş bir sigma harfine işaret eder. İlk n doğal sayının toplamı, örneğin, şeklinde tanımlanabilir.
Uzun toplam işlemleri ve değişken uzunlukta olan toplam işlemleri için (üç nokta veya Σ notasyonu ile ifade edilenler), sonucun ulaşmak sık karşılaşılan bir problemdir. Örneğin,
Bu tür formüllerin her zaman bulunabilir olmadığı durumlar olmakla birlikte, birçok toplam formülü tespit edilmiştir; bu makalede yer alan bölümler, en yaygın ve temel formüllerden bazılarını içermektedir.
Notasyon
Büyük-sigma notasyonu

Matematiksel notasyon, birçok benzer terimin toplamını kompakt bir şekilde temsil eden bir sembol kullanır: toplama sembolü, 
şeklinde tanımlanır; burada i toplama endeksi olarak adlandırılır; ai toplamın her terimini temsil eden dizinli değişkendir; m toplamın alt sınırı ve n toplamın üst sınırıdır. Toplama sembolünün altında yer alan "i = m" ifadesi, indeks i'nin m ile başladığını belirtir. İndeks, i, her ardışık terim için bir arttırılarak, i = n olduğunda durur.
Bu ifade, "i = m ile başlayıp n ile biten değerlerin toplamı" şeklinde okunur.
Karelerin toplamını gösteren bir örnek aşağıda verilmiştir:
Genelde, bir toplama işleminin indeksi olarak belirsizlik oluşturmayacak şekilde herhangi bir değişken kullanılabilir. Toplama indeksi olarak en sık kullanılan semboller arasında 
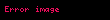


Alternatif bir yaklaşım olarak, eğer bağlam yeterince açıksa, toplama işlemi tanımından indeks ve sınırlar bazen çıkarılabilir. Bu durum, özellikle indeksin 1'den n'ye uzandığı hallerde uygulanır. Örnek olarak, aşağıdaki ifade kullanılabilir:
Bu gösterimlerin çeşitli genellemeleri sıklıkla tercih edilir; burada, belirlenen keyfi bir mantıksal koşul altında, bu koşulu karşılayan tüm değerlerin toplamı gerçekleştirilmek üzere tasarlanmıştır. Örnek olarak:



küme 





Çok sayıda sigma işaretinin kullanımı genelleştirilebilir şekilde ifade edilebilir. Örnek olarak,
ifadesi,
ile aynı anlamı taşır.
Dizi çarpımı için benzer bir notasyon kullanılır; burada, Yunan alfabesinin büyük harfi pi'nin genişletilmiş formu olan 

Özel durumlar
İki sayıdan daha az sayıda sayı ile toplam işlemi mümkündür:
- Eğer toplamda yalnızca bir toplama elemanı
bulunuyorsa, bu durumda elde edilen toplam
değeridir.
- Toplamda hiçbir toplama elemanı bulunmamaktaysa, elde edilen toplam sıfır olacaktır, çünkü sıfır toplama işlemi için birim eleman özelliği taşır. Bu durum, olarak adlandırılır.
Bu türden niteliksiz durumlar genellikle toplama notasyonu özel bir durumda geçersiz bir sonuç ürettiğinde tercih edilir. Örneğin, tanımda 

Resmi tanım
Toplam işlemi, yinelemeli olarak şöyle tanımlanabilir:
,
durumunda;
,
durumunda.
Ölçü teorisi notasyonu
Ölçü ve integrasyon teorileri çerçevesinde, bir toplam belirli integral şeklinde gösterilebilir,
burada 



Sonlu farklar kalkülüsü
Verilen bir f fonksiyonunun tam sayılar üzerinde tanımlandığı ve [m, n] içerisinde yer aldığı durumda, aşağıdaki eşitlik geçerlidir:
Bu durum, olarak tanımlanır ve sonlu farklar hesabı içindeki kalkülüsün temel teoremine benzer bir yaklaşım sunar. Bu teorem, şu şekilde ifade edilir:
burada
f fonksiyonunun türevi olarak belirtilir.
Yukarıdaki eşitliğin bir uygulama örneği şöyledir:
binom teoremi yardımıyla, bu ifade şu şekilde dönüştürülebilir:
Yukarıda verilen formül, aşağıda tanımı yapılan 
burada f, sıfır veya daha büyük tamsayılar üzerinde tanımlanmış bir fonksiyondur. Bu bağlamda, belirtilen f fonksiyonu için görev, f'nin , yani 


Bu tip toplamlar için her zaman bir mevcut olmayabilir; fakat , 
Belirli integrallerle yaklaşım
Birçok yaklaşım (İng. approximation), toplamlar ile integraller arasında kurulan ve herhangi bir f fonksiyonu için geçerli olan şu bağlantı ile sağlanabilir:
ve herhangi bir f fonksiyonu için:
Daha kapsamlı yaklaşımlar için, incelenebilir.
Toplama işlemi, indeksin bir integral fonksiyonu tarafından verilmiş veya bu yöntemle elde edilmişse, toplama işlemi ilgili belirli integralin tanımında yer alan bir Riemann toplamı olarak değerlendirilebilir. Bu bağlamda, örneğin
beklenir; zira sağ tarafta yer alan ifade, sol tarafta yer alan ifadenin 
Özdeşlikler
Aşağıdaki formüller, sonlu toplamlar için geçerlidir.
Genel özdeşlikler
(dağılma)
(Değişme özelliği ve birleşme özelliği)
(indeks öteleme)
(ifadesi, sonlu bir küme A üzerinden başka bir küme B'ye bir bijeksiyon σ aracılığıyla gerçekleşen bir eşleme durumunda geçerlidir; bu durum, önceki formülü daha genel bir bağlama taşır.)
(Birleşme özelliğini kullanarak toplamın parçalanması)
(bir önceki formülün bir başka formu)
(ifadesinde, serinin ilk elemanından son elemanına kadar olan toplamı, serinin son elemanından başlayıp ilk elemanına doğru olan toplamına eşdeğerdir. Bu durum, toplamın simetrisini ve ters çevrilebilirliğini vurgular.)
(bir önceki formülün bir başka formu)
(değişme özelliği ve birleşme özelliği)
(değişme ve birleşme özelliğinin bir başka uygulaması)
ifadesi, bir toplamın tek ve çift bileşenlerine ayrılmasını ifade eder, burada çift sayılı indeksler için bu ayrım yapılmaktadır. Bu yöntem, toplamın daha sistemli bir şekilde incelenmesini sağlar.
(toplamın tek indeks ile çift ve tek unsurlarına ayrılması)
(Dağılma özelliği)
(ifadesi, dağılma özelliğinin, çarpım işlemlerinin faktörler olarak ifade edilmesine olanak tanıdığını gösterir. Bu durum, iki farklı serinin çarpımının, her bir serinin toplamlarının çarpımına eşdeğer olduğunu ifade eder. Bu yöntem, serilerin çarpımını basitleştirerek analiz etmeyi kolaylaştırır.)
(ifadesi, bir çarpım işleminin logaritmasının, bu çarpımda yer alan bireysel terimlerin logaritmalarının toplamına denk olduğunu belirtir. Bu özellik, çarpım işlemlerinin logaritmik ifadesini analiz etmek için matematiksel bir kolaylık sağlar ve çarpım işlemlerinin logaritmalarını basitleştirerek toplama dönüştürmeyi mümkün kılar.)
(ifadesinin
tabanında üssü,
'den
'ye kadar olan
fonksiyonunun her bir değeri için
'nin alınmış üslerinin çarpımına eşittir)
(ifadesi,
üzerinde tanımlanmış herhangi bir
fonksiyonu için geçerlidir.)
Aritmetik dizilerin üs alınması ve logaritma hesaplamaları
ifadesi, c sabiti i'den bağımsız olduğunda her n için geçerlidir.
(n doğal sayının toplamı, bu sayılar en basit aritmetik diziyi oluşturur.):52
(tek doğal sayıların toplamı)
(çift doğal sayıların toplamı)
(bir dizi logaritmanın toplamı, bu değerlerin çarpımının logaritması ile eşdeğerdir)
(kare sayıların toplamı, ilgilidir.) :52
( göre) :52
Daha geniş bir perspektiften, 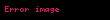
Bu ifadede, 

Üs değerlerindeki toplam indeksleri
Aşağıdaki toplam ifadelerde, a değerinin 1'den farklı olduğu kabul edilmektedir.
(bir toplamı olarak)
(a = 1/2 için özel bir durum)
(geometrik dizinin a'ya göre türetilmiş ifadesinin a ile çarpılması sonucu)
- (bir toplamı)
Binom katsayıları ve faktöriyeller
Binom katsayılarını içeren pek çok toplam özdeşliği mevcuttur; adlı eserin bir bölümü bu temel tekniklerin incelenmesine özel olarak ayrılmıştır. Bu özdeşliklerin en temel olanlarından bazıları aşağıda sunulmuştur.
Binom teoremi bağlamında
ifadesi binom teoremini temsil eder.
ifadesi, a = b = 1 durumunda, binom katsayılarının toplamının özel bir halidir.
, ifadesi p = a = 1 − b durumunda olup,
aralığında binom dağılımının toplam değerlerini gösterir.
ifadesi, a = b = 1 durumunda, binom teoreminin türetilmiş formunu verir.
ifadesi, a = b = 1 durumunda, binom teoreminin integral alınmış formunun bir değerini ifade eder.
Permütasyon sayıları bağlamında
Aşağıda verilen toplamlarda, 
ifadesi, verilen kapsamdaki permutasyon sayılarının bir toplamını ifade eder.
ifadesi, belirli bir kapsamdaki ardışık sayıların çarpımlarının toplamını ve bu toplamın matematiksel ifadesini gösterir.
ifadesi, faktöriyel ve permutasyon sayılarının toplamlarını hesaplar ve bu toplamların bir tam sayıya yuvarlanmış halini, yani kullanarak ifade eder.
Diğerleri
Harmonik sayılar
ifadesi, n'inci temsil eder.
ifadesi, bir ifade eder.
Büyüme hızları
Aşağıdaki ifadeler, çeşitli fonksiyonların büyüme hızlarını gösteren yaklaşık değerlerdir (theta notasyonu kullanılarak):
ifadesi, reel c değeri −1'den büyükse geçerlidir.
.
ifadesi, reel c değeri 1'den büyükse geçerlidir.
ifadesi, negatif olmayan reel c değeri için geçerlidir.
ifadesi, negatif olmayan reel c, d değerleri için geçerlidir.
ifadesi, negatif olmayan reel b > 1, c, d değerleri için geçerlidir.
Tarihçe
- 1675 yılında, Gottfried Wilhelm Leibniz, 'a gönderdiği bir mektupta, farklı diferansiyellerin toplamını göstermek için ∫ sembolünü önermiş ve bu öneri Latince 'calculus summatorius' (toplam hesabı) teriminden dolayı S şeklini almıştır. Bu sembolün integral olarak yeniden adlandırılması, sonradan Johann Bernoulli ile olan yazışmalar sırasında gerçekleşmiştir.
- 1755 yılında, sigma toplam sembolü, Leonhard Euler'ın adlı çalışmasında ilk kez kaydedilmiştir. Euler sembolü aşağıdaki denklikler için kullanmıştır:
- 1772 yılında, Σ and Σn sembolünün kullanımı Lagrange tarafından kayıt altına alınmıştır.
- 1823 yılında, büyük 'S' harfi, seriler için bir toplam sembolü olarak kullanılmış ve bu kullanım geniş çapta yaygınlaşmıştır.
- 1829 yılında, Σ toplam sembolü, Fourier ve C. G. J. Jacobi tarafından kullanılmış ve bu kullanım belgelenmiştir. Fourier'in metodolojisi, belirli alt ve üst sınırlar dahilinde değerlendirmeleri içermektedir. Örneğin:
ifadesi, sonsuz bir serinin toplamını ve bu toplamın nasıl ele alınacağını gösterir. Bu tür bir ifade, matematiksel analizde sıkça karşılaşılan karmaşık seri hesaplamalarını temsil eder.
Notlar
- ^ Detaylar için üçgensel sayı maddesine göz atınız.
- ^ Toplama notasyonu ve toplamlarla aritmetik üzerine detaylı bir inceleme için bkz. Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994). "Chapter 2: Sums". Concrete Mathematics: A Foundation for Computer Science (PDF) (2. bas.). Addison-Wesley Professional. ISBN .[]
- ^ i sayısı
ile karıştırılma ihtimali bulunmadığında
- ^ Serbest değişkenlerin ve bağlı değişkenlerin ismi, tanım itibariyle önemsizdir; ancak, karışıklık riski olduğunda genellikle alfabe ortasındaki harfler (
'den
'ya kadar) tam sayıları ifade etmek için kullanılır. Örneğin, yorumlamada kesin bir netlik olmasına karşın, birçok matematikçi yukarıdaki formüllerde
yerine
kullanılmasını muhtemelen anlaşılması güç bulabilir.
Kaynakça
- ^ "Summation Notation". www.columbia.edu. 31 Temmuz 2020 tarihinde kaynağından . Erişim tarihi: 16 Ağustos 2020.
- ^ a b c d Handbook of Discrete and Combinatorial Mathematics, Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, .
- ^ a b "Calculus I - Summation Notation". tutorial.math.lamar.edu. 11 Ağustos 2020 tarihinde kaynağından . Erişim tarihi: 16 Ağustos 2020.
- ^ Burton, David M. (2011). The History of Mathematics: An Introduction. 7th. McGraw-Hill. s. 414. ISBN .
- ^ Leibniz, Gottfried Wilhelm (1899). Gerhardt, Karl Immanuel (Ed.). Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band. Berlin: Mayer & Müller. s. 154.
- ^ a b Cajori (1929), ss. 181-182.
- ^ a b c d Cajori (1929), s. 61.
- ^ Euler, Leonhard (1755). Institutiones Calculi differentialis (Latin). Petropolis. s. 27. 4 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 28 Nisan 2024.
- ^ Lagrange, Joseph-Louis (1867–1892). Oeuvres de Lagrange. Tome 3 (Fransızca). Paris. s. 451. 8 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 28 Nisan 2024.
- ^ Mémoires de l'Académie royale des sciences de l'Institut de France pour l'année 1825, tome VIII (Fransızca). Paris: Didot. 1829. ss. 581-622.
- ^ Fourier, Jean-Baptiste Joseph (1888–1890). Oeuvres de Fourier. Tome 2 (Fransızca). Paris: Gauthier-Villars. s. 149. 7 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 28 Nisan 2024.
Bibliografya
- Cajori, Florian (1929). A History Of Mathematical Notations Volume II. Open Court Publishing. ISBN .
Dış bağlantılar
![image]() Wikimedia Commons'ta Summation ile ilgili çoklu ortam belgeleri bulunur
Wikimedia Commons'ta Summation ile ilgili çoklu ortam belgeleri bulunur
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematik alaninda toplam veya genel toplam olarak sonuclanan toplananlar ya da toplamalar diye adlandirilan bir sayi dizisinin eklenme surecine toplam toplama denir Sayilarin yani sira fonksiyonlar vektorler matrisler polinomlar ve genelde isareti ile tanimlanmis isleme sahip diger tum matematiksel nesne turleri de toplanabilir Sonsuz diziler uzerinde gerceklestirilen toplam islemleri seriler olarak isimlendirilir Bu tur toplamlar limit kavramini barindirir ve bu makale kapsaminda degerlendirilmemektedir Belirli bir diziye iliskin toplam ardisik toplama islemleri ile tanimlanir Ornek olarak 1 2 4 2 elemanlarinin toplami 1 2 4 2 seklinde ifade edilir ve bu islem sonucunda 9 degeri elde edilir bir diger deyisle 1 2 4 2 9 Toplama isleminin birlesme ve degisme ozellikleri dolayisiyla islem sirasinin degismesinden bagimsiz olarak sonuc degismez ve parantez kullanimina gerek kalmaz Tek bir eleman iceren bir dizinin toplami o elemanin kendisidir Eleman barindirmayan bos bir dizinin toplami ise konvansiyonel olarak sifir olarak kabul edilir Genellikle bir dizinin elemanlari bu elemanlarin dizideki konumlarina bagli olarak belirli bir duzen icinde bir fonksiyon olarak tanimlanmaktadir Basit duzenlerde uzun dizilerdeki toplamlar bircok toplananin uc nokta ile yer degistirmesi seklinde ifade edilebilir Ornek olarak ilk yuz dogal sayinin toplami 1 2 3 4 99 100 biciminde belirtilebilir Diger durumlarda toplama islemi S notasyonu ile ifade edilir burada textstyle sum buyutulmus bir sigma harfine isaret eder Ilk n dogal sayinin toplami ornegin i 1ni textstyle sum i 1 n i seklinde tanimlanabilir Uzun toplam islemleri ve degisken uzunlukta olan toplam islemleri icin uc nokta veya S notasyonu ile ifade edilenler sonucun ulasmak sik karsilasilan bir problemdir Ornegin i 1ni n n 1 2 displaystyle sum i 1 n i frac n n 1 2 Bu tur formullerin her zaman bulunabilir olmadigi durumlar olmakla birlikte bircok toplam formulu tespit edilmistir bu makalede yer alan bolumler en yaygin ve temel formullerden bazilarini icermektedir NotasyonBuyuk sigma notasyonu Toplama sembolu Matematiksel notasyon bircok benzer terimin toplamini kompakt bir sekilde temsil eden bir sembol kullanir toplama sembolu textstyle sum dik buyuk Yunan harfi sigma nin buyuk harfli formudur Bu i mnai am am 1 am 2 an 1 an displaystyle sum i mathop m n a i a m a m 1 a m 2 cdots a n 1 a n seklinde tanimlanir burada i toplama endeksi olarak adlandirilir ai toplamin her terimini temsil eden dizinli degiskendir m toplamin alt siniri ve n toplamin ust siniridir Toplama sembolunun altinda yer alan i m ifadesi indeks i nin m ile basladigini belirtir Indeks i her ardisik terim icin bir arttirilarak i n oldugunda durur Bu ifade i m ile baslayip n ile biten degerlerin toplami seklinde okunur Karelerin toplamini gosteren bir ornek asagida verilmistir i 36i2 32 42 52 62 86 displaystyle sum i 3 6 i 2 3 2 4 2 5 2 6 2 86 Genelde bir toplama isleminin indeksi olarak belirsizlik olusturmayacak sekilde herhangi bir degisken kullanilabilir Toplama indeksi olarak en sik kullanilan semboller arasinda i displaystyle i j displaystyle j k displaystyle k ve n displaystyle n yer alir bunlardan sonuncusu siklikla toplamalarin ust sinirini belirtmek icin tercih edilir Alternatif bir yaklasim olarak eger baglam yeterince aciksa toplama islemi tanimindan indeks ve sinirlar bazen cikarilabilir Bu durum ozellikle indeksin 1 den n ye uzandigi hallerde uygulanir Ornek olarak asagidaki ifade kullanilabilir ai2 i 1nai2 displaystyle sum a i 2 sum i 1 n a i 2 Bu gosterimlerin cesitli genellemeleri siklikla tercih edilir burada belirlenen keyfi bir mantiksal kosul altinda bu kosulu karsilayan tum degerlerin toplami gerceklestirilmek uzere tasarlanmistir Ornek olarak 0 k lt 100f k displaystyle sum 0 leq k lt 100 f k k 099f k textstyle sum k 0 99 f k gosteriminin alternatif bir bicimidir ve belirlenen aralikta yer alan tum tam sayilar k displaystyle k icin f k displaystyle f k degerlerinin toplamini temsil eder Ayni sekilde x Sf x displaystyle sum x mathop in S f x kume S displaystyle S icerisindeki tum elemanlar x displaystyle x icin f x displaystyle f x toplamini ifade eder ve d n m d displaystyle sum d n mu d n displaystyle n i bolen pozitif tamsayilar d displaystyle d uzerinden m d displaystyle mu d toplamini gosterir Cok sayida sigma isaretinin kullanimi genellestirilebilir sekilde ifade edilebilir Ornek olarak i j displaystyle sum i j ifadesi i j displaystyle sum i sum j ile ayni anlami tasir Dizi carpimi icin benzer bir notasyon kullanilir burada Yunan alfabesinin buyuk harfi pi nin genisletilmis formu olan textstyle prod textstyle sum isaretinin yerine tercih edilir Ozel durumlar Iki sayidan daha az sayida sayi ile toplam islemi mumkundur Eger toplamda yalnizca bir toplama elemani x displaystyle x bulunuyorsa bu durumda elde edilen toplam x displaystyle x degeridir Toplamda hicbir toplama elemani bulunmamaktaysa elde edilen toplam sifir olacaktir cunku sifir toplama islemi icin birim eleman ozelligi tasir Bu durum olarak adlandirilir Bu turden niteliksiz durumlar genellikle toplama notasyonu ozel bir durumda gecersiz bir sonuc urettiginde tercih edilir Ornegin tanimda n m displaystyle n m oldugunda toplam icerisinde yalnizca bir eleman bulunur n m 1 displaystyle n m 1 oldugunda ise herhangi bir eleman bulunmamaktadir Resmi tanimToplam islemi yinelemeli olarak soyle tanimlanabilir i abg i 0 displaystyle sum i a b g i 0 b lt a displaystyle b lt a durumunda i abg i g b i ab 1g i displaystyle sum i a b g i g b sum i a b 1 g i b a displaystyle b geqslant a durumunda Olcu teorisi notasyonuOlcu ve integrasyon teorileri cercevesinde bir toplam belirli integral seklinde gosterilebilir k abf k a b f dm displaystyle sum k mathop a b f k int a b f d mu burada a b displaystyle a b a displaystyle a dan b displaystyle b ye kadar olan tam sayilarin altkumesini ifade eder ve m displaystyle mu tam sayilar uzerinden alinan Sonlu farklar kalkulusuVerilen bir f fonksiyonunun tam sayilar uzerinde tanimlandigi ve m n icerisinde yer aldigi durumda asagidaki esitlik gecerlidir f n f m i mn 1 f i 1 f i displaystyle f n f m sum i m n 1 f i 1 f i Bu durum olarak tanimlanir ve sonlu farklar hesabi icindeki kalkulusun temel teoremine benzer bir yaklasim sunar Bu teorem su sekilde ifade edilir f n f m mnf x dx displaystyle f n f m int m n f x dx burada f x limh 0f x h f x h displaystyle f x lim h to 0 frac f x h f x h f fonksiyonunun turevi olarak belirtilir Yukaridaki esitligin bir uygulama ornegi soyledir nk i 0n 1 i 1 k ik displaystyle n k sum i 0 n 1 left i 1 k i k right binom teoremi yardimiyla bu ifade su sekilde donusturulebilir nk i 0n 1 j 0k 1 kj ij displaystyle n k sum i 0 n 1 biggl sum j 0 k 1 binom k j i j biggr Yukarida verilen formul asagida tanimi yapilan D displaystyle Delta icin tersine cevirme isleminde genellikle tercih edilir D f n f n 1 f n displaystyle Delta f n f n 1 f n burada f sifir veya daha buyuk tamsayilar uzerinde tanimlanmis bir fonksiyondur Bu baglamda belirtilen f fonksiyonu icin gorev f nin yani F D 1f displaystyle F Delta 1 f seklinde tanimlanacak oyle bir fonksiyonu hesaplamaktir ki DF f displaystyle Delta F f denklemini saglar Baska bir deyisle F n 1 F n f n displaystyle F n 1 F n f n Bu fonksiyon bir sabit deger eklenmesi disinda belirlenmistir ve su bicimde ifade edilebilir F n i 0n 1f i displaystyle F n sum i 0 n 1 f i Bu tip toplamlar icin her zaman bir mevcut olmayabilir fakat f n nk displaystyle f n n k durumunda ve dogrusallik prensibi geregi her polinom fonksiyonu icin kapali bir form sunar Belirli integrallerle yaklasimBircok yaklasim Ing approximation toplamlar ile integraller arasinda kurulan ve herhangi bir f fonksiyonu icin gecerli olan su baglanti ile saglanabilir s a 1bf s ds i abf i s ab 1f s ds displaystyle int s a 1 b f s ds leq sum i a b f i leq int s a b 1 f s ds ve herhangi bir f fonksiyonu icin s ab 1f s ds i abf i s a 1bf s ds displaystyle int s a b 1 f s ds leq sum i a b f i leq int s a 1 b f s ds Daha kapsamli yaklasimlar icin incelenebilir Toplama islemi indeksin bir integral fonksiyonu tarafindan verilmis veya bu yontemle elde edilmisse toplama islemi ilgili belirli integralin taniminda yer alan bir Riemann toplami olarak degerlendirilebilir Bu baglamda ornegin b an i 0n 1f a ib an abf x dx displaystyle frac b a n sum i 0 n 1 f left a i frac b a n right approx int a b f x dx beklenir zira sag tarafta yer alan ifade sol tarafta yer alan ifadenin n displaystyle n to infty limiti olarak tanimlanmistir Ancak belirli bir toplam icin n sabit kaldigindan f hakkinda ek varsayimlar yapilmadan yukaridaki yaklasimdaki hata hakkinda sinirli bilgi verilebilir Ozellikle siddetli dalgalanan fonksiyonlar icin Riemann toplami Riemann integralinden onemli olcude farkli olabilir OzdesliklerAsagidaki formuller sonlu toplamlar icin gecerlidir Genel ozdeslikler n stC f n C n stf n displaystyle sum n s t C cdot f n C cdot sum n s t f n quad dagilma n stf n n stg n n st f n g n displaystyle sum n s t f n pm sum n s t g n sum n s t left f n pm g n right quad Degisme ozelligi ve birlesme ozelligi n stf n n s pt pf n p displaystyle sum n s t f n sum n s p t p f n p quad indeks oteleme n Bf n m Af s m displaystyle sum n in B f n sum m in A f sigma m quad ifadesi sonlu bir kume A uzerinden baska bir kume B ye bir bijeksiyon s araciligiyla gerceklesen bir esleme durumunda gecerlidir bu durum onceki formulu daha genel bir baglama tasir n stf n n sjf n n j 1tf n displaystyle sum n s t f n sum n s j f n sum n j 1 t f n quad Birlesme ozelligini kullanarak toplamin parcalanmasi n abf n n 0bf n n 0a 1f n displaystyle sum n a b f n sum n 0 b f n sum n 0 a 1 f n quad bir onceki formulun bir baska formu n stf n n 0t sf t n displaystyle sum n s t f n sum n 0 t s f t n quad ifadesinde serinin ilk elemanindan son elemanina kadar olan toplami serinin son elemanindan baslayip ilk elemanina dogru olan toplamina esdegerdir Bu durum toplamin simetrisini ve ters cevrilebilirligini vurgular n 0tf n n 0tf t n displaystyle sum n 0 t f n sum n 0 t f t n quad bir onceki formulun bir baska formu i k0k1 j l0l1ai j j l0l1 i k0k1ai j displaystyle sum i k 0 k 1 sum j l 0 l 1 a i j sum j l 0 l 1 sum i k 0 k 1 a i j quad degisme ozelligi ve birlesme ozelligi k j i nai j i kn j kiai j j kn i jnai j j 0n k i kn jai j i displaystyle sum k leq j leq i leq n a i j sum i k n sum j k i a i j sum j k n sum i j n a i j sum j 0 n k sum i k n j a i j i quad degisme ve birlesme ozelliginin bir baska uygulamasi n 2s2t 1f n n stf 2n n stf 2n 1 displaystyle sum n 2s 2t 1 f n sum n s t f 2n sum n s t f 2n 1 quad ifadesi bir toplamin tek ve cift bilesenlerine ayrilmasini ifade eder burada cift sayili indeksler icin bu ayrim yapilmaktadir Bu yontem toplamin daha sistemli bir sekilde incelenmesini saglar n 2s 12tf n n s 1tf 2n n s 1tf 2n 1 displaystyle sum n 2s 1 2t f n sum n s 1 t f 2n sum n s 1 t f 2n 1 quad toplamin tek indeks ile cift ve tek unsurlarina ayrilmasi i 0nai j 0nbj i 0n j 0naibj displaystyle biggl sum i 0 n a i biggr biggl sum j 0 n b j biggr sum i 0 n sum j 0 n a i b j quad Dagilma ozelligi i sm j tnaicj i smai j tncj displaystyle sum i s m sum j t n a i c j biggl sum i s m a i biggr biggl sum j t n c j biggr quad ifadesi dagilma ozelliginin carpim islemlerinin faktorler olarak ifade edilmesine olanak tanidigini gosterir Bu durum iki farkli serinin carpiminin her bir serinin toplamlarinin carpimina esdeger oldugunu ifade eder Bu yontem serilerin carpimini basitlestirerek analiz etmeyi kolaylastirir n stlogb f n logb n stf n displaystyle sum n s t log b f n log b prod n s t f n quad ifadesi bir carpim isleminin logaritmasinin bu carpimda yer alan bireysel terimlerin logaritmalarinin toplamina denk oldugunu belirtir Bu ozellik carpim islemlerinin logaritmik ifadesini analiz etmek icin matematiksel bir kolaylik saglar ve carpim islemlerinin logaritmalarini basitlestirerek toplama donusturmeyi mumkun kilar n stf n displaystyle sum limits n s t f n ifadesinin C displaystyle C tabaninda ussu n s displaystyle n s den n t displaystyle n t ye kadar olan f n displaystyle f n fonksiyonunun her bir degeri icin C displaystyle C nin alinmis uslerinin carpimina esittir km 0 mn 0f m n km 0 kn mf n m displaystyle sum k m 0 sum m n 0 f m n sum k m 0 sum k n m f n m quad ifadesi Z Z textstyle mathbb Z times mathbb Z uzerinde tanimlanmis herhangi bir f textstyle f fonksiyonu icin gecerlidir Aritmetik dizilerin us alinmasi ve logaritma hesaplamalari i 1nc nc displaystyle sum i 1 n c nc quad ifadesi c sabiti i den bagimsiz oldugunda her n icin gecerlidir i 0ni i 1ni n n 1 2 displaystyle sum i 0 n i sum i 1 n i frac n n 1 2 qquad n dogal sayinin toplami bu sayilar en basit aritmetik diziyi olusturur 52 i 1n 2i 1 n2 displaystyle sum i 1 n 2i 1 n 2 qquad tek dogal sayilarin toplami i 0n2i n n 1 displaystyle sum i 0 n 2i n n 1 qquad cift dogal sayilarin toplami i 1nlog i log n displaystyle sum i 1 n log i log n qquad bir dizi logaritmanin toplami bu degerlerin carpiminin logaritmasi ile esdegerdir i 0ni2 i 1ni2 n n 1 2n 1 6 n33 n22 n6 displaystyle sum i 0 n i 2 sum i 1 n i 2 frac n n 1 2n 1 6 frac n 3 3 frac n 2 2 frac n 6 qquad kare sayilarin toplami ilgilidir 52 i 0ni3 i 0ni 2 n n 1 2 2 n44 n32 n24 displaystyle sum i 0 n i 3 biggl sum i 0 n i biggr 2 left frac n n 1 2 right 2 frac n 4 4 frac n 3 2 frac n 2 4 qquad gore 52 Daha genis bir perspektiften p gt 1 displaystyle p gt 1 durumu icin asagidaki gibidir k 1nkp np 1p 1 12np k 2p pk Bkp k 1 np k 1 displaystyle sum k 1 n k p frac n p 1 p 1 frac 1 2 n p sum k 2 p binom p k frac B k p k 1 n p k 1 Bu ifadede Bk displaystyle B k bir Bernoulli sayisi olarak tanimlanir ve pk displaystyle binom p k bir olarak bilinir Bu formul polinom derecesinin kuvvetleri toplamini hesaplamada kullanilir ve Bernoulli sayilari ile bu toplamlar arasindaki ili Us degerlerindeki toplam indeksleri Asagidaki toplam ifadelerde a degerinin 1 den farkli oldugu kabul edilmektedir i 0n 1ai 1 an1 a displaystyle sum i 0 n 1 a i frac 1 a n 1 a bir toplami olarak i 0n 112i 2 12n 1 displaystyle sum i 0 n 1 frac 1 2 i 2 frac 1 2 n 1 a 1 2 icin ozel bir durum i 0n 1iai a nan n 1 an 1 1 a 2 displaystyle sum i 0 n 1 ia i frac a na n n 1 a n 1 1 a 2 geometrik dizinin a ya gore turetilmis ifadesinin a ile carpilmasi sonucu i 0n 1 b id ai b i 0n 1ai d i 0n 1iai b 1 an1 a d a nan n 1 an 1 1 a 2 b 1 an n 1 dan1 a da 1 an 1 1 a 2 displaystyle begin aligned sum i 0 n 1 left b id right a i amp b sum i 0 n 1 a i d sum i 0 n 1 ia i amp b left frac 1 a n 1 a right d left frac a na n n 1 a n 1 1 a 2 right amp frac b 1 a n n 1 da n 1 a frac da 1 a n 1 1 a 2 end aligned bir toplami dd dd Binom katsayilari ve faktoriyeller Binom katsayilarini iceren pek cok toplam ozdesligi mevcuttur adli eserin bir bolumu bu temel tekniklerin incelenmesine ozel olarak ayrilmistir Bu ozdesliklerin en temel olanlarindan bazilari asagida sunulmustur Binom teoremi baglaminda i 0n ni an ibi a b n displaystyle sum i 0 n n choose i a n i b i a b n ifadesi binom teoremini temsil eder i 0n ni 2n displaystyle sum i 0 n n choose i 2 n ifadesi a b 1 durumunda binom katsayilarinin toplaminin ozel bir halidir i 0n ni pi 1 p n i 1 displaystyle sum i 0 n n choose i p i 1 p n i 1 ifadesi p a 1 b durumunda olup 0 p 1 displaystyle 0 leq p leq 1 araliginda binom dagiliminin toplam degerlerini gosterir i 0ni ni n 2n 1 displaystyle sum i 0 n i n choose i n 2 n 1 ifadesi a b 1 durumunda binom teoreminin turetilmis formunu verir i 0n ni i 1 2n 1 1n 1 displaystyle sum i 0 n frac n choose i i 1 frac 2 n 1 1 n 1 ifadesi a b 1 durumunda binom teoreminin integral alinmis formunun bir degerini ifade eder Permutasyon sayilari baglaminda Asagida verilen toplamlarda nPk displaystyle n P k sayisini temsil eder i 0niPk ni nPk 2n k displaystyle sum i 0 n i P k n choose i n P k 2 n k ifadesi verilen kapsamdaki permutasyon sayilarinin bir toplamini ifade eder i 1ni kPk 1 i 1n j 0k i j n k 1 n 1 k 2 displaystyle sum i 1 n i k P k 1 sum i 1 n prod j 0 k i j frac n k 1 n 1 k 2 ifadesi belirli bir kapsamdaki ardisik sayilarin carpimlarinin toplamini ve bu toplamin matematiksel ifadesini gosterir i 0ni ni i 0nnPi n e n Z displaystyle sum i 0 n i cdot n choose i sum i 0 n n P i lfloor n cdot e rfloor quad n in mathbb Z ifadesi faktoriyel ve permutasyon sayilarinin toplamlarini hesaplar ve bu toplamlarin bir tam sayiya yuvarlanmis halini yani kullanarak ifade eder Digerleri k 0m n kn n m 1n 1 displaystyle sum k 0 m binom n k n binom n m 1 n 1 i kn ik n 1k 1 displaystyle sum i k n i choose k n 1 choose k 1 i 0ni i n 1 1 displaystyle sum i 0 n i cdot i n 1 1 i 0n m i 1i m nn displaystyle sum i 0 n m i 1 choose i m n choose n i 0n ni 2 2nn displaystyle sum i 0 n n choose i 2 2n choose n i 0n1i n e n displaystyle sum i 0 n frac 1 i frac lfloor n e rfloor n Harmonik sayilar i 1n1i Hn displaystyle sum i 1 n frac 1 i H n quad ifadesi n inci temsil eder i 1n1ik Hnk displaystyle sum i 1 n frac 1 i k H n k quad ifadesi bir ifade eder Buyume hizlariAsagidaki ifadeler cesitli fonksiyonlarin buyume hizlarini gosteren yaklasik degerlerdir theta notasyonu kullanilarak i 1nic 8 nc 1 displaystyle sum i 1 n i c in Theta n c 1 ifadesi reel c degeri 1 den buyukse gecerlidir i 1n1i 8 loge n displaystyle sum i 1 n frac 1 i in Theta log e n i 1nci 8 cn displaystyle sum i 1 n c i in Theta c n ifadesi reel c degeri 1 den buyukse gecerlidir i 1nlog i c 8 n log n c displaystyle sum i 1 n log i c in Theta n cdot log n c ifadesi negatif olmayan reel c degeri icin gecerlidir i 1nlog i c id 8 nd 1 log n c displaystyle sum i 1 n log i c cdot i d in Theta n d 1 cdot log n c ifadesi negatif olmayan reel c d degerleri icin gecerlidir i 1nlog i c id bi 8 nd log n c bn displaystyle sum i 1 n log i c cdot i d cdot b i in Theta n d cdot log n c cdot b n ifadesi negatif olmayan reel b gt 1 c d degerleri icin gecerlidir Tarihce1675 yilinda Gottfried Wilhelm Leibniz a gonderdigi bir mektupta farkli diferansiyellerin toplamini gostermek icin sembolunu onermis ve bu oneri Latince calculus summatorius toplam hesabi teriminden dolayi S seklini almistir Bu sembolun integral olarak yeniden adlandirilmasi sonradan Johann Bernoulli ile olan yazismalar sirasinda gerceklesmistir 1755 yilinda sigma toplam sembolu Leonhard Euler in adli calismasinda ilk kez kaydedilmistir Euler sembolu asagidaki denklikler icin kullanmistir S 2wx w2 x2 displaystyle Sigma 2wx w 2 x 2 1772 yilinda S and Sn sembolunun kullanimi Lagrange tarafindan kayit altina alinmistir 1823 yilinda buyuk S harfi seriler icin bir toplam sembolu olarak kullanilmis ve bu kullanim genis capta yayginlasmistir 1829 yilinda S toplam sembolu Fourier ve C G J Jacobi tarafindan kullanilmis ve bu kullanim belgelenmistir Fourier in metodolojisi belirli alt ve ust sinirlar dahilinde degerlendirmeleri icermektedir Ornegin i 1 e i2t displaystyle sum i 1 infty e i 2 t ldots ifadesi sonsuz bir serinin toplamini ve bu toplamin nasil ele alinacagini gosterir Bu tur bir ifade matematiksel analizde sikca karsilasilan karmasik seri hesaplamalarini temsil eder Notlar Detaylar icin ucgensel sayi maddesine goz atiniz Toplama notasyonu ve toplamlarla aritmetik uzerine detayli bir inceleme icin bkz Graham Ronald L Knuth Donald E Patashnik Oren 1994 Chapter 2 Sums Concrete Mathematics A Foundation for Computer Science PDF 2 bas Addison Wesley Professional ISBN 978 0201558029 olu kirik baglanti i sayisi i displaystyle i ile karistirilma ihtimali bulunmadiginda Serbest degiskenlerin ve bagli degiskenlerin ismi tanim itibariyle onemsizdir ancak karisiklik riski oldugunda genellikle alfabe ortasindaki harfler i displaystyle i den q displaystyle q ya kadar tam sayilari ifade etmek icin kullanilir Ornegin yorumlamada kesin bir netlik olmasina karsin bircok matematikci yukaridaki formullerde k displaystyle k yerine x displaystyle x kullanilmasini muhtemelen anlasilmasi guc bulabilir Kaynakca Summation Notation www columbia edu 31 Temmuz 2020 tarihinde kaynagindan Erisim tarihi 16 Agustos 2020 a b c d Handbook of Discrete and Combinatorial Mathematics Kenneth H Rosen John G Michaels CRC Press 1999 0 8493 0149 1 a b Calculus I Summation Notation tutorial math lamar edu 11 Agustos 2020 tarihinde kaynagindan Erisim tarihi 16 Agustos 2020 Burton David M 2011 The History of Mathematics An Introduction 7th McGraw Hill s 414 ISBN 978 0 07 338315 6 Leibniz Gottfried Wilhelm 1899 Gerhardt Karl Immanuel Ed Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern Erster Band Berlin Mayer amp Muller s 154 a b Cajori 1929 ss 181 182 a b c d Cajori 1929 s 61 Euler Leonhard 1755 Institutiones Calculi differentialis Latin Petropolis s 27 4 Nisan 2023 tarihinde kaynagindan Erisim tarihi 28 Nisan 2024 KB1 bakim Tanimlanamayan dil link Lagrange Joseph Louis 1867 1892 Oeuvres de Lagrange Tome 3 Fransizca Paris s 451 8 Nisan 2023 tarihinde kaynagindan Erisim tarihi 28 Nisan 2024 Memoires de l Academie royale des sciences de l Institut de France pour l annee 1825 tome VIII Fransizca Paris Didot 1829 ss 581 622 Fourier Jean Baptiste Joseph 1888 1890 Oeuvres de Fourier Tome 2 Fransizca Paris Gauthier Villars s 149 7 Nisan 2023 tarihinde kaynagindan Erisim tarihi 28 Nisan 2024 BibliografyaCajori Florian 1929 A History Of Mathematical Notations Volume II Open Court Publishing ISBN 978 0 486 67766 8 Dis baglantilarWikimedia Commons ta Summation ile ilgili coklu ortam belgeleri bulunur
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans