| D├╝zg├╝n Tetrahedron | |
|---|---|
 (D├Čnen model animasyonu i├¦in buray─▒ t─▒klay─▒n─▒z) | |
| Tip | Platonik cisim |
| Elemanlar | F = 4, E = 6 V = 4 (Žć = 2) |
| Y├╝zler | 4{3} |
| {3,3} and s{2,2} | |
| 3 | 2 3 | 2 2 2 | |
veya (*332) | |
| 01, 15, 1 | |
| Ûzellikler | |
| 70.528779┬░ = arccos(1/3) | |
 3.3.3 () |  [[{{{T-├¦ifte┼¤}}}]] () |
 | |
Geometride tetrahedron veya d├Črt y├╝zl├╝, d├Črt ├╝├¦gen y├╝zden olu┼¤an bir ├¦oky├╝zl├╝d├╝r (polihedron), her k├Č┼¤esinde ├╝├¦ ├╝├¦gen birle┼¤ir. D├╝zg├╝n d├Črt y├╝zl├╝ d├Črt ├╝├¦genin e┼¤kenar oldu─¤u bir d├Črt y├╝zl├╝d├╝r ve Platonik cisimlerden biridir. D├Črty├╝zl├╝, d├Črt y├╝z├╝ olan tek . Tetrahedron isminin s─▒fat hali (tetrahedrona ait veya tetrahedronla ili┼¤kili anlam─▒nda) "tetrahedral"d─▒r.
D├Črty├╝zl├╝, kavram─▒n─▒n ├╝├¦ boyutlu h├ólidir.
D├Črty├╝zl├╝, bir cins piramittir. Piramit, ├¦okgen bir taban─▒ tek bir noktada birle┼¤tiren ├╝├¦gen y├╝zlerden olu┼¤ur. D├Črty├╝zl├╝ durumunda taban bir ├╝├¦gendir (d├Črt y├╝z├╝n herhangi biri taban say─▒labilir), dolay─▒s─▒yla d├Črt y├╝zl├╝ ayr─▒ca ├╝├¦gen piramit olarak da bilinir.
T├╝m d─▒┼¤b├╝key () ├¦okgenler gibi, d├Črt y├╝zl├╝ de tek bir sayfa k├ó─¤─▒d─▒n katlanmas─▒ ile meydana gelebilir. ─░ki olu┼¤ur.
Her bir d├Črt y├╝zl├╝ i├¦in ├Čyle bir k├╝re () vard─▒r ki d├Črt y├╝zl├╝n├╝n k├Č┼¤eleri bu k├╝renin y├╝zeyinde yer al─▒rlar.
D├╝zg├╝n d├Črt y├╝zl├╝ler i├¦in form├╝ller
Kenar uzunlu─¤u 
| Taban y├╝zeyin y├╝z├Čl├¦├╝m├╝ |  |
| y├╝z├Čl├¦├╝m | 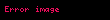 |
| Y├╝kseklik |  |
| Hacim |  |
| Bir kenar ile bir y├╝z aras─▒ndaki a├¦─▒ |  (yakla┼¤─▒k 54.7356┬░) |
| ─░ki y├╝z aras─▒ndaki a├¦─▒ |  (yakla┼¤─▒k 70.5288┬░) |
| Merkezi k├Č┼¤elere birle┼¤tiren do─¤rular aras─▒ndaki a├¦─▒ |  (yakla┼¤─▒k 109.4712┬░) |
| Kar┼¤─▒s─▒nda bir y├╝z olan bir k├Č┼¤edeki |  (yakla┼¤─▒k 0.55129 ) |
| yar─▒├¦ap─▒ | 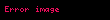 |
| Y├╝zlere te─¤et olan yar─▒├¦ap─▒ |  |
| Kenarlara te─¤et olan yar─▒├¦ap─▒ |  |
| yar─▒├¦aplar─▒ | 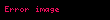 |
| Bir k├Č┼¤eden merkezine uzakl─▒k |  |
Taban y├╝ze g├Čre bir y├╝z├╝n e─¤imi, bir kenar─▒n e─¤iminin iki kat─▒d─▒r, ├¦├╝nk├╝ taban ├╝zerinde, bir kenar boyunca k├Č┼¤eye olan yatay uzakl─▒k, bir y├╝z├╝n kenarortay─▒ndan o k├Č┼¤eye olan uzakl─▒─¤─▒n iki kat─▒d─▒r. Bir di─¤er deyi┼¤le, e─¤er C, taban─▒n a─¤─▒rl─▒k merkezi (ortac─▒) ise, C'den taban─▒n k├Č┼¤elerinden birine olan uzakl─▒k, C'den taban kenarlar─▒ndan birinin orta noktas─▒na olan uzakl─▒─¤─▒n iki kat─▒d─▒r. Bunun nedeni, kenarortaylar─▒n birbirini k├╝tle merkezinde kesmeleri ve bu noktan─▒n her bir kenarortay─▒ uzunluklar─▒ 1:2 oranl─▒ olan iki par├¦aya b├Člmesidir.
Hacim
D├Črty├╝zl├╝n├╝n hacmi, piramit hacim form├╝l├╝d├╝r:
burada 
A┼¤a─¤─▒daki k├Č┼¤elere sahip bir d├Črt y├╝zl├╝ i├¦in a = (a1, a2, a3), b = (b1, b2, b3), c = (c1, c2, c3) ve d = (d1, d2, d3), hacim (1/6)┬Ę|det(aŌłÆb, bŌłÆc, cŌłÆd)|. Birbirleriyle basit bir ├¦izge olu┼¤turan k├Č┼¤e ├¦iftlerinin herhangi bir di─¤er kombinasyonu ile de hacmi veren bir form├╝l olu┼¤turulabilir. Bu form├╝l, nokta ├¦arp─▒m ve ├¦apraz ├¦arp─▒m kullan─▒larak da yaz─▒labilir:
E─¤er koordinat sisteminin orijini d k├Č┼¤esine rastlayacak ┼¤ekilde se├¦ilirse, d = 0 olur, dolay─▒s─▒yla
burada a, b ve c bir k├Č┼¤ede kesi┼¤en ├╝├¦ kenara kar┼¤─▒l─▒k gelir ve 
├£├¦l├╝ skaler ├¦arp─▒m a┼¤a─¤─▒daki determinantla g├Čsterilebilir:
┬Ā┬Ā veya ┬Ā┬Ā
┬Ā┬Ā burada ┬Ā┬Ā
┬Ā┬Ā sat─▒r veya s├╝tun vekt├Čr olarak g├Čsterilebilir
- Dolay─▒s─▒yla
┬Ā┬Ā burada ┬Ā┬Ā
┬Ā┬Ā vb.
- bunun sonucu
,
burada 

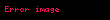

burada 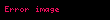

Kenarlar aras─▒ndaki uzakl─▒k
D├Črty├╝zl├╝n├╝n iki kar┼¤─▒ kenar─▒, iki ├╝zerinde yer al─▒rlar (ayk─▒r─▒ do─¤rular birbirlerine ne paralel ne de birbirini kesen do─¤rulard─▒r). Bu iki do─¤ru aras─▒ndaki en yak─▒n noktalar kenarlara ait noktalarsa bu noktalar kenarlar aras─▒ndaki en yak─▒n uzakl─▒─¤─▒ tan─▒mlar; aksi halde, kenarlar aras─▒ndaki uzakl─▒k, u├¦ noktalar ve kar┼¤─▒ kenar aras─▒ndaki uzakl─▒klardan en k─▒sa olan─▒d─▒r. a ve b-c kar┼¤─▒ kenarlar─▒n─▒n olu┼¤turdu─¤u ayk─▒r─▒ do─¤rular aras─▒ndaki uzakl─▒k 
Geometrik ili┼¤kiler

Animasyonu izle
D├Črty├╝zl├╝ bir 3-'tir. Di─¤er Platonik cisimlerden farkl─▒ olarak, bir d├╝zg├╝n d├Črt y├╝zl├╝n├╝n t├╝m k├Č┼¤eleri birbirinden e┼¤it uzakl─▒ktad─▒r. K├Č┼¤eler, ├╝├¦ boyutlu uzayda d├Črt noktan─▒n birbirine e┼¤it uzakl─▒kta olabilece─¤i tek konumdad─▒r.
D├Črty├╝zl├╝, ├╝├¦gensel bir piramittir. D├╝zg├╝n d├Črt y├╝zl├╝ (─░ng. self-dual).
D├╝zg├╝n bir d├Črt y├╝zl├╝ bir k├╝p├╝n i├¦ine iki farkl─▒ ┼¤ekilde yerle┼¤tirilebilir, her k├Č┼¤e k├╝p├╝n bir k├Č┼¤esi ve her kenar k├╝p├╝n y├╝zlerinden birinin ├¦apraz─▒ olacak ┼¤ekilde. Bu yerle┼¤tirmelerden biri i├¦in, k├Č┼¤elerin koordinatlar─▒ ┼¤├Čyledir:
- (+1, +1, +1);
- (ŌłÆ1, ŌłÆ1, +1);
- (ŌłÆ1, +1, ŌłÆ1);
- (+1, ŌłÆ1, ŌłÆ1).
Meydana gelen bu d├Črt y├╝zl├╝n├╝n orijin merkezli olup kenar uzunlu─¤u 2ŌłÜ2'dir. ├¢b├╝r d├Črt y├╝zl├╝ (birincisinin ├Čz-├¦ifte┼¤idir) i├¦in t├╝m i┼¤aretlerin tersini al─▒n. Bu iki d├Črt y├╝zl├╝n├╝n k├Č┼¤eleri birlikte k├╝p├╝n k├Č┼¤elerini meydana getirirler. B├Čylece bir d├╝zg├╝n d├Črt y├╝zl├╝n├╝n bir 3- (3-demicube) oldu─¤u g├Čsterilmi┼¤ olur.

Bu d├Črt y├╝zl├╝n├╝n hacmi k├╝b├╝n hacminin 1/3'├╝d├╝r. ─░ki d├Črt y├╝zl├╝y├╝ birle┼¤tirince bir (ayn─▒ merkeze sahip birden ├¦ok ├¦oky├╝zl├╝) olu┼¤ur, bunun ad─▒ (compound of two tetrahedra) veya (stellated octahedron)'dur.
Y─▒ld─▒zla┼¤m─▒┼¤ sekiz y├╝zl├╝n├╝n i├¦i bir sekiz y├╝zl├╝d├╝r. Dolay─▒s─▒yla, d├╝zg├╝n bir d├Črt y├╝zl├╝den yar─▒m kenar uzunlu─¤unda d├Črt tane d├╝zg├╝n d├Črt y├╝zl├╝ kesilmesinin sonucu, d├╝zg├╝n bir sekiz y├╝zl├╝d├╝r. Bu i┼¤leme d├Črt y├╝zl├╝n├╝n denir.
K├╝p├╝n i├¦ine bir d├Črt y├╝zl├╝ yerle┼¤tirince be┼¤ d├Črt y├╝zl├╝ meydana gelir, bunlardan biri d├╝zg├╝nd├╝r. Bir k├╝p├╝ olu┼¤turmak i├¦in gereken d├Črt y├╝zl├╝ say─▒s─▒ en az 5'tir.
D├╝zg├╝n ├¦oky├╝zl├╝ler uzay─▒ karolayamazlar. Bunun olabilece─¤i o kadar makul g├Čr├╝nm├╝┼¤t├╝r ki Aristo bunun olabilece─¤ini iddia etmi┼¤tir. Ancak, iki d├╝zg├╝n d├Črt y├╝zl├╝ ve bir sekiz y├╝zl├╝ ile birle┼¤tirilerek bir (rhombohedron) olu┼¤ur, bununla uzay karolanabilir.
Ancak, uzay─▒n karolayabilen en az bir d├╝zensiz d├Črt y├╝zl├╝ vard─▒r. D├Črty├╝zl├╝lerin hepsinin ayn─▒ boyda olmas─▒ ┼¤art─▒ esnetilirse, sadece d├Črt y├╝zl├╝ler kullanarak uzay─▒ kaplamak m├╝mk├╝nd├╝r. ├¢rne─¤in bir sekiz y├╝zl├╝y├╝ d├Črt d├Čry├╝zl├╝ye b├Čl├╝p bunlar─▒ iki d├╝zg├╝n d├Črt y├╝zl├╝ ile birle┼¤tirilebilir (bu iki tip d├Črt y├╝zl├╝n├╝n hacimleri e┼¤ittir).
D├╝zg├╝n ├¦oky├╝zl├╝ler aras─▒nda paralel y├╝zlere sahip olmayan tek cisim d├Črt y├╝zl├╝d├╝r.
─░lgili ├¦oky├╝zl├╝ler
Bir d├Črt y├╝zl├╝ye uygulanacak bir kesme i┼¤lemi d├╝zg├╝n bir ├¦oky├╝zl├╝ler serisi meydana getirir. Kalan kenarlar─▒ nokta haline getirecek ┼¤ekilde kesmek, rektifiye bir d├Črt y├╝zl├╝ olan bir sekiz y├╝zl├╝ olu┼¤turur. Bu i┼¤lem devam ettirilirse sonunda ikili rektifikasyon (birectification) olur, ba┼¤lang─▒├¦taki y├╝zler birer noktaya indirgenir ve ├Čz-├¦ifte┼¤ d├Črt y├╝zl├╝ yeni ba┼¤tan ortaya ├¦─▒kar.
| Ad | d├Črty├╝zl├╝ | rektifiye d├Črty├╝zl├╝ (sekizy├╝zl├╝) | cantellated tetrahedron () | omnitruncated tetrahedron () | Snub tetrahedron () | |
|---|---|---|---|---|---|---|
| {3,3} | t1{3,3} | t0,1{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} | |
     |      |      |      |      |      | |
| ├ćizge (A3) |  |  |  |  |  |  |
| ├ćizge (A2) |  |  |  |  |  |  |
| Kat─▒ |  |  |  |  |  |  |
 |  |  |  |  |  |
Kesi┼¤en d├Črt y├╝zl├╝ler
ile ilgin├¦ bir ├¦oky├╝zl├╝ in┼¤a edilebilir. Be┼¤ tane d├Črtl├╝den olu┼¤an bu y├╝zy─▒llard─▒r bilinmektedir. Origamide s─▒k s─▒k g├Čr├╝l├╝r. 20 k├Č┼¤enin birle┼¤tirilmesi ile bir dodekahedron (yirmiy├╝zl├╝) meydana gelir. Birbirinin olan ve bi├¦imleri vard─▒r.
Izometri
D├╝zg├╝n d├Črt y├╝zlerde izometriler

Bir k├╝p├╝n k├Č┼¤eleri, her biri bir d├Črt y├╝zl├╝ olu┼¤turan, d├Črtl├╝ iki gruba ayr─▒labilir (bkz. yukar─▒s─▒ ve ayr─▒ca animasyon). D├╝zg├╝n bir d├Črt y├╝zl├╝n├╝n simetrileri bir k├╝p├╝n simetrilerinin yar─▒s─▒na kar┼¤─▒l─▒k gelir: d├Črt y├╝zl├╝leri kendilerine d├Čn├╝┼¤t├╝renler ve birbirine d├Čn├╝┼¤t├╝rmeyenler.
D├Črty├╝zl├╝, platonik cisimler aras─▒nda ile kendi kendine rastlamayan tek cisimdir.
D├╝zg├╝n d├Črt y├╝zl├╝n├╝n 24 izometrisi vard─▒r, Td simetri grubu ve ona e┼¤bi├¦imli(izomorfik) olan olu┼¤turur. Bunlar ┼¤├Čyle kategorilendirilebilir:
- T, A4 (├Čzde┼¤lik ve 11 d├Čnme i┼¤lemi) ile izomorfiktir, a┼¤a─¤─▒daki e┼¤lenik s─▒n─▒flar─▒ vard─▒r (parantez i├¦inde k├Č┼¤elerin perm├╝tasyonlar─▒ ve birim kuaterniyon g├Čsterimleri verilmi┼¤tir):
- ├Čzde┼¤lik
- bir k├Č┼¤eden ge├¦en ve kar┼¤─▒ y├╝ze dik bir eksen etraf─▒nda ┬▒120┬░ d├Čnme: 4 eksen, eksen ba┼¤─▒na 2, birlikte 8┬Ā((1┬Ā2┬Ā3) vb.; (1┬Ā┬▒┬Āi┬Ā┬▒┬Āj┬Ā┬▒┬Āk)/2)
- 180┬░ bir a├¦─▒yla d├Čnme ├Čyle ki kenar kar┼¤─▒ kenar ile ├¦ak─▒┼¤s─▒n. 3 ((1 2)(3 4) vb.; i,┬Āj,┬Āk)
- bir kenara dik bir d├╝zlemde yans─▒ma: 6
- bir d├╝zlemde yans─▒ma ile o d├╝zleme dik bir eksen etraf─▒nda 90┬░ d├Čnme: 3 eksen, eksen ba┼¤─▒na 2, birlikte 6; buna e┼¤de─¤er olarak, 90┬░ d├Čnmelerle ters d├Čnmeler (x'in ŌłÆx'e d├Čn├╝┼¤mesi) birle┼¤imidir: d├Čnmeler bir k├╝pte bir y├╝z├╝ ├Čb├╝r y├╝ze d├Čn├╝┼¤t├╝ren d├Čnmelere kar┼¤─▒l─▒k gelir.
D├╝zensiz d├Črt y├╝zl├╝lerin izometrileri
D├╝zensiz bir d├Črt y├╝zl├╝n├╝n izometrileri (e┼¤├Čl├¦er d├Čn├╝┼¤├╝mleri) d├Črt y├╝zl├╝n├╝n geometrisine ba─¤l─▒d─▒r, 7 durum olabilir. Her durumda bir meydana gelir.
- E┼¤kenar ├╝├¦gen bir taban ve (e┼¤kenar olmayan) ikizkenar ├╝├¦gen kenarlar durumunda 6 izometri vard─▒r, bunlara taban─▒n 6 izometrisine kar┼¤─▒l─▒k gelir. K├Č┼¤elerin perm├╝tasyonlar─▒na kar┼¤─▒l─▒k gelen bu 6 izometri ┼¤unlard─▒r: ├Čzde┼¤lik 1, (123), (132), (12), (13) ve (23). Bunlar S3 ile izomorfik olan C3vsimetri grubunu olu┼¤turur.
- D├Črt (e┼¤kenar olmayan) ikizkenar ├╝├¦gen 8 izometri verir. E─¤er (1,2) ve (3,4) kenarlar─▒ di─¤er d├Črt kenardan farkl─▒ uzunluktaysa bu 8 izometri ┼¤unlard─▒r: ├Čzde┼¤lik 1, yans─▒malar (12) ve (34) ve 180┬░ d├Čnmeler (12)(34), (13)(24), (14)(23) ve 90┬░ d├Čnmeleri (1234) ve (1432). Bunlar D2d simetri grubunu olu┼¤turur.
- D├Črt ├¦e┼¤itkenar ├╝├¦gen 4 izometri verir. ─░zometriler ┼¤unlard─▒r: 1 ve 180┬░ d├Čnmeleri (12)(34), (13)(24) ve (14)(23). Bu, V4 Ōēģ Z22 (nokta k├╝mesi D2 olan).
- ─░ki ├¦ift izomorfik (e┼¤kenar olmayan) ikizkenar ├╝├¦gen. Birbirine dik ve farkl─▒ uzunlukta (1,2) and (3,4) kenarlar─▒ vard─▒r. 4 izometeriler ┼¤unlard─▒r: 1, yans─▒ma (12) ve (34) ve 180┬░ d├Čnmeleri (12)(34). Simetri grubu C2v'd─▒r, V4'e izomorfiktir.
- ─░ki ├¦ift izomofik ├¦e┼¤itkenar ├╝├¦gen. ─░ki ├¦ift e┼¤it uzunluklu kenar vard─▒r (1,3), (2,4) ve (1,4), (2,3) ama bunlar d─▒┼¤─▒nda hi├¦bir kenar e┼¤it de─¤ildir. Olan izometriler 1 ve (12)(34) d├Čnmesidir. Simetri grubu C2'd─▒r, Z2'e izomorfiktir.
- Ortak kenarl─▒ iki farkl─▒ e┼¤kenar ├╝├¦gen. ─░ki ├¦ift e┼¤it uzunluklu kenarlar vard─▒r (1,3), (1,4) ve (2,3), (2,4), ama bunlar d─▒┼¤─▒nda hi├¦bir kenar e┼¤it de─¤ildir. Olan izometriler 1 ve (34) yans─▒mas─▒d─▒r. Simetri grubu Cs'd─▒r, Z2'e izomorfiktir.
- Hi├¦bir kenar birbirine e┼¤it de─¤ildir, tek izometri ├Čzde┼¤liktir ve simetri grubu trivial gruptur.
D├Črty├╝zl├╝ler i├¦in sin├╝sler kanunu ve t├╝m d├Črt y├╝zl├╝ ┼¤ekillerinin uzay─▒

Sin├╝s teoreminin bir sonucu olarak, k├Č┼¤eleri O, A, B, C olan bir d├Črt y├╝zl├╝de
Bu e┼¤itli─¤in iki taraf─▒, y├╝zlerin saat y├Čnl├╝ ve ters saat y├Čnl├╝ okunu┼¤u gibi d├╝┼¤├╝n├╝lebilir.
D├Črt k├Č┼¤eden her birini O k├Č┼¤esi yerine koymak buna benzer d├Črt e┼¤itlik yarat─▒r, ama bunlar─▒n en fazla ├╝├¦ tanesi ba─¤─▒ms─▒zd─▒r: e─¤er e┼¤itliklerin "saat y├Čnl├╝" taraflar─▒ birbiriyle ├¦arp─▒l─▒rsa, sonucun "ters saat y├Čnl├╝" taraflar─▒n ├¦arp─▒m─▒na e┼¤it oldu─¤u ├¦─▒kar─▒m─▒ yap─▒labilir. Her iki taraftaki ortak ├¦arpanlar at─▒l─▒rsa geriye kalan, d├Črd├╝nc├╝ e┼¤itliktir. Bu "ba─¤─▒ms─▒zl─▒k" ili┼¤kisinin ├Čnemli olmas─▒n─▒n bir nedeni ┼¤udur: ├╝├¦ a├¦─▒n─▒n bir ├╝├¦gene ait olmas─▒ i├¦in toplamlar─▒n─▒n yar─▒m ├¦embere (180┬░) e┼¤it olmas─▒ gerekir. 12 a├¦─▒ i├¦in hangi ┼¤art bunlar─▒n bir d├Črt y├╝zl├╝ye ait olmas─▒n─▒ sa─¤lar? D├Črty├╝zl├╝n├╝n her bir y├╝z├╝ndeki a├¦─▒lar─▒n toplam─▒ yar─▒m ├¦emberdir. Bu ┼¤ekilde d├Črt ├╝├¦gen oldu─¤una g├Čre a├¦─▒ toplamlar─▒na etki eden d├Črt k─▒s─▒t vard─▒r. Dolay─▒s─▒yla serbestlik derecesi 12'den 8'e d├╝┼¤er. Bu sin├╝s teoreminindeki d├Črt ili┼¤ki, serbestlik derecelerini 8'den 4'e de─¤il, 5'e indirir, ├¦├╝nk├╝ d├Črd├╝nc├╝ k─▒s─▒t ilk ├╝├¦ten ba─¤─▒ms─▒z de─¤ildir. Dolay─▒s─▒yla olas─▒l t├╝m d├Črt y├╝zl├╝lerin olu┼¤turdu─¤u a├¦─▒ de─¤erlerinin uzay─▒ 5 boyutludur.
Uygulamalar


Say─▒sal analiz
Say─▒sal analizde, ├Čzellikle k─▒smi diferansiyel denklemlerin say─▒sal ├¦├Čz├╝mlerinde, sonlu eleman analizi i├¦in denklemler kurarken, karma┼¤─▒k ├╝├¦ boyutlu ┼¤ekiller ├¦o─¤u zaman d├╝zensiz d├Črt y├╝zl├╝lerden olu┼¤an bir ├¦okgen a─¤ ile yakla┼¤─▒klan─▒r. Bu y├Čntemler ├¦e┼¤itli m├╝hendislik dallar─▒nda yayg─▒n olarak kullan─▒lmaktad─▒r.
Kimya
Kimyada kuaterner faz diyagramlar─▒ grafik olarak tetrahedron olarak g├Čsterilir. (Ancak, ileti┼¤im m├╝hendisli─¤inde kuaterner faz diyagramlar─▒ grafik olarak iki boyutlu g├Čsterilir.)
Elektrik ve elektronik
E─¤er d├Črt e┼¤it birbirine ba─¤lanarak bir tetrahedron olu┼¤turursa, iki k├Č┼¤e aras─▒ndaki diren├¦, bir rezist├Čr├╝n direncinin yar─▒s─▒ kadard─▒r.
Oyun
├¢zellikle d├Črt-y├╝zl├╝ zar s─▒k kullan─▒l─▒r. At─▒lan say─▒ ya taban─▒n etraf─▒nda ya da ├╝st k├Č┼¤ede yaz─▒l─▒ olur. M├¢ 2600'den kalma Ur Kraliyet Oyunu, bir dizi d├Črt y├╝zl├╝ zarla oynanm─▒┼¤t─▒r. Baz─▒ Rubik K├╝p├╝ benzeri bulmacalar d├Črt y├╝zl├╝d├╝r, ├Črne─¤in ve .
Renk uzay─▒
Renk uzay─▒ d├Čn├╝┼¤├╝m algoritmalar─▒nda, ├Čzellikle ekseni renk uzay─▒n─▒ ├¦apraz kesti─¤i durumlarda (├Črne─¤in RGB, CMY), tetrahedral interpolasyon kullan─▒l─▒r.
Jeoloji
taraf─▒ndan ilk yay─▒mlanan ve D├╝nyan─▒n olu┼¤umunu a├¦─▒klamak i├¦in ├Čne s├╝r├╝len , 20. y├╝zy─▒l─▒n ba┼¤lar─▒nda pop├╝lerdi.
Do─¤ada
Kimya

D├Črty├╝zl├╝ (tetrahedron) ┼¤ekli, molek├╝llerin kovalent ba─¤lar─▒nda g├Čr├╝l├╝r. sp3-hibritlenmi┼¤ atomlara ├¦evreleyen atomlar bir d├Črt y├╝zl├╝n├╝n k├Č┼¤elerinde yer al─▒r, yani tetrahedral molek├╝ler geometriye sahiptir. ├¢rne─¤in, bir metan molek├╝l├╝ (CH4) veya bir amonyum iyonunda (NH4+), merkezdeki karbon veya azot atomu, tetrahedral simetriye sahip d├Črt hidrojen atomu ile ├¦evrilidir. Bu y├╝zden organik kimyan─▒n ├Čnde gelen dergilerinden biri olarak adland─▒r─▒lm─▒┼¤t─▒r.
D├╝zg├╝n bir d├Črt y├╝zl├╝n├╝n iki k├Č┼¤esi aras─▒ndaki merkez a├¦─▒ ╬Ė = 
Elektronikte kullan─▒lan en yayg─▒n yar─▒ iletken olan silikonun de─¤erlik say─▒s─▒ d├Črtt├╝r. Silikon atomunun ba─¤lar─▒n─▒n tetrahedral ┼¤ekli, silikon kristallerinin olu┼¤umunu ve ┼¤ekillerini belirler.
Kaynak├¦a
- ^ a b Eric W. Weisstein, Tetrahedron (MathWorld)
- ^ a b c d e f : (Methuen and Co., 1948). Table I(i).
- ^ . 30 May─▒s 2015 tarihinde kayna─¤─▒ndan ar┼¤ivlendi. Eri┼¤im tarihi: 19 Ekim 2010.
- ^ . 27 Eyl├╝l 2010 tarihinde kayna─¤─▒ndan ar┼¤ivlendi. Eri┼¤im tarihi: 19 Ekim 2010.
- ^ "Skew_lines". 29 May─▒s 2015 tarihinde kayna─¤─▒ndan ar┼¤ivlendi. Eri┼¤im tarihi: 19 Ekim 2010.
- ^ Klein, Douglas J. (2002). (PDF). Croatica Chemica Acta. 75 (2). ss.┬Ā633-649. 10 Haziran 2007 tarihinde kayna─¤─▒ndan (PDF) ar┼¤ivlendi. Eri┼¤im tarihi: 15 Eyl├╝l 2006.
- ^ Vondran, Gary L. (Nisan 1998). "Radial and Pruned Tetrahedral Interpolation Techniques" (PDF). HP Technical Report. Cilt┬ĀHPL-98-95. ss.┬Ā1-32. 7 Haziran 2011 tarihinde kayna─¤─▒ndan (PDF). Eri┼¤im tarihi: 19 Ekim 2010.
- ^ (1875). Vestiges of the Molten Globe, as exhibited in the figure of the earth, volcanic action and physiography. Part I. Londra: E. Stanford. OCLC┬Ā3571917. 25 May─▒s 2013 tarihinde kayna─¤─▒ndan . Eri┼¤im tarihi: 19 Ekim 2010.
- ^ (1965). Principles of physical geology. Nelson. s.┬Ā32. 26 May─▒s 2013 tarihinde kayna─¤─▒ndan . Eri┼¤im tarihi: 19 Ekim 2010.
- ^ Charles Henry Hitchcock (Ocak 1900). Newton Horace Winchell (Ed.). William Lowthian Green and his Theory of the Evolution of the Earth's Features. The American geologist. XXV. Geological Publishing Company. ss.┬Ā1-10. 25 May─▒s 2013 tarihinde kayna─¤─▒ndan . Eri┼¤im tarihi: 19 Ekim 2010.
Ayr─▒ca bak─▒n─▒z
wikipedia, wiki, viki, vikipedia, oku, kitap, k├╝t├╝phane, k├╝t├╝bhane, ara, ara bul, bul, her┼¤ey, ne arasan─▒z burada,hikayeler, makale, kitaplar, ├Č─¤ren, wiki, bilgi, tarih, yukle, izle, telefon i├¦in, turk, t├╝rk, t├╝rk├¦e, turkce, nas─▒l yap─▒l─▒r, ne demek, nas─▒l, yapmak, yap─▒l─▒r, indir, ├╝cretsiz, ├╝cretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, m├╝zik, ┼¤ark─▒, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Duzgun Tetrahedron Donen model animasyonu icin burayi tiklayiniz Tip Platonik cisimElemanlar F 4 E 6 V 4 x 2 Yuzler 4 3 3 3 and s 2 2 3 2 3 2 2 2veya 332 01 15 1Ozellikler70 528779 arccos 1 3 3 3 3 T ciftes Geometride tetrahedron veya dort yuzlu dort ucgen yuzden olusan bir cokyuzludur polihedron her kosesinde uc ucgen birlesir Duzgun dort yuzlu dort ucgenin eskenar oldugu bir dort yuzludur ve Platonik cisimlerden biridir Dortyuzlu dort yuzu olan tek Tetrahedron isminin sifat hali tetrahedrona ait veya tetrahedronla iliskili anlaminda tetrahedral dir Dortyuzlu kavraminin uc boyutlu halidir Dortyuzlu bir cins piramittir Piramit cokgen bir tabani tek bir noktada birlestiren ucgen yuzlerden olusur Dortyuzlu durumunda taban bir ucgendir dort yuzun herhangi biri taban sayilabilir dolayisiyla dort yuzlu ayrica ucgen piramit olarak da bilinir Tum disbukey cokgenler gibi dort yuzlu de tek bir sayfa kagidin katlanmasi ile meydana gelebilir Iki olusur Her bir dort yuzlu icin oyle bir kure vardir ki dort yuzlunun koseleri bu kurenin yuzeyinde yer alirlar Duzgun dort yuzluler icin formullerKenar uzunlugu a displaystyle a olan bir duzgun dort yuzlu icin Taban yuzeyin yuzolcumu A0 34a2 displaystyle A 0 sqrt 3 over 4 a 2 yuzolcum A 4A0 3a2 displaystyle A 4 A 0 sqrt 3 a 2 Yukseklik 23a displaystyle sqrt 2 over 3 a Hacim V 13A0h 212a3 displaystyle V 1 over 3 A 0 h sqrt 2 over 12 a 3 Bir kenar ile bir yuz arasindaki aci arccos 13 arctan 2 displaystyle arccos left 1 over sqrt 3 right arctan sqrt 2 yaklasik 54 7356 Iki yuz arasindaki aci arccos 13 arctan 22 displaystyle arccos left 1 over 3 right arctan 2 sqrt 2 yaklasik 70 5288 Merkezi koselere birlestiren dogrular arasindaki aci arccos 13 2arctan 2 displaystyle arccos left 1 over 3 right 2 arctan sqrt 2 yaklasik 109 4712 Karsisinda bir yuz olan bir kosedeki 3arccos 13 p displaystyle 3 arccos left 1 over 3 right pi yaklasik 0 55129 yaricapi R 38a displaystyle R sqrt 3 over 8 a Yuzlere teget olan yaricapi r 13R a24 displaystyle r 1 over 3 R a over sqrt 24 Kenarlara teget olan yaricapi rM rR a8 displaystyle r M sqrt rR a over sqrt 8 yaricaplari rE a6 displaystyle r E a over sqrt 6 Bir koseden merkezine uzaklik 32a displaystyle sqrt 3 over 2 a Taban yuze gore bir yuzun egimi bir kenarin egiminin iki katidir cunku taban uzerinde bir kenar boyunca koseye olan yatay uzaklik bir yuzun kenarortayindan o koseye olan uzakligin iki katidir Bir diger deyisle eger C tabanin agirlik merkezi ortaci ise C den tabanin koselerinden birine olan uzaklik C den taban kenarlarindan birinin orta noktasina olan uzakligin iki katidir Bunun nedeni kenarortaylarin birbirini kutle merkezinde kesmeleri ve bu noktanin her bir kenarortayi uzunluklari 1 2 oranli olan iki parcaya bolmesidir HacimDortyuzlunun hacmi piramit hacim formuludur V 13A0h displaystyle V frac 1 3 A 0 h burada A0 displaystyle A 0 tabanin alani ve h tabandan tepeye olan yuksekliktir Bu formul her yuz icin gecerlidir dolayisiyla koselerden karsi yuzlere olan uzaklik o yuzun alani ile ters orantilidir Asagidaki koselere sahip bir dort yuzlu icin a a1 a2 a3 b b1 b2 b3 c c1 c2 c3 ve d d1 d2 d3 hacim 1 6 det a b b c c d Birbirleriyle basit bir cizge olusturan kose ciftlerinin herhangi bir diger kombinasyonu ile de hacmi veren bir formul olusturulabilir Bu formul nokta carpim ve capraz carpim kullanilarak da yazilabilir V a d b d c d 6 displaystyle V frac mathbf a mathbf d cdot mathbf b mathbf d times mathbf c mathbf d 6 Eger koordinat sisteminin orijini d kosesine rastlayacak sekilde secilirse d 0 olur dolayisiyla V a b c 6 displaystyle V frac mathbf a cdot mathbf b times mathbf c 6 burada a b ve c bir kosede kesisen uc kenara karsilik gelir ve a b c displaystyle mathbf a cdot mathbf b times mathbf c bir Bu formulu bir hacmi ile karsilastirinca bir dort yuzlunun hacminin onunla uc kesisen yuz paylasan bir paralelyuzun hacminin 1 6 si oldugu sonucuna varabiliriz Uclu skaler carpim asagidaki determinantla gosterilebilir 6 V abc displaystyle 6 cdot V begin vmatrix mathbf a amp mathbf b amp mathbf c end vmatrix veya 6 V abc displaystyle 6 cdot V begin vmatrix mathbf a mathbf b mathbf c end vmatrix burada a a1 a2 a3 displaystyle mathbf a a 1 a 2 a 3 satir veya sutun vektor olarak gosterilebilirDolayisiyla36 V2 a2a ba ca bb2b ca cb cc2 displaystyle 36 cdot V 2 begin vmatrix mathbf a 2 amp mathbf a cdot mathbf b amp mathbf a cdot mathbf c mathbf a cdot mathbf b amp mathbf b 2 amp mathbf b cdot mathbf c mathbf a cdot mathbf c amp mathbf b cdot mathbf c amp mathbf c 2 end vmatrix burada a b abcos g displaystyle mathbf a cdot mathbf b ab cos gamma vb bunun sonucuV abc61 2cos acos bcos g cos2 a cos2 b cos2 g displaystyle V frac abc 6 sqrt 1 2 cos alpha cos beta cos gamma cos 2 alpha cos 2 beta cos 2 gamma burada a b g displaystyle alpha beta gamma d kosesinde olusan duzlemsel acilardir a displaystyle alpha acisi d kosesini b ve c koselerine baglayan kenarlar arasindaki acidir b displaystyle beta acisi a ve c koseleri icin ayni seyi yapar g displaystyle gamma de a ve b koselerinin konumlari ile tanimlanmistir Dortyuzlunun koseleri arasindaki uzakliklar kullanilarak hacim hesaplamak icin kullanilir 288 V2 0111110d122d132d1421d1220d232d2421d132d2320d3421d142d242d3420 displaystyle 288 cdot V 2 begin vmatrix 0 amp 1 amp 1 amp 1 amp 1 1 amp 0 amp d 12 2 amp d 13 2 amp d 14 2 1 amp d 12 2 amp 0 amp d 23 2 amp d 24 2 1 amp d 13 2 amp d 23 2 amp 0 amp d 34 2 1 amp d 14 2 amp d 24 2 amp d 34 2 amp 0 end vmatrix burada i j 1 2 3 4 displaystyle i j in 1 2 3 4 indisleri a b c d displaystyle mathbf a mathbf b mathbf c mathbf d koselerini temsil eder ve dij displaystyle d ij bunlar arasindaki ikili uzakliklardir yani iki koseyi birlestiren kenarin uzunlugu Determinantin negatif degerli olmasi verilen uzunluklara sahip bir dort yuzlunun olamayacagi anlamina gelir Bu formul bazen olarak da bilinir 15 yuzyilda yasamis ressam Piero della Francesca dan kaynaklanir Bir ucgenin alanini hesaplamakta kullanilan 1 yuzyilda kesfedilmis Heron formulu nun uc boyuttaki karsiligidir Kenarlar arasindaki uzaklikDortyuzlunun iki karsi kenari iki uzerinde yer alirlar aykiri dogrular birbirlerine ne paralel ne de birbirini kesen dogrulardir Bu iki dogru arasindaki en yakin noktalar kenarlara ait noktalarsa bu noktalar kenarlar arasindaki en yakin uzakligi tanimlar aksi halde kenarlar arasindaki uzaklik uc noktalar ve karsi kenar arasindaki uzakliklardan en kisa olanidir a ve b c karsi kenarlarinin olusturdugu aykiri dogrular arasindaki uzaklik d displaystyle d olsun Bu durumda hacim icin bir diger formul soyledir V d a b c 6 displaystyle V frac d mathbf a times mathbf b c 6 Geometrik iliskilerDortyuzlu ilustrasyonu yapisini vurgulamak icin dort farkli yontem kullanilmistir cevirme katlanma katlanmama yari seffaflik ve En onemlisi stereogram 50 70 cm tam cozunurlukte izlenmesi onerilir Animasyonu izle Dortyuzlu bir 3 tir Diger Platonik cisimlerden farkli olarak bir duzgun dort yuzlunun tum koseleri birbirinden esit uzakliktadir Koseler uc boyutlu uzayda dort noktanin birbirine esit uzaklikta olabilecegi tek konumdadir Dortyuzlu ucgensel bir piramittir Duzgun dort yuzlu Ing self dual Duzgun bir dort yuzlu bir kupun icine iki farkli sekilde yerlestirilebilir her kose kupun bir kosesi ve her kenar kupun yuzlerinden birinin caprazi olacak sekilde Bu yerlestirmelerden biri icin koselerin koordinatlari soyledir 1 1 1 1 1 1 1 1 1 1 1 1 Meydana gelen bu dort yuzlunun orijin merkezli olup kenar uzunlugu 2 2 dir Obur dort yuzlu birincisinin oz ciftesidir icin tum isaretlerin tersini alin Bu iki dort yuzlunun koseleri birlikte kupun koselerini meydana getirirler Boylece bir duzgun dort yuzlunun bir 3 3 demicube oldugu gosterilmis olur Stella octangula Bu dort yuzlunun hacmi kubun hacminin 1 3 udur Iki dort yuzluyu birlestirince bir ayni merkeze sahip birden cok cokyuzlu olusur bunun adi compound of two tetrahedra veya stellated octahedron dur Yildizlasmis sekiz yuzlunun ici bir sekiz yuzludur Dolayisiyla duzgun bir dort yuzluden yarim kenar uzunlugunda dort tane duzgun dort yuzlu kesilmesinin sonucu duzgun bir sekiz yuzludur Bu isleme dort yuzlunun denir Kupun icine bir dort yuzlu yerlestirince bes dort yuzlu meydana gelir bunlardan biri duzgundur Bir kupu olusturmak icin gereken dort yuzlu sayisi en az 5 tir Duzgun cokyuzluler uzayi karolayamazlar Bunun olabilecegi o kadar makul gorunmustur ki Aristo bunun olabilecegini iddia etmistir Ancak iki duzgun dort yuzlu ve bir sekiz yuzlu ile birlestirilerek bir rhombohedron olusur bununla uzay karolanabilir Ancak uzayin karolayabilen en az bir duzensiz dort yuzlu vardir Dortyuzlulerin hepsinin ayni boyda olmasi sarti esnetilirse sadece dort yuzluler kullanarak uzayi kaplamak mumkundur Ornegin bir sekiz yuzluyu dort doryuzluye bolup bunlari iki duzgun dort yuzlu ile birlestirilebilir bu iki tip dort yuzlunun hacimleri esittir Duzgun cokyuzluler arasinda paralel yuzlere sahip olmayan tek cisim dort yuzludur Ilgili cokyuzluler Bir dort yuzluye uygulanacak bir kesme islemi duzgun bir cokyuzluler serisi meydana getirir Kalan kenarlari nokta haline getirecek sekilde kesmek rektifiye bir dort yuzlu olan bir sekiz yuzlu olusturur Bu islem devam ettirilirse sonunda ikili rektifikasyon birectification olur baslangictaki yuzler birer noktaya indirgenir ve oz ciftes dort yuzlu yeni bastan ortaya cikar Ad dortyuzlu rektifiye dortyuzlu sekizyuzlu cantellated tetrahedron omnitruncated tetrahedron Snub tetrahedron 3 3 t1 3 3 t0 1 3 3 t0 2 3 3 t0 1 2 3 3 s 3 3 Cizge A3 Cizge A2 Kati Kesisen dort yuzluler ile ilginc bir cokyuzlu insa edilebilir Bes tane dortluden olusan bu yuzyillardir bilinmektedir Origamide sik sik gorulur 20 kosenin birlestirilmesi ile bir dodekahedron yirmiyuzlu meydana gelir Birbirinin olan ve bicimleri vardir IzometriDuzgun dort yuzlerde izometriler Duzgun dort yuzlulerin simetri grubunda donme ve yansimalar Bir kupun koseleri her biri bir dort yuzlu olusturan dortlu iki gruba ayrilabilir bkz yukarisi ve ayrica animasyon Duzgun bir dort yuzlunun simetrileri bir kupun simetrilerinin yarisina karsilik gelir dort yuzluleri kendilerine donusturenler ve birbirine donusturmeyenler Dortyuzlu platonik cisimler arasinda ile kendi kendine rastlamayan tek cisimdir Duzgun dort yuzlunun 24 izometrisi vardir Td simetri grubu ve ona esbicimli izomorfik olan olusturur Bunlar soyle kategorilendirilebilir T A4 ozdeslik ve 11 donme islemi ile izomorfiktir asagidaki eslenik siniflari vardir parantez icinde koselerin permutasyonlari ve birim kuaterniyon gosterimleri verilmistir ozdeslik bir koseden gecen ve karsi yuze dik bir eksen etrafinda 120 donme 4 eksen eksen basina 2 birlikte 8 1 2 3 vb 1 i j k 2 180 bir aciyla donme oyle ki kenar karsi kenar ile cakissin 3 1 2 3 4 vb i j k bir kenara dik bir duzlemde yansima 6 bir duzlemde yansima ile o duzleme dik bir eksen etrafinda 90 donme 3 eksen eksen basina 2 birlikte 6 buna esdeger olarak 90 donmelerle ters donmeler x in x e donusmesi birlesimidir donmeler bir kupte bir yuzu obur yuze donusturen donmelere karsilik gelir Duzensiz dort yuzlulerin izometrileri Duzensiz bir dort yuzlunun izometrileri esolcer donusumleri dort yuzlunun geometrisine baglidir 7 durum olabilir Her durumda bir meydana gelir Eskenar ucgen bir taban ve eskenar olmayan ikizkenar ucgen kenarlar durumunda 6 izometri vardir bunlara tabanin 6 izometrisine karsilik gelir Koselerin permutasyonlarina karsilik gelen bu 6 izometri sunlardir ozdeslik 1 123 132 12 13 ve 23 Bunlar S3 ile izomorfik olan C3vsimetri grubunu olusturur Dort eskenar olmayan ikizkenar ucgen 8 izometri verir Eger 1 2 ve 3 4 kenarlari diger dort kenardan farkli uzunluktaysa bu 8 izometri sunlardir ozdeslik 1 yansimalar 12 ve 34 ve 180 donmeler 12 34 13 24 14 23 ve 90 donmeleri 1234 ve 1432 Bunlar D2d simetri grubunu olusturur Dort cesitkenar ucgen 4 izometri verir Izometriler sunlardir 1 ve 180 donmeleri 12 34 13 24 ve 14 23 Bu V4 Z22 nokta kumesi D2 olan Iki cift izomorfik eskenar olmayan ikizkenar ucgen Birbirine dik ve farkli uzunlukta 1 2 and 3 4 kenarlari vardir 4 izometeriler sunlardir 1 yansima 12 ve 34 ve 180 donmeleri 12 34 Simetri grubu C2v dir V4 e izomorfiktir Iki cift izomofik cesitkenar ucgen Iki cift esit uzunluklu kenar vardir 1 3 2 4 ve 1 4 2 3 ama bunlar disinda hicbir kenar esit degildir Olan izometriler 1 ve 12 34 donmesidir Simetri grubu C2 dir Z2 e izomorfiktir Ortak kenarli iki farkli eskenar ucgen Iki cift esit uzunluklu kenarlar vardir 1 3 1 4 ve 2 3 2 4 ama bunlar disinda hicbir kenar esit degildir Olan izometriler 1 ve 34 yansimasidir Simetri grubu Cs dir Z2 e izomorfiktir Hicbir kenar birbirine esit degildir tek izometri ozdesliktir ve simetri grubu trivial gruptur Dortyuzluler icin sinusler kanunu ve tum dort yuzlu sekillerinin uzayiSinus teoreminin bir sonucu olarak koseleri O A B C olan bir dort yuzlude sin OAB sin OBC sin OCA sin OAC sin OCB sin OBA displaystyle sin angle OAB cdot sin angle OBC cdot sin angle OCA sin angle OAC cdot sin angle OCB cdot sin angle OBA Bu esitligin iki tarafi yuzlerin saat yonlu ve ters saat yonlu okunusu gibi dusunulebilir Dort koseden her birini O kosesi yerine koymak buna benzer dort esitlik yaratir ama bunlarin en fazla uc tanesi bagimsizdir eger esitliklerin saat yonlu taraflari birbiriyle carpilirsa sonucun ters saat yonlu taraflarin carpimina esit oldugu cikarimi yapilabilir Her iki taraftaki ortak carpanlar atilirsa geriye kalan dorduncu esitliktir Bu bagimsizlik iliskisinin onemli olmasinin bir nedeni sudur uc acinin bir ucgene ait olmasi icin toplamlarinin yarim cembere 180 esit olmasi gerekir 12 aci icin hangi sart bunlarin bir dort yuzluye ait olmasini saglar Dortyuzlunun her bir yuzundeki acilarin toplami yarim cemberdir Bu sekilde dort ucgen olduguna gore aci toplamlarina etki eden dort kisit vardir Dolayisiyla serbestlik derecesi 12 den 8 e duser Bu sinus teoreminindeki dort iliski serbestlik derecelerini 8 den 4 e degil 5 e indirir cunku dorduncu kisit ilk ucten bagimsiz degildir Dolayisiyla olasil tum dort yuzlulerin olusturdugu aci degerlerinin uzayi 5 boyutludur UygulamalarDortyuzlu zarDort yuzlu bir isik cismi Martina AvusturyaSayisal analiz Sayisal analizde ozellikle kismi diferansiyel denklemlerin sayisal cozumlerinde sonlu eleman analizi icin denklemler kurarken karmasik uc boyutlu sekiller cogu zaman duzensiz dort yuzlulerden olusan bir cokgen ag ile yaklasiklanir Bu yontemler cesitli muhendislik dallarinda yaygin olarak kullanilmaktadir Kimya Kimyada kuaterner faz diyagramlari grafik olarak tetrahedron olarak gosterilir Ancak iletisim muhendisliginde kuaterner faz diyagramlari grafik olarak iki boyutlu gosterilir Elektrik ve elektronik Eger dort esit birbirine baglanarak bir tetrahedron olusturursa iki kose arasindaki direnc bir rezistorun direncinin yarisi kadardir Oyun Ozellikle dort yuzlu zar sik kullanilir Atilan sayi ya tabanin etrafinda ya da ust kosede yazili olur MO 2600 den kalma Ur Kraliyet Oyunu bir dizi dort yuzlu zarla oynanmistir Bazi Rubik Kupu benzeri bulmacalar dort yuzludur ornegin ve Renk uzayi Renk uzayi donusum algoritmalarinda ozellikle ekseni renk uzayini capraz kestigi durumlarda ornegin RGB CMY tetrahedral interpolasyon kullanilir Jeoloji tarafindan ilk yayimlanan ve Dunyanin olusumunu aciklamak icin one surulen 20 yuzyilin baslarinda populerdi DogadaKimya Amonyum NH4 iyonu dort yuzludur Dortyuzlu tetrahedron sekli molekullerin kovalent baglarinda gorulur sp3 hibritlenmis atomlara cevreleyen atomlar bir dort yuzlunun koselerinde yer alir yani tetrahedral molekuler geometriye sahiptir Ornegin bir metan molekulu CH4 veya bir amonyum iyonunda NH4 merkezdeki karbon veya azot atomu tetrahedral simetriye sahip dort hidrojen atomu ile cevrilidir Bu yuzden organik kimyanin onde gelen dergilerinden biri olarak adlandirilmistir Duzgun bir dort yuzlunun iki kosesi arasindaki merkez aci 8 arccos 13 displaystyle arccos left tfrac 1 3 right veya yaklasik 109 47 dir Elektronikte kullanilan en yaygin yari iletken olan silikonun degerlik sayisi dorttur Silikon atomunun baglarinin tetrahedral sekli silikon kristallerinin olusumunu ve sekillerini belirler Kaynakca a b Eric W Weisstein Tetrahedron MathWorld a b c d e f Methuen and Co 1948 Table I i 30 Mayis 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 19 Ekim 2010 27 Eylul 2010 tarihinde kaynagindan arsivlendi Erisim tarihi 19 Ekim 2010 Skew lines 29 Mayis 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 19 Ekim 2010 Klein Douglas J 2002 PDF Croatica Chemica Acta 75 2 ss 633 649 10 Haziran 2007 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 15 Eylul 2006 Vondran Gary L Nisan 1998 Radial and Pruned Tetrahedral Interpolation Techniques PDF HP Technical Report Cilt HPL 98 95 ss 1 32 7 Haziran 2011 tarihinde kaynagindan PDF Erisim tarihi 19 Ekim 2010 1875 Vestiges of the Molten Globe as exhibited in the figure of the earth volcanic action and physiography Part I Londra E Stanford OCLC 3571917 25 Mayis 2013 tarihinde kaynagindan Erisim tarihi 19 Ekim 2010 1965 Principles of physical geology Nelson s 32 26 Mayis 2013 tarihinde kaynagindan Erisim tarihi 19 Ekim 2010 Charles Henry Hitchcock Ocak 1900 Newton Horace Winchell Ed William Lowthian Green and his Theory of the Evolution of the Earth s Features The American geologist XXV Geological Publishing Company ss 1 10 25 Mayis 2013 tarihinde kaynagindan Erisim tarihi 19 Ekim 2010 Ayrica bakinizMatematiksel sekillerin listesi Dortyuzlusel sayi Tetra Pak
 Azərbaycanca
Az╔Örbaycanca ąæąĄą╗ą░čĆčāčüą║č¢
ąæąĄą╗ą░čĆčāčüą║č¢ Dansk
Dansk Deutsch
Deutsch Espa├▒ola
Espa├▒ola Fran├¦ais
Fran├¦ais Indonesia
Indonesia Italiana
Italiana µŚźµ£¼Ķ¬×
µŚźµ£¼Ķ¬× ęÜą░ąĘą░ęø
ęÜą░ąĘą░ęø Lietuvos
Lietuvos Nederlands
Nederlands Português
Portugu├¬s ąĀčāčüčüą║ąĖą╣
ąĀčāčüčüą║ąĖą╣ ÓĘāÓĘÆÓČéÓĘäÓČĮ
ÓĘāÓĘÆÓČéÓĘäÓČĮ Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó
Ó╣üÓĖÜÓĖÜÓ╣äÓĖŚÓĖó T├╝rk├¦e
T├╝rk├¦e ąŻą║čĆą░茹Įčüčīą║ą░
ąŻą║čĆą░茹Įčüčīą║ą░ õĖŁÕ£ŗõ║║
õĖŁÕ£ŗõ║║ United State
United State Afrikaans
Afrikaans