Çevrel çember, geometride, bir çokgenin tüm köşelerinden geçen çember. Bu çemberin merkezi çevrel özek (çevrel çemberin merkezi) olarak isimlendirilir.

Çevrel çemberi olan çokgenler, devirsel çokgen olarak isimlendirilir. Bütün , üçgenler ve dörtgenler bu özelliği gösterir.
Üçgende çevrel çember

Her üçgen devirseldir; bir başka ifadeyle tüm üçgenlerin bir çevrel çemberi bulunur.
Bir üçgenin çevrel çemberinin merkezi herhangi iki kenar kesişim noktası alınarak bulunabilir. (Ortadikme üçgenin bir kenarıyla doksan derecelik açı yapan ve aynı zamanda bu kenarı orta noktasında kesen doğrudur.) Çünkü çevrel çemberin merkezi, üçgendeki herhangi iki köşe çiftine eşit uzaklıktadır ve ortadikme üzerindeki tüm noktalar da üçgenin iki köşesine aynı mesafede bulunma şartını sağlar.
Çevrel çember merkezinin konumu üçgenin türüne göre değişir. Çevrel çemberin merkezi:
- Ancak ve ancak üçgen dar açılı (tüm açıları doksan dereceden küçük) ise, üçgenin içindedir.
- Ancak ve ancak üçgen geniş açılı ise (doksan dereceden büyük bir açıya sahip), üçgenin dışındadır.
- Ancak ve ancak üçgen dik açılı ise, hipotenüsün orta noktasındadır. Bu durum Thales teoreminin bir türüdür.
-
![image]() Dar açılı bir üçgenin çevrel çemberinin merkezi, üçgenin içinde yer alır
Dar açılı bir üçgenin çevrel çemberinin merkezi, üçgenin içinde yer alır -
![image]() Dik açılı bir üçgenin çevrel çemberinin merkezi, üçgen hipotenüsünün orta noktasıdır
Dik açılı bir üçgenin çevrel çemberinin merkezi, üçgen hipotenüsünün orta noktasıdır -
![image]() Geniş açılı bir üçgenin çevrel çemberinin merkezi, üçgenin dışında yer alır
Geniş açılı bir üçgenin çevrel çemberinin merkezi, üçgenin dışında yer alır
Çevrel çemberin çapı, üçgenin herhangi bir kenar uzunluğunun, kenarı gören açının sinüsüne bölünmesiyle hesaplanabilir. (Sinüs teoreminin bir sonucu olarak, hangi kenar seçilirse seçilsin sonuç aynı olacaktır.) Üçgenin dokuz nokta çemberinin çapı, çevrel çemberin çapının yarısına eşittir. ΔABC üçgenin çevrel çemberinin çapı:
burada R çap uzunluğunu, a, b, c üçgenin kenar uzunluklarını ve s = (a + b + c)/2 yarı çevre uzunluğunu simgeler. Yukarıda ikinci paydadaki köklü ifade, Heron formülüne göre, üçgenin alan ifadesidir.[1] Çemberin çapı için yazılabilecek trigonometrik ifadelerden biri
Verilen herhangi bir üçgende, çevrel çemberin merkezi daima (kenarotayların kesişim noktası) ve kesişim noktası doğrusaldır. Bu noktaların tümünden geçen doğru olarak bilinir.
Çevrel çember merkezinin yüksekliklerin kesişim noktasıdır.
Üç doğrusal noktanın çevrel çemberi olan, bu noktalardan geçen doğru sonsuz yarıçaplı çember olarak anılır. Neredeyse doğrusal olan noktaların çevrel çember hesaplamalarında genellikle görülür.
Üçgen çevrel çemberlerinin, bir noktalar kümesinin ile yakın ilişkisi vardır.
Çevrel çember denklemleri
Öklid düzleminde, bir çevrel çember denklemi ait olduğu üçgeninin köşelerinin Kartezyen koordinatlarından elde edilebilir. Buna göre
A, B ve C noktalarının koordinatları olarak alınsın. Burada çevrel çember, Kartezyen düzlemde geometrik yeri aşağıdaki denklemleri sağlayan v = (vx,vy) noktalarıdır.
Denklemlerle A, B, C ve v'nin, çemberin merkezi u' dan eşit r2 uzaklıkta olması sağlanır. kullanılarak denklemler
matrisine indirgenebilir. Böylece çevrel çember, matris determinantının sıfırlarının geometrik yeriyle ifade edilir:
ile,
a|v|2 − 2Sv − b = 0 elde edilir ve üç noktanın doğrusal olmadığı varsayımıyla (aksi durumda çevrel çember S'nin sonsuzda olduğu bir doğru halini alır), |v − S/a|2 = b/a + |S|2/a2, S/a çevrel çember merkezi ve √ (b/a + |S|2/a2) yarıçapı hesaplanır. Benzer yaklaşımla bir dörtyüzlünün denklemi de bulunabilir.
Çevrel çemberin ifade edilmiş bir denklemi x : y : z is a/x + b/y + c/z = 0 ve ifade edilmiş bir denklemi x : y : z is a2/x + b2/y + c2/z = 0 şeklindedir.
Çevrel çemberin sonsuzdaki doğrudur; trilineer koordinatlarla ax + by + cz = 0 ve barisentrik koordinatlarla x + y + z = 0 olarak gösterilebilir.
Bunun yanında, d boyuttaki bir üçgenin çevrel çemberi, genelleştirilmiş bir yöntemle bulunabilir. A, B ve C üçgenin köşelerini ifade eden d-boyutlu noktalar olsun. İşlemler C orijine taşınarak başlar:
Çevrel çemberin yarıçapı, r,
burada θ a ve b arasındaki iç açıdır. Çevrel çemberin merkezi, p0,
şeklinde ifade edilebilir.
Çevrel çember merkezinin koordinatları
Kartezyen koordinatlar
Çevrel çember merkezinin Kartezyen koordinatları
ve
Denklemler, genelleştirilmiş durum kaybolmadan, A köşesi Kartezyen koordinat sisteminin orijinine taşınarak yazılabilir; yani 
burada
Kenar uzunluklarının fonksiyonu olarak barisentrik koordinatlar
Çevrel çemberin merkezi
ifade edilir. Burada a, b, c üçgenin kenar uzunluklarını (sırasıyla BC, CA, AB) göstermektedir.
Vektörel ve skaler çarpımla barisentrik koordinatlar
Öklid uzayında alınan, doğrusal olmayan herhangi P1, P2 ve P3 noktasından geçen bir çember bulunur. Kartezyen koordinatlar kullanılarak bu noktalar vektör olarak yazılırsa, vektörel çarpım ve skaler çarpımla çevrel çember yarıçapı ile merkezi hesaplanabilir.
olsun. Bu noktalardan geçecek çemberin yarıçapı şöyle ifade edilir:
Çemberin merkezi ise lineer kombinasyonla:
şeklinde gösterilir. Burada
Parametrik denklemler
Çevrel çemberin bulunduğu düzeleme dik bir birim vektör şöyle yazılabilir:
Böylece çevrel çember yarıçapı, r, merkezi, Pc, çember üzerindeki bir nokta, P0 ve çemberin bulunduğu yüzeye ait birim normal, 
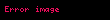
Çemberin kenarlarla yaptığı açılar
 |  |
Çevrel çemberin üçgenin kenarlarıyla yaptığı açılar, bu kenarların üçüncü kenarla oluşturduğu üçgen iç açılarına eşittir.
Çevrel çemberin diğer özellikleri
Çevrel çemberin yarıçapı, iç teğet çemberin yarıçapının iki katından küçük değildir. (Euler'in üçgen eşitsizliği)
Çevrel çemberin merkezi ile iç teğet çemberin merkezi arasındaki uzaklık 
a, b ve c kenarlarına sahip üçgenin çevrel çemberinin yarıçapının, iç teğet çemberinin yarıçapıyla çarpımı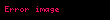
Notlar
- ^ Bu durum Kartezyen koordinat sisteminde alınacak r yarıçaplı ve merkez koordinatları a, b olan bir genel çember denklemi üzerinden ispatlanabilir:
Kaynakça
- ^ "TDK Matematik Terimleri Sözlüğü". TDK. Erişim tarihi: 9 Ağustos 2011.[]
- ^ Dörrie, Heinrich, 100 Great Problems of Elementary Mathematics, Dover, 1965. :s.379
- ^ "Wolfram barisentrik koordinatlar (İngilizce)". 20 Temmuz 2017 tarihinde kaynağından . Erişim tarihi: 8 Ağustos 2011.
- ^ a b Nelson, Roger, "Euler's triangle inequality via proof without words," Mathematics Magazine 81(1), February 2008, 58-61.
- ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover, 2007 (orij. 1929), s. 189, #298(d).
- ^Coxeter, H.S.M. (1969). "Chapter 1". Introduction to geometry. Wiley. s. 12–13. ISBN .
- ^Megiddo, N. (1983). "Linear-time algorithms for linear programming in R3 and related problems". SIAM Journal on Computing. 12 (4). ss. 759-776. doi:10.1137/0212052.
- Kimberling, Clark (1998). "Triangle centers and central triangles". Congressus Numerantium. Cilt 129. ss. i-xxv, 1-295.
- ^ (1988). Geometry: a comprehensive course. Dover.
Dış bağlantılar
- Eric W. Weisstein, Circumcircle (MathWorld)
- Eric W. Weisstein, Cyclic Polygon (MathWorld)
- Eric W. Weisstein, Steiner circumellipse (MathWorld)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Cevrel cember geometride bir cokgenin tum koselerinden gecen cember Bu cemberin merkezi cevrel ozek cevrel cemberin merkezi olarak isimlendirilir P cokgeninin cevrel cemberi C ve cevrel cemberinin merkezi O Cevrel cemberi olan cokgenler devirsel cokgen olarak isimlendirilir Butun ucgenler ve dortgenler bu ozelligi gosterir Ucgende cevrel cemberBir cevrel cember kirmizi ve merkezinin O noktasi olusturulmasi Her ucgen devirseldir bir baska ifadeyle tum ucgenlerin bir cevrel cemberi bulunur Bir ucgenin cevrel cemberinin merkezi herhangi iki kenar kesisim noktasi alinarak bulunabilir Ortadikme ucgenin bir kenariyla doksan derecelik aci yapan ve ayni zamanda bu kenari orta noktasinda kesen dogrudur Cunku cevrel cemberin merkezi ucgendeki herhangi iki kose ciftine esit uzakliktadir ve ortadikme uzerindeki tum noktalar da ucgenin iki kosesine ayni mesafede bulunma sartini saglar Cevrel cember merkezinin konumu ucgenin turune gore degisir Cevrel cemberin merkezi Ancak ve ancak ucgen dar acili tum acilari doksan dereceden kucuk ise ucgenin icindedir Ancak ve ancak ucgen genis acili ise doksan dereceden buyuk bir aciya sahip ucgenin disindadir Ancak ve ancak ucgen dik acili ise hipotenusun orta noktasindadir Bu durum Thales teoreminin bir turudur Dar acili bir ucgenin cevrel cemberinin merkezi ucgenin icinde yer alir Dik acili bir ucgenin cevrel cemberinin merkezi ucgen hipotenusunun orta noktasidir Genis acili bir ucgenin cevrel cemberinin merkezi ucgenin disinda yer alir Cevrel cemberin capi ucgenin herhangi bir kenar uzunlugunun kenari goren acinin sinusune bolunmesiyle hesaplanabilir Sinus teoreminin bir sonucu olarak hangi kenar secilirse secilsin sonuc ayni olacaktir Ucgenin dokuz nokta cemberinin capi cevrel cemberin capinin yarisina esittir DABC ucgenin cevrel cemberinin capi R abc2 alan AB BC CA 2 DABC abc2s s a s b s c 2abc a b c a b c a b c a b c displaystyle begin aligned text R amp frac abc 2 cdot text alan frac AB BC CA 2 Delta ABC amp frac abc 2 sqrt s s a s b s c amp frac 2abc sqrt a b c a b c a b c a b c end aligned burada R cap uzunlugunu a b c ucgenin kenar uzunluklarini ve s a b c 2 yari cevre uzunlugunu simgeler Yukarida ikinci paydadaki koklu ifade Heron formulune gore ucgenin alan ifadesidir 1 Cemberin capi icin yazilabilecek trigonometrik ifadelerden biri R 2 Alansin Asin Bsin C displaystyle text R sqrt frac 2 cdot text Alan sin A sin B sin C Verilen herhangi bir ucgende cevrel cemberin merkezi daima kenarotaylarin kesisim noktasi ve kesisim noktasi dogrusaldir Bu noktalarin tumunden gecen dogru olarak bilinir Cevrel cember merkezinin yuksekliklerin kesisim noktasidir Uc dogrusal noktanin cevrel cemberi olan bu noktalardan gecen dogru sonsuz yaricapli cember olarak anilir Neredeyse dogrusal olan noktalarin cevrel cember hesaplamalarinda genellikle gorulur Ucgen cevrel cemberlerinin bir noktalar kumesinin ile yakin iliskisi vardir Cevrel cember denklemleri Oklid duzleminde bir cevrel cember denklemi ait oldugu ucgeninin koselerinin Kartezyen koordinatlarindan elde edilebilir Buna gore A Ax Ay displaystyle mathbf A A x A y B Bx By displaystyle mathbf B B x B y C Cx Cy displaystyle mathbf C C x C y A B ve C noktalarinin koordinatlari olarak alinsin Burada cevrel cember Kartezyen duzlemde geometrik yeri asagidaki denklemleri saglayan v vx vy noktalaridir v u 2 r2 displaystyle mathbf v mathbf u 2 r 2 A u 2 r2 displaystyle mathbf A mathbf u 2 r 2 B u 2 r2 displaystyle mathbf B mathbf u 2 r 2 C u 2 r2 displaystyle mathbf C mathbf u 2 r 2 Denklemlerle A B C ve v nin cemberin merkezi u dan esit r2 uzaklikta olmasi saglanir kullanilarak denklemler v 2 2vx 2vy 1 A 2 2Ax 2Ay 1 B 2 2Bx 2By 1 C 2 2Cx 2Cy 1 displaystyle begin vmatrix mathbf v 2 amp 2v x amp 2v y amp 1 mathbf A 2 amp 2A x amp 2A y amp 1 mathbf B 2 amp 2B x amp 2B y amp 1 mathbf C 2 amp 2C x amp 2C y amp 1 end vmatrix matrisine indirgenebilir Boylece cevrel cember matris determinantinin sifirlarinin geometrik yeriyle ifade edilir det v 2vxvy1 A 2AxAy1 B 2BxBy1 C 2CxCy1 0 displaystyle det begin vmatrix mathbf v 2 amp v x amp v y amp 1 mathbf A 2 amp A x amp A y amp 1 mathbf B 2 amp B x amp B y amp 1 mathbf C 2 amp C x amp C y amp 1 end vmatrix 0 ile Sx 12det A 2Ay1 B 2By1 C 2Cy1 Sy 12det Ax A 21Bx B 21Cx C 21 displaystyle quad S x frac 1 2 det begin vmatrix mathbf A 2 amp A y amp 1 mathbf B 2 amp B y amp 1 mathbf C 2 amp C y amp 1 end vmatrix quad S y frac 1 2 det begin vmatrix A x amp mathbf A 2 amp 1 B x amp mathbf B 2 amp 1 C x amp mathbf C 2 amp 1 end vmatrix a det AxAy1BxBy1CxCy1 b det AxAy A 2BxBy B 2CxCy C 2 displaystyle a det begin vmatrix A x amp A y amp 1 B x amp B y amp 1 C x amp C y amp 1 end vmatrix quad b det begin vmatrix A x amp A y amp mathbf A 2 B x amp B y amp mathbf B 2 C x amp C y amp mathbf C 2 end vmatrix a v 2 2Sv b 0 elde edilir ve uc noktanin dogrusal olmadigi varsayimiyla aksi durumda cevrel cember S nin sonsuzda oldugu bir dogru halini alir v S a 2 b a S 2 a2 S a cevrel cember merkezi ve b a S 2 a2 yaricapi hesaplanir Benzer yaklasimla bir dortyuzlunun denklemi de bulunabilir Cevrel cemberin ifade edilmis bir denklemi x y z is a x b y c z 0 ve ifade edilmis bir denklemi x y z is a2 x b2 y c2 z 0 seklindedir Cevrel cemberin sonsuzdaki dogrudur trilineer koordinatlarla ax by cz 0 ve barisentrik koordinatlarla x y z 0 olarak gosterilebilir Bunun yaninda d boyuttaki bir ucgenin cevrel cemberi genellestirilmis bir yontemle bulunabilir A B ve C ucgenin koselerini ifade eden d boyutlu noktalar olsun Islemler C orijine tasinarak baslar a A C displaystyle mathbf a mathbf A mathbf C b B C displaystyle mathbf b mathbf B mathbf C Cevrel cemberin yaricapi r r a b a b 2 a b a b 2sin 8 A B 2sin 8 displaystyle r frac left mathbf a right left mathbf b right left mathbf a mathbf b right 2 left mathbf a times mathbf b right frac left mathbf a mathbf b right 2 sin theta frac left mathbf A mathbf B right 2 sin theta burada 8 a ve b arasindaki ic acidir Cevrel cemberin merkezi p0 p0 a 2b b 2a a b 2 a b 2 C displaystyle p 0 frac left mathbf a right 2 mathbf b left mathbf b right 2 mathbf a times mathbf a times mathbf b 2 left mathbf a times mathbf b right 2 mathbf C seklinde ifade edilebilir Cevrel cember merkezinin koordinatlariKartezyen koordinatlar Cevrel cember merkezinin Kartezyen koordinatlari Ay2 Ax2 By Cy By2 Bx2 Cy Ay Cy2 Cx2 Ay By D displaystyle A y 2 A x 2 B y C y B y 2 B x 2 C y A y C y 2 C x 2 A y B y D Ay2 Ax2 Cx Bx By2 Bx2 Ax Cx Cy2 Cx2 Bx Ax D displaystyle A y 2 A x 2 C x B x B y 2 B x 2 A x C x C y 2 C x 2 B x A x D ve D 2 Ax By Cy Bx Cy Ay Cx Ay By displaystyle D 2 A x B y C y B x C y A y C x A y B y Denklemler genellestirilmis durum kaybolmadan A kosesi Kartezyen koordinat sisteminin orijinine tasinarak yazilabilir yani A A A Ax Ay 0 0 displaystyle A A A A x A y 0 0 alinir Bu durumda kose koordinatlari B B A and C C A A dan koselere cizilmis vektorleri gosteren Bu ucgensel ceviri tum ucgenler icin gecerlidir ve A B C ucgeninin cevrel cemberinin merkez koordinatlari soyledir Cy Bx 2 By 2 By Cx 2 Cy 2 D displaystyle C y B x 2 B y 2 B y C x 2 C y 2 D Bx Cx 2 Cy 2 Cx Bx 2 By 2 D displaystyle B x C x 2 C y 2 C x B x 2 B y 2 D burada D 2 Bx Cy By Cx displaystyle D 2 B x C y B y C x Kenar uzunluklarinin fonksiyonu olarak barisentrik koordinatlar Cevrel cemberin merkezi a2 a2 b2 c2 b2 a2 b2 c2 c2 a2 b2 c2 displaystyle left a 2 a 2 b 2 c 2 b 2 a 2 b 2 c 2 c 2 a 2 b 2 c 2 right ifade edilir Burada a b c ucgenin kenar uzunluklarini sirasiyla BC CA AB gostermektedir Vektorel ve skaler carpimla barisentrik koordinatlar Oklid uzayinda alinan dogrusal olmayan herhangi P1 P2 ve P3 noktasindan gecen bir cember bulunur Kartezyen koordinatlar kullanilarak bu noktalar vektor olarak yazilirsa vektorel carpim ve skaler carpimla cevrel cember yaricapi ile merkezi hesaplanabilir P1 x1y1z1 P2 x2y2z2 P3 x3y3z3 displaystyle mathrm P 1 begin bmatrix x 1 y 1 z 1 end bmatrix mathrm P 2 begin bmatrix x 2 y 2 z 2 end bmatrix mathrm P 3 begin bmatrix x 3 y 3 z 3 end bmatrix olsun Bu noktalardan gececek cemberin yaricapi soyle ifade edilir r P1 P2 P2 P3 P3 P1 2 P1 P2 P2 P3 displaystyle mathrm r frac left P 1 P 2 right left P 2 P 3 right left P 3 P 1 right 2 left left P 1 P 2 right times left P 2 P 3 right right Cemberin merkezi ise lineer kombinasyonla Pc aP1 bP2 gP3 displaystyle mathrm P c alpha P 1 beta P 2 gamma P 3 seklinde gosterilir Burada a P2 P3 2 P1 P2 P1 P3 2 P1 P2 P2 P3 2 displaystyle alpha frac left P 2 P 3 right 2 left P 1 P 2 right cdot left P 1 P 3 right 2 left left P 1 P 2 right times left P 2 P 3 right right 2 b P1 P3 2 P2 P1 P2 P3 2 P1 P2 P2 P3 2 displaystyle beta frac left P 1 P 3 right 2 left P 2 P 1 right cdot left P 2 P 3 right 2 left left P 1 P 2 right times left P 2 P 3 right right 2 g P1 P2 2 P3 P1 P3 P2 2 P1 P2 P2 P3 2 displaystyle gamma frac left P 1 P 2 right 2 left P 3 P 1 right cdot left P 3 P 2 right 2 left left P 1 P 2 right times left P 2 P 3 right right 2 Parametrik denklemlerCevrel cemberin bulundugu duzeleme dik bir birim vektor soyle yazilabilir n P2 P1 P3 P1 P2 P1 P3 P1 displaystyle hat n frac left P 2 P 1 right times left P 3 P 1 right left left P 2 P 1 right times left P 3 P 1 right right Boylece cevrel cember yaricapi r merkezi Pc cember uzerindeki bir nokta P0 ve cemberin bulundugu yuzeye ait birim normal n displaystyle hat n olmak uzere P0 noktasindan baslayarak n displaystyle hat n ye pozitif yonelen sag el yonunde cemberin bir parametrik ifadesi R s Pc cos sr P0 Pc sin sr n P0 Pc displaystyle mathrm R left s right mathrm P c cos left frac mathrm s mathrm r right left P 0 P c right sin left frac mathrm s mathrm r right left hat n times left P 0 P c right right Cemberin kenarlarla yaptigi acilar Cevrel cemberin ucgenin kenarlariyla yaptigi acilar bu kenarlarin ucuncu kenarla olusturdugu ucgen ic acilarina esittir Cevrel cemberin diger ozellikleriCevrel cemberin yaricapi ic teget cemberin yaricapinin iki katindan kucuk degildir Euler in ucgen esitsizligi Cevrel cemberin merkezi ile ic teget cemberin merkezi arasindaki uzaklik R R 2r displaystyle sqrt R R 2r dir r ic teget cember yaricapini ve R cevrel cember yaricapini simgelemektedir a b ve c kenarlarina sahip ucgenin cevrel cemberinin yaricapinin ic teget cemberinin yaricapiyla carpimiabc2 a b c displaystyle frac abc 2 a b c seklinde olacaktir Notlar Bu durum Kartezyen koordinat sisteminde alinacak r yaricapli ve merkez koordinatlari a b olan bir genel cember denklemi uzerinden ispatlanabilir x a 2 y b 2 r2 displaystyle left x a right 2 left y b right 2 r 2 Bu denklem uc degiskenli oldugundan a b r bir cemberin denklemini belirlemek icin sadece uc nokta cifti gerekir Ucgenlerin uc kose uzerinden tanimlandigi dusunuldugunde her ucgen icin bir cevrel cember belirlenebilecegi gorulur Kaynakca TDK Matematik Terimleri Sozlugu TDK Erisim tarihi 9 Agustos 2011 olu kirik baglanti Dorrie Heinrich 100 Great Problems of Elementary Mathematics Dover 1965 s 379 Wolfram barisentrik koordinatlar Ingilizce 20 Temmuz 2017 tarihinde kaynagindan Erisim tarihi 8 Agustos 2011 a b Nelson Roger Euler s triangle inequality via proof without words Mathematics Magazine 81 1 February 2008 58 61 Johnson Roger A Advanced Euclidean Geometry Dover 2007 orij 1929 s 189 298 d Coxeter H S M 1969 Chapter 1 Introduction to geometry Wiley s 12 13 ISBN 0471504580 Megiddo N 1983 Linear time algorithms for linear programming in R3 and related problems SIAM Journal on Computing 12 4 ss 759 776 doi 10 1137 0212052 Kimberling Clark 1998 Triangle centers and central triangles Congressus Numerantium Cilt 129 ss i xxv 1 295 1988 Geometry a comprehensive course Dover Dis baglantilarEric W Weisstein Circumcircle MathWorld Eric W Weisstein Cyclic Polygon MathWorld Eric W Weisstein Steiner circumellipse MathWorld
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State



































