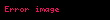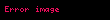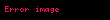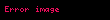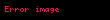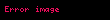Trigonometri (Yunanca trigōnon "üçgen" + metron "ölçmek"), üçgenlerin açıları ile kenarları arasındaki bağıntıları konu edinen matematik dalı. Trigonometri, sinüs ve kosinüs gibi trigonometrik işlevlerin (fonksiyon) üzerine kurulmuştur ve günümüzde fizik ve mühendislik alanlarında sıkça kullanılmaktadır.
Tarihçe
Matematiğin doğrudan doğruya astronomiden çıkmış bir kolu olan trigonometrinin bazı ögeleri, daha Babilliler ve Eski Mısırlılar döneminde biliniyor, Sümerli astronomlar ilk kez bir çemberi 360 eşit parçaya bölerek açı ölçümünü yaptılar. Eski Yunanlar Menelaos’un aracılığıyla, bir daire içine çizilebilen dörtgenden yola çıkarak daire yaylarının kirişlerinin değerlerini veren çizgiler oluşturuyorlardı. Daha sonra Araplar, yay kirişlerinin yerine sinüsleri koyup; tanjant, kotanjant, sekant, kosekant kavramlarını geliştirdiler.[].İlk kez Akdeniz'in çevresi trigonometre ile Abbasiler döneminde ölçülmüştür.[]
Batıda Nasîrüddin Tûsî’den büyük ölçüde yararlanan Regiomontanus’un üçgen üstüne adlı eseriyle gerçek trigonometri doğmuş oldu. François Viète ve , hesaplarda ondalık sayılardan yararlandılar. John Napier logaritmayı işe kattı. Isaac Newton ve öğrencileri trigonometri işlevlerinin ve logaritmalarının hesabına tam serileri uyguladılar. Daha sonra da Leonhard Euler, birim olarak trigonometrik cetvelin yarıçapını alarak, modern trigonometrinin temellerini attı.[].
Genel bakış
Trigonometrik işlevler

Trigonometrik işlevler bir dik üçgen ya da birim çember üzerinden tanımlanır. Temel olarak üç tane trigonometrik işlev ve bunların çarpma işlemine göre terslerinden oluşan üç tane daha işlev vardır. Yandaki ABC üçgeninde
- Sinüs işlevi (sin), karşı kenarın hipotenüse oranıdır.
- Kosinüs işlevi (cos), komşu kenarın hipotenüse oranıdır.
- Tanjant işlevi (tan), karşı kenarın komşu kenarı oranıdır.
Bir de bu işlevlerin çarpmaya göre tersi vardır. kosekant, sekant ve kotanjant:
Bu işlevler geometrinin dolayısıyla fiziğin ve mühendisliğin pek çok alanında kullanılır. Sinüs ve kosinüs teoremleri bir üçgenin açıları ve kenarlarını hesaplamakta kullanılır ki herhangi bir çokgen üçgenlerin birleşimi olduğundan çokgenleri incelemede de yararlıdır.
Birim çember ve esas ölçü

Yukarıda dik üçgen üzerinden yapılan tanım sadece 0-90 derece aralığını kapsar (0-π/2 radyan).
90-360 derece arasındaki açıların trigonometrik değerleri birim çember üzerinden hesaplanır. 360 dereceden büyük açılar 360 üzerinden devrettirilerek 0-360 arasındaki esas ölçüsü bulunur.
- 0° ≤x <360° ve k bir tam sayı olmak üzere ölçüsü (x + 360k) olan açıların esas ölçüsü x derecedir.
- 0 ≤ x< 2π ve k bir tam sayı olmak üzere, ölçüsü (x + 2πk) olan açıların esas ölçüsü x radyandır.
Merkezi orijin ve yarıçapı 1 birim olan çembere birim çember veya trigonometrik çember denir. Birim çemberin denklemi x2+y2=1 şeklindedir.
Sarma işlevi
Gerçel sayılar kümesinden birim çember üzerindeki noktalara tanımlanan işleve sarma işlevi denir.
Sarma işlevini s ile, birim çemberi de C ile gösterirsek işlev
şeklinde yazılabilir ve 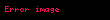

İşlevler arasındaki ilişkiler
Yukarıdaki tanımlardan görülebileceği gibi, bu işlevler arasında
ilişkileri vardır.
Sık kullanılan açıların trigonometrik oranları
 |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  |
 |  |  |  |  |  |  |  |  |
 |  |  |  |  | 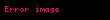 |  | 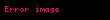 |  |
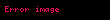 | 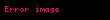 |  |  |  |  |  |  |  |
 |  |  |  |  |  | 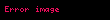 | 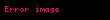 |  |
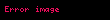 | 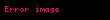 |  |  |  |  |  |  | 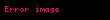 |
Gerçek veya karmaşık değişkenlerin trigonometrik fonksiyonları
Trigonometrik fonksiyon grafikleri
6 ana trigonometrik fonksiyonun özelliklerini özetleyen diyagramlar:
| Fonksiyon | Periyot | Alan | Aralık | Diyagram |
|---|---|---|---|---|
| sinüs |  |  | 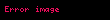 |  |
| cosinüs |  |  | 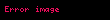 |  |
| tanjant |  | 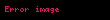 |  |  |
| sekant |  | 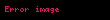 | 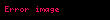 |  |
| cosekant |  | 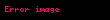 | 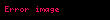 |  |
| cotanjant |  | 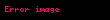 |  |  |
Ters trigonometrik fonksiyonlar
6 ana trigonometrik fonksiyon periyodik olduğu için birebir değillerdir yani ters çevrilemezler, ancak trigonometrik bir fonksiyonun alanını kısıtlayarak ters çevrilebilirler.:48ff
| Fonksiyon | Genel gösterim | İfade | x değer aralığı | Asıl değer aralığı (radyan) | Asıl değer aralığı (derece) |
|---|---|---|---|---|---|
| arcsinüs | y = arcsin x | x = sin y | −1 ≤ x ≤ 1 | −π/2 ≤ y ≤ π/2 | −90° ≤ y ≤ 90° |
| arckosinüs | y = arccos x | x = cos y | −1 ≤ x ≤ 1 | 0 ≤ y ≤ π | 0° ≤ y ≤ 180° |
| arctanjant | y = arctan x | x = tan y | tüm reel sayılar | −π/2 < y < π/2 | −90° < y < 90° |
| arckotanjant | y = arccot x | x = cot y | tüm reel sayılar | 0 < y < π | 0° < y < 180° |
| arcsekant | y = arcsec x | x = sec y | x ≤ −1 or 1 ≤ x | 0 ≤ y < π/2 or π/2 < y ≤ π | 0° ≤ y < 90° or 90° < y ≤ 180° |
| arckosekant | y = arccsc x | x = csc y | x ≤ −1 or 1 ≤ x | −π/2 ≤ y < 0 or 0 < y ≤ π/2 | -90° ≤ y < 0° or 0° < y ≤ 90° |
Kullanım alanları

Trigonometri birçok fen biliminde, matematiğin diğer alanlarında ve çeşitli sanatlarda yaygın bir biçimde kullanılmaktadır. Trigonometriyi kullanan bazı dallar şunlardır:
jeofizik, kristalografi, ekonomi (özellikle de finansal pazarların analizinde), elektrik mühendisliği, inşaat mühendisliği, elektronik, jeodezi, makine mühendisliği, meteoroloji, müzik kuramı, sayı kuramı (ve dolayısıyla kriptografi), oşinografi (okyanus bilimi), farmakoloji (eczacılık), optik, fonetik, olasılık kuramı, psikoloji, sismoloji...
Trigonometri yukarıda örneklendiği gibi birçok farklı alana farklı katkılarda bulunmuştur. Örneğin Pisagor kuramının isim babası Pisagor matematiksel müzik kuramına ilk katkıda bulunan isimlerdendir. Oşinografide bazı dalgaların sinüs dalgalarına benzerliği ilgili incelemelerde trigonometrinin kullanımına olanak tanımıştır. Bunun dışında Fourier serileri sayesinde trigonometrik işlevler farklı fonksiyonları temsil etmekte kullanılırlar ve bu sayede trigonometri birçok yararlanılan dallarda kullanım olanağı bulmuştur.
Özdeşlikler
Üçgen özdeşlikleri
Sinüs teoremi
Kosinüs teoremi
Tanjant teoremi
Trigonometrik özdeşlikler
Euler bağıntısı
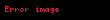
Bu bağıntıyla iki matematiksel ifade olan i ve 
de Moivre formülü
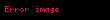
Diğer özdeşlikler
Toplam fark formülleri
Trigonometrik değerleri bilinen iki açının toplamının veya farkının trigonometrik değerlerini hesaplamak için kullanılan formüllerdir.
sin(α+β) = sin α.cos β + cos α.sin β
sin(α-β) = sin α.cos β - cos α.sin β
cos(α+β) = cos α.cos β - sin α.sin β
cos(α-β) = cos α.cos β + sin α.sin β
tan(α+β) = (tan α + tan β) / (1 - tan α . tan β)
tan(α-β) = (tan α - tan β) / (1 + tan α . tan β)
cot(α+β) = (cot α . cot β - 1) / (cot α + cot β)
cot(α-β) = (cot α . cot β + 1) / (cot β - cot α)
Yarım açı formülleri
Yarım açı formülleri ya da iki kat açı formülleri, trigonometrik değerleri bilinen bir açının iki katının veya yarısının trigonometrik değerlerini hesaplamak için kullanılan formüllerdir.
sin2α = 2sin α.cos α
cos2α = cos2 α - sin2 α
cos2α = 2cos2 α - 1
cos2α = 1- 2sin2 α
tan2α = 2tan α / 1-tan2 α
tan2α = 2 / cot α - tan α
cot2α = cot2 α - 1 / 2cot α
Dönüşüm formülleri
Dönüşüm formülleri, toplam durumundaki iki trigonometrik ifadeyi çarpım haline getirmeye yarar. Bu işlemin amacı bazı özel durumlarda işlem kolaylığı sağlamaktır.
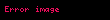
Ayrıca bakınız
Notlar
- ^ "Arşivlenmiş kopya". 11 Temmuz 2015 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 20 Aralık 2014 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ "Arşivlenmiş kopya". 27 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 28 Kasım 2020.
- ^ Mary P Attenborough (30 Haziran 2003). Mathematics for Electrical Engineering and Computing. Elsevier. s. 418. ISBN . 12 Mart 2022 tarihinde kaynağından . Erişim tarihi: 22 Mart 2022.
- ^ Ron Larson; Bruce H. Edwards (10 Kasım 2008). Calculus of a Single Variable. Cengage Learning. s. 21. ISBN . 22 Mayıs 2022 tarihinde kaynağından . Erişim tarihi: 22 Mart 2022.
- ^ Elizabeth G. Bremigan; Ralph J. Bremigan; John D. Lorch (2011). Mathematics for Secondary School Teachers. MAA. ISBN . 5 Mayıs 2022 tarihinde kaynağından . Erişim tarihi: 22 Mart 2022.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Trigonometri Yunanca trigōnon ucgen metron olcmek ucgenlerin acilari ile kenarlari arasindaki bagintilari konu edinen matematik dali Trigonometri sinus ve kosinus gibi trigonometrik islevlerin fonksiyon uzerine kurulmustur ve gunumuzde fizik ve muhendislik alanlarinda sikca kullanilmaktadir TarihceMatematigin dogrudan dogruya astronomiden cikmis bir kolu olan trigonometrinin bazi ogeleri daha Babilliler ve Eski Misirlilar doneminde biliniyor Sumerli astronomlar ilk kez bir cemberi 360 esit parcaya bolerek aci olcumunu yaptilar Eski Yunanlar Menelaos un araciligiyla bir daire icine cizilebilen dortgenden yola cikarak daire yaylarinin kirislerinin degerlerini veren cizgiler olusturuyorlardi Daha sonra Araplar yay kirislerinin yerine sinusleri koyup tanjant kotanjant sekant kosekant kavramlarini gelistirdiler kaynak belirtilmeli Ilk kez Akdeniz in cevresi trigonometre ile Abbasiler doneminde olculmustur kaynak belirtilmeli Batida Nasiruddin Tusi den buyuk olcude yararlanan Regiomontanus un ucgen ustune adli eseriyle gercek trigonometri dogmus oldu Francois Viete ve hesaplarda ondalik sayilardan yararlandilar John Napier logaritmayi ise katti Isaac Newton ve ogrencileri trigonometri islevlerinin ve logaritmalarinin hesabina tam serileri uyguladilar Daha sonra da Leonhard Euler birim olarak trigonometrik cetvelin yaricapini alarak modern trigonometrinin temellerini atti kaynak belirtilmeli Genel bakisTrigonometrik islevler Bir dik ucgenin kenarlari Trigonometrik islevler bir dik ucgen ya da birim cember uzerinden tanimlanir Temel olarak uc tane trigonometrik islev ve bunlarin carpma islemine gore terslerinden olusan uc tane daha islev vardir Yandaki ABC ucgeninde Sinus islevi sin karsi kenarin hipotenuse oranidir sin A karsihipotenus ac displaystyle sin A frac text karsi text hipotenus frac a c dd Kosinus islevi cos komsu kenarin hipotenuse oranidir cos A komsuhipotenus bc displaystyle cos A frac text komsu text hipotenus frac b c dd Tanjant islevi tan karsi kenarin komsu kenari oranidir tan A karsikomsu ab sin Acos A displaystyle tan A frac text karsi text komsu frac a b frac sin A cos A dd Bir de bu islevlerin carpmaya gore tersi vardir kosekant sekant ve kotanjant csc A 1sin A ca displaystyle csc A frac 1 sin A frac c a sec A 1cos A cb displaystyle sec A frac 1 cos A frac c b cot A 1tan A cos Asin A ba displaystyle cot A frac 1 tan A frac cos A sin A frac b a Bu islevler geometrinin dolayisiyla fizigin ve muhendisligin pek cok alaninda kullanilir Sinus ve kosinus teoremleri bir ucgenin acilari ve kenarlarini hesaplamakta kullanilir ki herhangi bir cokgen ucgenlerin birlesimi oldugundan cokgenleri incelemede de yararlidir Birim cember ve esas olcu Birim cember uzerinde butun islevler Yukarida dik ucgen uzerinden yapilan tanim sadece 0 90 derece araligini kapsar 0 p 2 radyan 90 360 derece arasindaki acilarin trigonometrik degerleri birim cember uzerinden hesaplanir 360 dereceden buyuk acilar 360 uzerinden devrettirilerek 0 360 arasindaki esas olcusu bulunur 0 x lt 360 ve k bir tam sayi olmak uzere olcusu x 360k olan acilarin esas olcusu x derecedir 0 x lt 2p ve k bir tam sayi olmak uzere olcusu x 2pk olan acilarin esas olcusu x radyandir Merkezi orijin ve yaricapi 1 birim olan cembere birim cember veya trigonometrik cember denir Birim cemberin denklemi x2 y2 1 seklindedir Sarma islevi Gercel sayilar kumesinden birim cember uzerindeki noktalara tanimlanan isleve sarma islevi denir Sarma islevini s ile birim cemberi de C ile gosterirsek islev s R C displaystyle s mathbb R to C seklinde yazilabilir ve s x P displaystyle s x P oldugunda s x 2kp P displaystyle s x 2k pi P olur Baska bir deyisle sarma islevi gercel sayilar uzerinde donemi periyodu 2p displaystyle 2 pi olan bir islevdir Islevler arasindaki iliskiler Yukaridaki tanimlardan gorulebilecegi gibi bu islevler arasinda cos2 x sin2 x 1 displaystyle cos 2 x sin 2 x 1 Pisagor teoremi sec2 A tan2 A 1 displaystyle sec 2 A tan 2 A 1 csc2 A cot2 A 1 displaystyle csc 2 A cot 2 A 1 iliskileri vardir Sik kullanilan acilarin trigonometrik oranlari 0 displaystyle 0 circ 30 p6 displaystyle 30 circ frac pi 6 45 p4 displaystyle 45 circ frac pi 4 60 p3 displaystyle 60 circ frac pi 3 90 p2 displaystyle 90 circ frac pi 2 180 p displaystyle 180 circ pi 270 3p2 displaystyle 270 circ frac 3 pi 2 360 2p displaystyle 360 circ 2 pi sin x displaystyle sin x 0 displaystyle 0 12 displaystyle frac 1 2 22 displaystyle frac sqrt 2 2 32 displaystyle frac sqrt 3 2 1 displaystyle 1 0 displaystyle 0 1 displaystyle 1 0 displaystyle 0 cos x displaystyle cos x 1 displaystyle 1 32 displaystyle frac sqrt 3 2 22 displaystyle frac sqrt 2 2 12 displaystyle frac 1 2 0 displaystyle 0 1 displaystyle 1 0 displaystyle 0 1 displaystyle 1 tan x displaystyle tan x 0 displaystyle 0 13 displaystyle frac 1 sqrt 3 1 displaystyle 1 3 displaystyle sqrt 3 displaystyle tilde infty 0 displaystyle 0 displaystyle tilde infty 0 displaystyle 0 cot x displaystyle cot x displaystyle tilde infty 3 displaystyle sqrt 3 1 displaystyle 1 13 displaystyle frac 1 sqrt 3 0 displaystyle 0 displaystyle tilde infty 0 displaystyle 0 displaystyle tilde infty sec x displaystyle sec x 1 displaystyle 1 23 displaystyle frac 2 sqrt 3 2 displaystyle sqrt 2 2 displaystyle 2 displaystyle tilde infty 1 displaystyle 1 displaystyle tilde infty 1 displaystyle 1 csc x displaystyle csc x displaystyle tilde infty 2 displaystyle 2 2 displaystyle sqrt 2 23 displaystyle frac 2 sqrt 3 1 displaystyle 1 displaystyle tilde infty 1 displaystyle 1 displaystyle tilde infty Gercek veya karmasik degiskenlerin trigonometrik fonksiyonlariTrigonometrik fonksiyon grafikleri 6 ana trigonometrik fonksiyonun ozelliklerini ozetleyen diyagramlar Fonksiyon Periyot Alan Aralik Diyagramsinus 2p displaystyle 2 pi displaystyle infty infty 1 1 displaystyle 1 1 cosinus 2p displaystyle 2 pi displaystyle infty infty 1 1 displaystyle 1 1 tanjant p displaystyle pi x p 2 np displaystyle x neq pi 2 n pi displaystyle infty infty sekant 2p displaystyle 2 pi x p 2 np displaystyle x neq pi 2 n pi 1 1 displaystyle infty 1 cup 1 infty cosekant 2p displaystyle 2 pi x np displaystyle x neq n pi 1 1 displaystyle infty 1 cup 1 infty cotanjant p displaystyle pi x np displaystyle x neq n pi displaystyle infty infty Ters trigonometrik fonksiyonlar 6 ana trigonometrik fonksiyon periyodik oldugu icin birebir degillerdir yani ters cevrilemezler ancak trigonometrik bir fonksiyonun alanini kisitlayarak ters cevrilebilirler 48ff Fonksiyon Genel gosterim Ifade x deger araligi Asil deger araligi radyan Asil deger araligi derece arcsinus y arcsin x x sin y 1 x 1 p 2 y p 2 90 y 90 arckosinus y arccos x x cos y 1 x 1 0 y p 0 y 180 arctanjant y arctan x x tan y tum reel sayilar p 2 lt y lt p 2 90 lt y lt 90 arckotanjant y arccot x x cot y tum reel sayilar 0 lt y lt p 0 lt y lt 180 arcsekant y arcsec x x sec y x 1 or 1 x 0 y lt p 2 or p 2 lt y p 0 y lt 90 or 90 lt y 180 arckosekant y arccsc x x csc y x 1 or 1 x p 2 y lt 0 or 0 lt y p 2 90 y lt 0 or 0 lt y 90 Kullanim alanlariFreiberger Denizcilik Sekstanti Trigonometri bircok fen biliminde matematigin diger alanlarinda ve cesitli sanatlarda yaygin bir bicimde kullanilmaktadir Trigonometriyi kullanan bazi dallar sunlardir jeofizik kristalografi ekonomi ozellikle de finansal pazarlarin analizinde elektrik muhendisligi insaat muhendisligi elektronik jeodezi makine muhendisligi meteoroloji muzik kurami sayi kurami ve dolayisiyla kriptografi osinografi okyanus bilimi farmakoloji eczacilik optik fonetik olasilik kurami psikoloji sismoloji Trigonometri yukarida orneklendigi gibi bircok farkli alana farkli katkilarda bulunmustur Ornegin Pisagor kuraminin isim babasi Pisagor matematiksel muzik kuramina ilk katkida bulunan isimlerdendir Osinografide bazi dalgalarin sinus dalgalarina benzerligi ilgili incelemelerde trigonometrinin kullanimina olanak tanimistir Bunun disinda Fourier serileri sayesinde trigonometrik islevler farkli fonksiyonlari temsil etmekte kullanilirlar ve bu sayede trigonometri bircok yararlanilan dallarda kullanim olanagi bulmustur OzdesliklerUcgen ozdeslikleri Sinus teoremi Kosinus teoremi Tanjant teoremi Trigonometrik ozdeslikler Euler bagintisi ei8 cos 8 isin 8 displaystyle e i theta cos theta i sin theta Bu bagintiyla iki matematiksel ifade olan i ve p displaystyle pi birbirine baglanmis olur de Moivre formulu cos x isin x n cos nx isin nx displaystyle left cos x i sin x right n cos left nx right i sin left nx right Diger ozdeslikler Toplam fark formulleri Trigonometrik degerleri bilinen iki acinin toplaminin veya farkinin trigonometrik degerlerini hesaplamak icin kullanilan formullerdir sin a b sin a cos b cos a sin b sin a b sin a cos b cos a sin b cos a b cos a cos b sin a sin b cos a b cos a cos b sin a sin b tan a b tan a tan b 1 tan a tan b tan a b tan a tan b 1 tan a tan b cot a b cot a cot b 1 cot a cot b cot a b cot a cot b 1 cot b cot a Yarim aci formulleri Yarim aci formulleri ya da iki kat aci formulleri trigonometrik degerleri bilinen bir acinin iki katinin veya yarisinin trigonometrik degerlerini hesaplamak icin kullanilan formullerdir sin2a 2sin a cos a cos2a cos2 a sin2 a cos2a 2cos2 a 1 cos2a 1 2sin2 a tan2a 2tan a 1 tan2 a tan2a 2 cot a tan a cot2a cot2 a 1 2cot a Donusum formulleri Donusum formulleri toplam durumundaki iki trigonometrik ifadeyi carpim haline getirmeye yarar Bu islemin amaci bazi ozel durumlarda islem kolayligi saglamaktir sin a sin b 2sin a b2cos a b2 displaystyle sin a sin b 2 sin a b over 2 cos a b over 2 sin a sin b 2cos a b2sin a b2 displaystyle sin a sin b 2 cos a b over 2 sin a b over 2 cos a cos b 2cos a b2cos a b2 displaystyle cos a cos b 2 cos a b over 2 cos a b over 2 cos a cos b 2sin a b2sin a b2 displaystyle cos a cos b 2 sin a b over 2 sin a b over 2 tan a tan b sin a b cos acos b displaystyle tan a tan b frac sin a b cos a cos b tan a tan b sin a b cos acos b displaystyle tan a tan b frac sin a b cos a cos b cot a cot b sin a b sin asin b displaystyle cot a cot b frac sin a b sin a sin b cot a cot b sin a b sin asin b displaystyle cot a cot b frac sin a b sin a sin b Ayrica bakinizTrigonometrinin ana hatlariNotlar Arsivlenmis kopya 11 Temmuz 2015 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 20 Aralik 2014 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Arsivlenmis kopya 27 Subat 2021 tarihinde kaynagindan Erisim tarihi 28 Kasim 2020 Mary P Attenborough 30 Haziran 2003 Mathematics for Electrical Engineering and Computing Elsevier s 418 ISBN 978 0 08 047340 6 12 Mart 2022 tarihinde kaynagindan Erisim tarihi 22 Mart 2022 Ron Larson Bruce H Edwards 10 Kasim 2008 Calculus of a Single Variable Cengage Learning s 21 ISBN 978 0 547 20998 2 22 Mayis 2022 tarihinde kaynagindan Erisim tarihi 22 Mart 2022 Elizabeth G Bremigan Ralph J Bremigan John D Lorch 2011 Mathematics for Secondary School Teachers MAA ISBN 978 0 88385 773 1 5 Mayis 2022 tarihinde kaynagindan Erisim tarihi 22 Mart 2022
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans