Pergeli Apollonius

Pergeli Apollonius (Grekçe: Ἀπολλώνιος ὁ Περγαῖος; Latince: Apollonius Pergaeus; d. yaklaşık MÖ 240 Perge - ö. yaklaşık MÖ 190, İskenderiye), konik kesitler üzerindeki çalışmaları ile tanınan Antik Yunan geometri uzmanı ve astronom. Öklid ve Arşimet'in konuya katkılarından başlayarak, onları analitik geometrinin icadından önceki duruma getirdi. Elips, parabol ve hiperbol terimlerinin tanımları bugün kullanımda olanlardır.

Pergeli Apollonius
Giovanni Battista Memo'nun eserlerinin 1537 baskısından Pergeli Apollonius'un yakından görünümü.
Kendi dilinde adı	Ἀπολλώνιος ὁ Περγαῖος
Doğum	MÖ 262/240 Perge, Pamfilya (Pamphylia)
Ölüm	MÖ 190 İskenderiye
Milliyet	Antik Yunan
Diğer ad(lar)ı	Apollonius Pergaeus, Apollonios, Apollonius of Perga, أبلونيوس البرغاوي
Meslek	Matematikçi (Geometrici), astronom, yazar
Önemli eser(ler)	Konikler (Conics)

Apollonius, astronomi de dahil olmak üzere çok sayıda başka konu üzerinde çalıştı. Tipik olarak diğer yazarlar tarafından atıfta bulunulan parçalar haricinde bu çalışmanın çoğu günümüze ulaşmadı. Yaygın olarak Orta Çağ'a kadar inanılan gezegenlerin görünüşte anormal hareketini açıklamak için eksantrik yörüngeler hipotezi, Rönesans sırasında yerini aldı.

Hayatı

Matematik alanına böylesine önemli katkılarda bulunan bir kişi için, yetersiz biyografik bilgi mevcuttur. 6. yüzyıl Yunan yorumcusu Ascalonlu Eutocius, Apollonius'un ana eseri olan Konikler (İngilizce: Conics) üzerine şöyle diyor:

Perge, o zamanlar Anadolu'da Helenleşmiş bir Pamphylia kentiydi. Şehrin kalıntıları halen ayaktadır. Helenistik bir kültür merkeziydi. Euergetes, "hayırsever", diadochi mirasında Mısır'ın üçüncü Yunan hanedanı olan Ptolemy III Euergetes'i tanımlar. Muhtemelen “zamanları”, MÖ 246-222/221 dönemine aittir. Zamanlar her zaman hükümdar veya yetkili yargıç tarafından kaydedilir, böylece Apollonius 246'dan önce doğmuş olsaydı, Euergetes'in babasının "zamanları" olurdu. Herakleios'un kimliği belirsizdir. Apollonius'un yaklaşık zamanları bu nedenle kesindir, ancak tam tarihler verilemez. Çeşitli bilim adamları tarafından belirtilen belirli doğum ve ölüm yılları rakamı yalnızca spekülatiftir.

Eutocius, Perge'yi Mısır'ın Ptolemaios hanedanı ile ilişkilendiriyor gibi görünmektedir. Mısır altında, MÖ 246'da Perge, Seleukos hanedanı tarafından yönetilen bağımsız bir diadochi devleti olan Seleukos İmparatorluğu'na ait değildi. MÖ 3. yüzyılın son yarısında, Perge birkaç kez el değiştirdi, alternatif olarak Seleukoslar ve kuzeyde Attalid hanedanı tarafından yönetilen Bergama Krallığı altında. "Pergeli" olarak adlandırılan birinin orada yaşamış ve çalışmış olması pekala beklenebilir. Aksine, Apollonius daha sonra Perge ile özdeşleştirilmişse, onun ikametgâhına dayanmıyordu. Kalan otobiyografik materyaller, onun İskenderiye'de yaşadığını, okuduğunu ve yazdığını ima etmektedir.

Yunan matematikçi ve astronom Hypsicles'ın bir mektubu, aslında Öklid'in Elementler kitabının, on üç kitabının bir parçası olan Öklid'in XIV. Kitabından alınan ekin bir parçasıydı.

“	"Tyreli Basilides, Ey Protarchus İskenderiye'ye gelip babamla tanıştığında, ikametinin büyük bir kısmını, matematiğe olan ortak ilgileri nedeniyle aralarındaki bağ nedeniyle geçirdi. Ve bir keresinde, Apollonius'un (Pergalı Apollonius) bir ve aynı alanda çizili 12 yüzlü (dodecahedron) ile 20 yüzlü (ikosahedron)'nün karşılaştırılmasıyla ilgili yazdığı, yani birbirlerine oranlarının ne olduğu sorusuyla ilgili yazılan sayfaya bakıldığında, Apollonius'un bu kitaptaki değerlendirmesinin doğru olmadığı sonucuna vardılar; buna göre, babamdan anladığım gibi, onu değiştirip yeniden yazmaya başladılar. Ancak daha sonra Apollonius tarafından yayınlanan, söz konusu konunun bir gösterimini içeren başka bir kitaba rastladım ve problemle ilgili araştırmasından çok etkilendim. Apollonius'un yayınladığı kitap artık herkesin erişimine açık; çünkü daha sonra dikkatli bir şekilde ayrıntılandırmanın sonucu gibi görünen bir biçimde geniş bir sirkülasyona sahip." "Benim açımdan, gerekli gördüklerimi size yorum yoluyla aktarmaya karar verdim, kısmen de yapabileceğiniz için, tüm matematik ve özellikle geometri alanındaki yeterliliğiniz nedeniyle, yazmak üzere olduğum şey hakkında uzman bir yargıya varmak ve kısmen de babamla yakınlığınız ve kendime karşı dostça duygularınız nedeniyle keşfime nazikçe kulak verin, araştırmamı iyi dinleyeceksiniz. Ancak, ön sözü yapmanın ve incelememe kendisinin başlamasının zamanı geldi."	„

Zamanında çok bilinmeyen, fakat 1600 yıllarında değeri anlaşılan Yunan matematikçilerinden biri Pergeli Apollonius'tur. Eski devirlerin en büyük matematikçilerinden biridir. MÖ 267 veya 262 yıllarında, Pamfiye denilen Teke sancağının Perge kentinde dünyaya gelmiştir. Mısır'ın İskenderiye kentine giderek, Öklid'ten sonra gelen matematikçilerden dersler alarak kendini yetiştirmiştir. Bir aralık Bergama'ya giderek orada kalmış, burada matematikçi Ödemus ve eski Bergama hükümdarı Atal ile ilmi ilişkilerde bulunmuştur. Matematikçi Pappus, Apollonius'un, bencil, üne düşkün, kibirli ve gururlu birisi olduğunu yazmaktadır. Apollonius'un yaptığı çalışmalar ve buluşları onun bu zayıf taraflarını örtecek kadar kuvvetlidir. Çarpmaya ait birçok buluşu vardır. Tümü geometriye ait olan yedi sekiz kitabı vardır. Koniklere ait buluşları onu şöhretin zirvesine çıkarmıştır. Birçok eserinin kaybolmasına karşın, bazı yapıtları Pappus tarafından yeniden ortaya çıkarılmıştır.

Öklid geometrisini benimseyerek onu daha ileri düzeylere götürmüştür. Teorik ve sentetik geometrici olarak, 19. yüzyıldaki Steiner'e kadar Apollonius'un bir eşine daha rastlanamaz. Konikler adı altında bugün bildiğimiz elips, çember, (hiperbol) ve parabol kesişimlerine ait problemlerin birçoğu Apollonius tarafından bulunmuştur. Konikler her ne kadar Apollonius'tan 150 yıl kadar önce üzerinde çalışılmışsa da, Apollonius kendisinden önceki çalışmaları ve kendi öz buluşlarını sekiz kitapta toplamıştır. Bunların çoğu onun çalışmaları ile ilerlemiştir. Yedi tane de yeni araştırması vardır. Bu araştırmaların bazıları Arapça'dan çevirmedir. Yine, analitik geometri özelliklerinin hemen hemen tümünü Apollonius'a borçluyuz.

Dairesel tabanlı ve tepesinin her iki tarafından sonsuza kadar uzatılmış bir koni bir düzlemle kesilirse, düzlemle koni yüzeyinin kesişimi olan eğri, doğru, çember, hiperbol, elips veya parabol olacağını ilk kez Apollonius göstermiştir. Merminin yörünge denkleminin bir parabol olacağı yine Apollonius tarafından bulunmuştur. Ayrıca, astronomide önemli buluşları vardır.

Elips, hiperbol ve parabol, Eflatun tarafından mekanik eğriler olarak adlandırılmıştır. Bu eğriler, yalnız cetvel ve pergel yardımıyla çizilemezler. Buna karşın, pergel ve cetvel yardımıyla, bu eğrilerin istenilen sayıda noktalarını elde edebiliriz. Apollonius ve konikler üzerine çalışma yapanların diğer bir hizmeti de, Kepler ve Kopernik'in Güneş ve gezegenlerin yörüngelerini hesaplamasında kullanmasıdır. Eğer bu geometriciler olmasaydı, Newton çekim kanununu belki de hiç bulamayacaktı. Yani, Kepler'in gezegenlerin yörüngeleri hakkındaki ince ve ustalıklı kullandığı hesaplamaları, Newton'un çekim kanununa ortam hazırlamıştır. Pergel ve cetvel yardımıyla üç çembere teğet çizme, Apollonius problemi olarak bilinir. Yine, sabit iki noktaya olan uzaklıkları oranı sabit olan noktaların geometrik yeri, bu sabit noktaları birleştiren doğru parçasını, verilen orana göre içten ve dıştan bölen noktalar arasındaki uzaklığı çap kabul eden bir çemberdir.

Apollonius'un zamanları

Apollonius, Helen kültürünün geniş Helenik olmayan bölgelerde çeşitli derinliklere, bazı yerlerde radikal, diğerlerinde hemen hemen hiç radikal olmayan bir şekilde üst üste binmesiyle karakterize edilen ve şimdi Hellenistik Dönem olarak adlandırılan tarihi bir dönemin sonuna doğru yaşadı. Değişiklik, Makedonyalı II. Philip ve oğlu Büyük İskender tarafından başlatıldı, o da tüm Yunanistan'ı bir dizi çarpıcı zafere maruz bırakarak Pers İmparatorluğunu fethetmeye devam etti. Mısır'dan Pakistan'a kadar bölgeleri yöneten Philip, MÖ 336'da suikasta kurban gitti. İskender, geniş Pers imparatorluğunu fethederek planını gerçekleştirmeye devam etti.

Apollonius'un kısa otobiyografisi

Materyal, Konikler kitaplarının hayatta kalan sahte “Önsözlerinde” yer almaktadır. Bunlar Apollonius'un nüfuzlu arkadaşlarına gönderilen ve mektupla birlikte verilen kitabı gözden geçirmelerini isteyen mektuplardır. Bir Eudemus'a hitap eden Birinci Kitabın Önsözü, ona Koniklerin başlangıçta İskenderiye'deki bir ev konuğu olan geometri uzmanı Naucrates tarafından talep edildiğini hatırlatır. Naucrates ziyaretin sonunda sekiz kitabın ilk taslağını elinde tuttu. Apollonius, bunlardan “tam bir arındırma olmaksızın” (Yunanca ou diakatharantes, Latince ea non perpurgaremus) olarak söz eder. Kitapları doğrulayıp düzeltmeyi, her birini tamamlandığı gibi yayınlamayı amaçladı.

Bu planı Apollonius'un daha sonraki Bergama ziyaretinde duyan Eudemus, Apollonius'un her kitabı yayınlanmadan önce kendisine göndermesinde ısrar etmişti. Koşullar, bu aşamada Apollonius'un topluluğu ve yerleşik profesyonellerin tavsiyelerini arayan genç bir geometri olduğunu gösteriyor. Pappus, İskenderiye'de Öklid öğrencilerinin yanında olduğunu belirtir. Öklid çoktan gitmişti. Bu kalma, belki de Apollonius'un eğitiminin son aşamasıydı. Eudemus, muhtemelen Pergamon'daki ilk eğitiminde kıdemli bir figürdü; Her halükarda, Bergama Kütüphanesi ve Araştırma Merkezi'nin (Müze) başkanı olduğuna veya başına geçtiğine inanmak için sebepler vardır. Apollonius, ilk dört kitabın unsurların gelişimi ile ilgilendiğini, son dördünün ise özel konularla ilgilendiğini belirtiyor.

Önsözler I ve II arasında bir boşluk vardır. Apollonius, oğlu Apollonius'u II. Eudemus'un kitabı özel çalışma gruplarında kullandığını öne sürerek daha özgüvenle konuşuyor, bu da Eudemus'un araştırma merkezinde müdür değilse de kıdemli bir önemli isim olduğunu ima ediyor. Büyük İskender ve onun kuzey kolundaki arkadaşlarının ikametgâhı nedeniyle Atina'daki Aristo Lycaeum modelini izleyen bu tür kurumlarda araştırma, kütüphane ve müzenin tamamlandığı, eğitim çabasının bir parçasıydı. Eyalette böyle tek bir okul vardı. Kralın sahip olduğu bina, tipik olarak kıskanç, coşkulu ve katılımcı olan kraliyet himayesindeydi. Krallar, değerli kitapları ellerinden geldiğince ve her yerde satın aldı, yalvardı, ödünç aldı ve çaldı. Kitaplar en yüksek değere sahipti ve yalnızca zengin müşteriler için karşılanabilirdi. Onları toplamak kraliyet yükümlülüğüydü. Bergama, parşömen endüstrisiyle biliniyordu ve "parşömen", "Pergamon" dan türemiştir.

Apollonius, Efes'te Eudemus ile tanıştığı bir geometrici olan Laodikeia'lı Philonides'i akla getiriyor. Philonides, Eudemus'un öğrencisi oldu. MÖ 2. yüzyılın 1. yarısında esas olarak Suriye'de yaşadı. Görüşmenin Apollonius'un Efes'te yaşadığını gösterip göstermediği ise çözülmedi. Akdeniz'in entelektüel topluluğu kültür olarak uluslararasıydı. Akademisyenler iş ararken hareket halindeydiler. Hepsi bir tür posta servisi aracılığıyla, kamuya açık veya özel olarak iletişim kurdular. Hayatta kalan mektuplar boldur. Birbirlerini ziyaret ettiler, birbirlerinin çalışmalarını okudular, birbirlerine önerilerde bulundular, öğrenciler tavsiye ettiler ve bazıları “matematiğin altın çağı” olarak adlandırılan bir gelenek biriktirdiler.

Önsöz III eksiktir. IV. Önsözde Apollonius "Eudemus'un öldüğü zaman aralığında" diyor, yine Eudemus'un Apollonius'tan daha kıdemli olduğu görüşünü destekliyor. Önsöz IV – VII daha resmidir, kişisel bilgileri çıkarır ve kitapları özetlemeye odaklanır. Bunların hepsi gizemli bir Attalus'a, Apollonius'un Attalus'a yazdığı gibi, "eserlerime sahip olma konusundaki ciddi arzunuzdan dolayı" yapılan bir seçimdir. O zamana kadar Bergama'da pek çok insan böyle bir istek duydu. Muhtemelen bu Attalus, Apollonius'un şaheserinin kopyalarını yazarın elinden yeni alan özel biriydi. Güçlü bir teoriye göre Attalus, Attalus II Philadelphus, MÖ 220-138, genel ve kardeşinin krallığının savunucusu (Eumenes II), ikincisinin MÖ 160'taki hastalığına eş-naip ve MÖ 158'de tahtının ve dul eşinin varisidir. O ve erkek kardeşi, kütüphaneyi uluslararası ihtişamla genişleten büyük sanat hamileriydi. Tarihler Philonides'inkilerle uyumluyken, Apollonius'un amacı Attalus'un kitap toplama girişimi ile de uyumludur.

Apollonius Önsöz V–VII'yı Attalus'a gönderdi. Önsöz VII'de, Kitap VIII'i "bir ek" ... "size olabildiğince çabuk göndermeye özen göstereceğim" şeklinde tanımlıyor. Gönderildiğine veya tamamlandığına dair hiçbir kayıt yoktur. Tarihte hiç olmadığı için de eksik olabilir, Apollonius tamamlanmadan ölmüştür. Ancak İskenderiyeli Pappus bunun için lemmalar sağladı, bu nedenle en azından bazı baskıları bir zamanlar dolaşımda olmalıydı.

Apollonius'un belgelenmiş eserleri

Apollonius, çok sayıda eser ortaya çıkaran üretken bir geometriciydi. Ne yazık ki bunlardan sadece biri, Konikler (İngilizce: Conics) adlı eseri hayatta kaldı. Bugünün standartlarına göre bile konu üzerine yoğun ve kapsamlı bir referans çalışmasıdır ve şu anda az bilinen geometrik önermelerin bir deposu ve Apollonius tarafından tasarlanan bazı yeni öğrenenler için bir araç olarak hizmet vermektedir. Dinleyicileri okuyamayan veya yazamayan genel nüfus değildi. Her zaman matematik bilginleri, devlet okulları ve ilgili kütüphaneleriyle bağlantılı az sayıdaki eğitimli okuyucular için tasarlandı. Başka bir deyişle, her zaman bir kütüphane referans çalışmasıydı. Temel tanımları önemli bir matematiksel miras haline gelmiştir. Çoğunlukla yöntemlerinin ve sonuçlarının yerini Analitik Geometri almıştır.

Sekiz kitabından yalnızca ilk dördü, Apollonius'un orijinal metinlerinden geldiği konusunda güvenilir bir iddiaya sahiptir. 5-7. kitaplar Arapçadan Latinceye çevrilmiştir. Orijinal Yunanca hali kaybolmuştur. Kitap VIII'in durumu ise bilinmemektedir. İlk taslak vardı ama nihai taslağın kitaba dönüşüp dönüşmediği bilinmemektedir. Edmond Halley tarafından Latince olarak "yeniden yapılanmış" bir versiyonu vardır ama ne kadarının Apollonius'a çok benzediğini bilmenin bir yolu yoktur. Halley ayrıca De Rationis Sectione ve De Spatii Sectione adlı eserleri de yeniden inşa etti. Bu eserlerin ötesinde, bir avuç bölüm dışında, herhangi bir şekilde Apollonius'tan gelme olarak yorumlanabilecek belgeler son bulmaktadır.

Kayıp eserlerinin çoğu yorumcular tarafından anlatılmakta veya bahsedilmektedir. Ek olarak, belgeler olmadan diğer yazarlar tarafından Apollonius'a atfedilen fikirler vardır. İnanılır ya da değil, onlar kulaktan dolmadır ve nakledilmiştir. Bazı yazarlar, Apollonius'u belirli fikirlerin yazarı olarak tanımlar ve dolayısıyla onun adını verir. Diğerleri, Apollonius'u modern gösterim veya deyimlerle belirsiz derecelerde sadakatle ifade etmeye çalışır.

Konikler (Conics)

Bir düzlemin farklı açılarda bir koni ile kesişmesiyle oluşturulan konik kesitler veya iki boyutlu şekiller. Bu şekillerin teorisi, eski Yunan matematikçiler tarafından kapsamlı bir şekilde geliştirildi ve özellikle Pergeli Apollonius'unki gibi çalışmalarda günümüze ulaştı. Konik kesitler, modern matematikte de yerini almıştır.

Yunanca Konikler metni, tanımların, şekillerin ve parçalarının Öklid düzenlemesini kullanır yani "verilenler", ardından "kanıtlanacak" önermeler yer alır. Kitaplar I-VII, 387 önerme sunar. Bu tür bir düzenleme, geleneksel konunun herhangi bir modern geometri ders kitabında görülebilir. Herhangi bir matematik dersinde olduğu gibi, materyal çok yoğundur ve dikkate alınması zorunlu olarak yavaştır. Apollonius'un her kitap için Önsözler bölümünde kısmen açıklanan bir planı vardı. Planın başlıkları veya işaretçileri bir şekilde eksiktir, Apollonius konuların mantıksal akışına daha çok bağlıydı.

Böylece çağın yorumcuları için entelektüel bir niş yaratılır. Her biri Apollonius'u kendi zamanına göre en anlaşılır ve en alakalı şekilde sunmalıdır. Çeşitli yöntemler kullanırlar: ek açıklama, kapsamlı ön hazırlık materyali, farklı biçimler, ek çizimler, kişi eklenmesiyle yüzeysel yeniden düzenleme, vb. Yorumda ince farklılıklar vardır. Modern İngilizce konuşmacı, İngiliz akademisyenlerin Yeni Latinceyi tercih etmesinden dolayı İngilizce materyal eksikliği ile karşılaşır. Hellenistik matematik ve astronomi geleneğinin soyundan gelen Edmund Halley ve Isaac Newton gibi entelektüel İngiliz devleri, çoğu klasik dilleri bilmeyen, İngilizce konuşan topluluklar tarafından yalnızca çevirisinden okunabilir ve yorumlanabilir.

Tamamen anadili İngilizce olan sunumlar 19. yüzyılın sonlarında başlar. Heath'in Konik Kesitler Üzerine İnceleme (İngilizce: Treatise on Conic Sections özel bir notu. Kapsamlı önsöz yorumu, Yunancayı, anlamlarını ve kullanımını veren Apolloncu geometrik terimler sözlüğü gibi öğeleri içerir. "Tezin görünüşte alçak gönüllü büyük çoğunluğunun birçok kişiyi tanışma girişiminden caydırdığı" yorumunu yaparak, organizasyonu yüzeysel olarak değiştirmek ve metni modern notasyonla netleştirmek üzere başlık eklemeye söz veriyor. Dolayısıyla çalışması, parantez içinde uygunlukların verildiği iki organizasyon sistemine atıfta bulunuyor; kendisine ait ve Apollonius'a ait.

Heath'in çıkarttığı iş vazgeçilmezdir. 20. yüzyılın başlarında öğretmenlik yaptı, 1940'ta vefat etti, ancak bu arada başka bir bakış açısı gelişiyordu. Komşu olduğu Maryland, Annapolis'teki Birleşik Devletler Donanma Akademisi'nden önce sömürge döneminden beri askerî okul olan St. John's College (Annapolis/Santa Fe), 1936'da akreditasyonunu kaybetmiş ve iflasın eşiğindeydi. Yönetim kurulu çaresizlik içinde, Klasikler öğretimi için yeni bir teorik program geliştirdikleri Chicago Üniversitesi'nden Stringfellow Barr ve Scott Buchanan'ı çağırdı. Fırsattan yararlanarak, 1937'de St. John's'ta “yeni programı” başlattılar, daha sonra Batı medeniyetinin kültürüne katkıda bulunan seçkin önemli kişilerin eserlerini öğretecek sabit bir müfredat olan Büyük Kitaplar (Great Books) programını adlandırdılar. St. John's'ta Apollonius, analitik geometriye ek olarak değil, kendisi olarak öğretilmeye başlandı.

Apollonius'un konularının "eğitmeni", 1937'de Virginia Üniversitesi'nden yeni bir doktor olan R. Catesby Taliaferro idi. 1942'ye kadar ders verdi ve daha sonra 1948'de bir yıl boyunca İngilizce çevirileri kendisi sağlayarak Batlamyus'un Almagest ve Apollonius'un Koniklerini tercüme etti. Bu çeviriler Encyclopædia Britannica'nın Batı Dünyası'nın Büyük Kitapları serisinin bir parçası oldu. Özel konular için bir ek ile birlikte yalnızca Kitaplar I-III dahil edilmiştir. Heath'in aksine Taliaferro, Apollonius'u yüzeysel olarak bile yeniden düzenlemeye ya da onu yeniden yazmaya kalkışmadı. Modern İngilizceye çevirisi Yunancayı oldukça yakından takip eder. Modern geometrik gösterimi bir dereceye kadar kullanmıştır.

Taliaferro'nun çalışmalarıyla eşzamanlı olarak, II. Dünya Savaşı döneminden bir Oxford bağışçısı olan Ivor Thomas, Yunan matematiğine yoğun bir ilgi duyuyordu. Kraliyet Norfolk Alayında bir subay olarak askerlik hizmeti sırasında meyve veren bir seçimler özeti planladı. Savaştan sonra, Loeb Klasik Kütüphanesi'nde, Loeb serisinde alışılmış olduğu gibi, sayfanın bir tarafında Yunanca ve diğer tarafında İngilizce ile Thomas tarafından çevrilmiş iki ciltlik bir yer buldu. Thomas'ın çalışması, Yunan matematiğinin altın çağı için bir el kitabı görevi gördü. Bu çalışma, Apollonius için yalnızca Kitap I'in bölümleri tanımlayan kısımlarını içerir.

Heath, Taliaferro ve Thomas, 20. yüzyılın büyük bölümünde halkın Apollonius'a olan talebini karşıladı. Ancak konu devam etmektedir. Daha yeni çeviriler ve araştırmalar, eski bilgileri incelemenin yanı sıra yeni bilgi ve bakış açılarını da içermektedir.

Kitap I

Kitap I, 58 önerme sunmaktadır. En dikkat çekici içeriği, koniler ve konik kesitler ile ilgili tüm temel tanımlardır. Bu tanımlar aynı kelimelerin modern tanımlarıyla tamamen aynı değildir. Etimolojik olarak modern sözcükler eskiden türetilmiştir, ancak sözcük kökü, anlam açısından refleksinden sıklıkla farklıdır.

Konik bir yüzey, bir açıortay noktası etrafında döndürülen bir çizgi parçası tarafından üretilir, öyle ki uç noktalar, her biri kendi düzleminde daireler çizer. Çift konik yüzeyin bir dalı olan bir koni, nokta (apeks veya verteks), daire (taban) ve tepe ile tabanın merkezini birleştiren bir çizgi olan eksen ile oluşan yüzeydir.

Bir "kesit" (Latince sectio, Yunanca tome), bir koninin bir düzlem tarafından hayali bir "dilimi"dir.

• Önerme I.3: "Bir koni, tepe noktasından bir düzlem tarafından kesilirse, bölüm bir üçgendir." Bir çift koni durumunda, bölüm, tepe noktasındaki açılar dikey açılar olacak şekilde iki üçgendir.
• Önerme I.4, bir koninin tabana paralel bölümlerinin eksen üzerinde merkezleri olan daireler olduğunu ileri sürer.* Önerme I.13, tabanın düzlemine eğimli bir düzlem tarafından tek bir koninin kesilmesi ve ikincisiyle koninin dışına uzanan tabanın çapına dik bir çizgide kesişmesi olarak tasarlanan elipsi tanımlar (gösterilmemiştir). Eğik düzlemin açısı sıfırdan büyük olmalıdır, aksi takdirde bölüm bir daire olacaktır. Şeklin bir parabol haline geldiği eksenel üçgenin karşılık gelen taban açısından da daha küçük olmalıdır.
• Önerme I.11 bir parabolü tanımlar. Düzlemi, eksenel üçgenin konik yüzeyinde bir kenara paraleldir.
• Önerme I.12 bir hiperbolu tanımlar. Düzlemi eksene paraleldir. Çiftin her iki konisini de keserek iki farklı dal elde eder (yalnızca bir tanesi gösterilmiştir).

Yunan geometriciler, Arşimet gibi büyük mucitlerin yapmaya alıştıkları gibi, mühendislik ve mimarinin çeşitli uygulamalarında envanterlerinden seçilmiş şekilleri düzenlemekle ilgilendiler. Konik kesitler için bir talep vardı ve halen vardır. Matematiksel karakterizasyonun gelişimi, geometriyi, bu tür cebirsel temelleri, değişkenler olarak çizgi parçalarına değer atamak gibi görsel olarak öne çıkaran Yunan geometrik cebirine doğru kaydırmıştı. Bir ölçüm kılavuzu ile Kartezyen koordinat sistemi arasında bir koordinat sistemi kullandılar. Oran teorileri ve alanların uygulanması, görsel denklemlerin geliştirilmesine izin verdi. (Aşağıda Apollonius'un Yöntemleri bölümüne bakın).

Animasyonlu şekil, bir parabolü karakterize eden matematiksel ilişkiyi ifade etmek için "alanların uygulanması" yöntemini tasvir etmektedir. Sol taraftaki değişen dikdörtgenin sol üst köşesi ve sağ taraftaki sağ üst köşesi "kesit üzerindeki herhangi bir nokta" dır. Animasyon, kesiti takip ediyor. Üstteki turuncu kare, "noktadan çapa kadar olan mesafedeki karedir; yani koordinatın bir karesidir. Apollonius'ta, yönelim burada gösterilen dikeyden ziyade yataydır. Burada apsisin karesidir. Yönelimden bağımsız olarak, denklem aynıdır, isimler değişmiştir. Dıştaki mavi dikdörtgen, diğer koordinattaki dikdörtgen ve mesafe ${\displaystyle p}$'dir. Cebirde, ${\displaystyle x^{2}=py}$, bir parabol denklemidir. 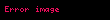Dış dikdörtgen ${\displaystyle py}$ alanını aşıyorsa, bölüm bir hiperbol, daha azsa bir elips olmalıdır.

"Alanların uygulanması", bir alan ve bir çizgi parçası verildiğinde dolaylı olarak bu alanın geçerli olup olmadığını sorar; yani, parçadaki kareye eşit mi? Evet ise, bir uygulanabilirlik (parabol) oluşturulmuştur. Apollonius Öklid'i takip ederek kesitin herhangi bir noktasının apsisindeki dikdörtgenin koordinatın karesine uygulanıp uygulanmadığını sordu. Eğer öyleyse, kelime denklemi, bir parabolün modern denklemlerinden biri olan 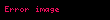${\textstyle y^{2}{=}kx}$'e eşdeğerdir. Dikdörtgenin kenarları ${\displaystyle k}$ ve ${\displaystyle x}$'tir. Buna göre şekle, parabol, "uygulama" adını veren oydu.

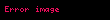
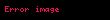
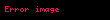
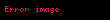
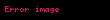
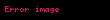
"Uygulanabilirlik yok" durumu ayrıca iki olasılığa bölünmüştür. Bir işlev verildiğinde, ${\textstyle f(x)}$, uygulanabilirlik durumunda ${\textstyle y^{2}{=}g(x)}$, uygulanabilirlik olmadığı durumda ${\textstyle y^{2}>g(x)}$ veya ${\textstyle y^{2}<g(x)}$. Birincisinde, ${\textstyle g(x)}$, "eksiklik (deficit)" olarak adlandırılan bir miktar nedeniyle ${\textstyle y^{2}}$ altında kalıyor. İkincisinde ise, ${\textstyle g(x)}$, "fazlalık (surfeit)" olarak adlandırılan bir miktar tarafından aşılır.

Uygulanabilirlik, eksiklik, ${\textstyle y^{2}{=}f(x){=}g(x)+d}$ eklenerek veya ${\textstyle g(x)-s}$ fazlalık çıkarılarak sağlanabilir. Bir açığı kapatan şekil elips olarak; bir fazlalık ise hiperbol olarak adlandırıldı. Modern denklemin terimleri şeklin orijinden ötelenmesi ve döndürülmesine bağlıdır, ancak bir elips için genel denklem;

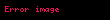
Ax² + By² = C

aşağıdaki biçime dönüştürülebilir;

${\displaystyle y^{2}{=}\left|{\frac {A}{B}}x^{2}\right|+{\frac {C}{B}}}$

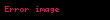
burada, denklem bir hiperbol içinse C/B, d'dir. (deficit=eksik miktar)

Ax² - By² = C

olur,

${\displaystyle y^{2}{=}\left|{\frac {A}{B}}x^{2}\right|-{\frac {C}{B}}}$

burada C/B s'dir. (surfeit=fazla miktar)

Kitap II

Kitap II, 53 önerme içerir. Apollonius, "olasılık sınırları için çaplar ve eksenlerle ilgili özellikleri ve ayrıca asimptotları ve diğer şeyleri" kapsamayı amaçladığını söylüyor. Onun "çap" tanımı gelenekselden farklıdır, çünkü mektubun hedeflenen alıcısını bir tanım için çalışmasına yönlendirmeyi gerekli bulmaktadır. Bahsedilen unsurlar, figürlerin şeklini ve oluşumunu belirten unsurlardır. Teğetler, kitabın sonunda ele alınmıştır.

Kitap III

Kitap III, 56 önerme içerir. Apollonius "katı lokusların inşası için kullanım ... üç-doğrulu ve dört-doğrulu lokus ..." teoremleri için orijinal keşfi iddia ediyor. Konik kesitin lokusu (geometrik yeri) kesittir. Üç-doğrulu lokus problemi (Taliafero'nun III. Kitap ekinde belirtildiği gibi), "verilen üç sabit düz çizgiden uzaklıkları olan noktaların yerini bulur ... mesafelerden birinin karesi her zaman diğer iki mesafenin içerdiği dikdörtgene sabit bir oranda olacak şekildedir." Bu, parabol ile sonuçlanan alanların uygulanmasının kanıtıdır. Dört doğru problemi elips ve hiperbol ile sonuçlanır. Analitik geometri, Descartes'ın övgüyle karşıladığı geometriden ziyade cebir tarafından desteklenen daha basit kriterlerden aynı lokusları türetir. Yöntemlerinde ise Apollonius'un yerini alır.

Kitap IV

Kitap IV, 57 önerme içerir. Eudemus'tan ziyade Attalus'a gönderilen ilki, onun daha olgun geometrik düşüncesini temsil eder. Konu oldukça uzmanlaşmıştır: "bir koninin bölümlerinin birbiriyle buluşabileceği veya bir çemberin çevresini karşılayabileceği en yüksek nokta sayısı ..." Yine de, coşkuyla konuşuyor ve onları problem çözmede "önemli ölçüde işe yarar" olarak nitelendiriyor. (Önsöz 4).

Kitap V

Yalnızca Arapçadan çevrilerek bilinen V. Kitap, tüm kitapların çoğu olan 77 önerme içerir. Elipsi (50 önerme), parabolü (22 önerme) ve hiperbolü (28 önerme) kapsar. Bunlar, Önsözler I ve V'de açık bir şekilde konu olarak yer almaz. Apollonius, maksimum ve minimum çizgiler olduğunu belirtir. Bu terimler açıklanmamıştır. Kitap I'in aksine, Kitap V hiçbir tanım ve açıklama içermez.

Belirsizlik, kitabın ana terimlerinin anlamını kesin olarak bilmeden yorumlaması gereken Apollonius'un yorumcuları için bir mıknatıs görevi gördü. Yakın zamana kadar Heath'in görüşü galip geldi: doğrular, kesitler için normal olarak değerlendirilecektir. Bu durumda bir normal, bazen ayak olarak adlandırılan teğet noktasındaki bir eğriye diktir. Bir kesit, Apollonius'un koordinat sistemine göre çizilirse (aşağıdaki Apollonius'un Yöntemleri bölümüne bakın), çap (Heath tarafından eksen olarak çevrilmiştir) x ekseni üzerinde ve tepe noktası solda orijinde olacak şekilde, önermeler, minimum/maksimumların kesit ve eksen arasında bulunacağını belirtir. Heath, hem teğet noktası hem de doğrunun bir ucu olarak hizmet eden kesitte sabit bir p noktası dikkate alınarak onun görüşüne bırakır. Eksendeki p ile bazı g noktaları arasındaki minimum mesafe bu durumda p’den normal olmalıdır.

Modern matematikte, eğrilerin normalleri, ayağın etrafında bulunan eğrinin küçük kısmının konumu olarak bilinir. Ayaktan merkeze olan mesafe 'dır. İkincisi, bir dairenin yarıçapıdır, ancak dairesel eğriler dışında küçük yay, bir dairesel yay ile yaklaştırılabilir. Dairesel olmayan eğrilerin eğriliği; örneğin, konik kesitler, kesit üzerinde değişmelidir. Eğrilik merkezinin haritası; yani, ayak bölüm üzerinde hareket ederken onun konumu, kesitin olarak adlandırılır. Bir çizginin ardışık konumlarının kenarı olan böyle bir şekil bugün olarak adlandırılır. Heath, V. Kitapta Apollonius'un normaller, evolütler ve zarflar teorisinin mantıksal temelini oluşturduğunu gördüğümüze inanıyordu.

Heath, 20. yüzyılın tamamı için Kitap V'in otoriter yorumu olarak kabul edildi, ancak yüzyılın değişmesi beraberinde bir görüş değişikliğini getirdi. 2001 yılında, Apollonius akademisyenleri Fried & Unguru, diğer Heath bölümlerine gereken saygıyı sunarak, Heath'in Kitap V analizinin tarihselliğine karşı çıktı ve “orijinali modern bir matematikçiye daha uygun hale getirmek için yeniden işlediğini … bu Heath'in çalışmasını tarihçi için şüpheli değer kılan, Apollonius'unkinden daha fazla Heath'in zihnini ortaya çıkaran türden bir şey.” olduğunu söylediler İddialarından bazıları özetle aşağıdaki gibidir. Ne önsözlerde ne de uygun kitaplarda maksimum/minimumun kendiliğinden normal olduğundan bahsedilmez. Heath'in, normalleri kapsadığı söylenen 50 önerme arasından sadece 7'si, Kitap V: 27-33, teğetlere dik olan maksimum/minimum çizgileri ifade eder veya ima eder. Bu 7 önerme, Fried tarafından kitabın ana önermeleri ile ilgisiz, izole olarak sınıflandırır. Hiçbir şekilde maksimum/minimumun genel olarak normal olduğu anlamına gelmez. Diğer 43 önermeyle ilgili kapsamlı araştırmasında Fried, çoğunun olamayacağını kanıtlıyor.

Fried ve Unguru, Apollonius'u geleceğin habercisi olmaktan çok geçmişin bir devamı olarak tasvir ederek karşı çıkıyor. Birincisi, standart bir ifadeyi ortaya çıkaran minimum ve maksimum satırlara yapılan tüm referansların eksiksiz bir filolojik çalışmasıdır. Her biri 20-25 önermeden oluşan üç grup vardır. İlk grup, varsayımsal bir "kesitteki bir noktadan eksene" tam karşısında olan "eksendeki bir noktadan kesite" ifadesini içerir. ki, öyle olsa da hiçbir şeye normal olmak zorunda değildir. Eksen üzerinde sabit bir nokta verildiğinde, onu kesitin tüm noktalarına bağlayan tüm çizgilerden biri en uzun (maksimum) ve biri en kısa (minimum) olacaktır. Diğer ifadeler "bir kesit içinde", "bir kesitten çizilmiş", "kesit ile ekseni arasında kesilmiş", eksen tarafından kesilmiş"dir ve hepsi aynı görüntüye atıfta bulunur.

Fried ve Unguru'nun görüşüne göre, Kitap V'in konusu tam olarak Apollonius'un söylediği şey, maksimum ve minimum çizgilerdir. Bunlar gelecekteki kavramlar için kod kelimeleri değil, o zamanlar kullanılan eski kavramlara atıfta bulunuyor. Yazarlar, kendisini dairelerle ve iç noktalardan çevreye maksimum ve minimum mesafelerle ilgili olan Öklid, Elemanlar, Kitap III'ten alıntı yapıyorlar. Herhangi bir genelliği kabul etmeden, "beğenmek" veya "benzeri" gibi terimler kullanırlar. "Neusis-benzeri" terimini yenilemesiyle tanınırlar. Bir , belirli bir parçayı verilen iki eğri arasına yerleştirme yöntemiydi. Bir P noktası ve üzerindeki eş bölümler işaretli olan bir cetvel verildiğinde, cetveli, bölüm aralarına sığana kadar iki eğriyi keserek P etrafında döndürür. Kitap V'de P, eksen üzerindeki noktadır. Etrafında bir cetvel döndürüldüğünde, minimum ve maksimumun ayırt edilebildiği bölüme olan mesafeler keşfedilir. Teknik duruma uygulanmaz, dolayısıyla neusis değildir. Yazarlar, eski yönteme arketipsel bir benzerlik görerek neusis-benzeri kullanıyorlar.

Kitap VI

Yalnızca Arapçadan çeviri yoluyla bilinen VI. Kitap, herhangi bir kitaptan daha az olan 33 önerme içerir. Ayrıca, önceki metinlerdeki hasar veya bozulma nedeniyle metinde büyük eksiklikler veya boşluklar vardır.

Konu nispeten açık ve tartışmasızdır. Önsöz 1, "konilerin eşit ve benzer kesitleri" olduğunu belirtir. Apollonius, Öklid tarafından sunulan uyum ve benzerlik kavramlarını üçgenler, dörtgenler gibi daha basit şekiller için konik kesitlere kadar genişletir. Önsöz 6, “eşit ve eşit olmayan” ve “benzer ve farklı” olan “kesitlerden ve bölümlerden” bahseder ve bazı yapısal bilgiler ekler.

Kitap VI, kitabın ön tarafındaki temel tanımlara bir dönüş sunar. "Eşitlik" alanların uygulanmasıyla belirlenir. Bir şekil varsa; yani, bir kesit veya bir bölüm diğerine "uygulanmış" (Halley tarafından si applicari possit altera super alteram olarak belirtilmiştir), çakışırlarsa ve birinin çizgisi diğerinin hiçbir çizgisini geçmiyorsa "eşittir" (Halley tarafından aequales olarak belirtilmiştir). Bu, Öklid, Kitap I, Ortak Kavramlar (Common Notions), 4: "ve birbiriyle çakışan şeyler (epharmazanta) eşittir (isa)" sonrasında açıkça bir uyum standardıdır. Tesadüf ve eşitlik örtüşür, ancak aynı değildir: Kesitleri tanımlamak için kullanılan alanların uygulanması, alanların nicel eşitliğine bağlıdır, ancak farklı şekillere ait olabilirler.

Aynı (homos), birbirine eşit ve farklı veya eşit olmayan örnekler arasında "aynı" (hom-oios) veya benzer şekiller vardır. Ne tamamen aynı ne de farklıdırlar, ancak aynı olan yönleri paylaşırlar ve farklı yönleri paylaşmazlar. Sezgisel olarak, geometrikçilerin akıllarında bir ölçek vardı; Örneğin, harita bir topoğrafik bölgeye benzer. Böylece şekiller kendilerinin daha büyük veya daha küçük versiyonlarına sahip olabilir.

Benzer şekillerde aynı olan yönler şekle bağlıdır. Öklid'in Elemanları kitabının 6. Kitabı, aynı karşılık gelen açılara sahip olanlarla benzer üçgenler sunar. Böylece bir üçgenin minyatürleri sizin istediğiniz kadar küçük olabilir veya dev versiyonları olabilir ve yine de orijinaliyle aynı üçgen olabilir.

Apollonius'un VI. Kitap'ın başındaki tanımlarında benzer sağ koniler, benzer eksenel üçgenlere sahiptir. Kesitlerin benzer bölümleri ve kesitler her şeyden önce benzer konilerdedir. Ayrıca her apsis için diğerinde istenen ölçekte bir apsis bulunmalıdır. Son olarak, birinin apsis ve ordinatı, diğeriyle aynı ordinat/apsis oranına sahip koordinatlarla eşleşmelidir. Toplam etki, farklı bir ölçek elde etmek için kesit veya bölümün koni üzerinde yukarı ve aşağı hareket ettirilmesi gibidir.

Kitap VII

Yine Arapçadan bir çeviri olan Kitap VII, 51 önerme içerir. Bunlar, Heath'in 1896 baskısında değerlendirdiği son şeylerdir. Önsöz I'de Apollonius bunlardan bahsetmiyor, bu da ilk taslağın yapıldığı tarihte bunların yeterince tutarlı bir biçimde tanımlanamayacaklarını ima ediyor. Apollonius, Halley'nin "de theorematis ad determinationem pertinentibus" olarak tercüme ettiği "peri dioristikon theorematon" ve Heath "limitlerin belirlenmesini içeren teoremler" olarak tercüme ettiği belirsiz bir dil kullanıyor. Bu tanımın dilidir, ancak hiçbir tanım yapılmaz. Referansın belirli bir tanım türüne ait olup olmayacağı bir değerlendirmedir ancak bugüne kadar inandırıcı bir şey önerilmemiştir. Apollonius'un yaşamının ve kariyerinin sonlarına doğru tamamlanan VII. Kitap konusu, Önsöz VII'de, büyük ölçüde bunlara dayandığı için eşlenik çapları içermesi gereken çaplar ve "bunlara göre tanımlanan şekiller" olarak belirtilmiştir. "Sınırlar" veya "tespitler" terimlerinin ne şekilde geçerli olabileceği belirtilmemiştir.

Çaplar ve bunların eşlenikleri Kitap I'de (Tanımlar: 4-6) tanımlanmıştır. Her çapın bir eşleniği yoktur. Bir çapın topoğrafyası (Yunanca diametros) düzgün bir kavisli şekil gerektirir. Modern zamanlarda ele alınan düzensiz şekilli alanlar antik tertip planında yoktur. Apollonius, elbette, genellikle dolambaçlı bir dille tanımladığı konik kesitleri aklında tutuyor: "aynı düzlemdeki bir eğri" bir daire, elips veya paraboldür, "aynı düzlemdeki iki eğri" ise bir hiperbol. Kiriş, iki uç noktası şeklin üzerinde olan düz bir çizgidir; yani şekli iki yerden keser. Şekle paralel kirişlerden oluşan bir kılavuz uygulanmışsa, çap, tüm kirişleri ikiye bölen ve eğrinin kendisine tepe (verteks) adı verilen bir noktada ulaşan çizgi olarak tanımlanır. Kapalı bir şekil olmasına gerek yoktur; örneğin, bir parabolün de bir çapı vardır.

Bir parabolün tek boyutta simetrisi vardır. Tek çapına katlandığını hayal ederseniz, iki yarım uyumludur veya birbirinin üzerine oturur. Aynı şey bir hiperbolün bir dalı için de söylenebilir. Bununla birlikte eşlenik çaplar (suzugeis'in "birbirine bağlı" olduğu, Yunanca suzugeis diametroi) iki boyutta simetriktir. Uygulandıkları şekiller, aynı zamanda, bugün olarak adlandırılan ve iki yönde simetri merkezi olarak hizmet eden bir alan merkezi (Yunanca kentron) gerektirir. Bu şekiller daire, elips ve iki dallı hiperboldür. Odaklarla karıştırılmaması gereken tek bir centroid vardır. Çap, merkezden geçen ve her zaman onu ikiye bölen bir kiriştir.

Daire ve elips için, paralel kirişlerden oluşan bir kılavuzun şeklin üzerine bindirilmesine izin verin, öyle ki, en uzun olan bir çaptır ve diğerleri, sonuncusu bir kiriş olmayıp bir teğet noktası olana kadar art arda daha kısadır. Teğet, çapa paralel olmalıdır. Eşlenik çap, merkez ve teğet nokta arasına yerleştirilen kirişleri ikiye böler. Dahası, her iki çap da birbirine eşleniktir ve buna eşlenik çift denir. Bir dairenin herhangi bir eşlenik çiftinin birbirine dik olduğu açıktır, ancak bir elipste, yalnızca ana ve küçük eksenler, diğer tüm durumlarda dikliği yok eden uzanımdır.

Eşlenikler, bir çift koninin tek bir düzlemle kesilmesinden kaynaklanan bir hiperbol'un iki dalı için tanımlanır ve eşlenik dallar denir. Aynı çapa sahipler. Centroid, köşeler arasındaki bölümü ikiye böler. Çapa benzer bir çizgi için daha yer vardır: çapa paralel bir çizgi kılavuzu, hiperbolün her iki dalını da kessin. Bu doğrular, aynı sürekli eğri üzerinde bitmemeleri dışında kiriş gibidir. Kiriş benzeri doğruları ikiye bölmek için ağırlık merkezinden bir eşlenik çap çizilebilir.

Bu kavramlar, esas olarak Kitap I'den, bölümler, çaplar ve eşlenik çaplar arasındaki ilişkileri ayrıntılı olarak tanımlayan Kitap VII'nin 51 önermesine başlamamızı sağlar. Apollonius'un diğer bazı özel konularda olduğu gibi, Analitik Geometri ile karşılaştırıldığında bugünkü faydaları görülmeye devam ediyor, ancak Önsöz VII'de hem yararlı hem de yenilikçi olduklarını doğruluyor; yani, onlar için itibarı hak ediyor.

Pappus tarafından tanımlanan kayıp ve yeniden yapılmış eserler

Pappus, Apollonius'un diğer incelemelerinden bahseder:

1. Λόγου ἀποτομή, De Rationis Sectione ("Cutting of a Ratio", "Oranların Paylaştırılması")
2. Χωρίου ἀποτομή, De Spatii Sectione ("Cutting of an Area", "Alanların Paylaştırılması")
3. Διωρισμένη τομή, De Sectione Determinata ("Determinate Section", "Kesit Belirlenmesi")
4. Ἐπαφαί, De Tactionibus ("Tangencies", "Teğetler")
5. Νεύσεις, De Inclinationibus ("Inclinations", "Eğimler")
6. Τόποι ἐπίπεδοι, De Locis Planis ("Plane Loci", "Düzlem Yerleşimleri").

Öklid'in Data, Porizmalar (Porisms) ve Yüzey-Yerleşimleri (Surface-Loci) ile Apollonius'un Konikleri (Conics) ile antik analizin gövdesinde yer alan Pappus'a göre bunların her biri iki kitaba ayrıldı. Yukarıda bahsedilen altı çalışmanın açıklamaları aşağıdadır.

De Rationis Sectione

De Rationis Sectione basit bir problemi çözmeye çalıştı: Her birinde iki düz çizgi ve bir nokta verildiğinde, üçüncü bir noktadan, iki sabit çizgiyi kesen düz bir çizgi çizin, böylelikle parçalar, verilen noktalar arasında kesişir ve bu üçüncü çizgi ile kesişme noktaları belirli bir orana sahip olabilir.

De Spatii Sectione

De Spatii Sectione, iki kesişimin içerdiği dikdörtgenin belirli bir dikdörtgene eşit olmasını gerektiren benzer bir problemi tartıştı.

17. yüzyılın sonlarında , Bodleian Kütüphanesi 'nde De Rationis Sectione’nin bir versiyonunu keşfetti. Bir çeviriye başlamasına rağmen, onu bitiren ve De Spatii Sectione restorasyonu ile 1706 ciline dahil eden Halley olmuştur.

De Sectione Determinata

De Sectione Determinata problemleri tek boyutlu analitik geometri olarak adlandırılabilecek bir şekilde ele alır; diğerlerine oranla bir doğru üzerinde noktalar bulma sorusuyla uğraşır. Spesifik problemler şunlardır: Düz bir çizgi üzerindeki iki, üç veya dört nokta verildiğinde, üzerinde öyle başka bir nokta bulun ki, verilen noktalara olan mesafeleri, üzerindeki karenin veya ikisinin içerdiği dikdörtgenin belirli bir orana sahip olması koşulunu sağlasın (1) Kalan kareye veya kalan ikisinin içerdiği dikdörtgene veya (2) geri kalanının içerdiği dikdörtgene ve verilen bir başka düz çizgiye. Bazıları Apollonius'un çözümünü keşfetmek için metni restore etmeye çalıştı, aralarında Snellius (, Leiden, 1698); Aberdeen 'den , Apollonius Redivivus’unun ekinde (Paris, 1612); ve Opera quaedam relquasında (Glasgow, 1776), açık ara en iyi girişimdi.

De Tactionibus

Daha fazla bilgi için 'ne bakın.

De Tactionibus aşağıdaki genel problemi benimsedi: Konumdaki üç şey (noktalar, düz çizgiler veya daireler) verildiğinde, verilen noktalardan geçen ve verilen düz çizgilere veya dairelere değen bir daireyi tanımlayın. En zor ve tarihsel olarak ilginç durum, verilen üç şey daire olduğunda ortaya çıkar. 16. yüzyılda, François Viète bu problemi (bazen Apollon problemi olarak da bilinir) hiperbol ile çözen 'a sundu. Bunun üzerine Vieta daha basit bir çözüm önerdi ve sonunda Apollonius'un küçük eseri olan Apollonius Gallus'taki (Paris, 1600) incelemesinin tamamını restore etmeye yöneltti. Problemin tarihi, 'ın özeti Apollonii Pergaei quae supersunt, ac maxime Lemmata Pappi in hos Libras, cum Observationibus, &c (Gothae, 1795, 8vo)'da araştırılmıştır.

De Inclinationibus

De Inclinationibus’un amacı, belirli bir noktaya doğru eğilimli, belirli bir uzunluktaki düz bir çizginin verilen (düz veya dairesel) iki çizgi arasına nasıl eklenebileceğini göstermekti. Marin Getaldić ve ("Geometrik Analiz", "Geometrical Analysis", Cadiz, 1698) restorasyon girişiminde bulunsa da, en iyisi Samuel Horsley (1770) tarafından yapılmıştır.

De Locis Planis

De Locis Planis, düz çizgilere veya dairelere ait olan lokuslarla (geometrik yer/yerleşimlerle) ilgili önermelerin bir koleksiyonudur. Pappus önermelerinin tüm ayrıntılarını verdiği için, bu metin sadece P. Fermat (Oeuvres, i., 1891, s. 3–51) ve (Leiden, 1656) tarafından değil ama aynı zamanda en başarılı şekilde R. Simson (Glasgow, 1749) tarafından da restore edilme çabalarını konu oldu.

Diğer antik yazarların bahsettiği kayıp eserler

Antik yazarlar, Apollonius'un artık var olmayan diğer eserlerine atıfta bulunur:

1. Περὶ τοῦ πυρίου, On the Burning-Glass (Yanan Aynalar Üzerine), muhtemelen parabolün odak özelliklerini araştıran bir inceleme
2. Περὶ τοῦ κοχλίου, On the Cylindrical Helix (Silindirik Helezon Üzerine) (Proclus tarafından bahsedildi)
3. Aynı küreye çizilmiş on iki yüzlü (dodecahedron) ve yirmi yüzlü (ikosahedron)'nün bir karşılaştırması
4. Ἡ καθόλου πραγματεία, Apollonius'un Öklid'in Elemanlarının iyileştirilmesi için belki de eleştirilerini ve önerilerini içeren matematiğin genel ilkeleri üzerine bir çalışma
5. Ὠκυτόκιον ("Quick Bringing-to-birth"), Eutocius'a göre Apollonius, π'nin değeri için Arşimet'inkinden daha yakın sınırların, 3+¹⁄₇ üst sınır olarak ve 3+¹⁰⁄₇₁ alt sınır olarak, nasıl bulunacağını gösterdi.
6. Hem büyük sayıları her gün Arşimet'in adlı eserindekinden daha fazla ifade etmek ve hem de bu büyük sayıları çarpmak için bir aritmetik çalışma (bkz. Pappus)
7. Öklid, Kitap X'te açıklanan irrasyonellik teorisinin büyük bir uzantısı, binomiyalden çok terimliye ve sıralıdan (ordered) sırasız (unordered) irrasyonellere (Pappus' comm. on Eucl. X.'ten alıntılara bakın, Arapça olarak korunmuş ve tarafından 1856'da yayınlanmıştır).

İlk basılmış yayınlar

Koniklerin 9. yüzyıl Arapça çevirisinden sayfalar

tarafından düzenlenmiş Apollonius'un Conica adlı kitabının 1654 baskısı

İlk basılı yayınlar çoğunlukla 16. yüzyılda başladı. O zamanlar, akademik kitapların Latince, bugünün Yeni Latincesi olması bekleniyordu. Neredeyse hiçbir el yazması Latince olmadığından, erken basılmış eserlerin editörleri Yunancadan veya Arapçadan Latinceye çevirdi. Yunanca ve Latince tipik olarak yan yana getirilmiştir, ancak yalnızca Yunanca orijinaldir ya da editör tarafından orijinal olduğunu düşündüğü şekilde restore edilmiştir. Kritik malzemeler Latince idi. Antik yorumlar, ancak, eski veya Orta Çağ Yunancası idi. Modern diller ancak 18. ve 19. yüzyıllarda ortaya çıkmaya başladı. Erken basılmış basımların temsili bir listesi aşağıda verilmiştir. Bu baskıların orijinalleri nadir ve pahalıdır. Modern dillerdeki modern baskılar için referanslara bakılmalıdır.

1. Pergaeus, Apollonius (1566). Conicorum libri quattuor: una cum Pappi Alexandrini lemmatibus, et commentariis Eutocii Ascalonitae. Sereni Antinensis philosophi libri duo ... quae omnia nuper Federicus Commandinus Vrbinas mendis quampluris expurgata e Graeco conuertit, & commentariis illustrauit (Latince). Bononiae: Ex officina Alexandri Benatii.  Fredericus Commandinus'un Yunanca Konikler (Conics) adlı eserin ilk dört kitabının İskenderiyeli Pappus, Ascalonlu Eutocius ve Antinouplisli Serenus yorumlarıyla birlikte Latinceye kendi tercümesiyle sunumu.
2. Apollonius; Barrow, I (1675). Apollonii conica: methodo nova illustrata, & succinctè demonstrata (Latince). Londini: Excudebat Guil. Godbid, voeneunt apud Robertum Scott, in vico Little Britain.  Barrow'un Konik adlı eserin ilk dört kitabının eski Yunancadan Neo-Latinceye çevirisi. Boston Halk Kütüphanesi'nde bulunan burada bağlantısı verilen kopya bir zamanlar John Adams'a aitti.
3. Apollonius; Pappus; Halley, E. (1706). Apollonii Pergaei de sectione rationis libri duo: Ex Arabico ms. Latine versi. Accedunt ejusdem de sectione spatii libri duo restituti (Latince). Oxonii. 16 Temmuz 2017 tarihinde kaynağından . Erişim tarihi: 7 Ekim 2020.  Apollonius'un kayıp ancak yeniden inşa edilmiş iki eserinin sunumu. De Sectione Rationis Oxford'daki Bodleian Kütüphanesi'nde orijinal olarak tarafından kısmen çevrilmiş ancak ölümüyle kesintiye uğramış Arapça olarak yayımlanmamış bir el yazmasından geliyor. Daha sonra Halley Kuyruklu Yıldızına adını veren Profesör, astronom, matematikçi ve kaşif Edmond Halley'e verildi. Bozuk metni deşifre edemedi ve onu terk etti. Daha sonra, , için Arapçayı restore etti ve onu Halley'e verdi. Arapça öğrenen Halley, De Sectione Rationisi tekrar yarattı ve okuyucu için ek bir kar olarak Pappus Commentary'den yeniden yapılandırılan De Sectione Spatiinin Neo-Latince çevirisini yarattı. İki Neo-Latin eseri ve Pappus'un eski Yunan yorumu, 1706 tarihli tek ciltte birbirine bağlanmıştır. Arapça el yazmasının yazarı bilinmemektedir. 825'te Bağdat'ın astronomu ve Halifesi Latin El-Me'mun "himayesinde" yazıldığına dair bir ifadeye dayanarak Halley, Praefatio ad Lectoremde bunu 820'ye tarihlendiriyor.
4. Apollonius; Alexandrinus Pappus; Halley, Edmond; Eutocius; Serenus (1710). Apollonii Pergaei Conicorum libri octo, et Sereni Antissensis De sectione cylindri & coni libri duo (PDF) (Latince). Oxoniae: e Theatro Sheldoniano. 4 Ekim 2020 tarihinde kaynağından (PDF). Erişim tarihi: 7 Ekim 2020.  David Gregory'nin 1706'da yayınlanan düzeltilmiş Arapça metni de Sectione rationis çevirisinin başarısından cesaret alan Halley, Apollonius'un bütün elementa conicasını restore edip Latinceye çevirmeye devam etti. Kitaplar I-IV hiç kaybolmamıştı. Grekçe tek sütunda ve Halley Latincesi paralel bir sütunda görünürler. Kitap V-VI, 1626'da Halep'de antika bilimci tarafından satın alınan ve Yunancadan Arapçaya daha önce takdir edilmeyen bir tercümenin beklenmedik bir şekilde keşfinden geldi. 1696'daki ölümü üzerine bir satın alma ve miras zinciriyle Bodleian Kütüphanesine geçti (orijinal olarak MS Marsh 607, 1070 tarihli). Çok daha erken tarihli çeviri, Almamon'un okulunun , "Musa'nın oğulları" adlı şubesinden geliyor. 9. yüzyıl çevirisi, onlar için çalışan yazarlar tarafından yapılmıştır. Halley'in çalışmasında, sadece V-VII Kitaplarının Latince çevirisi verilmektedir. Bu, ilk basılı yayınıdır. VIII. Kitap, Almamon bilginleri onu korumaya el atamadan kayboldu. Kitap VII'de geliştirilen beklentilere ve Pappus lemmalarına dayanan Halley'in uydurması Latince olarak verilmiştir. Eutocius'un yorumları, Pappus'un lemmaları ve Serenus'un iki ilgili eseri Koniklerin yorumlanmasına bir rehber olarak dahil edilmiştir.

Diğer yazarlar tarafından Apollonius'a atfedilen fikirler

Apollonius'un astronomiye katkısı

Gezegen hareketlerinin iki tanımının denkliği ona atfedilir, biri dışmerkezlilik, diğeri yörünge ve dış çemberler kullanır. Batlamyus, bu denkliği "Almagest" XII.1'de Apollonius teoremi olarak tanımlar.

Ay üzerindeki kraterinin ve Apollonius deliğinin (Rimae Apollonius) adı onuruna verilmiştir.

Apollonius'un Yöntemleri

Heath'e göre, "Apollonius'un Yöntemleri" ona ait ve kişisel değildi. Daha sonraki teorisyenler üzerindeki etkisi ne olursa olsun, kendi teknik yeniliğinden değil, geometriden kaynaklanıyordu. Heath'in bu konudaki ifadesi;

“	"Koniklerde kullanılan yöntemlerin ayrıntılı olarak değerlendirilmesine bir başlangıç olarak, genelde, kesin ifadesini Öklid'in Elemanlarında bulduğu kabul edilen geometrik inceleme ilkelerini istikrarlı bir şekilde takip ettikleri söylenebilir."	„

şeklindedir. Altın çağ geometricilerinden bahseden modernlerle ilgili olarak, "yöntem" terimi, özellikle, geometrinin bilmeden bugün kullanılan cebirsel bir yöntemle aynı sonucu ürettiği görsel, yeniden yapılandırıcı yol anlamına gelir. Basit bir örnek olarak, cebir bir karenin alanını, kenarının karesini alarak bulur. Aynı sonucu elde etmenin geometrik yöntemi, görsel bir kare oluşturmaktır. Altın çağdaki geometrik yöntemler, temel cebir sonuçlarının çoğunu üretebilir.

Geometrik cebir

Pisagor teoreminin antik Yunanların gördüğü görsel biçimi. Mavi kare, diğer iki karenin toplamına eşittir.

Heath, tüm altın çağın yöntemleri için geometrik cebir terimini kullanmaya devam eder. Terim buna "uygunsuz bir şekilde değil" deniyor der. Bugün terim başka anlamlarda kullanılmak üzere yeniden dirilmiştir (bkz. ). Heath, bunu 1890'da veya daha önce tarafından tanımlandığı şekliyle kullanıyordu. Fine bunu Analitik geometrinin ilk tam gelişmiş çalışması olan René Descartes'ın adlı eseri için uygular. Fine, "temel işlemleri biçimsel olarak aynı olan iki cebrin resmi olarak özdeş olduğunu" bir ön koşul olarak ortaya koyan Fine, "Descartes’ın çalışmasının ... yalnızca sayısal cebir olmadığını ama daha iyi bir isim istemek için çizgi parçalarının cebri denebileceğini söylüyor. Sembolizmi sayısal cebrinki ile aynıdır; ...."

Örneğin, Apollonius'ta bir doğru parçası AB (A noktası ile B noktası arasındaki çizgi) aynı zamanda parçanın sayısal uzunluğudur. Herhangi bir uzunlukta olabilir. Dolayısıyla AB, herhangi bir değerin atanabileceği x (bilinmeyen) gibi cebirsel değişken ile aynı olur; örn. x = 3.

Değişkenler Apollonius'ta bugün cebirde devam eden bir uygulama olan “AB kesitin herhangi bir noktasından çapa olan uzaklık olsun” gibi kelime ifadeleriyle tanımlanır. Her temel cebir öğrencisi, "kelime problemlerini" cebirsel değişkenlere ve cebir kurallarının x için çözümlemede geçerli olduğu denklemlere dönüştürmeyi öğrenmelidir. Apollonius'un böyle kuralları yoktu. Çözümleri geometrikti.

Resimsel çözümlere kolayca yatkın olmayan ilişkiler, onun kavrayamayacağı bir şeydi; ancak, resimsel çözümler repertuvarı, bugün genellikle bilinmeyen (veya gerekli olmayan) karmaşık geometrik çözümler havuzundan geldi. Bunun iyi bilinen bir istisnası, kaçınılmaz olan Pisagor Teoremi'dir, şimdi bile yanlarında kareler bulunan ve a² + b² = c² gibi bir ifadeyi gösteren bir dik üçgenle temsil edilir. Yunan geometriciler, bu terimleri "AB üzerindeki kare" vb. olarak adlandırdı. Benzer şekilde, AB ve CD'den oluşan bir dikdörtgenin alanı "AB ve CD'deki dikdörtgen" idi.

Bu kavramlar, Yunan geometricilerin doğrusal fonksiyonlara ve ikinci dereceden fonksiyonlara cebirsel erişimini sağladı, bunlar daha sonra konik kesitlerdir. Sırasıyla 1 veya 2'nin kuvvetlerini içerirler. Apollonius, bir koni katı olsa bile küpleri pek kullanmamıştı ('de gösteriliyor). İlgi alanı, düzlem şekiller olan konik kesitlerdi. 4 ve üzeri kuvvetler görselleştirmenin ötesindeydi ve geometride bulunmayan ancak cebirde elinizin altında olan bir soyutlama derecesi gerektiriyordu.

Apollonius'un koordinat sistemi

Kartezyen koordinat sistemi, analitik geometride standarttır.

Bir cetvel gibi standart kamuya açık araçlar kullanılarak, inç gibi genel birimlerdeki tüm olağan uzunluk ölçümü, bir Kartezyen sisteminin kamu tarafından tanınması anlamına gelir; yani, bir inç kare gibi birim karelere bölünmüş bir yüzey ve bir inç küp gibi birim küplere bölünmüş bir uzay. Antik Yunan ölçü birimleri, Bronz Çağı'ndan beri Yunan matematikçilere böyle bir sistem sağlamıştı.

Apollonius'tan önce, Menaechmus ve Arşimet, düşük bir ölçüyü işaretleyen sol taraftaki dikey bir çizgi ve düşük bir ölçüyü işaretleyen bir alt yatay çizgi ölçülmek üzere tasarlanmış mesafelere atıfta bulunarak şekillerini ortak kılavuzun zımni bir penceresine yerleştirmeye başlamıştı, yönler doğrusal veya birbirine diktir. Pencerenin bu kenarları Kartezyen koordinat sisteminde eksenler haline gelir. Eksenlerden herhangi bir noktanın doğrusal uzaklıkları, koordinatlar olarak belirtilir. Eski Yunanlar bu düzene sahip değildi. Sadece mesafelere atıfta bulundular.

Apollonius'un şekillerini yerleştirdiği standart bir penceresi vardı. Dikey ölçüm, "çap" olarak adlandırdığı yatay bir çizgiden yapılır. Kelime Yunancada İngilizce ile aynıdır, ancak Yunanca anlam bakımından biraz daha geniştir. Konik kesitin şekli, paralel çizgilerden oluşan bir ızgara ile kesilmişse, çap, şeklin dalları arasında bulunan tüm çizgi parçalarını ikiye böler. Tepe noktasından (koruphe, "crown" "taç") geçmelidir. Böylelikle bir çap, bir daire gibi bir parabol gibi açık ve kapalı şekiller içerir. Çapın paralel çizgilere dik olması gerektiğine dair bir özellik yoktur, ancak Apollonius yalnızca doğrusal olanları kullanır.

Kesit üzerindeki bir noktadan çapa kadar olan doğrusal uzaklık Yunanca tetagmenos olarak adlandırılır ve etimolojik olarak basitçe "uzatılmış" olarak adlandırılır. Yalnızca "aşağı" (kata-) veya "yukarı" (ana-) genişletildiği için, çevirmenler bunu olarak yorumlarlar. Bu durumda çap, x-ekseni ve tepe noktası başlangıç noktası olur. y-ekseni daha sonra tepe noktasındaki eğriye teğet olur. Apsis daha sonra ordinat ile tepe arasındaki çapın parçası olarak tanımlanır.

Apollonius, kendi koordinat sistemi versiyonunu kullanarak, konik kesitler için denklemlerin geometrik eşdeğerlerini resimsel formda geliştirmeyi başarır ve bu, koordinat sisteminin Kartezyen olarak kabul edilip edilemeyeceği sorusunu gündeme getirir. Bazı farklılıklar vardır. Kartezyen sistemi, herhangi bir hesaplama yapılmadan önce uygulanan tüm uzaydaki tüm rakamları kapsayan evrensel olarak kabul edilmelidir. Çapraz eksene bölünmüş dört kadrana sahiptir. Üç kadran, sıfırın referans eksenlerinin karşısındaki yönler anlamına gelen negatif koordinatları içerir.

Apollonius'un negatif sayıları yoktur, açıkça sıfır için de bir sayıya sahip değildir ve koordinat sistemini konik bölümlerden bağımsız olarak geliştirmez. Esasen sadece 1. Çeyrekte, hepsi pozitif koordinatlarda çalışır. Modern bir matematik tarihçisi olan Carl Boyer bu nedenle şöyle diyor:

“	”Ancak, Yunan geometrik cebri negatif büyüklükler sağlamadı; dahası, koordinat sistemi, özelliklerini incelemek için her durumda belirli bir eğri üzerine "a posteriori" eklenmiştir ... Antik çağın en büyük geometrisi Apollonius, analitik geometriyi geliştirmede başarısız olmuştur ..."	„

Bununla birlikte, Apollonius'un geleneksel ölçümün kılavuz sistemi ile Analitik Geometrinin tam gelişmiş Kartezyen Koordinat Sistemi arasında bir tür ara niş işgal ettiğini kimse inkâr edemez. Apollonius'u okurken, onun terimleri için modern anlamlar üstlenmemeye özen gösterilmelidir.

Oranlar teorisi

Apollonius, Öklid’in Elemanlar, Kitap 5 ve 6'da ifade edildiği gibi "Oranlar Teorisi"ni kullanır. Knidoslu Eudoxus tarafından geliştirilen teori, tamamen grafik yöntemler ve modern sayı teorisi arasında bir aracıdır. Kesirlerin standart işlemesi gibi standart bir ondalık sayı sistemi eksiktir. Ancak önermeler, aritmetikte kesirleri işlemek için kuralları kelimelerle ifade eder. Heath, çarpma ve bölmenin yerini aldıklarını ileri sürer.

"Büyüklük" terimi ile Eudoxus, sayıların ötesine geçip genel bir boyut duygusuna geçmeyi umuyordu, bu da onun günümüzde hala koruduğu bir anlama geliyordu. Öklid şekillerine gelince, çoğu zaman Pisagor yaklaşımı olan sayılar anlamına gelir. Pisagor, evrenin niceliklerle karakterize edilebileceğine inanıyordu ve bu inanç, mevcut bilimsel dogma haline geldi. Öklid'in 5. Kitabı, bir büyüklüğün (megethos, “size”, "boyut") birimlere (meros, “part”, "parça") eşit olarak bölünmesi gerektiği konusunda ısrar ederek başlar. Dolayısıyla büyüklük, birimlerin katlarıdır. Metre veya feet gibi standart ölçü birimleri olmaları gerekmez. Bir birim herhangi bir atanmış çizgi parçası olabilir.

Bunu, bilimde şimdiye kadar tasarlanmış belki de en yararlı temel tanım takip etmektedir: oran (Yunanca logos, kabaca “explanation”, "açıklama" anlamına gelir), göreceli büyüklükte bir ifadedir. AB ve CD segmentleri gibi iki büyüklük verildiğinde. CD'nin birim olarak kabul edildiği AB'nin CD'ye oranı, AB'deki CD sayısıdır; örneğin, 3 parça 4 veya milyonda 60 parça, burada gösterim başına parça (ppm - Parts per notation) hala "parçalar" terminolojisini kullanıyor. Oran, modern kesirlerin temelidir ve bu aynı zamanda kırıkla aynı Latince kökünden "parça" veya "fragman" anlamına da gelir.

Oran, "proporsiyon" (Yunanca analogos) olarak adlandırılan mantıksal yapıdaki matematiksel tahminin temelidir. Oran, iki bölüm, AB ve CD, diğer ikisi, EF ve GH ile aynı orana sahipse, AB ve CD'nin EF ve GH ile orantılı olduğunu veya Öklid'de söylendiği gibi EF, GH'ye olduğu gibi AB, CD'ye olduğunu belirtir.

Cebir, bu genel kavramı AB/CD = EF/GH ifadesine indirger. Terimlerin herhangi üçü göz önüne alındığında, dördüncü terim bilinmeyen olarak hesaplanabilir. Yukarıdaki denklemi yeniden düzenlediğimizde, AB = (CD/GH)•EF elde edilir, burada y = kx olarak ifade edilir ve CD/GH "orantılılık sabiti" olarak bilinir. Yunanlar, muhtemelen art arda ekleyerek, katları (Yunanca pollaplasiein) almakta çok az zorluk yaşadılar.

Apollonius, kareler ve dikdörtgenlerle gösterilen neredeyse yalnızca çizgi parçalarının ve alanlarının oranlarını kullanır. Çevirmenler, 1684'te Gottfried Wilhelm Leibniz tarafından sunulan ’da iki nokta işaretini kullanmayı taahhüt ettiler.Konikler, Kitap I'den Önerme 11'deki bir örnek aşağıda verilmiştir:

Yunancanın birebir çevirisi: FH'nin FA için olduğu gibi BC'nin (kare) BAC'nin (dikdörtgen) olması tasarlansın

Taliaferro’nun çevirisi: “kr. BC : dkdrt. BA.AC :: FH : FA olması tasarlansın”

Cebirsel eşdeğeri: BC²/BA•BC = FH/FA

Ayrıca bakınız

• Descartes teoremi

Kaynakça

1. ^ Eutocius, Commentary on Conica, Book I, Lines 5-10, to be found translated in Apollonius of Perga & Thomas 1953, s. 277
2. ^ Apollonius'un tarihleri üzerine yapılan araştırmalar, özünde Apollonius ve diğer antik yazarların bahsettiği bireylerin tarihlerinin bir hokkabazlığıdır. 246-222'de, doğum ya da eğitim, tam olarak hangi olayın meydana geldiği sorusu var. 19. ve 20. yüzyıl bilim adamları, Apollonius'u Arşimet'in yaş eşi haline getirmek için daha erken bir doğum olan 260 veya 262'yi tercih etme eğilimindedir. Pompeii'de ortaya çıkan bazı yazıt kanıtları Philonides'i en iyi tarihli karakter yapıyor. MÖ 2. yüzyılda yaşadı. Apollonius'un yaşamının 2. yüzyıla kadar uzatılması gerektiğinden, erken doğum tarihleri daha az olasıdır. Veri ve sorunların daha ayrıntılı bir sunumu Knorr (1986)'da bulunabilir. Gelenekten kaynaklanan geleneksel tarihler ile daha gerçekçi bir yaklaşım arasındaki ikilik, McElroy (McElroy, Tucker (2005). "Apollonius of Perga". A to Z of Mathematicians. ), bir kerede 262-190 (yüksek tarihler) verir ve bu makaledeki gibi 3. yy geç-2. yy erken dönem olması gerektiğini açıklar.
3. ^ ^{a b} Fried & Unguru 2001, Introduction
4. ^ Thomas Little Heath (1908). . 8 Aralık 2010 tarihinde kaynağından arşivlendi. 
5. ^ Fried and Unguru 2001, Eutoocius'un versiyonunun başarısı, şüphesiz, Koniklerin son dört kitabının Yunanca orijinalinin kaybolmasına katkıda bulundu, ancak bu, geç antik çağda ve Bizans Döneminde yüksek öğrenimle ilgilenenler arasında matematiğe olan dar ilginin bir sonucu olarak belki de kaçınılmazdı. (s. 6)
6. ^ Apollonius of Perga & Heath 1896, ss. clvii-clxx
7. ^ Apollonius of Perga & Heath 1896, s. vii
8. ^ Yunan geometricilerinin çemberi, elipsi ve diğer şekilleri konik kesitler olarak tanımlamadığına dikkat edin. Koni bir daire ile tanımlandığı için bu dairesel bir tanım olacaktır. Her şeklin kendi geometrik tanımı vardır ve ek olarak konik bir kesit olarak gösterilmektedir.
9. ^ Apollonius of Perga & Heath 1896, s. c
10. ^ Eksikliğin başka bir durumu olan bir dairenin bazen iki odak yerine tek bir merkeze sahip bir tür elips olarak kabul edildiğini unutmayın.
11. ^ y²=g(x)'in bir parabolün denklemi olmadığını unutmayın, y²=kx, x daha düşük bir kuvvete sahiptir.
12. ^ ^{a b c d e f g h i} Heath 1911, s. 187.
13. ^ Pek çok yorumcu ve çevirmen, şüphesiz, kopyacılar olarak, özellikle problemlerin çoğunu herhangi bir yapı stoku olmadan cebirle gerçekleştirebilen analitik geometriden sonra, kullanımları konusunda açıkça hevesli değillerdir. Taliaferro, Kitap III'te durur. Heath, kitabın bir özetini okuyucu için daha lezzetli hale getirmeye çalışır (Apollonius of Perga & Heath 1896, Intersecting Conics) Fried Apollonius'a daha nettir, bunun yerine kapsamlı bir kritik malzeme sağlar (Apollonius of Perga & Fried 2002, Footnotes).
14. ^ Fried & Unguru 2001, s. 146
15. ^ Fried & Unguru 2001, s. 188
16. ^ Apollonius of Pergas & Heath 1896, Normals as Maxima and Minima
17. ^ Apollonius of Perga & Heath 1896, Propositions Leading Immediately to the Determination of the Evolute
18. ^ ^{a b} Fried & Unguru 2001, s. 148
19. ^ Normalis, "norma ile ölçülmüş" veya kare anlamına gelen mükemmel bir Latince kelimedir. Halley, bunu, daha genel bir yönsel doğru duygusu olan Pappus'un eutheia'sını çevirmek için kullanır. "Dik (the perpendicular to)" için matematiksel Yunanca, nesnesinin herhangi bir şekil, genellikle düz bir çizgi olabileceği "normal (the normal of)" tabirini kullandılar. Fried'in söylediği şey, normalin, normalden normal bir eğrinin normal kullanımı anlamına gelmediği ve Apollonius'un bunu tanıtmadığı, ancak birkaç istisnai durumda bir tanesini tanımladığıdır.
20. ^ Fried & Unguru, bu eleştirilere bütün bir bölüm ayırıyor: Fried & Unguru 2001, Maximum and Minimum Lines: Book V of the Conica
21. ^ Bir özet tablo Fried & Unguru 2001, s. 190'de verilmiştir.
22. ^ Fried & Unguru 2001, s. 182
23. ^ Kitaptaki her önermenin kesinliği kadar matematiksel bir açıklama da şu adreste bulunabilir: (Toomer 1990, ss. lxi-lxix). Her bir İngiliz yazar, karmaşıklıkları açık ve özlü İngilizce olarak açıklamaya çalıştıkça, tanımların çevirilerinin büyük ölçüde değiştiğini unutmayın. Özünde, böyle bir İngilizce mevcut değildir.
24. ^ Sorunun bir özeti, (Heath 1896, s. lxx) adresinde bulunabilir. Çoğu yazarın bu konuda söyleyecek bir şeyi vardır; örneğin, Toomer, GJ (1990). Apollonius Conics Book V to VII: the Arabic Translation of the Lost Greek Original in the Version of the Banu Musa. Sources in the History of Mathematics and Physical Sciences 9. I. New York: Springer. ss. lxix-lxx. çözüm sınırlarının belirlenmesini ana amacı olarak görebiliriz . Toomer’in görüşü, Önsöz hariç VII. Kitabın herhangi bir metnine herhangi bir ayrıntı veya atıf olmaksızın verilmiştir.
25. ^ Mackenzie, Dana. "A Tisket, a Tasket, an Apollonian Gasket". American Scientist. 98, January–February 2010 (1): 10-14. 10 Nisan 2017 tarihinde kaynağından . Erişim tarihi: 7 Ekim 2020. 
26. ^ Boyer, Carl B. (1991). "Apollonius of Perga". A History of Mathematics (Second bas.). John Wiley & Sons, Inc. s. 142. ISBN . Apollonian'ın Kesit Belirlenmesi Üzerine (On Determinate Section) incelemesi tek boyutlu analitik geometri denebilecek şeydir. Geometrik formdaki tipik Yunan cebirsel analizini kullanarak aşağıdaki genel problemi değerlendirdi: Düz bir çizgi üzerinde A, B, C, D olmak üzere dört nokta verildiğinde, AP ve CP’deki dikdörtgen BP ve DP’deki dikdörtgene belirli bir oranda olacak şekilde beşinci bir P noktası belirleyin. Burada da problem kolaylıkla ikinci dereceden bir çözüme indirgenir; ve diğer durumlarda olduğu gibi, Apollonius, olasılıkların sınırları ve çözümlerin sayısı dahil olmak üzere soruyu kapsamlı bir şekilde ele aldı. 
27. ^ 1710 tarihli Praefatioda Apollonius, Arşimet'den sonra ikinci sırada yer almasına rağmen, elementa conicanın büyük bir kısmının "kesilmiş" ve geri kalan kısmının "daha az sadık”; sonuç olarak şimdi onu düzeltecekti dedi. Tam olarak hangi öğelerin "sadık" olarak kabul edileceği sorusu günümüz literatürüne yayılmıştır.
28. ^ Zincirin daha kesin bir versiyonu için bkz. (Wakefield, Colin. "Arabic Manuscripts in the Bodleian Library" (PDF). ss. 136-137. 28 Mart 2016 tarihinde kaynağından (PDF). Erişim tarihi: 7 Ekim 2020. )
29. ^ Apollonius krateri
30. ^ Apollonius of Perga & Heath 1896, s. ci
31. ^ (1902). The number-system of algebra treated theoretically and historically. Boston: Leach. ss. 119-120. 
32. ^ Apollonius of Perga & Heath 1896, s. cxv
33. ^ Apollonius, Konikler, Kitap I, Tanım 4. Ayrıca bkz. (Apollonius of Perga & Heath 1896, s. clxi)
34. ^ Boyer, Carl B. (1991). "Apollonius of Perga". A History of Mathematics (Second bas.). John Wiley & Sons, Inc. ss. 156-157. ISBN . 
35. ^ Apollonius of Perga & Heath 1896, ss. ci – cii
36. ^ Cajori, Florian (1993). A history of mathematical notations. New York: Dover Publications. s. 295. 

Dış bağlantılar

Vikisöz'de Απολλώνιος ο Περγάμου ile ilgili sözleri bulabilirsiniz.

Vikikaynak'ta Apollonius of Perga ile ilgili metin bulabilirsiniz.

• (PDF). Dictionary of Scientific Biography. 7 Şubat 2020 tarihinde kaynağından (PDF) arşivlendi. 
• . Encyclopaedia Britannica. 22 Ekim 2020 tarihinde kaynağından arşivlendi. 
• . MathSciNet Author profile. 11 Haziran 2017 tarihinde kaynağından arşivlendi. 
• Heinz Klaus Strick. (PDF). 14 Ocak 2021 tarihinde kaynağından (PDF) arşivlendi. Pergeli Apollonius'un Biyografisi 
• . 7 Şubat 2020 tarihinde kaynağından arşivlendi. 

Kaynakça

• M. Chasles (1837), Aperçu historique sur l'origine et le développement des méthodes en géométrie (Fransızca), Paris 
• B. Elsner (1988), 'Apollonius Saxonicus' : Die Restitution eines verlorenen Werkes des Apollonius von Perga durch Joachim Jungius, Woldeck Weland und Johannes Müller (Almanca), Göttingen 
• M. N. Fried (çev.) Apollonius of Perga: Conics Book IV (Santa Fe, 2002).
• M. N. Fried & S. Unguru (2001), , Leiden, 13 Ağustos 2020 tarihinde kaynağından arşivlendi 
• T. L. Heath, Apollonius of Perga: Treatise on Conic Sections (Oxford, 1961).
• T. L. Heath, A History of Greek Mathematics (2 vols.),1.Cilt, 2.Cilt (Oxford, 1921).
• R. C. Taliaferro (çev.) Apollonius of Perga: Conics Books I-III (Santa Fe, 1998).
• H. Wussing, Apollonius, in H. Wussing & W. Arnold, Biographien bedeutender Mathematiker (Berlin, 1983).
• A. Abdurahmanov, New information about the Arabic translation of the 'Conica' of Apollonius of Perga (Rusça), Taşkent. Gos. Univ. Naucn. Trudy Vyp. 490 Voprosy Matematiki (1976), 7-8, 259.
• A. Bilimovitch, Apollonius theorem on station of the planet (Serbo-Croatian), Glas Srpske Akad. Nauka Od. Prirod.-Mat. Nauka (N.S.) 206(5) (1953), 49-56.
• A. V. Dorofeeva, Apollonius (ca. 260-190 B.C.) (Rusça), Mat. v Shkole (5) (1988), i.
• J. P. Hogendijk, Desargues' 'Brouillon project' and the 'Conics' of Apollonius, Centaurus 34 (1) (1991), 1-43.
• J. P. Hogendijk, Arabic traces of lost works of Apollonius, Arch. Hist. Exact Sci. 35 (3) (1986), 187-253.
• O. Neugebauer, The equivalence of eccentric and epicyclic motion according to Apollonius, Scripta Math. 24 (1959), 5-21.
• O. Neugebauer (1955), , Comm. Pure Appl. Math., cilt 8, ss. 641-648, 16 Haziran 2018 tarihinde kaynağından arşivlendi 
• B. A. Rozenfeld, Inversion with respect to the circle and inversion with respect to the ellipse, the hyperbola and the parabola in the 'Conic sections' of Apollonius (Rusça), Istor.-Mat. Issled. 30 (1986), 195-199.
• (PDF) (İngilizce). Boris Rosenfeld tarafından çevrildi. The Pennsylvania State University. 4 Temmuz 2016 tarihinde kaynağından (PDF) arşivlendi.  & (PDF) (İngilizce). Boris Rosenfeld tarafından çevrildi. The Pennsylvania State University. 29 Kasım 2020 tarihinde kaynağından (PDF) arşivlendi. 
• K. Saito, Quelques observations sur l'édition des 'Coniques' d'Apollonius de Francesco Maurolico, Boll. Storia Sci. Mat. 14 (2) (1994), 239-258.
• K. Saito, Compounded ratio in Euclid and Apollonius, Historia Sci. 31 (1986), 25-59.
• M. E. Di Stefano & M. Ginepro Tinti, The circumference as a special conic, from the viewpoint of Apollonius (İtalyanca), Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 116 (1-2) (1982), 127-135.

Konuyla ilgili yayınlar

• Bergamalı Apollonius, Kitâb el-Mahrutât (Koni Kesitleri), Tıpkı Basım, İstanbul: İ.Ü. Fen Fakültesi Nazım Terzioğlu Araştırma Merkezi, 1996.
• Apollonius (of Perga.), (1827) Die bücher des Apollonius von Perga De sectione spatii
• Robert Simson, (1822) Die Bücher des Apollonius von Perga de Sectione Determinata
• Edmond Halley, Wilhelm Adolf Diesterweg, Apollonius (1824), Die Bücher des Apollonius von Perga de Sectione rationis
• (1889) Das fünfte Buch der Conica des Apollonius von Perga [microform] : in der arabischen Uebersetzung des Thabit ibn Corrah
• G.B.M. (1896), "Apollonius of Perga: Treatise on Conic Sections", Nature, cilt 54, ss. 314-315, doi:10.1038/054314a01896 
• (1836) Des Apollonius von Perga zwei Bücher vom Verhältnissschnitt, de sectione rationis, aus dem Lat
• H. Balsamj, Apollonius (1861) Des Apollonius von Perga sieben Bücher über Kegelschnitte: Nebst dem durch Halley wieder hergestellten achten Buche
• Bernard R. Goldstein (2009). (PDF). 10 Ocak 2020 tarihinde kaynağından (PDF) arşivlendi. 
• Maghribī, Muḥyī al-Dīn, y. 1281, Tahdhīb Makhrūṭāt Abulūniyūs (Apollonius'un Koniklerinin yedi bölümünün açıklamaları, çizimleri ve özeti.)