Trigonometride, trigonometrik özdeşlikler trigonometrik fonksiyonları içeren ve eşitliğin her iki tarafının da tanımlandığı değişkenlerin her değeri için doğru olan . Geometrik olarak, bunlar bir veya daha fazla açının belirli fonksiyonlarını içeren özdeşliklerdir. Bunlar (üçgen özdeşliklerinden) farklıdır, bunlar potansiyel olarak açıları içeren ama aynı zamanda kenar uzunluklarını veya bir üçgenin diğer uzunluklarını da içeren özdeşliklerdir.
Bu özdeşlikler, trigonometrik fonksiyonları içeren ifadelerin basitleştirilmesi gerektiğinde kullanışlıdır. Önemli bir uygulama, trigonometrik olmayan fonksiyonların integrasyonudur: yaygın bir teknik, önce bir trigonometrik fonksiyonla ikame kuralı kullanmayı ve ardından ortaya çıkan integrali bir trigonometrik özdeşlikle basitleştirmeyi içerir.
Pisagor özdeşlikleri

 ,
, 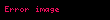 ve
ve  için birim uzunluktaki yarıçap, onları tanımlayan üçgenin hipotenüsünü oluşturur. Karşılıklı özdeşlikler, bu birim çizginin artık hipotenüs olmadığı üçgenlerde kenarların oranları olarak ortaya çıkar. Mavi gölgeli üçgen
için birim uzunluktaki yarıçap, onları tanımlayan üçgenin hipotenüsünü oluşturur. Karşılıklı özdeşlikler, bu birim çizginin artık hipotenüs olmadığı üçgenlerde kenarların oranları olarak ortaya çıkar. Mavi gölgeli üçgen  özdeşliğini, kırmızı gölgeli üçgen ise
özdeşliğini, kırmızı gölgeli üçgen ise  özdeşliğini göstermektedir.
özdeşliğini göstermektedir.arasındaki temel ilişki Pisagor özdeşliği ile verilir:

burada 

Bu Pisagor teoreminin bir versiyonu olarak görülebilir ve birim çember için 

Burada işaret 
Bu özdeşliği 


Bu özdeşlikleri kullanarak, herhangi bir trigonometrik fonksiyonu diğer herhangi bir fonksiyon cinsinden (artı veya eksi işaretin) ifade etmek mümkündür:
| cinsinden |  |  | 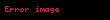 |  |  |  |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  | 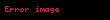 |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
Yansımalar, kaymalar ve periyodiklik
Birim çember incelenerek trigonometrik fonksiyonların aşağıdaki özellikleri belirlenebilir.
Yansımalar

 yansıma açısını
yansıma açısını  artışlarla kaydırırken (a, b) koordinatlarının dönüşümü.
artışlarla kaydırırken (a, b) koordinatlarının dönüşümü.Bir Öklid vektörünün yönü bir 






Bu açıların trigonometrik fonksiyonlarının değerleri 

 'da yansıtılan 'da yansıtılan  tek/çift özdeşlikler |  'te yansıtılan 'te yansıtılan  |  'de yansıtılan 'de yansıtılan  |  'te yansıtılan 'te yansıtılan  |  'de yansıtılan 'de yansıtılan   ile karşılaştıtma ile karşılaştıtma |
|---|---|---|---|---|
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
Kaymalar ve periyodiklik

 açısını
açısını 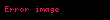 artışlarla kaydırırken
artışlarla kaydırırken(a, b) koordinatlarının dönüşümü.
| Bir çeyrek periyot kaydırma | Bir yarım periyot kaydırma | Tam periyotlarla kaydırma | Periyot |
|---|---|---|---|
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
İşaretler
Trigonometrik fonksiyonların işareti açının çeyreğine (kuadrantına) bağlıdır. Eğer 

Trigonometrik fonksiyonlar ortak periyot 

Açı toplam ve fark özdeşlikleri
 |  | |
Dar açıların sinüs ve kosinüsleri için açı toplam formüllerinin gösterimi. Vurgulanan parça birim uzunluktadır. |  ve ve  için açı farkı özdeşliklerini gösteren şekil. için açı farkı özdeşliklerini gösteren şekil. |
Bunlar aynı zamanda açı toplam ve fark teoremleri (veya formülleri) olarak da bilinir.







Bu özdeşlikler, diğer trigonometrik fonksiyonlar için toplam ve fark özdeşliklerini de içeren aşağıdaki tablonun ilk iki satırında özetlenmiştir.
| Sinüs |  |  |  | ||
|---|---|---|---|---|---|
| Kosinüs |  |  |  | ||
| Tanjant |  |  |  | ||
| Kosekant |  |  |  | ||
| Sekant |  |  |  | ||
| Kotanjant |  |  |  | ||
| Arksinüs |  |  |  | ||
| Arkkosinüs |  |  |  | ||
| Arktanjant |  |  |  | ||
| Arkkotanjant |  |  |  | ||
Sonsuz sayıda açının toplamlarının sinüs ve kosinüsleri







Toplamların tanjantları ve kotanjantları





Öyleyse yukarıdaki sinüs ve kosinüs toplam formüllerini kullanarak,

Sağ taraftaki terim sayısı sol taraftaki terim sayısına bağlıdır.
Örneğin: 
ve bunun gibi. Sadece sonlu sayıda terim olması durumu matematiksel tümevarım ile kanıtlanabilir. Sonsuz sayıda terim olması durumu, bazı temel eşitsizlikler kullanılarak kanıtlanabilir.
Toplamların sekantları ve kosekantları

Burada 


Örneğin,

Batlamyus teoremi

Batlamyus teoremi, trigonometrik özdeşlikler tarihinde önemlidir, çünkü sinüs ve kosinüs için toplam ve fark formüllerine eşdeğer sonuçlar ilk kez bu şekilde kanıtlanmıştır. Teorem, yandaki şekilde gösterildiği gibi 
Thales teoremi ile, 








Çevre açı teoremine göre, çemberin merkezindeki 








Bu değerler, Batlamyus teoreminin 




Açının katları ve yarım açı formülleri
| Tn, ninci |  |
|---|---|
| de Moivre formülü, i sanal birimdir |  |
Açının katları formülleri
Çift açı formülleri

 açılı yukarıdaki ikizkenar üçgen için alan 12 × taban × yükseklik iki yönde hesaplanır. Dik durumdayken alan
açılı yukarıdaki ikizkenar üçgen için alan 12 × taban × yükseklik iki yönde hesaplanır. Dik durumdayken alan  şeklindedir. Yan yattığında ise aynı alan
şeklindedir. Yan yattığında ise aynı alan  . Bu nedenle,
. Bu nedenle, 
Bir açının iki katı için formüller.
Üç kat açı formülleri
Üç kat açılar için formüller.
Çok kat açı formülleri
Çok katlı açılar için formüller.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu sayfanin herhangi bir incelenmis surumu bulunmuyor bu yuzden standartlara uygunluk acisindan kontrol edilmemis olabilir Trigonometride trigonometrik ozdeslikler trigonometrik fonksiyonlari iceren ve esitligin her iki tarafinin da tanimlandigi degiskenlerin her degeri icin dogru olan Geometrik olarak bunlar bir veya daha fazla acinin belirli fonksiyonlarini iceren ozdesliklerdir Bunlar ucgen ozdesliklerinden farklidir bunlar potansiyel olarak acilari iceren ama ayni zamanda kenar uzunluklarini veya bir ucgenin diger uzunluklarini da iceren ozdesliklerdir Bu ozdeslikler trigonometrik fonksiyonlari iceren ifadelerin basitlestirilmesi gerektiginde kullanislidir Onemli bir uygulama trigonometrik olmayan fonksiyonlarin integrasyonudur yaygin bir teknik once bir trigonometrik fonksiyonla ikame kurali kullanmayi ve ardindan ortaya cikan integrali bir trigonometrik ozdeslikle basitlestirmeyi icerir Pisagor ozdeslikleriTrigonometrik fonksiyonlar ve bunlarin birim cember uzerindeki karsiliklari Tum dik acili ucgenler benzerdir yani karsilik gelen kenarlari arasindaki oranlar aynidir Sin displaystyle Sin cos displaystyle cos ve tan displaystyle tan icin birim uzunluktaki yaricap onlari tanimlayan ucgenin hipotenusunu olusturur Karsilikli ozdeslikler bu birim cizginin artik hipotenus olmadigi ucgenlerde kenarlarin oranlari olarak ortaya cikar Mavi golgeli ucgen 1 cot2 8 csc2 8 displaystyle 1 cot 2 theta csc 2 theta ozdesligini kirmizi golgeli ucgen ise tan2 8 1 sec2 8 displaystyle tan 2 theta 1 sec 2 theta ozdesligini gostermektedir arasindaki temel iliski Pisagor ozdesligi ile verilir sin2 8 cos2 8 1 displaystyle sin 2 theta cos 2 theta 1 burada sin2 8 sin 8 2 displaystyle sin 2 theta sin theta 2 ve cos2 8 cos 8 2 displaystyle cos 2 theta cos theta 2 anlamina gelir Bu Pisagor teoreminin bir versiyonu olarak gorulebilir ve birim cember icin x2 y2 1 displaystyle x 2 y 2 1 denkleminden cikar Bu denklem sinus ya da kosinus icin cozulebilir sin 8 1 cos2 8 cos 8 1 sin2 8 displaystyle begin aligned sin theta amp pm sqrt 1 cos 2 theta cos theta amp pm sqrt 1 sin 2 theta end aligned Burada isaret 8 displaystyle theta nin kuadrantina baglidir Bu ozdesligi sin2 8 displaystyle sin 2 theta cos2 8 displaystyle cos 2 theta veya her ikisine boldugunuzde asagidaki ozdeslikler elde edilir 1 cot2 8 csc2 81 tan2 8 sec2 8sec2 8 csc2 8 sec2 8csc2 8 displaystyle begin aligned amp 1 cot 2 theta csc 2 theta amp 1 tan 2 theta sec 2 theta amp sec 2 theta csc 2 theta sec 2 theta csc 2 theta end aligned Bu ozdeslikleri kullanarak herhangi bir trigonometrik fonksiyonu diger herhangi bir fonksiyon cinsinden arti veya eksi isaretin ifade etmek mumkundur Her bir trigonometrik fonksiyon diger bes fonksiyonun her biri cinsinden cinsinden sin 8 displaystyle sin theta csc 8 displaystyle csc theta cos 8 displaystyle cos theta sec 8 displaystyle sec theta tan 8 displaystyle tan theta cot 8 displaystyle cot theta sin 8 displaystyle sin theta sin 8 displaystyle sin theta 1csc 8 displaystyle frac 1 csc theta 1 cos2 8 displaystyle pm sqrt 1 cos 2 theta sec2 8 1sec 8 displaystyle pm frac sqrt sec 2 theta 1 sec theta tan 81 tan2 8 displaystyle pm frac tan theta sqrt 1 tan 2 theta 11 cot2 8 displaystyle pm frac 1 sqrt 1 cot 2 theta csc 8 displaystyle csc theta 1sin 8 displaystyle frac 1 sin theta csc 8 displaystyle csc theta 11 cos2 8 displaystyle pm frac 1 sqrt 1 cos 2 theta sec 8sec2 8 1 displaystyle pm frac sec theta sqrt sec 2 theta 1 1 tan2 8tan 8 displaystyle pm frac sqrt 1 tan 2 theta tan theta 1 cot2 8 displaystyle pm sqrt 1 cot 2 theta cos 8 displaystyle cos theta 1 sin2 8 displaystyle pm sqrt 1 sin 2 theta csc2 8 1csc 8 displaystyle pm frac sqrt csc 2 theta 1 csc theta cos 8 displaystyle cos theta 1sec 8 displaystyle frac 1 sec theta 11 tan2 8 displaystyle pm frac 1 sqrt 1 tan 2 theta cot 81 cot2 8 displaystyle pm frac cot theta sqrt 1 cot 2 theta sec 8 displaystyle sec theta 11 sin2 8 displaystyle pm frac 1 sqrt 1 sin 2 theta csc 8csc2 8 1 displaystyle pm frac csc theta sqrt csc 2 theta 1 1cos 8 displaystyle frac 1 cos theta sec 8 displaystyle sec theta 1 tan2 8 displaystyle pm sqrt 1 tan 2 theta 1 cot2 8cot 8 displaystyle pm frac sqrt 1 cot 2 theta cot theta tan 8 displaystyle tan theta sin 81 sin2 8 displaystyle pm frac sin theta sqrt 1 sin 2 theta 1csc2 8 1 displaystyle pm frac 1 sqrt csc 2 theta 1 1 cos2 8cos 8 displaystyle pm frac sqrt 1 cos 2 theta cos theta sec2 8 1 displaystyle pm sqrt sec 2 theta 1 tan 8 displaystyle tan theta 1cot 8 displaystyle frac 1 cot theta cot 8 displaystyle cot theta 1 sin2 8sin 8 displaystyle pm frac sqrt 1 sin 2 theta sin theta csc2 8 1 displaystyle pm sqrt csc 2 theta 1 cos 81 cos2 8 displaystyle pm frac cos theta sqrt 1 cos 2 theta 1sec2 8 1 displaystyle pm frac 1 sqrt sec 2 theta 1 1tan 8 displaystyle frac 1 tan theta cot 8 displaystyle cot theta Yansimalar kaymalar ve periyodiklikBirim cember incelenerek trigonometrik fonksiyonlarin asagidaki ozellikleri belirlenebilir Yansimalar a displaystyle alpha yansima acisini p4 displaystyle frac pi 4 artislarla kaydirirken a b koordinatlarinin donusumu Bir Oklid vektorunun yonu bir 8 displaystyle theta acisi ile temsil edildiginde bu aci serbest vektor orijinden baslayan ve pozitif x displaystyle x birim vektoru tarafindan belirlenen acidir Ayni kavram Oklid uzayinda dogrulara da uygulanabilir burada aci verilen dogruya orijinden ve pozitif x displaystyle x ekseninden gecen bir paralel dogru tarafindan belirlenen acidir 8 displaystyle theta dogrultulu bir dogru vektor a displaystyle alpha dogrultulu bir dogru etrafinda yansitilirsa bu yansitilan dogrunun vektorun 8 displaystyle theta prime dogrultu acisi 8 2a 8 theta prime 2 alpha theta degerine sahiptir Bu acilarin trigonometrik fonksiyonlarinin degerleri 8 8 displaystyle theta theta prime belirli acilar a displaystyle alpha icin basit ozdeslikleri karsilar ya esittirler ya zit isaretlidirler ya da tamamlayici trigonometrik fonksiyon kullanirlar Bunlar indirgeme formulleri olarak da bilinir a 0 displaystyle alpha 0 da yansitilan 8 displaystyle theta tek cift ozdeslikler a p4 displaystyle alpha frac pi 4 te yansitilan 8 displaystyle theta a p2 displaystyle alpha frac pi 2 de yansitilan 8 displaystyle theta a 3p4 displaystyle alpha frac 3 pi 4 te yansitilan 8 displaystyle theta a p displaystyle alpha pi de yansitilan 8 displaystyle theta a 0 displaystyle alpha 0 ile karsilastitmasin 8 sin 8 displaystyle sin theta sin theta sin p2 8 cos 8 displaystyle sin left tfrac pi 2 theta right cos theta sin p 8 sin 8 displaystyle sin pi theta sin theta sin 3p2 8 cos 8 displaystyle sin left tfrac 3 pi 2 theta right cos theta sin 2p 8 sin 8 sin 8 displaystyle sin 2 pi theta sin theta sin theta cos 8 cos 8 displaystyle cos theta cos theta cos p2 8 sin 8 displaystyle cos left tfrac pi 2 theta right sin theta cos p 8 cos 8 displaystyle cos pi theta cos theta cos 3p2 8 sin 8 displaystyle cos left tfrac 3 pi 2 theta right sin theta cos 2p 8 cos 8 cos 8 displaystyle cos 2 pi theta cos theta cos theta tan 8 tan 8 displaystyle tan theta tan theta tan p2 8 cot 8 displaystyle tan left tfrac pi 2 theta right cot theta tan p 8 tan 8 displaystyle tan pi theta tan theta tan 3p2 8 cot 8 displaystyle tan left tfrac 3 pi 2 theta right cot theta tan 2p 8 tan 8 tan 8 displaystyle tan 2 pi theta tan theta tan theta csc 8 csc 8 displaystyle csc theta csc theta csc p2 8 sec 8 displaystyle csc left tfrac pi 2 theta right sec theta csc p 8 csc 8 displaystyle csc pi theta csc theta csc 3p2 8 sec 8 displaystyle csc left tfrac 3 pi 2 theta right sec theta csc 2p 8 csc 8 csc 8 displaystyle csc 2 pi theta csc theta csc theta sec 8 sec 8 displaystyle sec theta sec theta sec p2 8 csc 8 displaystyle sec left tfrac pi 2 theta right csc theta sec p 8 sec 8 displaystyle sec pi theta sec theta sec 3p2 8 csc 8 displaystyle sec left tfrac 3 pi 2 theta right csc theta sec 2p 8 sec 8 sec 8 displaystyle sec 2 pi theta sec theta sec theta cot 8 cot 8 displaystyle cot theta cot theta cot p2 8 tan 8 displaystyle cot left tfrac pi 2 theta right tan theta cot p 8 cot 8 displaystyle cot pi theta cot theta cot 3p2 8 tan 8 displaystyle cot left tfrac 3 pi 2 theta right tan theta cot 2p 8 cot 8 cot 8 displaystyle cot 2 pi theta cot theta cot theta Kaymalar ve periyodiklik 8 displaystyle theta acisini p2 displaystyle frac pi 2 artislarla kaydirirken a b koordinatlarinin donusumu Bir ceyrek periyot kaydirma Bir yarim periyot kaydirma Tam periyotlarla kaydirma Periyotsin 8 p2 cos 8 displaystyle sin theta pm tfrac pi 2 pm cos theta sin 8 p sin 8 displaystyle sin theta pi sin theta sin 8 k 2p sin 8 displaystyle sin theta k cdot 2 pi sin theta 2p displaystyle 2 pi cos 8 p2 sin 8 displaystyle cos theta pm tfrac pi 2 mp sin theta cos 8 p cos 8 displaystyle cos theta pi cos theta cos 8 k 2p cos 8 displaystyle cos theta k cdot 2 pi cos theta 2p displaystyle 2 pi csc 8 p2 sec 8 displaystyle csc theta pm tfrac pi 2 pm sec theta csc 8 p csc 8 displaystyle csc theta pi csc theta csc 8 k 2p csc 8 displaystyle csc theta k cdot 2 pi csc theta 2p displaystyle 2 pi sec 8 p2 csc 8 displaystyle sec theta pm tfrac pi 2 mp csc theta sec 8 p sec 8 displaystyle sec theta pi sec theta sec 8 k 2p sec 8 displaystyle sec theta k cdot 2 pi sec theta 2p displaystyle 2 pi tan 8 p4 tan 8 11 tan 8 displaystyle tan theta pm tfrac pi 4 tfrac tan theta pm 1 1 mp tan theta tan 8 p2 cot 8 displaystyle tan theta tfrac pi 2 cot theta tan 8 k p tan 8 displaystyle tan theta k cdot pi tan theta p displaystyle pi cot 8 p4 cot 8 11 cot 8 displaystyle cot theta pm tfrac pi 4 tfrac cot theta mp 1 1 pm cot theta cot 8 p2 tan 8 displaystyle cot theta tfrac pi 2 tan theta cot 8 k p cot 8 displaystyle cot theta k cdot pi cot theta p displaystyle pi Isaretler Trigonometrik fonksiyonlarin isareti acinin ceyregine kuadrantina baglidir Eger p lt 8 p displaystyle pi lt theta leq pi ve sgn isaret fonksiyonu ise sgn sin 8 sgn csc 8 1 0 lt 8 lt p ise 1 p lt 8 lt 0 ise0 8 0 p isesgn cos 8 sgn sec 8 1 12p lt 8 lt 12p ise 1 p lt 8 lt 12p veya 12p lt 8 lt p ise0 8 12p 12p isesgn tan 8 sgn cot 8 1 p lt 8 lt 12p veya 0 lt 8 lt 12p ise 1 12p lt 8 lt 0 veya 12p lt 8 lt p ise0 8 12p 0 12p p ise displaystyle begin aligned operatorname sgn sin theta operatorname sgn csc theta amp begin cases 1 amp 0 lt theta lt pi text ise 1 amp pi lt theta lt 0 text ise 0 amp theta in 0 pi text ise end cases 5mu operatorname sgn cos theta operatorname sgn sec theta amp begin cases 1 amp tfrac 1 2 pi lt theta lt tfrac 1 2 pi text ise 1 amp pi lt theta lt tfrac 1 2 pi text veya tfrac 1 2 pi lt theta lt pi text ise 0 amp theta in bigl tfrac 1 2 pi tfrac 1 2 pi bigr text ise end cases 5mu operatorname sgn tan theta operatorname sgn cot theta amp begin cases 1 amp pi lt theta lt tfrac 1 2 pi text veya 0 lt theta lt tfrac 1 2 pi text ise 1 amp tfrac 1 2 pi lt theta lt 0 text veya tfrac 1 2 pi lt theta lt pi text ise 0 amp theta in bigl tfrac 1 2 pi 0 tfrac 1 2 pi pi bigr text ise end cases end aligned Trigonometrik fonksiyonlar ortak periyot 2p displaystyle 2 pi ile periyodiktir bu nedenle p p displaystyle pi pi araliginin disindaki 8 degerleri icin tekrar eden degerler alirlar yukaridaki Kaymalar ve periyodiklik bolumune bakin Aci toplam ve fark ozdeslikleriDar acilarin sinus ve kosinusleri icin aci toplam formullerinin gosterimi Vurgulanan parca birim uzunluktadir sin a b displaystyle sin alpha beta ve cos a b displaystyle cos alpha beta icin aci farki ozdesliklerini gosteren sekil Bunlar ayni zamanda aci toplam ve fark teoremleri veya formulleri olarak da bilinir sin a b sin acos b cos asin bsin a b sin acos b cos asin bcos a b cos acos b sin asin bcos a b cos acos b sin asin b displaystyle begin aligned sin alpha beta amp sin alpha cos beta cos alpha sin beta sin alpha beta amp sin alpha cos beta cos alpha sin beta cos alpha beta amp cos alpha cos beta sin alpha sin beta cos alpha beta amp cos alpha cos beta sin alpha sin beta end aligned sin a b displaystyle sin alpha beta ve cos a b displaystyle cos alpha beta icin aci farki ozdeslikleri b displaystyle beta yerine b displaystyle beta koyarak ve sin b sin b displaystyle sin beta sin beta ile cos b cos b displaystyle cos beta cos beta gerceklerini kullanarak aci toplami versiyonlarindan turetilebilir Aci toplami ozdeslikleri icin seklin biraz degistirilmis bir versiyonu kullanilarak da elde edilebilirler her ikisi de burada gosterilmektedir Bu ozdeslikler diger trigonometrik fonksiyonlar icin toplam ve fark ozdesliklerini de iceren asagidaki tablonun ilk iki satirinda ozetlenmistir Sinus sin a b displaystyle sin alpha pm beta displaystyle sin acos b cos asin b displaystyle sin alpha cos beta pm cos alpha sin beta Kosinus cos a b displaystyle cos alpha pm beta displaystyle cos acos b sin asin b displaystyle cos alpha cos beta mp sin alpha sin beta Tanjant tan a b displaystyle tan alpha pm beta displaystyle tan a tan b1 tan atan b displaystyle frac tan alpha pm tan beta 1 mp tan alpha tan beta Kosekant csc a b displaystyle csc alpha pm beta displaystyle sec asec bcsc acsc bsec acsc b csc asec b displaystyle frac sec alpha sec beta csc alpha csc beta sec alpha csc beta pm csc alpha sec beta Sekant sec a b displaystyle sec alpha pm beta displaystyle sec asec bcsc acsc bcsc acsc b sec asec b displaystyle frac sec alpha sec beta csc alpha csc beta csc alpha csc beta mp sec alpha sec beta Kotanjant cot a b displaystyle cot alpha pm beta displaystyle cot acot b 1cot b cot a displaystyle frac cot alpha cot beta mp 1 cot beta pm cot alpha Arksinus arcsin x arcsin y displaystyle arcsin x pm arcsin y displaystyle arcsin x1 y2 y1 x2y displaystyle arcsin left x sqrt 1 y 2 pm y sqrt 1 x 2 vphantom y right Arkkosinus arccos x arccos y displaystyle arccos x pm arccos y displaystyle arccos xy 1 x2 1 y2 displaystyle arccos left xy mp sqrt left 1 x 2 right left 1 y 2 right right Arktanjant arctan x arctan y displaystyle arctan x pm arctan y displaystyle arctan x y1 xy displaystyle arctan left frac x pm y 1 mp xy right Arkkotanjant arccot x arccot y displaystyle operatorname arccot x pm operatorname arccot y displaystyle arccot xy 1y x displaystyle operatorname arccot left frac xy mp 1 y pm x right Sonsuz sayida acinin toplamlarinin sinus ve kosinusleri i 1 8i sum i 1 infty theta i serisi mutlak yakinsar oldugunda sin i 1 8i tek k 1 1 k 12 A 1 2 3 A k i Asin 8i i Acos 8i cos i 1 8i cift k 0 1 k2 A 1 2 3 A k i Asin 8i i Acos 8i displaystyle begin aligned sin biggl sum i 1 infty theta i biggl amp sum text tek k geq 1 1 frac k 1 2 sum begin smallmatrix A subseteq 1 2 3 dots left A right k end smallmatrix biggl prod i in A sin theta i prod i not in A cos theta i biggr cos biggl sum i 1 infty theta i biggr amp sum text cift k geq 0 1 frac k 2 sum begin smallmatrix A subseteq 1 2 3 dots left A right k end smallmatrix biggl prod i in A sin theta i prod i not in A cos theta i biggr end aligned i 1 8i sum i 1 infty theta i serisi mutlak yakinsadigi icin limi 8i 0 lim i to infty theta i 0 limi sin 8i 0 lim i to infty sin theta i 0 ve limi cos 8i 1 lim i to infty cos theta i 1 Ozellikle bu iki ozdeslikte sonlu sayida acinin toplamlari durumunda gorulmeyen bir asimetri ortaya cikar her carpimda yalnizca sonlu sayida sinus carpani vardir ancak cok sayida kosinus carpani vardir Sonsuz sayida sinus carpani olan terimler zorunlu olarak sifira esit olacaktir 8i displaystyle theta i acilarinin yalnizca sonlu sayida olani sifirdan farkli oldugunda sag taraftaki terimlerin yalnizca sonlu sayida olani sifirdan farklidir cunku sonlu sayida sinus carpani haric hepsi yok olur sadelesir Ayrica her bir terimde sonlu sayida kosinus carpani haric hepsi birimdir tekildir Toplamlarin tanjantlari ve kotanjantlari ek displaystyle e k k 0 1 2 3 displaystyle k 0 1 2 3 ldots icin degiskenler icinde k inci derece olsun xi tan 8i displaystyle x i tan theta i i 0 1 2 3 displaystyle i 0 1 2 3 ldots icin yani e0 1e1 ixi itan 8ie2 i lt jxixj i lt jtan 8itan 8je3 i lt j lt kxixjxk i lt j lt ktan 8itan 8jtan 8k displaystyle begin aligned e 0 amp 1 6pt e 1 amp sum i x i amp amp sum i tan theta i 6pt e 2 amp sum i lt j x i x j amp amp sum i lt j tan theta i tan theta j 6pt e 3 amp sum i lt j lt k x i x j x k amp amp sum i lt j lt k tan theta i tan theta j tan theta k amp vdots amp amp vdots end aligned Oyleyse yukaridaki sinus ve kosinus toplam formullerini kullanarak tan i8i sin i8i icos 8icos i8i icos 8i tek k 1 1 k 12 A 1 2 3 A k i Atan 8i cift k 0 1 k2 A 1 2 3 A k i Atan 8i e1 e3 e5 e0 e2 e4 cot i8i e0 e2 e4 e1 e3 e5 displaystyle begin aligned tan Bigl sum i theta i Bigr amp frac sin bigl sum i theta i bigr prod i cos theta i cos bigl sum i theta i bigr prod i cos theta i 10pt amp frac displaystyle sum text tek k geq 1 1 frac k 1 2 sum begin smallmatrix A subseteq 1 2 3 dots left A right k end smallmatrix prod i in A tan theta i displaystyle sum text cift k geq 0 1 frac k 2 sum begin smallmatrix A subseteq 1 2 3 dots left A right k end smallmatrix prod i in A tan theta i frac e 1 e 3 e 5 cdots e 0 e 2 e 4 cdots 10pt cot Bigl sum i theta i Bigr amp frac e 0 e 2 e 4 cdots e 1 e 3 e 5 cdots end aligned Sag taraftaki terim sayisi sol taraftaki terim sayisina baglidir Ornegin tan 81 82 e1e0 e2 x1 x21 x1x2 tan 81 tan 821 tan 81tan 82 tan 81 82 83 e1 e3e0 e2 x1 x2 x3 x1x2x3 1 x1x2 x1x3 x2x3 tan 81 82 83 84 e1 e3e0 e2 e4 x1 x2 x3 x4 x1x2x3 x1x2x4 x1x3x4 x2x3x4 1 x1x2 x1x3 x1x4 x2x3 x2x4 x3x4 x1x2x3x4 displaystyle begin aligned tan theta 1 theta 2 amp frac e 1 e 0 e 2 frac x 1 x 2 1 x 1 x 2 frac tan theta 1 tan theta 2 1 tan theta 1 tan theta 2 8pt tan theta 1 theta 2 theta 3 amp frac e 1 e 3 e 0 e 2 frac x 1 x 2 x 3 x 1 x 2 x 3 1 x 1 x 2 x 1 x 3 x 2 x 3 8pt tan theta 1 theta 2 theta 3 theta 4 amp frac e 1 e 3 e 0 e 2 e 4 8pt amp frac x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 1 x 2 x 4 x 1 x 3 x 4 x 2 x 3 x 4 1 x 1 x 2 x 1 x 3 x 1 x 4 x 2 x 3 x 2 x 4 x 3 x 4 x 1 x 2 x 3 x 4 end aligned ve bunun gibi Sadece sonlu sayida terim olmasi durumu matematiksel tumevarim ile kanitlanabilir Sonsuz sayida terim olmasi durumu bazi temel esitsizlikler kullanilarak kanitlanabilir Toplamlarin sekantlari ve kosekantlari sec i8i isec 8ie0 e2 e4 csc i8i isec 8ie1 e3 e5 displaystyle begin aligned sec Bigl sum i theta i Bigr amp frac prod i sec theta i e 0 e 2 e 4 cdots 8pt csc Bigl sum i theta i Bigr amp frac prod i sec theta i e 1 e 3 e 5 cdots end aligned Burada ek displaystyle e k n degiskenlerinde k inci derece olup xi tan 8i displaystyle x i tan theta i i 1 n displaystyle i 1 dots n ve paydadaki terim sayisi ile paydaki carpimdaki carpan sayisi soldaki toplamdaki terim sayisina baglidir Sadece sonlu sayida terim olmasi durumu bu tur terimlerin sayisi uzerine matematiksel tumevarim yoluyla kanitlanabilir Ornegin sec a b g sec asec bsec g1 tan atan b tan atan g tan btan gcsc a b g sec asec bsec gtan a tan b tan g tan atan btan g displaystyle begin aligned sec alpha beta gamma amp frac sec alpha sec beta sec gamma 1 tan alpha tan beta tan alpha tan gamma tan beta tan gamma 8pt csc alpha beta gamma amp frac sec alpha sec beta sec gamma tan alpha tan beta tan gamma tan alpha tan beta tan gamma end aligned Batlamyus teoremi Batlamyus teoremi ile sinus icin aci toplami trigonometri ozdesligi arasindaki iliskiyi gosteren sekil Batlamyus teoremi karsilikli kenarlarin uzunluklarinin carpimlarinin toplaminin kosegenlerin uzunluklarinin carpimina esit oldugunu belirtir Bu kenar uzunluklari yukaridaki sekilde gosterilen sin ve cos degerleri cinsinden ifade edildiginde sinus icin aci toplami trigonometrik ozdesligi elde edilir sin a b sin a cos b cos a sin b Batlamyus teoremi trigonometrik ozdeslikler tarihinde onemlidir cunku sinus ve kosinus icin toplam ve fark formullerine esdeger sonuclar ilk kez bu sekilde kanitlanmistir Teorem yandaki sekilde gosterildigi gibi ABCD displaystyle ABCD cembersel dortgeninde karsilikli kenarlarin uzunluklarinin carpimlarinin toplaminin kosegenlerin uzunluklarinin carpimina esit oldugunu belirtir Kosegenlerden veya kenarlardan birinin dairenin capi oldugu ozel durumlarda bu teorem dogrudan aci toplami ve fark trigonometrik ozdesliklerine yol acar Bu iliski en kolay sekilde burada gosterildigi gibi daire bir cap uzunlugunda olacak sekilde insa edildiginde ortaya cikar Thales teoremi ile DAB displaystyle angle DAB ve DCB displaystyle angle DCB her ikisi de dik acidir Dik acili DAB displaystyle DAB ve DCB displaystyle DCB ucgenlerinin her ikisi de uzunlugu 1 olan BD displaystyle overline BD hipotenusunu paylasir Boylece kenar AB sin a displaystyle overline AB sin alpha AD cos a displaystyle overline AD cos alpha BC sin b displaystyle overline BC sin beta ve CD cos b displaystyle overline CD cos beta olur Cevre aci teoremine gore cemberin merkezindeki AC displaystyle overline AC akorunun merkezde olusturdugu aci ADC displaystyle angle ADC acisinin iki katidir yani 2 a b displaystyle 2 alpha beta Dolayisiyla simetrik kirmizi ucgen ciftinin her birinin merkezinde a b displaystyle alpha beta acisi vardir Bu ucgenlerin her birinin 12 frac 1 2 uzunlugunda bir hipotenusu vardir dolayisiyla AC displaystyle overline AC uzunlugu 2 12sin a b 2 times frac 1 2 sin alpha beta yani basitce sin a b displaystyle sin alpha beta Dortgenin diger kosegeni 1 uzunlugundaki captir dolayisiyla kosegenlerin uzunluklarinin carpimi da sin a b displaystyle sin alpha beta dir Bu degerler Batlamyus teoreminin AC BD AB CD AD BC displaystyle overline AC cdot overline BD overline AB cdot overline CD overline AD cdot overline BC ifadesinde yerine konuldugunda sinus icin aci toplami trigonometrik ozdesligi elde edilir sin a b sin acos b cos asin b displaystyle sin alpha beta sin alpha cos beta cos alpha sin beta sin a b displaystyle sin alpha beta icin aci farki formulu CD displaystyle overline CD kenarinin BD displaystyle overline BD yerine cap olarak kullanilmasiyla benzer sekilde turetilebilir Acinin katlari ve yarim aci formulleriTn n inci cos n8 Tn cos 8 displaystyle cos n theta T n cos theta de Moivre formulu i sanal birimdir cos n8 isin n8 cos 8 isin 8 n displaystyle cos n theta i sin n theta cos theta i sin theta n Acinin katlari formulleri Cift aci formulleri Sinus icin cift aci formulunun gorsel ifadesi Birim kenarli ve 28 displaystyle 2 theta acili yukaridaki ikizkenar ucgen icin alan 1 2 taban yukseklik iki yonde hesaplanir Dik durumdayken alan sin 8cos 8 displaystyle sin theta cos theta seklindedir Yan yattiginda ise ayni alan 12sin 28 frac 1 2 sin 2 theta Bu nedenle sin 28 2sin 8cos 8 displaystyle sin 2 theta 2 sin theta cos theta Bir acinin iki kati icin formuller sin 28 2sin 8cos 8 sin 8 cos 8 2 1 2tan 81 tan2 8 displaystyle sin 2 theta 2 sin theta cos theta sin theta cos theta 2 1 frac 2 tan theta 1 tan 2 theta cos 28 cos2 8 sin2 8 2cos2 8 1 1 2sin2 8 1 tan2 81 tan2 8 displaystyle cos 2 theta cos 2 theta sin 2 theta 2 cos 2 theta 1 1 2 sin 2 theta frac 1 tan 2 theta 1 tan 2 theta tan 28 2tan 81 tan2 8 displaystyle tan 2 theta frac 2 tan theta 1 tan 2 theta cot 28 cot2 8 12cot 8 1 tan2 82tan 8 displaystyle cot 2 theta frac cot 2 theta 1 2 cot theta frac 1 tan 2 theta 2 tan theta sec 28 sec2 82 sec2 8 1 tan2 81 tan2 8 displaystyle sec 2 theta frac sec 2 theta 2 sec 2 theta frac 1 tan 2 theta 1 tan 2 theta csc 28 sec 8csc 82 1 tan2 82tan 8 displaystyle csc 2 theta frac sec theta csc theta 2 frac 1 tan 2 theta 2 tan theta Uc kat aci formulleri Uc kat acilar icin formuller sin 38 3sin 8 4sin3 8 4sin 8sin p3 8 sin p3 8 displaystyle sin 3 theta 3 sin theta 4 sin 3 theta 4 sin theta sin left frac pi 3 theta right sin left frac pi 3 theta right cos 38 4cos3 8 3cos 8 4cos 8cos p3 8 cos p3 8 displaystyle cos 3 theta 4 cos 3 theta 3 cos theta 4 cos theta cos left frac pi 3 theta right cos left frac pi 3 theta right tan 38 3tan 8 tan3 81 3tan2 8 tan 8tan p3 8 tan p3 8 displaystyle tan 3 theta frac 3 tan theta tan 3 theta 1 3 tan 2 theta tan theta tan left frac pi 3 theta right tan left frac pi 3 theta right cot 38 3cot 8 cot3 81 3cot2 8 displaystyle cot 3 theta frac 3 cot theta cot 3 theta 1 3 cot 2 theta sec 38 sec3 84 3sec2 8 displaystyle sec 3 theta frac sec 3 theta 4 3 sec 2 theta csc 38 csc3 83csc2 8 4 displaystyle csc 3 theta frac csc 3 theta 3 csc 2 theta 4 Cok kat aci formulleri Cok katli acilar icin formuller sin n8 k tek 1 k 12 nk cosn k 8sink 8 sin 8 i 0 n 1 2 j 0i 1 i j n2i 1 ij cosn 2 i j 1 8 2 n 1 k 0n 1sin kp n 8 displaystyle begin aligned sin n theta amp sum k text tek 1 frac k 1 2 n choose k cos n k theta sin k theta sin theta sum i 0 n 1 2 sum j 0 i 1 i j n choose 2i 1 i choose j cos n 2 i j 1 theta amp 2 n 1 prod k 0 n 1 sin k pi n theta end aligned cos n8 k cift 1 k2 nk cosn k 8sink 8 i 0n 2 j 0i 1 i j n2i ij cosn 2 i j 8 displaystyle cos n theta sum k text cift 1 frac k 2 n choose k cos n k theta sin k theta sum i 0 n 2 sum j 0 i 1 i j n choose 2i i choose j cos n 2 i j theta cos 2n 1 8 1 n22n k 02ncos kp 2n 1 8 displaystyle cos 2n 1 theta 1 n 2 2n prod k 0 2n cos k pi 2n 1 theta cos 2n8 1 n22n 1 k 02n 1cos 1 2k p 4n 8 displaystyle cos 2n theta 1 n 2 2n 1 prod k 0 2n 1 cos 1 2k pi 4n theta tan n8 k tek 1 k 12 nk tank 8 k cift 1 k
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans















