Pergel ve cetvel çizimi

Pergel ve çizgilik çizimi, belli uzunlukta doğrular, belli büyüklükte açılar ve diğer geometrik şekilleri çizmek için sadece ideal bir çizgilik (işaretsiz cetvel veya cetvel tahtası) ve pergel kullanılmasıdır.

Pergel ve çizgilik kullanarak altıgen çizimi

Eşkenar beşgen çizimi

Kullanılacak cetvelin sonsuz uzunlukta olduğu, üzerinde işaretleri olmadığı ve tek bir kenara sahip olduğu varsayılır, bu araç çizgilik olarak adlandırılır. Pergelin ise, sayfadan kaldırıldığı zaman kapandığı, yanı uzaklıkları doğrudan taşımak için kullanılamayacağı varsayılır. (Aslında bu önemsiz bir kısıtlamadır, çünkü ile bu amaca ulaşılabilir.)

Çizgilik ve pergel kullanılarak çizilebilcek her nokta, sadece pergel kullanılarak da elde edilebilir. Düzlem geometrisindeki bazı eski problemler bu kısıtlamayı getirirler.

Pergel ve çizgilik problemlerinin en meşhurlarından birkaçı, tarafından, matematiksel alan teorisi kullanarak ispatlanmıştır. İmkânsızlık kanıtlarına rağmen bazı kişiler bu problemleri çözmek için uğraşmaya devam etmektedir. Bu problemlerin çoğu, başka geometrik dönüşümlere izin verilmesi hâlinde kolaylıkla çözülebilir: örneğin, Küpü iki katına çıkarma, geometrik inşaat yöntemleri ile mümkündür, ama sadece çizgilik ve pergelle yapılamaz.

Matematikçi , çizgilik ve pergel çizimi için sahte kanıtları ve diğer matematiksel saçmalıkları toplamayı kendine hobi edinmiştir.

Pergel ve çizgilik araçları

Bir pergel

Çizgilik ve pergel çizimlerindeki "çizgilik" ve "pergel", gerçek hayattaki çizgilik ve pergellerin bir idealizasyonudur.

• Pergel istenildiği kadar açılabilir, ama (gerçek pergellerden farklı olarak) üzerinde işaret yoktur. Çizimin daha evvelki adımlarında elde edilmiş genişlikler kadar açılabilir sadece. Çizim yapmak için kullanılmadığında kapanır (yani hafızası yoktur).
• Çizgilik sonsuz uzunluktadır, üzerinde işaretler yoktur ve, adi cetvellerden farklı olarak, tek bir kenara sahiptir. Sadece iki nokta arasında bir doğru çizmek için veya mevcut bir çizgiyi uzatmak için kullanılabilir.

Her çizim tam olmalıdır. "Göz kararı" çizim yapmak, yani çizime bakarak onun doğruluğuna hüküm vermek veya ölçüm yaparak (bir cetveli kenarındaki işaretleri kullanmak gibi) yaklaşık bir sonuç bulmak, gerçek bir çözüm olarak sayılmaz.

Şartlar bu şekilde ifade edilince, çizgilik ve pergel çizimleri bir salon oyunu gibi görünebilir, ciddi bir pratik problemden çok; ama bu kısıtlamaların amacı, çizimin tam olarak doğru olduğunun kanıtlanmasını sağlamaktır. Yunan matematikçilerinin ana amaçlarından biri belli uzunluklara karşılık gelen hatasız çizim yöntemleri bulmaktı; örneğin, verilen bir çemberin içine teğet bir beşgenin bir kenarı gibi. Yunanlar üç problem için çizim yöntemi bulamamışlardır:

• Daireyi kareyle çevreleme: Verilen bir çember ile aynı alana sahip bir kare çizimi.
• Küpü iki katına çıkarma: Verilen bir küpün iki katı hacme sahip bir küpün kenar uzunluğunun çizimi.
• : Verilen bir açıyı birbirine eşit üç küçük açıya bölme.

2000 yıl boyunca, yukarıda belirtilen kuralların dahilinde bu problemleri çözecek çizimleri bulmak için çeşitli kişiler uğraş verdiler. Her üç problemin de genel olarak imkânsız olduğu artık kanıtlanmıştır. (Bazı değerlere sahip açılar üçe bölünebilir ama her açı üçe bölünemez.)

Temel çizimler

Temel çizimler

Tüm pergel ve çizgilik çizimleri, daha evvel çizilmiş olan nokta, çizgi ve çemberler kullanılarak yapılan beş temel çizim yönteminin gerektikçe uygulanmasıyla elde edilir. Bunlar:

• İki nokta kullanarak bir çizgi elde edilmesi.
• Bir noktadan geçen ve başka bir noktayı merkez alan bir çember çizilmesi.
• Mevcut, paralel olmayan, iki doğrunun kesişimi olan bir noktanın bulunması.
• Bir doğru ve bir çemberin kesiştiği bir veya iki kesişim noktasının bulunması (eğer kesişiyorlarsa).
• İki çemberin kesişim noktalarının bulunması (eğer kesişiyorlarsa).

Örneğin, bir çizimin en basit hâli olan iki ayrık noktadan başlanarak, bir doğru veya iki çember çizebiliriz. İki çemberin kesişim yerleri ile iki yeni nokta meydana gelir. Bu iki notadan biri ve başlangıçtaki iki nokta arasında doğrular çizerek, bir eşkenar üçgenin çizimi tamamlanır.

Dolayısıyla, herhangi bir geometrik problemde semboller (nokta ve doğrular) içeren bir başlangıç kümesi, bir algoritma ve bir sonuç vardır. Bu bakış açısıyla, geometri, aksiyomatik bir cebire denktir, cebirsel elemanlar yerine semboller kullanır. Muhtemelen Gauss bunu ilk fark eden kişi olmuştur ve bazı çizimlerin imkânsızlığını kanıtlamak için bu yaklaşımı kullanmıştır. Çok sonraları David Hilbert, tam kümesini bulmuştur.

Çizim noktaları ve uzunluklar

Bir doğru parçasının çizgilik ve pergel kullanarak üç eşit parçaya bölünmesi.

Biçimsel kanıt

Bir şeyin imkânsız olduğunu kanıtlamanın çeşitli yolları vardır. Güçlü bir kanıt, olabilirin sınırlarını belirleyip, bu problemleri çözmek için bu sınırı aşmak gerektiğini göstermektir. Çizilebilen şeylerin çoğu Thales'in kesişim kuramı kapsamındadır.

Geometrimiz ile bir cebir arasında bir ilişki kurabiliriz: iki doğrudan oluşan bir Kartezyen koordinat sistemi içinde noktalar sıralı ikililer (vektörler) şeklinde gösterilebilir. Bu vektörler karmaşık sayılar olarak da yazılabilir.

Doğru ve çember denklemleri kullanarak, kesişimlerindeki noktaların bir F alanının olduğu gösterilebilir. Bu alan, doğru üzerindeki iki nokta, çemberin merkezi ve çemberin yarıçapından oluşur. Yani ${\displaystyle x+y{\sqrt {k}}}$ biçimindedirler, burada x, y ve k F'ye aittir.

Çizilebilir noktalar alanı, karekök fonksiyonu içinde kapalı olduğu için, rasyonel katsayılı karmaşık sayılar alanının kadratik uzantılarının sonlu bir dizisinden elde edilebilecek tüm noktaları içerir. Yukarıdaki paragraf gereği, çizilebilecek her bir noktanın, bir uzantılar dizisi ile elde edilebileceği gösterilebilir. Bu önermenin doğal bir sonucu, çizilebilir bir nokta için (ve dolayısıyla herhangi uzunlukta bir doğru parçası için) en düşük polinomiyalin derecesinin 2'nin bir üssü olduğu bulunur. Özellikle, herhangi bir çizilebilir nokta, (veya uzunluk) bir cebirsel sayıdır, ama her cebirsel sayı (örneğin ${\displaystyle {\sqrt[{3}]{2}}}$) çizilebilir değildir (yani, çizilebilir uzunluklar ile cebirsel sayılar arasındaki ilişki birebir değildir)

Çizilebilir açılar

çizilebilir açılar ile, çizilebilir bir halkanın üzerinde çizilebilen noktalar arasında birebir ilişki vardır. Çizilebilen açılar modulo 2π toplaması için (ki bu işlem birim halka üzerinde karmaşık sayılar olarak görünen noktaların çarpımına karşılık gelir) bir Abel grubu oluşturur. Çizilebilen açılar, tanjantı (veya, buna denk olarak, sinüs ve kosinüsü) bir sayı olarak çizilebilen sayılara tam olarak karşılık gelir. Örneğin, düzgün on yedigen çizilebilir, Gauss tarafından keşfedildiği üzere: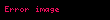${\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}}}$

Çizilebilir açılar grubu, açıların yarısını elde etme işlemi için (ki bu karekök almaya karşılık gelir) kapalı bir gruptur. İki noktadan başlanarak çizilebilen, sonlu mertebeye (finite order) sahip açılar, ya ikinin katına sahip olanlar ya da ikinin bir katı ile bazı Fermat sayılarının çarpımı olanlardır. Bunlara ilaveten, sonsuz mertebeli, yoğun bir çizilebilir açılar kümesi de mevcuttur.

Karmaşık aritmetik olarak pergel ve çizgilik çizimleri

Öklid düzleminde bir noktalar kümesi verilirse, bunlardan biri 0, bir diğeri 1 olarak adlandırmak için seçilirse, ayrıca bir de herhangi bir seçilirse, kümedeki diğer noktalar bir karmaşık sayılar kümesi olarak değerlendirilebilir.

Bir noktalar kümesinin bu şekilde bir karmaşık sayılar kümesi olarak yorumlarsak, sadece pergel ve çizgilik ile çizilebilen noktaların kümesi, orijinal noktaları da kapsayan ve, ve karekök işlemleri için kapalı olan, en küçük alandır (anlamda muğlaklık olmaması için, karmaşık argümanı π'den küçük olan karekök kastedilir). Bu alanın üyeleri, orijinal noktalar için toplama, çıkarma, çarpma, bölme, kompleks argüman ve karekök işlemleri ile ifade edilebilecek bir formüle karşılık gelir; bunların düzlemdeki noktaların yoğun, ama sonlu sayılı bir alt kümesi olduğu görülebilir. Bu altı işlemin her biri bir pergel ve çizgilik işlemine karşılık gelir. Böylesi bir formülden yola çıkarak, her bir aritmetik işleme karşılık gelen çizim işlemini kullanarak, her bir noktayı elde etmek için gereken çizim adımları belirlenebilir. Bazı noktaları elde etmek için bilinen daha kestirme çim yöntemleri, aritmetik işlemlerdeki kestirmelere (kısa yollara) karşılık gelir.

Buna denk olarak (ve herhangi iki noktanın seçilmesine gerek olmadan), herhangi bir doğrultu seçilirse, bir noktalar kümesinde herhangi iki çift nokta arasındaki farklar oranına karşılık gelen karmaşık oranlar, bu noktalar kümesi tarafından belirlenir. Pergel ve çizgilik tarafından bu oranlar kümesi kullanılarak çizilebilen oranların kümesi, orijinal oranları içeren, karmaşık eşlenikler ve karekökler için kapalı olan, en küçük alan ile tıpatıp aynıdır.

Örneğin, bir z noktası veya oranının (yukarıda belirtilen iki bakış açısı da kullanılabilir) gerçel kısmı, sanal kısmı ve modulusu çizimle elde edilebilir, çünkü bunlar şu şekilde ifade edilebilir:

${\displaystyle \mathrm {Re} (z)={\frac {z+{\bar {z}}}{2}}\;}$

${\displaystyle \mathrm {Im} (z)={\frac {z-{\bar {z}}}{2i}}\;}$

${\displaystyle \left|z\right|={\sqrt {z{\bar {z}}}}.\;}$

Küpün iki katına çıkarılması ve açının üçe bölünmesi için kübik denklemlerin çözümü olan oranlar gerekir. "Çemberin karesinin bulunması" ise bir aşkın oran gerektirmektedir. Bunlar, yukarıda tanımlanan alanlar içinde yer almamaktadır, dolayısıyla pergel ve çizgilik ile bunların çizimi için bir çözüm mevcut değildir. (Bir φ açısının üçte birinin bulunması probleminin istisnası, φ/6π'nın bir rasyonel sayı olması ve bu rasyonel sayının paydasının, ikinin bir katı ile bazı Fermat sayılarından birinin çarpımı olmasıdır).

İmkansız çizimler

Çemberin karesinin bulunması

Çemberin karesinin bulunması

Bu problemlerin en meşhuru olan Çemberin karesinin bulunması, verilen bir çember ile aynı alana sahip olan bir karenin çizimidir, sadece pergel ve çizgilik kullanarak.

Çemberin karesinin bulunmasının imkânsızlığı kanıtlanmıştır, çünkü bu problem aşkın bir oran, yani 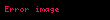${\displaystyle 1/{\sqrt {\pi }}}$, üretilmesine karşılık gelir. Çizgilik ve pergel kullanılarak sadece bazı cebirsel oranlar üretilebilir. Bunlar tam sayılardan başlanarak sonlu sayıda toplam, çıkarma, çarpma, bölme ve karekök işlemiyle elde edilenlerdir. Bu yüzden "çemberi karelemek" terimi, "imkansızı yapmak" anlamında kullanılır.

Çizgilik ve pergel kullanma sınırlaması olmazsa, çeşitli geometrik ve cebirsel yöntemlerle problem kolaylıkla çözülebilir, nitekim antik çağlarda birçok kere çözülmüştür.

Küpün iki katına çıkarılması

Küpün iki katına çıkarılması: sadece pergel ve çizgilik kullanarak, kenar uzunluğu verilen bir küpün iki katı hacimli başka bir küpün kenarını çizilmesi problemidir. Bu problemin çözümü imkânsızdır, çünkü 2'nin küp kökü, cebirsel olmakla birlikte, tam sayılardan başlanarak toplama, çıkarma, çarpma, bölme ve karekök alma yoluyla hesaplanamaz. Rasyonel sayılar üzerinden 2'nin küpköküne karşılık gelen minimal polinom denklem 3. derecedendir. Ancak, pergel ve üzerinde iki işaret olan bir cetvel kullanılarak bu problem çözülebilir.

Açının üçe bölünmesi

Açının üçe bölünmesi: sadece pergel ve çizgilik kullanarak, verilen herhangi bir açının üçte biri olan bir açı çizilmesi problemidir. Genel hâliyle bu problem imkânsızdır. Örneğin, π/3 radyan (60°) bölünemez ama 2π/5 radyan (72° = 360°/5) üçe bölünebilir.

Düzgün çokgenlerin çizimi

Bir karenin çizimi.

Yedigen çizimi

Bazı (örneğin bir düzgün beşgen) pergel ve çizgilikle kolayca çizilebilir; diğerleri kolayca çizilemez. Bu durumdan şu soru ortaya çıkar: bütün düzgün çokgenler pergel ve çizgilik ile çizilebilir mi?

Carl Friedrich Gauss 1796'da düzgün bir n-gen'in pergel ve çizgilik ile çizilebilmesi için n'nin tek sayılı asal çarpanların ayrık Fermat sayıları gerektiğini gösterdi. Gauss bu şartın ayrıca olduğunu da öne sürdü ama buna bir kanıt göstermedi. Gereklilik 1837'de tarafından kanıtlandı.

Yaklaşık çizimler

Pergel ve çizgilikle çizimi çok karmaşık veya imkânsız olan şekiller için yaklaşık çizim yolları mevcuttur. Bu çizimler, amaçlanan çizimin yaklaştırımlarıdır. Bu tür çizimlerin örnekleri arasında, π sayısının yaklaşık çizimi, çemberin yaklaşık karelenmesi, düzgün yedigenin yaklaşık çizimi ve düzgün dokuzgenin yaklaşık çizimi sayilabilir.

Sadece çizgilik veya sadece pergelle çizim

göre, eğer bir şey çizgilik ve pergelle çizilebilirse, sadece pergelle de çizilebilir, eğer verilen ve elde edilecek bilgiler ayrık noktalardan oluşuyorsa (yani çizgi ve çember değil). Sadece çizgilik kullanarak karekök almak mümkün değildir, bu yüzden çizgilikle çizilemeyen bazı şeyler pergelle çizilebilir. Ama ( göre) pergel ve çizgilik ile çizilebilen her şey, eğer bir çember ve merkezi verilirse, sadece bir çizgilik kullanılarak da çizilebilir.

Geniş kapsamlı çizimler

İşaretli cetveller

Neusis yöntemiyle bir açının üçe bölünmesi. Sadece cetvelin uzunluğu kullanılarak, ${\displaystyle \theta >135^{\circ }}$ bir açı için ${\displaystyle \phi ={\frac {\theta }{3}}}$ bulunur. Yayın yarıçapı cetvelin uzunluğuna eşittir. ${\displaystyle \theta <135^{\circ }}$ olan açılar için de aynı çizim uygulanır ama ${\displaystyle P}$, ${\displaystyle [AB]}$'nin dışında yer alır.

Arşimet ve Pergeli Apollonius çizgilik (işaretsiz cetvel) yerine, üzeri işaretli cetvel kullanarak yapılabilecek çizimleri gösterdiler. Bir doğru parçası, iki doğru (veya çember) ve bir noktadan başlayarak, bu yolla, verilen noktadan geçen ve her iki doğruyu kesen ve kesim noktaları arasındaki uzaklığın verilen doğru parçasına eşit olan bir dogru çizmek mümkündür. Yunanlar buna ("eğilim", "temayül", "sınırında olmak") adını vermiştir, çünkü çizilen doğru, noktaya temayül eder. İşaretli cetvelli çizimlerde, bulunacak bir uzaklığın verilen bir uzaklığa oranı eğer üçüncü veya dördüncü dereceden bir denklemin çözümü ise, bu uzaklık çizim yoluyla bulunabilir. Dolayısıyla, eğer işaretli cetvel ve neusis'e izin verilirse, açını üçe bölünmesi (bakınız Arşimet'in üçe bölme yöntemi) ve küpün iki katına çıkarılması mümkündür. ancak çemberin karelenmesi hâlâ imkânsızdır. Bazi düzgün çokgenler, örneğin yedigen, bu yöntemle çizilebilir ve John H. Conway bunların bazılarının çizimini nasıl yapıldığını göstermiştir ancak 11-gen ve sonsuz sayıda başka düzgün çokgen hâlâ imkânsızdır.

Eğer bir açıyı üçe bölücü sanal bir aracın olduğu varsayılır ve kullanımına izin verilirse, çizilebilecek tüm çokgenlerin bir listesi verilmiştir (bunların arasında yedigen, 13-gen ve 19-gen vardır). Bir açı-üçe-bölücüsü, çizgilik ve pergel kullanarak çizilebilecek p-genlerin sayısının sonsuz olup olmadığı, p'nin asal sayı olması hâlinde, henüz cevabı bilinmeyen bir sorudur.

Origami

, pergel ve çizgilik çizimlerinden daha güçlüdür. Huzita–Hatori aksiyomlarını tatmin eden katlamalar ile bulunabilen noktaların kümesi ile, pergel ve işaretli cetvel kullanılarak bulunabilecek noktalar kümesi aynıdır. Dolayısıyla, origami ile üçüncü ve dördüncü dereceden denklemlerin çözümünü bulmak ve klasik problemlerden ikisini çözmek mümkündür.

Uzantı alanı

İşaretli cetvele dayanan neusis yöntemi veya origami yöntemi, çizilebilir sayılar alanını genişletir. Bu genişlemiş alanda, karmaşık sayıların sadece karekökleri değil, küpkökleri de bulunur. Yukarıda bahsedilen, çizilebilir noktalara karşılık gelen aritmetik formüllerin bu genişlemiş alanda karşılıkları vardır, böylece formüllerde küpkökler de yer alır. Bu genişlemiş alanda çizilebilen yeni noktaların oluşturduğu alan genişlemesindeki noktaların derecesi, ikinin bir kuvveti ile üçün bir kuvvetinin çarpımıdır.

İkili sayı sistemiyle ilişki

, çizgilik ve pergel kullanarak bazı sayıların ikili sayı sistemindeki bitlerinin hesaplanmasının mümkün olduğunu göstermiştir.

Sanat

'D' harfi için tasarım, Felice Feliciano, Alphabetum Romanum [Codex Vaticanus 6852].

pergel ve çizgilik ile harf tasarımı yapan ilk kişi olmuştur. 1463'te, Roma yazıtlarındaki alfabeyi geomterik olarak yaratılabileceğini göstermiştir. Latin alfabesindeki aş harflerin bir kare ve çember kullanılarak çizilebildiğini gösteren yapıtı Vatikan Kütüphanesinde bulunmaktadır. Pergel ve çizgiliği tipografiye uygulayan diğer Rönesans sanatçıları arasında ve Luca Pacioli sayılabilir.

Luca Pacioli sanatta altın oranın kullanımı üzerine De Divina Proportione (İlahi Oran) adlı eserini yayımlamıştır (1509); altın oran pergel ve çizgilik ile elde edilebilen bir oranıdır.

Albrecht Dürer İtalya'da perspektif konusunu çalıştıktan sonra "Pergel ve Çizgilik ile Çizim Hakkında İnceleme" (Underweysung der Messung, mit dem Zirckel und Richtscheyt) adlı eseri yazmıştır. "Insan orantıları Hakkında Dört Kitap" (1532-1534) adlı eserinde geometrinin insan bedeninini çizimine uygulamıştır.Adem ve Havva adlı tablosundaki insan figürlerinin oranlarının estetik mükemelliğini sağlamak için pergel ve çizgilik kullandığını belirtmiştir.

Mimaride

Eflatun, diğer sanatlar arasında inşaat zanaatının yerinin ayrı olduğunu belirtmiştir, çünkü kullanılan araçların (pergel, düzkenar, gönye, çekül ve ip-ve-kazık) ölçümlerde bilimsel bir doğruluğa olanak vermektedir.

Roma mimarisinde bazı yapılarını planlarının pergel ve çizgilik olmadan çizilememiş olduğu barizdir. Günümüze yazılı eseri kalmış ilk Romalı mimar, MÖ 1. yüzyılda yaşayan, De Architectura'nın yazarı Vitruvius'dır. Vitruvius, bu eserinin birinci cildinde, pergel ve düz çizgilerin doğru kullanımı sayısinde boş bir sahanın toprağının üzerine şekillerin çizilebildiğini belirtmiştir. Pergel ve çizgilik Orta Çağ mimarları tarafından da kullanılırdı. 13. yüzyıl Fransız mimarı 'ın pergel ve çizgilik kullandığı bilinmektedir.

Günümüzde bilgisayar destekli tasarım programlarının yaygınlaşmadan evvel, teknik çizim için pergel ve çizgilik tekniklerinin temel bir yeri vardı.

Matematik eğitimi

Okullarda geometri kavramlarının pergel ve çizgilik çizimleri ile öğretilmesi gelenekseldir.

Kaynakça

1. ^ Underwood Dudley (1983). "What To Do When the Trisector Comes" (PDF). The Mathematical Intelligencer. 5 (1). ss. 20-25. 19 Haziran 2018 tarihinde kaynağından (PDF). Erişim tarihi: 23 Aralık 2011. 
2. ^ Eric W. Weisstein, Trigonometry Angles--Pi/17 (MathWorld)
3. ^ Kazarinoff, Nicholas D. (2003). Ruler and the Round. Mineola, N.Y.: Dover. ss. 29-30. ISBN . 
4. ^ Conway, John H. and Richard Guy: The Book of Numbers
5. ^ : "Angle trisection, the heptagon, and the triskaidecagon", Amer. Math. Monthly 95 (1988), no. 3, 185-194.
6. ^ Row, T. Sundara (1966). Geometric Exercises in Paper Folding. New York: Dover. 
7. ^ Simon Plouffe (1998). "The Computation of Certain Numbers Using a Ruler and Compass". Journal of Integer Sequences. Cilt 1. ISSN 1530-7638. 29 Şubat 2012 tarihinde kaynağından . Erişim tarihi: 23 Aralık 2011. 
8. ^ John H. Lienhard. "Albrecht Dürer". 9 Kasım 2015 tarihinde kaynağından . Erişim tarihi: 1 Ocak 2012. 
9. ^ Albrecht Dürer, Larry Silver, Jeffrey Chipps Smith (2010). The Essential Dürer. University of Pennsylvania Press. s. 28. ISBN . KB1 bakım: Birden fazla ad: yazar listesi ()
10. ^ John R. Senseney (2011). The Art of Building in the Classical World: Vision, Craftsmanship, and Linear Perspective in Greek and Roman Architecture. Cambridge University Press. s. 112. ISBN . 
11. ^ Mark Wilson Jones (2003). Principles of Roman Architecture. Yale University Press. s. 94. ISBN . 31 Aralık 2013 tarihinde kaynağından . Erişim tarihi: 2 Ocak 2012. 
12. ^ Indra Kagis McEwen (2004). Vitruvius: writing the body of architecture. MIT Press. s. 181. ISBN . 
13. ^ Carl F. Barnes (2009). The portfolio of Villard de Honnecourt (Paris, Bibliothèque nationale de France, MS Fr 19093): a new critical edition and color facsimile. Ashgate Publishing, Ltd. s. 20. ISBN . 

Ayrıca bakınız

• kullanıcılara pergel ve çizgilik inşaatları yapmalarını sağlar.
• , çoğu pergel ve çizgilik çizimleri gösterir

Dış bağlantılar

• at Convergence25 Haziran 2007 tarihinde Wayback Machine sitesinde .
• 25 Haziran 2007 tarihinde Wayback Machine sitesinde .}nt&sa=viewDocument&nodeId=1056&bodyId=1245 Rönesans artistleri tarafından düzgün poligonların çizimi] (Convergence 12 Şubat 2006 tarihinde Wayback Machine sitesinde .25 Haziran 2007 tarihinde Wayback Machine sitesinde .25 Haziran 2007 tarihinde Wayback Machine sitesinde .)
• Hippokrat tarafından açının üçe bölünmesi14 Mayıs 2008 tarihinde Wayback Machine sitesinde .
• Eric W. Weisstein, Açının üçe bölünmesi (MathWorld)
• pergel ve çizgilik ile çeşitli çizimler21 Haziran 2010 tarihinde Wayback Machine sitesinde . adım adım animasyonlu talimatlarla