D'Hondt yöntemi

D'Hondt yöntemi, Belçikalı hukukçu ve matematikçi Victor D'Hondt tarafından 1878'de tasarlanmış nispi temsil hesaplama yöntemidir. Türkiye’de 1961’den bu yana –1965 Millet Meclisi genel seçimi ile 1966 Millet Meclisi ara seçimi dışında– bütün milletvekili genel ve ara seçimlerinde d’Hondt sistemi uygulanmıştır; günümüzde de yürürlükte olan sistem budur.

Kullanım nedeni

Orantılı temsil sistemleri, partilere, aldıkları oy sayısına yaklaşık olarak orantılı olarak koltuklar tahsis etmeyi amaçlar. Örneğin, bir parti oyların üçte birini kazanırsa, yaklaşık olarak koltukların üçte birini kazanmalıdır. Genel olarak, tam orantılılık mümkün olmamaktadır çünkü bu bölmeler kesirli koltuk sayıları üretir. Sonuç olarak, D'Hondt yöntemi de dahil olmak üzere birkaç yöntem geliştirilmiştir, bu yöntemler partilerin koltuk tahsislerinin tam sayılar olduğu ve mümkün olduğunca orantılı olduğu şekilde sağlar. Bu yöntemlerin hepsi orantısızlığı minimize ederek orantılılığa yaklaşır. D'Hondt yöntemi ise en büyük koltuk oranını minimize eder. Diğer daha popüler orantısızlık kavramlarına dayanan deneysel çalışmalar, D'Hondt yönteminin orantılı temsil yöntemleri arasında en az orantılı olanlardan biri olduğunu göstermektedir. D'Hondt, stratejik oy kullanımından dolayı büyük partilere ve koalisyonlara küçük partilerden daha fazla avantaj sağlar. Buna karşılık, Sainte-Laguë yöntemi büyük partilere karşı orantısızlık eğilimini azaltır ve farklı boyuttaki partiler için genellikle daha eşit bir koltuk-oy oranına sahiptir.

D'Hondt yönteminin aksiyomatik özellikleri incelenmiş ve D'Hondt yönteminin tutarlı ve monoton bir yöntem olduğu kanıtlanmıştır. Bu yöntem, siyasi parçalanmayı azaltarak koalisyonları teşvik eder. Bir yöntem, eşit oy alan partilere eşit davranıyorsa tutarlıdır. Monotonluk ilkesine göre, herhangi bir devlet veya partiye verilen koltuk sayısı, meclis büyüklüğü arttığında azalmaz.

Kullanılan ülkeler

D'Hondt yöntemi, Åland, Angola, Arjantin, Arnavutluk, Aruba, Avusturya, Belçika, Bolivya, Brezilya, Burundi, Cape Verde, Şili, Kolombiya, Hırvatistan, Danimarka, Dominik Cumhuriyeti, Doğu Timor, Ekvador, Ermenistan, Estonya, Fiji, Finlandiya, Grönland, Guatemala, Hollanda, İspanya, İsrail, İsviçre, İtalya (karma sistemde), İzlanda, Japonya, Kamboçya, Karadağ, KKTC, Kuzey Makedonya, Lüksemburg, Macaristan (karma sistemde), Moldova, Monako, Mozambik, Nikaragua, Paraguay, Peru, Polonya, Portekiz, Romanya, San Marino, Sırbistan, Slovenya, Türkiye, Uruguay ve Venezuela'da yasama organlarını seçmek için kullanılmaktadır.

İşlem

Tüm oylar sayıldıktan sonra, her parti için bölüm hesaplanır. Bölüm formülü şu şekildedir:

${\displaystyle {\text{Bölüm}}={\frac {T}{s+1}}}$

burada:

• T partinin aldığı toplam oy sayısı,
• s partinin şimdiki aşamaya kadar kazanmış olduğu sandalye sayısı, başlangıçta tüm partiler için 0'dır.

Hangi parti en yüksek orana sahipse, bir sonraki sandalyeyi alır ve oranları yeniden hesaplanır. Tüm sandalyeler tahsis edilene kadar işlem tekrarlanır. Bir seçim çevresinde her partinin aldığı oy toplamı, sırasıyla 1’e, 2’ye, 3’e, 4’e ... bölünür ve o seçim çevresinin çıkaracağı milletvekili sayısına ulaşıncaya kadar bu işleme devam edilir. Elde edilen paylar, parti farkı gözetmeksizin, büyükten küçüğe doğru sıralanır. Milletvekillikleri bu sıralamaya göre partilere tahsis edilir.

Örnek

7 milletvekili çıkaracak bir seçim bölgesinde A Partisi 60.000, B Partisi 25.000, C Partisi 14.000 oy almış olsun.

Partiler	Oy/1	Oy/2	Oy/3	Oy/4	Oy/5	Partinin çıkardığı milletvekili sayısı
A Partisi	60.000	30.000	20.000	15.000	12.000	4
B Partisi	25.000	12.500	8.333	6.250	5.000	2
C Partisi	14.000	7.000	4.667	3.500	2.800	1

Bu seçim çevresinden 7 milletvekili çıkacağından en yüksek 7 rakam ve bu rakamın denk geldiği partiler tespit edilerek çıkarılacak milletvekillikleri bulunur. Buna göre yeşil ile işaretlendiği üzere A partisi 4, B partisi 2 ve C partisi 1 milletvekili çıkarır.

Aşağıda aynı örnek var, ancak farklı bir şekilde açıklanmıştır.

	A Partisi	B Partisi	C Partisi
Aldığı oy	60.000	25.000	14.000
1. milletvekili	60.000	25.000	14.000
2. milletvekili	30.000	25.000	14.000
3. milletvekili	20.000	25.000	14.000
4. milletvekili	20.000	12.500	14.000
5. milletvekili	15.000	12.500	14.000
6. milletvekili	12.000	12.500	14.000
7. milletvekili	12.000	12.500	7.000
Partinin çıkardığı milletvekili sayısı	4	2	1
Milletvekili başına düşen oy	15.000	12.500	14.000

A Partisine 1. olduğu için bir milletvekili verilir. A Partisinin oyu 2'ye bölünür. A Partisinin oyu hâlâ en çok olduğu için A Partisinin oyu bu sefer 3'e bölünür. (60.000/3=20.000). Bu işlemden sonra en çok oy B Partisinde olduğu için B'ye bir milletvekili verilir ve oyu 2'ye bölünür (25.000/2=12.500). Kalan sayılar arasında en büyük A olduğu için bir milletvekili daha verilir ve A'nın oyu bu defa 4'e bölünür (60.000/4=15.000). Ortaya çıkan sayılar arasında en büyük oy yine A'nın oyu olduğundan yine bir milletvekili verilir ve bu kez de oyları 5'e bölünür (60.000/5=12.000). Bu işlemden sonra en büyük oy C'ye aittir ve C'nin hanesine 1 milletvekili eklenir; C'nin oyları 2'ye bölünür (14.000/2=7.000). Bu yedinci ve son işlem sonucunda en büyük sayı B'ye ait olduğu için son milletvekilini B Partisi alır.

D'Hondt altında yaklaşık orantılılık

D'Hondt yöntemi, seçimler sonucu tüm siyasal partiler arasında ortaya çıkan en yüksek milletvekili sayısı-oy oranını düşürerek orantısızlığın önüne geçmektedir. En yüksek milletvekili sayısı-oy oranı, avantaj oranı olarak bilinir. Genel parti sayısının ${\displaystyle P}$ olduğunu düşünelim. Parti ${\displaystyle p\in \{1,\dots ,P\}}$ için avantaj oranı;

${\displaystyle a_{p}={\frac {s_{p}}{v_{p}}},}$

bu denklemde

${\displaystyle s_{p}}$ – ${\displaystyle p}$ partisinin meclisteki sandalye payı, ${\displaystyle s_{p}\in [0,1],\;\sum _{p}s_{p}=1}$,

${\displaystyle v_{p}}$ – ${\displaystyle p}$ partisinin oy payı, ${\displaystyle v_{p}\in [0,1],\;\sum _{p}v_{p}=1}$.

En yüksek avantaj oranı,

${\displaystyle \delta =\max _{p}a_{p},}$

tüm siyasal partiler arasında en fazla temsil edilen siyasi partinin ne kadar orantısız olarak temsil edildiğini ortaya çıkarır. D'Hondt yöntemi, siyasal partilere parlamento sandalyesi tahsis eder ve ortaya çıkan en büyük avantaj oranını mümkün olduğu kadar azaltır,

${\displaystyle \delta ^{*}=\min _{\mathbf {s} \in {\mathcal {S}}}\max _{p}a_{p}}$.

Bu koltuk tahsisi ${\displaystyle \mathbf {s} =\{s_{1},\dots ,s_{P}\}}$, olası tüm ${\displaystyle {\mathcal {S}}}$’lerin bir ögesidir. Bu sayede, D'Hondt yöntemi oyları orantılı olarak temsil edilenlere ve kalanlara ayırır ve işlem sonucunda ortaya çıkan fazlalığı en aza indirir. Geri kalan oyların genel oranı:

${\displaystyle \pi ^{*}=1-{\frac {1}{\delta ^{*}}}}$.

${\displaystyle p}$ partisinin fazla sandalye sayısı bu şekilde hesaplanır,

${\displaystyle r_{p}=v_{p}-(1-\pi ^{*})s_{p},\;r_{p}\in [0,v_{p}],\sum _{p}\,r_{p}=\pi ^{*}}$.

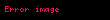
Bunun nasıl çalıştığını daha iyi anlayabilmek için seçimlerde rekabet eden üç siyasal parti düşünün. A partisi oyların yüzde 60,6'sını, B partisi yüzde 25,3'ünü ve C partisi yüzde 14,1'ini almıştır. D'Hondt yöntemi meclis sandalyelerinin yüzde 57,1'ini A partisine, yüzde 28,6'sını B partisine, yüzde 14,1'ini C partisine verir. Bu süreç, A partisine 0,94, B partisine 1,13, C partisine 1,01 avantaj oranı verir. Böylece B en büyük avantaj oranını elde eder. Fazlalığın toplam payı 1 - 1 / 1,13 = 0,12 veya yüzde 12'dir. Bu, A partisi fazlalıklarının yüzde 10,1, B partisi fazlalıklarının yüzde 0 ve C partisi fazlalıklarının yüzde 1,5 olduğu anlamına gelir. Yukarıdaki tablo bu durumu özetlemektedir.

Jefferson ve D'Hondt

Yöntem ilk kez 1792'de Thomas Jefferson tarafından, Amerika Birleşik Devletleri Temsilciler Meclisi'ndeki koltuk dağılımı konusunda George Washington'a yazdığı bir mektupta açıklandı.

Milletvekilleri için böyle ortak bir oran veya bölen olamaz, ki onları tam olarak ve kalan veya kesir olmadan bölebilsin. Ben o zaman şöyle cevap veririm... ki milletvekilleri, en yakın orana mümkün olduğunca yakın şekilde bölünmelidir; ve kesirler göz ardı edilmelidir.

Avrupa'da, Belçikalı matematikçi Victor D'Hondt tarafından 1878 yılında bağımsız olarak icat edildi ve şu şekilde tanımlandı:

Birkaç sayı arasında orantılı olarak ayrılacak ayrık öğeleri tahsis etmek için bu sayıları ortak bir bölenle bölmek gereklidir, bu da payların toplamının tahsis edilecek öğe sayısına eşit olduğu katsayıları üretir.

Jefferson ve D'Hondt yöntemleri eşdeğerdir. Her zaman aynı sonuçları verirler, ancak hesaplamanın sunumu yöntemleri farklıdır. George Washington, Kuzey eyaletlerinin temsilci koltuklarını artıracak yeni bir planı içeren bir yasa tasarısında veto yetkisini ilk kez kullandı. Vetodan on gün sonra Kongre, Jefferson'un Yöntemi olarak bilinen yeni bir paylaştırma yöntemi kabul etti. Devlet adamı ve gelecekteki ABD Başkanı Thomas Jefferson, 1792'de Birleşik Devletler'in İlk Nüfus Sayımı'na dayanarak ABD kongre paylaştırması için bu yöntemi geliştirdi. Bu yöntem, 1842'ye kadar, Temsilciler Meclisindeki koltukların eyaletler arasında orantılı bir şekilde dağıtılmasını sağlamak için kullanıldı.

Victor D'Hondt, yöntemini Fransızca: "Système pratique et raisonné de représentation proportionnelle" adlı yayınında 1882 yılında Brüksel'de sunmuştur.

Bu sistem, hem nüfusa göre eyaletler arasında koltukların dağıtılması hem de seçim sonucuna göre partiler arasında kullanılabilir. Görevler matematiksel olarak eşdeğerdir, eyaletleri partilerin yerine koyar ve nüfusu oyların yerine koyar. Bazı ülkelerde, Jefferson sistemi, yerel politikacıların veya uzmanların yerel olarak tanıttığı isimlerle bilinir. Örneğin, İsrail'de bu yöntem:

Bader–Ofer sistemi

Jefferson yöntemi, en büyük kalan yöntemiyle benzer şekilde bir kota (bir bölen olarak adlandırılır) kullanır. Bölen, gereken toplama eşit olacak şekilde, kesirli kalanları dikkate almadan elde edilen kotalara göre seçilir; yani, kalanları incelemeye gerek olmadığı bir sayı seçilir. Bu, kotaların bir aralığındaki herhangi bir sayıyla gerçekleştirilebilir. Bu aralıktaki en yüksek sayı her zaman D'Hondt yöntemi tarafından bir koltuk vermek için kullanılan en düşük sayıya (Jefferson yöntemi yerine kullanılıyorsa) eşit olurken, aralıktaki en düşük sayı, D'Hondt hesaplamalarında bir koltuk veren bir sonraki sayıdan daha büyük olan en küçük sayıdır.

Yukarıdaki parti listesi örneğine uygulandığında, bu aralık 20.001 ile 25.000 arasında tam sayılar olarak genişler. Daha kesin bir şekilde, 20.000 < n ≤ 25.000 şeklinde ifade edilen herhangi bir n sayısı kullanılabilir.

Seçim eşiği

D'Hondt yöntemi, daha büyük partilere daha fazla koltuk tahsis ederek siyasi parçalanmayı azaltır; bu etki, seçim bölgelerinin küçük olduğu durumlarda daha belirgindir. Siyasi parçalanmayı azaltmak için bir diğer yaklaşım ise seçim eşikleridir; bu eşikleri sağlayamayan herhangi bir liste (boşa harcanan oy), bir koltuk almak için yeterli oyları alsalar bile hiçbir koltuk tahsis edilmez. D'Hondt yöntemiyle seçim eşiği kullanan ülkelerin örnekleri şunlardır: Arnavutluk (tek partiler için %3, iki veya daha fazla partinin koalisyonları için %5, bağımsız adaylar için %1); Danimarka (%2); Doğu Timor, İspanya, Sırbistan ve Karadağ (%3); İsrail (%3.25); Slovenya ve Bulgaristan (%4); Hırvatistan, Fiji, Romanya, Rusya ve Tanzanya (%5); Türkiye (%7); Polonya (%5 veya koalisyonlar için %8; ancak etnik azınlık partileri için uygulanmaz), Macaristan (tek parti için %5, iki parti koalisyonları için %10, 3 veya daha fazla parti koalisyonları için %15) ve Belçika (bölgesel olarak %5). Hollanda'da bir parti, alt mecliste tamamen orantılı bir koltuk için yeterli oy kazanmalıdır (dikkat edilmesi gereken nokta, bunun sadece düz D'Hondt'ta gerekli olmamasıdır); alt mecliste 150 koltuk olduğu için etkili bir seçim eşiği olan %0.67'lik bir oy eşiği bulunmaktadır. Estonya'da, seçim bölgelerinde basit kota alan adaylar seçilmiş sayılır, ancak ikinci (bölge düzeyi) ve üçüncü (ulusal düzeyde, değiştirilmiş D'Hondt yöntemi) sayım turunda, ulusal düzeyde oyların %5'inin üzerinde olan aday listelerine sadece koltuklar verilir. Oy eşiği, koltuk tahsis sürecini basitleştirir ve (çok az oy alması muhtemel olan) marjinal partilerin seçimlere katılmasını engeller. Oy eşiği ne kadar yüksekse, parlamentoda temsil edilecek parti sayısı o kadar az olacaktır.

Ayrıca bakınız

• Saint-Lague yöntemi

Kaynakça

1. ^ Çınar, Yetkin (1 Mart 2022). (PDF). Türkiye Ekonomi Politikaları Araştırma Vakfı. 29 Mart 2022 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 8 Nisan 2023. 
2. ^ 25.5.1961 tarih ve 306 sayılı Milletvekili Seçimi Kanunu m. 32/II, 10.6.1983 tarih ve 2839 sayılı Milletvekili Seçimi Kanunu m. 34/III
3. ^ Gallagher, Michael (1991). (PDF). Electoral Studies. 10 (1): 33-51. doi:10.1016/0261-3794(91)90004-C. 16 Kasım 2013 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 30 Ocak 2016. 
4. ^ Juraj Medzihorsky (2019). "Rethinking the D'Hondt method". Political Research Exchange. 1 (1): 1625712. doi:10.1080/2474736X.2019.1625712. 
5. ^ ^{a b} Pukelsheim, Friedrich (2007). (PDF). 4th ECPR General Conference. 7 Şubat 2009 tarihinde kaynağından (PDF) arşivlendi. 
6. ^ Schuster, Karsten; Pukelsheim, Friedrich; Drton, Mathias; Draper, Norman R. (2003). (PDF). Electoral Studies. 22 (4): 651-676. doi:10.1016/S0261-3794(02)00027-6. 15 Şubat 2016 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 2 Şubat 2016. 
7. ^ Benoit, Kenneth (2000). (PDF). Political Analysis. 8 (4): 381-388. doi:10.1093/oxfordjournals.pan.a029822. 28 Temmuz 2018 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 11 Şubat 2016. 
8. ^ Lijphart, Arend (1990). "The Political Consequences of Electoral Laws, 1945-85". The American Political Science Review. 84 (2): 481-496. doi:10.2307/1963530. JSTOR 1963530. 
9. ^ Balinski, M. L.; Young, H. P. (1978). "The Jefferson method of Apportionment" (PDF). SIAM Rev. 20 (2): 278-284. doi:10.1137/1020040. 22 Eylül 2017 tarihinde kaynağından (PDF). Erişim tarihi: 19 Haziran 2023. 
10. ^ Balinski, M. L.; Young, H. P. (1979). "Criteria for proportional representation" (PDF). . 27: 80-95. doi:10.1287/opre.27.1.80. 
11. ^ André Sainte-Laguë (1910). "La représentation Proportionnelle et la méthode des moindres carrés" (PDF). Annales scientifiques de l'École Normale Supérieure. Cilt 27. l'École Normale Supérieure. 6 Ekim 2019 tarihinde kaynağından (PDF). Erişim tarihi: 10 Ekim 2019. 
12. ^ Gallagher, Michael (1991). "Proportionality, disproportionality and electoral systems". Electoral Studies. 10 (1). doi:10.1016/0261-3794(91)90004-C. 
13. ^ Juraj Medzihorsky (2019). "Rethinking the D'Hondt method". Political Research Exchange. 1 (1). 24 Mayıs 2020 tarihinde kaynağından . Erişim tarihi: 10 Ekim 2019. 
14. ^ Kaynak hatası: Geçersiz <ref> etiketi; :0 isimli refler için metin sağlanmadı (Bkz: )
15. ^ "Founders Online: Proportional Representation, [22 March] 1792". 18 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 19 Haziran 2023. 
16. ^ Caulfield, Michael. "Apportioning Representatives in the United States Congress – Jefferson's Method of Apportionment". Mathematical Association of America. 31 Mayıs 2017 tarihinde kaynağından . Erişim tarihi: 25 Haziran 2017. 
17. ^ King, Charles. "Electoral Systems". Prof. King’s Teaching and Learning Resources. 13 Mayıs 2018 tarihinde kaynağından . Erişim tarihi: 5 Mayıs 2018.