Ayar teorisi veya ayar kuramÄą, kuramsal fizikte temel etileÅmeleri aÃ§Äąklar. TÞrkçede bazen yerelleÅtirilmiÅ bakÄąÅÄąm kuramÄą olarak da geçer.
Fizikte, bir YerelleÅtirilmiÅ BakÄąÅÄąm KuramÄą (Gauge Teorisi) Lagrange yerel dÃķnÞÅÞmlerin sÞrekli gruplar altÄąnda deÄiÅmez deÄerlerin olduÄu alan teorisinin bir tÞrÞdÞr.

Terim olarak yerelleÅtirilmiÅ bakÄąÅÄąm Lagrangian içindeki gereksiz serbestlik derecelerine iÅaret eder. Ayar dÃķnÞÅÞmleri denilen olasÄą gÃķstergeleri arasÄąndaki dÃķnÞÅÞmler, bir Lie grubu-sevk simetri grubu ya da teorinin gÃķsterge grubu olarak oluÅturur. Grup jeneratÃķrlerin Lie cebiri herhangi Lie grubu ile iliÅkilendirilmiÅtir. Her grup jeneratÃķr için mutlaka bir karÅÄąlÄąk gelen alan (genellikle bir vektÃķr alanÄą) gauge alanÄą denilen alan ortaya Ã§Äąkar. Gauge alanlarÄą yerel grup dÃķnÞÅÞmleri altÄąnda deÄiÅmezliÄi (denilen gauge deÄiÅmezliÄi) saÄlamak için Lagrange dahildir. BÃķyle bir teori nicemlenmis olduÄunda, Gauge alanlarÄąnÄąn kuantumuna Gauge bozonlarÄą denir. Simetri grubu deÄiÅmeli deÄil ise ise, normal olan Ãķrnek Yang-Mills teorisidir.
Fizikteki birçok gÞçlÞ teoriler Lagrangeler altÄąnda sabit simetrik dÃķnÞÅÞm gruplarÄą tarafÄąndan aÃ§ÄąklanmÄąÅtÄąr. Onlar aynÄą fiziksel sÞreçler ortaya Ã§ÄąktÄąÄÄą zaman uzayÄąn her noktasÄąnda yapÄąlan bir dÃķnÞÅÞm altÄąnda deÄiÅmezdir, onlarÄąn kÞresel bir simetriye sahip olduÄu sÃķylenir. Gauge teorilerinin temel taÅÄą olan yerel simetri daha sÄąkÄą bir engeldir. AslÄąnda, kÞresel simetri uzayda sabitlenmiÅ olan yerel simetrinin grup parametlereleridir.
Guage teorileri temel parçacÄąklarÄąn dinamiklerini aÃ§Äąklayan baÅarÄąlÄą alan teorileri kadar Ãķnemlidir. Kuantum elektrodinamiÄi gauge teorisinin simetrik grubu U(1) ile deÄiÅmelidir. Kuantum elektrodinamiÄi bir tane gauge alanÄąna sahiptir. Standart Modelin toplamda on iki tane gauge bozonu vardÄąr. Bunlar foton, Þç tane zayÄąf bozon ve 8 tane gluondur. U (1) SU à simetri grubu ile deÄiÅmeli olmayan gauge teorisi (2) à SU (3) ve on iki bozonlarÄąnÄąn toplam vardÄąr: fotonun, Þç zayÄąf bozonlarÄą ve sekiz gluonlarÄąn.
Gauge teorileri genel gÃķrelilik teorisi içindeki yerçekimini aÃ§Äąklamada Ãķnemlidir. Onun vaka gÃķstergesi alan bir tensÃķr, Lanczos tensÃķr olduÄunu biraz benzersizdir. Gauge çekim teorisi ile baÅlayan kuantum yerçekimi teorisi, aynÄą zamanda kÞtleçekimi olarak bilinen bir ÃķlçÞ bozonunun varlÄąÄÄąna inanmaktayÄąz. Gauge simetrilerinin koordinat sistemi uzay keyfi diffeomorphisms altÄąnda serbestçe seçilebilir olduÄu genel genel gÃķrelilik kovaryans ilkesi analoglarÄą olarak gÃķrÞlebilir. Hem gauge deÄiÅmezliÄi ve Diffeomorfizm deÄiÅmezliÄi sisteminin aÃ§ÄąklamasÄąnda bir fazlalÄąk gÃķstermektedir. Bir alternatif kÞtleçekimi teorisi olarak gauge kÞtleçekim teorisi yeni gauge alanlarÄą ile gerçek bir gauge ilkesinin genel kovaryans ilkesini deÄiÅtirir.
Tarihsel olarak, bu fikirler ilk klasik elektromanyetizma baÄlamÄąnda ve daha sonra genel gÃķrelilik ile belirtilmiÅtir. Ancak, gauge simetrilerinin modern fizikteki Ãķnemi elektron gÃķreli kuantum mekaniÄiyle ilk olarak ortaya Ã§ÄąktÄą. BugÞn, Gauge teorileri yoÄun madde fiziÄinde, nÞkleer ve yÞksek enerji fiziÄinde ve diÄer alt baÅlÄąklar arasÄąnda yararlÄądÄąr.
GeçmiÅi
Bir gauge simetriye sahip ilk alan teorisi, 1864-65 yÄąlÄąnda, Maxwell'in formÞlasyonu olan elektrodinamiktir. ( "Elektromanyetik Alan Bir Dinamik Teorisi"). Bu simetrinin Ãķnemi erken formÞlasyonlarda fark edilememiÅtir. Benzer Åekilde fark edilemeyen, Hilbert'Äąn Einstein'Äąn alan denklemlerinden tÞrettiiÄi genel koordinat dÃķnÞÅÞmÞ altÄąnda eylem deÄiÅmezliÄini varsaymÄąÅtÄą. Daha sonra Hermann Weyl, genel gÃķrelilik ve elektromanyetizma birleÅtirmek amacÄąyla, ayar (ya da "Gauge") deÄiÅikliÄi altÄąnda genel gÃķrelilikte yerel simetri olabileceÄini tahmin etti. Kuantum mekaniÄinin geliÅiminden sonra Weyl, Vladimir Fock ve Fritz London karmaÅÄąk bir miktar ayar katsayÄąsÄąnÄą deÄiÅtirerek gague deÄiÅtirilmiÅ oldu ve U (1) gauge simetrisi olan faz deÄiÅikliÄi içine Ãķlçekli dÃķnÞÅÞme dÃķndÞ. Bu olay yÞklÞ kuantum mekaniksel parçacÄąÄÄąn dalga fonksiyonu Þzerinde elektromanyetik alan etkisi olarak aÃ§ÄąklandÄą. Bu 1940'larda Pauli tarafÄąndan yaygÄąnlaÅtÄąrÄąlan ilk tanÄąnmÄąÅ ayar teorisi, oldu.
1954 yÄąlÄąnda, temel parçacÄąk fiziÄinde bÞyÞk bir karÄąÅÄąklÄąÄÄą bazÄą çÃķzmek için çalÄąÅÄąrken, Chen Ning Yang ve Robert Mills birlikte atom çekirdeklerindeki nÞkleonlarÄą tutan gÞçlÞ etkileÅimi anlamak için model olarak deÄiÅmeyen gauge teorileri tanÄątÄąldÄą. (Ronald Shaw, Abdus Salam altÄąnda çalÄąÅan, baÄÄąmsÄąz doktora tezi aynÄą kavramÄąnÄą tanÄąttÄą.) Elektromanyetizma gÃķstergesi deÄiÅmezliÄi yaygÄąnlaÅtÄąrÄąlmasÄą, onlar (non-deÄiÅmeli) SU (2) simetri grubunun eylem dayalÄą bir teori inÅa etmek için proton ve nÃķtronlarÄąn izospin duble Þzerinde çalÄąÅtÄą. Bu, kuantum elektrodinamik spinÃķr alanlarÄą U (1) grubunun hareketine benzerdir. ParçacÄąk fiziÄindeki odak kuantize gauge teorilerini kullanarak oldu.
Bu fikir daha sonra kuantum alan teorisinin zayÄąf kuvvet uygulamasÄą ve elektrozayÄąf teoride elektromanyetizma ile birleÅmesine vesile oldu. DeÄiÅmez gauge teorileri asimptotik ÃķzgÞrlÞk olarak adlandÄąrÄąlan bir Ãķzellik ile yeniden fark edildiÄinde gauge teorileri daha da çekici hale geldi. gÞçlÞ etkileÅimlerin Ãķnemli bir ÃķzelliÄi olduÄuna inanÄąlÄąyordu. Bu gÞçkÞ kuvvetler için gauge teorisini aramaya taÅvik etti. Åimdi kuantum renk teorisi olarak bilinen bu teori, kuarklarÄąn renk ÞçlÞsÞ SU (3) grubunun eylemi ile birlikte bir gauge teorisidir. Standart Model, gauge teorisi dilinde elektromanyetizma, zayÄąf etkileÅimler ve gÞçlÞ etkileÅimlerin aÃ§ÄąklamasÄąnÄą birleÅtirir.
1970'li yÄąllarda, Michael Atiyah klasik Yang-Mills matematiksel denklemlerinin çÃķzÞmlerinin çalÄąÅsmasÄąna baÅladÄą. 1983 yÄąlÄąnda, Atiyah'Äąn ÃķÄrencisi pÞrÞzsÞz 4-manifoldlarÄą tÞrevlenebilir sÄąnÄąflandÄąrma ile homeomorfizma kadar onlarÄąn sÄąnÄąflandÄąrmadan çok farklÄą olduÄunu gÃķstermek için bÞtÞn çalÄąÅmasÄąnÄą bunun Þzerine inÅa etti. Michael Freedman Ãklid 4-boyutlu uzayda Þzerinde yapÄąlarÄąnÄą sergilemek için Donaldson çalÄąÅmalarÄąnÄą kullandÄą. Bu temel fizik baÅarÄąlarÄąndan baÄÄąmsÄąz, kendi iyiliÄi için gauge teorisi giderek artan ilgiye yol açtÄą. 1994 yÄąlÄąnda, Edward Witten ve bazÄą topolojik deÄiÅmezler (Seiberg-Witten deÄiÅmezler) hesaplanmasÄąnÄą etkin SÞpersimetri dayalÄą gauge teorisinin tekniklerini icat etti. Gauge teorisinden matematiÄe olan bu katkÄąlar bu alanda yenilenmiÅ bir ilgiye yol açmÄąÅtÄąr.
Fizikteki gauge teorilerinin Ãķnemi elektromanyetizmanÄąn kuantum alan teorisi aÃ§Äąklamak için birleÅik bir çerçeve, zayÄąf kuvvet ve gÞçlÞ kuvvet saÄlayan matematiksel biçimcilik gibi muazzam baÅarÄąlara Ãķrnek olmuÅtur. Standart Model olarak bilinen bu teori, doÄanÄąn dÃķrt temel kuvvetten ÞçÞne iliÅkin deneysel tahminleri aÃ§Äąklar. Sicim teorisi gibi modern teorilerin, yanÄą sÄąra genel gÃķrelilik, teorilerinin içinde bir Åekilde gauge teorileri vardÄąr.
TanÄąmÄą
Global ve Lokal Simetriler
Global Simetri
Fizikte, herhangi bir fiziksel durum için matematiksel aÃ§Äąklama, genellikle fazla serbestlik dereceleri ihtiva eder; aynÄą fiziksel durum ise, aynÄą zamanda birçok eÅdeÄer matematiksel yapÄąlandÄąrmalar için tarif edilir. Bu dÃķnÞÅÞmler teorinin "simetrileri" bir grubu olduÄu ve fiziksel durumu baÄÄąmsÄąz bir matematik yapÄąlandÄąrmaya ancak bu simetri grubu ile birbirine baÄlÄą sÄąnÄąflardaki konfigÞrasyonlarda karÅÄąlÄąk gelir.
Bu fikir tÞm fiziksel sistemi kapsar hiçbir tercih "eylemsizlik" koordinat sistemi vardÄąr bir durumda çok daha soyut "koordinatlarÄąn deÄiÅiklikler" benzer yerel yanÄą sÄąra kÞresel simetri içerecek Åekilde genel olabilir. Bir gauge teorisi modelin simetrileri ile birlikte tutarlÄą fiziksel tahminler yapmak için gerekli teknikler sete sahip bir matematiksel modeldir.
Global Simetriye Ãrnek
Matematiksel konfigÞrasyonda meydana gelen miktarÄą sadece bir sayÄą deÄil de bir hÄąz ya da bir dÃķnme ekseni, bir vektÃķr veya bir matris halinde dÞzenlenmiÅ sayÄąlarÄą da koordinat transformasyonu ile deÄiÅtirilebilir  olarak geometrik Ãķneme sahip olduÄunu  temsili  olarak gÃķrmek gerekir.
Lokal Simetri
Lokal Simetriyi tanÄąmlamak için lif demetlerinin kullanÄąlmasÄą
Gauge teorilerinin çoÄunda, uzay ve zamanda bireysel bir noktada soyut ÃķlçÞ bazÄąnda olasÄą dÃķnÞÅÞmlerin kÞmesi sonlu boyutlu Lie grubudur. En basit Åekliyle bÃķyle bir grup karmaÅÄąk sayÄąlar kullanÄąmÄą yoluyla kuantum elektrodinamik (QED) modern formÞlasyonu gÃķrÞnen U (1) 'dir. Kuantum elektrodinamik genellikle ilk ve en basit fiziksel ÃķlçÞ teorisi olarak kabul edilir. Belirli bir gauge teorisinin tÞm yapÄąlandÄąrma için mÞmkÞn gauge dÃķnÞÅÞmlerinin kÞmesi de bir grup oluÅturmaktadÄąr. Bu grupta gauge grubunun teorisini oluÅturmaktadÄąr. Gauge grubunun bir elemanÄą (sonlu boyutlu) Lie grubu, ÃķrneÄin her noktada fonksiyonun deÄerini ve tÞrevlerinin gÃķstergesi dÃķnÞÅÞm eylem Þzerinde temsil ettiÄi için uzay-zamanÄąn noktalarÄąndan bir dÞzgÞn deÄiÅen fonksiyonu tarafÄąndan deÄiÅtirilebilen bu nokta Þzerindedir.
Uzay ve zaman içinde her noktada sabit bir parametre ile bir gauge dÃķnÞÅÞmÞ geometrik koordinat sisteminindeki katÄą bir rotasyona benzerdir. Bu gauge temsilinin kÞresel simetrisini temsil eder. Sert bir dÃķnÞŠdurumunda olduÄu gibi, bu gauge dÃķnÞÅÞmÞ gerçekten yerel miktarÄą temsili ile aynÄą Åekilde gauge baÄÄąmlÄą miktarÄąnÄąn bir yol boyunca deÄiÅiklik oranÄąnÄą temsil eden ifadeleri etkiler. olan parametre sabit fonksiyon yerel simetri olarak adlandÄąrÄąlÄąr olmayan bir gÃķstergesi dÃķnÞÅÞmÞ; Bir tÞrev içeren ifadeler Þzerindeki etkisi yok ifadelerden o niteliksel olarak farklÄą olduÄunu. (Bu Coriolis etkisi Þretebilir referans çerçevesi olmayan bir atalet deÄiÅimine benzer.)
Gauge AlanlarÄą
Gauge alanĹ matematiksel yapÄąlandÄąrmayĹ aÃ§Äąklamak için Ãķnemli bir parça haline gelir. Gauge alan bir gauge dÃķnÞÅÞmÞ ile yok edilebilecek bir yapÄąlandÄąrma (matematiksel dili, kendi eÄriliÄi olarak) kendi alan Åiddeti her yerde sÄąfÄąr ÃķzelliÄine sahip; Gauge teorisi bu yapÄąlandÄąrmalar ile sÄąnÄąrlÄą deÄildir. BaÅka bir deyiÅle, bir gauge teorisinin ayÄąrt edici ÃķzelliÄi gauge alanÄą sadece koordinat sisteminin kÃķtÞ bir seçimi ile telafi olmamasÄądÄąr. BaÅka bir deyiÅle genellkile gauge alanÄąnÄą yok eden hiçbir gauge dÃķnÞÅÞm yoktur.
Bir gauge teorisinin dinamiklerini analiz ederken, gauge alanĹ dinamik bir deÄiÅken gibi davranmalÄądÄąr. Ek olarak diÄer nesneler ile etkileÅimi yÞzÞnden gauge alanÄą tipik olarak "kendi kendine enerji" terimi Åeklinde enerjiye katkÄąda bulunur. Gauge teorisi için denklemleri elde etmek için
- gauge alanÄą olmadan naif baÅlangÄąÃ§
- (Genel olarak, bir dÃķnme aÃ§ÄąsÄą için soyut eÅdeÄeri) sÞrekli bir parametre ile karekterize edilebilir teorinin kiÅilerce genel simetri listesi;
- bir yerden baÅka bir yere deÄiÅen izin verlien simetri parametresinden kaynaklanan dÞzeltme terimlerini hesaplamak;
- Bir veya daha fazla ÃķlçÞ alanlarÄąna kavramalarÄą olarak bu dÞzeltme terimleri yeniden yorumlanmasÄąna ve bu alanlarÄą uygun Ãķz enerji terimleri ve dinamik davranÄąÅÄą vererek.
Bu bir anlamda gauge teorisinin global simetriden lokal simetriye uzanÄąÅtÄąr. AyrÄąca bu oldukça yakÄąn bir Åekilde gauge kÞtleçekimi teorisinin bilenen adÄąyla genel gÃķrelilik teorisinin tarihsel geliÅimini andÄąrÄąyor.
Fiziksel Deneyler
Gauge teorilerinin esas fiziksel deneylerin sonuçlarÄąnÄą modellemek için
- evreni sÄąnÄąrlayan olasÄą yapÄąlandÄąrmalarÄą deneyi kurmak için bilgilerle uyumlu olanlar
- deneyi Ãķlçmek için olasÄą sonuçlarÄąn olasÄąlÄąk daÄÄąlÄąmÄą hesaplama
bu ikisi kullanÄąlÄąr.
Ãzel bir referans olmadan genellikle deneyin kurulum bilgileri ve olasÄą ÃķlçÞm sonuçlarÄą matematiksel aÃ§Äąklamalarla anlatÄąlamaz buna gauge seçimide dahildir. Gauge teorisinin hesaplamalarÄąnda anormalliklerin sÄąk gÃķrÞlen kaynaÄÄą hor kullanÄąlan sÄąnÄąr durumlardaki gauge baÄÄąmlÄąlÄąÄÄądÄąr.
SÞreklilik teorileri
(SÞreklilik elektrodinamik ve genel gÃķrelilik) YukarÄąda belirtilen iki gauge teorileri sÞreklilik alan teorileri Ãķrnekleridir.  SÞreklilik teorisindeki hesaplama tekniklerini dolaylÄą olarak varsayarÄąz:
- gauge tamamen sabit seçenek sunulur, tek bir yapÄąlandÄąrma sÄąnÄąr koÅullarÄą prensipte tamamen tarif edilebilir
- tamamen sabit gauge ve sÄąnÄąr koÅullarÄą komple bir set verilen en az eylem ilkesi, bu sÄąnÄąrlarÄą ile tutarlÄą eÅsiz bir matematiksel bir yapÄąlandÄąrma (ve dolayÄąsÄąyla eÅsiz bir fiziksel durum) belirler;
- muhtemel ÃķlçÞm sonuçlarÄą olasÄąlÄąÄÄą ile belirlenebilir:
- kurulum bilgileri ile tutarlÄą sÄąnÄąr koÅullarÄą tarafÄąndan belirlenmektedir tÞm fiziksel durumlar Þzerinde bir olasÄąlÄąk daÄÄąlÄąmÄą kurulmasÄą,
- Her olasÄą fiziksel durum için ÃķlçÞm sonuçlarÄąnÄąn bir olasÄąlÄąk daÄÄąlÄąmÄą kurulmasÄą,
- Bu iki olasÄąlÄąk daÄÄąlÄąmlarÄąnÄą  toplamÄąnÄąn olasÄą bir ÃķlçÞm daÄÄątÄąm kurulum bilgileri ile tutarlÄą sonuçlarÄąnÄą almak için;
- Gauge sabitlemek hesaplamalarda anormalik gÃķstermez.
Bu varsayÄąmlar, enerji Ãķlçekleri ve deneysel koÅullar için  geniÅ bir yelpazede geçerlidir. Bu teoriler ÄąÅÄąÄÄąnda, gÞnÞmÞzde karÅÄąlaÅÄąlan  ĹÅÄąktan ÄąsÄą ve elektrik dÞÅÞÅlerinden ve yÞkselmelerinden gelen bÞtÞn fenomenleri doÄru tahmin etmede kullanÄąlÄąr. Bu tahminler sadece çok kÞçÞk ve çok bÞyÞk Ãķlçeklerde doÄru deÄildir.
Kuantum Alan Teorileri
Bu klasik sÞreklilik alan teorileri dÄąÅÄąnda, en yaygÄąn olarak bilinen gauge teorileri, kuantum elektrodinamik ve temel parçacÄąk fiziÄinin Standart Modeli dahil kuantum alan teorisi vardÄąr. En az eylem ilkesine gÃķre "izin verilen" fiziksel durumlarÄą niteleyen bir gauge-kovaryantÄą eylem ayrÄąlmaz. Ancak, gauge dÃķnÞÅÞmleri tarafÄąndan aÅÄąrÄą derecelerde serbest davranÄąÅlarÄąndan dolayÄą sÞreç (continuum) ve kuantum teorileri bÞyÞk farklÄąlÄąklar gÃķstermektedir. SÞreç (continuum) teorileri ve basit kuantum alan teorilerinin çoÄu matematiksel dÞzenlemelerin yÃķrÞngelerini dÞÅÞrmeden gauge reçetesini kullanÄąrlar.
Daha sofistike olan kuantum alan teorileri Ãķzellikle deÄiÅme olmayan gauge gruplarÄąnÄą içerenler baÅta olmak Þzere gauge simetrisine karÄąÅÄąklÄąk teorisi teknikleriyle yok ederler ve ve karÅÄą terimler BRST nicelemesinde bilindiÄi gibi birbirlerini anormal bir Åekilde iptal etmek için motive ederler. Bu endiÅeler bir anlamda son derece teknik olmakla birlikte, aynÄą zamanda yakÄąndan ÃķlçÞmÞ, fiziksel bir durum bilgisine sÄąnÄąrlarÄą ve eksik belirtilen deneysel koÅullar nedeniyle tam olarak anlaÅÄąlmamÄąÅtÄąr. Matematiksel teknikler iÅlenebilir gauge teorilerini uygulamak için birçok alanda geliÅtirildi. Bunlara Ãķrnek dÞÅÞk boyutlu topoloji katÄą hal fiziÄi ve kristalografisi verilebilir.
Klasik Gauge teorisi
Klasik elektromanyetizma
Tarihsel olarak, Gauge simetrisinin ilk ÃķrneÄinin keÅfi klasik elektromanyetizmadÄąr. Elektrostatikte, elektrik alan E ya da onun karÅÄąlÄąÄÄą elektrik potansiyel V . 



Genel Gauge dÃķnÞÅÞmÞ sadece 


Burada f zamana ve pozisyona dayalÄą herhangi bir fonksiyondur. Gauge dÃķnÞÅÞmleri altÄąnda alanlar aynÄą kalÄąr ve sonuç olarak Maxwell denklemleri hala geçerlidir. Buda Maxvell denklemlerinin gauge simetrisine sahip olduÄunu sÃķyler.
Skaler Gauge Teorisin ÃrneÄi
AÅaÄÄądaki formÞllerle sezgisel kÞresel simetri Ãķzelliklerinden baÅlayarak "motive" nasÄąl yerel gauge  deÄiÅmezliÄi gÃķsterir ve baÅlangÄąÃ§ta olmayan etkileÅim alanlarÄą arasÄąndaki etkileÅime nasÄąl yol açar. AÅaÄÄądaki formÞllerle ÃķrneklendirilmiÅtir.
n burada etkileÅime girmeyen gerçek skaler alanlar, m burada kÞtleye eÅittir. Sistem burada hareket halindedir. ve toplam hareket halindeki skaler alanlar
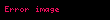
Lagrange(yoÄunluÄu) kÞçÞk sÄąkÄą bir Åekilde yazÄąlabilir.

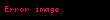
AlanlarÄąn vektÃķrÞnÞn gÃķsterimiyle

4 boyutun her birinde Terim olan 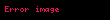

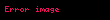
G Â n-by-n ortogonal gruba ait olan sabit matrisdir. 


Bu bu Ãķzel Lagrangian kÞresel simetri karakterize ve simetri grup genellikle ÃķlçÞ grubu denir; Matematiksel terim Ãķzellikle G-yapÄąlarÄąn teorik olarak yapÄą grubudur. Bu arada, Noether teoremi dÃķnÞÅÞmleri bu grup altÄąnda deÄiÅmezlik akÄąmlarÄąn korunmasÄąna yol açtÄąÄÄąnÄą ima edilir.

Burada Ta matrisleri SO(n) gruplarÄąnÄąn jeneratÃķrleridir. Her jeneratÃķr için korunmuÅ bir akÄąm vardÄąr.
Åimdi Lagrangian lokal deÄiÅmeyen O(n) sahip olmalÄądÄąr. G matrisleri x koordinatÄąnda uzayzaman fonksiyonun olmasÄąna izin vermelidir.
Bu durumda G=G(x) iken G matrisi geçemez.

Bu sorunu çÃķzmek için yeni bir tÞrev alÄąrÄąz.
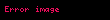
Bu yeni tÞrev eÅdeÄiÅken gauge tÞrevi olarak adlandÄąrÄąlÄąr ve bu forma sahiptir.

Burada g eÅleÅen sabit olarak adlandÄąrÄąlÄąr ve etkileÅimin gÞcÞnÞ tanÄąmlamada Ãķnemlidir. Basit birkaç hesaplamadan sonra Gauge AlanÄą A(x) aÅaÄÄądaki gibi dÃķnÞÅmek zorundadÄąr.
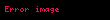
Gauge alanÄą Lie cebirinin bir elementidir. Sonuç olarak aÅaÄÄądaki gibi geniÅletilebilir.

Son olarak Åimdi elimizde lokal Gauge deÄiÅmeyen bir Lagrangian' ÄąmÄąz var.

Bu Lagrange ve ÃķzgÞn kÞresel gauge  deÄiÅmeyen Lagrangian arasÄąndaki fark Lagrange EtileÅimi olduÄu gÃķrÞlÞr.

Bu terim sadece yerel gauge deÄiÅmezliÄi için talebin bir sonucu olarak n skaler alanlar arasÄąndaki etkileÅimleri tanÄątÄąr. Bununla birlikte, bu etkileÅimin fiziksel olup tamamen rastgele hale getirmek için, arabulucu A (X) uzayda yayÄąlmasÄą gerekir. Bununla baÅa Ã§Äąkmak için bir sonraki aÅama 
Gauge alanÄą için Yang-Mills Lagrangesi
Bir Ãķnceki bÃķlÞmde geliÅtirilen bir klasik gauge teorisinin çizilen o resmi neredeyse bitmek Þzere.  Uzayzamanda ki gauge alan A(x) deÄerinin bulunmasÄą için sadece eÅdeÄiÅken tÞrvelerin (D) tanÄąmlanmasÄą kaldÄą.  Bu alanÄąn manuel deÄerlerini belirlemek yerine, bu bize alan denklemlerinin çÃķzÞmÞnÞ verilebilir. DahasÄą bu alan denkleme Lagrange yanÄą sÄąra yerel gauge deÄiÅmez olduÄunu gerektiren, gauge alanÄą için  Lagrangian olasÄą bir formu (geleneksel) Åeklinde yazÄąlÄąr

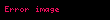
ve Ä°zler vektÃķr uzay alanlarÄą Þzerinden atÄąlÄąyor. Buna Yang-mills hareketi denir. DiÄer gauge deÄiÅmez haretleri hala mevcuttur. ÃrneÄin doÄrusal olmayan elektrodinamik, Born-Infeld hareketi Chern-Simons model gibi.
Gauge teorisi için tamamlanmÄąÅ Lagrangian aÅaÄÄądaki gibidir.

ElektrodinamiÄe Ãrnek
Daha Ãķnceki bÃķlÞmlerde geliÅtirilen biçimcilik basit bir uygulama olarak, sadece elektron alanÄą ile, elektrodinamik davayÄą dÞÅÞnÞn.  Bare-bones hareketi elektrik alanÄąn Dirac denklemini Þretir.

Bu sistem için global simetri aÅaÄÄądaki gibidir.
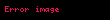
Buradaki gauge grubu U(1)dir. parçacÄąk dÃķnmeleriyle alanÄąn faz aÃ§ÄąsÄąnÄąn dÃķnmeleri sabit Îļ ile belirlenir. Bu sistemin lokalleÅmesinin anlamÄą Îļ ile Îļ(x) yer deÄiÅtirmesidir. YaklaÅÄąk eÅ deÄiÅken tÞrevi
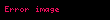
OlaÄan elektrik yÞkÞyle e yÞkÞnÞ belirler ve elektromanyetizmanÄąn 4-vektÃķr potansiyeliyle  gauge alanÄąnÄą Langrangian etkileÅimiyle sonuçlandÄąrÄąr.

Burada 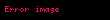
Gauge alan 
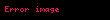
Matematiksel FormÞlleme
Gauge  teorileri genellikle diferansiyel geometrinin dilinde tartÄąÅÄąlmÄąÅtÄąr. Matematiksel olarak, bir gauge  bazÄą temel yÄąÄÄąnlarÄąn bir (yerel) bÃķlÞmÞnde sadece bir seçimdir. Bir gauge dÃķnÞÅÞmÞ sadece iki bÃķlge arasÄąndaki dÃķnÞÅÞmdÞr.
Gauge teorisi baÄlantÄąlarÄąn çalÄąÅmasÄąyla (Ãķncelikle yÞksek enerjili fizikçiler tarafÄąndan çalÄąÅÄąlmÄąÅtÄąr.) hakim olmasÄąna raÄmen, baÄlantÄą fikri genelde gauge teorisinin merkezi olmamÄąÅtÄąr. AslÄąnda, genel gauge teorisindeki bir sonuç gauge dÃķnÞÅÞmlerinin  temsillerini afine etmektedir. ÃrneÄin afin modÞlleri.  Bu temsiller belli Ãķzellikleri karÅÄąlayan jet paket bÃķlÞmleri olarak sÄąnÄąflandÄąrÄąlabilir. BazÄą temsiller nokta tabanlÄą ( fizikçiler tarafÄąndan ilk tÞr gauge dÃķnÞÅÞmleri için kullanÄąlÄąr)  eÅdeÄiÅkenli olarak dÃķnÞÅÞrler.  BaÅka temsiller baÄlantÄą formu ( fizikçiler tarafÄąndan ikinci tÞr gauge dÃķnÞÅÞm olarak adlandÄąrÄąlÄąr.) Åeklinde dÃķnÞÅÞr. DiÄer genel temsiller dÞz olmayan temsillerdir ancak bunlar çok karÄąÅÄąktÄąr. Hala dÞz olmayan sigma modelleri dÞz olmayan bir Åekilde dÃķnÞÅÞr.
EÄer taban alanÄą uzay ya da uzayzaman ve yapÄą grubu Lie grup olan ana P demeti varsa, P formlarÄąnÄąn  bÃķlÞmleri gauge dÃķnÞÅÞm gruplarÄąnn homojen uzayÄąnÄąn temelidir.
BaÄlantÄąlar (gauge  baÄlantÄąsÄą) temel demetleri tanÄąmlar. Bu demetler her vektor demetinde birleÅmiÅ Â gevÅek eÅdeÄiÅkenli tÞrevlerdir. EÄer yerel bir çerçeve seçilmiÅ ise, eÅdeÄiÅkenli tÞrev  A baÄlantÄą formu ile temsil edilir. Lie cebiri 1-form deÄerini vermiÅtir bu fizikte Gauge potansiyeli olarak anÄąlÄąr. AÃ§Äąkça gerçek deÄildir ancak çerçeve niceliÄe baÄlÄądÄąr. EÄrilik formu F lie cebiri tarafÄąndan 2 deÄer formuna atanmÄąÅtÄąr. Bu baÄlantÄą formlarÄąyla kurulmuÅtur.

Burada d dÄąÅÅal tÞrevdir. 
Sonsuz derecede kÞçÞk  gauge  dÃķnÞÅÞmleri Lie cebirini oluÅturur. Lie cebri  pÞrÞzsÞz skaler deÄerde olmasÄąyla karakterize edilir. Sonsuz derecede kÞçÞk gauge dÃķÞÅÞmleri altÄąnda

eÄer 
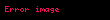

AyrÄąca 

TÞm gauge dÃķnÞÅÞmleri  genel olarak sonsuz dercede kÞçÞk  gauge dÃķnÞÅÞmleri tarafÄąndan oluÅturulmuÅ olmayabilir. Baz manifoldu Lie grubu bu manifoldundan dÃķnÞÅÞmlerin homotopi sÄąnÄąf nontrivial Åekilde sÄąnÄąr olmadan kompakt manifoldu olduÄunda bir Ãķrnektir.
Yang-Mills hareketi Åimdi bu formÞlle 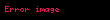
Gauge deÄiÅmeyen niceliÄi Wilson dÃķngÞsÞdÞr.  Bu dÃķngÞ aÅaÄÄąda gÃķrÞldÞÄÞ Þzere herhangi kapalÄą bir yol için  Îģ tanÄąmlanÄąr.
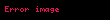

Gauge Teorilerini Kuantumlama
Gauge teorileri herhangi kuantum alan teorisi için geçerli olan yÃķntemlerin uzmanlÄąk ile kuantize olabilir. Ancak, gauge kÄąsÄątlamalarÄą dayattÄąÄÄą inceliklerini nedeniyle diÄer alan teorileri ortaya Ã§Äąkmazsa çÃķzÞlmesi gereken birçok teknik sorunlar var.Gauge teorileri zengin yapÄąsÄą bazÄą hesaplamalarÄąn basitleÅtirilmesi saÄlar. ÃrneÄin, FarklÄą renormalizasyon sabitlerini Ward kimliklerine baÄlamak gibi.
YÃķntemler ve Amaçlar
Niceleme ilk olarak gauge teorisinde kuantum elektrodinamik (QED) idi. Ä°lk yÃķntemler gauge yer sabitlemesi için geliÅtirildi ve daha sonra meÅru kuantumlama için kullanÄąldÄą. Gupta-Bleuler yÃķntemi de bu sorunu ele almak geliÅtirilmiÅtir. DeÄiÅmeyen gauge teorileri artÄąk çeÅitli araçlarla tarafÄąndan ele alÄąnÄąr. KuantumlamanÄąn yÃķntemleri kuantumlama ile alakalÄą makalede bahsedilmektedir.
Teori tarafÄąndan izin verilen çeÅitli iÅemler için kuantum genliklerinin hesaplanamamasĹ kuantumlamanÄąn ana noktasÄą olmuÅtur. Teknik olarak vakum durumdaki belli korelasyon fonksiyonlarÄąnÄąn hesaplamalarÄąnÄą azaltmak. Bu teorinin bir renormalizasyona içerir.
Teorinin çalÄąÅan eÅleÅmelerde yeteri kadar kÞçÞk olduÄu zaman, bundan sonra gerekli tÞm miktarlar pertÞrbasyon teoride hesaplanabilir. (ÃrneÄin kanonik nicemleme gibi)Nicemleme ÅemalarÄą bu tÞr hesaplamalarÄą kolaylaÅtÄąrmak için tasarlanmÄąÅtÄąr. Nicemleme ÅemalarÄąna pertÞrbatif nicemleme ÅemalarÄą denebilir. Åu anda bu yÃķntemlerden bazÄąlarÄą gauge teorileri en hassas deneysel testlere ÃķncÞlÞk ediyor.
Ancak, çoÄu gauge teorilerinde çok fazla ilginç sorunlar bulunuyor. Niceleme ÅemalarÄą bu problemlere uyum saÄlÄąyor. sigara tedirgemesiz birçok ilginç soru vardÄąr. (ÃrneÄin kafes gauge teorisi gibi) bu sorunlara uygun niceleme dÞzenleri olmayan pertÞrbatif niceleme ÅemalarÄą denebilir.Hassas hesaplamalar genellikle mÞkemmel hesaplama gerektirir ve bu nedenle dÄier Åemalara gÃķre daha az geliÅmiÅtir.
Anomaliler
Kuantum teorisi içerisinde klasik teorinin bazi simetrileri tutunamadÄą. Bu fenomen anormallik olarak adlandÄąrÄąldÄą. En iyi bilinen anormalliklerden bazÄąlarÄą
- Ãlçek anomali: Kuantum elektrodinamiÄinde Ãķlçek anomali Landau kutubuna neden olur. Kuantum RenkliÄinde bu asimptotik serbestliÄe yol açar
- Kiral anomal:: Bu anlÄąk eÄlimler yoluyola topoloji ile yanÄądan bir baÄlantÄąsÄą vardÄąr. Kuantum elektrodinamiÄinde kiral anomali iki foton ve bir pion çÞrÞmesine neden olur.
- Gauge anomali: Bu anomali herhangi tutarlÄą fiziksel bir teoride iptal etmemiz gerekir. Elektro zayÄąf teoride bu iptal için gerekli olan elektronlarÄąn ve kuarklarÄąn eÅitliÄidir.
Saf Gauge
Saf gauge, yani bir sÄąfÄąr gauge-dÃķnÞÅÞmÞdÞr. Saf gauge elde etmek için gauge dÃķnÞÅÞmÞnÞ boÅ bir alan Þzerinde uygulamak gerekir. Yani alan yapÄąlandÄąrmanÄąn uzayda belirli bir "gauge yÃķrÞnge" sindedir.
Sonuç olarak, deÄiÅmeli durumda 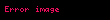

AyrÄąca bakÄąnÄąz
- ElektrozayÄąf kuvvet
- Lie cebiri
- Lie grubu
- Kuantum renk dinamiÄi
- Kuantum mekaniÄi
- Kuantum kÞtleçekimi
- Simetri (fizik)
- Standart Model
- [1] 11 Temmuz 2016 tarihinde Wayback Machine sitesinde arÅivlendi.
- Kuantum Alan KuramÄą Tarihi
- Kuantum elektrodinamiÄi
Bibliyografi
Genel Okuyucular
- Schumm, Bruce (2004) Deep Down Things. Johns Hopkins University Press. Esp. chpt. 8. A serious attempt by a physicist to explain gauge theory and the Standard Model with little formal mathematics.
Metinler
- Bromley, D.A. (2000). Gauge Theory of Weak Interactions. . ISBNÂ .
- Cheng, T.-P.; Li, L.-F. (1983). Gauge Theory of Elementary Particle Physics. Oxford University Press. ISBNÂ .
- (2008). Gauge Field Theories (3.3yayÄąncÄą=Wiley-VCH bas.).
- Kane, G.L. (1987). Modern Elementary Particle Physics. Perseus Books. ISBNÂ .
Makaleler
- Becchi, C. (1997). "Introduction to Gauge Theories". arXiv:hep-ph/9705211âŊ$2.
- Gross, D. (1992). . 23 Åubat 2016 tarihinde kaynaÄÄąndan arÅivlendi. EriÅim tarihi: 23 Nisan 2009.
- (2002). "From Lorenz to Coulomb and other explicit gauge transformations". Am. J. Phys. 70 (9). ss. 917-928. arXiv:physics/0204034âŊ$2. Bibcode:2002AmJPh..70..917J. doi:10.1119/1.1491265.
- Svetlichny, George (1999). "Preparation for Gauge Theory". arXiv:math-ph/9902027âŊ$2.
Kaynakça
- ^ Wolfgang Pauli (1941). "Relativistic Field Theories of Elementary Particles," Rev. Mod. Phys. 13: 203â32.
- ^ Pickering, A. (1984). Constructing Quarks. University of Chicago Press. ISBN .
- ^ J. J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley, 1967, sect. 1â4.
DÄąÅ baÄlantÄąlar
- Hazewinkel, Michiel, (Ed.) (2001), "Gauge transformation", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBNÂ
- Gauge theories on Scholarpedia 1 Temmuz 2016 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kÞtÞphane, kÞtÞbhane, ara, ara bul, bul, herÅey, ne arasanÄąz burada,hikayeler, makale, kitaplar, ÃķÄren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, tÞrk, tÞrkçe, turkce, nasÄąl yapÄąlÄąr, ne demek, nasÄąl, yapmak, yapÄąlÄąr, indir, Þcretsiz, Þcretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, mÞzik, ÅarkÄą, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Ayar teorisi veya ayar kurami kuramsal fizikte temel etilesmeleri aciklar Turkcede bazen yerellestirilmis bakisim kurami olarak da gecer Fizikte bir Yerellestirilmis Bakisim Kurami Gauge Teorisi Lagrange yerel donusumlerin surekli gruplar altinda degismez degerlerin oldugu alan teorisinin bir turudur Kuantum alan kurami Terim olarak yerellestirilmis bakisim Lagrangian icindeki gereksiz serbestlik derecelerine isaret eder Ayar donusumleri denilen olasi gostergeleri arasindaki donusumler bir Lie grubu sevk simetri grubu ya da teorinin gosterge grubu olarak olusturur Grup jeneratorlerin Lie cebiri herhangi Lie grubu ile iliskilendirilmistir Her grup jenerator icin mutlaka bir karsilik gelen alan genellikle bir vektor alani gauge alani denilen alan ortaya cikar Gauge alanlari yerel grup donusumleri altinda degismezligi denilen gauge degismezligi saglamak icin Lagrange dahildir Boyle bir teori nicemlenmis oldugunda Gauge alanlarinin kuantumuna Gauge bozonlari denir Simetri grubu degismeli degil ise ise normal olan ornek Yang Mills teorisidir Fizikteki bircok guclu teoriler Lagrangeler altinda sabit simetrik donusum gruplari tarafindan aciklanmistir Onlar ayni fiziksel surecler ortaya ciktigi zaman uzayin her noktasinda yapilan bir donusum altinda degismezdir onlarin kuresel bir simetriye sahip oldugu soylenir Gauge teorilerinin temel tasi olan yerel simetri daha siki bir engeldir Aslinda kuresel simetri uzayda sabitlenmis olan yerel simetrinin grup parametlereleridir Guage teorileri temel parcaciklarin dinamiklerini aciklayan basarili alan teorileri kadar onemlidir Kuantum elektrodinamigi gauge teorisinin simetrik grubu U 1 ile degismelidir Kuantum elektrodinamigi bir tane gauge alanina sahiptir Standart Modelin toplamda on iki tane gauge bozonu vardir Bunlar foton uc tane zayif bozon ve 8 tane gluondur U 1 SU simetri grubu ile degismeli olmayan gauge teorisi 2 SU 3 ve on iki bozonlarinin toplam vardir fotonun uc zayif bozonlari ve sekiz gluonlarin Gauge teorileri genel gorelilik teorisi icindeki yercekimini aciklamada onemlidir Onun vaka gostergesi alan bir tensor Lanczos tensor oldugunu biraz benzersizdir Gauge cekim teorisi ile baslayan kuantum yercekimi teorisi ayni zamanda kutlecekimi olarak bilinen bir olcu bozonunun varligina inanmaktayiz Gauge simetrilerinin koordinat sistemi uzay keyfi diffeomorphisms altinda serbestce secilebilir oldugu genel genel gorelilik kovaryans ilkesi analoglari olarak gorulebilir Hem gauge degismezligi ve Diffeomorfizm degismezligi sisteminin aciklamasinda bir fazlalik gostermektedir Bir alternatif kutlecekimi teorisi olarak gauge kutlecekim teorisi yeni gauge alanlari ile gercek bir gauge ilkesinin genel kovaryans ilkesini degistirir Tarihsel olarak bu fikirler ilk klasik elektromanyetizma baglaminda ve daha sonra genel gorelilik ile belirtilmistir Ancak gauge simetrilerinin modern fizikteki onemi elektron goreli kuantum mekanigiyle ilk olarak ortaya cikti Bugun Gauge teorileri yogun madde fiziginde nukleer ve yuksek enerji fiziginde ve diger alt basliklar arasinda yararlidir GecmisiBir gauge simetriye sahip ilk alan teorisi 1864 65 yilinda Maxwell in formulasyonu olan elektrodinamiktir Elektromanyetik Alan Bir Dinamik Teorisi Bu simetrinin onemi erken formulasyonlarda fark edilememistir Benzer sekilde fark edilemeyen Hilbert in Einstein in alan denklemlerinden turettiigi genel koordinat donusumu altinda eylem degismezligini varsaymisti Daha sonra Hermann Weyl genel gorelilik ve elektromanyetizma birlestirmek amaciyla ayar ya da Gauge degisikligi altinda genel gorelilikte yerel simetri olabilecegini tahmin etti Kuantum mekaniginin gelisiminden sonra Weyl Vladimir Fock ve Fritz London karmasik bir miktar ayar katsayisini degistirerek gague degistirilmis oldu ve U 1 gauge simetrisi olan faz degisikligi icine olcekli donusume dondu Bu olay yuklu kuantum mekaniksel parcacigin dalga fonksiyonu uzerinde elektromanyetik alan etkisi olarak aciklandi Bu 1940 larda Pauli tarafindan yayginlastirilan ilk taninmis ayar teorisi oldu 1954 yilinda temel parcacik fiziginde buyuk bir karisikligi bazi cozmek icin calisirken Chen Ning Yang ve Robert Mills birlikte atom cekirdeklerindeki nukleonlari tutan guclu etkilesimi anlamak icin model olarak degismeyen gauge teorileri tanitildi Ronald Shaw Abdus Salam altinda calisan bagimsiz doktora tezi ayni kavramini tanitti Elektromanyetizma gostergesi degismezligi yayginlastirilmasi onlar non degismeli SU 2 simetri grubunun eylem dayali bir teori insa etmek icin proton ve notronlarin izospin duble uzerinde calisti Bu kuantum elektrodinamik spinor alanlari U 1 grubunun hareketine benzerdir Parcacik fizigindeki odak kuantize gauge teorilerini kullanarak oldu Bu fikir daha sonra kuantum alan teorisinin zayif kuvvet uygulamasi ve elektrozayif teoride elektromanyetizma ile birlesmesine vesile oldu Degismez gauge teorileri asimptotik ozgurluk olarak adlandirilan bir ozellik ile yeniden fark edildiginde gauge teorileri daha da cekici hale geldi guclu etkilesimlerin onemli bir ozelligi olduguna inaniliyordu Bu gucku kuvvetler icin gauge teorisini aramaya tasvik etti Simdi kuantum renk teorisi olarak bilinen bu teori kuarklarin renk uclusu SU 3 grubunun eylemi ile birlikte bir gauge teorisidir Standart Model gauge teorisi dilinde elektromanyetizma zayif etkilesimler ve guclu etkilesimlerin aciklamasini birlestirir 1970 li yillarda Michael Atiyah klasik Yang Mills matematiksel denklemlerinin cozumlerinin calissmasina basladi 1983 yilinda Atiyah in ogrencisi puruzsuz 4 manifoldlari turevlenebilir siniflandirma ile homeomorfizma kadar onlarin siniflandirmadan cok farkli oldugunu gostermek icin butun calismasini bunun uzerine insa etti Michael Freedman Oklid 4 boyutlu uzayda uzerinde yapilarini sergilemek icin Donaldson calismalarini kullandi Bu temel fizik basarilarindan bagimsiz kendi iyiligi icin gauge teorisi giderek artan ilgiye yol acti 1994 yilinda Edward Witten ve bazi topolojik degismezler Seiberg Witten degismezler hesaplanmasini etkin Supersimetri dayali gauge teorisinin tekniklerini icat etti Gauge teorisinden matematige olan bu katkilar bu alanda yenilenmis bir ilgiye yol acmistir Fizikteki gauge teorilerinin onemi elektromanyetizmanin kuantum alan teorisi aciklamak icin birlesik bir cerceve zayif kuvvet ve guclu kuvvet saglayan matematiksel bicimcilik gibi muazzam basarilara ornek olmustur Standart Model olarak bilinen bu teori doganin dort temel kuvvetten ucune iliskin deneysel tahminleri aciklar Sicim teorisi gibi modern teorilerin yani sira genel gorelilik teorilerinin icinde bir sekilde gauge teorileri vardir TanimiGlobal ve Lokal Simetriler Global Simetri Fizikte herhangi bir fiziksel durum icin matematiksel aciklama genellikle fazla serbestlik dereceleri ihtiva eder ayni fiziksel durum ise ayni zamanda bircok esdeger matematiksel yapilandirmalar icin tarif edilir Bu donusumler teorinin simetrileri bir grubu oldugu ve fiziksel durumu bagimsiz bir matematik yapilandirmaya ancak bu simetri grubu ile birbirine bagli siniflardaki konfigurasyonlarda karsilik gelir Bu fikir tum fiziksel sistemi kapsar hicbir tercih eylemsizlik koordinat sistemi vardir bir durumda cok daha soyut koordinatlarin degisiklikler benzer yerel yani sira kuresel simetri icerecek sekilde genel olabilir Bir gauge teorisi modelin simetrileri ile birlikte tutarli fiziksel tahminler yapmak icin gerekli teknikler sete sahip bir matematiksel modeldir Global Simetriye Ornek Matematiksel konfigurasyonda meydana gelen miktari sadece bir sayi degil de bir hiz ya da bir donme ekseni bir vektor veya bir matris halinde duzenlenmis sayilari da koordinat transformasyonu ile degistirilebilir olarak geometrik oneme sahip oldugunu temsili olarak gormek gerekir Lokal Simetri Lokal Simetriyi tanimlamak icin lif demetlerinin kullanilmasi Gauge teorilerinin cogunda uzay ve zamanda bireysel bir noktada soyut olcu bazinda olasi donusumlerin kumesi sonlu boyutlu Lie grubudur En basit sekliyle boyle bir grup karmasik sayilar kullanimi yoluyla kuantum elektrodinamik QED modern formulasyonu gorunen U 1 dir Kuantum elektrodinamik genellikle ilk ve en basit fiziksel olcu teorisi olarak kabul edilir Belirli bir gauge teorisinin tum yapilandirma icin mumkun gauge donusumlerinin kumesi de bir grup olusturmaktadir Bu grupta gauge grubunun teorisini olusturmaktadir Gauge grubunun bir elemani sonlu boyutlu Lie grubu ornegin her noktada fonksiyonun degerini ve turevlerinin gostergesi donusum eylem uzerinde temsil ettigi icin uzay zamanin noktalarindan bir duzgun degisen fonksiyonu tarafindan degistirilebilen bu nokta uzerindedir Uzay ve zaman icinde her noktada sabit bir parametre ile bir gauge donusumu geometrik koordinat sisteminindeki kati bir rotasyona benzerdir Bu gauge temsilinin kuresel simetrisini temsil eder Sert bir donus durumunda oldugu gibi bu gauge donusumu gercekten yerel miktari temsili ile ayni sekilde gauge bagimli miktarinin bir yol boyunca degisiklik oranini temsil eden ifadeleri etkiler olan parametre sabit fonksiyon yerel simetri olarak adlandirilir olmayan bir gostergesi donusumu Bir turev iceren ifadeler uzerindeki etkisi yok ifadelerden o niteliksel olarak farkli oldugunu Bu Coriolis etkisi uretebilir referans cercevesi olmayan bir atalet degisimine benzer Gauge Alanlari Gauge alani matematiksel yapilandirmayi aciklamak icin onemli bir parca haline gelir Gauge alan bir gauge donusumu ile yok edilebilecek bir yapilandirma matematiksel dili kendi egriligi olarak kendi alan siddeti her yerde sifir ozelligine sahip Gauge teorisi bu yapilandirmalar ile sinirli degildir Baska bir deyisle bir gauge teorisinin ayirt edici ozelligi gauge alani sadece koordinat sisteminin kotu bir secimi ile telafi olmamasidir Baska bir deyisle genellkile gauge alanini yok eden hicbir gauge donusum yoktur Bir gauge teorisinin dinamiklerini analiz ederken gauge alani dinamik bir degisken gibi davranmalidir Ek olarak diger nesneler ile etkilesimi yuzunden gauge alani tipik olarak kendi kendine enerji terimi seklinde enerjiye katkida bulunur Gauge teorisi icin denklemleri elde etmek icin gauge alani olmadan naif baslangic Genel olarak bir donme acisi icin soyut esdegeri surekli bir parametre ile karekterize edilebilir teorinin kisilerce genel simetri listesi bir yerden baska bir yere degisen izin verlien simetri parametresinden kaynaklanan duzeltme terimlerini hesaplamak Bir veya daha fazla olcu alanlarina kavramalari olarak bu duzeltme terimleri yeniden yorumlanmasina ve bu alanlari uygun oz enerji terimleri ve dinamik davranisi vererek Bu bir anlamda gauge teorisinin global simetriden lokal simetriye uzanistir Ayrica bu oldukca yakin bir sekilde gauge kutlecekimi teorisinin bilenen adiyla genel gorelilik teorisinin tarihsel gelisimini andiriyor Fiziksel Deneyler Gauge teorilerinin esas fiziksel deneylerin sonuclarini modellemek icin evreni sinirlayan olasi yapilandirmalari deneyi kurmak icin bilgilerle uyumlu olanlar deneyi olcmek icin olasi sonuclarin olasilik dagilimi hesaplama bu ikisi kullanilir Ozel bir referans olmadan genellikle deneyin kurulum bilgileri ve olasi olcum sonuclari matematiksel aciklamalarla anlatilamaz buna gauge secimide dahildir Gauge teorisinin hesaplamalarinda anormalliklerin sik gorulen kaynagi hor kullanilan sinir durumlardaki gauge bagimliligidir Sureklilik teorileri Sureklilik elektrodinamik ve genel gorelilik Yukarida belirtilen iki gauge teorileri sureklilik alan teorileri ornekleridir Sureklilik teorisindeki hesaplama tekniklerini dolayli olarak varsayariz gauge tamamen sabit secenek sunulur tek bir yapilandirma sinir kosullari prensipte tamamen tarif edilebilir tamamen sabit gauge ve sinir kosullari komple bir set verilen en az eylem ilkesi bu sinirlari ile tutarli essiz bir matematiksel bir yapilandirma ve dolayisiyla essiz bir fiziksel durum belirler muhtemel olcum sonuclari olasiligi ile belirlenebilir kurulum bilgileri ile tutarli sinir kosullari tarafindan belirlenmektedir tum fiziksel durumlar uzerinde bir olasilik dagilimi kurulmasi Her olasi fiziksel durum icin olcum sonuclarinin bir olasilik dagilimi kurulmasi Bu iki olasilik dagilimlarini toplaminin olasi bir olcum dagitim kurulum bilgileri ile tutarli sonuclarini almak icin Gauge sabitlemek hesaplamalarda anormalik gostermez Bu varsayimlar enerji olcekleri ve deneysel kosullar icin genis bir yelpazede gecerlidir Bu teoriler isiginda gunumuzde karsilasilan isiktan isi ve elektrik dususlerinden ve yukselmelerinden gelen butun fenomenleri dogru tahmin etmede kullanilir Bu tahminler sadece cok kucuk ve cok buyuk olceklerde dogru degildir Kuantum Alan Teorileri Bu klasik sureklilik alan teorileri disinda en yaygin olarak bilinen gauge teorileri kuantum elektrodinamik ve temel parcacik fiziginin Standart Modeli dahil kuantum alan teorisi vardir En az eylem ilkesine gore izin verilen fiziksel durumlari niteleyen bir gauge kovaryanti eylem ayrilmaz Ancak gauge donusumleri tarafindan asiri derecelerde serbest davranislarindan dolayi surec continuum ve kuantum teorileri buyuk farkliliklar gostermektedir Surec continuum teorileri ve basit kuantum alan teorilerinin cogu matematiksel duzenlemelerin yorungelerini dusurmeden gauge recetesini kullanirlar Daha sofistike olan kuantum alan teorileri ozellikle degisme olmayan gauge gruplarini icerenler basta olmak uzere gauge simetrisine karisiklik teorisi teknikleriyle yok ederler ve ve karsi terimler BRST nicelemesinde bilindigi gibi birbirlerini anormal bir sekilde iptal etmek icin motive ederler Bu endiseler bir anlamda son derece teknik olmakla birlikte ayni zamanda yakindan olcumu fiziksel bir durum bilgisine sinirlari ve eksik belirtilen deneysel kosullar nedeniyle tam olarak anlasilmamistir Matematiksel teknikler islenebilir gauge teorilerini uygulamak icin bircok alanda gelistirildi Bunlara ornek dusuk boyutlu topoloji kati hal fizigi ve kristalografisi verilebilir Klasik Gauge teorisiKlasik elektromanyetizma Tarihsel olarak Gauge simetrisinin ilk orneginin kesfi klasik elektromanyetizmadir Elektrostatikte elektrik alan E ya da onun karsiligi elektrik potansiyel V V V C displaystyle V rightarrow V C bu haric elektrik alan ya da elektrik potansiyelden birnin bilinmesi muhtemelen digerinin bulunmasini saglar elektrik alan uzayda bir noktadan digerine potansiyel degisimlerle ilgilidir Vektor hesabi acisindan elektrik alan potansiyelin negatif degisim derecesine esittir E V displaystyle mathbf E nabla V Elektrostatikten elektromanyetizmaya genellersek elimizde ikinci bir vektor potansiyeli A ile E V A t displaystyle mathbf E nabla V frac partial mathbf A partial t B A displaystyle mathbf B nabla times mathbf A Genel Gauge donusumu sadece V V C displaystyle V rightarrow V C degildir A A f displaystyle mathbf A rightarrow mathbf A nabla f V V f t displaystyle V rightarrow V frac partial f partial t Burada f zamana ve pozisyona dayali herhangi bir fonksiyondur Gauge donusumleri altinda alanlar ayni kalir ve sonuc olarak Maxwell denklemleri hala gecerlidir Buda Maxvell denklemlerinin gauge simetrisine sahip oldugunu soyler Skaler Gauge Teorisin Ornegi Asagidaki formullerle sezgisel kuresel simetri ozelliklerinden baslayarak motive nasil yerel gauge degismezligi gosterir ve baslangicta olmayan etkilesim alanlari arasindaki etkilesime nasil yol acar Asagidaki formullerle orneklendirilmistir n burada etkilesime girmeyen gercek skaler alanlar m burada kutleye esittir Sistem burada hareket halindedir ve toplam hareket halindeki skaler alanlar S d4x i 1n 12 mfi mfi 12m2fi2 displaystyle mathcal S int mathrm d 4 x sum i 1 n left frac 1 2 partial mu varphi i partial mu varphi i frac 1 2 m 2 varphi i 2 right Lagrange yogunlugu kucuk siki bir sekilde yazilabilir L 12 mF T mF 12m2FTF displaystyle mathcal L frac 1 2 partial mu Phi T partial mu Phi frac 1 2 m 2 Phi T Phi Alanlarin vektorunun gosterimiyle F f1 f2 fn T displaystyle Phi varphi 1 varphi 2 ldots varphi n T 4 boyutun her birinde Terim olan m displaystyle partial mu Einstein simgesi F displaystyle Phi kismi turevidir Donusumun altindaki degismeyen Lagrange simdi daha seffaf oldu F F GF displaystyle Phi mapsto Phi G Phi G n by n ortogonal gruba ait olan sabit matrisdir F displaystyle Phi turevi benzer bicimde F displaystyle Phi ve her iki nicelikte nokta carpiminin icindeki Lagrange belirdigi icin Lagrange nin korunudugu gorunur mF mF G mF displaystyle partial mu Phi mapsto partial mu Phi G partial mu Phi Bu bu ozel Lagrangian kuresel simetri karakterize ve simetri grup genellikle olcu grubu denir Matematiksel terim ozellikle G yapilarin teorik olarak yapi grubudur Bu arada Noether teoremi donusumleri bu grup altinda degismezlik akimlarin korunmasina yol actigini ima edilir Jma i mFTTaF displaystyle J mu a i partial mu Phi T T a Phi Burada Ta matrisleri SO n gruplarinin jeneratorleridir Her jenerator icin korunmus bir akim vardir Simdi Lagrangian lokal degismeyen O n sahip olmalidir G matrisleri x koordinatinda uzayzaman fonksiyonun olmasina izin vermelidir Bu durumda G G x iken G matrisi gecemez m GF G mF displaystyle partial mu G Phi neq G partial mu Phi Bu sorunu cozmek icin yeni bir turev aliriz DmF GDmF displaystyle D mu Phi GD mu Phi Bu yeni turev esdegisken gauge turevi olarak adlandirilir ve bu forma sahiptir Dm m igAm displaystyle D mu partial mu igA mu Burada g eslesen sabit olarak adlandirilir ve etkilesimin gucunu tanimlamada onemlidir Basit birkac hesaplamadan sonra Gauge Alani A x asagidaki gibi donusmek zorundadir Am GAmG 1 ig mG G 1 displaystyle A mu GA mu G 1 frac i g partial mu G G 1 Gauge alani Lie cebirinin bir elementidir Sonuc olarak asagidaki gibi genisletilebilir Am aAmaTa displaystyle A mu sum a A mu a T a Son olarak simdi elimizde lokal Gauge degismeyen bir Lagrangian imiz var Lloc 12 DmF TDmF 12m2FTF displaystyle mathcal L mathrm loc frac 1 2 D mu Phi T D mu Phi frac 1 2 m 2 Phi T Phi Bu Lagrange ve ozgun kuresel gauge degismeyen Lagrangian arasindaki fark Lagrange Etilesimi oldugu gorulur Lint ig2FTAmT mF ig2 mF TAmF g22 AmF TAmF displaystyle mathcal L mathrm int i frac g 2 Phi T A mu T partial mu Phi i frac g 2 partial mu Phi T A mu Phi frac g 2 2 A mu Phi T A mu Phi Bu terim sadece yerel gauge degismezligi icin talebin bir sonucu olarak n skaler alanlar arasindaki etkilesimleri tanitir Bununla birlikte bu etkilesimin fiziksel olup tamamen rastgele hale getirmek icin arabulucu A X uzayda yayilmasi gerekir Bununla basa cikmak icin bir sonraki asama Lgf displaystyle mathcal L mathrm gf teriminin Lagrangiana eklenmesidir Elde edilen klasik alan teorisi kuantize surumunde kuantum gauge alani A x gauge bozonlari denir Kuantum alan teorisinde Lagrangian etkilesiminin yorumlanmasi skaler bozonlarin degisen gauge bozonlariyla etkilesimidir Gauge alani icin Yang Mills Lagrangesi Bir onceki bolumde gelistirilen bir klasik gauge teorisinin cizilen o resmi neredeyse bitmek uzere Uzayzamanda ki gauge alan A x degerinin bulunmasi icin sadece esdegisken turvelerin D tanimlanmasi kaldi Bu alanin manuel degerlerini belirlemek yerine bu bize alan denklemlerinin cozumunu verilebilir Dahasi bu alan denkleme Lagrange yani sira yerel gauge degismez oldugunu gerektiren gauge alani icin Lagrangian olasi bir formu geleneksel seklinde yazilir Lgf 12Tr FmnFmn displaystyle mathcal L mathrm gf frac 1 2 operatorname Tr F mu nu F mu nu ile Fmn 1ig Dm Dn displaystyle F mu nu frac 1 ig D mu D nu ve Izler vektor uzay alanlari uzerinden atiliyor Buna Yang mills hareketi denir Diger gauge degismez haretleri hala mevcuttur Ornegin dogrusal olmayan elektrodinamik Born Infeld hareketi Chern Simons model gibi Gauge teorisi icin tamamlanmis Lagrangian asagidaki gibidir L Lloc Lgf Lglobal Lint Lgf displaystyle mathcal L mathcal L mathrm loc mathcal L mathrm gf mathcal L mathrm global mathcal L mathrm int mathcal L mathrm gf Elektrodinamige Ornek Daha onceki bolumlerde gelistirilen bicimcilik basit bir uygulama olarak sadece elektron alani ile elektrodinamik davayi dusunun Bare bones hareketi elektrik alanin Dirac denklemini uretir S ps iâcgm m mc2 psd4x displaystyle mathcal S int bar psi i hbar c gamma mu partial mu mc 2 psi mathrm d 4 x Bu sistem icin global simetri asagidaki gibidir ps ei8ps displaystyle psi mapsto e i theta psi Buradaki gauge grubu U 1 dir parcacik donmeleriyle alanin faz acisinin donmeleri sabit 8 ile belirlenir Bu sistemin lokallesmesinin anlami 8 ile 8 x yer degistirmesidir Yaklasik es degisken turevi Dm m ieâAm displaystyle D mu partial mu i frac e hbar A mu Olagan elektrik yukuyle e yukunu belirler ve elektromanyetizmanin 4 vektor potansiyeliyle gauge alanini Langrangian etkilesimiyle sonuclandirir Lint eâps x gmps x Am x Jm x Am x displaystyle mathcal L mathrm int frac e hbar bar psi x gamma mu psi x A mu x J mu x A mu x Burada Jm x displaystyle J mu x olagan 4 vektor elektrik yogunlugudur Sonuc olarak gauge prensibi minimal eslesme olarak adlandirilan elektromanyetik alanin elektrik alan uretmesi gozlenir Gauge alan Am x displaystyle A mu x icin Lagrangian eklenmesi diger bir terimle elektrodinamik de ayni olan alan guc sensoru eklenmesiyle kuantum elektrodinamikteki baslangic noktasini kullanarak Lagrangian elde edilir LQED ps iâcgmDm mc2 ps 14m0FmnFmn displaystyle mathcal L mathrm QED bar psi i hbar c gamma mu D mu mc 2 psi frac 1 4 mu 0 F mu nu F mu nu Matematiksel Formulleme Gauge teorileri genellikle diferansiyel geometrinin dilinde tartisilmistir Matematiksel olarak bir gauge bazi temel yiginlarin bir yerel bolumunde sadece bir secimdir Bir gauge donusumu sadece iki bolge arasindaki donusumdur Gauge teorisi baglantilarin calismasiyla oncelikle yuksek enerjili fizikciler tarafindan calisilmistir hakim olmasina ragmen baglanti fikri genelde gauge teorisinin merkezi olmamistir Aslinda genel gauge teorisindeki bir sonuc gauge donusumlerinin temsillerini afine etmektedir Ornegin afin modulleri Bu temsiller belli ozellikleri karsilayan jet paket bolumleri olarak siniflandirilabilir Bazi temsiller nokta tabanli fizikciler tarafindan ilk tur gauge donusumleri icin kullanilir esdegiskenli olarak donusurler Baska temsiller baglanti formu fizikciler tarafindan ikinci tur gauge donusum olarak adlandirilir seklinde donusur Diger genel temsiller duz olmayan temsillerdir ancak bunlar cok karisiktir Hala duz olmayan sigma modelleri duz olmayan bir sekilde donusur Eger taban alani uzay ya da uzayzaman ve yapi grubu Lie grup olan ana P demeti varsa P formlarinin bolumleri gauge donusum gruplarinn homojen uzayinin temelidir Baglantilar gauge baglantisi temel demetleri tanimlar Bu demetler her vektor demetinde birlesmis gevsek esdegiskenli turevlerdir Eger yerel bir cerceve secilmis ise esdegiskenli turev A baglanti formu ile temsil edilir Lie cebiri 1 form degerini vermistir bu fizikte Gauge potansiyeli olarak anilir Acikca gercek degildir ancak cerceve nicelige baglidir Egrilik formu F lie cebiri tarafindan 2 deger formuna atanmistir Bu baglanti formlariyla kurulmustur F dA A A displaystyle mathbf F mathrm d mathbf A mathbf A wedge mathbf A Burada d dissal turevdir displaystyle wedge dis cebiri temsiz eder Sonsuz derecede kucuk gauge donusumleri Lie cebirini olusturur Lie cebri puruzsuz skaler degerde olmasiyla karakterize edilir Sonsuz derecede kucuk gauge dousumleri altinda deA e A de displaystyle delta varepsilon mathbf A varepsilon mathbf A mathrm d varepsilon eger deX eX displaystyle delta varepsilon X varepsilon X esitligi olursa deDX eDX displaystyle delta varepsilon DX varepsilon DX olur Burada D esdegisken turevidir DX def dX AX displaystyle DX stackrel mathrm def mathrm d X mathbf A X Ayrica deF eF displaystyle delta varepsilon mathbf F varepsilon mathbf F Buradaki F displaystyle mathbf F esdegiskenli donusumlerdir Tum gauge donusumleri genel olarak sonsuz dercede kucuk gauge donusumleri tarafindan olusturulmus olmayabilir Baz manifoldu Lie grubu bu manifoldundan donusumlerin homotopi sinif nontrivial sekilde sinir olmadan kompakt manifoldu oldugunda bir ornektir Yang Mills hareketi simdi bu formulle 14g2 Tr F F displaystyle frac 1 4g 2 int operatorname Tr F wedge F verilir Formuldeki Hodge Dual simgeler ve integral diferansiyel geometri olarak tanimlanir Gauge degismeyen niceligi Wilson dongusudur Bu dongu asagida goruldugu uzere herhangi kapali bir yol icin g tanimlanir x r P e gA displaystyle chi rho left mathcal P left e int gamma A right right Burada x karmasik temsili r karakteri ve P displaystyle mathcal P emredilen operator yolunu temsil eder Gauge Teorilerini KuantumlamaGauge teorileri herhangi kuantum alan teorisi icin gecerli olan yontemlerin uzmanlik ile kuantize olabilir Ancak gauge kisitlamalari dayattigi inceliklerini nedeniyle diger alan teorileri ortaya cikmazsa cozulmesi gereken bircok teknik sorunlar var Gauge teorileri zengin yapisi bazi hesaplamalarin basitlestirilmesi saglar Ornegin Farkli renormalizasyon sabitlerini Ward kimliklerine baglamak gibi Yontemler ve Amaclar Niceleme ilk olarak gauge teorisinde kuantum elektrodinamik QED idi Ilk yontemler gauge yer sabitlemesi icin gelistirildi ve daha sonra mesru kuantumlama icin kullanildi Gupta Bleuler yontemi de bu sorunu ele almak gelistirilmistir Degismeyen gauge teorileri artik cesitli araclarla tarafindan ele alinir Kuantumlamanin yontemleri kuantumlama ile alakali makalede bahsedilmektedir Teori tarafindan izin verilen cesitli isemler icin kuantum genliklerinin hesaplanamamasi kuantumlamanin ana noktasi olmustur Teknik olarak vakum durumdaki belli korelasyon fonksiyonlarinin hesaplamalarini azaltmak Bu teorinin bir renormalizasyona icerir Teorinin calisan eslesmelerde yeteri kadar kucuk oldugu zaman bundan sonra gerekli tum miktarlar perturbasyon teoride hesaplanabilir Ornegin kanonik nicemleme gibi Nicemleme semalari bu tur hesaplamalari kolaylastirmak icin tasarlanmistir Nicemleme semalarina perturbatif nicemleme semalari denebilir Su anda bu yontemlerden bazilari gauge teorileri en hassas deneysel testlere onculuk ediyor Ancak cogu gauge teorilerinde cok fazla ilginc sorunlar bulunuyor Niceleme semalari bu problemlere uyum sagliyor sigara tedirgemesiz bircok ilginc soru vardir Ornegin kafes gauge teorisi gibi bu sorunlara uygun niceleme duzenleri olmayan perturbatif niceleme semalari denebilir Hassas hesaplamalar genellikle mukemmel hesaplama gerektirir ve bu nedenle dgier semalara gore daha az gelismistir Anomaliler Kuantum teorisi icerisinde klasik teorinin bazi simetrileri tutunamadi Bu fenomen anormallik olarak adlandirildi En iyi bilinen anormalliklerden bazilari Olcek anomali Kuantum elektrodinamiginde olcek anomali Landau kutubuna neden olur Kuantum Renkliginde bu asimptotik serbestlige yol acar Kiral anomal Bu anlik eglimler yoluyola topoloji ile yanidan bir baglantisi vardir Kuantum elektrodinamiginde kiral anomali iki foton ve bir pion curumesine neden olur Gauge anomali Bu anomali herhangi tutarli fiziksel bir teoride iptal etmemiz gerekir Elektro zayif teoride bu iptal icin gerekli olan elektronlarin ve kuarklarin esitligidir Saf Gauge Saf gauge yani bir sifir gauge donusumudur Saf gauge elde etmek icin gauge donusumunu bos bir alan uzerinde uygulamak gerekir Yani alan yapilandirmanin uzayda belirli bir gauge yorunge sindedir Sonuc olarak degismeli durumda Am x Am x Am x mf x displaystyle A mu x rightarrow A mu x A mu x partial mu f x Saf gauge butun f x icin alan yapilandirmalari Am x mf x displaystyle A mu x partial mu f x olarak ayarlanir Ayrica bakinizElektrozayif kuvvet Lie cebiri Lie grubu Kuantum renk dinamigi Kuantum mekanigi Kuantum kutlecekimi Simetri fizik Standart Model 1 11 Temmuz 2016 tarihinde Wayback Machine sitesinde arsivlendi Kuantum Alan Kurami Tarihi Kuantum elektrodinamigiBibliyografiGenel Okuyucular Schumm Bruce 2004 Deep Down Things Johns Hopkins University Press Esp chpt 8 A serious attempt by a physicist to explain gauge theory and the Standard Model with little formal mathematics Metinler Bromley D A 2000 Gauge Theory of Weak Interactions Springer ISBN 3 540 67672 4 Cheng T P Li L F 1983 Gauge Theory of Elementary Particle Physics Oxford University Press ISBN 0 19 851961 3 2008 Gauge Field Theories 3 3yayinci Wiley VCH bas Kane G L 1987 Modern Elementary Particle Physics Perseus Books ISBN 0 201 11749 5 Makaleler Becchi C 1997 Introduction to Gauge Theories arXiv hep ph 9705211 2 Gross D 1992 23 Subat 2016 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Nisan 2009 2002 From Lorenz to Coulomb and other explicit gauge transformations Am J Phys 70 9 ss 917 928 arXiv physics 0204034 2 Bibcode 2002AmJPh 70 917J doi 10 1119 1 1491265 Svetlichny George 1999 Preparation for Gauge Theory arXiv math ph 9902027 2 Kaynakca Wolfgang Pauli 1941 Relativistic Field Theories of Elementary Particles Rev Mod Phys 13 203 32 Pickering A 1984 Constructing Quarks University of Chicago Press ISBN 0 226 66799 5 J J Sakurai Advanced Quantum Mechanics Addison Wesley 1967 sect 1 4 Dis baglantilarHazewinkel Michiel Ed 2001 Gauge transformation Encyclopaedia of Mathematics Kluwer Academic Publishers ISBN 978 1556080104 Gauge theories on Scholarpedia 1 Temmuz 2016 tarihinde Wayback Machine sitesinde
 AzÉrbaycanca
AzÉrbaycanca ÐÐĩÐŧаŅŅŅКŅ
ÐÐĩÐŧаŅŅŅКŅ Dansk
Dansk Deutsch
Deutsch EspaÃąola
EspaÃąola Français
Français Indonesia
Indonesia Italiana
Italiana æĨæŽčŠ
æĨæŽčŠ ŌазаŌ
ŌазаŌ Lietuvos
Lietuvos Nederlands
Nederlands PortuguÊs
PortuguÊs Ð ŅŅŅКÐļÐđ
Ð ŅŅŅКÐļÐđ ā·ā·āķā·āķ―
ā·ā·āķā·āķ― āđāļāļāđāļāļĒ
āđāļāļāđāļāļĒ TÞrkçe
TÞrkçe ÐĢКŅаŅÐ―ŅŅКа
ÐĢКŅаŅÐ―ŅŅКа äļåäšš
äļåäšš United State
United State Afrikaans
Afrikaans