Matematikte, tetrasyon (hiper-4 olarak da bilinir), üslü sayıdan sonra gelen ilk tekrarlı üssüdür. Tetrasyonun İngilizce karşılığı olan tetration kelimesi ilk kez matematikçi tarafından, (dört) ve (tekrar)dan türetilerek kullanılmaya başlandı. Tetrasyon (çok büyük sayıların gösterimi) için kullanıldı. Fakat birkaç pratik uygulaması vardır. Bu yüzden sadece incelenir. Burada aşırı işlecin ilk dört örneğin gösteriliyor. Tekrasyon dördüncüsüdür:
- toplama
- Normal bilinen toplama işlemi.
- çarpma
-
- genellikle temel işlemlerden birini ifade eder. Fakat doğal sayılar gibi özel durumlar için kendine n kere eklenen a olabilir.
-
- üs alma
-
- a nın kendisi ile n kere çarpılması.
-
- tetrasyon
-
- a 'nın kendisiyle n kere üssünün alınması.
-

buradaki her bir işlem, bir öncekinin tekrarı şeklinde tanımlanır. Tetrasyonunu bu işlemlerden ayıran özellik, ilk üçü, (toplama, çarpma ve üs alma) n nin karmaşık değerler ile genelleşmesiyken, tetrasyonun henüz keşfedilen düzenli bir genelleştirilmesi yoktur ve tetrasyon, bir temel fonksiyon olarak nitelendirilmez.
Toplama (a + n), en temel işlemdir. Çarpma (an) da temel fonksiyondur. Tetrasyon (), n nin a tane kuvvetini içeren bir dizi olarak düşünülebilir. a değişkeni ilerleyen bölümlerde temel değişken olarak adlandırılırken n değişkeni de yükseklik değişkeni olarak adlandırılacak (integral ilk yaklaşımdır, fakat kesirli olarak genelleştirilebilir, gerçel ve karmaşık yükseklik gibi).
Tanım
Her pozitif reel 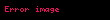


(
ise) ve
(eğer
ise)
Tekrarlı kuvvetler
Tanımdan da görüldüğü üzere, tetrasyon "üslü kuvvet" olarak hesaplandığında üs, öncelikle en derin seviyede alınır (gösterimdeki en yüksek derece) Diğer ifadeyle:
Üssün birleşme olmadığına dikkat edin. Böylece, diğer sıradaki hesaplama, farklı bir cevaba gider:
Burada, üslü kuvvetler, yukarıdan aşağıya doğru (veya sağdan sola doğru) hesaplanmalıdır.
Terimbilim
Tetrasyon için birçok terim ve her birinin kullanımı için mantıksal düşünceler vardır. Fakat bazıları, birçok nedenden dolayı yaygınlık kazanamadı. Burada birkaçından bahsedilecektir.
- Tetration (tetrasyon) terimi, 1947'de Goodstein tarafından geliştirildi.
- Superexponentiation (süper üs) terimi Bromer tarafından geliştirildi.
- Hyperpower (aşırı kuvvet), hyper (aşırı) ve power (kuvvet) kelimelerinin birleşimidir ve tetrasyonun uygun şekilde açıklar.
- Power tower (üslü kule), ara sıra kullanılır. Örneğin,
" n sırasının üslü kulesi"
Tetrasyon birbirine yakın ilişkiye sahip fonksiyon ve ifadelerle genellikle karıştırılıyor. Bundan dolayıdır ki tetrasyon ile ilgili birçok terim kullanılıyor. Burada birkaçını vereceğiz:
Form Terimbilimi Tetrasyon Tekrarlı üsler İçiçe üsler (kuleler) Sonsuz üsler (kuleler)
İlk iki ifadede a, tabandır. Kez (kere) sayısı olan diğer a, yükseklikdir. Üçüncü ifadede n, yüksekliktir, fakat her birinin tabanı farklıdır.
Gösterim
Tetrasyonun yazılabileceği gösterimler şunlardır:
Ad Form Açıklama Standart gösterim Maurer [1901] ve Goodstein [1947] tarafından kullanıldı; kitabı olan , bu gösterimi popüler yaptı. Knuth yukarı ok gösterimi Daha fazla oklar koyarak genişlemeyi veya daha güçlü olmayı sağlar. Conway dizisi ok gösterimi 2 sayısının artırarak genişlemeyi sağlar (yukarıdakinin genişlemesiyle eşdeğerdir). Ayrıca, dizi genişletilerek daha da güçlenir. Ackermann işlevi Ackermann işlevinin için yazılan özel durumudur.
Tekrarlı üstel gösterimi 1'den farklı başlangıç değerlerine sahip olan tekrarlı üstellerin basit genişlemesini sağlar. Hooshmand gösterimi gösterimi 4 sayısını arttırarak genişleme sağlar. Bu aşırı işleçlerin ailesini oluşturur ASCII gösterimi a^^nYukarı ok, düzeltme işareti ( ^) ile aynı kullanıldığında, tetrasyon işleci de (^^) olarak yazılır.
Yukarıdaki gösterimlerden biri, tekrarlı üstel gösterimi kullanır. Bu genellikle şöyle tanımlanır:
n tane "a".
Tekrarlı üsler için çok fazla gösterim yoktur. Fakat birkaçını verelim:
Ad Form Açıklama Standart gösterim Euler dizi gösterimi ve tekrar gösterimi
.
Knuth yukarı ok gösterimi Okların sayısını arttırarak süper kuvvetler ve süper üslü fonksiyonları sağlar. Bu gösterim büyük sayılarda kullanılır. Ioannis Galidakis gösterimi Büyük ifadelerin temelini oluşturun. ASCII (yardımcı) a^^n@xTekrarlı üstelin görünüm temeli yardımcı tetrasyondur. ASCII (standart) exp_a^n(x)Standart gösterimin temelidir.
Örnekler
Aşağıdaki tablodaki çoğu değerler, bilimsel gösterimde yazmak çok zordur. Bundan dolayı tekrarlı üstel gösterim onları 10 tabanında ifade etti. Değerlerdeki ondalık nokta yaklaşıktır.
1 1 1 1 2 4 16 65.536 3 27 7.625.597.484.987 4 256 5 3.125 6 46.656 7 823.543 8 16.777.216 9 387.420.489 10 10.000.000.000
Çok ilkel fonksiyonlardaki yaklaşımlar
Polinom yaklaşımları
Lineer yaklaşım
Lineer yaklaşımı (süreklilik isteğinin çözümüe, differensiyellenebilirlik yaklaşımı) şöyle elde edilir:
Bundan dolayı:
Yaklaşım Tanım kümesi için
için
için
ve böylece devam eder.
Örnekler: 
Ana teorem Hooshmand'e göre: 

,
'de türevlenebilir,
fonksiyonu,
'da azalmayan veya artmayan bir fonksiyondur,
Daha sonra 
Buradaki 



İkinci ve dördüncü şartlar ispattır.

Eğer 
için,
,
'de yakınsar,
Sonra 
Buradaki ispat bir öncekine çok benzer. Özyineleme eşitliği, 

Bundan dolayı doğal tetrasyondaki lineer yaklaşımı, sadece 


Yüksek sıralı yaklaşımlar
İkinci dereceden yaklaşım şöyledir:
Bu ifade tüm 

Genişlemeler
Tetrasyon, 
Tabanlarda tanım kümesi genişlemesi
Sıfır tabanında genişleme
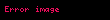


Buradan 

Bu genişleme altında, 

Karmaşık tabanlarda genişleme


Karmaşık sayılar kuvvetlerle arttarken, tetrasyon, 



Bu, 

Aşağıdaki yaklaşım değerleri türetilebilir:
Yaklaşım Değeri i
Önceki bölümle ters ilişkiyi çözme, n nin negatif değerli beklenen 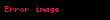

(Tekrarlı) "yükseklikler" için tanım kümesi genişlemeleri
Sonsuz yükseklik genişlemesi
Tetrasyon sonsuz yüksekliklere genişletilebilir (

Genellikle 

Negatif yüksekliklere (sınırlı) genişleme
Asıl kuralı korumak için:

Buradan:
Bununla beraber daha küçük negatif değerler, bu yolla iyi tanım verme. Çünkü,
iyi tanımlı değildir.


- her
için,
'dir.
Gerçek yüksekliklere genişleme
Burada, genişleme tetrasyonunun genel problemlerinin çözümü için 
Genelde problem, a > 0 ve, 

tüm reel x > -1 için.
- Dördüncü koşul genellikle şunlardan biridir:
- Bir süreklilik koşulu (genellikle sadece
, her iki değişken için
şartılya süreklidir).
- Bir türevlenebilirlik koşulu (x 'de bir kez, iki kez, k kez veya sonsuz kez türevlenebilir).
- Bir uygunluk şartı (x 'de iki kez türevlenebilirliği ifade eder) şöyledir:
tüm
için
- Bir süreklilik koşulu (genellikle sadece
Dördüncü koşul kişiden kişiye ve yaklaşımlara göre değişirr. Tetrasyonunu gerçel yüksekliklere genişletmek için iki ana yaklaşım vardır. Birincisi uygunluk koşulu, diğeri de türevlenebilirlik koşuludur. Bu iki yaklaşım, birbirleriyle tutarsız sonuçlar üretmesi, onların çok farklı olduğunu gösterdi.
Neyse ki, bir uzunluğun içindekilerden biri, tüm pozitif reel sayılar için genişletilebilir. Bir içsel uzunluk için 

Karmaşık yüksekliklere genişleme

 tetrasyonunun karmaşık düzlemde analitik genişlemesinin çizimi.
tetrasyonunun karmaşık düzlemde analitik genişlemesinin çizimi.  ve
ve  dereceleri kalın eğimlerle gösteriliyor.
dereceleri kalın eğimlerle gösteriliyor.Şöyle bir konjektür vardır: F(z+1)=exp(F(z)) eşitliğinin çözümü için eşsiz bir F fonksiyonu vardır ve ek F(0)=1 ve F(z) yaklaşımlarını sağlar. Bu fonksiyon sağdaki şekilde görülüyor.
Ters fonksiyonlar
Tetrasyonun Ters fonksiyonları genellikle süper kök ve süper logaritma olarak adlandırılır. 

Her n > tam sayıları için nx şeklinde fonksiyon vardır ve bu fonksiyon x ≥ için artarak 1=n1 = eşitliği elde edilir. Böylece x in n. süper kökü x ≥ 1 için elde edilir.
Yine de, eğer yukarıdaki lineer yaklaşım kullanılır ve -1≤y≤0 şart sağlanırsa, 1= yx = y + 1 olur. Böylece 1=ysroot(y + 1) elde edilemez.
slogax süper algoritması, tüm gerçel x ve a > 1 sayıları için geçerlidir.

İnfra logaritma fonksiyonu, ultra üstel fonksiyonun iki katıdır ve 


Süper kök
Süper kök, tetrasyonun iki ters fonksiyonundan biridir. Sadece, ve logaritma üstel olarak iki ters fonksiyonken, keza tetrasyonunda iki ters fonksiyonu vardır: süper kök ve süper logaritma. Süper kök, tetrasyonun tabanını ifade eden ters fonksiyonudur: eğer 
böylece 2, 65.536'nın 4. köküdür ve
olur.
Böylece 3, 7.625.597.484.987'nin 3. süper kökü (veya süper küpü)dür.
Süper kökün birkaç pratik uygulaması vardır. Bunlar sadece çalışılır.
Kare kök
2. sıra süper kök veya "süper kare kök" is noteworthy for its simple expression in terms of Lambert W fonksiyonunda terimlerinin basit ifadesi için önemlidir. İfadesi;
buradaki
,
'in süper kare köküdür.
Fonksiyon her ne kadar süper karenin karşıtı olarak tanımlanmış olsa bile, sonsuz üstelin de karşıtıdır. Sonsuz şöyledir;

Kare kök örnekleri
Aşağıdaki tablo ilk 27 tam sayının süper kare köklerini gösteriyor.
 | 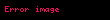 | 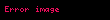 | 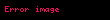 | 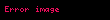 |  |
|---|---|---|---|---|---|
| 1 | 1 | 10 | 2,506184... | 19 | 2,830223... |
| 2 | 1,559610... | 11 | 2,555604... | 20 | 2,855308... |
| 3 | 1,825455... | 12 | 2,600295... | 21 | 2,879069... |
| 4 | 2 | 13 | 2,641061... | 22 | 2,901637... |
| 5 | 2,129372... | 14 | 2,678523... | 23 | 2,923122... |
| 6 | 2,231828... | 15 | 2,713163... | 24 | 2,943621... |
| 7 | 2,316454... | 16 | 2,745368... | 25 | 2,963219... |
| 8 | 2,388423... | 17 | 2,775449... | 26 | 2,981990... |
| 9 | 2,450953... | 18 | 2,803663... | 27 | 3 |
Eğer bir sayının süper kare kökü tam sayı değilse, o irrasyoneldir. Fakat bununla ilgili herhangi bir ispat bilinmiyor.
Diğer süper kökler
Diğer süper kökler, kullanılan aynı tabanda ifade edilebilir: süper küp kökler, 



Süper logaritma
Tetrasyonun iki ters fonksiyonundan biridir. Sadece, ve logaritma üstel olarak iki ters fonksiyonken, keza tetrasyonunda iki ters fonksiyonu vardır: süper logaritma ve süper kök. Süper logaritmayı açıklayan birkaç yol vardır:
- Üstel fonksiyonların olarak,
- Tetrasyonun yüksekliğini ifade eden ters fonksiyonu olarak,
- Logaritmanın 1'e gitmesi için kaç kez gerektiğinin sayısı,
- As a generalization of Robert Munafo's large number class system16 Mayıs 2017 tarihinde Wayback Machine sitesinde .,
- bir sınırsız sürümü olarak.
Süper logaritma tanımları

ve
Bu tanımın sadece tam sayılar verebileceğine ve sadece tam sayı üretebilecek sayıları kabul edebileceğine dikkat edin. Bu tanımın kabul edeceği sayılar 
Yaklaşımlar
Genellikle özel fonksiyonlar, argüman(lar)ın reel değerleri için değil, karmaşık düzlem, diferansiyel ve integral ifadeleri içinde tanımlanır. Slag fonksiyonu için mevcut ifadeler olmadığı için, basit yaklaşımlar şöyle öneriliyor.
Süper logaritmaya lineer yaklaşım
Süper logaritmaya lineer yaklaşım şöyledir:
Bu fonksiyon, tüm reel z (
İkinci dereceden yaklaşım
Süper logaritmaya ikinci dereceden yaklaşım şöyledir:
Bu fonksiyon tüm reel z (
Abel fonksiyonuna yaklaşımlar
Abel fonksiyonu, şu eşitliği sağlayan herhangi bir fonksiyondur:
Verilen bir 


Özellikler
Süper logaritmanın diğer eşitlikleri:
tüm reel z için
Tetrasyonun tersi olarak slag

 fonksiyonu.
fonksiyonu.Tetrasyon olarak 



Ayrıca bakınız
Alıntılar
- Daniel Geisler, tetration.org 20 Temmuz 2011 tarihinde Wayback Machine sitesinde .
- Ioannis Galidakis, (2006'dan önce) (A simpler, easier to read review of the next reference)
- Ioannis Galidakis, (undated, 2006 or earlier).
- Robert Munafo, Extension of the hyper4 function to reals 17 Ağustos 2010 tarihinde Wayback Machine sitesinde . (An informal discussion about extending tetration to the real numbers.)
- Lode Vandevenne, Tetration of the Square Root of Two 10 Kasım 2012 tarihinde Wayback Machine sitesinde ., (2004). (Attempt to extend tetration to real numbers.)
- Ioannis Galidakis, , (Definitive list of references to tetration research. Lots of information on the Lambert W function, Riemann surfaces, and analytic continuation.)
- Galidakis, Ioannis and Weisstein, Eric W. Power Tower27 Nisan 2014 tarihinde Wayback Machine sitesinde .
- Joseph MacDonell, Some Critical Points of the Hyperpower Function 17 Ocak 2010 tarihinde Wayback Machine sitesinde ..
- Dave L. Renfro, Web pages for infinitely iterated exponentials 18 Şubat 2005 tarihinde Wayback Machine sitesinde . (Compilation of entries from questions about tetration on sci.math.)
- Andrew Robbins, Home of Tetration11 Aralık 2008 tarihinde Wayback Machine sitesinde . (An infinitely differentiable extension of tetration to real numbers.)
- R. Knobel. "Exponentials Reiterated." Amerikan Matematik Aylığı 88, (1981), p. 235-252.
- Hans Maurer. "Über die Funktion
für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft in Hamburg 4, (1901), p. 33-50. (Reference to usage of
from Knobel's paper.)
Dış bağlantılar
- Andrew Robbins'in tetrasyon sitesi11 Aralık 2008 tarihinde Wayback Machine sitesinde .
- Daniel Geisler'in tetrasyon sitesi 20 Temmuz 2011 tarihinde Wayback Machine sitesinde .
- Tetrasyon Forumu 22 Temmuz 2010 tarihinde Wayback Machine sitesinde .
- citizendium'daki tetrasyon 27 Ekim 2010 tarihinde Wayback Machine sitesinde .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte tetrasyon hiper 4 olarak da bilinir uslu sayidan sonra gelen ilk tekrarli ussudur Tetrasyonun Ingilizce karsiligi olan tetration kelimesi ilk kez matematikci tarafindan dort ve tekrar dan turetilerek kullanilmaya baslandi Tetrasyon cok buyuk sayilarin gosterimi icin kullanildi Fakat birkac pratik uygulamasi vardir Bu yuzden sadece incelenir Burada asiri islecin ilk dort ornegin gosteriliyor Tekrasyon dorduncusudur toplama Normal bilinen toplama islemi dd carpma a n a a a n displaystyle a times n underbrace a a cdots a n genellikle temel islemlerden birini ifade eder Fakat dogal sayilar gibi ozel durumlar icin kendine n kere eklenen a olabilir dd us alma an a a a n displaystyle a n underbrace a times a times cdots times a n a nin kendisi ile n kere carpilmasi dd tetrasyon na aa a n displaystyle n a underbrace a a cdot cdot a n a nin kendisiyle n kere ussunun alinmasi dd e 1 e x ee 1 displaystyle e 1 e leq x leq e e 1 tabanlari icin limn xn displaystyle lim n rightarrow infty x frac n sonsuz uslu kulesi buradaki her bir islem bir oncekinin tekrari seklinde tanimlanir Tetrasyonunu bu islemlerden ayiran ozellik ilk ucu toplama carpma ve us alma n nin karmasik degerler ile genellesmesiyken tetrasyonun henuz kesfedilen duzenli bir genellestirilmesi yoktur ve tetrasyon bir temel fonksiyon olarak nitelendirilmez Toplama a n en temel islemdir Carpma an da temel fonksiyondur Tetrasyon na displaystyle n a n nin a tane kuvvetini iceren bir dizi olarak dusunulebilir a degiskeni ilerleyen bolumlerde temel degisken olarak adlandirilirken n degiskeni de yukseklik degiskeni olarak adlandirilacak integral ilk yaklasimdir fakat kesirli olarak genellestirilebilir gercel ve karmasik yukseklik gibi TanimHer pozitif reel a gt 0 displaystyle a gt 0 ve negatif olmayan tam sayi n 0 displaystyle n geq 0 icin na displaystyle n a soyle tanimlanir 0a 1 displaystyle 0 a 1 n 0 displaystyle n 0 ise ve na a n 1a displaystyle n a a n 1 a eger n gt 0 displaystyle n gt 0 ise Tekrarli kuvvetlerTanimdan da goruldugu uzere tetrasyon uslu kuvvet olarak hesaplandiginda us oncelikle en derin seviyede alinir gosterimdeki en yuksek derece Diger ifadeyle 42 2222 2 2 22 2 24 216 65 536 displaystyle 4 2 2 2 2 2 2 left 2 left 2 2 right right 2 left 2 4 right 2 16 65 536 Ussun birlesme olmadigina dikkat edin Boylece diger siradaki hesaplama farkli bir cevaba gider 2222 22 2 2 22 2 2 256 displaystyle 2 2 2 2 neq left left 2 2 right 2 right 2 2 2 cdot 2 cdot 2 256 Burada uslu kuvvetler yukaridan asagiya dogru veya sagdan sola dogru hesaplanmalidir TerimbilimTetrasyon icin bircok terim ve her birinin kullanimi icin mantiksal dusunceler vardir Fakat bazilari bircok nedenden dolayi yayginlik kazanamadi Burada birkacindan bahsedilecektir Tetration tetrasyon terimi 1947 de Goodstein tarafindan gelistirildi Superexponentiation super us terimi Bromer tarafindan gelistirildi Hyperpower asiri kuvvet hyper asiri ve power kuvvet kelimelerinin birlesimidir ve tetrasyonun uygun sekilde aciklar Power tower uslu kule ara sira kullanilir Ornegin aa a n displaystyle atop underbrace a a cdot cdot a atop n n sirasinin uslu kulesi Tetrasyon birbirine yakin iliskiye sahip fonksiyon ve ifadelerle genellikle karistiriliyor Bundan dolayidir ki tetrasyon ile ilgili bircok terim kullaniliyor Burada birkacini verecegiz Form Terimbilimiaa aa displaystyle a a cdot cdot a a Tetrasyonaa ax displaystyle a a cdot cdot a x Tekrarli uslera1a2 an displaystyle a 1 a 2 cdot cdot a n Icice usler kuleler a1a2a3 displaystyle a 1 a 2 a 3 cdot cdot cdot Sonsuz usler kuleler Ilk iki ifadede a tabandir Kez kere sayisi olan diger a yukseklikdir Ucuncu ifadede n yuksekliktir fakat her birinin tabani farklidir GosterimTetrasyonun yazilabilecegi gosterimler sunlardir Ad Form AciklamaStandart gosterim na displaystyle n a Maurer 1901 ve Goodstein 1947 tarafindan kullanildi kitabi olan bu gosterimi populer yapti Knuth yukari ok gosterimi a n displaystyle a uparrow uparrow n Daha fazla oklar koyarak genislemeyi veya daha guclu olmayi saglar Conway dizisi ok gosterimi a n 2 displaystyle a rightarrow n rightarrow 2 2 sayisinin artirarak genislemeyi saglar yukaridakinin genislemesiyle esdegerdir Ayrica dizi genisletilerek daha da guclenir Ackermann islevi n2 A 4 n 3 3 displaystyle n 2 operatorname A 4 n 3 3 Ackermann islevinin a 2 displaystyle a 2 icin yazilan ozel durumudur Tekrarli ustel gosterimi na expan 1 displaystyle n a exp a n 1 1 den farkli baslangic degerlerine sahip olan tekrarli ustellerin basit genislemesini saglar Hooshmand gosterimi uxpa n an displaystyle operatorname uxp a n a frac n gosterimi a 4 n hiper4 a n displaystyle a 4 n operatorname hiper 4 a n 4 sayisini arttirarak genisleme saglar Bu asiri isleclerin ailesini olustururASCII gosterimi a n Yukari ok duzeltme isareti ile ayni kullanildiginda tetrasyon isleci de olarak yazilir Yukaridaki gosterimlerden biri tekrarli ustel gosterimi kullanir Bu genellikle soyle tanimlanir expan x aa ax displaystyle exp a n x a a cdot cdot a x n tane a Tekrarli usler icin cok fazla gosterim yoktur Fakat birkacini verelim Ad Form AciklamaStandart gosterim expan x displaystyle exp a n x Euler dizi gosterimi expa x ax displaystyle exp a x a x ve tekrar gosterimi fn x displaystyle f n x Knuth yukari ok gosterimi a n x displaystyle a uparrow n x Oklarin sayisini arttirarak super kuvvetler ve super uslu fonksiyonlari saglar Bu gosterim buyuk sayilarda kullanilir Ioannis Galidakis gosterimi n a x displaystyle n a x Buyuk ifadelerin temelini olusturun ASCII yardimci a n x Tekrarli ustelin gorunum temeli yardimci tetrasyondur ASCII standart exp a n x Standart gosterimin temelidir OrneklerAsagidaki tablodaki cogu degerler bilimsel gosterimde yazmak cok zordur Bundan dolayi tekrarli ustel gosterim onlari 10 tabaninda ifade etti Degerlerdeki ondalik nokta yaklasiktir x displaystyle x 2x displaystyle 2 x 3x displaystyle 3 x 4x displaystyle 4 x 1 1 1 12 4 16 65 5363 27 7 625 597 484 987 exp103 1 09902 displaystyle exp 10 3 1 09902 4 256 exp102 2 18788 displaystyle exp 10 2 2 18788 exp103 2 18726 displaystyle exp 10 3 2 18726 5 3 125 exp102 3 33931 displaystyle exp 10 2 3 33931 exp103 3 33928 displaystyle exp 10 3 3 33928 6 46 656 exp102 4 55997 displaystyle exp 10 2 4 55997 exp103 4 55997 displaystyle exp 10 3 4 55997 7 823 543 exp102 5 84259 displaystyle exp 10 2 5 84259 exp103 5 84259 displaystyle exp 10 3 5 84259 8 16 777 216 exp102 7 18045 displaystyle exp 10 2 7 18045 exp103 7 18045 displaystyle exp 10 3 7 18045 9 387 420 489 exp102 8 56784 displaystyle exp 10 2 8 56784 exp103 8 56784 displaystyle exp 10 3 8 56784 10 10 000 000 000 exp103 1 displaystyle exp 10 3 1 exp104 1 displaystyle exp 10 4 1 Cok ilkel fonksiyonlardaki yaklasimlarPolinom yaklasimlari Lineer yaklasim Lineer yaklasimi sureklilik isteginin cozumue differensiyellenebilirlik yaklasimi soyle elde edilir xa loga x 1 a x 1 icin1 x 1 lt x 0 icina x 1 a x gt 0 icin displaystyle x a approx begin cases log a x 1 a amp x leq 1 mbox icin 1 x amp 1 lt x leq 0 mbox icin a left x 1 a right amp x gt 0 mbox icin end cases Bundan dolayi Yaklasim Tanim kumesixa x 1 displaystyle x a approx x 1 1 lt x lt 0 displaystyle 1 lt x lt 0 icinxa ax displaystyle x a approx a x 0 lt x lt 1 displaystyle 0 lt x lt 1 icinxa aa x 1 displaystyle x a approx a a x 1 1 lt x lt 2 displaystyle 1 lt x lt 2 icin ve boylece devam eder Ornekler p 2 e 5 868 4 30 5 4 03335 displaystyle pi 2 e approx 5 868 dots 4 3 0 5 approx 4 03335 dots Ana teorem Hooshmand e gore 0 lt a 1 displaystyle 0 lt a neq 1 dir Eger f 2 R displaystyle f 2 infty rightarrow mathbb R istenmeyen durumlara dogru giderse f x af x 1 tumx gt 1 vef 0 1 icin displaystyle f x a f x 1 mbox tum x gt 1 mbox ve f 0 1 mbox icin f displaystyle f 1 0 displaystyle 1 0 de turevlenebilir f displaystyle f prime fonksiyonu 1 0 displaystyle 1 0 da azalmayan veya artmayan bir fonksiyondur f 0 ln a f 0 veya f 1 f 0 displaystyle f prime 0 ln a f prime 0 mbox veya f prime 1 f prime 0 Daha sonra f displaystyle f su denklemle benzersiz tanimlanir f x expa x a x expa x 1 x tumx gt 2 icin displaystyle f x exp a x a x exp a x 1 x mbox tum x gt 2 mbox icin Buradaki x x x displaystyle x x x x in kismi parcasini ifade eder ve expa x displaystyle exp a x fonksiyonu expa displaystyle exp a fonksiyonunun x displaystyle x Ikinci ve dorduncu sartlar ispattir xe displaystyle x e dogal tetrasyon fonksiyonundaki lineer yaklasimi surekli olarak turevlenebilir Fakat ikinci turevi argumaninin tam sayisinda bulunmaz Hooshmand onun icin de soyle bir essiz teorem turetti Eger f 2 R displaystyle f 2 infty rightarrow mathbb R ise surekli fonksiyon soyledir f x ef x 1 tumx gt 1 f 0 1 displaystyle f x e f x 1 mbox tum x gt 1 f 0 1 icin f displaystyle f 1 0 displaystyle 1 0 de yakinsar f 0 f 0 displaystyle f prime 0 leq f prime 0 Sonra f uxp displaystyle f mbox uxp olur Buradaki ispat bir oncekine cok benzer Ozyineleme esitligi f 1 f 0 displaystyle f prime 1 f prime 0 oldugunu saglar ve yakinsaklik sarti 1 0 de f displaystyle f fonksiyonunun lineer oldugunu ifade eder Bundan dolayi dogal tetrasyondaki lineer yaklasimi sadece f x ef x 1 x gt 1 displaystyle f x e f x 1 x gt 1 esitliginin cozumudur ve f 0 1 displaystyle f 0 1 1 displaystyle 1 infty de Diger tum uygun turevlenebilir cozumlerin 1 0 araliginda bir olmasi gerekir Yuksek sirali yaklasimlar Ikinci dereceden yaklasim soyledir xa loga x 1 a x 1 icin 1 2log a 1 log a x 1 log a 1 log a x2 1 lt x 0 icin a x 1 a x gt 0 icin displaystyle x a approx begin cases log a x 1 a amp x leq 1 mbox icin 1 frac 2 log a 1 log a x frac 1 log a 1 log a x 2 amp 1 lt x leq 0 mbox icin a left x 1 a right amp x gt 0 mbox icin end cases Bu ifade tum x gt 0 displaystyle x gt 0 icin turevlenebilir Faka iki kez turevlenemez Eger a e displaystyle a e ise bu lineer yaklasim gibidir GenislemelerTetrasyon n0 displaystyle n 0 ve diger tanim kumelerini ifade etmek icin genisletilebilir Tabanlarda tanim kumesi genislemesi Sifir tabaninda genisleme 00 displaystyle 0 0 us ifadesi surekli olarak tanimlanmaz n0 displaystyle n 0 tetrasyonu da daha onceki formule gore iyi tanimlanmaz Yine de limx 0nx displaystyle lim x rightarrow 0 n x soyle tanimlanabilir limx 0nx 1 n cift0 n tek displaystyle lim x rightarrow 0 n x begin cases 1 amp n mbox cift 0 amp n mbox tek end cases Buradan n0 limx 0nx displaystyle n 0 lim x rightarrow 0 n x ifadesini surekli tanimlayabiliriz Bu 00 1 displaystyle 0 0 1 taniminin esdegeridir Bu genisleme altinda 00 1 displaystyle 0 0 1 Boylece asil tanim koruyarak 0a 1 displaystyle 0 a 1 kurali saglanir Karmasik tabanlarda genisleme Periyoda gore tetrasyonSizintiya gore tetrasyon Karmasik sayilar kuvvetlerle arttarken tetrasyon z a bi displaystyle z a bi formunun tabanlarinda uygulanabilir Buradaki i displaystyle i 1 in karekokudur Ornegin nz displaystyle n z z i displaystyle z i tetrasyonu dogal logaritma prensibi kullanilarak ifade edilebilir Euler formulunu kullanarak soyle bir iliski elde edebiliriz ia bi eip2 a bi e bp2 cos ap2 isin ap2 displaystyle i a bi e i pi over 2 a bi e b pi over 2 left cos a pi over 2 i sin a pi over 2 right Bu n 1 i a b i displaystyle n 1 i a b i icin tekrarli bir tanim ortaya cikartir Her ni a bi displaystyle n i a bi icin a e bp2cos ap2 displaystyle a e b pi over 2 cos a pi over 2 b e bp2sin ap2 displaystyle b e b pi over 2 sin a pi over 2 Asagidaki yaklasim degerleri turetilebilir ni displaystyle n i Yaklasim Degeri1i i displaystyle 1 i i i2i i 1i displaystyle 2 i i left 1 i right 0 2079 displaystyle 0 2079 3i i 2i displaystyle 3 i i left 2 i right 0 9472 0 3208i displaystyle 0 9472 0 3208i 4i i 3i displaystyle 4 i i left 3 i right 0 0501 0 6021i displaystyle 0 0501 0 6021i 5i i 4i displaystyle 5 i i left 4 i right 0 3872 0 0305i displaystyle 0 3872 0 0305i 6i i 5i displaystyle 6 i i left 5 i right 0 7823 0 5446i displaystyle 0 7823 0 5446i 7i i 6i displaystyle 7 i i left 6 i right 0 1426 0 4005i displaystyle 0 1426 0 4005i 8i i 7i displaystyle 8 i i left 7 i right 0 5198 0 1184i displaystyle 0 5198 0 1184i 9i i 8i displaystyle 9 i i left 8 i right 0 5686 0 6051i displaystyle 0 5686 0 6051i Onceki bolumle ters iliskiyi cozme n nin negatif degerli beklenen 0i 1 displaystyle 0 i 1 ve 1 i 0 displaystyle 1 i 0 i saglar Bunun icin sanal eksene sonsuz sonuc verilir Tekrarli yukseklikler icin tanim kumesi genislemeleri Sonsuz yukseklik genislemesi Tetrasyon sonsuz yuksekliklere genisletilebilir na displaystyle n a deki n Ornegin 222 displaystyle sqrt 2 sqrt 2 sqrt 2 cdot cdot cdot ifadesi 2 ye yakinsar bundan dolayi 2 ye esittir denir 2 ye dogru gidis kucuk sonlu kuleyi hesaplayarak gorulebilir 222221 41 22221 63 2221 76 221 84 21 89 1 93 displaystyle begin aligned sqrt 2 sqrt 2 sqrt 2 sqrt 2 sqrt 2 1 41 amp sqrt 2 sqrt 2 sqrt 2 sqrt 2 1 63 amp sqrt 2 sqrt 2 sqrt 2 1 76 sqrt 2 sqrt 2 1 84 amp sqrt 2 1 89 1 93 end aligned Genellikle xx displaystyle x x cdot cdot cdot sonsuz kuvvet kulesi nx displaystyle n x in limiti siniri olarak tanimlanir Burada n e e x e1 e icin sonsuzluga gider Negatif yuksekliklere sinirli genisleme Asil kurali korumak icin k 1 a a ka displaystyle k 1 a a k a k displaystyle k nin negatif degerleri icin ozyineleme iliskisini kullanmaliyiz ka loga k 1 a displaystyle k a log a left k 1 a right Buradan 1 a loga 0a loga 1 0 displaystyle 1 a log a left 0 a right log a 1 0 Bununla beraber daha kucuk negatif degerler bu yolla iyi tanim verme Cunku 2 a loga 1a loga 0 displaystyle 2 a log a left 1 a right log a 0 iyi tanimli degildir 1 1 displaystyle 1 1 in her tanimi n 1 displaystyle n 1 icin kuralla uyumlu olduguna dikkat edin Cunku her n 1 1 displaystyle n 1 1 icin 01 1 1n displaystyle 0 1 1 1 n dir Gercek yuksekliklere genisleme Burada genisleme tetrasyonunun genel problemlerinin cozumu icin n displaystyle n nin reel veya karmasik degerlerinde yaygin olarak kullanilan kabul edilmis bir cozum yoktur Cesitli yaklasimlar asagidaki gosteriliyor Genelde problem a gt 0 ve x gt 2 displaystyle x gt 2 degerleri icin f x xa displaystyle f x x a gibi bir super ustel fonksiyon bulunuyor ki bu da yeterince tatminkardir 1 a 0 displaystyle 1 a 0 0a 1 displaystyle 0 a 1 xa a x 1 a displaystyle x a a left x 1 a right tum reel x gt 1 icin Dorduncu kosul genellikle sunlardan biridir Bir sureklilik kosulu genellikle sadece xa displaystyle x a her iki degisken icin x gt 0 displaystyle x gt 0 sartilya sureklidir Bir turevlenebilirlik kosulu x de bir kez iki kez k kez veya sonsuz kez turevlenebilir Bir uygunluk sarti x de iki kez turevlenebilirligi ifade eder soyledir d2dx2f x gt 0 displaystyle left frac d 2 dx 2 f x gt 0 right tum x gt 0 displaystyle x gt 0 icin dd Dorduncu kosul kisiden kisiye ve yaklasimlara gore degisirr Tetrasyonunu gercel yuksekliklere genisletmek icin iki ana yaklasim vardir Birincisi uygunluk kosulu digeri de turevlenebilirlik kosuludur Bu iki yaklasim birbirleriyle tutarsiz sonuclar uretmesi onlarin cok farkli oldugunu gosterdi Neyse ki bir uzunlugun icindekilerden biri tum pozitif reel sayilar icin genisletilebilir Bir icsel uzunluk icin xa displaystyle x a tanimliysa tam fonksiyon tum x gt 2 displaystyle x gt 2 icin gecerlidir Karmasik yuksekliklere genisleme f F x iy displaystyle f F x rm i y tetrasyonunun karmasik duzlemde analitik genislemesinin cizimi f 1 e 1 e 2 displaystyle f 1 e pm 1 e pm 2 ldots ve arg f 0 1 2 displaystyle arg f 0 pm 1 pm 2 ldots dereceleri kalin egimlerle gosteriliyor Soyle bir konjektur vardir F z 1 exp F z esitliginin cozumu icin essiz bir F fonksiyonu vardir ve ek F 0 1 ve F z yaklasimlarini saglar Bu fonksiyon sagdaki sekilde goruluyor Ters fonksiyonlarTetrasyonun Ters fonksiyonlari genellikle super kok ve super logaritma olarak adlandirilir xx displaystyle x x in super kokun karesi olan ssrt x displaystyle mathrm ssrt x Lambert W fonksiyonu ile soyle ifade edilebilir ssqrt x eW ln x ln x W ln x displaystyle mathrm ssqrt x e W mathrm ln x frac mathrm ln x W mathrm ln x Her n gt tam sayilari icin nx seklinde fonksiyon vardir ve bu fonksiyon x icin artarak 1 n1 esitligi elde edilir Boylece x in n super koku x 1 icin elde edilir Yine de eger yukaridaki lineer yaklasim kullanilir ve 1 y 0 sart saglanirsa 1 yx y 1 olur Boylece 1 ysroot y 1 elde edilemez slogax super algoritmasi tum gercel x ve a gt 1 sayilari icin gecerlidir sloga displaystyle mathrm slog a fonksiyonu slogaxa x displaystyle mathrm slog a x a x slogaax 1 slogax displaystyle mathrm slog a a x 1 mathrm slog a x slogax 1 slogaloga x displaystyle mathrm slog a x 1 mathrm slog a log a x slogax gt 2 displaystyle mathrm slog a x gt 2 Infra logaritma fonksiyonu ultra ustel fonksiyonun iki katidir ve ioga displaystyle mathrm iog a seklinde ifade edilir Eger a gt 1 displaystyle a gt 1 ise uxpa displaystyle mathrm uxp a fonksiyonunun tersi olur Super kok Super kok tetrasyonun iki ters fonksiyonundan biridir Sadece ve logaritma ustel olarak iki ters fonksiyonken keza tetrasyonunda iki ters fonksiyonu vardir super kok ve super logaritma Super kok tetrasyonun tabanini ifade eden ters fonksiyonudur eger ny x displaystyle n y x ise y de x in n super koku olur Ornegin 42 2222 65 536 displaystyle 4 2 2 2 2 2 65 536 boylece 2 65 536 nin 4 kokudur ve 33 333 7 625 597 484 987 displaystyle 3 3 3 3 3 7 625 597 484 987 olur Boylece 3 7 625 597 484 987 nin 3 super koku veya super kupu dur Super kokun birkac pratik uygulamasi vardir Bunlar sadece calisilir Kare kok 2 sira super kok veya super kare kok is noteworthy for its simple expression in terms of Lambert W fonksiyonunda terimlerinin basit ifadesi icin onemlidir Ifadesi xs eW ln x displaystyle sqrt x s e W ln x buradaki xs displaystyle sqrt x s x displaystyle x in super kare kokudur Fonksiyon her ne kadar super karenin karsiti olarak tanimlanmis olsa bile sonsuz ustelin de karsitidir Sonsuz soyledir xs xxxx displaystyle sqrt x s sqrt sqrt sqrt sqrt x x x x Kare kok ornekleri Asagidaki tablo ilk 27 tam sayinin super kare koklerini gosteriyor x displaystyle x xs displaystyle sqrt x s x displaystyle x xs displaystyle sqrt x s x displaystyle x xs displaystyle sqrt x s 1 1 10 2 506184 19 2 830223 2 1 559610 11 2 555604 20 2 855308 3 1 825455 12 2 600295 21 2 879069 4 2 13 2 641061 22 2 901637 5 2 129372 14 2 678523 23 2 923122 6 2 231828 15 2 713163 24 2 943621 7 2 316454 16 2 745368 25 2 963219 8 2 388423 17 2 775449 26 2 981990 9 2 450953 18 2 803663 27 3 Eger bir sayinin super kare koku tam sayi degilse o irrasyoneldir Fakat bununla ilgili herhangi bir ispat bilinmiyor Diger super kokler Diger super kokler kullanilan ayni tabanda ifade edilebilir super kup kokler x yyy displaystyle x y y y oldugunda y ureten fonksiyon x3s displaystyle sqrt 3 x s olarak ifade edilebilir 4 super kok x4s displaystyle sqrt 4 x s olarak ifade edilebilir ve bundan dolayi n super kok xns displaystyle sqrt n x s dir denilebilir Super logaritma Tetrasyonun iki ters fonksiyonundan biridir Sadece ve logaritma ustel olarak iki ters fonksiyonken keza tetrasyonunda iki ters fonksiyonu vardir super logaritma ve super kok Super logaritmayi aciklayan birkac yol vardir Ustel fonksiyonlarin olarak Tetrasyonun yuksekligini ifade eden ters fonksiyonu olarak Logaritmanin 1 e gitmesi icin kac kez gerektiginin sayisi As a generalization of Robert Munafo s large number class system16 Mayis 2017 tarihinde Wayback Machine sitesinde bir sinirsiz surumu olarak Super logaritma tanimlari slogb z displaystyle mathrm slog b z olarak yazilan super logaritma tam olarak soyle tanimlanir slogb bz slogb z 1 displaystyle mathrm slog b b z mathrm slog b z 1 ve slogb 1 0 displaystyle mathrm slog b 1 0 Bu tanimin sadece tam sayilar verebilecegine ve sadece tam sayi uretebilecek sayilari kabul edebilecegine dikkat edin Bu tanimin kabul edecegi sayilar b bb bbb displaystyle b b b b b b vb formdadir Yaklasimlar Genellikle ozel fonksiyonlar arguman lar in reel degerleri icin degil karmasik duzlem diferansiyel ve integral ifadeleri icinde tanimlanir Slag fonksiyonu icin mevcut ifadeler olmadigi icin basit yaklasimlar soyle oneriliyor Super logaritmaya lineer yaklasim Super logaritmaya lineer yaklasim soyledir slogb z slogb bz 1z 0icin 1 z0 lt z 1icin slogb logb z 11 lt zicin displaystyle mathrm slog b z approx begin cases mathrm slog b b z 1 amp z leq 0 mbox icin 1 z amp 0 lt z leq 1 mbox icin mathrm slog b log b z 1 amp 1 lt z mbox icin end cases Bu fonksiyon tum reel z C0 displaystyle C 0 sureklilik icin sureklidir Ikinci dereceden yaklasim Super logaritmaya ikinci dereceden yaklasim soyledir slogb z slogb bz 1z 0icin 1 2log b 1 log b z 1 log b 1 log b z20 lt z 1icin slogb logb z 11 lt zicin displaystyle mathrm slog b z approx begin cases mathrm slog b b z 1 amp z leq 0 mbox icin 1 frac 2 log b 1 log b z frac 1 log b 1 log b z 2 amp 0 lt z leq 1 mbox icin mathrm slog b log b z 1 amp 1 lt z mbox icin end cases Bu fonksiyon tum reel z C1 displaystyle C 1 sureklilik icin turevlenebilir Abel fonksiyonuna yaklasimlar Abel fonksiyonu su esitligi saglayan herhangi bir fonksiyondur Af f x Af x 1 displaystyle A f f x A f x 1 Verilen bir Af x displaystyle A f x Abel fonksiyonunun diger cozumu herhangi sabit Af x Af x c displaystyle A f x A f x c eklenerek elde edilebilir Verilen bu super logaritma slogb 1 0 displaystyle mathrm slog b 1 0 olarak tanimlanir ve ucuncu ozelligi ustel fonksiyonun Abel fonksiyonu essiz olarak tanimlanabilmesidir Ozellikler Super logaritmanin diger esitlikleri slogb z slogb logb z 1 displaystyle mathrm slog b z mathrm slog b log b z 1 slogb z gt 2 displaystyle mathrm slog b z gt 2 tum reel z icinTetrasyonun tersi olarak slag Karmasik z duzlemindeki f sloge z displaystyle f rm slog rm e z fonksiyonu Tetrasyon olarak sexpb z displaystyle rm sexp b z analitik fonksiyon olmasi husunuda suphelidir En azindan b displaystyle b nin bazi degerleri icin slogb sexpb 1 ters fonksiyonu analitik olabilir Karmasik z duzlemindeki slogb z displaystyle rm slog b z nin davranisi yukaridaki sekilde b e displaystyle b e durumu icin cizilmistir slog fonksiyonunun sanal kisminin reel ve tam sayi degerlerinin dereceleri kalin cizgilerle gosteriliyor Ayrica bakinizAckermann isleviAlintilar D Kouznetsov Temmuz 2009 Karmasik z displaystyle z duzleminde F z 1 exp F z displaystyle F z 1 exp F z nin cozumu PDF Hesap Matematigi 78 267 s 1647 1670 doi 10 1090 S0025 5718 09 02188 7 Daniel Geisler tetration org 20 Temmuz 2011 tarihinde Wayback Machine sitesinde Ioannis Galidakis 2006 dan once A simpler easier to read review of the next reference Ioannis Galidakis undated 2006 or earlier Robert Munafo Extension of the hyper4 function to reals 17 Agustos 2010 tarihinde Wayback Machine sitesinde An informal discussion about extending tetration to the real numbers Lode Vandevenne Tetration of the Square Root of Two 10 Kasim 2012 tarihinde Wayback Machine sitesinde 2004 Attempt to extend tetration to real numbers Ioannis Galidakis Definitive list of references to tetration research Lots of information on the Lambert W function Riemann surfaces and analytic continuation Galidakis Ioannis and Weisstein Eric W Power Tower27 Nisan 2014 tarihinde Wayback Machine sitesinde Joseph MacDonell Some Critical Points of the Hyperpower Function 17 Ocak 2010 tarihinde Wayback Machine sitesinde Dave L Renfro Web pages for infinitely iterated exponentials 18 Subat 2005 tarihinde Wayback Machine sitesinde Compilation of entries from questions about tetration on sci math Andrew Robbins Home of Tetration11 Aralik 2008 tarihinde Wayback Machine sitesinde An infinitely differentiable extension of tetration to real numbers R Knobel Exponentials Reiterated Amerikan Matematik Ayligi 88 1981 p 235 252 Hans Maurer Uber die Funktion y x x x displaystyle y x x x cdots fur ganzzahliges Argument Abundanzen Mittheilungen der Mathematische Gesellschaft in Hamburg 4 1901 p 33 50 Reference to usage of na displaystyle n a from Knobel s paper Dis baglantilarAndrew Robbins in tetrasyon sitesi11 Aralik 2008 tarihinde Wayback Machine sitesinde Daniel Geisler in tetrasyon sitesi 20 Temmuz 2011 tarihinde Wayback Machine sitesinde Tetrasyon Forumu 22 Temmuz 2010 tarihinde Wayback Machine sitesinde citizendium daki tetrasyon 27 Ekim 2010 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans