Olasılık teorisi ya da ihtimaliyet teorisi olayların analizi ile ilgilenen bir matematik bilim dalıdır. Olasılık teorisinin ana ögeleri rassal değişkenler, , olarak sayılabilir. Bunlar ya tek olarak ortaya çıkan veya bir zaman dönemi içinde gelişerek meydana gelen, ilk görünüşü rastgele bir şekilde olan deterministik olmayan olayların veya ölçülebilir miktarların matematiksel soyutlamalarıdır. Bir madeni parayı yazı-tura denemesi için havaya atmak veya bir zarı atmak ile ortaya çıkan sonuç ilk bakışta rastgele bir olay olarak görülebilirse bile eğer birbirini takip eden rastgele olaylar tekrar tekrar ortaya çıkartılırsa incelenebilecek ve tahmin edilebilecek belirli bir istatistiksel seyir takip ettikleri görülecektir. Bu türlü olaylar ve sonuçların seyirlerini betimleyen iki temsilci matematiksel sonuç büyük sayılar yasası ve merkezsel limit teoremidir.
İstatistik bilim dalının matematiksel temelini oluşturan olasılık teorisi, büyük veri serilerinin niceliksel analizini gerektiren birçok insan faaliyetinin incelenebilmesi ve anlaşılabilmesi için gereken temel esasları oluşturur. Bunun yanında, olasılık teorisinin yöntemleri, durumları hakkında sadece kısımsal bilgimiz olabilecek karmaşık sistemlerin tanımlanmasına da uygulanabilir. Örneğin; İstatistiksel Mekanik. Yirminci yüzyılda fizik biliminde en büyük buluşlardan biri, atomik düzeyde fiziksel olayların tabiatının olasılıklı olduğu ve bunların kuantum mekanik bilgisi ile açıklanıp, incelenip, kullanılabileceğidir.
Tarihçe
Bilinen en eski olasılık ve istatistik hesaplamaları, 8 ve 13. yüzyıllar arasında kriptografi üzerine çalışan Arap matematikçiler tarafından geliştirilmiştir. Halil ibn Ahmed el-Ferahidi (717-786) sesli ve sessiz harflerle olası tüm Arapça kelimeleri listelemek için tarihte ilk defa permütasyon ve kombinasyonun kullanıldığı Şifreleme Mesajları Kitabı'nı yazmıştır. Kindî (801-873), kriptanaliz ve frekans analizi konusundaki çalışmalarında bilinen en erken istatistiksel çıkarımlarda bulunmuştur. İbn Adlan (1187-1268) ise frekans analizi kullanımı için örneklem büyüklüğü üzerine çalışmalar yapmıştır.
Matematiksel olasılık teorisinin tarihsel kökleri 16. yüzyılda Gerolamo Cardano ve 17. yüzyılda Pierre de Fermat ile Blaise Pascal tarafından yapılan matematiksel incelemelerine dayanır.
Başlangıçta, olasılık teorisi genellikle ayrık olayları incelemek için geliştirilmiş ve kullanılan yöntemler genellikle matematik kurallarına dayandırılmıştır. Fakat giderek görüşleri daha ağır basarak olasılık teorisine sürekli değişkenlerin incelenmesinin de katılması gerektirmiştir. Bu gelişmenin şu andaki en son aşamasının temelleri, tarafından, bağlantılı olan modern olasılık teorisi olarak ortaya çıkartılmıştır. Kolmogorov, Richard von Mises tarafından ortaya atılan örnek uzay kavramlarını kavramları ile birleştirerek 1933'te modern olasılık teorisi için esas olan Kolmogorov aksiyomlarını ortaya atmıştır. Bu gelişme bilim camiası tarafından çabucak, hiç karşı çıkan kuram olmadan, modern olasılık teorisinin ana olarak benimsenmiştir.
İnceleme
Olasılık teorisine girişlerin çoğunda, ayrık olasılık dağılımları ve sürekli olasılık dağılımları ayrı ayrı olarak incelemeye alınmaktadır. Halbuki olasılığın daha ileri matematiksel yaklaşımla incelenmesinin, hem ayrık, hem sürekli ve hem de bunların karışığı ve daha ilerisinde olan dağılımların hep birlikte yapılmasını gerektirmektedir.
Ayrık olasılık dağılımları
Ayrık olasılık teorisi örneklem uzayında ortaya çıkan olayları inceler. Örneğin: Zar atılması, küp deneyleri, çekmek veya rastgele yürüyüş olayları.
Klasik tanım: Olasılık teorisi geliştirilmesinin ilk safhalarında, belirtilmiş bir olay ortaya çıkması için olasılık, her mümkün sonucu eşit olasılıklı olan örneklem uzayında incelendiği kabul edilmiş ve incelenen olaya uygun sonuç sayısının toplam tüm sonuçlar sayısına oranı olarak tanımlanmıştı. Örneğin, incelenecek sorun "tek bir zar atılınca çift sayıların gelme olasılığı nedir" şeklinde sorulursun. Zar yansız olup her altı yüzü de eşit olasılıkla gelebileceği için, 2, 4, 6 sonuçları 3 tane olduğu ve toplam mümkün sonuç sayısı 6 yüze dayanarak 6 olduğu için, aranan olasılık
- P( 2 veya 4 veya 6 ) =
olarak bulunur.
Modern tanım: Modern tanıma örneklem uzayı adı verilen bir küme ile başlanır; bu klasik tanımda kullanılan mümkün tüm sonuçlar seti ile aynı anlamlıdır; ve şu notasyon kullanılarak ifade edilir: 
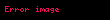

Bu demektir ki olasılık fonksiyonu olan f(x) Ω örneklem uzayında bulunan her x değeri için 0 ile 1 arasında bulunmaktadır ve x için tüm mümkün değerler için f(x) değerlerinin toplamı tama tam (1'e) eşit olur. Bir olay 
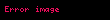
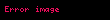
Buna göre tüm örneklem uzayının olasılığı 1e eşittir ve boş örneklem uzayı veya 0 olay için de olasılık 0a eşit olur.
Örnekleme uzayındaki bir noktayı "olasılık" değerine eşleyen fonksiyona, yani 
Sürekli olasılık dağılımları
Sürekli olasılık teorisi sürekli örneklem uzayında ortaya çıkan olayları inceler.
Klasik tanım: Sürekli olasılık hâlleri ile karşılaşınca klasik tanım geçerli olmaz. maddesine bakin.
Modern tanım: Eğer örneklem uzayı reel sayılardan oluşursa (yani 
Yığmalı dağılım fonksiyonu şu özellikleri göstermelidir:
, bir fonksiyondur;
Eğer 
bulunur.

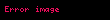
Eğer bir olasılık yoğunluk fonksiyonu var ise, bu şöyle ifade edilebilir:
Olasılık yoğunluk fonksiyonu sadece sürekli rassal değişkenler için var olmakta ise de, yığmalı dağılım fonksiyonu 
Bu kavramlar 
Ölçüm kuramsal olasılık teorisi
Modern olasılık teorisi yaklaşımı kullanılması suretiyle yapılmakta ve bu kuram olasılık uzayında Kolmogorov aksiyomlarına dayandırılmaktadır. Olasılık uzayı üç kısımdan oluşmuştur. Olasılığın bu ölçüm teorisine göre uygulanmasının esas nedeni bu teorisin ayrık ve sürekli değişkenleri birlikte ele alabilmesinden ve aralarındaki farkları kullanılan ölçü ile açıklamasındandır. Bundan başka saf ayrık veya saf sürekli dağılımlar yanında bu iki kategoriye tam uymayan dağılımları da inceleme imkânı sağlamaktadır.
Herhangi bir set 
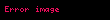

non-negatifdir;
Eğer 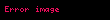
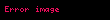
σ-cebiri 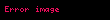
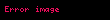
Burada entegrasyon 
Temel Prensipler
Belirli bir olay A için olasılık 
| Olay | Olasılık |
|---|---|
| A olayı olması için olasılık |  |
| A olayı olmaması için olasılık | 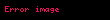 |
| A veya B olması için olasılık |  |
| A ve B olması için olasılık |  |
| A verilmiş B olması (B koşullu A) | 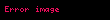 |
Olasılık dağılımları
Bazı rassal değişkenler olasılık teorisi içinde daha sık olarak isimleri geçmektedir; çünkü bu değişkenler birçok doğal veya fiziksel süreçleri belirlemektedirler veya özellikle çıkarımsal istatistikte çok öneme haizdirler. Bunun için bu tür değişkenler için olasılık dağılımları olasılık teorisi içinde özel önem taşımaktadırlar.
Temel ayrık olasılık dağılımları listesi şöyle verilebilir:
- Ayrık tekdüze dağılım
- Bernoulli dağılımı
- Binom dağılımı
- Negatif binom dağılımı
- Poisson dağılımı
- Geometrik dağılım
- Hipergeometrik dağılım
Temel sürekli olasılık dağılımları listesi şöyle verilebilir:
Rassal değişkenlerin yakınsaması
- Olasılık teorisi içinde rassal değişkenler in yakınsama kavramı birkaç değişik şekilde tanımlanır. Aşağıdaki listede bu değişik tanımlar tanımın geçerlilik gücüne göre sıralanmıştır. Bu sıralamaya göre sıranın içindeki herhangi bir tanım daha önce verilmiş olan tüm tanımları da içinde kapsamaktadır.
- Dağılım içinde yakınsama: Bir seri rassal değişken olan
,
rassal değişkenine dağılım içinde yakınsama göstermesi, ancak her bir X_i rassal değişkeni için yığmalı dağılım fonksiyonu olan
fonksiyonlarının
in yığmalı dağılım fonksiyonu olan
ye yakınsama göstermesi hâlinde ortaya çıkar. Burada
sürekli bir fonksiyondur.
- En iyi bilinir kısaltılmış notasyon ile:
- En iyi bilinir kısaltılmış notasyon ile:
- Zayıf yakınsama: Bir seri rassal değişken olan
rassal değişkenine zayıf yakınsama gösterirlerse, her ε > 0 için
olur. Zayıf yakınsama 'olasılık içinde yakınsama olarak da bilinmektedir.
- En iyi bilinir kısaltılmış notasyon ile:
- En iyi bilinir kısaltılmış notasyon ile:
- Güçlü yakınsama: Bir seri rassal değişken olan
rassal değişkenine güçlü yakınsama gösterirlerse
ifadesi gerçekleşir. Güçlü yakınsama hemen hemen kesinlikle yakınsama olarak da isimlendirilir.
- En iyi bilinir kısaltılmış notasyon ile:
- En iyi bilinir kısaltılmış notasyon ile:
Güçlü yakınsamanın bir zayıf yakınsamanın daha güçlü bir şekli olduğu gerçeğinin sezilmesi kolaydır ve her iki hâlde de rassal değişkenler 

Büyük sayılar yasası
Yaygın olan bir sezgiye göre eğer yansız olan bir madeni para birkaç kere havaya atılıp yazı-tura sonuçları kayıt edilirse, sonuçların kabaca yarısı yazı olacak ve kalan yarısı da tura olacaktır. Üstelik, madeni parayı daha da çok defa havaya atıp sonuç kayıt edildikçe giderek yazı sonuçları sayısının tura sonuçları sayısına oranının gittikçe daha çok bire yaklaştığı gözümlenecektir. Bu sezgi ile geliştirilen bu düşünce prensibine istatistik bilimde daha formel bir şekil verilmekte ve bunu büyük sayılar yasasi olarak isimlendirilmektedir. Bu dikkate değerdir; çünkü bu yasa olasılık teorisinin hiçbir yerinde, bu teorisin temel taşdır şeklinde bir bahis görmemektedir; fakat bu yasa olasılık teorisi temelinden bir teorem olarak geliştirilip ortaya çıkarılmaktadır. Bununla beraber, teorik olarak elde edilen olasılıkları, pratik reel hâllerde gerçek olarak ortaya çıkan çokluklara (frekanslara) bağladığı için, bu yasa istatistik teorisinin tarihinin içinde çok önemli bir orta direk taşı olarak kabul edilmektedir.
Büyük sayılar yasasına göre örneklem ortalaması, yani bağımsız ve birbiri ile sonsuz olmayan beklenen değeri 

- Güçlü yasa:
- Zayıf yasa:
Ayrıca bakınız
- İstatistiksel bağımsızlık
- İstatistiksel terimler, kavramlar ve konular listesi
- - Olasılık teorisi ve mantık bileşimi
Kaynakça
- ^ "Probability theory, Encyclopaedia Britannica". 15 Nisan 2008 tarihinde kaynağından . Erişim tarihi: 18 Nisan 2008.
- ^ Broemeling, Lyle D. (1 Kasım 2011). "An Account of Early Statistical Inference in Arab Cryptology". The American Statistician. 65 (4). ss. 255-257. doi:10.1198/tas.2011.10191.
- ^ (PDF). 5 Şubat 2012 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 18 Nisan 2008.
- ^ . 26 Ocak 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 18 Nisan 2008.
Bibliyografya
- Billingsley, P., (1995) Probability and Measure, 3ncu ed., John Wiley, New York
- Gut, A., (2005) Probability: A Graduate Course. Springer-Verlag. .
- Jeffreys, H., (1939) The Theory of Probability
- Kolmogorov, A.N., (1933) Grundbegriffe der Wahrscheinlichkeitrechnung.
- Laplace, P.S., (1812) Theorie Analytique des Probabilités.
- Nelson, E., (1987) Radically Elementary Probability Theory
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Olasilik teorisi ya da ihtimaliyet teorisi olaylarin analizi ile ilgilenen bir matematik bilim dalidir Olasilik teorisinin ana ogeleri rassal degiskenler olarak sayilabilir Bunlar ya tek olarak ortaya cikan veya bir zaman donemi icinde geliserek meydana gelen ilk gorunusu rastgele bir sekilde olan deterministik olmayan olaylarin veya olculebilir miktarlarin matematiksel soyutlamalaridir Bir madeni parayi yazi tura denemesi icin havaya atmak veya bir zari atmak ile ortaya cikan sonuc ilk bakista rastgele bir olay olarak gorulebilirse bile eger birbirini takip eden rastgele olaylar tekrar tekrar ortaya cikartilirsa incelenebilecek ve tahmin edilebilecek belirli bir istatistiksel seyir takip ettikleri gorulecektir Bu turlu olaylar ve sonuclarin seyirlerini betimleyen iki temsilci matematiksel sonuc buyuk sayilar yasasi ve merkezsel limit teoremidir Istatistik bilim dalinin matematiksel temelini olusturan olasilik teorisi buyuk veri serilerinin niceliksel analizini gerektiren bircok insan faaliyetinin incelenebilmesi ve anlasilabilmesi icin gereken temel esaslari olusturur Bunun yaninda olasilik teorisinin yontemleri durumlari hakkinda sadece kisimsal bilgimiz olabilecek karmasik sistemlerin tanimlanmasina da uygulanabilir Ornegin Istatistiksel Mekanik Yirminci yuzyilda fizik biliminde en buyuk buluslardan biri atomik duzeyde fiziksel olaylarin tabiatinin olasilikli oldugu ve bunlarin kuantum mekanik bilgisi ile aciklanip incelenip kullanilabilecegidir TarihceBilinen en eski olasilik ve istatistik hesaplamalari 8 ve 13 yuzyillar arasinda kriptografi uzerine calisan Arap matematikciler tarafindan gelistirilmistir Halil ibn Ahmed el Ferahidi 717 786 sesli ve sessiz harflerle olasi tum Arapca kelimeleri listelemek icin tarihte ilk defa permutasyon ve kombinasyonun kullanildigi Sifreleme Mesajlari Kitabi ni yazmistir Kindi 801 873 kriptanaliz ve frekans analizi konusundaki calismalarinda bilinen en erken istatistiksel cikarimlarda bulunmustur Ibn Adlan 1187 1268 ise frekans analizi kullanimi icin orneklem buyuklugu uzerine calismalar yapmistir Matematiksel olasilik teorisinin tarihsel kokleri 16 yuzyilda Gerolamo Cardano ve 17 yuzyilda Pierre de Fermat ile Blaise Pascal tarafindan yapilan matematiksel incelemelerine dayanir Baslangicta olasilik teorisi genellikle ayrik olaylari incelemek icin gelistirilmis ve kullanilan yontemler genellikle matematik kurallarina dayandirilmistir Fakat giderek gorusleri daha agir basarak olasilik teorisine surekli degiskenlerin incelenmesinin de katilmasi gerektirmistir Bu gelismenin su andaki en son asamasinin temelleri tarafindan baglantili olan modern olasilik teorisi olarak ortaya cikartilmistir Kolmogorov Richard von Mises tarafindan ortaya atilan ornek uzay kavramlarini kavramlari ile birlestirerek 1933 te modern olasilik teorisi icin esas olan Kolmogorov aksiyomlarini ortaya atmistir Bu gelisme bilim camiasi tarafindan cabucak hic karsi cikan kuram olmadan modern olasilik teorisinin ana olarak benimsenmistir IncelemeOlasilik teorisine girislerin cogunda ayrik olasilik dagilimlari ve surekli olasilik dagilimlari ayri ayri olarak incelemeye alinmaktadir Halbuki olasiligin daha ileri matematiksel yaklasimla incelenmesinin hem ayrik hem surekli ve hem de bunlarin karisigi ve daha ilerisinde olan dagilimlarin hep birlikte yapilmasini gerektirmektedir Ayrik olasilik dagilimlari Ayrik olasilik teorisi orneklem uzayinda ortaya cikan olaylari inceler Ornegin Zar atilmasi kup deneyleri cekmek veya rastgele yuruyus olaylari Klasik tanim Olasilik teorisi gelistirilmesinin ilk safhalarinda belirtilmis bir olay ortaya cikmasi icin olasilik her mumkun sonucu esit olasilikli olan orneklem uzayinda incelendigi kabul edilmis ve incelenen olaya uygun sonuc sayisinin toplam tum sonuclar sayisina orani olarak tanimlanmisti Ornegin incelenecek sorun tek bir zar atilinca cift sayilarin gelme olasiligi nedir seklinde sorulursun Zar yansiz olup her alti yuzu de esit olasilikla gelebilecegi icin 2 4 6 sonuclari 3 tane oldugu ve toplam mumkun sonuc sayisi 6 yuze dayanarak 6 oldugu icin aranan olasilik P 2 veya 4 veya 6 36 12 displaystyle tfrac 3 6 tfrac 1 2 olarak bulunur Modern tanim Modern tanima orneklem uzayi adi verilen bir kume ile baslanir bu klasik tanimda kullanilan mumkun tum sonuclar seti ile ayni anlamlidir ve su notasyon kullanilarak ifade edilir W x1 x2 displaystyle Omega left x 1 x 2 dots right Sonra x W displaystyle x in Omega icinde bulunan her bir olasilik degeri f x displaystyle f x bagli oldugu varsayilir ve bu olasilik degerinde su ozelliklerin bulundugu kabul edilir f x 0 1 butun x W displaystyle f x in 0 1 mbox butun x in Omega x Wf x 1 displaystyle sum x in Omega f x 1 Bu demektir ki olasilik fonksiyonu olan f x W orneklem uzayinda bulunan her x degeri icin 0 ile 1 arasinda bulunmaktadir ve x icin tum mumkun degerler icin f x degerlerinin toplami tama tam 1 e esit olur Bir olay W displaystyle Omega orneklem uzayinin herhangi bir E displaystyle E altseti olarak tanimlanir E displaystyle E olayinin olasilik degeri ise soyle tanimlanir P E x Ef x displaystyle P E sum x in E f x Buna gore tum orneklem uzayinin olasiligi 1e esittir ve bos orneklem uzayi veya 0 olay icin de olasilik 0a esit olur Ornekleme uzayindaki bir noktayi olasilik degerine esleyen fonksiyona yani f x displaystyle f x fonksiyonuna olasilik kutle fonksiyonu adi verilir Modern tanim olasilik kutle fonksiyonunun nasil ortaya ciktigini aciklayan bir kuram yaratmaz sadece bu fonksiyonlarin varoldugunu kabul eden bir kuram ortaya cikartir Surekli olasilik dagilimlari Surekli olasilik teorisi surekli orneklem uzayinda ortaya cikan olaylari inceler Klasik tanim Surekli olasilik halleri ile karsilasinca klasik tanim gecerli olmaz maddesine bakin Modern tanim Eger orneklem uzayi reel sayilardan olusursa yani R displaystyle mathbb R yigmali dagilim fonksiyonu adi verilen bir fonsksiyonun var oldugu kabul edilir bu bir rassal degisken olan X icin P X le x F x lt math gt ifadesini gosterir yani P X le x F x lt math gt rassal degiskenin X x sayi degerine esit veya xden daha dusuk olmasi halindeki olasiligi gosterir Yigmali dagilim fonksiyonu su ozellikleri gostermelidir F displaystyle F bir fonksiyondur limx F x 0 displaystyle lim x rightarrow infty F x 0 limx F x 1 displaystyle lim x rightarrow infty F x 1 Eger F displaystyle F fonksiyonun turevi alinabilirse rassal degisken X icin bir olasilik yogunluk fonksiyonu f x dF x dx displaystyle f x frac dF x dx bulunur E R displaystyle E subseteq mathbb R seti icin rassal degisken Xin E displaystyle E seti icinde bulunma olasiligi soyle tanimlanir P X E x EdF x displaystyle P X in E int x in E dF x Eger bir olasilik yogunluk fonksiyonu var ise bu soyle ifade edilebilir P X E x Ef x dx displaystyle P X in E int x in E f x dx Olasilik yogunluk fonksiyonu sadece surekli rassal degiskenler icin var olmakta ise de yigmali dagilim fonksiyonu R displaystyle mathbb R icinde degerleri olan aralikli rassal degiskenler dahil tum rassal degisken icin mevcut bulunmaktadir Bu kavramlar Rn displaystyle mathbb R n ve diger surekli orneklem uzaylari icin hallere de genellestirilmistir Olcum kuramsal olasilik teorisi Modern olasilik teorisi yaklasimi kullanilmasi suretiyle yapilmakta ve bu kuram olasilik uzayinda Kolmogorov aksiyomlarina dayandirilmaktadir Olasilik uzayi uc kisimdan olusmustur Olasiligin bu olcum teorisine gore uygulanmasinin esas nedeni bu teorisin ayrik ve surekli degiskenleri birlikte ele alabilmesinden ve aralarindaki farklari kullanilan olcu ile aciklamasindandir Bundan baska saf ayrik veya saf surekli dagilimlar yaninda bu iki kategoriye tam uymayan dagilimlari da inceleme imkani saglamaktadir Herhangi bir set W displaystyle Omega verilsin ve bu orneklem uzayi olarak da anilmaktadir Bu set uzerinde bir ile F displaystyle mathcal F bulunsun bir olcum P displaystyle P nin bir olasilik olcumu olarak adlandirmasi ancak ve ancak su kosullar altinda mumkun olur P displaystyle P non negatifdir P W 1 displaystyle P Omega 1 Eger F displaystyle mathcal F bir ise o halde herhangi bir yigmali dagilim fonksiyonu F displaystyle mathcal F uzerinde tek ve tek bir olasilik olcumu bulunur ve bunun aksi onerim de dogrudur Bu olcum ayrik degiskenler icin olasilik kutle fonksiyonu ve surekli degiskenler icin olasilik yogunluk fonksiyonu ile cakismaktadir ve boylece olcum teorisine bagli yaklasim yaniltici mantiktan uzaklastirmaktadir s cebiri F displaystyle mathcal F icinde E displaystyle E seti icin olasilik soyle tanimlanir P X E x EdF x displaystyle P X in E int x in E dF x Burada entegrasyon F displaystyle F tarafindan ortaya cikartilan olcuye goredir Temel PrensiplerBelirli bir olay A icin olasilik P A displaystyle textstyle mathbb P A 0 ile 1 arasinda degisen bir sayi ile temsil edilir Hic olanaksiz bir olay icin olasilik 0 olur ve kesinlikle olacak bir olayin olasiligi 1 olur Bazi istatistikciler bu ucsal olasilik degerlerinin sadece teorik oldugunu iddia etmektedirler cunku kabul ettikleri deneylemelerle limitte goresel cokluluk relatif frekans degerine dayanir Diger Bayes tipi ozellikle subjektif gore bu ucsal olasilik degerlerini subjektif olarak dusunmek ve olaylara bu degerleri koymak imkan dahilindedir Bazi temel ozellikler Olay OlasilikA olayi olmasi icin olasilik P A 0 1 displaystyle mathbb P A in 0 1 A olayi olmamasi icin olasilik P Ac 1 P A displaystyle mathbb P A c 1 mathbb P A A veya B olmasi icin olasilik P A B P A P B P A B displaystyle begin aligned mathbb P A cup B amp mathbb P A mathbb P B mathbb P A cap B end aligned A ve B olmasi icin olasilik P A B P A B P B P A P B eger A ve B bagimsizlarsa displaystyle begin aligned mathbb P A cap B amp mathbb P A B mathbb P B amp mathbb P A mathbb P B qquad mbox eger A ve B bagimsizlarsa end aligned A verilmis B olmasi B kosullu A P A B P A B P B displaystyle mathbb P A B frac mathbb P A cap B mathbb P B Olasilik dagilimlariBazi rassal degiskenler olasilik teorisi icinde daha sik olarak isimleri gecmektedir cunku bu degiskenler bircok dogal veya fiziksel surecleri belirlemektedirler veya ozellikle cikarimsal istatistikte cok oneme haizdirler Bunun icin bu tur degiskenler icin olasilik dagilimlari olasilik teorisi icinde ozel onem tasimaktadirlar Temel ayrik olasilik dagilimlari listesi soyle verilebilir Ayrik tekduze dagilim Bernoulli dagilimi Binom dagilimi Negatif binom dagilimi Poisson dagilimi Geometrik dagilim Hipergeometrik dagilim Temel surekli olasilik dagilimlari listesi soyle verilebilir Surekli tekduze dagilim Normal dagilim Student in t dagilimi F dagilimi Ki kare dagilimi Ustel dagilim Beta dagilimi Gamma dagilimiRassal degiskenlerin yakinsamasiOlasilik teorisi icinde rassal degiskenler in yakinsama kavrami birkac degisik sekilde tanimlanir Asagidaki listede bu degisik tanimlar tanimin gecerlilik gucune gore siralanmistir Bu siralamaya gore siranin icindeki herhangi bir tanim daha once verilmis olan tum tanimlari da icinde kapsamaktadir Dagilim icinde yakinsama Bir seri rassal degisken olan X1 X2 displaystyle X 1 X 2 dots X displaystyle X rassal degiskenine dagilim icinde yakinsama gostermesi ancak her bir X i rassal degiskeni icin yigmali dagilim fonksiyonu olan F1 F2 displaystyle F 1 F 2 dots fonksiyonlarinin X displaystyle X in yigmali dagilim fonksiyonu olan F displaystyle F ye yakinsama gostermesi halinde ortaya cikar Burada F displaystyle F surekli bir fonksiyondur En iyi bilinir kisaltilmis notasyon ile Xn DX displaystyle X n xrightarrow mathcal D X dd Zayif yakinsama Bir seri rassal degisken olan X1 X2 displaystyle X 1 X 2 dots X displaystyle X rassal degiskenine zayif yakinsama gosterirlerse her e gt 0 icinlimn P Xn X e 0 displaystyle lim n rightarrow infty P left left X n X right geq varepsilon right 0 olur Zayif yakinsama olasilik icinde yakinsama olarak da bilinmektedir En iyi bilinir kisaltilmis notasyon ile Xn PX displaystyle X n xrightarrow P X dd Guclu yakinsama Bir seri rassal degisken olan X1 X2 displaystyle X 1 X 2 dots X displaystyle X rassal degiskenine guclu yakinsama gosterirlerseP limn Xn X 1 displaystyle P lim n rightarrow infty X n X 1 ifadesi gerceklesir Guclu yakinsama hemen hemen kesinlikle yakinsama olarak da isimlendirilir En iyi bilinir kisaltilmis notasyon ile Xn a s X displaystyle X n xrightarrow mathrm a s X dd Guclu yakinsamanin bir zayif yakinsamanin daha guclu bir sekli oldugu gerceginin sezilmesi kolaydir ve her iki halde de rassal degiskenler X1 X2 displaystyle X 1 X 2 dots X displaystyle X ile artan bir korelasyon gostermektedirler Ancak dagilim icin yakinsama halinde rasssal degiskenlerin gerceklesen degerlerinin gercekte yakinsama gostermeleri gerekli degildir ve bunlarin arasindaki herhangi bir korelasyonun hicbir pratik onemi bulunmaz Buyuk sayilar yasasiYaygin olan bir sezgiye gore eger yansiz olan bir madeni para birkac kere havaya atilip yazi tura sonuclari kayit edilirse sonuclarin kabaca yarisi yazi olacak ve kalan yarisi da tura olacaktir Ustelik madeni parayi daha da cok defa havaya atip sonuc kayit edildikce giderek yazi sonuclari sayisinin tura sonuclari sayisina oraninin gittikce daha cok bire yaklastigi gozumlenecektir Bu sezgi ile gelistirilen bu dusunce prensibine istatistik bilimde daha formel bir sekil verilmekte ve bunu buyuk sayilar yasasi olarak isimlendirilmektedir Bu dikkate degerdir cunku bu yasa olasilik teorisinin hicbir yerinde bu teorisin temel tasdir seklinde bir bahis gormemektedir fakat bu yasa olasilik teorisi temelinden bir teorem olarak gelistirilip ortaya cikarilmaktadir Bununla beraber teorik olarak elde edilen olasiliklari pratik reel hallerde gercek olarak ortaya cikan cokluklara frekanslara bagladigi icin bu yasa istatistik teorisinin tarihinin icinde cok onemli bir orta direk tasi olarak kabul edilmektedir Buyuk sayilar yasasina gore orneklem ortalamasi yani bagimsiz ve birbiri ile sonsuz olmayan beklenen degeri m displaystyle mu olan ayni bir dagilim gosteren rassal degiskenler limitte teorik beklenen degere yani m displaystyle mu ya yaklasilik gosterirler gosterdikleri degisik sekillere gore bu yasa iki sekilde matematik olarak ifade edilebilir Guclu yasa X n a s mforn displaystyle overline X n xrightarrow mathrm a s mu qquad textrm for qquad n to infty Zayif yasa X n Pmforn displaystyle overline X n xrightarrow P mu qquad textrm for qquad n to infty Ayrica bakinizIstatistiksel bagimsizlik Istatistiksel terimler kavramlar ve konular listesi Olasilik teorisi ve mantik bilesimiKaynakca Probability theory Encyclopaedia Britannica 15 Nisan 2008 tarihinde kaynagindan Erisim tarihi 18 Nisan 2008 Broemeling Lyle D 1 Kasim 2011 An Account of Early Statistical Inference in Arab Cryptology The American Statistician 65 4 ss 255 257 doi 10 1198 tas 2011 10191 PDF 5 Subat 2012 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 18 Nisan 2008 26 Ocak 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 18 Nisan 2008 BibliyografyaBillingsley P 1995 Probability and Measure 3ncu ed John Wiley New York Gut A 2005 Probability A Graduate Course Springer Verlag ISBN 0 387 22833 0 Jeffreys H 1939 The Theory of Probability Kolmogorov A N 1933 Grundbegriffe der Wahrscheinlichkeitrechnung Laplace P S 1812 Theorie Analytique des Probabilites Nelson E 1987 Radically Elementary Probability Theory
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans