Niccolò Fontana Tartaglia (İtalyanca telaffuz: ; 1499/1500 - 13 Aralık 1557), o zamanki Venedik Cumhuriyetinden (şimdi İtalya'nın bir parçası) İtalyan bir matematikçi, (tahkimatlar tasarlayan) bir mühendis, (topoğrafya, en iyi savunma veya saldırı araçlarını arayan) bir haritacı ve bir muhasebeciydi. Arşimet ve Öklid'in ilk İtalyanca çevirileri ve beğenilen bir matematik derlemesi de dahil olmak üzere birçok kitap yayınladı. Tartaglia, Nova Scientia (Yeni Bir Bilim, 1537) adlı eserinde balistik olarak bilinen top güllelerinin yollarının araştırılmasına matematiği uygulayan ilk kişiydi; çalışmaları daha sonra kısmen doğrulandı ve Galileo'nun düşen cisimler üzerindeki çalışmaları tarafından kısmen değiştirildi. Ayrıca batık gemilerin kurtarılması üzerine bir inceleme yayınladı.
Niccolò Fontana Tartaglia | |
|---|---|
 | |
| Doğum | Niccolò Fontana 1499/1500 Brescia, Lombardiya, Kuzey İtalya |
| Ölüm | 13 Aralık 1557 (58 yaşında) Venedik, Kuzeydoğu İtalya |
| Milliyet | İtalyan |
| Vatandaşlık | Venedik Cumhuriyeti |
| Tanınma nedeni |
|
| Kariyeri | |
| Dalı | Matematik, mühendislik |
| Önemli öğrencileri | , |
Kişisel yaşamı
Niccolò Fontana, Brescia'da, komşu kasabalara posta dağıtmak için seyahat eden bir sevk memuru olan Michele Fontana'nın oğlu olarak doğdu. 1506'da Michele, soyguncular tarafından öldürüldü ve iki kardeşi, Niccolò ve annesi yoksul kaldı. Niccolò, 1512'de Kral XII. Louis'in birlikleri sırasında Venedik'e karşı Brescia'yı işgal ettiğinde daha fazla trajedi yaşadı. Brescia milisleri şehirlerini yedi gün boyunca savundu. Fransızlar nihayet sızdığında, Brescia sakinlerini katlederek intikamlarını aldılar. Savaşın sonunda 45.000'den fazla kişi öldü. Katliam sırasında, Niccolò ve ailesi yerel katedralde sığınak aradılar. Ama Fransızlar içeri girdi ve bir asker Niccolò'nun çenesini ve damağını bir kılıçla kesti ve onu ölüme terk etti. Annesi onu sağlığına kavuşturdu, ancak genç çocuk bir konuşma engeli ile kaldı ve "Tartaglia" ("kekeme") takma adını aldı. Bundan sonra asla tıraş olmaz ve yaralarını kamufle etmek için sakal bırakırdı.
Tartaglia'nın biyografisini yazan Arnoldo Masotti şöyle yazıyor:
| “ | Yaklaşık on dört yaşında, [Tartaglia] alfabeyi yazmayı öğrenmek için bir Usta Francesco'ya gitti; ancak “k” ye ulaştığında artık öğretmene ödeme yapamaz hale geldi. Daha sonra hareketli bir otobiyografik eskizde, “O günden sonra, asla bir öğretmene geri dönmedim, ancak yalnızca endüstri denilen yoksulluğun kızıyla birlikte ölü adamların işleri üzerinde kendi başıma çalışmaya devam ettim” ” diye yazdı. (Quesiti, bk. VI, question 8) | „ |
Tartaglia, 1517 civarında Verona'ya, ardından 1534'te büyük bir Avrupa ticaret merkezi ve o dönemde İtalyan rönesansının en büyük merkezlerinden biri olan Venedik'e taşındı. Venedik'in on altıncı yüzyılda Avrupa matbaacılık kültürünün ön saflarındaki yeri de konuyla ilgilidir; yeterince motive olmuş veya iyi bağlantıları varsa, erken basılmış metinleri fakir bilim insanlarına bile erişilebilir kılar -örneğin Tartaglia, Arşimet'in parabolün karesi üzerindeki çalışmasını biliyordu, Guarico'nun "1531'de Verona'da bir sosis satıcısının elinde" bulduğu 1503 tarihli Latince baskısından (kendi sözleriyle "in mano di un salzizaro in Verona, l'anno 1531").
Tartaglia, 'nda pratik matematik öğreterek geçimini sağladı ve yapabildiğinde para kazandı:
| “ | Bu olağanüstü adam [Tartaglia], topçulara ve mimarlara matematiksel tavsiyeler, on peniye bir soru satan ve kendisine Öklid üzerine verdiği dersler için ödeme yerine yıpranmış bir pelerin verdiklerinde üzerinde mütabakata varmak yerine müşterilerine dava açmak zorunda kalan, kendi kendini yetiştirmiş bir matematik öğretmeniydi. | „ |
Venedik'te öldü.
Balistik

Matteo Valleriani tarafından aşağıdaki gibi tarif edilen Nova Scientia (1537), Tartaglia'nın ilk yayınlanmış eseriydi:
| “ | .. Rönesans mekaniği üzerine en temel çalışmalardan biri, aslında, erken modern topçular tarafından biriktirilen pratik bilginin yönünü teorik "ve" matematiksel bir çerçeveye dönüştüren ilk kişi. | „ |
Daha sonra baskın Aristoteles fiziği, hareketi tanımlamak için genellikle matematiksel açıklamalardan kaçınarak "ağır" ve "doğal" ve "şiddetli" gibi kategorileri tercih etti. Tartaglia, Mary J. Henninger-Voss'un sözleriyle "Aristotelesçi mermi hareketi terimlerini içini boşaltan" matematiksel modelleri ön plana çıkardı. Bulgularından biri, bir merminin maksimum menzilinin, topu ufka 45°'lik bir açıyla yönlendirerek elde edilmesiydi.
Tartaglia'nın top güllesinin uçuş modeli, toptan düz bir çizgide ilerlemesi, sonra bir süre sonra dairesel bir yol boyunca dünyaya doğru kavis çizmeye başlaması ve sonunda doğrudan dünyaya doğru başka bir düz çizgide düşmesiydi. "Nova Scientia" adlı eserin 2. kitabının sonunda, Tartaglia, Öklid tarzı bir argümanla meşgul olan, 45° yükseklikte ateşlenen bir mermi için bu ilk doğrusal yolun uzunluğunu bulmayı önerir, ama doğru parçalarına ve alanlarına sayılar eklenmiş ve sonunda istenen miktarı bulmak için cebirsel olarak ilerler (onun deyimiyle procederemo per algebra).
Mary J. Henninger-Voss, "Tartaglia'nın askeri bilim üzerine çalışmasının Avrupa'da muazzam bir sirkülasyona sahip olduğunu" ve bazen atıf yapılmayan çeviriler yoluyla on sekizinci yüzyıla sıradan topçular için bir referans olduğunu belirtiyor. Mermi problemini bir kez ve herkes için çözmeye koyulurken, balistik konusundaki çalışmalarının "zengin açıklamalı" kopyalarına sahip olan Galileo'yu da etkiledi.
Çeviriler
Arşimet'in çalışmaları, Tartaglia'nın zamanında, matematiğin fiziği anlamanın anahtarı olduğu fikrinin bir örneği olarak üniversitelerin dışında incelenmeye başlandı, 1558'de şunu söylerken bu fikri yansıttı: "Geometri konusunda aklı başında hiç kimse Arşimet'in biraz tanrı olduğunu inkar edemez." Tartaglia, 1543'te Arşimet'in parabol, daire, ağırlık merkezleri ve yüzen cisimler üzerindeki çalışmalarının 71 sayfalık Latince baskısını içeren Opera Archimedis Syracusani philosophi et mathematici ingeniosissimi adlı eseri yayınladı. Guarico, 1503'te ilk ikisinin Latince baskılarını yayınlamıştı, ancak ağırlık merkezleri ve yüzen cisimler üzerindeki çalışmalar daha önce yayınlanmamıştı. Tartaglia, bazı Arşimet metinlerinin İtalyanca versiyonlarını daha sonraki yaşamında yayınladı, vasisi ölümünden sonra çevirilerini yayınlamaya devam etti. Galileo, muhtemelen Arşimet'in çalışmalarını bu geniş çapta dağıtılan baskılar aracılığıyla öğrendi.
Tartaglia'nın Öklid'in 1543'teki İtalyanca baskısı, Euclide Megarense philosopho özellikle önemliydi. Öklid'in Elementlerinin herhangi bir modern Avrupa diline ilk çevirisidir. İki yüzyıl boyunca Öklid, Arapça bir kaynaktan alınan iki Latin çeviriden öğrenilmişti; bunlar Kitap V'de, Eudoxian orantı teorisini kullanılamaz hale getiren hatalar içeriyordu. Tartaglia'nın baskısı, 'nin bozulmamış bir Yunanca metnin Latince çevirisine dayanıyordu ve Kitap V'i doğru bir şekilde yorumladı. Ayrıca teori üzerine ilk modern ve faydalı yorumu yazdı. Bu çalışma on altıncı yüzyılda birçok baskıdan geçti ve matematik bilgisinin İtalya'da akademik olmayan ancak giderek daha iyi bilgilendirilmiş okur-yazar ve sayısal bilgili bir halka yayılmasına yardımcı oldu. Teori, Arşimet için olduğu gibi Galileo için de temel bir araç haline geldi.
General Trattato di Numeri et Misure

Tartaglia, onikinci yüzyıldan beri İtalya'da gelişen ve tüccar topluluklar tarafından sürdürülen öğretilen somut bir ticari matematik geleneği olan abacco geleneğini temsil etti ve sonunda aştı. Tartaglia gibi Maestros d'abaco, abaküsle değil, kağıt kalemle, bugün ilkokullarda bulunan türden algoritmalar aşılayarak öğretiyordu.
Tartaglia'nın başyapıtı General Trattato di Numeri et Missure (İngilizce: General Treatise on Number and Measure,Türkçe: Sayı ve Ölçü Üzerine Genel İnceleme), altı bölümden oluşan 1500 sayfalık bir ansiklopediydi. Venedik lehçesinde, ilk üçü Tartaglia'nın ölümüyle ilgili olarak 1556'da çıktı ve son üçü, edebi vasisi ve yayıncısı Curtio Troiano tarafından 1560'ta ölümünden sonra yayınlandı. David Eugene Smith, "General Trattato" hakkında şunları yazdı:
| “ | İtalyan aritmetikçilerinin sayısal işlemleri ve ticari kurallarının çok kapsamlı bir tartışmasını içeren, kendi yüzyılında İtalya'da ortaya çıkan en iyi aritmetik incelemesi. 16. yüzyılda halkın hayatı, tüccarların örf ve adetleri, aritmetiği geliştirme çabaları bu dikkate değer eserde anlatılmaktadır. | „ |
Bölüm I, 554 sayfa uzunluğundadır ve günün karmaşık para birimleri (ducat, soldi, pizolli vb.) ile temel işlemler, döviz alışverişi, faiz hesaplama ve anonim şirketlerde kârları bölüştürme gibi konuları ele alan esasen ticari bir aritmetik oluşturur. Kitap, yöntem ve kurallara (yani, algoritmalara) çok önem veren, hepsi sanal olarak olduğu gibi kullanıma hazır, çalışılmış örneklerle doludur.
Bölüm II, ilerlemeler, kuvvetler, iki terimli açılımlar, Tartaglia üçgeni ("Pascal üçgeni" olarak da bilinir), köklerle hesaplamalar ve oranlar / kesirler dahil olmak üzere daha genel aritmetik problemlerini ele alır.
Bölüm IV, üçgenler, düzgün çokgenler, Platonik katılar ile daireyi kareyle çevreleme ve bir kürenin etrafında bir silindirin çevrelenmesi gibi Arşimet konuları ile ilgilidir.
Tartaglia üçgeni

Tartaglia, iki terimli açılımlar konusunda uzmandı ve General Trattatonun II. bölümünde pek çok çalışılmış örnek içeriyordu; bunlardan biri, uygun ile 
Tartaglia, General Trattatodan alınan bu resimde gösterildiği gibi, Pascal üçgeni'ni Pascal'dan yüz yıl önce biliyordu. Örnekleri sayısaldır, ancak bunu geometrik olarak düşünür, üçgenin tepesindeki yatay 


Kübik denklemlerin çözümü
Tartaglia belki de bugün en çok Gerolamo Cardano ile olan çatışmalarıyla tanınıyor. 1539'da Cardano, Tartaglia'yı kübik denklemlere yönelik çözümünü, onları yayınlamamaya söz vererek açıklamaya ikna etti. Tartaglia, kübik denklemin üç farklı formunun çözümlerinin sırlarını manzum olarak ifşa etmiştir. Birkaç yıl sonra Cardano, bağımsız olarak Tartaglia ile aynı çözümü bulan Scipione del Ferro'nun yayınlanmamış çalışmasını gördü. Yayımlanmamış eser Tartaglia'nınkinden daha eski olduğundan, Cardano sözünün tutulmayabileceğine karar verdi ve bir sonraki yayınına Tartaglia'nın çözümünü dahil etti. Cardano keşfine inansa da, Tartaglia son derece üzgündü ve kendisi ile Cardano'nun öğrencisi arasında ünlü bir meydan okuma maçı yaşandı. Tartaglia'nın hayatının geri kalanını Cardano'yu mahvetmeye adadığı yaygın hikâyeler tamamen uydurma gibi görünmektedir. Matematik tarihçileri şimdi hem Cardano hem de Tartaglia'yı kübik denklemleri çözme formülüyle "" olarak adlandırıyorlar.
Bir tetrahedronun hacmi

Tartaglia, olağanüstü bir hesap makinesi ve katı geometri ustasıydı. General Trattatonun IV. bölümünde, üçgen bir taban, yani düzensiz bir tetrahedron üzerindeki bir piramidin yüksekliğinin nasıl hesaplanacağını örnekle gösterir.
Piramidin tabanı, kenarları 
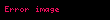
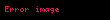




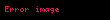

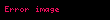
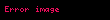


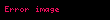



Kosinüs yasası'ndan türetilen bir formüldür. (General Trattatonun bu bölümünde herhangi bir gerekçe göstermiyor.).
Tartaglia, 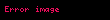

Piramidin hacmi bundan sonra kolayca elde edilir (Tartaglia'nın verdiğinden değil):
, daha sonra on altıncı yüzyılda icat etti, bu nedenle son rakam her zaman kesirleri kullanan Tartaglia'ya yabancı oldu. Yine de, yaklaşımı bazı yönlerden moderndir, örnek olarak düzensiz dörtyüzlülerin çoğunun veya tamamının yüksekliğini hesaplamak için bir algoritma önerir, ancak (onun için her zaman olduğu gibi) açık bir formül vermez.
Notlar
- ^ (1978), Galileo at Work: His Scientific Biography, Dover, s. 3
- ^ Strathern 2013, s.189
- ^ Masotti, Arnoldo, "Niccolò Tartaglia", Dictionary of Scientific Biography, 25 Kasım 2020 tarihinde kaynağından , erişim tarihi: 29 Temmuz 2021
- ^ Tartaglia, Niccolò. Part IV"General Trattato di Numeri et Misure". Book 3. s. 43v. 28 Temmuz 2021 tarihinde kaynağından . Erişim tarihi: 28 Temmuz 2021.
Sosis satıcısı için bakınız.
- ^ Zilsel, Edgar, The Social Origins of Modern Science, s. 35
- ^ Valleriani, Matteo (2013). . s. 1. 16 Aralık 2016 tarihinde kaynağından arşivlendi.
- ^ Henninger-Voss, Mary J. (Temmuz 2002), ""How the 'New Science' of Cannons Shook up the Aristotelian Cosmos"", Journal of the History of Ideas, 63 (3), ss. 371-397,
"eviscerated": s.376
- ^ Valleriani, Matteo (2013), Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia, ss. 169-181, 15 Ağustos 2020 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Valleriani, Matteo (2013), Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia, ss. 176-177, 26 Eylül 2020 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Henninger-Voss, Mary J. (Temmuz 2002), ""How the 'New Science' of Cannons Shook up the Aristotelian Cosmos"", Journal of the History of Ideas, 63 (3), ss. 391-393,
Tartışma ve alıntılar için bakınız.
- ^ Clagett, Marshall, "William of Moerbeke: Translator of Archimedes", ss. 356-366
- ^ Archimedes; Tartaglia, Niccolo (1543), Opera Archimedis Syracvsani philosophi et mathematici ingeniosissimi, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 13 Nisan 2022
- ^ Henninger-Voss, Mary J., "'New Science' of Cannons", s. 392
- ^ "Ruffinelli, Venturino, Guglielmo da Fontaneto & Facolo, Pietro & Tartaglia, Niccolò, Gesuiti : Casa Professa : Biblioteca, Gesuiti : Collegio Romano, Collegio di San Francesco di Paola : Biblioteca", Euclide megarense philosopho: solo introduttore delle scientie mathematice: diligentemente reassettato, et alla integrita ridotto per il degno professore di tal scientie Nicolo Tartalea, brisciano, secondo le due tradottioni: e per commune commodo & vtilita di latino in volgar tradotto. con vna ampla espositione dello istesso tradottore di nouo aggionta., Roma Ulusal Merkez Kütüphanesi, 1543, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Bakınız Malet, Antoni, "Euclid's Swan Song: Euclid's Elements in Early Modern Europe", burada Tartaglia'nın Öklid üzerine çalışması "matematiksel olarak ikna edici, yenilikçi ve etkili" olarak tanımlanıyor." (s. 207).
- ^ Tartaglia, Niccolò, 1556-1560
- ^ Smith 1985, s.298.
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part I, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part II, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part IV, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part II, Book 2, s. 51v, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021,
'yi genişletmek için bakınız.
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part II, Book 2, s. 72, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021,
"Pascal üçgeni"ndeki toplama kuralının tartışması için bakınız.
- ^ Katz 1998, s.359
- ^ , Cardano v Tartaglia: The Great Feud Goes Supernatural (PDF), 29 Eylül 2020 tarihinde kaynağından (PDF), erişim tarihi: 28 Temmuz 2021
- ^ Tartaglia, Niccolò, General Trattato di Numeri et Misure, Part IV, Book 2, s. 35r, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021,
13-14-15-20-18-16 piramidinin yüksekliğinin hesaplanması için bakınız.
Kaynakça
![image]() Chisholm, Hugh, (Ed.) (1911). "Tartaglia, Niccolò". Encyclopædia Britannica. 26 (11. bas.). Cambridge University Press.
Chisholm, Hugh, (Ed.) (1911). "Tartaglia, Niccolò". Encyclopædia Britannica. 26 (11. bas.). Cambridge University Press.- Clagett, Marshall (1982). "William of Moerbeke: Translator of Archimedes". Proceedings of the American Philosophical Society. 126 (5): 356-366..
- Henninger-Voss, Mary J. (Temmuz 2002). "How the 'New Science' of Cannons Shook up the Aristotelian Cosmos". Journal of the History of Ideas. 63 (3): 371-397. doi:10.1353/jhi.2002.0029.
![image]() Herbermann, Charles, (Ed.) (1913). "Nicolò Tartaglia". Katolik Ansiklopedi (İngilizce). New York: Robert Appleton Company.
Herbermann, Charles, (Ed.) (1913). "Nicolò Tartaglia". Katolik Ansiklopedi (İngilizce). New York: Robert Appleton Company.- Charles Hutton (1815). "Tartaglia or Tartaglia (Nicholas)". A philosophical and mathematical dictionary. Printed for the author. s. 482.
- Katz, Victor J. (1998), A History of Mathematics: An Introduction, Reading, Addison Wesley Longman, ISBN .
- Malet, Antoni (2012). "Euclid's Swan Song: Euclid's Elements in Early Modern Europe". Olmos, Paula (Ed.). Greek Science in the Long Run: Essays on the Greek Scientific Tradition (4th c. BCE-17th c. CE). Cambridge Scholars Publishing. ss. 205-234. ISBN ..
- Masotti, Arnoldo (1970). "Niccolò Tartaglia". Gillispie, Charles (Ed.). Dictionary of Scientific Biography. New York: Scribner & American Council of Learned Societies.
- Smith, D.E. (1958), History of Mathematics, I, New York: Dover Publications, ISBN .
- Strathern, Paul (2013), Venetians, New York, NY: Pegasus Books.
- Tartaglia, Niccolò (1543). Opera Archimedis Syracusani philosophi et mathematici ingeniosissimi. Venedik. 28 Temmuz 2021 tarihinde kaynağından . Erişim tarihi: 13 Nisan 2022.
- Tartaglia, Niccolò (1543). Euclide Megarense philosopho. Venedik. 28 Temmuz 2021 tarihinde kaynağından . Erişim tarihi: 28 Temmuz 2021.
- Tartaglia, Niccolò (1556–1560), General Trattato di Numeri et Misure, Venedik: Curtio Troiano.
- Valleriani, Matteo (2013), Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia, Berlin: Edition Open Access / Max Planck Research Library, ISBN .
- Zilsel, Edgar (2000), Raven, Diederick; Krohn, Wolfgang; Cohen, Robert S. (Ed.), The Social Origins of Modern Science, Springer Netherlands, ISBN .
Dış bağlantılar
- . 22 Ocak 2012 tarihinde kaynağından arşivlendi.
- . 6 Ekim 2013 tarihinde kaynağından arşivlendi.
- O'Connor, John J.; Robertson, Edmund F., "Niccolò Tartaglia", MacTutor Matematik Tarihi arşivi
- . MAA Convergence. 30 Eylül 2007 tarihinde kaynağından arşivlendi.
- . Venedik. 1550. 3 Ocak 2018 tarihinde kaynağından arşivlendi.
- Tartaglia, Niccolò (1556), General Trattato di Numeri et Misure, Part I, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Tartaglia, Niccolò (1556), General Trattato di Numeri et Misure, Part II, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Tartaglia, Niccolò (1556), General Trattato di Numeri et Misure, Part III, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Tartaglia, Niccolò (1560), General Trattato di Numeri et Misure, Part IV, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Tartaglia, Niccolò (1560), General Trattato di Numeri et Misure, Part V, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Tartaglia, Niccolò (1560), General Trattato di Numeri et Misure, Part VI, Venedik, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Valleriani, Matteo, Metallurgy, Ballistics and Epistemic Instruments: The Nova scientia of Nicolò Tartaglia, 28 Temmuz 2021 tarihinde kaynağından , erişim tarihi: 28 Temmuz 2021
- Favaro, Antonio (1913), "PER LA BIOGRAFIA DI NICCOLÒ TARTAGLIA", Archivio Storico Italiano (İtalyanca), 71 (2 (270)), ss. 335-372, JSTOR 44458852
- Serafina Cuomo (1997), "Shooting by the Book: Notes on Niccolò Tartaglia's Nova Scientia", History of Science, 35 (2), ss. 155-188, doi:10.1177/007327539703500202
- Bernardoni A. (2015), Sgarbi M. (Ed.), "Tartaglia, NIccolò", Encyclopedia of Renaissance Philosophy, Springer, Cham., doi:10.1007/978-3-319-02848-4_81-1, ISBN
- Ricahrd W. Feldmann (Mart 1961), "The Cardano-Tartaglia Dispute" (PDF), The Mathematics Teacher, National Council of Teachers of Mathematics, 54 (3), ss. 160-163, JSTOR 27956338, 28 Temmuz 2021 tarihinde kaynağından (PDF), erişim tarihi: 28 Temmuz 2021
- Tony Rothman, Cardano v Tartaglia:The Great Feud Goes Supernatural (PDF), 29 Eylül 2020 tarihinde kaynağından (PDF), erişim tarihi: 28 Temmuz 2021
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Niccolo Fontana Tartaglia Italyanca telaffuz nikkoˈlɔ ffonˈtaːna tarˈtaʎʎa 1499 1500 13 Aralik 1557 o zamanki Venedik Cumhuriyetinden simdi Italya nin bir parcasi Italyan bir matematikci tahkimatlar tasarlayan bir muhendis topografya en iyi savunma veya saldiri araclarini arayan bir haritaci ve bir muhasebeciydi Arsimet ve Oklid in ilk Italyanca cevirileri ve begenilen bir matematik derlemesi de dahil olmak uzere bircok kitap yayinladi Tartaglia Nova Scientia Yeni Bir Bilim 1537 adli eserinde balistik olarak bilinen top gullelerinin yollarinin arastirilmasina matematigi uygulayan ilk kisiydi calismalari daha sonra kismen dogrulandi ve Galileo nun dusen cisimler uzerindeki calismalari tarafindan kismen degistirildi Ayrica batik gemilerin kurtarilmasi uzerine bir inceleme yayinladi Niccolo Fontana TartagliaDogumNiccolo Fontana 1499 1500 Brescia Lombardiya Kuzey ItalyaOlum13 Aralik 1557 58 yasinda Venedik Kuzeydogu ItalyaMilliyetItalyanVatandaslikVenedik CumhuriyetiTaninma nedeniBalistik ile ilgili erken donem arastirmalari Tartaglia ucgeniKariyeriDaliMatematik muhendislikOnemli ogrencileri Kisisel yasamiNiccolo Fontana Brescia da komsu kasabalara posta dagitmak icin seyahat eden bir sevk memuru olan Michele Fontana nin oglu olarak dogdu 1506 da Michele soyguncular tarafindan olduruldu ve iki kardesi Niccolo ve annesi yoksul kaldi Niccolo 1512 de Kral XII Louis in birlikleri sirasinda Venedik e karsi Brescia yi isgal ettiginde daha fazla trajedi yasadi Brescia milisleri sehirlerini yedi gun boyunca savundu Fransizlar nihayet sizdiginda Brescia sakinlerini katlederek intikamlarini aldilar Savasin sonunda 45 000 den fazla kisi oldu Katliam sirasinda Niccolo ve ailesi yerel katedralde siginak aradilar Ama Fransizlar iceri girdi ve bir asker Niccolo nun cenesini ve damagini bir kilicla kesti ve onu olume terk etti Annesi onu sagligina kavusturdu ancak genc cocuk bir konusma engeli ile kaldi ve Tartaglia kekeme takma adini aldi Bundan sonra asla tiras olmaz ve yaralarini kamufle etmek icin sakal birakirdi Tartaglia nin biyografisini yazan Arnoldo Masotti soyle yaziyor Yaklasik on dort yasinda Tartaglia alfabeyi yazmayi ogrenmek icin bir Usta Francesco ya gitti ancak k ye ulastiginda artik ogretmene odeme yapamaz hale geldi Daha sonra hareketli bir otobiyografik eskizde O gunden sonra asla bir ogretmene geri donmedim ancak yalnizca endustri denilen yoksullugun kiziyla birlikte olu adamlarin isleri uzerinde kendi basima calismaya devam ettim diye yazdi Quesiti bk VI question 8 Tartaglia 1517 civarinda Verona ya ardindan 1534 te buyuk bir Avrupa ticaret merkezi ve o donemde Italyan ronesansinin en buyuk merkezlerinden biri olan Venedik e tasindi Venedik in on altinci yuzyilda Avrupa matbaacilik kulturunun on saflarindaki yeri de konuyla ilgilidir yeterince motive olmus veya iyi baglantilari varsa erken basilmis metinleri fakir bilim insanlarina bile erisilebilir kilar ornegin Tartaglia Arsimet in parabolun karesi uzerindeki calismasini biliyordu Guarico nun 1531 de Verona da bir sosis saticisinin elinde buldugu 1503 tarihli Latince baskisindan kendi sozleriyle in mano di un salzizaro in Verona l anno 1531 Tartaglia nda pratik matematik ogreterek gecimini sagladi ve yapabildiginde para kazandi Bu olaganustu adam Tartaglia topculara ve mimarlara matematiksel tavsiyeler on peniye bir soru satan ve kendisine Oklid uzerine verdigi dersler icin odeme yerine yipranmis bir pelerin verdiklerinde uzerinde mutabakata varmak yerine musterilerine dava acmak zorunda kalan kendi kendini yetistirmis bir matematik ogretmeniydi Venedik te oldu BalistikNova Scientia 3 Agustos 2020 tarihinde Wayback Machine sitesinde dan cesitli mermi yorungeleri Matteo Valleriani tarafindan asagidaki gibi tarif edilen Nova Scientia 1537 Tartaglia nin ilk yayinlanmis eseriydi Ronesans mekanigi uzerine en temel calismalardan biri aslinda erken modern topcular tarafindan biriktirilen pratik bilginin yonunu teorik ve matematiksel bir cerceveye donusturen ilk kisi Daha sonra baskin Aristoteles fizigi hareketi tanimlamak icin genellikle matematiksel aciklamalardan kacinarak agir ve dogal ve siddetli gibi kategorileri tercih etti Tartaglia Mary J Henninger Voss un sozleriyle Aristotelesci mermi hareketi terimlerini icini bosaltan matematiksel modelleri on plana cikardi Bulgularindan biri bir merminin maksimum menzilinin topu ufka 45 lik bir aciyla yonlendirerek elde edilmesiydi Tartaglia nin top gullesinin ucus modeli toptan duz bir cizgide ilerlemesi sonra bir sure sonra dairesel bir yol boyunca dunyaya dogru kavis cizmeye baslamasi ve sonunda dogrudan dunyaya dogru baska bir duz cizgide dusmesiydi Nova Scientia adli eserin 2 kitabinin sonunda Tartaglia Oklid tarzi bir argumanla mesgul olan 45 yukseklikte ateslenen bir mermi icin bu ilk dogrusal yolun uzunlugunu bulmayi onerir ama dogru parcalarina ve alanlarina sayilar eklenmis ve sonunda istenen miktari bulmak icin cebirsel olarak ilerler onun deyimiyle procederemo per algebra Mary J Henninger Voss Tartaglia nin askeri bilim uzerine calismasinin Avrupa da muazzam bir sirkulasyona sahip oldugunu ve bazen atif yapilmayan ceviriler yoluyla on sekizinci yuzyila siradan topcular icin bir referans oldugunu belirtiyor Mermi problemini bir kez ve herkes icin cozmeye koyulurken balistik konusundaki calismalarinin zengin aciklamali kopyalarina sahip olan Galileo yu da etkiledi CevirilerArsimet in calismalari Tartaglia nin zamaninda matematigin fizigi anlamanin anahtari oldugu fikrinin bir ornegi olarak universitelerin disinda incelenmeye baslandi 1558 de sunu soylerken bu fikri yansitti Geometri konusunda akli basinda hic kimse Arsimet in biraz tanri oldugunu inkar edemez Tartaglia 1543 te Arsimet in parabol daire agirlik merkezleri ve yuzen cisimler uzerindeki calismalarinin 71 sayfalik Latince baskisini iceren Opera Archimedis Syracusani philosophi et mathematici ingeniosissimi adli eseri yayinladi Guarico 1503 te ilk ikisinin Latince baskilarini yayinlamisti ancak agirlik merkezleri ve yuzen cisimler uzerindeki calismalar daha once yayinlanmamisti Tartaglia bazi Arsimet metinlerinin Italyanca versiyonlarini daha sonraki yasaminda yayinladi vasisi olumunden sonra cevirilerini yayinlamaya devam etti Galileo muhtemelen Arsimet in calismalarini bu genis capta dagitilan baskilar araciligiyla ogrendi Tartaglia nin Oklid in 1543 teki Italyanca baskisi Euclide Megarense philosopho ozellikle onemliydi Oklid in Elementlerinin herhangi bir modern Avrupa diline ilk cevirisidir Iki yuzyil boyunca Oklid Arapca bir kaynaktan alinan iki Latin ceviriden ogrenilmisti bunlar Kitap V de Eudoxian oranti teorisini kullanilamaz hale getiren hatalar iceriyordu Tartaglia nin baskisi nin bozulmamis bir Yunanca metnin Latince cevirisine dayaniyordu ve Kitap V i dogru bir sekilde yorumladi Ayrica teori uzerine ilk modern ve faydali yorumu yazdi Bu calisma on altinci yuzyilda bircok baskidan gecti ve matematik bilgisinin Italya da akademik olmayan ancak giderek daha iyi bilgilendirilmis okur yazar ve sayisal bilgili bir halka yayilmasina yardimci oldu Teori Arsimet icin oldugu gibi Galileo icin de temel bir arac haline geldi General Trattato di Numeri et MisureGeneral trattato di numeri et misure 1556 Tartaglia onikinci yuzyildan beri Italya da gelisen ve tuccar topluluklar tarafindan surdurulen ogretilen somut bir ticari matematik gelenegi olan abacco gelenegini temsil etti ve sonunda asti Tartaglia gibi Maestros d abaco abakusle degil kagit kalemle bugun ilkokullarda bulunan turden algoritmalar asilayarak ogretiyordu Tartaglia nin basyapiti General Trattato di Numeri et Missure Ingilizce General Treatise on Number and Measure Turkce Sayi ve Olcu Uzerine Genel Inceleme alti bolumden olusan 1500 sayfalik bir ansiklopediydi Venedik lehcesinde ilk ucu Tartaglia nin olumuyle ilgili olarak 1556 da cikti ve son ucu edebi vasisi ve yayincisi Curtio Troiano tarafindan 1560 ta olumunden sonra yayinlandi David Eugene Smith General Trattato hakkinda sunlari yazdi Italyan aritmetikcilerinin sayisal islemleri ve ticari kurallarinin cok kapsamli bir tartismasini iceren kendi yuzyilinda Italya da ortaya cikan en iyi aritmetik incelemesi 16 yuzyilda halkin hayati tuccarlarin orf ve adetleri aritmetigi gelistirme cabalari bu dikkate deger eserde anlatilmaktadir Bolum I 554 sayfa uzunlugundadir ve gunun karmasik para birimleri ducat soldi pizolli vb ile temel islemler doviz alisverisi faiz hesaplama ve anonim sirketlerde karlari bolusturme gibi konulari ele alan esasen ticari bir aritmetik olusturur Kitap yontem ve kurallara yani algoritmalara cok onem veren hepsi sanal olarak oldugu gibi kullanima hazir calisilmis orneklerle doludur Bolum II ilerlemeler kuvvetler iki terimli acilimlar Tartaglia ucgeni Pascal ucgeni olarak da bilinir koklerle hesaplamalar ve oranlar kesirler dahil olmak uzere daha genel aritmetik problemlerini ele alir Bolum IV ucgenler duzgun cokgenler Platonik katilar ile daireyi kareyle cevreleme ve bir kurenin etrafinda bir silindirin cevrelenmesi gibi Arsimet konulari ile ilgilidir Tartaglia ucgeniGeneral Trattato di Numeri et Misure Bolum II Kitap 2 s 69 28 Temmuz 2021 tarihinde Wayback Machine sitesinde dan Tartaglia ucgeni Tartaglia iki terimli acilimlar konusunda uzmandi ve General Trattatonun II bolumunde pek cok calisilmis ornek iceriyordu bunlardan biri uygun ile 6 4 7 displaystyle 6 4 7 in toplamlarinin nasil hesaplanacagina dair ayrintili bir aciklamaydi Tartaglia General Trattatodan alinan bu resimde gosterildigi gibi Pascal ucgeni ni Pascal dan yuz yil once biliyordu Ornekleri sayisaldir ancak bunu geometrik olarak dusunur ucgenin tepesindeki yatay ab displaystyle ab dogrusu ac displaystyle ac ve cb displaystyle cb olarak iki bolume ayrilir burada c displaystyle c noktasi ucgenin tepe noktasidir Iki terimli acilimlar ucgende asagi inerken n 2 3 4 displaystyle n 2 3 4 cdots usleri icin ac cb n displaystyle ac cb n almak anlamina gelir Dis kisimdaki semboller cebirsel gosterimin bu erken asamasindaki kuvvetleri temsil eder ce 2 cu 3 ce ce 4 displaystyle ce 2 cu 3 ce ce 4 vb Toplamali olusum kurali hakkinda acikca yazmistir ornegin besinci siradaki bitisik 15 ve 20 nin toplami altinci sirada onlarin altinda gorunen 35 e kadar cikar Kubik denklemlerin cozumuTartaglia belki de bugun en cok Gerolamo Cardano ile olan catismalariyla taniniyor 1539 da Cardano Tartaglia yi kubik denklemlere yonelik cozumunu onlari yayinlamamaya soz vererek aciklamaya ikna etti Tartaglia kubik denklemin uc farkli formunun cozumlerinin sirlarini manzum olarak ifsa etmistir Birkac yil sonra Cardano bagimsiz olarak Tartaglia ile ayni cozumu bulan Scipione del Ferro nun yayinlanmamis calismasini gordu Yayimlanmamis eser Tartaglia ninkinden daha eski oldugundan Cardano sozunun tutulmayabilecegine karar verdi ve bir sonraki yayinina Tartaglia nin cozumunu dahil etti Cardano kesfine inansa da Tartaglia son derece uzgundu ve kendisi ile Cardano nun ogrencisi arasinda unlu bir meydan okuma maci yasandi Tartaglia nin hayatinin geri kalanini Cardano yu mahvetmeye adadigi yaygin hikayeler tamamen uydurma gibi gorunmektedir Matematik tarihcileri simdi hem Cardano hem de Tartaglia yi kubik denklemleri cozme formuluyle olarak adlandiriyorlar Bir tetrahedronun hacmiGeneral Trattato di Numeri et Misure Part IV Book 2 s 35 28 Temmuz 2021 tarihinde Wayback Machine sitesinde ten 13 14 15 20 18 16 piramidi Tartaglia olaganustu bir hesap makinesi ve kati geometri ustasiydi General Trattatonun IV bolumunde ucgen bir taban yani duzensiz bir tetrahedron uzerindeki bir piramidin yuksekliginin nasil hesaplanacagini ornekle gosterir Piramidin tabani kenarlari 20 18 displaystyle 20 18 ve 16 displaystyle 16 olan bir 13 14 15 displaystyle 13 14 15 ucgeni bcd displaystyle bcd dir Sirasiyla b displaystyle b c displaystyle c ve d displaystyle d noktalarindan a displaystyle a tepe noktasina yukselir bcd displaystyle bcd taban ucgeni dik aciyi d displaystyle d noktasindan bc displaystyle bc kenarina indirerek 5 12 13 displaystyle 5 12 13 ve 9 12 15 displaystyle 9 12 15 ucgenlerine bolunur Piramidin tepe noktasi olan a displaystyle a noktasindan gecen bc displaystyle bc dogrusuna dik duzlemde bir ucgen kurmaya devam eder bu ucgenin uc tarafini da hesaplar ve yuksekliginin piramidin yuksekligi olduguna dikkat ceker Son adimda bir ucgenin h displaystyle h yuksekliginin p q r displaystyle p q r p displaystyle p tarafindan karsi kosesine kadar olan yukseklik kenarlarina gore miktarini bulmak icin bu formulu uygular h2 r2 p2 r2 q22p 2 displaystyle h 2 r 2 left p 2 r 2 q 2 over 2p right 2 Kosinus yasasi ndan turetilen bir formuldur General Trattatonun bu bolumunde herhangi bir gerekce gostermiyor Tartaglia 3053149 displaystyle 305 frac 31 49 i 305349 displaystyle 305 frac 3 49 olarak alarak hesaplamanin baslarinda bir basamak dusurur ancak yontemi saglamdir Son dogru cevap height of pyramid 2406153136 displaystyle text height of pyramid sqrt 240 frac 615 3136 Piramidin hacmi bundan sonra kolayca elde edilir Tartaglia nin verdiginden degil V 1 3 taban yukseklik 1 3 Alan bcd yukseklik 1 3 84 2406153136 433 9513222 displaystyle begin aligned V amp 1 3 times text taban times text yukseklik amp 1 3 times text Alan triangle bcd times text yukseklik amp 1 3 times 84 times sqrt 240 frac 615 3136 amp approx 433 9513222 end aligned daha sonra on altinci yuzyilda icat etti bu nedenle son rakam her zaman kesirleri kullanan Tartaglia ya yabanci oldu Yine de yaklasimi bazi yonlerden moderndir ornek olarak duzensiz dortyuzlulerin cogunun veya tamaminin yuksekligini hesaplamak icin bir algoritma onerir ancak onun icin her zaman oldugu gibi acik bir formul vermez Notlar 1978 Galileo at Work His Scientific Biography Dover s 3 Strathern 2013 s 189 Masotti Arnoldo Niccolo Tartaglia Dictionary of Scientific Biography 25 Kasim 2020 tarihinde kaynagindan erisim tarihi 29 Temmuz 2021 Tartaglia Niccolo Part IV General Trattato di Numeri et Misure Book 3 s 43v 28 Temmuz 2021 tarihinde kaynagindan Erisim tarihi 28 Temmuz 2021 Sosis saticisi icin bakiniz Zilsel Edgar The Social Origins of Modern Science s 35 Valleriani Matteo 2013 s 1 16 Aralik 2016 tarihinde kaynagindan arsivlendi Henninger Voss Mary J Temmuz 2002 How the New Science of Cannons Shook up the Aristotelian Cosmos Journal of the History of Ideas 63 3 ss 371 397 eviscerated s 376 Valleriani Matteo 2013 Metallurgy Ballistics and Epistemic Instruments The Nova Scientia of Nicolo Tartaglia ss 169 181 15 Agustos 2020 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Valleriani Matteo 2013 Metallurgy Ballistics and Epistemic Instruments The Nova Scientia of Nicolo Tartaglia ss 176 177 26 Eylul 2020 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Henninger Voss Mary J Temmuz 2002 How the New Science of Cannons Shook up the Aristotelian Cosmos Journal of the History of Ideas 63 3 ss 391 393 Tartisma ve alintilar icin bakiniz Clagett Marshall William of Moerbeke Translator of Archimedes ss 356 366 Archimedes Tartaglia Niccolo 1543 Opera Archimedis Syracvsani philosophi et mathematici ingeniosissimi 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 13 Nisan 2022 Henninger Voss Mary J New Science of Cannons s 392 Ruffinelli Venturino Guglielmo da Fontaneto amp Facolo Pietro amp Tartaglia Niccolo Gesuiti Casa Professa Biblioteca Gesuiti Collegio Romano Collegio di San Francesco di Paola Biblioteca Euclide megarense philosopho solo introduttore delle scientie mathematice diligentemente reassettato et alla integrita ridotto per il degno professore di tal scientie Nicolo Tartalea brisciano secondo le due tradottioni e per commune commodo amp vtilita di latino in volgar tradotto con vna ampla espositione dello istesso tradottore di nouo aggionta Roma Ulusal Merkez Kutuphanesi 1543 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Bakiniz Malet Antoni Euclid s Swan Song Euclid s Elements in Early Modern Europe burada Tartaglia nin Oklid uzerine calismasi matematiksel olarak ikna edici yenilikci ve etkili olarak tanimlaniyor s 207 Tartaglia Niccolo 1556 1560 Smith 1985 s 298 Tartaglia Niccolo General Trattato di Numeri et Misure Part I 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo General Trattato di Numeri et Misure Part II 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo General Trattato di Numeri et Misure Part IV 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo General Trattato di Numeri et Misure Part II Book 2 s 51v 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 6 4 7 displaystyle 6 4 7 yi genisletmek icin bakiniz Tartaglia Niccolo General Trattato di Numeri et Misure Part II Book 2 s 72 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Pascal ucgeni ndeki toplama kuralinin tartismasi icin bakiniz Katz 1998 s 359 Cardano v Tartaglia The Great Feud Goes Supernatural PDF 29 Eylul 2020 tarihinde kaynagindan PDF erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo General Trattato di Numeri et Misure Part IV Book 2 s 35r 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 13 14 15 20 18 16 piramidinin yuksekliginin hesaplanmasi icin bakiniz Kaynakca Chisholm Hugh Ed 1911 Tartaglia Niccolo Encyclopaedia Britannica 26 11 bas Cambridge University Press Clagett Marshall 1982 William of Moerbeke Translator of Archimedes Proceedings of the American Philosophical Society 126 5 356 366 Henninger Voss Mary J Temmuz 2002 How the New Science of Cannons Shook up the Aristotelian Cosmos Journal of the History of Ideas 63 3 371 397 doi 10 1353 jhi 2002 0029 Herbermann Charles Ed 1913 Nicolo Tartaglia Katolik Ansiklopedi Ingilizce New York Robert Appleton Company Charles Hutton 1815 Tartaglia or Tartaglia Nicholas A philosophical and mathematical dictionary Printed for the author s 482 Katz Victor J 1998 A History of Mathematics An Introduction Reading Addison Wesley Longman ISBN 0 321 01618 1 Malet Antoni 2012 Euclid s Swan Song Euclid s Elements in Early Modern Europe Olmos Paula Ed Greek Science in the Long Run Essays on the Greek Scientific Tradition 4th c BCE 17th c CE Cambridge Scholars Publishing ss 205 234 ISBN 978 1 4438 3775 0 Masotti Arnoldo 1970 Niccolo Tartaglia Gillispie Charles Ed Dictionary of Scientific Biography New York Scribner amp American Council of Learned Societies Smith D E 1958 History of Mathematics I New York Dover Publications ISBN 0 486 20429 4 Strathern Paul 2013 Venetians New York NY Pegasus Books Tartaglia Niccolo 1543 Opera Archimedis Syracusani philosophi et mathematici ingeniosissimi Venedik 28 Temmuz 2021 tarihinde kaynagindan Erisim tarihi 13 Nisan 2022 Tartaglia Niccolo 1543 Euclide Megarense philosopho Venedik 28 Temmuz 2021 tarihinde kaynagindan Erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1556 1560 General Trattato di Numeri et Misure Venedik Curtio Troiano Valleriani Matteo 2013 Metallurgy Ballistics and Epistemic Instruments The Nova Scientia of Nicolo Tartaglia Berlin Edition Open Access Max Planck Research Library ISBN 978 3 8442 5258 3 Zilsel Edgar 2000 Raven Diederick Krohn Wolfgang Cohen Robert S Ed The Social Origins of Modern Science Springer Netherlands ISBN 0 7923 6457 0 Dis baglantilar 22 Ocak 2012 tarihinde kaynagindan arsivlendi 6 Ekim 2013 tarihinde kaynagindan arsivlendi O Connor John J Robertson Edmund F Niccolo Tartaglia MacTutor Matematik Tarihi arsivi MAA Convergence 30 Eylul 2007 tarihinde kaynagindan arsivlendi Venedik 1550 3 Ocak 2018 tarihinde kaynagindan arsivlendi Tartaglia Niccolo 1556 General Trattato di Numeri et Misure Part I Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1556 General Trattato di Numeri et Misure Part II Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1556 General Trattato di Numeri et Misure Part III Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1560 General Trattato di Numeri et Misure Part IV Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1560 General Trattato di Numeri et Misure Part V Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Tartaglia Niccolo 1560 General Trattato di Numeri et Misure Part VI Venedik 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Valleriani Matteo Metallurgy Ballistics and Epistemic Instruments The Nova scientia of Nicolo Tartaglia 28 Temmuz 2021 tarihinde kaynagindan erisim tarihi 28 Temmuz 2021 Favaro Antonio 1913 PER LA BIOGRAFIA DI NICCOLO TARTAGLIA Archivio Storico Italiano Italyanca 71 2 270 ss 335 372 JSTOR 44458852 Serafina Cuomo 1997 Shooting by the Book Notes on Niccolo Tartaglia s Nova Scientia History of Science 35 2 ss 155 188 doi 10 1177 007327539703500202 Bernardoni A 2015 Sgarbi M Ed Tartaglia NIccolo Encyclopedia of Renaissance Philosophy Springer Cham doi 10 1007 978 3 319 02848 4 81 1 ISBN 978 3 319 02848 4 Ricahrd W Feldmann Mart 1961 The Cardano Tartaglia Dispute PDF The Mathematics Teacher National Council of Teachers of Mathematics 54 3 ss 160 163 JSTOR 27956338 28 Temmuz 2021 tarihinde kaynagindan PDF erisim tarihi 28 Temmuz 2021 Tony Rothman Cardano v Tartaglia The Great Feud Goes Supernatural PDF 29 Eylul 2020 tarihinde kaynagindan PDF erisim tarihi 28 Temmuz 2021
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans