Knidos'lu Eudoxus veya Knidoslu Ödoksus (; Grekçe: Εὔδοξος ὁ Κνίδιος; Eúdoxos ho Knídios y. 408 – y. MÖ 355), antik bir Yunan astronomu, matematikçi, bilim insanı ve Archytas ile Platon'un öğrencisiydi. Hipparchus'un Aratus'un astronomi üzerine şiiriyle ilgili yorumunda bazı parçalar korunsa da tüm eserleri kaybolmuştur.Bithynialı Theodosius tarafından yazılan , Eudoxus'un bir çalışmasına dayanabilir.
Knidoslu Eudoxus (Ödoksus) | |
|---|---|
| Doğum | y. MÖ 400 Knidos, Küçük Asya |
| Ölüm | y. MÖ 350 Knidos, Küçük Asya |
| Tanınma nedeni | (Kampyle of Eudoxus) Ortak merkezli küreler kuramı |
| Kariyeri | |
| Dalı | |
Takımyıldızların tanımlanmasına katkıda bulundu Ve böylece Yunan dünyasında gözlemsel astronominin gelişmesine ve ilk gelişmiş, geometrik gök hareket modelini kurdu. Coğrafya üzerine yazılar yazdı ve Platon Akademisi'nde felsefi tartışmalara katkıda bulundu. Yazılarının hiçbiri hayatta kalmasa da, katkıları Antik Çağ'daki birçok tartışmadan bilinmektedir.
Aristoteles, Eudoksos’un metafizik ve etik hakkındaki görüşlerini korumuştur. Platon'dan farklı olarak, Eudoksos formların algılanabilir şeyler olduğunu iddia etti. Ayrıca, iyiliği her şeyin amaçladığı, zevke ulaşmayı hedefleyen şey olarak tanımladı.
Hayatı
Eudoxus, günümüz Türkiye'sinin güneybatı kıyısında bir şehir olan Cnidus'ta (bazen Knidos olarak da söylenir) doğdu ve öldü. Eudoxus'un doğum ve ölüm yılları tam olarak bilinmemektedir, ancak aralık yaklaşık y. 408 – y. MÖ 355, veya y. 390 – y. MÖ 337 olabilir. Adı Eudoxus "onurlu [honored]" veya "iyi şöhretli [of good repute]" anlamına gelir (εὔδοξος, eu "iyi [good]" ve doxa’dan "fikir [opinion], inanç [belief], şöhret [fame]"). Latince adı Benedictus'a benzer.
Eudoxus'un babası Cnidus'lu Aeschines geceleri yıldızları izlemeyi severdi. Eudoxus, matematik öğrendiği Archytas ile çalışmak için önce Tarentum'a gitti. İtalya'dayken Eudoxus, ile tıp eğitimi aldığı Sicilya'yı ziyaret etti.
23 yaşında, (Diogenes Laërtius'a göre) bazılarının sevgilisi olduğuna inandığı doktor ile Sokrates'in takipçileriyle çalışmak için Atina'ya gitti. Sonunda birkaç ay boyunca Platon ve diğer filozofların derslerine katıldı, ancak bir anlaşmazlık nedeniyle araları açıldı. Eudoxus oldukça fakirdi ve sadece Pire'de bir daire alabiliyordu. Platon'un derslerine katılmak için her gün geliş ve dönüşte 7 mil (11 km) yürüdü. Yoksulluğundan dolayı arkadaşları onu astronomi ve matematik çalışmalarını sürdürmesi için 'ın Heliopolis kentine gönderecek kadar para topladılar. 16 ay orada yaşadı. Mısır'dan kuzeye, Marmara Denizi'nin güney kıyısındaki Propontis'te bulunan Kyzikos'a gitti. Güneye, Mausolus'un sarayına gitti. Seyahatleri sırasında birçok öğrenciyi bir araya getirdi.
MÖ 368 civarında Eudoxus öğrencileriyle Atina'ya döndü. Bazı kaynaklara göre, 367 civarında, Platon'un Syracuse döneminde Akademi başkanlığını üstlendi ve Aristo'ya öğretmenlik yaptı.[] Sonunda, şehir meclisinde görev yaptığı memleketi Knidos'a geri döndü. Burada yasa koyucu oldu ve araştırmasını 53 yaşında ölene kadar sürdürdü. Menaechmus ve Callippus dahil olmak üzere Eudoksos'un takipçileri hem Atina'da hem de Kyzikos'ta gelişti. Cnidus'tayken bir gözlemevi inşa etti ve teoloji, astronomi ve meteoroloji üzerine yazmaya ve ders vermeye devam etti. Bir oğlu Aristagoras ve üç kızı Actis, Philtis ve Delphis vardı.
Matematiksel astronomide ünü, eş merkezli kürelerin ortaya çıkması ve gezegenlerin hareketini anlamaya yaptığı erken katkılardan kaynaklanmaktadır.
Oranlar üzerine yaptığı çalışma, gerçel sayılar hakkında fikir verir; sadece tam sayıların ve hatta rasyonel sayıların değil, sürekli büyüklüklerin titiz bir şekilde ele alınmasını sağlar. 16. yüzyılda Tartaglia ve diğerleri tarafından yeniden canlandırıldığında, bilimde nicel çalışmanın temeli haline geldi ve Richard Dedekind'in çalışmalarına ilham verdi.
ve Ay'daki onun adına verilmiştir. Bir olan ( [Kampyle of Eudoxus]) de adını ondan almıştır.
Eudoksos, Arşimet'ten önceki en yenilikçi Yunan matematikçisidir. Çalışmaları, Öklid'in Unsurları'ndaki en ileri tartışmaların temelini oluşturuyor ve Arşimet'in hacim ve yüzey çalışmalarına zemin hazırlıyor. Oranlar teorisi, tamamen eklemlenmiş ilk büyüklük teorisidir. Çoğu gök bilimci, MÖ 2. yüzyılın ortalarında astronomik görüşlerini terk etmiş gibi görünse de, merkezdeki her göksel hareketin merkezdeki tekdüze ve dairesel olması ilkesi 17. yüzyıl gök bilimcisi Johannes Kepler'e kadar devam etti. Batlamyus'un bu prensibi (üniform hareketin merkezini hareket çemberinin merkezinden farklı kıldığı yerde) değiştirmesinden duyulan memnuniyetsizlik, Nicolaus Copernicus (1473–1543) dahil olmak üzere birçok Orta Çağ ve Rönesans astronomunu motive etti.
Bilimsel çalışmaları
Matematik
Eudoxus, bazıları tarafından klasik Yunan matematikçilerinin en büyüğü olarak kabul edilir ve tüm Antik Çağ'da sadece Arşimet'ten sonra ikinci sırada yer alır. Eudoxus, muhtemelen Öklid'in Elementler V. kitabının çoğunun kaynağıydı.'un, sonraki yüzyılda Arşimet tarafından ustaca bir şekilde kullanılan integral hesabın bir öncüsü olan tükenme yöntemini titizlikle geliştirdi. Yöntemi uygularken, Eudoxus aşağıdaki gibi matematiksel ifadeleri kanıtladı:
- dairelerin alanları, yarıçaplarının kareleri ile birbirine orantılıdır,
- kürelerin hacimleri, yarıçaplarının küpleri ile birbirine orantılıdır,
- bir piramidin hacmi, aynı taban ve yüksekliğe sahip bir prizmanın hacminin üçte biridir,
- bir koninin hacmi, karşılık gelen silindirin üçte biridir.
Eudoxus, çizgiler, açılar, alanlar ve hacimler gibi sürekli geometrik varlıkları tanımlamak ve bunlarla çalışmak için ölçülmemiş matematiksel büyüklük fikrini ortaya attı, böylece irrasyonel sayıların kullanımından kaçındı. Bunu yaparken, Pisagor'un sayı ve aritmetik üzerindeki vurgusunu tersine çevirdi ve bunun yerine katı matematiğin temeli olarak geometrik kavramlara odaklandı. Eudoxus'un öğretmeni Archytas gibi bazı Pisagorcular sadece aritmetiğin ispatlara temel oluşturabileceğine inanıyordu. anlama ve bunlarla çalışma ihtiyacının neden olduğu Eudoxus, açık aksiyomlar temelinde matematiğin ilk tümdengelimli düzeni olabilecek şeyi kurdu. Eudoxus'un odak noktasındaki değişiklik, matematikte iki bin yıl süren bir bölünmeyi tetikledi. Pratik sorunlarla ilgilenmeyen bir Yunan entelektüel yaklaşımı ile birlikte, aritmetik ve cebirdeki tekniklerin gelişiminde önemli bir gerileme yaşandı.
Pisagorcular, bir karenin köşegeninin karenin kenarlarıyla ortak bir ölçü birimine sahip olmadığını keşfetmişlerdi; bu, 2'nin karekökünün iki tam sayının oranı olarak ifade edilemeyeceğinin ünlü keşfidir. Bu keşif, tam sayıların ve rasyonel kesirlerin ötesinde ölçülemez büyüklüklerin varlığını müjdelemişti, ancak aynı zamanda bir bütün olarak geometride ölçüm ve hesaplamalar fikrini de sorguladı. Örneğin, Öklid, Pisagor teoreminin (Elementler I.47) ayrıntılı bir ispatını, alanların toplamasını kullanarak ve ancak çok daha sonra (Elementler VI.31), doğru parçalarının oranlarına dayanan benzer üçgenlerden daha basit bir kanıt sağlar.
Antik Yunan matematikçiler bugün yaptığımız gibi miktarlar ve denklemlerle hesaplama yapmadılar, bunun yerine nicelikler arasındaki ilişkiyi ifade etmek için orantıları kullandılar. Dolayısıyla, bugün düşündüğümüz gibi, iki benzer büyüklüğün oranı sadece sayısal bir değer değildi; iki benzer niceliğin oranı, aralarındaki ilkel bir ilişkiydi.
Eudoxus, iki oran arasındaki eşitliğin anlamı için şaşırtıcı bir tanım sağlayarak orantılılıkların kullanımına olan güveni yeniden sağladı. Bu oran tanımı, Öklid'in Elementler'inin V. kitabı'nın konusunu oluşturur.
Öklid'in V. kitabının 5. tanımında şunu okuyoruz:
| “ | Büyüklükleri aynı oranda olduğunda, birinci ile üçüncüden alınan eş çarpanlar ne olursa olsun ve ikinci ile dördüncünün eş çarpanları ne olursa olsun, eski eş çarpanlar aynı şekilde artar, benzer sırayla alınan ikinci eş çarpanlar benzer olurlar, veya benzer şekilde azalırlar. | „ |
Modern zaman gösterimini kullanılarak bu, aşağıdaki gibi açıklığa kavuşturulur. Dört miktar alırsak: 




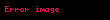
Şimdi 


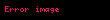
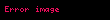


Eğer 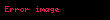





Tanımın benzer miktarlar 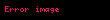

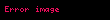

Tanımın karmaşıklığı, ilgili derin kavramsal ve metodolojik yeniliği yansıtır. Öklid'in paralelliklerle ilgili meşhur (beşinci postülatını) akla getiriyor ki bu tanım, ifadeleri açısından diğer postülalardan daha kapsamlı ve karmaşıktır.
Eudox'un orantılılık tanımı, modern limit ve sürekliliğin olduğu gibi, sonsuz ve sonsuz küçük olanı kullanmak için "her bir ... için" niceleyiciyi kullanır.
Ek olarak, Öklid'in V. kitabının 4. tanımı olarak belirtilen , aslında Arşimet'e değil, Eudoxus'a aittir.
Eudoksos'un tükenme yöntemi
Eudoksos, bir piramidin hacmini, hacmini “tüketen” art arda daha küçük prizmalar ile hesapladı.
Eudoksos da muhtemelen bir daire içine yazılan normal bir beşgenin yan ve diyagonal oranlarının, Çemberin çapı Atina'daki Theaetetus'un sınıflarına girmez (MÖ 417-369). Cyrene Eratosthenes'e göre (MÖ 276-194), Eudoksos ayrıca küpü ikiye katlama sorununa, yani belirli bir küpün iki katı hacminde bir küpün inşasına bir çözüm kattı.
Astronomi
Antik Yunanistan'da astronomi, matematiğin bir dalıdır; gök bilimciler göksel hareketlerin görünümünü taklit edebilecek geometrik modeller yaratmaya çalıştılar. Eudoxus'un astronomik çalışmasını ayrı bir kategori olarak tanımlamak bu nedenle modern bir kolaylıktır. Eudoxus'un günümüze ulaşan astronomik metinlerinden bazıları şunlardır:
- Güneşin kaybolması (Disappearances of the Sun), muhtemelen tutulmalarda
- Oktaeteris (Ὀκταετηρίς), takvimin sekiz yıllık Ay-Güneş-Venüs döngüsü üzerine
- Phaenomena (Φαινόμενα) ve Entropon (Ἔντροπον), üzerine, muhtemelen Eudoxus tarafından Mısır ve Knidus'ta yapılan gözlemlere dayanmaktadır.
- Hızlar Üzerine (On Speeds), gezegen hareketlerinde
Phaenomena’nın içeriği hakkında oldukça iyi bilgilendirildik, çünkü Eudoxus'un düz yazı metni Aratus'un aynı adlı bir şiirinin temelini oluşturuyordu. Hipparchus, Aratus üzerine yaptığı yorumda Eudoxus'un metninden alıntı yaptı.
İki eserde, Phaenomena ve Mirror, Eudoksos, takımyıldızları şematik olarak, sabit yıldızların fazlarını (görünür oldukları tarihler) ve farklı fazlarla ilişkili hava durumunu açıkladı. Aratos'un bir şiiri (MÖ 315-245 civarı) ve gökbilimci Hipparchus'un (MÖ 100 civarı) şiiri hakkındaki yorumlarıyla, bu eserler antik dönemde kalıcı bir etkiye sahipti. Eudoksos ayrıca Güneş, Ay ve Dünya'nın boyutlarını da tartıştı. Sekiz yıllık bir döngü takvimi (Oktaëteris) yapmış olabilir.
Eudoksos ayrıca parçalarının hayatta kaldığı bir etnografik eser (Dünyanın Devresi) yazdı. Eudoksos'un göksel kürenin bir bölünmesine göre küresel Dünya'yı da bilinen altı bölüme (kuzey ve güney tropikal, ılıman ve kutup bölgeleri) böldüğü düşünülebilir.
Eudoxus'a ait gezegen modelleri
On Speeds’in içeriğiyle ilgili genel bir fikir, Aristoteles'in Metafizik XII, 8'den ve Cilicia'lı Simplicius'un (MS 6. yüzyıl) De caelo adlı eserinde Aristoteles'in bir başka eseri üzerine yaptığı yorumdan elde edilebilir. Simplicius tarafından aktarılan bir hikayeye göre Platon, Yunan gökbilimciler için bir soru sordu: "Gezegenlerin görünen hareketleri hangi tek tip ve düzenli hareketler varsayımıyla açıklanabilir?" (Lloyd 1970, s. 84). Platon, gezegenlerin görünüşte kaotik gezinme hareketlerinin, küresel bir Dünya üzerinde merkezlenmiş tekdüze dairesel hareketlerin kombinasyonları ile açıklanabileceğini öne sürdü; bu, görünüşe göre MÖ 4. yüzyılda yeni bir fikirdi.
Eudoxan modelinin çoğu modern rekonstrüksiyonunda, Ay'a üç küre atanmıştır:
- En dıştaki kısım 24 saatte bir batıya doğru dönerek yükselmeyi ve batmayı açıklar.
- İkincisi ayda bir kez doğuya doğru döner ve Ay'ın burçlar boyunca aylık hareketini açıklar.
- Üçüncüsü de bir ayda devrimini tamamlar, ancak ekseni biraz farklı bir açıyla eğilir ve enlemdeki hareketi (ekliptikten sapma) ve hareketini açıklar.
Güneş'e ayrıca üç küre atanmıştır. İkincisi, bir ay yerine bir yılda hareketini tamamlar. Üçüncü bir kürenin dahil edilmesi, Eudoxus'un hatalı olarak Güneş'in enlemde hareket ettiğine inandığı anlamına gelir.


Görünür beş gezegenin (Venüs, Merkür, Mars, Jüpiter ve Satürn) her birine dört küre atanır:
- En dıştaki günlük hareketi açıklar.
- İkincisi, gezegenin burçtaki hareketini açıklar.
- Üçüncü ve dördüncü birlikte, bir gezegen yavaşlar göründüğünde, zodyak boyunca hareketini kısaca tersine çevirdiğinde açıklar. Eudoxus, iki kürenin eksenlerini birbirine göre eğerek ve bunları zıt yönlerde ancak eşit periyotlarla döndürerek, iç küre üzerinde sekiz şeklindeki bir şekli veya izleyen bir nokta yapabilirdi.
Eudoxus'a ait sisteminin önemi
4. yüzyılın Yunan gök bilimcisi Callippus, Eudoxus'un orijinal 27 küreli sistemine yedi küre daha ekledi (gezegensel kürelere ek olarak, Eudoxus sabit yıldızlar için bir küre içeriyordu). Aristoteles her iki sistemi de tanımladı, ancak dış kümenin hareketlerini iptal etmek için her küre kümesi arasına "yuvarlanan" küreler eklemekte ısrar etti. Aristoteles, sistemin fiziksel doğasıyla ilgileniyordu; silindirler olmadan, dış hareketler iç gezegenlere aktarılacaktır.
Eudoxian sistemindeki büyük bir kusur, gezegenlerin parlaklığındaki değişiklikleri Dünya'dan görüldüğü gibi açıklayamamasıdır. Küreler eşmerkezli olduğundan, gezegenler her zaman Dünya'dan aynı mesafede kalacaktır. Bu soruna Pitane'li Autolycus tarafından Antik Çağ'da işaret edilmiştir. Gök bilimciler, bir gezegenin mesafesini değiştirmesine neden olan 'ı tanıtarak yanıt verdi. Bununla birlikte, Eudoxus'un astronomi ve özellikle Yunan astronomisi için önemi büyüktür.
Etik
adlı eserindeAristoteles, Eudoxus'a hedonizm lehine bir argüman atfeder -yani, zevk, aktivitenin çabaladığı nihai iyiliktir. Aristoteles'e göre, Eudoxus bu pozisyon için şu argümanları ileri sürer:
- Mantıklı ve mantıksız her şey zevki hedefler; şeyler, iyi olduğuna inandıkları şeyi hedefler; Temel iyiliğin ne olduğuna dair iyi bir gösterge, çoğu şeyin hedeflediği şey olacaktır.
- Benzer şekilde, hazzın zıttı -acı- evrensel olarak önlenir ve bu da hazzın evrensel olarak iyi kabul edildiği fikrine ek destek sağlar.
- İnsanlar zevki başka bir şeyin aracı olarak değil, kendi başına bir amaç olarak ararlar.
- Aklınıza gelebilecek başka herhangi bir iyilik, ona zevk eklenseydi daha iyi olurdu ve iyilik ancak iyilikle artırılabilir.
- İyi olan her şey arasında mutluluk övülmemeye özgüdür, bu da onun taçlandıran iyilik olduğunu gösterebilir.
Ayrıca bakınız
- Arşimet
- Öklid
- Öklid'in Elementler'i
- (onun onuruna adı verilen gerçek sayıların oldukça yakın zamanda keşfedilen bir yapısı)
- Delos problemi (Küpün hacmini iki katına çıkarma problemi)
- Ölçülemez büyüklükler
- Speusippus
Bibliyografya
- Ball, Walter William Rouse (1908). A Short Account of the History of Mathematics (4 bas.). Dover Publications.
- De Santillana, G. (1968). "Eudoxus and Plato: A Study in Chronology". Reflections on Men and Ideas. Cambridge, MA: MIT Press.
- Evans, James (1998). The History and Practice of Ancient Astronomy. Oxford University Press. ISBN . OCLC 185509676.
- Huxley, GL (1980). Eudoxus of Cnidus. Dictionary of Scientific Biography. 4. ss. 465-7.
- Huxley, G. L. (1963). "Eudoxian Topics". Greek, Roman, and Byzantine Studies. 4: 83-96.
- Knorr, Wilbur Richard (1978). "Archimedes and the Pre-Euclidean Proportion Theory". Archives Internationales d'Histoire des Sciences. 28: 183-244.
- (1986). The Ancient tradition of geometric problems. Boston: Birkhäuser. ISBN .
- Lasserre, François (1966) Die Fragmente des Eudoxos von Knidos (de Gruyter: Berlin)
![image]() Laërtius, Diogenes (1925). "Pythagoreans: Eudoxus"
Laërtius, Diogenes (1925). "Pythagoreans: Eudoxus" ![image]() . . 2:8. Translated by (Two volume ed.). .
. . 2:8. Translated by (Two volume ed.). .- Lloyd, GER (1970). Early Greek Science: Thales to Aristotle. W.W. Norton.
- Manitius, C. (1894) Hipparchi in Arati et Eudoxi Phaenomena Commentariorum Libri Tres (Teubner)
- Neugebauer, O. (1975). A history of ancient mathematical astronomy. Berlin: Springer-Verlag. ISBN .
- Van der Waerden, B. L. (1988). Science Awakening (5 bas.). Leiden: Noordhoff.
Kaynakça
- ^ a b c d (2008). The Oxford Dictionary of Philosophy (2. revize bas.). Oxford: Oxford University Press. ISBN . 12 Eylül 2021 tarihinde kaynağından . Erişim tarihi: 30 Kasım 2020.
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Knidoslu Ödoksus", MacTutor Matematik Tarihi arşivi
- ^ Lasserre, François (1966) Die Fragmente des Eudoxos von Knidos (de Gruyter: Berlin)
- ^ Diogenes Laertius; VIII.87
- ^ Milenko Nikolić (2012) "The ancient idea of real number in Eudoxus' theory of ratios", page 226, and "The analogy between Eudoxus' theory of ratios and Dedekind's theory of cut", page 238 in For Jan Struik, Cohen-Stachel-Wartofsky editors,
- ^ Calinger, Ronald (1982). Classics of Mathematics. Oak Park, Illinois: Moore Publishing Company, Inc. s. 75. ISBN .
- ^ Ball 1908, s. 54.
- ^ a b Morris Kline (1972). Mathematical Thought from Ancient to Modern Times. Oxford University Press. ss. 48-50. ASIN B01FEKKDUC. ISBN .
- ^ (1951). Theory and Application of Infinite Series (İngilizce) (2 bas.). Londra & Glasgow: Blackie & Son, Ltd. s. 7.
- ^ Büyük ölçüde 10. kitapta.
- ^ Bu özel argüman 1. kitapta referans olarak verilmiştir.
Dış bağlantılar
| Wikimedia Commons'ta Eudoxus of Cnidus ile ilgili ortam dosyaları bulunmaktadır. |
- . 1 Kasım 2014 tarihinde kaynağından arşivlendi. (Eudoxus'un Kürelerinin çalışma modeli ve eksiksiz açıklaması)
- . 16 Ağustos 2018 tarihinde kaynağından arşivlendi.
a documentary on Eudoxus, including a description of his planetary model
(gezegen modelinin bir açıklamasını içeren Eudoxus üzerine bir belgesel) - Dennis Duke. (PDF). DIO. 19 Temmuz 2011 tarihinde kaynağından (PDF) arşivlendi.
bkz. sayfa 7-23
(Eudoxus Olaylarının İstatistiksel tarihlemesi) - . Britannica.com. 11 Mayıs 2008 tarihinde kaynağından arşivlendi.
- Professor Donald Allen. . Texas A&M University. 23 Temmuz 1997 tarihinde kaynağından arşivlendi.
- Henry Mendell. . LA: Cal. State Uni. 16 Mayıs 2011 tarihinde kaynağından arşivlendi. (astronomi ve homosentrik -eş merkezli- küreler)
- . 21 Ağustos 2008 tarihinde kaynağından arşivlendi. (Herodot Projesi: Cnidus'un kapsamlı Siyah Beyaz fotoğraf denemesi)
- Craig McConnell (Ph.D.). . Cal. State, Fullerton. 19 Temmuz 2011 tarihinde kaynağından arşivlendi. (Gezegensel Hareket Modelleri - Eudoxus)
- O'Connor, John J.; Robertson, Edmund F., "Knidoslu Ödoksus", MacTutor Matematik Tarihi arşivi
- . 21 Kasım 2007 tarihinde kaynağından arşivlendi. (Eudoxus'a Göre Evren - Java uygulaması)
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Knidos lu Eudoxus veya Knidoslu Odoksus ˈ juː d e k s e s Grekce Eὔdo3os ὁ Knidios Eudoxos ho Knidios y 408 y MO 355 antik bir Yunan astronomu matematikci bilim insani ve Archytas ile Platon un ogrencisiydi Hipparchus un Aratus un astronomi uzerine siiriyle ilgili yorumunda bazi parcalar korunsa da tum eserleri kaybolmustur Bithyniali Theodosius tarafindan yazilan Eudoxus un bir calismasina dayanabilir Knidoslu Eudoxus Odoksus Dogumy MO 400 Knidos Kucuk AsyaOlumy MO 350 Knidos Kucuk AsyaTaninma nedeni Kampyle of Eudoxus Ortak merkezli kureler kuramiKariyeriDaliMatematikFizikCografyaAstronomiTipFelsefe Takimyildizlarin tanimlanmasina katkida bulundu Ve boylece Yunan dunyasinda gozlemsel astronominin gelismesine ve ilk gelismis geometrik gok hareket modelini kurdu Cografya uzerine yazilar yazdi ve Platon Akademisi nde felsefi tartismalara katkida bulundu Yazilarinin hicbiri hayatta kalmasa da katkilari Antik Cag daki bircok tartismadan bilinmektedir Aristoteles Eudoksos un metafizik ve etik hakkindaki goruslerini korumustur Platon dan farkli olarak Eudoksos formlarin algilanabilir seyler oldugunu iddia etti Ayrica iyiligi her seyin amacladigi zevke ulasmayi hedefleyen sey olarak tanimladi HayatiEudoxus gunumuz Turkiye sinin guneybati kiyisinda bir sehir olan Cnidus ta bazen Knidos olarak da soylenir dogdu ve oldu Eudoxus un dogum ve olum yillari tam olarak bilinmemektedir ancak aralik yaklasik y 408 y MO 355 veya y 390 y MO 337 olabilir Adi Eudoxus onurlu honored veya iyi sohretli of good repute anlamina gelir eὔdo3os eu iyi good ve doxa dan fikir opinion inanc belief sohret fame Latince adi Benedictus a benzer Eudoxus un babasi Cnidus lu Aeschines geceleri yildizlari izlemeyi severdi Eudoxus matematik ogrendigi Archytas ile calismak icin once Tarentum a gitti Italya dayken Eudoxus ile tip egitimi aldigi Sicilya yi ziyaret etti 23 yasinda Diogenes Laertius a gore bazilarinin sevgilisi olduguna inandigi doktor ile Sokrates in takipcileriyle calismak icin Atina ya gitti Sonunda birkac ay boyunca Platon ve diger filozoflarin derslerine katildi ancak bir anlasmazlik nedeniyle aralari acildi Eudoxus oldukca fakirdi ve sadece Pire de bir daire alabiliyordu Platon un derslerine katilmak icin her gun gelis ve donuste 7 mil 11 km yurudu Yoksullugundan dolayi arkadaslari onu astronomi ve matematik calismalarini surdurmesi icin in Heliopolis kentine gonderecek kadar para topladilar 16 ay orada yasadi Misir dan kuzeye Marmara Denizi nin guney kiyisindaki Propontis te bulunan Kyzikos a gitti Guneye Mausolus un sarayina gitti Seyahatleri sirasinda bircok ogrenciyi bir araya getirdi MO 368 civarinda Eudoxus ogrencileriyle Atina ya dondu Bazi kaynaklara gore 367 civarinda Platon un Syracuse doneminde Akademi baskanligini ustlendi ve Aristo ya ogretmenlik yapti kaynak belirtilmeli Sonunda sehir meclisinde gorev yaptigi memleketi Knidos a geri dondu Burada yasa koyucu oldu ve arastirmasini 53 yasinda olene kadar surdurdu Menaechmus ve Callippus dahil olmak uzere Eudoksos un takipcileri hem Atina da hem de Kyzikos ta gelisti Cnidus tayken bir gozlemevi insa etti ve teoloji astronomi ve meteoroloji uzerine yazmaya ve ders vermeye devam etti Bir oglu Aristagoras ve uc kizi Actis Philtis ve Delphis vardi Matematiksel astronomide unu es merkezli kurelerin ortaya cikmasi ve gezegenlerin hareketini anlamaya yaptigi erken katkilardan kaynaklanmaktadir Oranlar uzerine yaptigi calisma gercel sayilar hakkinda fikir verir sadece tam sayilarin ve hatta rasyonel sayilarin degil surekli buyukluklerin titiz bir sekilde ele alinmasini saglar 16 yuzyilda Tartaglia ve digerleri tarafindan yeniden canlandirildiginda bilimde nicel calismanin temeli haline geldi ve Richard Dedekind in calismalarina ilham verdi ve Ay daki onun adina verilmistir Bir olan Kampyle of Eudoxus de adini ondan almistir Eudoksos Arsimet ten onceki en yenilikci Yunan matematikcisidir Calismalari Oklid in Unsurlari ndaki en ileri tartismalarin temelini olusturuyor ve Arsimet in hacim ve yuzey calismalarina zemin hazirliyor Oranlar teorisi tamamen eklemlenmis ilk buyukluk teorisidir Cogu gok bilimci MO 2 yuzyilin ortalarinda astronomik goruslerini terk etmis gibi gorunse de merkezdeki her goksel hareketin merkezdeki tekduze ve dairesel olmasi ilkesi 17 yuzyil gok bilimcisi Johannes Kepler e kadar devam etti Batlamyus un bu prensibi uniform hareketin merkezini hareket cemberinin merkezinden farkli kildigi yerde degistirmesinden duyulan memnuniyetsizlik Nicolaus Copernicus 1473 1543 dahil olmak uzere bircok Orta Cag ve Ronesans astronomunu motive etti Bilimsel calismalariMatematik Eudoxus bazilari tarafindan klasik Yunan matematikcilerinin en buyugu olarak kabul edilir ve tum Antik Cag da sadece Arsimet ten sonra ikinci sirada yer alir Eudoxus muhtemelen Oklid in Elementler V kitabinin cogunun kaynagiydi un sonraki yuzyilda Arsimet tarafindan ustaca bir sekilde kullanilan integral hesabin bir oncusu olan tukenme yontemini titizlikle gelistirdi Yontemi uygularken Eudoxus asagidaki gibi matematiksel ifadeleri kanitladi dairelerin alanlari yaricaplarinin kareleri ile birbirine orantilidir kurelerin hacimleri yaricaplarinin kupleri ile birbirine orantilidir bir piramidin hacmi ayni taban ve yukseklige sahip bir prizmanin hacminin ucte biridir bir koninin hacmi karsilik gelen silindirin ucte biridir Eudoxus cizgiler acilar alanlar ve hacimler gibi surekli geometrik varliklari tanimlamak ve bunlarla calismak icin olculmemis matematiksel buyukluk fikrini ortaya atti boylece irrasyonel sayilarin kullanimindan kacindi Bunu yaparken Pisagor un sayi ve aritmetik uzerindeki vurgusunu tersine cevirdi ve bunun yerine kati matematigin temeli olarak geometrik kavramlara odaklandi Eudoxus un ogretmeni Archytas gibi bazi Pisagorcular sadece aritmetigin ispatlara temel olusturabilecegine inaniyordu anlama ve bunlarla calisma ihtiyacinin neden oldugu Eudoxus acik aksiyomlar temelinde matematigin ilk tumdengelimli duzeni olabilecek seyi kurdu Eudoxus un odak noktasindaki degisiklik matematikte iki bin yil suren bir bolunmeyi tetikledi Pratik sorunlarla ilgilenmeyen bir Yunan entelektuel yaklasimi ile birlikte aritmetik ve cebirdeki tekniklerin gelisiminde onemli bir gerileme yasandi Pisagorcular bir karenin kosegeninin karenin kenarlariyla ortak bir olcu birimine sahip olmadigini kesfetmislerdi bu 2 nin karekokunun iki tam sayinin orani olarak ifade edilemeyeceginin unlu kesfidir Bu kesif tam sayilarin ve rasyonel kesirlerin otesinde olculemez buyukluklerin varligini mujdelemisti ancak ayni zamanda bir butun olarak geometride olcum ve hesaplamalar fikrini de sorguladi Ornegin Oklid Pisagor teoreminin Elementler I 47 ayrintili bir ispatini alanlarin toplamasini kullanarak ve ancak cok daha sonra Elementler VI 31 dogru parcalarinin oranlarina dayanan benzer ucgenlerden daha basit bir kanit saglar Antik Yunan matematikciler bugun yaptigimiz gibi miktarlar ve denklemlerle hesaplama yapmadilar bunun yerine nicelikler arasindaki iliskiyi ifade etmek icin orantilari kullandilar Dolayisiyla bugun dusundugumuz gibi iki benzer buyuklugun orani sadece sayisal bir deger degildi iki benzer niceligin orani aralarindaki ilkel bir iliskiydi Eudoxus iki oran arasindaki esitligin anlami icin sasirtici bir tanim saglayarak orantililiklarin kullanimina olan guveni yeniden sagladi Bu oran tanimi Oklid in Elementler inin V kitabi nin konusunu olusturur Oklid in V kitabinin 5 taniminda sunu okuyoruz Buyuklukleri ayni oranda oldugunda birinci ile ucuncuden alinan es carpanlar ne olursa olsun ve ikinci ile dorduncunun es carpanlari ne olursa olsun eski es carpanlar ayni sekilde artar benzer sirayla alinan ikinci es carpanlar benzer olurlar veya benzer sekilde azalirlar Modern zaman gosterimini kullanilarak bu asagidaki gibi acikliga kavusturulur Dort miktar alirsak a displaystyle a b displaystyle b c displaystyle c ve d displaystyle d o zaman birinci ve ikincinin bir orani olur ab displaystyle frac a b benzer sekilde ucuncu ve dorduncu de cd displaystyle frac c d gibi bir orana sahiptir Simdi ab cd displaystyle frac a b frac c d oldugunu soylersek Asagidakileri yapariz Herhangi iki rastgele tam sayi icin m displaystyle m ve n displaystyle n birinci ve ucuncunun m a displaystyle m cdot a ve m c displaystyle m cdot c es carpanlarini olustururuz benzer sekilde ikinci ve dorduncu n b displaystyle n cdot b ve n d displaystyle n cdot d es carpanlarini olusturur Eger m a gt n b displaystyle m cdot a gt n cdot b olursa o zaman m c gt n d displaystyle m cdot c gt n cdot d ye de sahip olmamiz gerekir Eger m a n b displaystyle m cdot a n cdot b olursa o zaman m c n d displaystyle m cdot c n cdot d ye de sahip olmamiz gerekir Son olarak eger m a lt n b displaystyle m cdot a lt n cdot b olursa o zaman m c lt n d displaystyle m cdot c lt n cdot d ye de sahip olmamiz gerekir Tanimin benzer miktarlar m a displaystyle m cdot a ve n b displaystyle n cdot b ile benzer miktarlar m c displaystyle m cdot c ve n d displaystyle n cdot d yi karsilastirmaya bagli olduguna ve bu miktarlari olcmek icin ortak bir birimin varligina bagli olmadigina dikkat edin Tanimin karmasikligi ilgili derin kavramsal ve metodolojik yeniligi yansitir Oklid in paralelliklerle ilgili meshur besinci postulatini akla getiriyor ki bu tanim ifadeleri acisindan diger postulalardan daha kapsamli ve karmasiktir Eudox un orantililik tanimi modern limit ve surekliligin oldugu gibi sonsuz ve sonsuz kucuk olani kullanmak icin her bir icin niceleyiciyi kullanir Ek olarak Oklid in V kitabinin 4 tanimi olarak belirtilen aslinda Arsimet e degil Eudoxus a aittir Eudoksos un tukenme yontemi Eudoksos bir piramidin hacmini hacmini tuketen art arda daha kucuk prizmalar ile hesapladi Eudoksos da muhtemelen bir daire icine yazilan normal bir besgenin yan ve diyagonal oranlarinin Cemberin capi Atina daki Theaetetus un siniflarina girmez MO 417 369 Cyrene Eratosthenes e gore MO 276 194 Eudoksos ayrica kupu ikiye katlama sorununa yani belirli bir kupun iki kati hacminde bir kupun insasina bir cozum katti Astronomi Antik Yunanistan da astronomi matematigin bir dalidir gok bilimciler goksel hareketlerin gorunumunu taklit edebilecek geometrik modeller yaratmaya calistilar Eudoxus un astronomik calismasini ayri bir kategori olarak tanimlamak bu nedenle modern bir kolayliktir Eudoxus un gunumuze ulasan astronomik metinlerinden bazilari sunlardir Gunesin kaybolmasi Disappearances of the Sun muhtemelen tutulmalarda Oktaeteris Ὀktaethris takvimin sekiz yillik Ay Gunes Venus dongusu uzerine Phaenomena Fainomena ve Entropon Ἔntropon uzerine muhtemelen Eudoxus tarafindan Misir ve Knidus ta yapilan gozlemlere dayanmaktadir Hizlar Uzerine On Speeds gezegen hareketlerinde Phaenomena nin icerigi hakkinda oldukca iyi bilgilendirildik cunku Eudoxus un duz yazi metni Aratus un ayni adli bir siirinin temelini olusturuyordu Hipparchus Aratus uzerine yaptigi yorumda Eudoxus un metninden alinti yapti Iki eserde Phaenomena ve Mirror Eudoksos takimyildizlari sematik olarak sabit yildizlarin fazlarini gorunur olduklari tarihler ve farkli fazlarla iliskili hava durumunu acikladi Aratos un bir siiri MO 315 245 civari ve gokbilimci Hipparchus un MO 100 civari siiri hakkindaki yorumlariyla bu eserler antik donemde kalici bir etkiye sahipti Eudoksos ayrica Gunes Ay ve Dunya nin boyutlarini da tartisti Sekiz yillik bir dongu takvimi Oktaeteris yapmis olabilir Eudoksos ayrica parcalarinin hayatta kaldigi bir etnografik eser Dunyanin Devresi yazdi Eudoksos un goksel kurenin bir bolunmesine gore kuresel Dunya yi da bilinen alti bolume kuzey ve guney tropikal iliman ve kutup bolgeleri boldugu dusunulebilir Eudoxus a ait gezegen modelleri On Speeds in icerigiyle ilgili genel bir fikir Aristoteles in Metafizik XII 8 den ve Cilicia li Simplicius un MS 6 yuzyil De caelo adli eserinde Aristoteles in bir baska eseri uzerine yaptigi yorumdan elde edilebilir Simplicius tarafindan aktarilan bir hikayeye gore Platon Yunan gokbilimciler icin bir soru sordu Gezegenlerin gorunen hareketleri hangi tek tip ve duzenli hareketler varsayimiyla aciklanabilir Lloyd 1970 s 84 Platon gezegenlerin gorunuste kaotik gezinme hareketlerinin kuresel bir Dunya uzerinde merkezlenmis tekduze dairesel hareketlerin kombinasyonlari ile aciklanabilecegini one surdu bu gorunuse gore MO 4 yuzyilda yeni bir fikirdi Eudoxan modelinin cogu modern rekonstruksiyonunda Ay a uc kure atanmistir En distaki kisim 24 saatte bir batiya dogru donerek yukselmeyi ve batmayi aciklar Ikincisi ayda bir kez doguya dogru doner ve Ay in burclar boyunca aylik hareketini aciklar Ucuncusu de bir ayda devrimini tamamlar ancak ekseni biraz farkli bir aciyla egilir ve enlemdeki hareketi ekliptikten sapma ve hareketini aciklar Gunes e ayrica uc kure atanmistir Ikincisi bir ay yerine bir yilda hareketini tamamlar Ucuncu bir kurenin dahil edilmesi Eudoxus un hatali olarak Gunes in enlemde hareket ettigine inandigi anlamina gelir Eudoxus un geriye donuk gezegen hareketi modelini gosteren animasyon Onun modelinin en icteki iki es merkezli homosentrik kuresi burada halkalar olarak temsil edilir her biri ayni periyotta ancak zit yonlerde donerek gezegeni sekiz seklindeki bir egri veya su aygiri boyunca hareket ettirir Eudoxus un gezegen hareketi modeli Es merkezli kurelerinin her biri burada gosterilen eksende donen bir halka olarak temsil edilmektedir En distaki sari kure gunde bir kez doner ikincisi mavi gezegenin burctaki hareketini tanimlar ucuncu yesil ve dorduncu kirmizi birlikte geriye donuk hareketi aciklamak icin gezegeni sekiz seklindeki bir egri veya hippopede boyunca hareket ettirir Gorunur bes gezegenin Venus Merkur Mars Jupiter ve Saturn her birine dort kure atanir En distaki gunluk hareketi aciklar Ikincisi gezegenin burctaki hareketini aciklar Ucuncu ve dorduncu birlikte bir gezegen yavaslar gorundugunde zodyak boyunca hareketini kisaca tersine cevirdiginde aciklar Eudoxus iki kurenin eksenlerini birbirine gore egerek ve bunlari zit yonlerde ancak esit periyotlarla dondurerek ic kure uzerinde sekiz seklindeki bir sekli veya izleyen bir nokta yapabilirdi Eudoxus a ait sisteminin onemi 4 yuzyilin Yunan gok bilimcisi Callippus Eudoxus un orijinal 27 kureli sistemine yedi kure daha ekledi gezegensel kurelere ek olarak Eudoxus sabit yildizlar icin bir kure iceriyordu Aristoteles her iki sistemi de tanimladi ancak dis kumenin hareketlerini iptal etmek icin her kure kumesi arasina yuvarlanan kureler eklemekte israr etti Aristoteles sistemin fiziksel dogasiyla ilgileniyordu silindirler olmadan dis hareketler ic gezegenlere aktarilacaktir Eudoxian sistemindeki buyuk bir kusur gezegenlerin parlakligindaki degisiklikleri Dunya dan goruldugu gibi aciklayamamasidir Kureler esmerkezli oldugundan gezegenler her zaman Dunya dan ayni mesafede kalacaktir Bu soruna Pitane li Autolycus tarafindan Antik Cag da isaret edilmistir Gok bilimciler bir gezegenin mesafesini degistirmesine neden olan i tanitarak yanit verdi Bununla birlikte Eudoxus un astronomi ve ozellikle Yunan astronomisi icin onemi buyuktur Etik adli eserindeAristoteles Eudoxus a hedonizm lehine bir arguman atfeder yani zevk aktivitenin cabaladigi nihai iyiliktir Aristoteles e gore Eudoxus bu pozisyon icin su argumanlari ileri surer Mantikli ve mantiksiz her sey zevki hedefler seyler iyi olduguna inandiklari seyi hedefler Temel iyiligin ne olduguna dair iyi bir gosterge cogu seyin hedefledigi sey olacaktir Benzer sekilde hazzin zitti aci evrensel olarak onlenir ve bu da hazzin evrensel olarak iyi kabul edildigi fikrine ek destek saglar Insanlar zevki baska bir seyin araci olarak degil kendi basina bir amac olarak ararlar Akliniza gelebilecek baska herhangi bir iyilik ona zevk eklenseydi daha iyi olurdu ve iyilik ancak iyilikle artirilabilir Iyi olan her sey arasinda mutluluk ovulmemeye ozgudur bu da onun taclandiran iyilik oldugunu gosterebilir Ayrica bakinizArsimet Oklid Oklid in Elementler i onun onuruna adi verilen gercek sayilarin oldukca yakin zamanda kesfedilen bir yapisi Delos problemi Kupun hacmini iki katina cikarma problemi Olculemez buyuklukler SpeusippusBibliyografyaBall Walter William Rouse 1908 A Short Account of the History of Mathematics 4 bas Dover Publications De Santillana G 1968 Eudoxus and Plato A Study in Chronology Reflections on Men and Ideas Cambridge MA MIT Press Evans James 1998 The History and Practice of Ancient Astronomy Oxford University Press ISBN 0 19 509539 1 OCLC 185509676 Huxley GL 1980 Eudoxus of Cnidus Dictionary of Scientific Biography 4 ss 465 7 Huxley G L 1963 Eudoxian Topics Greek Roman and Byzantine Studies 4 83 96 Knorr Wilbur Richard 1978 Archimedes and the Pre Euclidean Proportion Theory Archives Internationales d Histoire des Sciences 28 183 244 1986 The Ancient tradition of geometric problems Boston Birkhauser ISBN 0 8176 3148 8 Lasserre Francois 1966 Die Fragmente des Eudoxos von Knidos de Gruyter Berlin Laertius Diogenes 1925 Pythagoreans Eudoxus 2 8 Translated by Two volume ed Lloyd GER 1970 Early Greek Science Thales to Aristotle W W Norton Manitius C 1894 Hipparchi in Arati et Eudoxi Phaenomena Commentariorum Libri Tres Teubner Neugebauer O 1975 A history of ancient mathematical astronomy Berlin Springer Verlag ISBN 0 387 06995 X Van der Waerden B L 1988 Science Awakening 5 bas Leiden Noordhoff Kaynakca a b c d 2008 The Oxford Dictionary of Philosophy 2 revize bas Oxford Oxford University Press ISBN 9780199541430 12 Eylul 2021 tarihinde kaynagindan Erisim tarihi 30 Kasim 2020 a b O Connor John J Robertson Edmund F Knidoslu Odoksus MacTutor Matematik Tarihi arsivi Lasserre Francois 1966 Die Fragmente des Eudoxos von Knidos de Gruyter Berlin Diogenes Laertius VIII 87 Milenko Nikolic 2012 The ancient idea of real number in Eudoxus theory of ratios page 226 and The analogy between Eudoxus theory of ratios and Dedekind s theory of cut page 238 in For Jan Struik Cohen Stachel Wartofsky editors Calinger Ronald 1982 Classics of Mathematics Oak Park Illinois Moore Publishing Company Inc s 75 ISBN 0 935610 13 8 Ball 1908 s 54 a b Morris Kline 1972 Mathematical Thought from Ancient to Modern Times Oxford University Press ss 48 50 ASIN B01FEKKDUC ISBN 9780195012170 1951 Theory and Application of Infinite Series Ingilizce 2 bas Londra amp Glasgow Blackie amp Son Ltd s 7 Buyuk olcude 10 kitapta Bu ozel arguman 1 kitapta referans olarak verilmistir Dis baglantilarWikimedia Commons ta Eudoxus of Cnidus ile ilgili ortam dosyalari bulunmaktadir 1 Kasim 2014 tarihinde kaynagindan arsivlendi Eudoxus un Kurelerinin calisma modeli ve eksiksiz aciklamasi 16 Agustos 2018 tarihinde kaynagindan arsivlendi a documentary on Eudoxus including a description of his planetary model gezegen modelinin bir aciklamasini iceren Eudoxus uzerine bir belgesel Dennis Duke PDF DIO 19 Temmuz 2011 tarihinde kaynagindan PDF arsivlendi bkz sayfa 7 23 Eudoxus Olaylarinin Istatistiksel tarihlemesi Britannica com 11 Mayis 2008 tarihinde kaynagindan arsivlendi Professor Donald Allen Texas A amp M University 23 Temmuz 1997 tarihinde kaynagindan arsivlendi Henry Mendell LA Cal State Uni 16 Mayis 2011 tarihinde kaynagindan arsivlendi astronomi ve homosentrik es merkezli kureler 21 Agustos 2008 tarihinde kaynagindan arsivlendi Herodot Projesi Cnidus un kapsamli Siyah Beyaz fotograf denemesi Craig McConnell Ph D Cal State Fullerton 19 Temmuz 2011 tarihinde kaynagindan arsivlendi Gezegensel Hareket Modelleri Eudoxus O Connor John J Robertson Edmund F Knidoslu Odoksus MacTutor Matematik Tarihi arsivi 21 Kasim 2007 tarihinde kaynagindan arsivlendi Eudoxus a Gore Evren Java uygulamasi
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State
