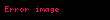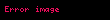Normal dağılım, aynı zamanda Gauss dağılımı veya Gauss tipi dağılım olarak isimlendirilen, birçok alanda pratik uygulaması olan, çok önemli bir sürekli olasılık dağılım ailesidir.
Olasılık yoğunluk fonksiyonu Standard normal dağılım yeşil çizgi ile gösterilir | |
Yığmalı dağılım fonksiyonu Renkler yukarıdaki gösterim ile aynıdır | |
| Parametreler | () kare (reel) |
|---|---|
| Olasılık yoğunluk fonksiyonu (OYF) | |
| Birikimli dağılım fonksiyonu (YDF) | |
| Ortalama | |
| Medyan | |
| Mod | |
| Varyans | |
| Çarpıklık | 0 |
| Fazladan basıklık | 0 |
| Entropi | |
| Moment üreten fonksiyon (mf) | |
| Karakteristik fonksiyon | |
Bu dağılım ailesinin her bir üyesi sadece iki parametreyle tam olarak tanımlanabilir: Bunlar konum gösteren ortalama (μ, aritmetik ortalama) ve ölçek gösteren varyans (σ2, "yayılım")dır.
Standart normal dağılım, ortalama değeri 0 ve varyans değeri 1 olan normal dağılım ailesinin tek bir elemanıdır. Carl Friedrich Gauss bu dağılımlar grubu ile, astronomik verileri analiz etmekte iken, ilgilenmiş ve bu dağılım için olasılık yoğunluk fonksiyonunu ilk defa tanımlamıştır. Bu olasılık fonksiyonunun grafiği, bir çana benzediği için çoğu kez çan eğrisi olarak da anılmaktadır.
Doğa ve davranış bilimleri içinde bulunan birçok fenomenin niceliksel modeli yapılmasında normal dağılımın kullanılmasına neden merkezsel limit teoreminin uygulanmasından doğmaktadır. Birçok psikolojik ölçümler ve fiziksel fenomen normal dağılım kullanılarak çok iyi yaklaşık olarak açıklanmaktadır. Bu fenomenlerin altında yatan mekanizmalar çoğu zaman bilinmemekte fakat normal dağılım modelinin açıklamada uygulanmaktadır. Bunun pratik yaklaşımın teorik olarak savunması ise her bir reel gözlemin oluşması için geri planda çok sayıda birbirinden bağımsız etkilerin ayrı ayrı toplam olarak katkıda bulundukları varsayımıdır.
Normal dağılım istatistik biliminin birçok alanında kullanılmaktadır. Örneğin için , örneğin kaynağı olan anakütle için dağılımın normal olmadığı gayet açık olsa bile, yaklaşık olarak normal dağılım göstermektedir. Bunun yanında, değerleri bilinen ortalaması ve varyansı olan bütün dağılımlar içinde maksimum yapan dağılımın normal olduğu ispat edilmiştir. Böylece örnek ortalaması ve varyansı ile özetlenen her veri için bilinmeyen kaynak dağılımı olarak normal dağılımı kullanmak gayet doğal bir yaklaşım olması çok uygun bir davranıştır. İstatistikte kullanılan dağılımlar aileleri arasında normal dağılım pratikte en çok kullanılanıdır ve birçok istatistiksel test, normal dağılımın varolduğu varsayımına dayanılarak geliştirilmiştir ve kullanılmaktadır. Olasılık kuramı içinde birkaç sürekli olasılık dağılımları ve ayrık olasılık dağılımlarının limite giden dağılımları yani kullanılmaktadır.
Tarihçe
İstatistik ve olasılığın önemli dağılımlarından biri olan normal dağılım, ilk olarak 1733'te Abraham de Moivre tarafından yayınlanan bir yazıda ilk ortaya çıkartılmıştır ve 1738'de yayınlanan adlı kitabının ikinci baskısında p değişmemek koşuluyla n değerinin artısıyla binom dağılımının limit şekli yaklaşım olarak gösterilmiştir. De Moivre'in bu sonucu tarafından 1812'de bastırılan geliştirilmiştir ve bu sonuç şimdi olarak isimlendirilmektedir.
Laplace normal dağılımı incelemekte olduğu deneylemelerde konusunda uygulamıştır. 1805'te Legendre çok önemli olan en küçük kareler yöntemini ortaya atmıştır. Gauss, bu yöntemi1794'ten beri kullandığını iddia etmiştir ama en kesin surette hataların normal dağılımı varsayımı ile birlikte yayınladığı eser 1809'dadır.
Çan eğrisi teriminin ilk kullanılışı tarafından 1875'te bir bağımsız parçalardan oluşan ikideğişirli normal hakkında yazıda çan yüzeyi teriminin kullanmasına kadar götürülebilir. Normal dağılım sözcüğü ise, Francis Galton ve tarafından ayrı ayrı 1875 civarlarında ortaya atılmıştır.
Bu dağılıma normal adı vermek bazen hatalı görülmektedir; çünkü bazı hallerde diğer dağılımlar pratiğe çok daha uygunluk göstermektedirler.
Karakteristikler
Bir olasılık dağılımını çeşitli şekilde matematiksel ifadelerle karakterize etmek mümkündür. Bunlar arasında göze en iyi hitap edeni olasılık yoğunluk fonksiyonu ile olur. Dağılımın özellikleri ayrıca birikimli dağılım fonksiyonu,momentler, kümülantlar, karakteristik fonksiyon, moment üreten fonksiyon, ve vasıtasıyla da belirtilebilir. Bu kavramların ayrıntıları için maddesine bakınız.
Matematiksel notasyon kullanılması ile, X rassal değeri için ortalama değeri μ ve varyansı σ² ≥ 0, olan bir normal dağılımın bulunduğu şöyle ifade edilir:
Normal dağılım için fazla kullanılmayan bir değişik parametreleme şekli de bulunmaktadır. Bu (bir üssü varyans yani 1/ σ²), değerine eşit olan parametresi τ kullanılarak yapılır. Bunun avantajı sıfır değerine çok yakın varyans (σ²) değerlerinin böler olmalarından doğan limit problemlerinden ayrılma imkânı sağlaması ve normal dağılımı bir bireyi olarak kullanılması gerektiği halde ortaya çıkar.
Bazı merkezsel limit teoremleri için (örneğin ) teorisi kullanışlı olmakla beraber, tüm olasılığı μ etrafında konsantre eden ve bir normal dağılıma benzer olarak ortalama μ ve varyans σ² = 0 değerleri bulunan bir normal dağılım olarak kabul edilmemektedir; buna matematiksel açıklama bu ölçümde kurallarına göre gereken yoğunluğun bulunmamasıdır.
Olasılık yoğunluk fonksiyonu

Normal dağılım için sürekli olasılık yoğunluk fonksiyonu şu :
Burada σ > 0 standart sapmadır; bir reel parametre olan μ beklenen değerdir; ve
ifadesi standart normal dağılım için yoğunluk fonksiyonudur. Standart normal dağılım μ = 0 ve σ = 1 parametreleri olan bir normal dağılımdır.
ifadesinin reel doğru üzerindeki integral değeridir. (Ayrıntıları için maddesine bakınız.)
Olasılık yoğunluk fonksiyonunun özellikleri arasında şunlar başta gelenlerdir:
- ortalama değer μ etrafında simetrik olma;
- hem modun hem de medyanın ortalama μ değerine eşit olması;
- yoğunluk eğrisinin üzerindeki, ortalamadan birer standart sapma altında ve üstündeki noktalar arasında (yani μ - σ ve μ+σ noktalarında) bir bulunması.
Birikimli dağılım fonksiyonu

Bir olasılık dağılımı için birikimli dağılım fonksiyonu, bir rassal değişken X için olay olasılığının dağılımının x sayısına eşit veya daha düşük olmasına kadar değerlendirilmesinden ortaya çıkar. Normal dağılım için birikimli dağılım fonksiyonu (yoğunluk fonksiyonunda kullanılan ayn terimlerle) şöyle ifade edilir:
Burada, parametreleri μ = 0 ve σ = 1 olan standart normal dağılımı için birikimli dağılım fonksiyonu, Φ, ile ifade edilmiştir ve bu fonksiyon şudur:
Standart normal birikimli dağılım fonksiyonu aynı zamanda adı verilen bir özel fonksiyon ifade edilebilir. şöyle ifade edilir:
Böylece terimleri ile standart normal dağılımı için birikimli dağılım fonksiyonu şöyle yazılır:
Standart normal dağılım için birikimli dağılım fonksiyonunun tamlayıcı fonksiyonu (yani 
Standart normal birikimli dağılım fonksiyonunun tersine adı verilir. Bunun formülünü ifade için önce şu ters hata fonksiyonu bulunur:
ve bu fonksiyon kullanılarak şu ters birikimli dağılım fonksiyonu ortaya çıkartılır:
Bu kuantil fonksiyonuna bazen fonksiyonu adı da verilir. Bir probit fonksiyonu için bir elemanter matematiksel olarak ispat edilmiştir. Normal dağılım için çok iyi sonuçlar verdiği anlaşılan yaklaşık fonksiyonlar ve yöntemler ortaya çıkarılmıştır. Bunlar arasında sayısal entegrasyon, , ve yöntemlerinin kullanılması anılabilir.
Birikimli dağılım fonksiyonu için kesin alt ve üst sınırlar
Büyük değerde bir x sayısı için standart normal dağılım birikimli dağılım fonksiyonun 


ifadesi yeterlidir.
Yerine koymak suretiyle entegresyon yöntemi kullanarak, üst sınır şöyle ortaya çıkartılabilir:
Aynı şekilde 
ifadesi ortaya çıkartılır. Bunun 
Üreten fonksiyonlar
Moment üreten fonksiyon
Genel olarak moment üreten fonksiyon, exp(tX) için olarak tanımlanır. Bir normal dağılım için moment üreten fonksiyonu şu olur:
Bu ifade, tanımda verilen üssel değerin, yöntemi dönüştürülmesi ile elde edilmiştir.
Kümülant üreten fonksiyon
, moment üreten fonksiyonun logaritmasidir:
- g(t) = μt + σ²t²/2.
Bu t terimleri ile bir kuadratik polinom olduğu için yalnız ilk iki kümülant için sıfır olmayan değer bulunabilinir.
Karakteristik fonksiyon
Karakteristik fonksiyon, 



Bir normal dağılımı için karakteristik fonksiyonu şudur:
Özellikleri
Normal dağılımın şu özellikleri vardır:
- Eğer
ve
ile
reel sayılar ise, o zaman
( ve varyans maddelerine bakınız.).
- Eğer
ve
ifadeleri bağımsız normal rassal değişkenler ise, o halde -
- Bunların toplamı
normal dağılım gösterir (). Daha ilgi çekici olarak bunun tersi de geçerlidir: Eğer iki bağımsız rassal değişkenlerin toplamı normal dağılım gösteriyorsa, her iki değişken de ayrı ayrı normal dağılım gösterirler. Bu olarak isimlendirilmiştir.
- Bunların arasındaki fark şu şekilde normal dağılım gösterir: Yani
.
- Eğer X ve Y rassal değişkenlerinin varyansları birbirine eşitse, U (toplam için rassal değişken) ve V (fark için rassal değişken) birbirinden bağımsızdırlar.
- şöyle ifade edilir
- Bunların toplamı
- Eğer
ve
birbirinden bağımsız normal rassal değişkenler ise; o zaman
- Bunların çarpımı, yani
,
ile şöyle ifade edilen yoğunluk fonksiyonu olan özel bir dağılım gösterir
burada
bir.
- Bunların birbirine oranı
şekilde Cauchy dağılımı gösterir. Böylece bu Cauchy dağılımı özel bir tip olur.
- Bunların çarpımı, yani
- Eğer
bir seri bağımsız standart normal değişkenler ise, o zaman bunların toplamı, yani
n serbestlik dereceli bir ki-kare dağılımı gösterir.
Normal rassal değişkenlerin standart forma dönüşümleri
Yukarıda verilen 1. özellik sonucu olarak tüm normal rassal değişkenleri standart normale dönüştürmek imkânı vardır: Eğer 

bir standart normal rassal değişken olur; yani 
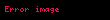
Bunun bir önemli sonucu birikimli olasılık fonksiyonun bir genel normal dağılımı olmasıdır:
Tersini ele alırsak, eğer 

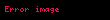
ifadesi de beklenen değeri 
Standart normal dağılım için çeşitli tablolar bulunmaktadır. Çok kere bu tablolar birikimli dağılım fonksiyonu, Φ şeklindedirler. Diğer normal dağılımlar basit bir dönüşüm ile standart normal dağılıma dönüştürülüp bu tablolardan biri kullanılabilir.
Momentler
Normal dağılım için ilk birkaç momentleri şunlardır:
| Sayı | Ham moment | Merkezsel moment | Kümülant |
|---|---|---|---|
| 0 | 1 | 1 | |
| 1 |  | 0 |  |
| 2 |  | 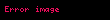 | 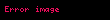 |
| 3 |  | 0 | 0 |
| 4 |  |  | 0 |
| 5 |  | 0 | 0 |
| 6 |  |  | 0 |
| 7 |  | 0 | 0 |
| 8 |  |  | 0 |
Normal dağılım için ilk iki kümülant dışındaki kümülant değerler hep sıfıra eşittir.
Daha büyük sayıya bağlı (

Normal rassal değişirler için üretici değerler
Bilgisayarla simulasyon yapılmakta iken, çok kere bir normal dağılım için değerlerin üretilmesi gerekir. Bunun için birkaç değişik yöntem kullanılabilir. En basit şekilde bir standart normal dağılım birikimli olasılık fonksiyonunun tersini almak suretiyle elde edilir. Daha etkin yöntemler de geliştirilmiştir.
Çok popüler olarak kullanılan yöntem . Box-Muller algoritması kullanılması, [0,1] arasında bulunan sürekli tekdüze dağılım gösteren iki sayı a ve b ile başlar; bunlardan şu formüllere göre iki standart normal dağılım gösteren c ve d sayıları şöyle elde edilir:
Bunların elde edilmesi, dönüşümün bazında (yukarıda 4. özellikte gösterilen) 2 serbestlik derecesi olan bir ki-kare dağılımının kolayca üretilebilinen bir üstel rassal değişken olması gerçeğine dayandırılır.
Halen en etkin şekilde normal dağılımı simulasyonu için, kullanılmaktadır.
Merkezi limit teoremi

Sonlu varyansları olan rassal değişkenler ve benzeri koşullar altında, büyük sayıda rassal değişkenlerin toplamı yaklaşık olarak normal dağılım gösterir. Bu merkezsel limit teoremidir.
Merkezsel limit teoreminin pratik önemi normal birikimli dağılım fonksiyonunun bazı diğer birikimli dağılım fonksiyonunun yaklaşık olarak kullanabilmesindedir. Örneğin
- Parametreleri n ve p olan bir binom dağılım için, eğer büyük değerlerde, ama 0 veya 1e çok yakın olmayan n vep bulunursa bir normal dağılımına yaklaşmış oldukları kabul edilebilir. (Bazı istatistik kitapları bu yaklaşımın np ve n(1 -p değerlerinin her ikisi için en aşağı 5 olması halinde uygulanmasını ve eğer 5 olurlarsa bir kullanılmasını tavsiye ederler.)
Eğer yaklaşık olarak normal dağılımı kullanılırsa bunun parametreleri μ = np ve σ2 = np(1-p) olarak bulunması gerekir. - Eğer λ'nin değeri büyük ise, λ parametreli Poisson dağılımı için yaklaşık olarak normal dağılım kullanılabilir ve bu halde yaklaşık normal dağılımın parametreleri μ = σ2 = λ olarak bulunur.
Bu yaklaşımların yeter derecede doğru olup olmayacağı, sonuçların ne maksatlarla kullanacaklarına ve normal dağılımın yakınsalama oranına bağlıdır. Bu tip yaklaşımlar dağılımın kuyruk değerlerine yaklaştıkça gittikçe daha çok hatalı olacaklardır. birikimli dağılım fonksiyonu için yaklaşım hatası için genel üst sınırları gösterir.
Sonsuz olarak bölünebilme
Normal dağılımlar olasılık dağılımlarıdır: Bir ortalama değeri μ, bir varyans değeri σ2≥ 0 ve bir doğal sayı değeri n verildiği zaman, n bağımsız rassal değişkenlerin toplamı olan 'X1 + . . . +Xn' şu normal dağılımı gösterir:
ç
(Daha fazla ayrıntı için ile maddelerine bakınız.)
Dengelilik
Normal dağılımlar kesinlikle gösteren olasılık dağılımlarıdır.
Standart sapma ve güven aralıkları (açıklıkları)

Bir normal dağılımdan seçilmiş değerlerin %68i ortalama olan μ'in bir standart sapma σ > 0 uzaklığındaki noktalar arasındadır; değerlerin neredeyse %95i μ'den iki standart sapma uzaklıklar aralığında; ve %99,7 üç standart sapma uzaklıklar aralığında bulunur. Buna veya adı da verilir.
Daha doğru bir kesin ifadeyle μ - nσ ve μ + nσ arasındaki çan eğrisinin altında kalan alanın birikimli normal dağılım fonksiyonu şöyle verilir:
Burada erf . Ondalık sayılarla 12 basamak kullanılarak 1-, 2- .. 6- sigma noktalarına kadar değerler şöyle verilir:
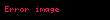 |  |
|---|---|
| 1 | 0.682689492137 |
| 2 | 0.954499736104 |
| 3 | 0.997300203937 |
| 4 | 0.999936657516 |
| 5 | 0.999999426697 |
| 6 | 0.999999998027 |
İkinci tablo çan eğrisinin altındaki alan için değerlerin bulunmasını sağlamak üzere, çok zaman kullanılan katsayı değerlerindeki, sigma çarpanlarının ters ilişkisini gösterir. Normal dağılım gösteren veya asimtotda normal olan kestirimler için belirtilmiş olan seviyelerde (asimtotik) saptamak için bu değerler çok kullanışlıdır:
 | 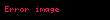 |
|---|---|
| 0.80 | 1.28155 |
| 0.90 | 1.64485 |
| 0.95 | 1.95996 |
| 0.98 | 2.32635 |
| 0.99 | 2.57583 |
| 0.995 | 2.80703 |
| 0.998 | 3.09023 |
| 0.999 | 3.29052 |
Bu tabloda sol taraftaki sütun bilinen bir aralığa düşecek değerlerin oranı verilmekte ve soldaki n sütunu ise aralığın genişliğinin kaç tane standart sapma birimini ihtiva ettiğini göstermektedir.
Üstel ailesi şekli
Normal dağılım bir iki parametreli elemanıdır. İki tane doğal parametresi μ ve 1/σ2 olur ve doğal istatistikleri X ve X2 dir. Kanonik şeklinin parametreleri 



İlişkili dağılımlar
- Eğer
ise ve burada
ave
iki bağımsız normal dağılımlarsa, o halde
bir Rayleigh dağılımı olur.
- Eğer
ise ve burada
için
ise ve bunların hepsi bağımsızlarsa; o zaman
serbestlik derecesi
olan bir ki-kare dağılımıolur.
- Eğer iki bağımsız normal dağılımlı
ve
için 

- Eğer
ve
ise, o zaman
bir.
- ilişki : Eğer
ise o halde
.
- . Eğer
o halde Xi alttan
'da ve üstten
'de kesmek suretiyle, ortalaması
olan bir rassal değişken ortaya çıkarılır.
Burada 

- Eğer
normal dağılım gösteren bir rassal değişken ise ve
ise, o halde
bir gösterir.
Betimsel ve çıkarımsal istatistikler
Puanlar
Puan verme çeşitlerinin çoğu normal dağılıma bağlı olarak ortaya çıkarılmıştır. Değişik puanlama yöntemleri arasında , , , ve T-puanlaması vb. sayılabilir. Davranışsal bilimlerde kullanılan birçok istatistiksel yordamlar puanların normal dağılım gösterdiği varsayımına dayanılarak geliştirilmiştir. Örneğin çok kişiye uygulanan imtihan veya zeka testleri için bir çan eğrisine dayanan not verilip imtihan veya test sonuçlarının gruplanması veya sıralanması imtihan veya test notlarının normal dağılım gösterdiği varsayımına dayandırılır.
Normallik sınamaları
Normallik sınamaları, verilmiş bir veri dizisinin normal dağılıma benzerliğinin incelenmesidir. Bu sınamalarda veri dizisinin normal dağılıma benzer olmasıdır. Bu nedenle normal olmayan veri için yeter derecede küçük bir p-değeri (yani genellikle %0,05'ten veya 0,01den küçük) ortaya çıkacak ve sıfır hipotez olan veri dizisinin normal dağılıma benzerliği hipotezinin ret edilmesine neden olacaktır.
- Kolmogorov-Smirnov sınaması
- Anderson-Darling sınaması
- Shapiro-Wilk sınaması
- ( gösterimi)
- Jarque-Bera sınaması
Parametrelerin kestirimi
Parametrelerin maksimum olabilirlik kestirimi
Bir düşünce denemesi olarak, bir seri normal dağılım için

ifadesinin her biri diğerinden bağımsız olduğu düşünülsün. Her bir ifade beklenen değersi μ ve varyansı σ2>0 olan normal dağılımlar göstermektedir. İstatistikçiler bu n rassal değişkenin gözümlenen değerlerinin normal dağılım gösteren bir anakütleden ortaya çıkan bir n büyüklüğünde bir örneklem olduğunu kabul etmektedirler. Bu örneklemden gözlenen değerlere dayanarak "anakütle ortalaması" μ ve "anakütle standart sapması" kestirimcilerini bulmak arzu edilmektedir. Bu n sayıdaki bağımsız rassal değişken için sürekli ortak olasılık yoğunluk fonksiyonu şöyle verilir:
μ ve σ fonksiyonları olarak, X1, ..., Xn gözlemlerine dayanan şudur:
Burada C>0 herhangi bir sabittir. Bunun genellikle X1,...,Xn değişkenlerine bile dayanarak bağlandığı kabul edilmektedir; ama hesaplanan parametrelere göre log-olabilirlik fonksiyonların kısmî türevleri bulunduğu zaman sabit oldukları için elimine edilmektedirler.
Maksimum olabilirlik yöntemine göre olabilirlik fonksiyonu maksimize eden μ ve σ değerleri, teorik anakütle parametreleri olan μ ve σ için kestirim oldukları kabul edilmektedir. Genel olarak iki değişkenli bir fonksiyonun maksimum değerini hesaplanmaktayken kullanılır. Ancak burada maksimum hesaplama daha kolaylaşmaktadır çünkü olabilirlik fonksiyonunu maksimize eden μ değeri bulunmakta iken σ anakütle parametresi olan σya bağımlı olmayan bir sabittir. Bundan dolayı ilk olarakμ değeri bulunur; bu değer olabilirlik fonksiyonundaki μ değişkeni yerine konulur ve bu yeni tek değişkenli fonksiyonu maksimize eden σ değeri bulunur.
olabilirlik fonksiyonunun şu toplam ifadesinin bir azalan fonksiyonu olduğu bilinmektedir:
Bu toplam ifadeyi minimize edecek μ değerini bulmak istenmektedir. Şu ifade
n gözleme dayanan bir "örneklem ortalamasıdır. Böylece
Bu ifadede so terim μ değişkenine bağlıdır ve bu terimin minimum değeri şöyle bulunur:
İşte bu ifade n sayıda X1,....,Xn gözlem kullanarak μnun maksimum olabilirlik kestirimidir. Sonuç olarak
elde edilir. olabilirlik fonksiyonunun logaritmasi olan log-olabilirlik fonksiyonu matematik notasyona göre küçük harflerle (yani
Sonra
olur. Bu türev, σ2 değeri 0 ile
değeri arasında ise pozitif olur; bu değere eşitse türev sıfıra eşittir; bu değerden büyükse türev negatif olur.
Bu analizin sonucu olarak bu bulunan n gözlemli örneklem için σ2 bir maksimum olabilirlik kestirimidir ve bunun kare kökü σ için maksimum olabilirlik kestirimdir. Bu kestirim yani
Parametrelerin yansız kestirimi
Bir örneklemden elde edilen anakütle ortalamasının maksimum olabilirlik kestirimcisi, anakütle ortalamasının bilinir. Aynı şekilde anakütle ortalaması önsel olarak bilinirse, varyans için maksimum olabilirlik kestrimcisi de yansız kestirimcidir. Ancak eğer elimizde bir örneklem bulunuyorsa ama bu örneklemin geldiği anakütlenin ne ortalamasının ne de varyansının değerlerin bilmiyorsak, anakütle varyansının yansız kestrimicisi, 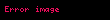
Eğer tüm Xi birbirinden bağımsız ve aynı şekilde dağılım gösterirlerse, bu "örneklem varyansı" bir Gamma dağılımıgösterir:
Ayrıca bakınız
- Standart normal dağılım
- - Verileri normal dağılıma dönüştürmek için basit teknikler
- , Sayı teorisi içinde normal dağılımın meydana çıkışı.
-
- Iannis Xenakis, Müzik için Gauss-tipi dağılımı.
- Log-normal dağılım
- Çokdeğişirli normal dağılım
- Matris normal dağılımı
- (İki tane birbirinden bağımsız olmadan birbirleri ile korelasyon göstermeyen normal dağılımlı rassal değişken için örnek verilmiştir. Bu örnek için geçerli değildir.)
- Student'in t dağılımı
Kaynakça
- ^ H. Gavil, 2003
Dış bağlantılar
Normal dağılım
- Mathworld: Normal dağılım 5 Temmuz 2008 tarihinde Wayback Machine sitesinde .
- GNU Bilimsel Kutuphane – Referans Elkitabı–Gauss-tipi dağılım 8 Haziran 2008 tarihinde Wayback Machine sitesinde .
- PlanetMath: Normal rassal değişken 16 Mayıs 2008 tarihinde Wayback Machine sitesinde .
Yazılım sonuçları ve uygulamaları
- Normal dağılım tablosu 18 Aralık 2020 tarihinde Wayback Machine sitesinde .
- Dağılım hesaplayıcısı – Normal, , ki-kare ve F-dağılımı için kritik değerler ve olasılık hesaplayıcısı29 Ocak 2007 tarihinde Wayback Machine sitesinde .
- Normal dağılımlar için Java Appleti 20 Mart 2008 tarihinde Wayback Machine sitesinde .
- Etkilişimli (normal dağılım da dahil) dağılım modelcisi 16 Şubat 2008 tarihinde Wayback Machine sitesinde .
- Etkileşimli Standart normal eğrisi gösterimi 22 Şubat 2008 tarihinde Wayback Machine sitesinde . Standart normal eğrinin tek kuyruk ve iki kuyruk alanı için çabuk göz önüne getirme yazılımı.
- Online hesap makinesi Normal dağılım 10 Mart 2014 tarihinde Wayback Machine sitesinde .
Algoritmalar ve yaklaşımlar
- , sitmo.com
- , Hazırlayan: Peter J. Acklam – Birkaç değişik örnekler var.
- , gatech.edu
- Matematiksel Fonksiyonlar için Elkitabı': P(x) ve Z(x) icin Polinom ve Rasyonel Yaklaşımlar 17 Nisan 2008 tarihinde Wayback Machine sitesinde . - Abramowitz ve Stegun
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Normal dagilim ayni zamanda Gauss dagilimi veya Gauss tipi dagilim olarak isimlendirilen bircok alanda pratik uygulamasi olan cok onemli bir surekli olasilik dagilim ailesidir Normal Olasilik yogunluk fonksiyonu Standard normal dagilim yesil cizgi ile gosterilirYigmali dagilim fonksiyonu Renkler yukaridaki gosterim ile aynidirParametreler m displaystyle mu s2 gt 0 displaystyle sigma 2 gt 0 kare reel x R displaystyle x in mathbb R Olasilik yogunluk fonksiyonu OYF 1s2pexp x m 22s2 displaystyle frac 1 sigma sqrt 2 pi exp left frac left x mu right 2 2 sigma 2 right Birikimli dagilim fonksiyonu YDF 12 1 erfx ms2 displaystyle frac 1 2 left 1 mathrm erf frac x mu sigma sqrt 2 right Ortalama m displaystyle mu Medyan m displaystyle mu Mod m displaystyle mu Varyans s2 displaystyle sigma 2 Carpiklik 0Fazladan basiklik 0Entropi ln s2pe displaystyle ln left sigma sqrt 2 pi e right Moment ureten fonksiyon mf MX t exp mt s2t22 displaystyle M X t exp left mu t frac sigma 2 t 2 2 right Karakteristik fonksiyon xX t exp mit s2t22 displaystyle chi X t exp left mu i t frac sigma 2 t 2 2 right Bu dagilim ailesinin her bir uyesi sadece iki parametreyle tam olarak tanimlanabilir Bunlar konum gosteren ortalama m aritmetik ortalama ve olcek gosteren varyans s2 yayilim dir Standart normal dagilim ortalama degeri 0 ve varyans degeri 1 olan normal dagilim ailesinin tek bir elemanidir Carl Friedrich Gauss bu dagilimlar grubu ile astronomik verileri analiz etmekte iken ilgilenmis ve bu dagilim icin olasilik yogunluk fonksiyonunu ilk defa tanimlamistir Bu olasilik fonksiyonunun grafigi bir cana benzedigi icin cogu kez can egrisi olarak da anilmaktadir Doga ve davranis bilimleri icinde bulunan bircok fenomenin niceliksel modeli yapilmasinda normal dagilimin kullanilmasina neden merkezsel limit teoreminin uygulanmasindan dogmaktadir Bircok psikolojik olcumler ve fiziksel fenomen normal dagilim kullanilarak cok iyi yaklasik olarak aciklanmaktadir Bu fenomenlerin altinda yatan mekanizmalar cogu zaman bilinmemekte fakat normal dagilim modelinin aciklamada uygulanmaktadir Bunun pratik yaklasimin teorik olarak savunmasi ise her bir reel gozlemin olusmasi icin geri planda cok sayida birbirinden bagimsiz etkilerin ayri ayri toplam olarak katkida bulunduklari varsayimidir Normal dagilim istatistik biliminin bircok alaninda kullanilmaktadir Ornegin icin ornegin kaynagi olan anakutle icin dagilimin normal olmadigi gayet acik olsa bile yaklasik olarak normal dagilim gostermektedir Bunun yaninda degerleri bilinen ortalamasi ve varyansi olan butun dagilimlar icinde maksimum yapan dagilimin normal oldugu ispat edilmistir Boylece ornek ortalamasi ve varyansi ile ozetlenen her veri icin bilinmeyen kaynak dagilimi olarak normal dagilimi kullanmak gayet dogal bir yaklasim olmasi cok uygun bir davranistir Istatistikte kullanilan dagilimlar aileleri arasinda normal dagilim pratikte en cok kullanilanidir ve bircok istatistiksel test normal dagilimin varoldugu varsayimina dayanilarak gelistirilmistir ve kullanilmaktadir Olasilik kurami icinde birkac surekli olasilik dagilimlari ve ayrik olasilik dagilimlarinin limite giden dagilimlari yani kullanilmaktadir TarihceIstatistik ve olasiligin onemli dagilimlarindan biri olan normal dagilim ilk olarak 1733 te Abraham de Moivre tarafindan yayinlanan bir yazida ilk ortaya cikartilmistir ve 1738 de yayinlanan adli kitabinin ikinci baskisinda p degismemek kosuluyla n degerinin artisiyla binom dagiliminin limit sekli yaklasim olarak gosterilmistir De Moivre in bu sonucu tarafindan 1812 de bastirilan gelistirilmistir ve bu sonuc simdi olarak isimlendirilmektedir Laplace normal dagilimi incelemekte oldugu deneylemelerde konusunda uygulamistir 1805 te Legendre cok onemli olan en kucuk kareler yontemini ortaya atmistir Gauss bu yontemi1794 ten beri kullandigini iddia etmistir ama en kesin surette hatalarin normal dagilimi varsayimi ile birlikte yayinladigi eser 1809 dadir Can egrisi teriminin ilk kullanilisi tarafindan 1875 te bir bagimsiz parcalardan olusan ikidegisirli normal hakkinda yazida can yuzeyi teriminin kullanmasina kadar goturulebilir Normal dagilim sozcugu ise Francis Galton ve tarafindan ayri ayri 1875 civarlarinda ortaya atilmistir Bu dagilima normal adi vermek bazen hatali gorulmektedir cunku bazi hallerde diger dagilimlar pratige cok daha uygunluk gostermektedirler KarakteristiklerBir olasilik dagilimini cesitli sekilde matematiksel ifadelerle karakterize etmek mumkundur Bunlar arasinda goze en iyi hitap edeni olasilik yogunluk fonksiyonu ile olur Dagilimin ozellikleri ayrica birikimli dagilim fonksiyonu momentler kumulantlar karakteristik fonksiyon moment ureten fonksiyon ve vasitasiyla da belirtilebilir Bu kavramlarin ayrintilari icin maddesine bakiniz Matematiksel notasyon kullanilmasi ile X rassal degeri icin ortalama degeri m ve varyansi s 0 olan bir normal dagilimin bulundugu soyle ifade edilir X N m s2 displaystyle X sim N mu sigma 2 Normal dagilim icin fazla kullanilmayan bir degisik parametreleme sekli de bulunmaktadir Bu bir ussu varyans yani 1 s degerine esit olan parametresi t kullanilarak yapilir Bunun avantaji sifir degerine cok yakin varyans s degerlerinin boler olmalarindan dogan limit problemlerinden ayrilma imkani saglamasi ve normal dagilimi bir bireyi olarak kullanilmasi gerektigi halde ortaya cikar Bazi merkezsel limit teoremleri icin ornegin teorisi kullanisli olmakla beraber tum olasiligi m etrafinda konsantre eden ve bir normal dagilima benzer olarak ortalama m ve varyans s 0 degerleri bulunan bir normal dagilim olarak kabul edilmemektedir buna matematiksel aciklama bu olcumde kurallarina gore gereken yogunlugun bulunmamasidir Olasilik yogunluk fonksiyonu Normal dagilim icin olasilik yogunluk fonksiyonu Normal dagilim icin surekli olasilik yogunluk fonksiyonu su fm s2 x 1s2pe x m 22s2 1sf x ms x R displaystyle varphi mu sigma 2 x frac 1 sigma sqrt 2 pi e frac x mu 2 2 sigma 2 frac 1 sigma varphi left frac x mu sigma right quad x in mathbb R Burada s gt 0 standart sapmadir bir reel parametre olan m beklenen degerdir ve f x f0 1 x 12pe x22 x R displaystyle varphi x varphi 0 1 x frac 1 sqrt 2 pi e frac x 2 2 quad x in mathbb R ifadesi standart normal dagilim icin yogunluk fonksiyonudur Standart normal dagilim m 0 ve s 1 parametreleri olan bir normal dagilimdir fm s2 displaystyle varphi mu sigma 2 ifadesinin reel dogru uzerindeki integral degeridir Ayrintilari icin maddesine bakiniz Olasilik yogunluk fonksiyonunun ozellikleri arasinda sunlar basta gelenlerdir ortalama deger m etrafinda simetrik olma hem modun hem de medyanin ortalama m degerine esit olmasi yogunluk egrisinin uzerindeki ortalamadan birer standart sapma altinda ve ustundeki noktalar arasinda yani m s ve m s noktalarinda bir bulunmasi Birikimli dagilim fonksiyonu Normal dagilim icin birikimli dagilim fonksiyonu Bir olasilik dagilimi icin birikimli dagilim fonksiyonu bir rassal degisken X icin olay olasiliginin dagiliminin x sayisina esit veya daha dusuk olmasina kadar degerlendirilmesinden ortaya cikar Normal dagilim icin birikimli dagilim fonksiyonu yogunluk fonksiyonunda kullanilan ayn terimlerle soyle ifade edilir Fm s2 x xfm s2 u du 1s2p xexp u m 22s2 du F x ms x R displaystyle begin aligned Phi mu sigma 2 x amp int infty x varphi mu sigma 2 u du amp frac 1 sigma sqrt 2 pi int infty x exp Bigl frac u mu 2 2 sigma 2 Bigr du amp Phi Bigl frac x mu sigma Bigr quad x in mathbb R end aligned Burada parametreleri m 0 ve s 1 olan standart normal dagilimi icin birikimli dagilim fonksiyonu F ile ifade edilmistir ve bu fonksiyon sudur F x F0 1 x 12p xexp u22 du x R displaystyle Phi x Phi 0 1 x frac 1 sqrt 2 pi int infty x exp Bigl frac u 2 2 Bigr du quad x in mathbb R Standart normal birikimli dagilim fonksiyonu ayni zamanda adi verilen bir ozel fonksiyon ifade edilebilir soyle ifade edilir F x 12 1 erf x2 x R displaystyle Phi x frac 1 2 Bigl 1 operatorname erf Bigl frac x sqrt 2 Bigr Bigr quad x in mathbb R Boylece terimleri ile standart normal dagilimi icin birikimli dagilim fonksiyonu soyle yazilir Fm s2 x 12 1 erf x ms2 x R displaystyle Phi mu sigma 2 x frac 1 2 Bigl 1 operatorname erf Bigl frac x mu sigma sqrt 2 Bigr Bigr quad x in mathbb R Standart normal dagilim icin birikimli dagilim fonksiyonunun tamlayici fonksiyonu yani Q x 1 F x displaystyle Q x 1 Phi x cok kere Q fonksiyonu olarak isimlendirilir ve ozellikle bu kavram muhendislik kitaplarinda buyuk onemle yer almaktadir Standart normal birikimli dagilim fonksiyonunun tersine adi verilir Bunun formulunu ifade icin once su ters hata fonksiyonu bulunur F 1 p 2erf 1 2p 1 p 0 1 displaystyle Phi 1 p sqrt 2 operatorname erf 1 2p 1 quad p in 0 1 ve bu fonksiyon kullanilarak su ters birikimli dagilim fonksiyonu ortaya cikartilir Fm s2 1 p m sF 1 p m s2erf 1 2p 1 p 0 1 displaystyle Phi mu sigma 2 1 p mu sigma Phi 1 p mu sigma sqrt 2 operatorname erf 1 2p 1 quad p in 0 1 Bu kuantil fonksiyonuna bazen fonksiyonu adi da verilir Bir probit fonksiyonu icin bir elemanter matematiksel olarak ispat edilmistir Normal dagilim icin cok iyi sonuclar verdigi anlasilan yaklasik fonksiyonlar ve yontemler ortaya cikarilmistir Bunlar arasinda sayisal entegrasyon ve yontemlerinin kullanilmasi anilabilir Birikimli dagilim fonksiyonu icin kesin alt ve ust sinirlar Buyuk degerde bir x sayisi icin standart normal dagilim birikimli dagilim fonksiyonun F x displaystyle scriptstyle Phi x degerinin bire 1 yakinsalandigi ve F x 1 F x displaystyle scriptstyle Phi x 1 Phi x in ise sifira 0 yakinsaladigi asikardir Yogunlukf displaystyle scriptstyle varphi terimleri kullanilarak su basit ust sinir x1 x2f x lt 1 F x lt f x x x gt 0 displaystyle frac x 1 x 2 varphi x lt 1 Phi x lt frac varphi x x qquad x gt 0 ifadesi yeterlidir Yerine koymak suretiyle entegresyon yontemi kullanarak ust sinir soyle ortaya cikartilabilir 1 F x x f u du lt x uxf u du x2 2 e vx2pdv e vx2p x2 2 f x x displaystyle begin aligned 1 Phi x amp int x infty varphi u du amp lt int x infty frac u x varphi u du int x 2 2 infty frac e v x sqrt 2 pi dv biggl frac e v x sqrt 2 pi biggr x 2 2 infty frac varphi x x end aligned Ayni sekilde f u uf u displaystyle scriptstyle varphi u u varphi u ifadesini ve kullanarak 1 1x2 1 F x x 1 1x2 f u du gt x 1 1u2 f u du f u u x f x x displaystyle begin aligned Bigl 1 frac 1 x 2 Bigr 1 Phi x amp int x infty Bigl 1 frac 1 x 2 Bigr varphi u du amp gt int x infty Bigl 1 frac 1 u 2 Bigr varphi u du biggl frac varphi u u biggr x infty frac varphi x x end aligned ifadesi ortaya cikartilir Bunun 1 F x displaystyle scriptstyle 1 Phi x terimleri ile cozumlenmesi yukarida ifade edilen ust siniri verir Ureten fonksiyonlar Moment ureten fonksiyon Genel olarak moment ureten fonksiyon exp tX icin olarak tanimlanir Bir normal dagilim icin moment ureten fonksiyonu su olur MX t E exp tX 1s2pexp x m 22s2 exp tx dx exp mt s2t22 displaystyle begin aligned M X t amp mathrm E left exp tX right amp int infty infty frac 1 sigma sqrt 2 pi exp left frac x mu 2 2 sigma 2 right exp tx dx amp exp left mu t frac sigma 2 t 2 2 right end aligned Bu ifade tanimda verilen ussel degerin yontemi donusturulmesi ile elde edilmistir Kumulant ureten fonksiyon moment ureten fonksiyonun logaritmasidir g t mt s t 2 Bu t terimleri ile bir kuadratik polinom oldugu icin yalniz ilk iki kumulant icin sifir olmayan deger bulunabilinir Karakteristik fonksiyon Karakteristik fonksiyon i displaystyle i sanal birim ile gosterilen exp itX displaystyle exp itX ifadesinin olarak tanimlanmistir Bu nedenle karakteristik fonksiyon moment ureten fonksiyon icindeki t displaystyle t terimininit displaystyle it ile degistirilmesi ile elde edilir Bir normal dagilimi icin karakteristik fonksiyonu sudur xX t m s MX it E exp itX 1s2pexp x m 22s2 exp itx dx exp imt s2t22 displaystyle begin aligned chi X t mu sigma amp M X it mathrm E left exp itX right amp int infty infty frac 1 sigma sqrt 2 pi exp left frac x mu 2 2 sigma 2 right exp itx dx amp exp left i mu t frac sigma 2 t 2 2 right end aligned OzellikleriNormal dagilimin su ozellikleri vardir Eger X N m s2 displaystyle X sim N mu sigma 2 ve a displaystyle a ile b displaystyle b reel sayilar ise o zaman aX b N am b as 2 displaystyle aX b sim N a mu b a sigma 2 ve varyans maddelerine bakiniz Eger X N mX sX2 displaystyle X sim N mu X sigma X 2 ve Y N mY sY2 displaystyle Y sim N mu Y sigma Y 2 ifadeleri bagimsiz normal rassal degiskenler ise o halde Bunlarin toplami U X Y N mX mY sX2 sY2 displaystyle U X Y sim N mu X mu Y sigma X 2 sigma Y 2 normal dagilim gosterir Daha ilgi cekici olarak bunun tersi de gecerlidir Eger iki bagimsiz rassal degiskenlerin toplami normal dagilim gosteriyorsa her iki degisken de ayri ayri normal dagilim gosterirler Bu olarak isimlendirilmistir Bunlarin arasindaki fark su sekilde normal dagilim gosterir Yani V X Y N mX mY sX2 sY2 displaystyle V X Y sim N mu X mu Y sigma X 2 sigma Y 2 Eger X ve Y rassal degiskenlerinin varyanslari birbirine esitse U toplam icin rassal degisken ve V fark icin rassal degisken birbirinden bagimsizdirlar soyle ifade edilir DKL X Y 12 log sY2sX2 sX2sY2 mY mX 2sY2 1 displaystyle D rm KL X Y 1 over 2 left log left sigma Y 2 over sigma X 2 right frac sigma X 2 sigma Y 2 frac left mu Y mu X right 2 sigma Y 2 1 right Eger X N 0 sX2 displaystyle X sim N 0 sigma X 2 ve Y N 0 sY2 displaystyle Y sim N 0 sigma Y 2 birbirinden bagimsiz normal rassal degiskenler ise o zaman Bunlarin carpimi yani XY displaystyle XY p displaystyle p ile soyle ifade edilen yogunluk fonksiyonu olan ozel bir dagilim gosterir p z 1psXsYK0 z sXsY displaystyle p z frac 1 pi sigma X sigma Y K 0 left frac z sigma X sigma Y right burada K0 displaystyle K 0 bir Bunlarin birbirine orani X Y Cauchy 0 sX sY displaystyle X Y sim mathrm Cauchy 0 sigma X sigma Y sekilde Cauchy dagilimi gosterir Boylece bu Cauchy dagilimi ozel bir tip olur Eger X1 Xn displaystyle X 1 dots X n bir seri bagimsiz standart normal degiskenler ise o zaman bunlarin toplami yani X12 Xn2 displaystyle X 1 2 cdots X n 2 n serbestlik dereceli bir ki kare dagilimi gosterir Normal rassal degiskenlerin standart forma donusumleri Yukarida verilen 1 ozellik sonucu olarak tum normal rassal degiskenleri standart normale donusturmek imkani vardir Eger X displaystyle X N m s2 displaystyle N mu sigma 2 ise bu halde Z X ms displaystyle Z frac X mu sigma bir standart normal rassal degisken olur yani Z displaystyle Z N 0 1 displaystyle N 0 1 Bunun bir onemli sonucu birikimli olasilik fonksiyonun bir genel normal dagilimi olmasidir Pr X x F x ms 12 1 erf x ms2 displaystyle Pr X leq x Phi left frac x mu sigma right frac 1 2 left 1 operatorname erf left frac x mu sigma sqrt 2 right right Tersini ele alirsak eger Z displaystyle Z bir standart normal dagilim ise yani Z displaystyle Z N 0 1 displaystyle N 0 1 ise o halde X sZ m displaystyle X sigma Z mu ifadesi de beklenen degeri m displaystyle mu ve varyansi s2 displaystyle sigma 2 olan bir normal rassal degiskendir Standart normal dagilim icin cesitli tablolar bulunmaktadir Cok kere bu tablolar birikimli dagilim fonksiyonu F seklindedirler Diger normal dagilimlar basit bir donusum ile standart normal dagilima donusturulup bu tablolardan biri kullanilabilir Momentler Normal dagilim icin ilk birkac momentleri sunlardir Sayi Ham moment Merkezsel moment Kumulant0 1 11 m displaystyle mu 0 m displaystyle mu 2 m2 s2 displaystyle mu 2 sigma 2 s2 displaystyle sigma 2 s2 displaystyle sigma 2 3 m3 3ms2 displaystyle mu 3 3 mu sigma 2 0 04 m4 6m2s2 3s4 displaystyle mu 4 6 mu 2 sigma 2 3 sigma 4 3s4 displaystyle 3 sigma 4 05 m5 10m3s2 15ms4 displaystyle mu 5 10 mu 3 sigma 2 15 mu sigma 4 0 06 m6 15m4s2 45m2s4 15s6 displaystyle mu 6 15 mu 4 sigma 2 45 mu 2 sigma 4 15 sigma 6 15s6 displaystyle 15 sigma 6 07 m7 21m5s2 105m3s4 105ms6 displaystyle mu 7 21 mu 5 sigma 2 105 mu 3 sigma 4 105 mu sigma 6 0 08 m8 28m6s2 210m4s4 420m2s6 105s8 displaystyle mu 8 28 mu 6 sigma 2 210 mu 4 sigma 4 420 mu 2 sigma 6 105 sigma 8 105s8 displaystyle 105 sigma 8 0 Normal dagilim icin ilk iki kumulant disindaki kumulant degerler hep sifira esittir Daha buyuk sayiya bagli 2k displaystyle 2k derecede ve m 0 displaystyle mu 0 merkezsel momenti su formul kullanilarak elde edilebilir E x2k 2k 2kk s2k displaystyle E left x 2k right frac 2k 2 k k sigma 2k Normal rassal degisirler icin uretici degerler Bilgisayarla simulasyon yapilmakta iken cok kere bir normal dagilim icin degerlerin uretilmesi gerekir Bunun icin birkac degisik yontem kullanilabilir En basit sekilde bir standart normal dagilim birikimli olasilik fonksiyonunun tersini almak suretiyle elde edilir Daha etkin yontemler de gelistirilmistir Cok populer olarak kullanilan yontem Box Muller algoritmasi kullanilmasi 0 1 arasinda bulunan surekli tekduze dagilim gosteren iki sayi a ve b ile baslar bunlardan su formullere gore iki standart normal dagilim gosteren c ve d sayilari soyle elde edilir c 2ln a cos 2pb displaystyle c sqrt 2 ln a cdot cos 2 pi b d 2ln a sin 2pb displaystyle d sqrt 2 ln a cdot sin 2 pi b Bunlarin elde edilmesi donusumun bazinda yukarida 4 ozellikte gosterilen 2 serbestlik derecesi olan bir ki kare dagiliminin kolayca uretilebilinen bir ustel rassal degisken olmasi gercegine dayandirilir Halen en etkin sekilde normal dagilimi simulasyonu icin kullanilmaktadir Merkezi limit teoremi n 48 ve p 1 4 parametreleri olan bir binom dagiliminin olasilik kutle fonksiyonun yaklasimi olarak m 12 ve s 3 parametreli bir normal dagilimin olasilik yogunluk fonksiyonunun gosterinimi Sonlu varyanslari olan rassal degiskenler ve benzeri kosullar altinda buyuk sayida rassal degiskenlerin toplami yaklasik olarak normal dagilim gosterir Bu merkezsel limit teoremidir Merkezsel limit teoreminin pratik onemi normal birikimli dagilim fonksiyonunun bazi diger birikimli dagilim fonksiyonunun yaklasik olarak kullanabilmesindedir Ornegin Parametreleri n ve p olan bir binom dagilim icin eger buyuk degerlerde ama 0 veya 1e cok yakin olmayan n vep bulunursa bir normal dagilimina yaklasmis olduklari kabul edilebilir Bazi istatistik kitaplari bu yaklasimin np ve n 1 p degerlerinin her ikisi icin en asagi 5 olmasi halinde uygulanmasini ve eger 5 olurlarsa bir kullanilmasini tavsiye ederler Eger yaklasik olarak normal dagilimi kullanilirsa bunun parametreleri m np ve s2 np 1 p olarak bulunmasi gerekir Eger l nin degeri buyuk ise l parametreli Poisson dagilimi icin yaklasik olarak normal dagilim kullanilabilir ve bu halde yaklasik normal dagilimin parametreleri m s2 l olarak bulunur Bu yaklasimlarin yeter derecede dogru olup olmayacagi sonuclarin ne maksatlarla kullanacaklarina ve normal dagilimin yakinsalama oranina baglidir Bu tip yaklasimlar dagilimin kuyruk degerlerine yaklastikca gittikce daha cok hatali olacaklardir birikimli dagilim fonksiyonu icin yaklasim hatasi icin genel ust sinirlari gosterir Sonsuz olarak bolunebilme Normal dagilimlar olasilik dagilimlaridir Bir ortalama degeri m bir varyans degeri s2 0 ve bir dogal sayi degeri n verildigi zaman n bagimsiz rassal degiskenlerin toplami olan X1 Xn su normal dagilimi gosterir X1 X2 Xn N m n s2 n displaystyle X 1 X 2 dots X n sim N mu n sigma 2 n c Daha fazla ayrinti icin ile maddelerine bakiniz Dengelilik Normal dagilimlar kesinlikle gosteren olasilik dagilimlaridir Standart sapma ve guven araliklari acikliklari Koyu mavi ortalamadan bir standart sapma daha kucuktur Bir normal dagilim icin bu koyu mavi egrinin altinda kalan alan toplam alanin 68 ini kapsar Ortalamadan iki standart sapma araliginda noktalar icin egrinin altinda kalan alan acik orta ve koyu mavi alan toplam alanin 99 7sini kapsar Bir normal dagilimdan secilmis degerlerin 68i ortalama olan m in bir standart sapma s gt 0 uzakligindaki noktalar arasindadir degerlerin neredeyse 95i m den iki standart sapma uzakliklar araliginda ve 99 7 uc standart sapma uzakliklar araliginda bulunur Buna veya adi da verilir Daha dogru bir kesin ifadeyle m ns ve m ns arasindaki can egrisinin altinda kalan alanin birikimli normal dagilim fonksiyonu soyle verilir Fm s2 m ns Fm s2 m ns F n F n 2F n 1 erf n 2 displaystyle begin aligned amp Phi mu sigma 2 mu n sigma Phi mu sigma 2 mu n sigma amp Phi n Phi n 2 Phi n 1 mathrm erf bigl n sqrt 2 bigr end aligned Burada erf Ondalik sayilarla 12 basamak kullanilarak 1 2 6 sigma noktalarina kadar degerler soyle verilir n displaystyle n erf n 2 displaystyle mathrm erf bigl n sqrt 2 bigr 1 0 6826894921372 0 9544997361043 0 9973002039374 0 9999366575165 0 9999994266976 0 999999998027 Ikinci tablo can egrisinin altindaki alan icin degerlerin bulunmasini saglamak uzere cok zaman kullanilan katsayi degerlerindeki sigma carpanlarinin ters iliskisini gosterir Normal dagilim gosteren veya asimtotda normal olan kestirimler icin belirtilmis olan seviyelerde asimtotik saptamak icin bu degerler cok kullanislidir erf n 2 displaystyle mathrm erf bigl n sqrt 2 bigr n displaystyle n 0 80 1 281550 90 1 644850 95 1 959960 98 2 326350 99 2 575830 995 2 807030 998 3 090230 999 3 29052 Bu tabloda sol taraftaki sutun bilinen bir araliga dusecek degerlerin orani verilmekte ve soldaki n sutunu ise araligin genisliginin kac tane standart sapma birimini ihtiva ettigini gostermektedir Ustel ailesi sekli Normal dagilim bir iki parametreli elemanidir Iki tane dogal parametresi m ve 1 s2 olur ve dogal istatistikleri X ve X2 dir Kanonik seklinin parametreleri ms2 displaystyle mu over sigma 2 ve 1s2 displaystyle 1 over sigma 2 olup yeterli istatistikleri x displaystyle sum x ve 12 x2 displaystyle 1 over 2 sum x 2 olur Iliskili dagilimlarEger R X2 Y2 displaystyle R sqrt X 2 Y 2 ise ve burada X N 0 s2 displaystyle X sim N 0 sigma 2 aveY N 0 s2 displaystyle Y sim N 0 sigma 2 iki bagimsiz normal dagilimlarsa o halde R Rayleigh s2 displaystyle R sim mathrm Rayleigh sigma 2 bir Rayleigh dagilimi olur Eger Y k 1nXk2 displaystyle Y sum k 1 nu X k 2 ise ve burada k 1 n displaystyle k 1 dots nu icin Xk N 0 1 displaystyle X k sim N 0 1 ise ve bunlarin hepsi bagimsizlarsa o zaman Y xn2 displaystyle Y sim chi nu 2 serbestlik derecesi n displaystyle nu olan bir ki kare dagilimiolur Eger iki bagimsiz normal dagilimli X1 N 0 1 displaystyle X 1 sim N 0 1 ve X2 N 0 1 displaystyle X 2 sim N 0 1 icin Y X1 X2 displaystyle Y X 1 X 2 ise o zaman Y Cauchy m 0 8 1 displaystyle Y sim mathrm Cauchy mu 0 theta 1 bir Cauchy dagilimidir Eger Y eX displaystyle Y e X ve X N m s2 displaystyle X sim N mu sigma 2 ise o zamanY Log N m s2 displaystyle Y sim mbox Log N mu sigma 2 bir iliski Eger X Levy SaS 2 b s 2 m displaystyle X sim textrm Levy S alpha textrm S 2 beta sigma sqrt 2 mu ise o halde X N m s2 displaystyle X sim N mu sigma 2 Eger X N m s2 displaystyle X sim N mu sigma 2 o halde Xi alttan A displaystyle A da ve usttenB displaystyle B de kesmek suretiyle ortalamasi E X m s f1 f2 T displaystyle E X mu frac sigma varphi 1 varphi 2 T olan bir rassal degisken ortaya cikarilir Burada T F B ms F A ms f1 f A ms f2 f B ms displaystyle T Phi left frac B mu sigma right Phi left frac A mu sigma right varphi 1 varphi left frac A mu sigma right varphi 2 varphi left frac B mu sigma right olur ve f displaystyle varphi bir standart normal rassal degisken icin bir olasilik yogunluk fonksiyonu olur Eger X displaystyle X normal dagilim gosteren bir rassal degisken ise ve Y X displaystyle Y X ise o halde Y displaystyle Y bir gosterir Betimsel ve cikarimsal istatistiklerPuanlar Puan verme cesitlerinin cogu normal dagilima bagli olarak ortaya cikarilmistir Degisik puanlama yontemleri arasinda ve T puanlamasi vb sayilabilir Davranissal bilimlerde kullanilan bircok istatistiksel yordamlar puanlarin normal dagilim gosterdigi varsayimina dayanilarak gelistirilmistir Ornegin cok kisiye uygulanan imtihan veya zeka testleri icin bir can egrisine dayanan not verilip imtihan veya test sonuclarinin gruplanmasi veya siralanmasi imtihan veya test notlarinin normal dagilim gosterdigi varsayimina dayandirilir Normallik sinamalari Normallik sinamalari verilmis bir veri dizisinin normal dagilima benzerliginin incelenmesidir Bu sinamalarda veri dizisinin normal dagilima benzer olmasidir Bu nedenle normal olmayan veri icin yeter derecede kucuk bir p degeri yani genellikle 0 05 ten veya 0 01den kucuk ortaya cikacak ve sifir hipotez olan veri dizisinin normal dagilima benzerligi hipotezinin ret edilmesine neden olacaktir Kolmogorov Smirnov sinamasi Anderson Darling sinamasi Shapiro Wilk sinamasi gosterimi Jarque Bera sinamasiParametrelerin kestirimi Parametrelerin maksimum olabilirlik kestirimi Bir dusunce denemesi olarak bir seri normal dagilim icin X1 Xn displaystyle X 1 dots X n Gauss Egrisi ifadesinin her biri digerinden bagimsiz oldugu dusunulsun Her bir ifade beklenen degersi m ve varyansi s2 gt 0 olan normal dagilimlar gostermektedir Istatistikciler bu n rassal degiskenin gozumlenen degerlerinin normal dagilim gosteren bir anakutleden ortaya cikan bir n buyuklugunde bir orneklem oldugunu kabul etmektedirler Bu orneklemden gozlenen degerlere dayanarak anakutle ortalamasi m ve anakutle standart sapmasi kestirimcilerini bulmak arzu edilmektedir Bu n sayidaki bagimsiz rassal degisken icin surekli ortak olasilik yogunluk fonksiyonu soyle verilir f x1 xn m s i 1nfm s2 xi 1 s2p n i 1nexp 12 xi ms 2 x1 xn Rn displaystyle begin aligned f x 1 dots x n mu sigma amp prod i 1 n varphi mu sigma 2 x i amp frac 1 sigma sqrt 2 pi n prod i 1 n exp biggl 1 over 2 Bigl x i mu over sigma Bigr 2 biggr quad x 1 ldots x n in mathbb R n end aligned m ve s fonksiyonlari olarak X1 Xn gozlemlerine dayanan sudur L m s Csnexp i 1n Xi m 22s2 m R s gt 0 displaystyle L mu sigma frac C sigma n exp left sum i 1 n X i mu 2 over 2 sigma 2 right quad mu in mathbb R sigma gt 0 Burada C gt 0 herhangi bir sabittir Bunun genellikle X1 Xn degiskenlerine bile dayanarak baglandigi kabul edilmektedir ama hesaplanan parametrelere gore log olabilirlik fonksiyonlarin kismi turevleri bulundugu zaman sabit olduklari icin elimine edilmektedirler Maksimum olabilirlik yontemine gore olabilirlik fonksiyonu maksimize eden m ve s degerleri teorik anakutle parametreleri olan m ve s icin kestirim olduklari kabul edilmektedir Genel olarak iki degiskenli bir fonksiyonun maksimum degerini hesaplanmaktayken kullanilir Ancak burada maksimum hesaplama daha kolaylasmaktadir cunku olabilirlik fonksiyonunu maksimize eden m degeri bulunmakta iken s anakutle parametresi olan sya bagimli olmayan bir sabittir Bundan dolayi ilk olarakm degeri bulunur bu deger olabilirlik fonksiyonundaki m degiskeni yerine konulur ve bu yeni tek degiskenli fonksiyonu maksimize eden s degeri bulunur olabilirlik fonksiyonunun su toplam ifadesinin bir azalan fonksiyonu oldugu bilinmektedir i 1n Xi m 2 displaystyle sum i 1 n X i mu 2 Bu toplam ifadeyi minimize edecek m degerini bulmak istenmektedir Su ifade X n X1 Xn n displaystyle overline X n X 1 cdots X n n n gozleme dayanan bir orneklem ortalamasidir Boylece i 1n Xi m 2 i 1n Xi X n X n m 2 i 1n Xi X n 2 2 X n m i 1n Xi X n 0 i 1n X n m 2 i 1n Xi X n 2 n X n m 2 displaystyle begin aligned sum i 1 n X i mu 2 amp sum i 1 n bigl X i overline X n overline X n mu bigr 2 amp sum i 1 n X i overline X n 2 2 overline X n mu underbrace sum i 1 n X i overline X n 0 sum i 1 n overline X n mu 2 amp sum i 1 n X i overline X n 2 n overline X n mu 2 end aligned Bu ifadede so terim m degiskenine baglidir ve bu terimin minimum degeri soyle bulunur m n X n displaystyle widehat mu n overline X n Iste bu ifade n sayida X1 Xn gozlem kullanarak mnun maksimum olabilirlik kestirimidir Sonuc olarak L X n s Csnexp i 1n Xi X n 22s2 s gt 0 displaystyle L overline X n sigma frac C sigma n exp biggl sum i 1 n X i overline X n 2 over 2 sigma 2 biggr quad sigma gt 0 elde edilir olabilirlik fonksiyonunun logaritmasi olan log olabilirlik fonksiyonu matematik notasyona gore kucuk harflerle yaniℓ displaystyle ell yazilmasi alisilagelmistir ℓ X n s log C nlog s i 1n Xi X n 22s2 s gt 0 displaystyle ell overline X n sigma log C n log sigma sum i 1 n X i overline X n 2 over 2 sigma 2 quad sigma gt 0 Sonra sℓ X n s ns i 1n Xi X n 2s3 ns3 s2 1n i 1n Xi X n 2 s gt 0 displaystyle begin aligned partial over partial sigma ell overline X n sigma amp n over sigma sum i 1 n X i overline X n 2 over sigma 3 amp n over sigma 3 biggl sigma 2 1 over n sum i 1 n X i overline X n 2 biggr quad sigma gt 0 end aligned olur Bu turev s2 degeri 0 ile s n2 1n i 1n Xi X n 2 displaystyle hat sigma n 2 1 over n sum i 1 n X i overline X n 2 degeri arasinda ise pozitif olur bu degere esitse turev sifira esittir bu degerden buyukse turev negatif olur Bu analizin sonucu olarak bu bulunan n gozlemli orneklem icin s2 bir maksimum olabilirlik kestirimidir ve bunun kare koku s icin maksimum olabilirlik kestirimdir Bu kestirim yanis n2 displaystyle hat sigma n 2 bir kestirimdir Alisilagelen yansiz kestirim n n 1 carpi bu kestirimdir Ancak yanli maksimum olabilirlik kestirimi icin yansiz kestirimden daha kucuktur Parametrelerin yansiz kestirimi Bir orneklemden elde edilen anakutle ortalamasinin maksimum olabilirlik kestirimcisi anakutle ortalamasinin bilinir Ayni sekilde anakutle ortalamasi onsel olarak bilinirse varyans icin maksimum olabilirlik kestrimcisi de yansiz kestirimcidir Ancak eger elimizde bir orneklem bulunuyorsa ama bu orneklemin geldigi anakutlenin ne ortalamasinin ne de varyansinin degerlerin bilmiyorsak anakutle varyansinin yansiz kestrimicisi s2 displaystyle sigma 2 soyle ifade edilir S2 1n 1 i 1n Xi X 2 displaystyle S 2 frac 1 n 1 sum i 1 n X i overline X 2 Eger tum Xi birbirinden bagimsiz ve ayni sekilde dagilim gosterirlerse bu orneklem varyansi bir Gamma dagilimigosterir S2 Gamma n 12 2s2n 1 displaystyle S 2 sim operatorname Gamma left frac n 1 2 frac 2 sigma 2 n 1 right Ayrica bakinizStandart normal dagilim Verileri normal dagilima donusturmek icin basit teknikler Sayi teorisi icinde normal dagilimin meydana cikisi Iannis Xenakis Muzik icin Gauss tipi dagilimi Log normal dagilim Cokdegisirli normal dagilim Matris normal dagilimi Iki tane birbirinden bagimsiz olmadan birbirleri ile korelasyon gostermeyen normal dagilimli rassal degisken icin ornek verilmistir Bu ornek icin gecerli degildir Student in t dagilimiKaynakca H Gavil 2003Dis baglantilarNormal dagilim Mathworld Normal dagilim 5 Temmuz 2008 tarihinde Wayback Machine sitesinde GNU Bilimsel Kutuphane Referans Elkitabi Gauss tipi dagilim 8 Haziran 2008 tarihinde Wayback Machine sitesinde PlanetMath Normal rassal degisken 16 Mayis 2008 tarihinde Wayback Machine sitesinde Yazilim sonuclari ve uygulamalari Normal dagilim tablosu 18 Aralik 2020 tarihinde Wayback Machine sitesinde Dagilim hesaplayicisi Normal ki kare ve F dagilimi icin kritik degerler ve olasilik hesaplayicisi29 Ocak 2007 tarihinde Wayback Machine sitesinde Normal dagilimlar icin Java Appleti 20 Mart 2008 tarihinde Wayback Machine sitesinde Etkilisimli normal dagilim da dahil dagilim modelcisi 16 Subat 2008 tarihinde Wayback Machine sitesinde Etkilesimli Standart normal egrisi gosterimi 22 Subat 2008 tarihinde Wayback Machine sitesinde Standart normal egrinin tek kuyruk ve iki kuyruk alani icin cabuk goz onune getirme yazilimi Online hesap makinesi Normal dagilim 10 Mart 2014 tarihinde Wayback Machine sitesinde Algoritmalar ve yaklasimlar sitmo com Hazirlayan Peter J Acklam Birkac degisik ornekler var gatech edu Matematiksel Fonksiyonlar icin Elkitabi P x ve Z x icin Polinom ve Rasyonel Yaklasimlar 17 Nisan 2008 tarihinde Wayback Machine sitesinde Abramowitz ve Stegun
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans