Kütleçekim dalgaları

Genel görelilik

Genel bakış Tarihçe Testler Einstein denklemleri Eşdeğerlik ilkesi Kara delik Kütleçekimsel dalga Kütleçekimsel mercek Olay ufku Schwarzschild çözümü Tekillik

İlgili başlıklar

Albert Einstein Astrofizik Kozmoloji Kütleçekim Özel görelilik Riemann geometrisi Stephen Hawking

düzenle

Kütleçekimsel dalga veya kütleçekim dalgası (KÇD), fizikte uzayzaman eğriliğinde oluşan kırışıklık olup kaynağından dışarıya doğru bir dalga olarak yayılır. Albert Einstein tarafından 1915'te varlığı öngörülen bu dalgalar,Genel Relativite Teorisi'ne dayanarakkütleçekimsel ışıma şeklinde enerji naklederler. Tespit edilebilir kütleçekimsel dalga kaynakları, beyaz cüce, nötron yıldızı veya kara delik içeren çift yıldız sistemleri olabilir. Kütleçekimsel dalgaların varlığı, kendisiyle fiziksel etkileşimlerin yayılma hızını sınırlama kavramını getiren ve genel relativite ile ilgili Lorentz değişmezliğinin muhtemel bir sonucudur. Bu dalgaların, etkileşim hızını sonsuz olarak kabul eden Newton'un Çekim Teorisi'nde varlığı mümkün değildir.

Doğrudan doğruya tespit edilemeyen kütleçekimsel ışımanın varlığı 2016 yılına kadar dolaylı olarak bilinmekteydi. Kütleçekimsel dalgaların matematiksel denksizliklerden ziyade olduğunu gösteren Hulse-Taylor çift yıldızı ile ilgili ölçümleri içeren çalışmalar, 1993'te Nobel Fizik Ödülü'ne layık görülmüştür. Muhtelif kütle-çekimsel dalga detektörleri mevcut olmakla birlikte bugüne kadar bu dalgaların tespitini yapamamışlardır.

11 Şubat 2016'da Lazer Interferometer Yerçekimi Dalgası Gözlemevi (LIGO) çalışma grubu, birbirleri ile çarpışan iki kara delikten yer çekimsel dalgalar tespit edildiğini açıkladı. Keşfedilen yerçekimi dalgalarının iki kara deliğin 1,3 milyar ışık yılı ötedeki çarpışmasıyla ortaya çıktığı ve çarpışma sesinin kaydedildiği ifade edildi.

Giriş

Einstein'in Genel Relativite Teorisi'ne göre çekim, uzayzamanın eğriliğinden doğan bir fenomen olarak ele alınır. Bir noktadaki bu eğrilik, orada bulunan bir kütlenin varlığından kaynaklanır. Genel olarak bir hacim ne kadar çok kütle içinde bulundurursa bu hacmin çeperindeki uzayzaman da o derece eğrilecektir. Kütleli cisimler hareket ettiğinde buradaki eğrilik, bu cisimlerin hareketini yansıtacak şekilde değişir. Özel durumlarda hızlana cisimler, bu eğriliği değiştirerek dışarıya doğru dalgasal biçimde ışık hızıyla yayılmasını sağlarlar.

Kütleçekimsel dalga uzaktaki bir gözlemcinin yanından geçtiğinde gözlemci, uzayzamanın oluşan zorlanmadan dolayı çarpıldığını fark eder. Serbest cisimlerarası uzaklıklar, dalga geçerken dalganın frekansına uygun şekilde ritmik olarak artar ve azalır. Bu hareket, serbest cisimlere dengede olmayan bir kuvvet etki etmemiş olmasına rağmen olur. Hareketin genliği, cismin dalga kaynağına olan uzaklığıyla ters orantılıdır. İçeri doğru birbirine yaklaşarak dönen (İng. İngilizce: inspiralling) kaynaştığında kütleçekimsel dalgalar için kuvvetli bir kaynak oldukları tahmin edilmektedir. Çünkü bu kaynaşma sırasında birbirine iyice yaklaşan gök cisimlerinin kütleleri çok büyük bir ivmeyle birbirlerine doğru hareket etmektedirler. Bu tür kaynaklara olan büyük uzaklıklardan dolayı Dünya'da eğriliklerin 1'e 10²⁰'den az olması beklenmektedir. Başka bir ifadeyle Dünya ile Güneş arası uzunluğunda olan hayalî bir detektörün en az 1,5 nm'lik bir değişikliği farketmesi yetersiz kalacaktır. Bilginler, bu dalgaların varlığını daha da hassas detektörlerle göstermeye çalışmaktadırlar. 2012'deki en hassas detektör, LİGO ve rasathanelerinde kullanılmakta olup 5×10^-22'lik bir değişimi fark edebilecek kapasitededirler. Bu rasathanelerde kütleçekimsel dalgaların tespit edilememesi, bu tür olayların çokluğuna bir üst sınırlama getirmektedir. Uzaya fırlatılmak üzere ESA'nın geliştirmekte olduğu rasathanesi daha bitmemiştir.

Prensip olarak KÇD'ler her genlikte yayılabilir. Fakat çok düşük frekanstaki KÇD'leri tespit etmek imkânsızken çok yüksek frekanslarda "yayın" yapabileceğine inanılan bir kaynak bilinmemektedir. Stephen W. Hawking ve , 10^-7 ilâ 10¹¹ Hz arası frekanslarda dalga üretebilecek muhtemel kaynakları listelemişlerdir.

Geçen kütleçekimsel dalgaların etkileri

Artı polarizasyonlu bir kütleçekimsel dalganın parçacık halkasında bıraktığı etki.

Çapraz polarizasyonlu bir kütleçekimsel dalganın parçacık halkasında bıraktığı etki.

Geçmekte olan bir KÇD'nın etkisi, (ekranınınız yüzeyi gibi) kusursuz düz bir uzayzaman düzleminde bulunan hareketsiz test parçacıklarınca görüntülenebilir. KÇD, parçacıklar arasından (ekranınıza bakış doğrultusu gibi) bu düzleme dik doğrultuda geçerken bu parçacıklar, animasyonda da görüldüğü üzere uzayzamanın çarpıklığını izleyerek çapraz şekilde salınırlar. Parçacıkların kapsadığı alan bu sırada değişmediği gibi parçacıklar, dalganın yayılma yönünde hareket etmezler.

Animasyonda gösterilen salınımlar, tartışmada anlaşılması için abartılmıştır. Gerçekte KÇD'nın genliği, belirtildiği gibi çok küçüktür. Fakat bu abartılmış salınımlar, mesela dairesel hareket eden bir kütle çiftince meydana getirilen KÇD'larla görülen salınım tarzını görüntülerler. Bu durumda KÇD'nın genliği sabitken polarizasyon düzlemi, dairesel hareketin periyodunun iki katıyla değişir veya döner. Böylece zamanla değişen KÇD boyu (veya periyodik uzayzaman gerinimi), animasyonda görülen bir değişime uğrar. Yörünge eliptikse KÇD'nın genliği, Einstein'ın göre zamanla değişir.

Diğer dalgalarda olduğu gibi KÇD'ları tanımlayan birkaç kullanışlı özellikleri vardır:

• Genlik: Genellikle ${\displaystyle h}$ ile simgelenir. Animasyonda gerilme veya sıkışma olarak görülen hareketin bir kesri olan genlik, dalganın boyudur. Burada gösterilen genlik, kabaca ${\displaystyle h=0{,}5}$ veya %50'dir. Dünya'dan geçmekte olan KÇD'ları, burada gösterilenin birçok bilyonda biri kadardır — ${\displaystyle h\approx 10^{-20}}$. Burada bu büyüklüğün elektromanyetik dalganın ${\displaystyle {\frac {dh}{dt}}}$ olan genliği ile benzeşmediğine dikkat çekilmelidir.
• Frekans: Genelde f ile simgelenir. 1/iki ardışık en büyük gerilme veya sıkışma arasında geçen zaman olan bu büyüklük, salınım frekansını gösterir.
• Dalga boyu: Genelde ${\displaystyle \lambda }$ ile gösterilen bu büyüklük, en büyük gerilme veya sıkışma arası uzaklıktır.
• Hız: Dalga üzerinde (mesela en büyük gerilme veya sıkışma yerindeki) bir noktanın hızıdır. Küçük genlikli KÇD'lar için bu hız, ışık hızına eşittir (${\displaystyle c}$).

Bir KÇD'nın hızı, dalga boyu ve frekansı, gibi ${\displaystyle c=\lambda {\dot {f}}}$ denklemiyle bağıntılıdır. Mesela buradaki animasyonlar, takriben her iki saniyede bir kere salınırlar. Bu salınım, 0,5 Hz'lik bir frekansa ve 600.000 km'lik ya da Dünya çapının 47 katındaki bir dalga boyuna tekabül eder.

Yukarıdaki örnekte aslında dalganın bir ayrıcalığı vardır. Dalganın edildiğini farz ettik. Böyle dalgalar ${\displaystyle h_{\,+}}$ şeklinde yazılır. Bir KÇD'nın polarizasyonu, bir elektromanyetik dalganın polarizasyonu gibi olmakla birlikte KÇD'da 90° yerine 45°'dir. Bilhassa "çapraz" polarizasyonlu bir KÇD (${\displaystyle h_{\,\times }}$) olsaydı, test parçacıkları üzerindeki tesiri temelde aynı, fakat ikinci animasyondaki gibi 45° dönmüş olacaktı. Işık polarizasyonundaki gibi KÇD'ların polarizasyonu da dairesel polarizasyon olarak da ifade edilebilirdi. KÇD'lar, kaynaklarının tabiatından dolayı polarizedirler. Bir dalganın polarizasyonu, bir sonraki bölümde görüleceği gibi kaynağından geldiği açıya bağlıdır.

Kütleçekimsel dalgaların kaynakları

Farklı kütlede iki yıldız dairesel yörüngededirler. Her biri, kırmızı küçük artı işaretiyle gösterilmiş ortak ağırlık merkezi etrafında dönmektedir. Bu çift yıldızda büyük kütle küçük yörüngededir.

Genel olarak KÇD'lar hızlanan cisimlerden kusursuz küresel ya da silindirik simetrik hareket yapmamaları halinde yayılırlar. Döner halter, bu tür hareketlere basit bir örnektir: eğer bir mile bağlı tekerlekler gibi tam ortadan çevrilirlerse KÇD yaymayacaktır. Eğer tekerlerler milin tam ortasından değil de birbiri etrafında dönen gök cisimleri gibi başka bir eksen etrafında dönerlerse KÇD'lar teoriye göre yayılır. Kütlesi ve dönüş hızı ne kadar yüksekse o derece fazla kütleçekimsel ışıma yayacaktır. Eğer iki halter tekerleğinin birbiri etrafında hızlıca dönen nötron yıldızları ya da kara delikler gibi büyük kütleli yıldızlar olduğunu farz edersek hatırı sayılır miktarda kütleçekimsel ışıma uzaya yayılacaktır.

Daha detaylı örnekler:

• Hemen hemen Kepler'si olan düzlemsel yörüngede birbiri etrafında bir gezegenin yıldızı etrafında döndüğü gibi dönen iki cisim ışıyacaktır.
• Eksenine göre simetrik olmayan (ve mesela ekvatorunda bir kabarık ya da çukuru olan bir planetoid ışıyacaktır.
• Teorik olarak simetrik olarak patlayanlar hariç bir süpernova ışıyacaktır.
• Yalıtılmış ve kendi etrafında dönmeyen katı bir cisim, sabit hızla hareket ettiğinde ışımayacaktır. Bu durum doğrusal momentumun korunumu prensibinin sonucu olarak düşünülebilir.
• Kendi etrafında dönen bir disk ışımayacaktır. Bu durum açısal momentumun korunumu prensibinin sonucu olarak düşünülebilir.
• Küresel simetrik nabız gibi titreşen (yani sıfırdan farklı monopol momenti veya kütlesi olup sıfır kuadrupol momenti olan) bir yıldız ışımayacaktır. Bu durum, uygundur.

Daha teknik bir ifadeyle yalıtılmış bir sistemin stres-enerji tensörünün kuadrupol momentinin üçüncü türevi (veya ninci çoklu kutup momentinin zamana göre ninci türevi), KÇD yayabilmesi için sıfırdan farklı olmalıdır. Bu da elektromanyetik ışıma için gereken elektriksel yük ya da akımın değişen dipol momentine benzer.

Birbiri etrafında dönen cisimlerin ışıdığı güç

KÇD'lar, kaynaklarından öteye enerji taşırlar. Birbiri etrafında dönen cisimlerde bu, zamanla içe doğru helezon şeklinde birbirlerine yaklaşmalarına ve yörünge çapının küçülmesine yol açar. Mesela iki kütleden meydana gelen Dünya-Güneş sistemi gibi birbiri etrafında ışık hızına nispetle yavaşça dönen basit bir sistem düşünün. Bu iki kütlenin birbiri etrafında dairesel bir yörüngede ${\displaystyle x}$-${\displaystyle y}$ düzleminde döndüğünü farzedelim. İyi bir yaklaşım için kütlelerin basit döndüğünü kabul ediyoruz. Fakat bu tür yörüngeler değişken kuadrupol momenti temsil ederler. Dolayısıyla sistem KÇD yayacaktır.

Her iki kütlenin ${\displaystyle m_{1}}$ ve ${\displaystyle m_{2}}$ olduğunu ve birbirlerinden ${\displaystyle r}$ uzakta bulunduklarını farz edelim. Bu sistemin yaydığı güç

${\displaystyle P={\frac {dE}{dt}}=-{\frac {32}{5}}\,{\frac {G^{4}}{c^{5}}}\,{\frac {(m_{1}m_{2})^{2}(m_{1}+m_{2})}{r^{5}}}}$,

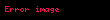
'dür. Burada G , c vakumdaki ışık hızı ve eksi işareti de gücün sistemden dışarıya doğru yayıldığını gösterir. Güneş ve Dünya sistemi gibi bir sistem için ${\displaystyle r}$ 1,5×10¹¹ m ve ${\displaystyle m_{1}}$ ve ${\displaystyle m_{2}}$ de 2×10³⁰ kg ve 6×10²⁴ kg civarıdır. Bu durumda güç 200 vattır. Bu değer, takrîben 3,86×10²⁶ watt olan ile kıyaslanınca küçüktür.

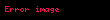
Teoride kütleçekimsel ışımayla enerji kaybı, zamanla Dünya'yı Güneş'in içine düşürür. Fakat Güneş etrafında dönen Dünya'nın toplam (potansiyel ve kinetik) enerji, takriben 1,14×10³⁶juldür. Bunun saniyede ancak 200 julü kütleçekimsel ışımayla kaybolduğundan yörünge, günde 1×10^-15 metre ya da takriben bir protonun çapı kadar büzülür. Bu büzülmeyle Dünya'nın helezonlar çizerek Güneş'le bu yüzden kaynaşması, Kâinat'ın yaşının 1×10¹³ katı kadar sürmelidir. Bu hesap r'nin zamanla azalmasını göz ardı etmek olmasına rağmen sürenin büyük bir kısmında cisimler birbirinden çok uzakta ve az miktarda ışımaktadır; yani bu örnekteki bu dikkatsizlikten doğan fark küçüktür. Sadece birkaç milyar sene sonra Dünya'nın kırmızı dev hâline gelen Güneş tarafından yutulacağı tahmin edilmektedir.

Işınan kütleçekimsel enerjinin daha dramatik bir örneği, birbiri etrafında 1,89×10⁸ m (sadece 0,63 ışık saniyesi) uzaklığında dönen ve her biri Güneş kütleli olan iki nötron yıldızı oluşturur. [Güneş, Dünya'dan ortalama sekiz dakika 20 saniye uzaktadır.] Bu cisimlerin kütlelerini yukarıdaki denkleme koyunca kütleçekimsel ışımanın 1,38×10²⁸ watt olduğu görülür. Bu da Güneş'in toplam elektromanyetik ışımasının 100 mislidir.

Kütleçekimsel ışımadan dolayı yörüngenin küçülmesi

Kütleçekimsel ışıma, birbiri etrafında dönen cisimlerin enerjisini alır. Evvelâ yörüngeleri daireselleştirir, sonra da çaplarını azaltır. Yörüngenin enerjisi azaltılınca cisimlerarası uzaklık azalarak birbiri etrafında daha çabuk dönmeye başlarlar. Buna rağmen toplam açısal momentum azalmaktadır. Bu azalma, kütleçekimsel ışımayla götürülen açısal momentuma karşılıktır. Cisimlerin birbirine olan uzaklığın zamana göre azalma nispeti şu formülle hesaplanır:

${\displaystyle {\frac {dr}{dt}}=-{\frac {64}{5}}\,{\frac {G^{3}}{c^{5}}}\,{\frac {(m_{1}m_{2})(m_{1}+m_{2})}{r^{3}}}\ }$.

Buradaki değişkenler, bir önceki denklemdekilerle aynıdır.

Yörünge, yarıçapın üçüncü kuvvetiyle ters orantılı olarak küçülür. Yarıçap, ilk değerinin yarısına indiğinde küçülmesi sekiz kere daha hızlanmış olur. Kepler'in üçüncü kanununa göre dönüş hızı bu noktada 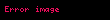${\displaystyle {\sqrt {8}}=2{,}828}$ katına ya da neredeyse başdaki hızın üç misline çıkacaktır. Yarıçap azalınca kütleçekimsel ışımaya giden güç daha da artar. Önceki denklemden de görülebileceği gibi ışıdığı güç, yarıçapın beşinci kuvvetiyle ters orantılı olarak artar. Bu da bu durumda 32 kat demektir.

Bundan önce verilen değerleri Güneş ve Dünya için kullanırsak Dünya yörüngesinin saniyede 1,1×10^-20 metre küçüldüğü ortaya çıkar. Bu da yılda 3,5×10^-13 m'dir ya da çapının 1/300'üdür. Başka bir ifadeyle kütleçekimsel ışımanın Dünya'nın yörüngesine etkisi, Kâinat'ın bütün ömrü boyunca dahî ihmâl edilebilecek kadar azdır. Birbirine daha yakın dolanan cisimler için bu böyle değildir.

Daha pratik bir örnek, Güneş benzeri bir yıldızın kütlesi çok bir kara delik etrafındaki yörüngesidir. Samanyolu'muz, merkezi olan Sagittarius A'da potansiyel olarak 4.000.000 Güneş kütlesi olan bir kara deliğe sahiptir. Buna benzer , neredeyse her galaksinin merkezinde bulunmaktadır. Bu örnek için iki milyon Güneş kütlesine sahip bir kara deliğin etrafında 1,89×10¹⁰ m (63 ışık saniyesi) uzaklıkta dönen bir Güneş kütleli bir yıldız farz edelim. Kara deliğin kütlesi 4×10³⁶ kg ve 6×10⁹ m'dir. Yörüngenin periyodu 1.000 s veya 17 dakikanın biraz altında olacaktır. Güneş kütleli yıldız, merkezdeki kara deliği saniyede 7,4 metre ya da her dolanımda 7,4 km yaklaşacaktır. Çarpışma çok sürmeden olacaktır.

Bir çift Güneş kütleli nötron yıldızı, birbirlerinden 1,89×10⁸ m (189.000 km) uzakta olduğu hâlde birbirleri etrafında dönmektedirler. Bu da Güneş'in çapının 1/7'sinden biraz daha az ya da 0,63 ışık saniyesidir. Yörünge periyodu 1.000 s olacaktır. Yeni kütle ve yarıçapı yukarıdaki formüldeki yerine koyunca yörüngenin küçülmesi 3,7×10^-6 m/s veya dönüş başına 3,7 mm'dir. Bu da yılda 116 metredir ve kozmik zaman ölçeğinde ihmâl edilemez.

Bunun yerine bu nötron yıldızlarının 1,89×10⁶ m (1890 km) uzaktan birbiri etrafında döndüklerini farz edelim. Periyotları 1 s ve yörüngesel hızları ışık hızının 1/50'sidir. Yörüngeleri her devirde 3,7 m küçülecektir. Yakın çarpışma kaçınılmazdır. Yörüngeden kontrolden çıkarcasına devam eden enerji kaybıyla yıldızlararası uzaklık daha hızlı şekilde küçülecektir. Sonuçta bir kara deliği oluşturup artık kütleçekimsel dalga yaymayacaklardır. Buna İngilizcede inspiral denir.

Yukarıdaki denklem, yarıçapın değişim hızı yarıçapa bağlı olduğu ve böylece sâbit olmadığından bu yörüngenin ömrünü doğrudan hesap etmek için kullanılamaz. Yörünge ömrü, bu denklemin entegrasyonuyla hesap edilebilir (bakınız bir sonraki bölüm).

Kütleçekimsel ışımadan dolayı yörüngesel ömür sınırları

Yörüngesel ömür, kütleçekimsel ışıma kaynaklarının en önemli özelliklerindendir. Kâinat'ta tespit edilebilecek kadar yakın olan çift yıldızların ortalama sayınsını belirler. Kısa ömürlü çift yıldızlar nispeten az olup kütleçekimsel ışıması kuvvetli olan kaynaklardandır. Uzun ömürlü çift yıldızlar sayıca daha çoktur, fakat zayıf kütleçekimsel dalga kaynağıdırlar. LIGO, iki nötron yıldızının kaynaşmak üzere olduğu frekans kuşağında en hassastır. Bu ışımanın olduğu zaman çerçevesi sadece birkaç saniye kadardır. Milyonlarca sene süren dönmeden sonra bir an meselesi olan bu olayı detektörün algılaması için tâlihin yaver gitmesi gerekmektedir. Böyle bir kaynaşmanın görülme ihtimâli onyılda bir kadardır.

Bir yörüngenin ömrü şu formülle hesaplanır:

${\displaystyle t={\frac {5}{256}}\,{\frac {c^{5}}{G^{3}}}\,{\frac {r^{4}}{(m_{1}m_{2})(m_{1}+m_{2})}}\ }$,

Burada r, birbiri etrafında dönen iki cismin ilk uzaklığıdır. Bu denklem, bir önceki denklemin yarıçap azalma hızına göre integralini alarak çıkarılır. Denklem, yörünge çapının sıfıra ne zaman ineceğini gösterir. Yörüngesel hız, ışık hızını hatırı sayılır bir yüzdesi olduğundan denklem hatâlı olur. Bu yüzden içeri doğru helezon yapan cisimlerin kaynaşmadan önceki birkaç milisaniyeye kadar kullanılabilir.

Kütlelerin yerine Güneş ve Dünya'nın kütlelerini ve yörünge yarıçapını koyunca bu yörünge için 3,44×10³⁰ s veya 1,09×10²³ yıl gibi çok uzun bir ömür çıkar (ki bu, takrîben Kâinat'ın yaşının 10¹⁵ katıdır). Gerçek değer, hesaplanandan az daha küçük olacaktır. Dünya, Güneş'e birkaç yarıçap uzaklıktan daha fazla yaklaştığında gelgitsel kuvvetlerin etkisiyle parçalanacaktır. Parçalar, Güneş etrafında bir halka oluşturur oluşturmaz KÇD ışıması da duracaktır.

İki milyon Güneş kütleli bir kara deliğin 1,89×10¹⁰ m etrafında dönen Güneş kütleli bir yıldızdan oluşan bir sistemin ömrü 6,50×10⁸ s veya 20,7 senedir.

10 kilometre çapında birbiri etrafında 1,89×10⁸ m (189.000 km) uzaktan dönen Güneş kütleli iki nötron yıldızı sisteminin ömrü 1,30×10¹³ saniye veya takrîben 414.000 yıldır. Yörünge periyodu 1.000 s olup çok uzakta olmaması halinde LISA ile izlenebilir. Yörüngesel periyodu bu civarda olan çok daha büyük sayıda beyaz cüce çiftleri bulunmaktadır. Beyaz cüce çiftlerinin kütleleri Güneş kütlesi, çapları da Dünya çapı civarında olur. Birbirleri ile kaynaşıp KÇD ışımaya son vermeden önce birbirleri etrafında dönerken aralarındaki uzaklık 10.000 km'den çok daha az olamaz. Sonuçta yeni bir nötron yıldızı ya da kara delik oluşur. Bu olana kadar kütleçekimsel ışımaları bir nötron yıldızı çiftiyle kıyaslanabilir. LISA, bu tür çift yıldızları tespit edebilecek tek kütleçekimsel deneydir.

Nötron yıldızı çiftinin yörünge çapı 1,89×10⁶ m'ye (1890 km) düşünce kalan ömrü 130.000 s veya 36 saat civarıdır. Yörüngesel frekansı başta saniyede 1 devirken aradaki uzaklık 20 km'ye inip kaynaşmak üzere olduğu anda frekansı 918'e çıkar, kütleçekimsel ışıma yörünge frekansının iki katı olur. Tam kaynaşmadan önceki yörüngesel helezon, çift yıldızlar yeteri kadar yakın olması halinde LIGO tarafından gözlenebilir. Toplam ömrü milyarlarca sene olan böyle bir sistemdeki bu kaynaşmayı izlemek için LIGO'nun ancak birkaç dakikalık bir zaman penceresi vardır. Kâinat'ta bu tür kaynaşmalar çok olmasına rağmen böyle olayları baştaki gibi ayarlanan LIGO ile izleme ihtimali bir hayli düşüktür. Bunun sebebi aletin hassasiyetinin yeteri kadar sisteme erişecek kadar olamamasıdır. İlk ayarlarındaki LIGO, birkaç yılda hiçbir kaynaşma tespit edememiştir. Bu ayarlarla LIGO'nun ancak birkaç on yılda bir böyle bir olayı izleyebileceği düşünülmektedir. Yenilenen LIGO detektörünün hassasiyeti on kat daha fazla ve erişebildiği uzaklık on mislidir. Böylece gözlediği hacim de bin misline çıkar ve gözleyebileceği yıldız çifti adayları da 1000 misline çıkar. Böylece yılda onlarca tespitin mümkün olacağı beklenmektedir.

Dünya–Güneş sisteminin dalga genlikleri

Dairesel yörüngede olan sistemleri yaydıkları KÇD genliğine göre de düşünebiliriz. ${\displaystyle \theta }$, yörünge düzleminin dikmesiyle gözlemcinin bakış doğrultusu arasındaki açı olsun. Bir gözlemcinin sistemin dışında kütle merkezinden ${\displaystyle R}$ uzaklığında olduğunu farz edelim. Eğer ${\displaystyle R}$, dalga boyundan çok daha büyükse dalganın iki polarizasyonu

${\displaystyle h_{+}=-{\frac {1}{R}}\,{\frac {G^{2}}{c^{4}}}\,{\frac {2m_{1}m_{2}}{r}}(1+\cos ^{2}\theta )\cos \left[2\omega (t-R)\right],}$

${\displaystyle h_{\times }=-{\frac {1}{R}}\,{\frac {G^{2}}{c^{4}}}\,{\frac {4m_{1}m_{2}}{r}}\,(\cos {\theta })\sin \left[2\omega (t-R)\right].}$

olacaktır. Burada Newton fiziğinde sabit açısal hızla dairesel bir yörünge kabul edilmiştir:

${\displaystyle \omega ={\sqrt {G(m_{1}+m_{2})/r^{3}}}.}$

Mesela gözlemci ${\displaystyle x}$-${\displaystyle y}$ düzleminde ise ${\displaystyle \theta =\pi /2}$ ve ${\displaystyle \cos(\theta )=0}$'dır. Böylece ${\displaystyle h_{\times }}$ polarizasyonu her zaman sıfır olur. Ayrıca ışınan dalga frekansının dönme frekansının iki katı olduğunu görülüyor. Sonucu Dünya–Güneş sisteminin değerlerini denkleme koyarsak

${\displaystyle h_{+}=-{\frac {1}{R}}\,{\frac {G^{2}}{c^{4}}}\,{\frac {4m_{1}m_{2}}{r}}=-{\frac {1}{R}}\,1{,}7\times 10^{-10}\,\mathrm {metre} .}$

olduğunu buluruz. Bu durumda dalga bulabilmek için en küçük uzaklık R ≈ 1 ışık yılıdır. Böylece tipik genlikler h ≈ 10⁻²⁶ olacaktır. Başka bir ifade ile bir parçacıklar halkası 10²⁶'da bir kadar genişleyip sıkışacaklardır. Bu değer, düşünülebilecek bütün detektörlerin hassasiyet sınırının bir hayli altındadır.

Başka kaynaklardan ışıma

Dünya-Güneş sisteminin oluşturduğu dalgalar çok ufak olmasına rağmen astronomlar, hatırı sayılır dalgalara sebep olan başka kaynakları gösterebilirler. Önemli bir örnek, birisinin çift pulsar olduğu . Yörüngelerinin karakteristiği, yaydıkları radyo sinyallerinin Doppler etkisiyle değişiminden çıkarılabilir. Her bir yıldızın kütlesi 1,4 Güneş kütlesi olup yörüngelerinin çapı, Dünya-Güneş yörüngesinin 1/75'idir. Başka bir ifadeyle bu çap, Güneş çapının birkaç katıdır. Büyük kütlelerin ve küçük bir çapın bir araya gelmesiyle Hulse-Taylor Sistemi'nin yaydığı enerji, Dünya-Güneş Sistemi'nin verdiği enerjiden çok daha fazladır - takrîben 10²² katı kadar.

Yörünge hakkındaki bilgiler, dalga hâlinde ne kadar enerji (ve açısal momentum) yayılacağını kestirmeye yarar. Enerji oradan yayılırken yıldızlar birbirlerine yaklaşırlar. Bu etkiye içeri doğru dönme (İng. İngilizce: inspiral) denir ve pulsarın sinyalinde gözlenebilir. Hulse-Taylor sistemi ölçümleri otuz seneden fazla bir süreden beri yapılmaktadır. Genel rölativitenin öngördüğü kütleçekimsel ışımanın gözlemlerle %0,2'lik bir hata ile uyuştuğu gösterilmiştir. 1993'te Russell Hulse ve Joe Taylor, kütleçekimsel dalgaların bu ilk dolaylı ispatından dolayı Fizik Nobel ödülüne lâyık görülmüşlerdir. Ne yazık ki bu ikili sistemin yörüngesel ömrü 1,84 milyar senedir. Bu süre, Kâinat'ın bilinen ömrünün hatırı sayılır bir kesridir.

İnspiraller, kütleçekimsel dalgaların önemli kaynaklarındandır. Her ne zaman beyaz cüceler, nötron yıldızları veya gibi yoğun cisimler yakın oldukları hâlde birbirleri etrafında dönerse etrafa kuvvetli kütleçekimsel dalga yayarlar. Birbirlerine yakaştıkça bu dalgalar daha da kuvvetleşir. Öyle bir nokta gelir ki bu dalgaların etkisi, Dünya'daki veya Kâinat'taki başka cisimlerde doğrudan tespiti mümkün olur. Kütleçekimsel dalgayı doğrudan tespit etmeyi hedefleyen birkaç büyük ölçekli deney yapılmaktadır.

Bu konudaki tek zorluk, Hulse-Taylor ikilisi gibi sistemlerin çoğunun o kadar uzakta olmasıdır. Hulse-Taylor ikilisinin yaydığı dalga genliği, Dünya'ya geldiğinde takrîben h ≈ 10⁻²⁶ olacaktır. Fakat astrofizikçilerin bulmayı ümidettiği çok daha büyük genlikli kaynaklar vardır (h ≈ 10⁻²⁰). En azından sekiz başka ikili pulsar keşfedilmiştir

Kaynakça

1. ^ Finley, Dave (25 Nisan 2013). "Einstein's gravity theory passes toughest test yet: Bizarre binary star system pushes study of relativity to new limits" [Einstein'in çekim teorisi şimdiye kadarki en sıkı testten geçiyor: Tuhaf çift yıldız sistemi, relativite çalışmalarını yeni sınırlara doğru itiyor] (HTML) (makale) (İngilizce). PHYS.ORG. 2 Mart 2014 tarihinde kaynağından . Erişim tarihi: 31 Mayıs 2013. 
2. ^ Barish, Barry C. (2010). "The Detection of Gravitational Waves with LIGO" [LİGO ile kütleçekimsel dalgaların tespiti] (PDF) (makale) (İngilizce). California Institute of Technology, Pasadena, CA 91125, ABD. 27 Nisan 2012 tarihinde kaynağından . Erişim tarihi: 31 Mayıs 2013. 
3. ^ Davide Castelvecchi & Alexandra Witze (11 Şubat 2016). "Einstein's gravitational waves found at last". Nature.com. 12 Şubat 2016 tarihinde kaynağından . Erişim tarihi: 11 Şubat 2016. 
4. ^ Nadia Drake (11 Şubat 2016). "Found! Gravitational Waves, or a Wrinkle in Spacetime". National Geographic. 12 Şubat 2016 tarihinde kaynağından . Erişim tarihi: 11 Şubat 2016. 
5. ^ LIGO Scientific Collaboration; Virgo Collaboration (2012). "Search for Gravitational Waves from Low Mass Compact Binary Coalescence in LIGO's Sixth Science Run and Virgo's Science Runs 2 and 3". Physical Review D. Cilt 85. s. 082002. arXiv:1111.7314 $2. 
6. ^ Hawking, S. W. and Israel, W., General Relativity: An Einstein Centenary Survey, Cambridge University Press, Cambridge, 1979, 98.
7. ^ Landau, L. D. and Lifshitz, E. M., The Classical Theory of Fields. Fourth Revised English Edition, Pergamon Press., 1975, 356–357.
8. ^ Einstein, A., "Über Gravitationswellen." Sitzungsberichte, Preussische Akademie der Wissenschaften, 154, (1918).
9. ^ ^{a b c} (PDF). eftaylor.com. 7 Temmuz 2010. 13 Temmuz 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 26 Nisan 2014. 
10. ^ "Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis" (PDF). 16 Kasım 2017 tarihinde kaynağından (PDF). Erişim tarihi: 8 Eylül 2013. 
11. ^ "Crashing Black Holes" (PDF). 7 Ocak 2011 tarihinde kaynağından (PDF). Erişim tarihi: 8 Eylül 2013. 
12. ^ (PDF). 1 Mart 2012 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 8 Eylül 2013.