Bell teoremi fizikteki birbiriyle yakından ilişkili birkaç sonucu kapsayan bir terimdir ve bu sonuçların tümü kuantum mekaniği'nin, ölçümün doğası hakkında bazı temel varsayımların olduğu ile uyumsuz olduğunu belirler. Buradaki "yerel", yerellik ilkesini, bir parçacığın yalnızca yakın çevresinden etkilenebileceği ve fiziksel alanların aracılık ettiği etkileşimlerin ışık hızından daha hızlı yayılamayacağı fikrini ifade eder. "", kuantum teorisine dahil olmayan ancak yine de deneylerin sonucunu etkileyen kuantum parçacıklarının varsayılan özellikleridir. Bu sonuç ailesine adını veren fizikçi John Stewart Bell'in sözleriyle, "Eğer gizli değişkenli bir teori yerel ise, kuantum mekaniği ile uyuşmaz ve eğer kuantum mekaniği ile uyuşursa, yerel olmaz."
Terim, geniş bir şekilde bir dizi farklı türetmeye uygulanır; bunlardan ilki Bell tarafından 1964'te "Einstein Podolsky Rosen Paradoksu Üzerine" başlıklı bir makalede tanıtıldı. Bell'in makalesi, Albert Einstein, ve Nathan Rosen'in, kuantum fiziğinin "eksik" bir teori olduğunu savunarak önerdiği 1935 tarihli bir düşünce deneyine bir yanıttı. 1935'te, kuantum fiziğinin tahminlerinin olasılığa dayalı olduğu zaten kabul edilmişti. Einstein, Podolsky ve Rosen, bir çift parçacığın kuantum durumunun dolanık olacağı şekilde hazırlanmasını ve ardından parçacıkları gelişigüzel şekilde büyük bir mesafeye ayırmayı içeren bir senaryo sundular. Deneyci, parçacıklardan biri üzerinde gerçekleştirilebilecek olası kuantum mekaniksel ölçüm seçeneklerine sahiptir. Bir ölçüm seçtiklerinde ve bir sonuç elde ettiklerinde, diğer parçacığın kuantum durumu, diğer parçacık ne kadar uzakta olursa olsun, o sonuca bağlı olarak bir anda yeni bir duruma çöker. Bu, ya birinci parçacığın ölçümünün bir şekilde ikinci parçacıkla ışık hızından daha hızlı etkileşime girdiğini ya da dolanık parçacıkların ayrılmadan önce son kuantum durumlarını önceden belirleyen bazı ölçülmemiş özelliklere sahip olduğunu düşündürür. Bu nedenle, yerellik varsayıldığında, parçacığın gerçek fiziksel özelliklerinin tam bir tanımını veremediği için kuantum mekaniği eksik olmalıdır. Başka bir deyişle, elektronlar ve fotonlar gibi kuantum parçacıkları, kuantum teorisinde yer almayan bazı özellik veya nitelikler taşımalıdır ve kuantum teorisinin tahminlerindeki belirsizlikler, daha sonra "gizli değişkenler" olarak adlandırılan bu özelliklerle ilgili cehaletten veya bilinmezlikten kaynaklanacaktır.
Bell, kuantum dolanıklık analizini çok daha ileriye taşıdı. Ölçümler, dolanık bir çiftin iki ayrı parçacığı üzerinde bağımsız olarak yapılırsa, sonuçların her bir yarıdaki gizli değişkenlere bağlı olduğu varsayımının, iki ölçümdeki sonuçların nasıl ilişkilendirildiğine ilişkin matematiksel bir kısıtlama anlamına geldiği sonucuna vardı. Bu kısıtlama daha sonra Bell eşitsizliği olarak adlandırılacaktı. Bell daha sonra kuantum fiziğinin bu eşitsizliği ihlal eden korelasyonları tahmin ettiğini gösterdi. Sonuç olarak, gizli değişkenlerin kuantum fiziğinin tahminlerini açıklayabilmesinin tek yolu, onların "yerel olmaması"dır; bu, iki parçacığın ne kadar geniş bir alana ayrılırsa ayrılsınlar, bir şekilde anında etkileşime girebildiklerini söylemektir.
Sonraki yıllarda, Bell teoreminin birden çok varyasyonu öne sürülerek, genellikle Bell eşitsizlikleri (veya "Bell-tipi eşitsizlikler") olarak bilinen yakından ilişkili diğer koşullar ortaya kondu. Bell'in teoremini test etmek için tasarlanan ilk ilkel deney, 1972'de John Clauser ve tarafından yapıldı. Toplu olarak olarak bilinen daha gelişmiş deneyler, o zamandan beri birçok kez gerçekleştirildi. Sıklıkla, bu deneylerin amacı "boşlukları kapatmak", yani prensipte daha önceki Bell testlerinin bulgularının geçerliliğini etkileyebilecek deneysel tasarım veya kurulum sorunlarını iyileştirmekti. Bugüne kadar Bell testleri, fiziksel sistemlerin kuantum mekaniğine uyduğunu ve Bell eşitsizliklerini ihlal ettiğini tutarlı bir şekilde bulmuştur; yani bu deneylerin sonuçları herhangi bir yerel gizli değişken teorisiyle bağdaşmaz.
Korelasyonlar üzerinde Bell tipi bir kısıtlamayı kanıtlamak için gereken varsayımların kesin doğası, fizikçiler ve filozoflar tarafından tartışıldı. Bell'in teoreminin önemi şüphe götürmezken, kuantum mekaniğinin yorumlanması üzerindeki tüm sonuçları çözümlenmemiştir.
Teorem
Temel fikir üzerinde birçok varyasyon vardır, bazıları diğerlerinden daha güçlü matematiksel varsayımlar kullanır. Önemli bir şekilde, Bell tipi teoremler herhangi bir yerel gizli değişkenler teorisine atıfta bulunmaz, bunun yerine kuantum fiziğinin klasik doğa resimlerinin ardındaki genel varsayımları ihlal ettiğini gösterir. Bell tarafından 1964'te ispatlanan orijinal teorem, deneye en uygun teorem değildir ve Bell tipi eşitsizlikler türünü daha sonraki bir örnekle tanıtmak uygundur.
Varsayımsal karakterler Alice ve Bob geniş ölçüde ayrılmış konumlarda duruyor. Meslektaşları Victor bir çift parçacık hazırlar ve birini Alice'e, diğerini Bob'a gönderir. Alice parçacığını aldığında, iki olası ölçümden birini yapmayı seçer (belki hangisine karar vermek için yazı tura atarak). Bu ölçümleri şu şekilde belirtin: 
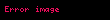

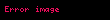


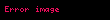
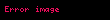

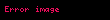
Her ölçümün parçacığın zaten sahip olduğu bir özelliği ortaya çıkardığını varsayalım. Örneğin, Alice 




Hem 
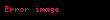
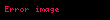







Bu bir Bell eşitsizliğidir, özellikle .:115 Buradaki türetilmesi iki varsayıma bağlıdır: birincisi, temel fiziksel özellikler 

Kuantum mekaniği, CHSH eşitsizliğini aşağıdaki gibi ihlal edebilir. Victor, ile tanımladığı bir çift qubit hazırlar.

burada 


Victor daha sonra ilk kübiti Alice'e ve ikincisini Bob'a iletir. Alice ve Bob'un olası ölçüm seçimleri de Pauli matrisleri cinsinden tanımlanır. Alice, iki gözlemlenebilir olan 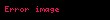
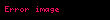






CHSH eşitsizliği, Alice ve Bob'un eylemlerini koordine etmeye çalıştıkları bir “oyun” olarak da düşünülebilir. Victor, 










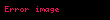

Varyasyonlar ve ilgili sonuçlar
Bell (1964)
Bell'in 1964 tarihli makalesi, sınırlı koşullar altında, yerel gizli değişken modellerinin kuantum mekaniğinin tahminlerini yeniden üretebileceğine işaret ediyor. Daha sonra bunun genel olarak doğru olamayacağını gösterir. Bell, Einstein–Podolsky–Rosen (EPR) düşünce deneyinin David Bohm tarafından geliştirilmiş hali üzerinde duruyor. Bu senaryoda, bir çift parçacık, bir spin tekli durumu (dolaşnık duruma bir örnektir) tarafından tanımlanacak şekilde birlikte oluşturulur. Parçacıklar daha sonra zıt yönlerde birbirinden uzaklaşır. Her parçacık bir Stern–Gerlach cihazı ile ölçülür; bu, farklı yönlerde yönlendirilebilen ve 
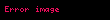



Özellikle, iki dedektörün oryantasyonu aynıysa (



Bell, bu korelasyonlar için yerel bir gizli değişken modelinin, bunları 





















Bell'in 1964 teoremi, mükemmel anti-korelasyon olasılığını gerektirir: birincinin sonucunu bilerek, ikinci detektörün sonucu hakkında bir olasılık tahmini yapma yeteneği. Bu, Einstein, Podolsky ve Rosen tarafından 1935 tarihli bir makalede tanıtılan bir kavram olan "EPR gerçeklik kriteri" ile ilgilidir. Bu makale, "Bir sistemi herhangi bir şekilde bozmadan, fiziksel bir niceliğin değerini kesin olarak (yani, bire eşit olasılıkla) tahmin edebiliyorsak, o zaman o niceliğe karşılık gelen bir gerçeklik unsuru vardır" diyor.
GHZ–Mermin (1990)
1990'da , ve Anton Zeilinger, daha sonra 'in yalnızca üç parçacık kullanacak şekilde basitleştirdiği, dört parçacıklı bir düşünce deneyi sundular. Bu düşünce deneyinde Victor, kuantum durumu 


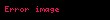
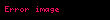


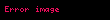

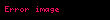







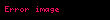



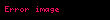


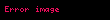

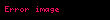

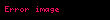


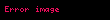










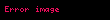
Bu düşünce deneyi, geleneksel bir Bell eşitsizliği olarak veya eşdeğer olarak, CHSH oyunuyla aynı ruhta yerel olmayan bir oyun olarak yeniden biçimlendirilebilir. İçinde Alice, Bob ve Charlie, Victor'dan 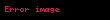





Kochen–Specker theorem (1967)
Kuantum teorisinde, bir Hilbert uzayı için ortonormal bazlar, o Hilbert uzayına sahip bir sistem üzerinde gerçekleştirilebilecek ölçümleri temsil eder. Bir bazdaki her vektör, o ölçümün olası bir sonucunu temsil eder. Farz edin ki gizli bir 




Özgür irade teoremi
Birbirine bağlı tabanların konfigürasyonlarını kullanan Kochen-Specker tipi argüman, Bell tipi eşitsizliklerin altında yatan dolanık çiftleri ölçme fikri ile birleştirilebilir. Bu, 1970'lerin başında Kochen, Heywood ve Redhead, Stairs ve Brown ve Svetlichny tarafından not edildi. EPR'nin işaret ettiği gibi, dolanık bir çiftin bir yarısında bir ölçüm sonucunun elde edilmesi, diğer yarısında karşılık gelen bir ölçümün sonucu hakkında kesinlik anlamına gelir. "EPR gerçeklik kriteri", çiftin ikinci yarısı rahatsız edilmediği için, bu kesinliğin ona ait fiziksel bir özellikten kaynaklanması gerektiğini varsayar. Başka bir deyişle, bu kritere göre, çiftin henüz ölçülmemiş ikinci yarısı içinde gizli bir 
Bu tür bir argüman, John Conway ve tarafından özgür irade teoremi adı altında bir örneği ileri sürüldüğünde dikkat çekti. Conway-Kochen teoremi, tarafından keşfedilen bir çift dolanık ve bir Kochen-Specker konfigürasyonu kullanır.
Yarı klasik dolanıklık
Bell'in işaret ettiği gibi, dolanıklıktan üretilen özel korelasyon durumları da dahil olmak üzere, kuantum mekaniğinin bazı tahminleri yerel gizli değişken modellerinde çoğaltılabilir. Bu konu, Bell'in teoreminden bu yana geçen zamanda sistematik olarak incelenmiştir. 1989'da , şimdi olarak adlandırılan, EPR tipi korelasyonlar sağlayan ama aynı zamanda bir gizli değişken modelini kabul eden bir çift sistem için ortak kuantum durumları olan şeyi tanıttı. Werner durumları, simetrik tensör-çarpım formunun birimleri altında değişmez olan iki parçalı kuantum durumlarıdır:

2004 yılında Robert Spekkens, yerel, ayrıklaştırılmış serbestlik dereceleri öncülüyle başlayan ve ardından bir gözlemcinin bu serbestlik dereceleri hakkında ne kadar bilebileceğini kısıtlayan ve böylece onları gizli değişkenlere dönüştüren bir "bilgi dengesi ilkesi" dayatan bir oyuncak modeli tanıttı. Altta yatan değişkenler ("ontik durumlar") hakkında izin verilen bilgi durumları ("epistemik durumlar"), kuantum durumlarının bazı özelliklerini taklit eder. Oyuncak modelindeki korelasyonlar, tek eşlilik gibi karışıklığın bazı yönlerini taklit edebilir, ancak yapı gereği, oyuncak modeli asla bir Bell eşitsizliğini ihlal edemez.
Geçmiş
Arka plan
Kuantum mekaniğinin gizli değişkenler tarafından "tamamlanıp" tamamlanamayacağı sorusu, kuantum teorisinin ilk yıllarına kadar uzanır. Macaristan doğumlu bilge John von Neumann, 'nda, "gizli parametreler" olamayacağına dair bir kanıt olduğunu iddia ettiği şeyi sundu. Von Neumann'ın ispatının geçerliliği ve kesinliği Hans Reichenbach tarafından, daha ayrıntılı olarak tarafından ve muhtemelen Albert Einstein tarafından basılı olmasa da konuşma sırasında sorgulandı. ( ve , von Neumann'ın temel varsayımını 1961 gibi erken bir tarihte reddettiler, ancak 1967'ye kadar bir eleştiri yayınlamadılar.)
Einstein ısrarla kuantum mekaniğinin tamamlanmış bir teori olamayacağını savundu. Tercih ettiği argüman bir yerellik ilkesine dayanıyordu:
- Birbiriyle yalnızca sınırlı bir süre boyunca etkileşime giren A ve B iki kısmi sistemden oluşan mekanik bir sistem düşünün. Etkileşimlerinden önce ψ fonksiyonu verilsin. O zaman Schrödinger denklemi, etkileşimleri gerçekleştikten sonra ψ fonksiyonunu sağlayacaktır. Şimdi A kısmi sisteminin fiziksel durumunu ölçümlerle mümkün olduğu kadar tam olarak belirleyelim. Daha sonra kuantum mekaniği, yapılan ölçümlerden ve toplam sistemin ψ fonksiyonundan kısmi sistem Bnin ψ fonksiyonunu belirlememizi sağlar. Ancak bu belirleme, A koşulunu belirten belirleyici büyüklüklerden hangisinin ölçüldüğüne bağlı bir sonuç verir (örneğin koordinatlar veya momentumlar). Etkileşimden sonra Bnin sadece bir fiziksel durumu olabileceğinden ve Bden ayrılmış A sisteminde gerçekleştirdiğimiz özel ölçüme bağlı olarak kabul edilemeyeceğinden, ψ fonksiyonunun fiziksel durumla açık bir şekilde koordine olmadığı sonucuna varılabilir. Birkaç ψ fonksiyonunun B sisteminin aynı fiziksel koşuluyla bu koordinasyonu, ψ fonksiyonunun bir birim sistemin fiziksel durumunun (tam) bir açıklaması olarak yorumlanamayacağını tekrar gösterir.
EPR düşünce deneyi de benzerdir, ayrıca birleşik bir dalga fonksiyonu tarafından açıklanan iki ayrı sistem A ve B dikkate alınır. Bununla birlikte, EPR makalesi, daha sonra gerçekliğin EPR kriteri olarak bilinen fikri ekler; buna göre, "B" üzerindeki bir ölçümün sonucunu 1 olasılıkla tahmin etme yeteneği, B içinde bir "gerçeklik unsurunun" varlığını ima eder.
1951'de David Bohm, EPR tarafından ele alınan konum ve momentum ölçümlerinin aksine, ölçümlerin farklı olası sonuç aralıklarına sahip olduğu, EPR düşünce deneyinin bir varyantını önerdi. Bir yıl önce, Chien-Shiung Wu ve Irving Shaknov, dolanık çiftler halinde üretilen fotonların polarizasyonlarını başarıyla ölçtüler, böylece EPR düşünce deneyinin Bohm versiyonunu pratikte uygulanabilir hale getirdiler.
1940'ların sonlarında, matematikçi kuantum fiziğinin temellerine ilgi duymaya başladı ve 1957'de kuantum mekaniğinin kesin bir tanımı olarak kabul ettiği bir varsayımlar listesi hazırladı. Mackey, varsayımlardan birinin gereksiz olduğunu tahmin etti ve kısa bir süre sonra Andrew M. Gleason, bunun gerçekten de diğer varsayımlardan çıkarsanabileceğini kanıtladı., geniş bir gizli değişken teorileri sınıfının kuantum mekaniği ile bağdaşmadığına dair bir argüman sağladı. Daha spesifik olarak, Gleason teoremi "bağlamsal olmayan" gizli değişken modellerini dışlar. Kuantum mekaniği için herhangi bir gizli değişken modeli, Gleason teoreminin imalarından kaçınmak için, yalnızca ölçülen sisteme ait özellikler olmayan, aynı zamanda ölçümün yapıldığı dış bağlama da bağlı olan gizli değişkenleri içermelidir. Bu tür bir bağımlılık genellikle yapmacık veya istenmeyen olarak görülür; bazı ayarlarda özel görelilik ile tutarsızdır. Kochen-Specker teoremi, üzerinde böyle bir olasılık ölçüsünün tanımlanamayacağı belirli bir sonlu ışın alt kümesi oluşturarak bu ifadeyi geliştirir.
Tsung-Dao Lee, 1960 yılında Bell'in teoremini türetmeye çok yaklaştı. Zıt yönlerde hareket eden iki kaon'un üretildiği olayları değerlendirdi ve gizli değişkenlerin bu tür durumlarda elde edilebilecek korelasyonları açıklayamayacağı sonucuna vardı. Ancak kaonların bozunması nedeniyle zorluklar ortaya çıktı ve Bell tipi bir eşitsizlik çıkaracak kadar ileri gitmedi.{{refn|group=note|This was reported by .:308 Lee en çok ile parite korunumunun ihlali tahminiyle tanınır; bu tahmin ödülü paylaşmayan Chien-Shiung Wu tarafından onaylandıktan sonra onlara Nobel Ödülü kazandırdı.
Bell'in yayınları
Bell, teoremini nispeten belirsiz bir dergide yayınlamayı seçti çünkü sayfa ücreti gerektirmiyordu ve o sırada aslında orada yayınlayan yazarlara ödeme yapıyordu. Dergi, yazarların dağıtması için makalelerin ücretsiz yeniden baskılarını sağlamadığından, Bell aldığı parayı diğer fizikçilere gönderebileceği kopyaları satın almak için harcamak zorunda kaldı. Dergide basılan makalelerin kendisinde yayının adı basitçe “Physics” olarak sıralanırken, kapaklarda İngilizce, Fransızca ve Rusça makaleler basılacağını yansıtmak için üç dilli “Physics Physique Физика” versiyonu yer alıyordu.:92–100, 289
Bell, 1964 sonucunu kanıtlamadan önce, Kochen-Specker teoremine eşdeğer bir sonuç da kanıtladı (bu nedenle, ikincisi bazen Bell-Kochen-Specker veya Bell-KS teoremi olarak da bilinir). Ancak, bu teoremin yayınlanması yanlışlıkla 1966 yılına kadar ertelendi. O yazıda Bell, kuantum fenomeninin gizli değişkenler açısından açıklanması yerel olmama gerektireceğinden, EPR paradoksunun "Einstein'ın en az seveceği şekilde çözüldüğünü" savundu.
Deneyler

S kaynağı, zıt yönlerde gönderilen "foton" çiftleri üretir. Her foton, yönü (a veya b) deneyi yapan kişi tarafından ayarlanabilen iki kanallı bir polarizörle karşılaşır. Her kanaldan gelen sinyaller tespit edilir ve çakışma monitörü tarafından dört türdeki (++, −−, +− ve −+) çakışmalar sayılır.
1967'de olağandışı "Physics Physique Физика" başlığı John Clauser'ın dikkatini çekti, o da Bell'in makalesini keşfetti ve laboratuvarda bir yapmayı düşünmeye başladı. Clauser ve , 1972'de bir Bell testi yaptılar. Bu sadece sınırlı bir testti, çünkü dedektör ayarlarının seçimi fotonlar kaynaktan ayrılmadan önce yapılmıştı. 1982'de Alain Aspect ve işbirlikçileri bu sınırlamayı kaldırmak için ilk Bell testini gerçekleştirdiler. Bu, giderek daha katı Bell testleri eğilimini başlattı. GHZ düşünce deneyi, 2000 yılında fotonların birbirine dolanık üçlüleri kullanılarak pratikte uygulandı. 2002 yılına gelindiğinde, lisans laboratuvar derslerinde CHSH eşitsizliğinin test edilmesi mümkündü.
Bell testlerinde, deneysel bulguların geçerliliğini etkileyen deneysel tasarım veya kurulum sorunları olabilir. Bu sorunlara genellikle "boşluklar" denir. Deneyin amacı, kuantum mekaniğinin tahminleriyle çelişecek olan ile doğanın açıklanıp tanımlanamayacağını test etmektir.
Gerçek deneylerdeki en yaygın boşluklar “tespit” ve “yerellik” boşluklarıdır. Deneyde parçacıkların (genellikle fotonlar) küçük bir kısmı algılandığında, algılama açık kapısı oluşur ve bu, algılanan parçacıkların, temsil olmayan bir örnek olduğunu varsayarak, verileri yerel gizli değişkenlerle açıklamayı mümkün kılar. Tespitler bir boşluk benzeri ayrım ile yapılmadığında, yerellik açık kapısı oluşur ve görelilikle çelişmeden bir ölçümün sonucunun diğerini etkilemesi mümkün olur. Bazı deneylerde, Bell testi ihlallerinin yerel-gizli-değişken açıklamalarını mümkün kılan ek kusurlar olabilir.
Farklı deneylerde hem yerellik hem de algılama boşlukları kapatılmış olsa da, aynı deneyde her ikisini de aynı anda kapatmak uzun süredir devam eden bir zorluktu.This was finally achieved in three experiments in 2015. Bu sonuçlarla ilgili olarak Alain Aspect, "... hiçbir deneyin ... tamamen açık kapısız olduğu söylenemez" diye yazıyor ama deneylerin yerel gizli değişkenlerden "vazgeçmemiz gerektiğine dair son şüpheleri de ortadan kaldırdığını" söylüyor ve kalan açıkkapıların ise örneklerini "çok zorlanmış" ve "fizikteki olağan akıl yürütme biçimine yabancı" olarak ifade ediyor.
Bell eşitsizliklerinin ihlallerini deneysel olarak doğrulamaya yönelik bu çabalar, daha sonra Clauser, Aspect ve Anton Zeilinger'ın 2022 Nobel Fizik Ödülü'ne layık görülmesiyle sonuçlanacaktı.
Bell teoreminin yorumları
Bell'in teoremine verilen tepkiler çok ve çeşitli olmuştur. Schlosshauer, Kofler ve Zeilinger, Bell eşitsizliklerinin "çok sayıda deneyle test edilmiş titiz bir teorik sonuca nasıl sahip olabileceğimize ve yine de sonuçlar konusunda nasıl anlaşamayacağımıza dair harika bir örnek" sağladığını yazıyor.
Kopenhag Yorumu
Kopenhag yorumu, temelde Niels Bohr ve Werner Heisenberg'e atfedilen kuantum mekaniğinin anlamı hakkındaki görüşlerin bir derlemesidir. Özellikleri 1925-1927 yılları arasında kuantum mekaniğinin gelişimine dayandığından, kuantum mekaniğinin önerilen sayısız yorumunun en eskilerinden biridir ve en yaygın olarak öğretilenlerden biri olmaya devam etmektedir. "Kopenhag" yorumunun ne olduğuna dair kesin bir tarihsel açıklama yoktur. Özellikle Bohr ve Heisenberg'in görüşleri arasında temel görüş ayrılıkları vardı. Kopenhag koleksiyonunun bir parçası olarak genel olarak kabul edilen bazı temel ilkeler, kuantum mekaniğinin özünde deterministik olmadığı (Belirlenimsizlik|belirlenimsiz olduğu) fikrini içerir ve olasılıklar ve tamamlayıcılık ilkesi kullanılarak hesaplanır. Tamamlayıcılık ilkesi, belirli özelliklerin, aynı sistem için aynı anda ortaklaşa tanımlanamayacağını söyler. Bir sistemin belirli bir özelliğinden söz edebilmek için, o sistemin belirli bir laboratuvar düzenlemesi kapsamında ele alınması gerekir. Birbirini dışlayan laboratuvar düzenlemelerine karşılık gelen gözlemlenebilir miktarlar birlikte tahmin edilemez, ancak bir sistemi karakterize etmek için bu tür birbirini dışlayan çok sayıda deneyi dikkate almak gerekir. Bohr'un kendisi, EPR "paradoksunun" yanıltıcı olduğunu iddia etmek için tamamlayıcılığı kullandı. Konum ve momentum ölçümleri tamamlayıcı olduğundan, birini ölçmeyi seçmek diğerini ölçme olasılığını dışlar. Sonuç olarak, laboratuvar cihazlarının bir düzenlemesiyle ilgili olarak çıkarılan bir gerçeğin, diğeri aracılığıyla çıkarılan bir gerçekle birleştirilemeyeceğini ve bu nedenle, ikinci parçacık için önceden belirlenmiş konum ve momentum değerlerinin çıkarımının geçerli olmayacağını savundu.:194–197 Bohr, EPR'nin "argümanlarının, kuantum tanımının esasen eksik olduğu yönündeki sonuçlarını haklı çıkarmadığı" sonucuna vardı.
Kopenhag tipi yorumlar genellikle Bell eşitsizliklerinin ihlalini, genellikle veya "gerçekçilik" olarak adlandırılan ve daha geniş bir felsefi anlamda gerçekçiliği terk etmekle aynı şey olmayan varsayımı reddetmek için gerekçe olarak alır. Örneğin, , gizli değişkenlerin reddedildiğini savunuyor ve şu sonuca varıyor: "kuantum mekaniği muhtemelen kapsamı ve olgunluğu bakımından şimdiye kadarki herhangi bir teori kadar realist.":531 Bu aynı zamanda (genellikle "Kopenhag doğru yapıldı" olarak ilan edilir) ve gibi Kopenhag geleneğinden gelen yorumların izlediği yoldur.
Kuantum mekaniğinin birçok dünya yorumu
Everett yorumu olarak da bilinen , kuantum mekaniğinin dalga fonksiyonu çökmeden, üniter kısmından oluştuğu için yerel ve deterministiktir. Bir Bell eşitsizliğini ihlal eden korelasyonlar üretebilir çünkü Bell'in ölçümlerin tek bir sonucu olduğu şeklindeki üstü kapalı varsayımını ihlal eder. Aslında, Bell'in teoremi, bir ölçümün tek bir sonucu olduğu varsayımından yola çıkarak Birçok Dünya çerçevesinde kanıtlanabilir. Bu nedenle, bir Bell eşitsizliğinin ihlali, ölçümlerin birden çok sonucu olduğunu gösteren bir kanıt olarak yorumlanabilir.
Bell korelasyonları için sağladığı açıklama, Alice ve Bob ölçümlerini yaptıklarında yerel dallara ayrılmalarıdır. Alice'in her kopyası açısından bakıldığında, Bob'un farklı sonuçlar yaşayan birden çok kopyası vardır, bu nedenle Bob'un kesin bir sonucu olamaz ve Bob'un her kopyası açısından da aynı şey geçerlidir. Yalnızca gelecekteki ışık konileri çakıştığında karşılıklı olarak iyi tanımlanmış bir sonuç elde edeceklerdir. Bu noktada Bell korelasyonunun var olmaya başladığını ancak tamamen yerel bir mekanizma tarafından üretildiğini söyleyebiliriz. Bu nedenle, bir Bell eşitsizliğinin ihlali, yerel olmamanın bir kanıtı olarak yorumlanamaz.
Yerel olmayan gizli değişkenler
Gizli değişkenler fikrinin çoğu savunucusu, deneylerin yerel gizli değişkenleri devre dışı bıraktığına inanıyor. Bell'in eşitsizliğinin ihlalini, parçacıkların durumları hakkında bilgi alışverişinde bulundukları yerel olmayan bir aracılığıyla açıklayarak yerellikten vazgeçmeye hazırlar. Bu, evrendeki tüm parçacıkların diğerleri ile anında bilgi alışverişi yapabilmesini gerektiren kuantum mekaniğinin temelidir. Yerel olmayan gizli değişken teorileri için bir zorluk, bu anlık iletişimin neden gizli değişkenler seviyesinde var olabileceğini, ancak sinyal göndermek için kullanılamayacağını açıklamaktır. 2007'de yapılan bir deney, Bohm mekaniğinin kendisi olmasa da, Bohmcu olmayan, yerel olmayan gizli değişken teorilerinin büyük bir sınıfını dışladı.
Zamanda hem geriye hem de ileriye doğru hareket eden dalgaları varsayan da aynı şekilde yerel değildir.
Süperdeterminizm
Bell teoremini türetmek için gerekli bir varsayım, gizli değişkenlerin ölçüm ayarlarıyla ilişkili olmamasıdır. Bu varsayım, deneycinin ayarları seçmek için "özgür irade"ye sahip olduğu ve her şeyden önce bilim yapmak için bunun gerekli olduğu şeklinde gerekçelendirildi. Ölçüm seçiminin mutlaka ölçülen sistemle ilişkili olduğu (varsayımsal) bir teori "süperdeterministik" olarak bilinir.
Deterministik modellerin birkaç savunucusu, yerel gizli değişkenlerden vazgeçmedi. Örneğin, Gerard 't Hooft süperdeterminizmin göz ardı edilemeyeceğini savundu.
Notlar
- ^ We are for convenience assuming that the response of the detector to the underlying property is deterministic. This assumption can be replaced; it is equivalent to postulating a joint probability distribution over all the observables of the experiment.
- ^ Daha ayrıntılı olarak, Paul Dirac,David Hilbert,John von Neumann ve Hermann Weyl tarafından geliştirildiği üzere, bir kuantum mekanik sisteminin durumu, ayrılabilir bir Hilbert uzayı
'ye ait bir
vektörüdür. İlgilenilen fiziksel nicelikler - konum, momentum, enerji, dönüş - Hilbert uzayı üzerinde etki eden kendine eş doğrusal operatörler olan "gözlemlenebilirler" tarafından temsil edilir. Bir gözlemlenebilir ölçüldüğünde sonuç, tarafından verilen olasılıkla özdeğerlerinden biri olacaktır: en basit durumda,
özdeğeri dejenere değildir ve olasılık,
'nın ilişkili özvektörü olduğu
tarafından verilir. Daha genel olarak, özdeğer dejeneredir ve olasılık
tarafından verilir; burada
, ilişkili özuzayının projektörüdür. Bu tartışmanın amaçları doğrultusunda, özdeğerleri dejenere olmayan olarak alabiliriz.
- ^ See Reichenbach and Jammer,:276 Mermin and Schack, and for Einstein's remarks, Clauser and Shimony and Wick.:286
- ^ Deterministik olan bir gizli değişken teorisi, belirli bir sonucun olasılığının "her zaman" ya 0 ya da 1 olduğunu ima eder. Örneğin, bir spin-1 atomu üzerindeki bir Stern-Gerlach ölçümü, atomun seçilen eksen boyunca açısal momentumunun,
,
ve
olarak adlandırılabilecek üç olası değerden biri olduğunu bildirecektir. Deterministik bir gizli değişken teorisinde, ölçümde bulunan sonucu sabitleyen temel bir fiziksel özellik vardır. Altta yatan fiziksel özelliğin değerine bağlı olarak, herhangi bir sonuç (örneğin,
sonucu) imkansız veya garantili olmalıdır. Ancak Gleason teoremi, böyle bir deterministik olasılık ölçüsünün olamayacağını ima eder, çünkü herhangi bir olasılık ölçüsünün, bazı yoğunluk operatörleri
için bir
eşleme biçimini alması gerektiğini kanıtlar. Bu eşleme Hilbert uzayının birim küre üzerinde süreklidir ve bu birim küre olduğundan, üzerinde hiçbir sürekli olasılık ölçüsü deterministik olamaz. Bu eşleme, Hilbert uzayının birim küresi üzerinde süreklidir ve bu birim küre bağlantılı olduğundan, üzerinde hiçbir sürekli olasılık ölçüsü deterministik olamaz.:§1.3
- ^ was one exception, but Jaynes' arguments have not generally been found persuasive.
Kaynakça
- ^ Bell, John S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. s. 65. ISBN . OCLC 15053677.
- ^ a b Einstein, A.; ; Rosen, N. (15 Mayıs 1935). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?". Physical Review. 47 (10): 777-780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777
![image]() .
. - ^ a b Bell, J. S. (1964). "On the Einstein Podolsky Rosen Paradox" (PDF). . 1 (3): 195-200. doi:10.1103/PhysicsPhysiqueFizika.1.195. 5 Mart 2017 tarihinde kaynağından (PDF). Erişim tarihi: 18 Mayıs 2023.
- ^ Parker, Sybil B. (1994). McGraw-Hill Encyclopaedia of Physics
![image]() (2. bas.). McGraw-Hill. s. 542. ISBN .
(2. bas.). McGraw-Hill. s. 542. ISBN . - ^ a b c d (July 1993). "Hidden Variables and the Two Theorems of John Bell" (PDF). Reviews of Modern Physics. 65 (3): 803-15. arXiv:1802.10119 $2. Bibcode:1993RvMP...65..803M. doi:10.1103/RevModPhys.65.803. 9 Temmuz 2020 tarihinde kaynağından (PDF). Erişim tarihi: 18 Mayıs 2023.
- ^ "The Nobel Prize in Physics 2022". (Basın açıklaması). . 4 Ekim 2022. 4 Ekim 2022 tarihinde kaynağından . Erişim tarihi: 6 Ekim 2022.
- ^ The BIG Bell Test Collaboration (9 Mayıs 2018). "Challenging local realism with human choices". Nature. 557 (7704): 212-216. arXiv:1805.04431 $2. Bibcode:2018Natur.557..212B. doi:10.1038/s41586-018-0085-3. (PMID) 29743691.
- ^ (7 Şubat 2017). . (İngilizce). 7 Şubat 2017 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Şubat 2020.
- ^ a b . "Bell's Theorem". (Ed.). Stanford Encyclopedia of Philosophy.
- ^ a b c d ; (2010). Quantum Computation and Quantum Information (2. bas.). Cambridge: Cambridge University Press. ISBN . OCLC 844974180.
- ^ Fine, Arthur (1 Şubat 1982). "Hidden Variables, Joint Probability, and the Bell Inequalities". Physical Review Letters (İngilizce). 48 (5): 291-295. Bibcode:1982PhRvL..48..291F. doi:10.1103/PhysRevLett.48.291. ISSN 0031-9007. 9 Eylül 2023 tarihinde kaynağından . Erişim tarihi: 20 Mayıs 2023.
- ^ Braunstein, Samuel L.; (August 1990). "Wringing out better Bell inequalities". (İngilizce). 202 (1): 22-56. Bibcode:1990AnPhy.202...22B. doi:10.1016/0003-4916(90)90339-P.
- ^ Rau, Jochen (2021). Quantum theory : an information processing approach. Oxford University Press. ISBN . OCLC 1256446911.
- ^ ; Hoyer, P.; Toner, B.; (2004). "Consequences and limits of nonlocal strategies". Proceedings. 19th IEEE Annual Conference on Computational Complexity, 2004. IEEE. ss. 236-249. arXiv:quant-ph/0404076 $2. Bibcode:2004quant.ph..4076C. doi:10.1109/CCC.2004.1313847. ISBN . OCLC 55954993.
- ^ Barnum, H.; Beigi, S.; Boixo, S.; Elliott, M. B.; Wehner, S. (6 Nisan 2010). "Local Quantum Measurement and No-Signaling Imply Quantum Correlations". Physical Review Letters (İngilizce). 104 (14): 140401. arXiv:0910.3952 $2. Bibcode:2010PhRvL.104n0401B. doi:10.1103/PhysRevLett.104.140401. ISSN 0031-9007. (PMID) 20481921.
- ^ Griffiths, David J. (2005). Introduction to Quantum Mechanics (2. bas.). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN . OCLC 53926857.
- ^ ; ; ; Zeilinger, A. (1990). "Bell's theorem without inequalities". American Journal of Physics. 58 (12): 1131. Bibcode:1990AmJPh..58.1131G. doi:10.1119/1.16243.
- ^ (1990). "Quantum mysteries revisited". American Journal of Physics. 58 (8): 731-734. Bibcode:1990AmJPh..58..731M. doi:10.1119/1.16503.
- ^ ; ; Tapp, Alain (2005). "Recasting Mermin's multi-player game into the framework of pseudo-telepathy". Quantum Information and Computation. 5 (7): 538-550. arXiv:quant-ph/0408052 $2. Bibcode:2004quant.ph..8052B. doi:10.26421/QIC5.7-2.
- ^ Dirac, Paul Adrien Maurice (1930). The Principles of Quantum Mechanics. Oxford: Clarendon Press.
- ^ Hilbert, David (2009). Sauer, Tilman; Majer, Ulrich (Ed.). Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology. Springer. doi:10.1007/b12915. ISBN . OCLC 463777694.
- ^ von Neumann, John (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer. English translation: Mathematical Foundations of Quantum Mechanics. tarafından çevrildi. Princeton University Press. 1955.
- ^ Weyl, Hermann (1950) [1931]. The Theory of Groups and Quantum Mechanics. tarafından çevrildi. Dover. ISBN . Translated from the German Gruppentheorie und Quantenmechanik (2. bas.). . 1931.
- ^ (1993). Quantum Theory: Concepts and Methods. . ISBN . OCLC 28854083.
- ^ ; (1 Temmuz 1991). "Nonlocality in Quantum Mechanics". (İngilizce). 65 (1): 119-160. doi:10.1093/aristoteliansupp/65.1.119. ISSN 0309-7013. JSTOR 4106773.
A similar approach was arrived at independently by Simon Kochen, although never published (private communication).
- ^ Heywood, Peter; (May 1983). "Nonlocality and the Kochen–Specker paradox". (İngilizce). 13 (5): 481-499. Bibcode:1983FoPh...13..481H. doi:10.1007/BF00729511. ISSN 0015-9018.
- ^ Stairs, Allen (December 1983). "Quantum Logic, Realism, and Value Definiteness". Philosophy of Science (İngilizce). 50 (4): 578-602. doi:10.1086/289140. ISSN 0031-8248.
- ^ ; Svetlichny, G. (November 1990). "Nonlocality and Gleason's lemma. Part I. Deterministic theories". (İngilizce). 20 (11): 1379-1387. Bibcode:1990FoPh...20.1379B. doi:10.1007/BF01883492. ISSN 0015-9018.
- ^ Glick, David; Boge, Florian J. (22 Ekim 2019). "Is the Reality Criterion Analytic?". Erkenntnis (İngilizce). 86 (6): 1445-1451. arXiv:1909.11893 $2. Bibcode:2019arXiv190911893G. doi:10.1007/s10670-019-00163-w. ISSN 0165-0106.
- ^ Conway, John; (2006). "The Free Will Theorem". . 36 (10): 1441. arXiv:quant-ph/0604079 $2. Bibcode:2006FoPh...36.1441C. doi:10.1007/s10701-006-9068-6.
- ^ Rehmeyer, Julie (15 Ağustos 2008). . (İngilizce). 13 Şubat 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Nisan 2022.
- ^ Thomas, Rachel (27 Aralık 2011). . (İngilizce). 12 Ocak 2012 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Nisan 2022.
- ^ Conway, John H.; (2009). "The strong free will theorem" (PDF). . 56 (2): 226-232. 20 Mart 2023 tarihinde kaynağından (PDF). Erişim tarihi: 22 Mayıs 2023.
- ^ Werner, Reinhard F. (1 Ekim 1989). "Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model". Physical Review A (İngilizce). 40 (8): 4277-4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. ISSN 0556-2791. (PMID) 9902666.
- ^ (19 Mart 2007). "Evidence for the epistemic view of quantum states: A toy theory". Physical Review A (İngilizce). 75 (3): 032110. arXiv:quant-ph/0401052 $2. Bibcode:2007PhRvA..75c2110S. doi:10.1103/PhysRevA.75.032110. ISSN 1050-2947.
- ^ Catani, Lorenzo; Browne, Dan E. (27 Temmuz 2017). "Spekkens' toy model in all dimensions and its relationship with stabiliser quantum mechanics". . 19 (7): 073035. Bibcode:2017NJPh...19g3035C. doi:10.1088/1367-2630/aa781c
![image]() . ISSN 1367-2630.
. ISSN 1367-2630. - ^ Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. s. 14. OCLC 872622725.
- ^ a b c (1974). The Philosophy of Quantum Mechanics. John Wiley and Sons. ISBN .
- ^ ; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". . 48 (9): 1007-1020. arXiv:1805.10311 $2. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5.
- ^ Clauser, J. F.; Shimony, A. (1978). "Bell's theorem: Experimental tests and implications" (PDF). Reports on Progress in Physics. 41 (12): 1881-1927. Bibcode:1978RPPh...41.1881C. CiteSeerX 10.1.1.482.4728 $2. doi:10.1088/0034-4885/41/12/002. 23 Eylül 2017 tarihinde kaynağından (PDF). Erişim tarihi: 28 Ekim 2017.
- ^ a b Wick, David (1995). The Infamous Boundary: Seven Decades of Heresy in Quantum Physics. New York: Springer. doi:10.1007/978-1-4612-4030-3_11. ISBN .
- ^ Conway, John; (2002). "The Geometry of the Quantum Paradoxes". ; Zeilinger, Anton (Ed.). Quantum [Un]speakables: From Bell to Quantum Information. Berlin: Springer. ss. 257-269. ISBN . OCLC 49404213.
- ^ Einstein, Albert (March 1936). "Physics and reality". Journal of the Franklin Institute. 221 (3): 349-382. Bibcode:1936FrInJ.221..349E. doi:10.1016/S0016-0032(36)91047-5.
- ^ Harrigan, Nicholas; Spekkens, Robert W. (2010). "Einstein, incompleteness, and the epistemic view of quantum states". . 40 (2): 125. arXiv:0706.2661 $2. Bibcode:2010FoPh...40..125H. doi:10.1007/s10701-009-9347-0.
- ^ Bohm, David (1989). Quantum Theory (Dover reprint bas.). Prentice-Hall. ss. 614-623. ISBN . OCLC 1103789975.
- ^ Wu, C.-S.; Shaknov, I. (1950). "The Angular Correlation of Scattered Annihilation Radiation". Physical Review. 77 (1): 136. Bibcode:1950PhRv...77..136W. doi:10.1103/PhysRev.77.136.
- ^ (1957). "Quantum Mechanics and Hilbert Space". . 64 (8P2): 45-57. doi:10.1080/00029890.1957.11989120. JSTOR 2308516.
- ^ Gleason, Andrew M. (1957). "Measures on the closed subspaces of a Hilbert space". . 6 (4): 885-893. doi:10.1512/iumj.1957.6.56050
![image]() . MR 0096113. 26 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 24 Mayıs 2023.
. MR 0096113. 26 Şubat 2021 tarihinde kaynağından . Erişim tarihi: 24 Mayıs 2023. - ^ "Andy Gleason and Quantum Mechanics" (PDF). . 56 (10): 1253-1259. 8 Aralık 2018 tarihinde kaynağından (PDF). Erişim tarihi: 24 Mayıs 2023.
- ^ Wilce, A. (2017). "Quantum Logic and Probability Theory". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ (1984). "Contextual Hidden Variable Theories and Bell's Inequalities". . 35 (1): 25-45. doi:10.1093/bjps/35.1.25.
- ^ (1991). "Two simple proofs of the Kochen-Specker theorem". (İngilizce). 24 (4): L175-L178. Bibcode:1991JPhA...24L.175P. doi:10.1088/0305-4470/24/4/003. ISSN 0305-4470.
- ^ Whitaker, Andrew (2016). John Stewart Bell and Twentieth Century Physics: Vision and Integrity (İngilizce). Oxford University Press. ISBN .
- ^ a b Bell, J. S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447-452. Bibcode:1966RvMP...38..447B. doi:10.1103/revmodphys.38.447. 1444158.
- ^ (30 Ocak 2012). . Scientific American (İngilizce). 4 Mart 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 11 Şubat 2020.
- ^ ; Clauser, J. F. (1972). "Experimental test of local hidden-variable theories" (PDF). Physical Review Letters. 28 (938): 938-941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938. 24 Mayıs 2023 tarihinde kaynağından (PDF). Erişim tarihi: 24 Mayıs 2023.
- ^ Freedman, Stuart Jay (5 Mayıs 1972). Experimental test of local hidden-variable theories (PDF) (PhD). University of California, Berkeley. 23 Mayıs 2023 tarihinde kaynağından (PDF). Erişim tarihi: 24 Mayıs 2023.
- ^ Aspect, Alain; Dalibard, Jean; Roger, Gérard (1982). "Experimental Test of Bell's Inequalities Using Time-Varying Analyzers". Physical Review Letters. 49 (25): 1804-7. Bibcode:1982PhRvL..49.1804A. doi:10.1103/PhysRevLett.49.1804
![image]() .
. - ^ Pan, Jian-Wei; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. (2000). "Experimental test of quantum nonlocality in three-photon GHZ entanglement". Nature. 403 (6769): 515-519. Bibcode:2000Natur.403..515P. doi:10.1038/35000514. (PMID) 10676953.
- ^ Dehlinger, Dietrich; Mitchell, M. W. (2002). "Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory". American Journal of Physics. 70 (9): 903-910. arXiv:quant-ph/0205171 $2. Bibcode:2002AmJPh..70..903D. doi:10.1119/1.1498860.
- ^ Larsson, Jan-Åke (2014). "Loopholes in Bell inequality tests of local realism". Journal of Physics A: Mathematical and Theoretical. 47 (42): 424003. arXiv:1407.0363 $2. Bibcode:2014JPhA...47P4003L. doi:10.1088/1751-8113/47/42/424003.
- ^ Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Scarani, V.; Makarov, V.; Kurtsiefer, C. (2011). "Experimentally faking the violation of Bell's inequalities". Physical Review Letters. 107 (17): 170404. arXiv:1106.3224 $2. Bibcode:2011PhRvL.107q0404G. doi:10.1103/PhysRevLett.107.170404. (PMID) 22107491.
- ^ Merali, Zeeya (27 Ağustos 2015). "Quantum 'spookiness' passes toughest test yet". Nature News. 525 (7567): 14-15. Bibcode:2015Natur.525...14M. doi:10.1038/nature.2015.18255
![image]() . (PMID) 26333448.
. (PMID) 26333448. - ^ Markoff, Jack (21 Ekim 2015). "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real". New York Times. 31 Temmuz 2019 tarihinde kaynağından . Erişim tarihi: 21 Ekim 2015.
- ^ Hensen, B. (21 Ekim 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682-686. arXiv:1508.05949 $2. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. (PMID) 26503041.
- ^ Shalm, L. K. (16 Aralık 2015). "Strong Loophole-Free Test of Local Realism". Physical Review Letters. 115 (25): 250402. arXiv:1511.03189 $2. Bibcode:2015PhRvL.115y0402S. doi:10.1103/PhysRevLett.115.250402. (PMC) 5815856 $2. (PMID) 26722906.
- ^ Giustina, M. (16 Aralık 2015). "Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons". Physical Review Letters. 115 (25): 250401. arXiv:1511.03190 $2. Bibcode:2015PhRvL.115y0401G. doi:10.1103/PhysRevLett.115.250401. (PMID) 26722905.
- ^ Aspect, Alain (16 Aralık 2015). "Closing the Door on Einstein and Bohr's Quantum Debate". . 8: 123. Bibcode:2015PhyOJ...8..123A. doi:10.1103/Physics.8.123
![image]() .
. - ^ Ahlander, Johan; Burger, Ludwig; Pollard, Niklas (4 Ekim 2022). "Nobel physics prize goes to sleuths of 'spooky' quantum science". Reuters (İngilizce). 4 Ekim 2022 tarihinde kaynağından . Erişim tarihi: 4 Ekim 2022.
- ^ Schlosshauer, Maximilian; Kofler, Johannes; Zeilinger, Anton (6 Ocak 2013). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222-230. arXiv:1301.1069 $2. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004.
- ^ Siddiqui, Shabnam; Singh, Chandralekha (2017). "How diverse are physics instructors' attitudes and approaches to teaching undergraduate level quantum mechanics?". European Journal of Physics. 38 (3): 035703. Bibcode:2017EJPh...38c5703S. doi:10.1088/1361-6404/aa6131
![image]() .
. - ^ a b (2019). "Copenhagen Interpretation of Quantum Mechanics". Zalta, Edward N. (Ed.). . Metaphysics Research Lab, Stanford University. 29 Nisan 2019 tarihinde kaynağından . Erişim tarihi: 16 Eylül 2021.
- ^ Camilleri, K.; Schlosshauer, M. (2015). "Niels Bohr as Philosopher of Experiment: Does Decoherence Theory Challenge Bohr's Doctrine of Classical Concepts?". . 49: 73-83. arXiv:1502.06547 $2. Bibcode:2015SHPMP..49...73C. doi:10.1016/j.shpsb.2015.01.005.
- ^ (2002). "Popper's experiment and the Copenhagen interpretation". . 33: 23. arXiv:quant-ph/9910078 $2. Bibcode:1999quant.ph.10078P. doi:10.1016/S1355-2198(01)00034-X.
- ^ Bohr, N. (13 Ekim 1935). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?" (PDF). Physical Review. 48 (8): 696-702. Bibcode:1935PhRv...48..696B. doi:10.1103/PhysRev.48.696
![image]() . 9 Ocak 2020 tarihinde kaynağından (PDF). Erişim tarihi: 16 Eylül 2021.
. 9 Ocak 2020 tarihinde kaynağından (PDF). Erişim tarihi: 16 Eylül 2021. - ^ Werner, Reinhard F. (24 Ekim 2014). "Comment on 'What Bell did'". . 47 (42): 424011. Bibcode:2014JPhA...47P4011W. doi:10.1088/1751-8113/47/42/424011. ISSN 1751-8113.
- ^ Żukowski, Marek (2017). "Bell's Theorem Tells Us Not What Quantum Mechanics Is, but What Quantum Mechanics Is Not". Bertlmann, Reinhold; Zeilinger, Anton (Ed.). Quantum [Un]Speakables II. The Frontiers Collection. Cham: Springer International Publishing. ss. 175-185. arXiv:1501.05640 $2. doi:10.1007/978-3-319-38987-5_10. ISBN .
- ^ (1994). The Interpretation of Quantum Mechanics. Princeton University Press. ISBN . OCLC 439453957.
- ^ (5 Ekim 2010). "Colloquium : An introduction to consistent quantum theory". Reviews of Modern Physics (İngilizce). 82 (4): 2835-2844. arXiv:0909.2359 $2. Bibcode:2010RvMP...82.2835H. doi:10.1103/RevModPhys.82.2835. ISSN 0034-6861.
- ^ Healey, Richard (2016). "Quantum-Bayesian and Pragmatist Views of Quantum Theory". Zalta, Edward N. (Ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. 17 Ağustos 2021 tarihinde kaynağından . Erişim tarihi: 16 Eylül 2021.
- ^ Deutsch, David; (2000). "Information flow in entangled quantum systems". . 456 (1999): 1759-1774. arXiv:quant-ph/9906007 $2. Bibcode:2000RSPSA.456.1759D. doi:10.1098/rspa.2000.0585.
- ^ ; Timpson, Christopher G. (2016). "Bell on Bell's Theorem: The Changing Face of Nonlocality". Bell, Mary; Gao, Shan (Ed.). Quantum Nonlocality and Reality: 50 years of Bell's theorem. Cambridge University Press. ss. 91-123. arXiv:1501.03521 $2. doi:10.1017/CBO9781316219393.008. ISBN .
- ^ Jaynes, E. T. (1989). "Clearing up Mysteries — the Original Goal". Clearing up Mysteries—The Original Goal (PDF). Maximum Entropy and Bayesian Methods. ss. 1-27. CiteSeerX 10.1.1.46.1264 $2. doi:10.1007/978-94-015-7860-8_1. ISBN . 28 Ekim 2011 tarihinde kaynağından (PDF). Erişim tarihi: 18 Ekim 2011.
- ^ Gill, Richard D. (2002). "Time, Finite Statistics, and Bell's Fifth Position". Proceedings of the Conference Foundations of Probability and Physics - 2 : Växjö (Soland), Sweden, June 2-7, 2002. 5. Växjö University Press. ss. 179-206. arXiv:quant-ph/0301059 $2.
- ^ Wood, Christopher J.; (3 Mart 2015). "The lesson of causal discovery algorithms for quantum correlations: causal explanations of Bell-inequality violations require fine-tuning". . 17 (3): 033002. arXiv:1208.4119 $2. Bibcode:2015NJPh...17c3002W. doi:10.1088/1367-2630/17/3/033002. ISSN 1367-2630. 20 Mart 2023 tarihinde kaynağından . Erişim tarihi: 30 Mayıs 2023.
- ^ Gröblacher, Simon; Paterek, Tomasz; Kaltenbaek, Rainer; Brukner, Časlav; Żukowski, Marek; Aspelmeyer, Markus; Zeilinger, Anton (2007). "An experimental test of non-local realism". Nature. 446 (7138): 871-5. arXiv:0704.2529 $2. Bibcode:2007Natur.446..871G. doi:10.1038/nature05677. (PMID) 17443179.
- ^ Kastner, Ruth E. (May 2010). "The quantum liar experiment in Cramer's transactional interpretation". (İngilizce). 41 (2): 86-92. arXiv:0906.1626 $2. Bibcode:2010SHPMP..41...86K. doi:10.1016/j.shpsb.2010.01.001. 24 Haziran 2018 tarihinde kaynağından . Erişim tarihi: 16 Eylül 2021.
- ^ 't Hooft, Gerard (2016). The Cellular Automaton Interpretation of Quantum Mechanics. Fundamental Theories of Physics. 185. Springer. doi:10.1007/978-3-319-41285-6. ISBN . OCLC 951761277. 29 Aralık 2021 tarihinde kaynağından . Erişim tarihi: 27 Ağustos 2020.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bell teoremi fizikteki birbiriyle yakindan iliskili birkac sonucu kapsayan bir terimdir ve bu sonuclarin tumu kuantum mekanigi nin olcumun dogasi hakkinda bazi temel varsayimlarin oldugu ile uyumsuz oldugunu belirler Buradaki yerel yerellik ilkesini bir parcacigin yalnizca yakin cevresinden etkilenebilecegi ve fiziksel alanlarin aracilik ettigi etkilesimlerin isik hizindan daha hizli yayilamayacagi fikrini ifade eder kuantum teorisine dahil olmayan ancak yine de deneylerin sonucunu etkileyen kuantum parcaciklarinin varsayilan ozellikleridir Bu sonuc ailesine adini veren fizikci John Stewart Bell in sozleriyle Eger gizli degiskenli bir teori yerel ise kuantum mekanigi ile uyusmaz ve eger kuantum mekanigi ile uyusursa yerel olmaz Terim genis bir sekilde bir dizi farkli turetmeye uygulanir bunlardan ilki Bell tarafindan 1964 te Einstein Podolsky Rosen Paradoksu Uzerine baslikli bir makalede tanitildi Bell in makalesi Albert Einstein ve Nathan Rosen in kuantum fiziginin eksik bir teori oldugunu savunarak onerdigi 1935 tarihli bir dusunce deneyine bir yanitti 1935 te kuantum fiziginin tahminlerinin olasiliga dayali oldugu zaten kabul edilmisti Einstein Podolsky ve Rosen bir cift parcacigin kuantum durumunun dolanik olacagi sekilde hazirlanmasini ve ardindan parcaciklari gelisiguzel sekilde buyuk bir mesafeye ayirmayi iceren bir senaryo sundular Deneyci parcaciklardan biri uzerinde gerceklestirilebilecek olasi kuantum mekaniksel olcum seceneklerine sahiptir Bir olcum sectiklerinde ve bir sonuc elde ettiklerinde diger parcacigin kuantum durumu diger parcacik ne kadar uzakta olursa olsun o sonuca bagli olarak bir anda yeni bir duruma coker Bu ya birinci parcacigin olcumunun bir sekilde ikinci parcacikla isik hizindan daha hizli etkilesime girdigini ya da dolanik parcaciklarin ayrilmadan once son kuantum durumlarini onceden belirleyen bazi olculmemis ozelliklere sahip oldugunu dusundurur Bu nedenle yerellik varsayildiginda parcacigin gercek fiziksel ozelliklerinin tam bir tanimini veremedigi icin kuantum mekanigi eksik olmalidir Baska bir deyisle elektronlar ve fotonlar gibi kuantum parcaciklari kuantum teorisinde yer almayan bazi ozellik veya nitelikler tasimalidir ve kuantum teorisinin tahminlerindeki belirsizlikler daha sonra gizli degiskenler olarak adlandirilan bu ozelliklerle ilgili cehaletten veya bilinmezlikten kaynaklanacaktir Bell kuantum dolaniklik analizini cok daha ileriye tasidi Olcumler dolanik bir ciftin iki ayri parcacigi uzerinde bagimsiz olarak yapilirsa sonuclarin her bir yaridaki gizli degiskenlere bagli oldugu varsayiminin iki olcumdeki sonuclarin nasil iliskilendirildigine iliskin matematiksel bir kisitlama anlamina geldigi sonucuna vardi Bu kisitlama daha sonra Bell esitsizligi olarak adlandirilacakti Bell daha sonra kuantum fiziginin bu esitsizligi ihlal eden korelasyonlari tahmin ettigini gosterdi Sonuc olarak gizli degiskenlerin kuantum fiziginin tahminlerini aciklayabilmesinin tek yolu onlarin yerel olmamasi dir bu iki parcacigin ne kadar genis bir alana ayrilirsa ayrilsinlar bir sekilde aninda etkilesime girebildiklerini soylemektir Sonraki yillarda Bell teoreminin birden cok varyasyonu one surulerek genellikle Bell esitsizlikleri veya Bell tipi esitsizlikler olarak bilinen yakindan iliskili diger kosullar ortaya kondu Bell in teoremini test etmek icin tasarlanan ilk ilkel deney 1972 de John Clauser ve tarafindan yapildi Toplu olarak olarak bilinen daha gelismis deneyler o zamandan beri bircok kez gerceklestirildi Siklikla bu deneylerin amaci bosluklari kapatmak yani prensipte daha onceki Bell testlerinin bulgularinin gecerliligini etkileyebilecek deneysel tasarim veya kurulum sorunlarini iyilestirmekti Bugune kadar Bell testleri fiziksel sistemlerin kuantum mekanigine uydugunu ve Bell esitsizliklerini ihlal ettigini tutarli bir sekilde bulmustur yani bu deneylerin sonuclari herhangi bir yerel gizli degisken teorisiyle bagdasmaz Korelasyonlar uzerinde Bell tipi bir kisitlamayi kanitlamak icin gereken varsayimlarin kesin dogasi fizikciler ve filozoflar tarafindan tartisildi Bell in teoreminin onemi suphe goturmezken kuantum mekaniginin yorumlanmasi uzerindeki tum sonuclari cozumlenmemistir TeoremTemel fikir uzerinde bircok varyasyon vardir bazilari digerlerinden daha guclu matematiksel varsayimlar kullanir Onemli bir sekilde Bell tipi teoremler herhangi bir yerel gizli degiskenler teorisine atifta bulunmaz bunun yerine kuantum fiziginin klasik doga resimlerinin ardindaki genel varsayimlari ihlal ettigini gosterir Bell tarafindan 1964 te ispatlanan orijinal teorem deneye en uygun teorem degildir ve Bell tipi esitsizlikler turunu daha sonraki bir ornekle tanitmak uygundur Varsayimsal karakterler Alice ve Bob genis olcude ayrilmis konumlarda duruyor Meslektaslari Victor bir cift parcacik hazirlar ve birini Alice e digerini Bob a gonderir Alice parcacigini aldiginda iki olasi olcumden birini yapmayi secer belki hangisine karar vermek icin yazi tura atarak Bu olcumleri su sekilde belirtin A0 displaystyle A 0 ve A1 displaystyle A 1 Hem A0 displaystyle A 0 hem de A1 displaystyle A 1 ikili olcumlerdir A0 displaystyle A 0 in sonucu ya 1 displaystyle 1 ya da 1 displaystyle 1 dir ve ayni sekilde A1 displaystyle A 1 icin de gecerlidir Bob parcacigini aldiginda ikisi de ikili olan B0 displaystyle B 0 ve B1 displaystyle B 1 olmak uzere iki olcumden birini secer Her olcumun parcacigin zaten sahip oldugu bir ozelligi ortaya cikardigini varsayalim Ornegin Alice A0 displaystyle A 0 i olcmeyi secer ve 1 displaystyle 1 sonucunu elde ederse aldigi parcacik a0 displaystyle a 0 ozelligi icin 1 displaystyle 1 degerini tasir Asagidaki kombinasyonu goz onunde bulundurun a0b0 a0b1 a1b0 a1b1 a0 a1 b0 a0 a1 b1 displaystyle a 0 b 0 a 0 b 1 a 1 b 0 a 1 b 1 a 0 a 1 b 0 a 0 a 1 b 1 Hem a0 displaystyle a 0 hem de a1 displaystyle a 1 1 displaystyle pm 1 degerlerini aldigindan o zaman ya a0 a1 displaystyle a 0 a 1 ya da a0 a1 displaystyle a 0 a 1 dir Ilk durumda a0 a1 b1 0 displaystyle a 0 a 1 b 1 0 ikinci durumda ise a0 a1 b0 0 displaystyle a 0 a 1 b 0 0 Boylece yukaridaki ifadenin sag tarafindaki terimlerden biri kaybolacak ve digeri 2 displaystyle pm 2 ye esit olacaktir Sonuc olarak Victor un yeni parcacik ciftleri hazirlamasiyla deney bircok denemede tekrarlanirsa a0b0 a0b1 a1b0 a1b1 displaystyle a 0 b 0 a 0 b 1 a 1 b 0 a 1 b 1 kombinasyonunun tum denemelerdeki ortalama degeri 2 den kucuk veya ona esit olacaktir Hicbir tek deneme bu miktari olcemez cunku Alice ve Bob her biri yalnizca bir olcum secebilir ancak altta yatan ozelliklerin var oldugu varsayimina gore toplamin ortalama degeri her terimin ortalamalarinin toplamidir Ortalamalari belirtmek icin koseli parantez kullanirsak A0B0 A0B1 A1B0 A1B1 2 displaystyle langle A 0 B 0 rangle langle A 0 B 1 rangle langle A 1 B 0 rangle langle A 1 B 1 rangle leq 2 Bu bir Bell esitsizligidir ozellikle 115 Buradaki turetilmesi iki varsayima baglidir birincisi temel fiziksel ozellikler a0 a1 b0 displaystyle a 0 a 1 b 0 ve b1 displaystyle b 1 in gozlemlenmekten veya olculmekten bagimsiz olarak var oldugu bazen gercekcilik varsayimi olarak adlandirilir ve ikincisi Alice in eylem secimi Bob un sonucunu etkileyemez veya tersi de etkileyemez genellikle yerellik varsayimi olarak adlandirilir 117 Kuantum mekanigi CHSH esitsizligini asagidaki gibi ihlal edebilir Victor ile tanimladigi bir cift qubit hazirlar ps 0 1 1 0 2 displaystyle psi rangle frac 0 rangle otimes 1 rangle 1 rangle otimes 0 rangle sqrt 2 burada 0 displaystyle 0 rangle ve 1 displaystyle 1 rangle Pauli matrisleri nin birinin ozdurumlaridir sz 100 1 displaystyle sigma z begin pmatrix 1 amp 0 0 amp 1 end pmatrix Victor daha sonra ilk kubiti Alice e ve ikincisini Bob a iletir Alice ve Bob un olasi olcum secimleri de Pauli matrisleri cinsinden tanimlanir Alice iki gozlemlenebilir olan sz displaystyle sigma z ve sx displaystyle sigma x den birini olcer A0 sz A1 sx 0110 displaystyle A 0 sigma z A 1 sigma x begin pmatrix 0 amp 1 1 amp 0 end pmatrix ve Bob iki gozlemlenebilirden birini olcer B0 sx sz2 B1 sx sz2 displaystyle B 0 frac sigma x sigma z sqrt 2 B 1 frac sigma x sigma z sqrt 2 Victor kullanarak bu gozlemlenebilirlerin ciftleri icin kuantum beklenti degerlerini hesaplayabilir A0 B0 12 A0 B1 12 A1 B0 12 A1 B1 12 displaystyle langle A 0 otimes B 0 rangle frac 1 sqrt 2 langle A 0 otimes B 1 rangle frac 1 sqrt 2 langle A 1 otimes B 0 rangle frac 1 sqrt 2 langle A 1 otimes B 1 rangle frac 1 sqrt 2 Deneyin bir denemesinde bu dort olcumden sadece biri yapilabilirken toplam A0 B0 A0 B1 A1 B0 A1 B1 22 displaystyle langle A 0 otimes B 0 rangle langle A 0 otimes B 1 rangle langle A 1 otimes B 0 rangle langle A 1 otimes B 1 rangle 2 sqrt 2 Victor un birden cok denemede bulmayi bekledigi ortalama degerlerin toplamini verir Bu deger yerel gizli degiskenler hipotezinden cikarilan klasik 2 ust sinirini asiyor 11622 displaystyle 2 sqrt 2 aslinda kuantum fiziginin bu beklenti degerleri kombinasyonu icin izin verdigi en buyuk degerdir ve onu bir yapar 140 CHSH oyununun bir ornegi hakem Victor Alice e ve Bob a birer bit gonderir ve Alice ve Bob hakeme birer bit geri gonderir CHSH esitsizligi Alice ve Bob un eylemlerini koordine etmeye calistiklari bir oyun olarak da dusunulebilir Victor x displaystyle x ve y displaystyle y olmak uzere iki biti bagimsiz olarak ve rastgele hazirlar x displaystyle x bitini Alice e ve y displaystyle y bitini Bob a gonderir Alice ve Bob a displaystyle a ve b displaystyle b yanit bitlerini Victor a dondurerek xy a bmod2 displaystyle xy a b mod 2 denklemini saglarlarsa kazanirlar Veya esdeger olarak x displaystyle x ve y displaystyle y nin mantiksal VE si a displaystyle a ve b displaystyle b nin mantiksal XOR u ise Alice ve Bob kazanir Alice ve Bob oyundan once istedikleri herhangi bir strateji uzerinde anlasabilirler ancak oyun basladiktan sonra iletisim kuramazlar Yerel gizli degiskenlere dayali herhangi bir teoride Alice ve Bob un kazanma olasiligi onceden hangi strateji uzerinde anlasirlarsa anlassinlar 3 4 displaystyle 3 4 ten buyuk degildir Ancak dolanik bir kuantum durumunu paylasiyorlarsa kazanma olasiliklari 2 24 0 85 displaystyle frac 2 sqrt 2 4 approx 0 85 kadar buyuk olabilir Varyasyonlar ve ilgili sonuclarBell 1964 Bell in 1964 tarihli makalesi sinirli kosullar altinda yerel gizli degisken modellerinin kuantum mekaniginin tahminlerini yeniden uretebilecegine isaret ediyor Daha sonra bunun genel olarak dogru olamayacagini gosterir Bell Einstein Podolsky Rosen EPR dusunce deneyinin David Bohm tarafindan gelistirilmis hali uzerinde duruyor Bu senaryoda bir cift parcacik bir spin tekli durumu dolasnik duruma bir ornektir tarafindan tanimlanacak sekilde birlikte olusturulur Parcaciklar daha sonra zit yonlerde birbirinden uzaklasir Her parcacik bir Stern Gerlach cihazi ile olculur bu farkli yonlerde yonlendirilebilen ve 1 displaystyle 1 ve 1 displaystyle 1 ile gosterilebilen iki olasi sonuctan birini raporlayan bir olcum aletidir Her olcum aletinin konfigurasyonu bir birim vektor ile temsil edilir ve a displaystyle vec a ve b displaystyle vec b ayarlarina sahip iki dedektor arasindaki korelasyon icin kuantum mekanik tahmini P a b a b displaystyle P vec a vec b vec a cdot vec b dir Ozellikle iki dedektorun oryantasyonu ayniysa a b displaystyle vec a vec b o zaman bir olcumun sonucu digerinin sonucunun negatifi olacagi kesindir ve P a a 1 displaystyle P vec a vec a 1 i verir Ve eger iki detektorun yonelimleri ortogonal a b 0 displaystyle vec a cdot vec b 0 ise o zaman sonuclar ilintisizdir ve P a b 0 displaystyle P vec a vec b 0 dir Bell bu ozel durumlarin gizli degiskenler acisindan aciklanabilecegini orneklerle kanitliyor ardindan ara acilari iceren tum olasiliklarin aciklanamayacagini gostermeye devam ediyor Bell bu korelasyonlar icin yerel bir gizli degisken modelinin bunlari l displaystyle lambda gizli parametresinin olasi degerleri uzerinden bir integral olarak aciklayacagini one surdu P a b dlr l A a l B b l displaystyle P vec a vec b int d lambda rho lambda A vec a lambda B vec b lambda burada r l displaystyle rho lambda bir olasilik yogunluk fonksiyonudur Iki islev A a l displaystyle A vec a lambda ve B b l displaystyle B vec b lambda yonlendirme vektorleri ve gizli degisken verilen iki dedektorun yanitlarini saglar A a l 1 B b l 1 displaystyle A vec a lambda pm 1 B vec b lambda pm 1 En onemlisi A displaystyle A dedektorunun sonucu b displaystyle vec b ye bagli degildir ve benzer sekilde B displaystyle B un sonucu a displaystyle vec a e bagli degildir cunku iki dedektor fiziksel olarak ayrilmistir Simdi deneyi yapan kisinin ikinci dedektor icin bir ayar secenegine sahip oldugunu varsayalim b displaystyle vec b veya c displaystyle vec c Bell bu iki dedektor ayari secenegi arasindaki korelasyon farkinin asagidaki esitsizligi karsilamasi gerektigini kanitliyor P a b P a c 1 P b c displaystyle P vec a vec b P vec a vec c leq 1 P vec b vec c Ancak kuantum mekaniginin Bell esitsizligini ihlal ettigi durumlari bulmak kolaydir 425 426 Ornegin a displaystyle vec a ve b displaystyle vec b vektorlerinin ortogonal oldugunu ve c displaystyle vec c un onlarin kendi duzlemlerinde her ikisinden de 45 acida oldugunu varsayalim Bu durumda P a b 0 displaystyle P vec a vec b 0 P a c P b c 22 displaystyle P vec a vec c P vec b vec c frac sqrt 2 2 iken ancak 22 1 22 displaystyle frac sqrt 2 2 nleq 1 frac sqrt 2 2 Bu nedenle tum a displaystyle vec a b displaystyle vec b ve c displaystyle vec c secimleri icin kuantum mekaniginin tahminlerini yeniden uretebilen yerel bir gizli degisken modeli yoktur Deneysel sonuclar klasik egrilerle celisir ve deneysel eksiklikler hesaba katildigi surece kuantum mekanigi tarafindan tahmin edilen egriyle eslesir Bell in 1964 teoremi mukemmel anti korelasyon olasiligini gerektirir birincinin sonucunu bilerek ikinci detektorun sonucu hakkinda bir olasilik tahmini yapma yetenegi Bu Einstein Podolsky ve Rosen tarafindan 1935 tarihli bir makalede tanitilan bir kavram olan EPR gerceklik kriteri ile ilgilidir Bu makale Bir sistemi herhangi bir sekilde bozmadan fiziksel bir niceligin degerini kesin olarak yani bire esit olasilikla tahmin edebiliyorsak o zaman o nicelige karsilik gelen bir gerceklik unsuru vardir diyor GHZ Mermin 1990 1990 da ve Anton Zeilinger daha sonra in yalnizca uc parcacik kullanacak sekilde basitlestirdigi dort parcacikli bir dusunce deneyi sundular Bu dusunce deneyinde Victor kuantum durumu ps 12 000 111 displaystyle psi rangle frac 1 sqrt 2 000 rangle 111 rangle tarafindan tanimlanan uc spin 1 2 parcacigi kumesi uretir burada yukaridaki gibi 0 displaystyle 0 rangle ve 1 displaystyle 1 rangle Pauli matrisi sz displaystyle sigma z nin ozvektorleridir Victor daha sonra birbirinden cok farkli yerlerde bekleyen Alice Bob ve Charlie ye birer parcacik gonderir Alice parcacigi uzerinde sx displaystyle sigma x veya sy displaystyle sigma y yi olcer Bob ve Charlie de oyle Her olcumun sonucu 1 displaystyle 1 veya 1 displaystyle 1 seklindedir Born kuralini uc kubitlik ps displaystyle psi rangle durumuna uygulayan Victor uc olcumun bir sx displaystyle sigma x ve iki sy displaystyle sigma y icerdiginde sonuclarin urununun her zaman 1 displaystyle 1 olacagini tahmin ediyor Bunun nedeni ps displaystyle psi rangle nin ozdegeri 1 displaystyle 1 olan sx sy sy displaystyle sigma x otimes sigma y otimes sigma y nin bir ozvektoru olmasidir ve ayni durum sy sx sy displaystyle sigma y otimes sigma x otimes sigma y ve sy sy sx displaystyle sigma y otimes sigma y otimes sigma x icin de gecerlidir Bu nedenle Alice in sx displaystyle sigma x olcumu icin sonucunu ve Bob un sy displaystyle sigma y olcumu icin sonucunu bilen Victor Charlie nin sy displaystyle sigma y olcumu icin hangi sonucu dondurecegini 1 olasilikla tahmin edebilir EPR gerceklik kriterine gore Charlie nin kubiti uzerindeki bir sy displaystyle sigma y olcumunun sonucuna karsilik gelen bir gerceklik unsuru olacaktir Aslinda ayni mantik hem olcumler hem de uc kubit icin gecerlidir O halde EPR gerceklik kriterine gore her parcacik uzerinde bir sx displaystyle sigma x veya sy displaystyle sigma y olcumunun sonucunu belirleyen bir komut seti icerir Uc parcacigin tamami daha sonra ax ay bx by cx cy displaystyle a x a y b x b y c x c y komut seti tarafindan aciklanacak ve her giris ya 1 displaystyle 1 ya da 1 displaystyle 1 olacak ve her sx displaystyle sigma x ya da sy displaystyle sigma y olcumu basitce uygun degeri dondurecektir Alice Bob ve Charlie nin hepsi sx displaystyle sigma x olcumunu yaparsa sonuclarinin carpimi axbxcx displaystyle a x b x c x olur Bu deger sundan cikarilabilir axbycy aybxcy aybycx axbxcxay2by2cy2 axbxcx displaystyle a x b y c y a y b x c y a y b y c x a x b x c x a y 2 b y 2 c y 2 a x b x c x cunku 1 displaystyle 1 veya 1 displaystyle 1 un karesi 1 displaystyle 1 dir Parantez icindeki her faktor 1 displaystyle 1 e esittir bu nedenle axbxcx 1 displaystyle a x b x c x 1 ve Alice Bob ve Charlie nin sonuclari soyle olacaktir olasilik birligi ile 1 displaystyle 1 Parantez icindeki her faktor 1 displaystyle 1 e esittir yani axbxcx 1 displaystyle a x b x c x 1 olur ve Alice Bob ve Charlie nin sonuclarinin carpimi olasilik birligi ile 1 displaystyle 1 olacaktir Ancak bu kuantum fizigi ile tutarsizdir Victor ps displaystyle psi rangle durumunu kullanarak sx sx sx displaystyle sigma x otimes sigma x otimes sigma x olcumunun bunun yerine olasilik birligi ile 1 displaystyle 1 i verecegini tahmin edebilir Bu dusunce deneyi geleneksel bir Bell esitsizligi olarak veya esdeger olarak CHSH oyunuyla ayni ruhta yerel olmayan bir oyun olarak yeniden bicimlendirilebilir Icinde Alice Bob ve Charlie Victor dan x y z displaystyle x y z bitlerini alirlar her zaman cift sayida bire yani x y z 0 displaystyle x oplus y oplus z 0 ye sahip olacaklarina soz verilirler ve ona a b c displaystyle a b c bitlerini geri gonderirler Cift sayida bire sahip olmalari gerektiginde a b c displaystyle a b c nin x y z 0 displaystyle x y z 0 disindaki tum girdiler icin tek sayida bire sahip olmasi durumunda oyunu kazanirlar Yani a b c x y z displaystyle a oplus b oplus c x lor y lor z olursa oyunu kazanirlar Yerel gizli degiskenlerle sahip olabilecekleri en yuksek zafer olasiligi 3 4 iken yukaridaki kuantum stratejisini kullanarak kesin olarak kazanirlar Bu kuantum sozde telepatinin bir ornegidir Kochen Specker theorem 1967 Kuantum teorisinde bir Hilbert uzayi icin ortonormal bazlar o Hilbert uzayina sahip bir sistem uzerinde gerceklestirilebilecek olcumleri temsil eder Bir bazdaki her vektor o olcumun olasi bir sonucunu temsil eder Farz edin ki gizli bir l displaystyle lambda degiskeni var oyle ki l displaystyle lambda nin degerini bilmek herhangi bir olcumun sonucu hakkinda kesinlik anlamina gelebilir Bir l displaystyle lambda degeri verildiginde her olcum sonucu yani Hilbert uzayindaki her vektor ya imkansizdir ya da garanti edilir Bir Kochen Specker konfigurasyonu icindeki bir vektorun bir tabana ait oldugu dusunuldugunde her zaman imkansiz ve baska bir tabana ait olarak alindiginda garantili olacagi ozelligine sahip birbirine kenetlenen coklu tabanlardan yapilmis sonlu bir vektorler kumesidir Diger bir deyisle bir Kochen Specker yapilandirmasi gizli bir l displaystyle lambda degiskeninin olcum sonuclarini kontrol edebilecegini varsaymanin tutarsizligini gosteren renklendirilemez bir kumedir Baska bir deyisle bir Kochen Specker yapilandirmasi gizli bir degisken olan l displaystyle lambda nin olcum sonuclarini kontrol edebilecegini varsaymanin tutarsizligini gosteren renklendirilemez bir kumedir 196 201 Ozgur irade teoremi Birbirine bagli tabanlarin konfigurasyonlarini kullanan Kochen Specker tipi arguman Bell tipi esitsizliklerin altinda yatan dolanik ciftleri olcme fikri ile birlestirilebilir Bu 1970 lerin basinda Kochen Heywood ve Redhead Stairs ve Brown ve Svetlichny tarafindan not edildi EPR nin isaret ettigi gibi dolanik bir ciftin bir yarisinda bir olcum sonucunun elde edilmesi diger yarisinda karsilik gelen bir olcumun sonucu hakkinda kesinlik anlamina gelir EPR gerceklik kriteri ciftin ikinci yarisi rahatsiz edilmedigi icin bu kesinligin ona ait fiziksel bir ozellikten kaynaklanmasi gerektigini varsayar Baska bir deyisle bu kritere gore ciftin henuz olculmemis ikinci yarisi icinde gizli bir l displaystyle lambda degiskeni bulunmalidir Ilk yarida sadece bir olcum dikkate alinirsa herhangi bir celiski ortaya cikmaz Bununla birlikte gozlemcinin birden fazla olasi olcum secenegi varsa ve bu olcumleri tanimlayan vektorler bir Kochen Specker konfigurasyonu olusturuyorsa o zaman ikinci yaridaki bazi sonuclar ayni anda imkansiz ve garanti olacaktir Bu tur bir arguman John Conway ve tarafindan ozgur irade teoremi adi altinda bir ornegi ileri suruldugunde dikkat cekti Conway Kochen teoremi tarafindan kesfedilen bir cift dolanik ve bir Kochen Specker konfigurasyonu kullanir Yari klasik dolaniklik Bell in isaret ettigi gibi dolanikliktan uretilen ozel korelasyon durumlari da dahil olmak uzere kuantum mekaniginin bazi tahminleri yerel gizli degisken modellerinde cogaltilabilir Bu konu Bell in teoreminden bu yana gecen zamanda sistematik olarak incelenmistir 1989 da simdi olarak adlandirilan EPR tipi korelasyonlar saglayan ama ayni zamanda bir gizli degisken modelini kabul eden bir cift sistem icin ortak kuantum durumlari olan seyi tanitti Werner durumlari simetrik tensor carpim formunun birimleri altinda degismez olan iki parcali kuantum durumlaridir rAB U U rAB U U displaystyle rho AB U otimes U rho AB U dagger otimes U dagger 2004 yilinda Robert Spekkens yerel ayriklastirilmis serbestlik dereceleri onculuyle baslayan ve ardindan bir gozlemcinin bu serbestlik dereceleri hakkinda ne kadar bilebilecegini kisitlayan ve boylece onlari gizli degiskenlere donusturen bir bilgi dengesi ilkesi dayatan bir oyuncak modeli tanitti Altta yatan degiskenler ontik durumlar hakkinda izin verilen bilgi durumlari epistemik durumlar kuantum durumlarinin bazi ozelliklerini taklit eder Oyuncak modelindeki korelasyonlar tek eslilik gibi karisikligin bazi yonlerini taklit edebilir ancak yapi geregi oyuncak modeli asla bir Bell esitsizligini ihlal edemez GecmisArka plan Kuantum mekaniginin gizli degiskenler tarafindan tamamlanip tamamlanamayacagi sorusu kuantum teorisinin ilk yillarina kadar uzanir Macaristan dogumlu bilge John von Neumann nda gizli parametreler olamayacagina dair bir kanit oldugunu iddia ettigi seyi sundu Von Neumann in ispatinin gecerliligi ve kesinligi Hans Reichenbach tarafindan daha ayrintili olarak tarafindan ve muhtemelen Albert Einstein tarafindan basili olmasa da konusma sirasinda sorgulandi ve von Neumann in temel varsayimini 1961 gibi erken bir tarihte reddettiler ancak 1967 ye kadar bir elestiri yayinlamadilar Einstein israrla kuantum mekaniginin tamamlanmis bir teori olamayacagini savundu Tercih ettigi arguman bir yerellik ilkesine dayaniyordu Birbiriyle yalnizca sinirli bir sure boyunca etkilesime giren A ve B iki kismi sistemden olusan mekanik bir sistem dusunun Etkilesimlerinden once ps fonksiyonu verilsin O zaman Schrodinger denklemi etkilesimleri gerceklestikten sonra ps fonksiyonunu saglayacaktir Simdi A kismi sisteminin fiziksel durumunu olcumlerle mumkun oldugu kadar tam olarak belirleyelim Daha sonra kuantum mekanigi yapilan olcumlerden ve toplam sistemin ps fonksiyonundan kismi sistem Bnin ps fonksiyonunu belirlememizi saglar Ancak bu belirleme A kosulunu belirten belirleyici buyukluklerden hangisinin olculdugune bagli bir sonuc verir ornegin koordinatlar veya momentumlar Etkilesimden sonra Bnin sadece bir fiziksel durumu olabileceginden ve Bden ayrilmis A sisteminde gerceklestirdigimiz ozel olcume bagli olarak kabul edilemeyeceginden ps fonksiyonunun fiziksel durumla acik bir sekilde koordine olmadigi sonucuna varilabilir Birkac ps fonksiyonunun B sisteminin ayni fiziksel kosuluyla bu koordinasyonu ps fonksiyonunun bir birim sistemin fiziksel durumunun tam bir aciklamasi olarak yorumlanamayacagini tekrar gosterir EPR dusunce deneyi de benzerdir ayrica birlesik bir dalga fonksiyonu tarafindan aciklanan iki ayri sistem A ve B dikkate alinir Bununla birlikte EPR makalesi daha sonra gercekligin EPR kriteri olarak bilinen fikri ekler buna gore B uzerindeki bir olcumun sonucunu 1 olasilikla tahmin etme yetenegi B icinde bir gerceklik unsurunun varligini ima eder 1951 de David Bohm EPR tarafindan ele alinan konum ve momentum olcumlerinin aksine olcumlerin farkli olasi sonuc araliklarina sahip oldugu EPR dusunce deneyinin bir varyantini onerdi Bir yil once Chien Shiung Wu ve Irving Shaknov dolanik ciftler halinde uretilen fotonlarin polarizasyonlarini basariyla olctuler boylece EPR dusunce deneyinin Bohm versiyonunu pratikte uygulanabilir hale getirdiler 1940 larin sonlarinda matematikci kuantum fiziginin temellerine ilgi duymaya basladi ve 1957 de kuantum mekaniginin kesin bir tanimi olarak kabul ettigi bir varsayimlar listesi hazirladi Mackey varsayimlardan birinin gereksiz oldugunu tahmin etti ve kisa bir sure sonra Andrew M Gleason bunun gercekten de diger varsayimlardan cikarsanabilecegini kanitladi genis bir gizli degisken teorileri sinifinin kuantum mekanigi ile bagdasmadigina dair bir arguman sagladi Daha spesifik olarak Gleason teoremi baglamsal olmayan gizli degisken modellerini dislar Kuantum mekanigi icin herhangi bir gizli degisken modeli Gleason teoreminin imalarindan kacinmak icin yalnizca olculen sisteme ait ozellikler olmayan ayni zamanda olcumun yapildigi dis baglama da bagli olan gizli degiskenleri icermelidir Bu tur bir bagimlilik genellikle yapmacik veya istenmeyen olarak gorulur bazi ayarlarda ozel gorelilik ile tutarsizdir Kochen Specker teoremi uzerinde boyle bir olasilik olcusunun tanimlanamayacagi belirli bir sonlu isin alt kumesi olusturarak bu ifadeyi gelistirir Tsung Dao Lee 1960 yilinda Bell in teoremini turetmeye cok yaklasti Zit yonlerde hareket eden iki kaon un uretildigi olaylari degerlendirdi ve gizli degiskenlerin bu tur durumlarda elde edilebilecek korelasyonlari aciklayamayacagi sonucuna vardi Ancak kaonlarin bozunmasi nedeniyle zorluklar ortaya cikti ve Bell tipi bir esitsizlik cikaracak kadar ileri gitmedi refn group note This was reported by 308 Lee en cok ile parite korunumunun ihlali tahminiyle taninir bu tahmin odulu paylasmayan Chien Shiung Wu tarafindan onaylandiktan sonra onlara Nobel Odulu kazandirdi Bell in yayinlari Bell teoremini nispeten belirsiz bir dergide yayinlamayi secti cunku sayfa ucreti gerektirmiyordu ve o sirada aslinda orada yayinlayan yazarlara odeme yapiyordu Dergi yazarlarin dagitmasi icin makalelerin ucretsiz yeniden baskilarini saglamadigindan Bell aldigi parayi diger fizikcilere gonderebilecegi kopyalari satin almak icin harcamak zorunda kaldi Dergide basilan makalelerin kendisinde yayinin adi basitce Physics olarak siralanirken kapaklarda Ingilizce Fransizca ve Rusca makaleler basilacagini yansitmak icin uc dilli Physics Physique Fizika versiyonu yer aliyordu 92 100 289 Bell 1964 sonucunu kanitlamadan once Kochen Specker teoremine esdeger bir sonuc da kanitladi bu nedenle ikincisi bazen Bell Kochen Specker veya Bell KS teoremi olarak da bilinir Ancak bu teoremin yayinlanmasi yanlislikla 1966 yilina kadar ertelendi O yazida Bell kuantum fenomeninin gizli degiskenler acisindan aciklanmasi yerel olmama gerektireceginden EPR paradoksunun Einstein in en az sevecegi sekilde cozuldugunu savundu Deneyler Iki kanalli Bell testi semasi S kaynagi zit yonlerde gonderilen foton ciftleri uretir Her foton yonu a veya b deneyi yapan kisi tarafindan ayarlanabilen iki kanalli bir polarizorle karsilasir Her kanaldan gelen sinyaller tespit edilir ve cakisma monitoru tarafindan dort turdeki ve cakismalar sayilir 1967 de olagandisi Physics Physique Fizika basligi John Clauser in dikkatini cekti o da Bell in makalesini kesfetti ve laboratuvarda bir yapmayi dusunmeye basladi Clauser ve 1972 de bir Bell testi yaptilar Bu sadece sinirli bir testti cunku dedektor ayarlarinin secimi fotonlar kaynaktan ayrilmadan once yapilmisti 1982 de Alain Aspect ve isbirlikcileri bu sinirlamayi kaldirmak icin ilk Bell testini gerceklestirdiler Bu giderek daha kati Bell testleri egilimini baslatti GHZ dusunce deneyi 2000 yilinda fotonlarin birbirine dolanik ucluleri kullanilarak pratikte uygulandi 2002 yilina gelindiginde lisans laboratuvar derslerinde CHSH esitsizliginin test edilmesi mumkundu Bell testlerinde deneysel bulgularin gecerliligini etkileyen deneysel tasarim veya kurulum sorunlari olabilir Bu sorunlara genellikle bosluklar denir Deneyin amaci kuantum mekaniginin tahminleriyle celisecek olan ile doganin aciklanip tanimlanamayacagini test etmektir Gercek deneylerdeki en yaygin bosluklar tespit ve yerellik bosluklaridir Deneyde parcaciklarin genellikle fotonlar kucuk bir kismi algilandiginda algilama acik kapisi olusur ve bu algilanan parcaciklarin temsil olmayan bir ornek oldugunu varsayarak verileri yerel gizli degiskenlerle aciklamayi mumkun kilar Tespitler bir bosluk benzeri ayrim ile yapilmadiginda yerellik acik kapisi olusur ve gorelilikle celismeden bir olcumun sonucunun digerini etkilemesi mumkun olur Bazi deneylerde Bell testi ihlallerinin yerel gizli degisken aciklamalarini mumkun kilan ek kusurlar olabilir Farkli deneylerde hem yerellik hem de algilama bosluklari kapatilmis olsa da ayni deneyde her ikisini de ayni anda kapatmak uzun suredir devam eden bir zorluktu This was finally achieved in three experiments in 2015 Bu sonuclarla ilgili olarak Alain Aspect hicbir deneyin tamamen acik kapisiz oldugu soylenemez diye yaziyor ama deneylerin yerel gizli degiskenlerden vazgecmemiz gerektigine dair son supheleri de ortadan kaldirdigini soyluyor ve kalan acikkapilarin ise orneklerini cok zorlanmis ve fizikteki olagan akil yurutme bicimine yabanci olarak ifade ediyor Bell esitsizliklerinin ihlallerini deneysel olarak dogrulamaya yonelik bu cabalar daha sonra Clauser Aspect ve Anton Zeilinger in 2022 Nobel Fizik Odulu ne layik gorulmesiyle sonuclanacakti Bell teoreminin yorumlariBell in teoremine verilen tepkiler cok ve cesitli olmustur Schlosshauer Kofler ve Zeilinger Bell esitsizliklerinin cok sayida deneyle test edilmis titiz bir teorik sonuca nasil sahip olabilecegimize ve yine de sonuclar konusunda nasil anlasamayacagimiza dair harika bir ornek sagladigini yaziyor Kopenhag Yorumu Kopenhag yorumu temelde Niels Bohr ve Werner Heisenberg e atfedilen kuantum mekaniginin anlami hakkindaki goruslerin bir derlemesidir Ozellikleri 1925 1927 yillari arasinda kuantum mekaniginin gelisimine dayandigindan kuantum mekaniginin onerilen sayisiz yorumunun en eskilerinden biridir ve en yaygin olarak ogretilenlerden biri olmaya devam etmektedir Kopenhag yorumunun ne olduguna dair kesin bir tarihsel aciklama yoktur Ozellikle Bohr ve Heisenberg in gorusleri arasinda temel gorus ayriliklari vardi Kopenhag koleksiyonunun bir parcasi olarak genel olarak kabul edilen bazi temel ilkeler kuantum mekaniginin ozunde deterministik olmadigi Belirlenimsizlik belirlenimsiz oldugu fikrini icerir ve olasiliklar ve tamamlayicilik ilkesi kullanilarak hesaplanir Tamamlayicilik ilkesi belirli ozelliklerin ayni sistem icin ayni anda ortaklasa tanimlanamayacagini soyler Bir sistemin belirli bir ozelliginden soz edebilmek icin o sistemin belirli bir laboratuvar duzenlemesi kapsaminda ele alinmasi gerekir Birbirini dislayan laboratuvar duzenlemelerine karsilik gelen gozlemlenebilir miktarlar birlikte tahmin edilemez ancak bir sistemi karakterize etmek icin bu tur birbirini dislayan cok sayida deneyi dikkate almak gerekir Bohr un kendisi EPR paradoksunun yaniltici oldugunu iddia etmek icin tamamlayiciligi kullandi Konum ve momentum olcumleri tamamlayici oldugundan birini olcmeyi secmek digerini olcme olasiligini dislar Sonuc olarak laboratuvar cihazlarinin bir duzenlemesiyle ilgili olarak cikarilan bir gercegin digeri araciligiyla cikarilan bir gercekle birlestirilemeyecegini ve bu nedenle ikinci parcacik icin onceden belirlenmis konum ve momentum degerlerinin cikariminin gecerli olmayacagini savundu 194 197 Bohr EPR nin argumanlarinin kuantum taniminin esasen eksik oldugu yonundeki sonuclarini hakli cikarmadigi sonucuna vardi Kopenhag tipi yorumlar genellikle Bell esitsizliklerinin ihlalini genellikle veya gercekcilik olarak adlandirilan ve daha genis bir felsefi anlamda gercekciligi terk etmekle ayni sey olmayan varsayimi reddetmek icin gerekce olarak alir Ornegin gizli degiskenlerin reddedildigini savunuyor ve su sonuca variyor kuantum mekanigi muhtemelen kapsami ve olgunlugu bakimindan simdiye kadarki herhangi bir teori kadar realist 531 Bu ayni zamanda genellikle Kopenhag dogru yapildi olarak ilan edilir ve gibi Kopenhag geleneginden gelen yorumlarin izledigi yoldur Kuantum mekaniginin bircok dunya yorumu Everett yorumu olarak da bilinen kuantum mekaniginin dalga fonksiyonu cokmeden uniter kismindan olustugu icin yerel ve deterministiktir Bir Bell esitsizligini ihlal eden korelasyonlar uretebilir cunku Bell in olcumlerin tek bir sonucu oldugu seklindeki ustu kapali varsayimini ihlal eder Aslinda Bell in teoremi bir olcumun tek bir sonucu oldugu varsayimindan yola cikarak Bircok Dunya cercevesinde kanitlanabilir Bu nedenle bir Bell esitsizliginin ihlali olcumlerin birden cok sonucu oldugunu gosteren bir kanit olarak yorumlanabilir Bell korelasyonlari icin sagladigi aciklama Alice ve Bob olcumlerini yaptiklarinda yerel dallara ayrilmalaridir Alice in her kopyasi acisindan bakildiginda Bob un farkli sonuclar yasayan birden cok kopyasi vardir bu nedenle Bob un kesin bir sonucu olamaz ve Bob un her kopyasi acisindan da ayni sey gecerlidir Yalnizca gelecekteki isik konileri cakistiginda karsilikli olarak iyi tanimlanmis bir sonuc elde edeceklerdir Bu noktada Bell korelasyonunun var olmaya basladigini ancak tamamen yerel bir mekanizma tarafindan uretildigini soyleyebiliriz Bu nedenle bir Bell esitsizliginin ihlali yerel olmamanin bir kaniti olarak yorumlanamaz Yerel olmayan gizli degiskenler Gizli degiskenler fikrinin cogu savunucusu deneylerin yerel gizli degiskenleri devre disi biraktigina inaniyor Bell in esitsizliginin ihlalini parcaciklarin durumlari hakkinda bilgi alisverisinde bulunduklari yerel olmayan bir araciligiyla aciklayarak yerellikten vazgecmeye hazirlar Bu evrendeki tum parcaciklarin digerleri ile aninda bilgi alisverisi yapabilmesini gerektiren kuantum mekaniginin temelidir Yerel olmayan gizli degisken teorileri icin bir zorluk bu anlik iletisimin neden gizli degiskenler seviyesinde var olabilecegini ancak sinyal gondermek icin kullanilamayacagini aciklamaktir 2007 de yapilan bir deney Bohm mekaniginin kendisi olmasa da Bohmcu olmayan yerel olmayan gizli degisken teorilerinin buyuk bir sinifini disladi Zamanda hem geriye hem de ileriye dogru hareket eden dalgalari varsayan da ayni sekilde yerel degildir Superdeterminizm Bell teoremini turetmek icin gerekli bir varsayim gizli degiskenlerin olcum ayarlariyla iliskili olmamasidir Bu varsayim deneycinin ayarlari secmek icin ozgur irade ye sahip oldugu ve her seyden once bilim yapmak icin bunun gerekli oldugu seklinde gerekcelendirildi Olcum seciminin mutlaka olculen sistemle iliskili oldugu varsayimsal bir teori superdeterministik olarak bilinir Deterministik modellerin birkac savunucusu yerel gizli degiskenlerden vazgecmedi Ornegin Gerard t Hooft superdeterminizmin goz ardi edilemeyecegini savundu Notlar We are for convenience assuming that the response of the detector to the underlying property is deterministic This assumption can be replaced it is equivalent to postulating a joint probability distribution over all the observables of the experiment Daha ayrintili olarak Paul Dirac David Hilbert John von Neumann ve Hermann Weyl tarafindan gelistirildigi uzere bir kuantum mekanik sisteminin durumu ayrilabilir bir Hilbert uzayi H displaystyle mathcal H ye ait bir ps displaystyle psi rangle vektorudur Ilgilenilen fiziksel nicelikler konum momentum enerji donus Hilbert uzayi uzerinde etki eden kendine es dogrusal operatorler olan gozlemlenebilirler tarafindan temsil edilir Bir gozlemlenebilir olculdugunde sonuc tarafindan verilen olasilikla ozdegerlerinden biri olacaktir en basit durumda h displaystyle eta ozdegeri dejenere degildir ve olasilik h displaystyle eta rangle nin iliskili ozvektoru oldugu h ps 2 displaystyle langle eta psi rangle 2 tarafindan verilir Daha genel olarak ozdeger dejeneredir ve olasilik ps Phps displaystyle langle psi P eta psi rangle tarafindan verilir burada Ph displaystyle P eta iliskili ozuzayinin projektorudur Bu tartismanin amaclari dogrultusunda ozdegerleri dejenere olmayan olarak alabiliriz See Reichenbach and Jammer 276 Mermin and Schack and for Einstein s remarks Clauser and Shimony and Wick 286 Deterministik olan bir gizli degisken teorisi belirli bir sonucun olasiliginin her zaman ya 0 ya da 1 oldugunu ima eder Ornegin bir spin 1 atomu uzerindeki bir Stern Gerlach olcumu atomun secilen eksen boyunca acisal momentumunun displaystyle 0 displaystyle 0 ve displaystyle olarak adlandirilabilecek uc olasi degerden biri oldugunu bildirecektir Deterministik bir gizli degisken teorisinde olcumde bulunan sonucu sabitleyen temel bir fiziksel ozellik vardir Altta yatan fiziksel ozelligin degerine bagli olarak herhangi bir sonuc ornegin displaystyle sonucu imkansiz veya garantili olmalidir Ancak Gleason teoremi boyle bir deterministik olasilik olcusunun olamayacagini ima eder cunku herhangi bir olasilik olcusunun bazi yogunluk operatorleri r displaystyle rho icin bir u ru u displaystyle u to langle rho u u rangle esleme bicimini almasi gerektigini kanitlar Bu esleme Hilbert uzayinin birim kure uzerinde sureklidir ve bu birim kure oldugundan uzerinde hicbir surekli olasilik olcusu deterministik olamaz Bu esleme Hilbert uzayinin birim kuresi uzerinde sureklidir ve bu birim kure baglantili oldugundan uzerinde hicbir surekli olasilik olcusu deterministik olamaz 1 3 was one exception but Jaynes arguments have not generally been found persuasive Kaynakca Bell John S 1987 Speakable and Unspeakable in Quantum Mechanics Cambridge University Press s 65 ISBN 9780521368698 OCLC 15053677 a b Einstein A Rosen N 15 Mayis 1935 Can Quantum Mechanical Description of Physical Reality be Considered Complete Physical Review 47 10 777 780 Bibcode 1935PhRv 47 777E doi 10 1103 PhysRev 47 777 a b Bell J S 1964 On the Einstein Podolsky Rosen Paradox PDF 1 3 195 200 doi 10 1103 PhysicsPhysiqueFizika 1 195 5 Mart 2017 tarihinde kaynagindan PDF Erisim tarihi 18 Mayis 2023 Parker Sybil B 1994 McGraw Hill Encyclopaedia of Physics 2 bas McGraw Hill s 542 ISBN 978 0 07 051400 3 a b c d July 1993 Hidden Variables and the Two Theorems of John Bell PDF Reviews of Modern Physics 65 3 803 15 arXiv 1802 10119 2 Bibcode 1993RvMP 65 803M doi 10 1103 RevModPhys 65 803 9 Temmuz 2020 tarihinde kaynagindan PDF Erisim tarihi 18 Mayis 2023 The Nobel Prize in Physics 2022 Basin aciklamasi 4 Ekim 2022 4 Ekim 2022 tarihinde kaynagindan Erisim tarihi 6 Ekim 2022 The BIG Bell Test Collaboration 9 Mayis 2018 Challenging local realism with human choices Nature 557 7704 212 216 arXiv 1805 04431 2 Bibcode 2018Natur 557 212B doi 10 1038 s41586 018 0085 3 PMID 29743691 7 Subat 2017 Ingilizce 7 Subat 2017 tarihinde kaynagindan arsivlendi Erisim tarihi 8 Subat 2020 a b Bell s Theorem Ed Stanford Encyclopedia of Philosophy a b c d 2010 Quantum Computation and Quantum Information 2 bas Cambridge Cambridge University Press ISBN 978 1 107 00217 3 OCLC 844974180 Fine Arthur 1 Subat 1982 Hidden Variables Joint Probability and the Bell Inequalities Physical Review Letters Ingilizce 48 5 291 295 Bibcode 1982PhRvL 48 291F doi 10 1103 PhysRevLett 48 291 ISSN 0031 9007 9 Eylul 2023 tarihinde kaynagindan Erisim tarihi 20 Mayis 2023 Braunstein Samuel L August 1990 Wringing out better Bell inequalities Ingilizce 202 1 22 56 Bibcode 1990AnPhy 202 22B doi 10 1016 0003 4916 90 90339 P Rau Jochen 2021 Quantum theory an information processing approach Oxford University Press ISBN 978 0 192 65027 6 OCLC 1256446911 Hoyer P Toner B 2004 Consequences and limits of nonlocal strategies Proceedings 19th IEEE Annual Conference on Computational Complexity 2004 IEEE ss 236 249 arXiv quant ph 0404076 2 Bibcode 2004quant ph 4076C doi 10 1109 CCC 2004 1313847 ISBN 0 7695 2120 7 OCLC 55954993 Barnum H Beigi S Boixo S Elliott M B Wehner S 6 Nisan 2010 Local Quantum Measurement and No Signaling Imply Quantum Correlations Physical Review Letters Ingilizce 104 14 140401 arXiv 0910 3952 2 Bibcode 2010PhRvL 104n0401B doi 10 1103 PhysRevLett 104 140401 ISSN 0031 9007 PMID 20481921 Griffiths David J 2005 Introduction to Quantum Mechanics 2 bas Upper Saddle River NJ Pearson Prentice Hall ISBN 0 13 111892 7 OCLC 53926857 Zeilinger A 1990 Bell s theorem without inequalities American Journal of Physics 58 12 1131 Bibcode 1990AmJPh 58 1131G doi 10 1119 1 16243 1990 Quantum mysteries revisited American Journal of Physics 58 8 731 734 Bibcode 1990AmJPh 58 731M doi 10 1119 1 16503 Tapp Alain 2005 Recasting Mermin s multi player game into the framework of pseudo telepathy Quantum Information and Computation 5 7 538 550 arXiv quant ph 0408052 2 Bibcode 2004quant ph 8052B doi 10 26421 QIC5 7 2 Dirac Paul Adrien Maurice 1930 The Principles of Quantum Mechanics Oxford Clarendon Press Hilbert David 2009 Sauer Tilman Majer Ulrich Ed Lectures on the Foundations of Physics 1915 1927 Relativity Quantum Theory and Epistemology Springer doi 10 1007 b12915 ISBN 978 3 540 20606 4 OCLC 463777694 von Neumann John 1932 Mathematische Grundlagen der Quantenmechanik Berlin Springer English translation Mathematical Foundations of Quantum Mechanics tarafindan cevrildi Princeton University Press 1955 Weyl Hermann 1950 1931 The Theory of Groups and Quantum Mechanics tarafindan cevrildi Dover ISBN 978 0 486 60269 1 Translated from the German Gruppentheorie und Quantenmechanik 2 bas de 1931 1993 Quantum Theory Concepts and Methods ISBN 0 7923 2549 4 OCLC 28854083 1 Temmuz 1991 Nonlocality in Quantum Mechanics Ingilizce 65 1 119 160 doi 10 1093 aristoteliansupp 65 1 119 ISSN 0309 7013 JSTOR 4106773 A similar approach was arrived at independently by Simon Kochen although never published private communication Heywood Peter May 1983 Nonlocality and the Kochen Specker paradox Ingilizce 13 5 481 499 Bibcode 1983FoPh 13 481H doi 10 1007 BF00729511 ISSN 0015 9018 Stairs Allen December 1983 Quantum Logic Realism and Value Definiteness Philosophy of Science Ingilizce 50 4 578 602 doi 10 1086 289140 ISSN 0031 8248 Svetlichny G November 1990 Nonlocality and Gleason s lemma Part I Deterministic theories Ingilizce 20 11 1379 1387 Bibcode 1990FoPh 20 1379B doi 10 1007 BF01883492 ISSN 0015 9018 Glick David Boge Florian J 22 Ekim 2019 Is the Reality Criterion Analytic Erkenntnis Ingilizce 86 6 1445 1451 arXiv 1909 11893 2 Bibcode 2019arXiv190911893G doi 10 1007 s10670 019 00163 w ISSN 0165 0106 Conway John 2006 The Free Will Theorem 36 10 1441 arXiv quant ph 0604079 2 Bibcode 2006FoPh 36 1441C doi 10 1007 s10701 006 9068 6 Rehmeyer Julie 15 Agustos 2008 Ingilizce 13 Subat 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Nisan 2022 Thomas Rachel 27 Aralik 2011 Ingilizce 12 Ocak 2012 tarihinde kaynagindan arsivlendi Erisim tarihi 23 Nisan 2022 Conway John H 2009 The strong free will theorem PDF 56 2 226 232 20 Mart 2023 tarihinde kaynagindan PDF Erisim tarihi 22 Mayis 2023 Werner Reinhard F 1 Ekim 1989 Quantum states with Einstein Podolsky Rosen correlations admitting a hidden variable model Physical Review A Ingilizce 40 8 4277 4281 Bibcode 1989PhRvA 40 4277W doi 10 1103 PhysRevA 40 4277 ISSN 0556 2791 PMID 9902666 19 Mart 2007 Evidence for the epistemic view of quantum states A toy theory Physical Review A Ingilizce 75 3 032110 arXiv quant ph 0401052 2 Bibcode 2007PhRvA 75c2110S doi 10 1103 PhysRevA 75 032110 ISSN 1050 2947 Catani Lorenzo Browne Dan E 27 Temmuz 2017 Spekkens toy model in all dimensions and its relationship with stabiliser quantum mechanics 19 7 073035 Bibcode 2017NJPh 19g3035C doi 10 1088 1367 2630 aa781c ISSN 1367 2630 Reichenbach Hans 1944 Philosophic Foundations of Quantum Mechanics University of California Press s 14 OCLC 872622725 a b c 1974 The Philosophy of Quantum Mechanics John Wiley and Sons ISBN 0 471 43958 4 Schack Rudiger 2018 Homer nodded von Neumann s surprising oversight 48 9 1007 1020 arXiv 1805 10311 2 Bibcode 2018FoPh 48 1007M doi 10 1007 s10701 018 0197 5 Clauser J F Shimony A 1978 Bell s theorem Experimental tests and implications PDF Reports on Progress in Physics 41 12 1881 1927 Bibcode 1978RPPh 41 1881C CiteSeerX 10 1 1 482 4728 2 doi 10 1088 0034 4885 41 12 002 23 Eylul 2017 tarihinde kaynagindan PDF Erisim tarihi 28 Ekim 2017 a b Wick David 1995 The Infamous Boundary Seven Decades of Heresy in Quantum Physics New York Springer doi 10 1007 978 1 4612 4030 3 11 ISBN 978 0 387 94726 6 Conway John 2002 The Geometry of the Quantum Paradoxes Zeilinger Anton Ed Quantum Un speakables From Bell to Quantum Information Berlin Springer ss 257 269 ISBN 3 540 42756 2 OCLC 49404213 Einstein Albert March 1936 Physics and reality Journal of the Franklin Institute 221 3 349 382 Bibcode 1936FrInJ 221 349E doi 10 1016 S0016 0032 36 91047 5 Harrigan Nicholas Spekkens Robert W 2010 Einstein incompleteness and the epistemic view of quantum states 40 2 125 arXiv 0706 2661 2 Bibcode 2010FoPh 40 125H doi 10 1007 s10701 009 9347 0 Bohm David 1989 Quantum Theory Dover reprint bas Prentice Hall ss 614 623 ISBN 978 0 486 65969 5 OCLC 1103789975 Wu C S Shaknov I 1950 The Angular Correlation of Scattered Annihilation Radiation Physical Review 77 1 136 Bibcode 1950PhRv 77 136W doi 10 1103 PhysRev 77 136 1957 Quantum Mechanics and Hilbert Space 64 8P2 45 57 doi 10 1080 00029890 1957 11989120 JSTOR 2308516 Gleason Andrew M 1957 Measures on the closed subspaces of a Hilbert space 6 4 885 893 doi 10 1512 iumj 1957 6 56050 MR 0096113 26 Subat 2021 tarihinde kaynagindan Erisim tarihi 24 Mayis 2023 Andy Gleason and Quantum Mechanics PDF 56 10 1253 1259 8 Aralik 2018 tarihinde kaynagindan PDF Erisim tarihi 24 Mayis 2023 Wilce A 2017 Quantum Logic and Probability Theory Stanford Encyclopedia of Philosophy Metaphysics Research Lab Stanford University 1984 Contextual Hidden Variable Theories and Bell s Inequalities 35 1 25 45 doi 10 1093 bjps 35 1 25 1991 Two simple proofs of the Kochen Specker theorem Ingilizce 24 4 L175 L178 Bibcode 1991JPhA 24L 175P doi 10 1088 0305 4470 24 4 003 ISSN 0305 4470 Whitaker Andrew 2016 John Stewart Bell and Twentieth Century Physics Vision and Integrity Ingilizce Oxford University Press ISBN 978 0 19 874299 9 a b Bell J S 1966 On the problem of hidden variables in quantum mechanics Reviews of Modern Physics 38 3 447 452 Bibcode 1966RvMP 38 447B doi 10 1103 revmodphys 38 447 1444158 30 Ocak 2012 Scientific American Ingilizce 4 Mart 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 11 Subat 2020 Clauser J F 1972 Experimental test of local hidden variable theories PDF Physical Review Letters 28 938 938 941 Bibcode 1972PhRvL 28 938F doi 10 1103 PhysRevLett 28 938 24 Mayis 2023 tarihinde kaynagindan PDF Erisim tarihi 24 Mayis 2023 Freedman Stuart Jay 5 Mayis 1972 Experimental test of local hidden variable theories PDF PhD University of California Berkeley 23 Mayis 2023 tarihinde kaynagindan PDF Erisim tarihi 24 Mayis 2023 Aspect Alain Dalibard Jean Roger Gerard 1982 Experimental Test of Bell s Inequalities Using Time Varying Analyzers Physical Review Letters 49 25 1804 7 Bibcode 1982PhRvL 49 1804A doi 10 1103 PhysRevLett 49 1804 Pan Jian Wei Bouwmeester D Daniell M Weinfurter H Zeilinger A 2000 Experimental test of quantum nonlocality in three photon GHZ entanglement Nature 403 6769 515 519 Bibcode 2000Natur 403 515P doi 10 1038 35000514 PMID 10676953 Dehlinger Dietrich Mitchell M W 2002 Entangled photons nonlocality and Bell inequalities in the undergraduate laboratory American Journal of Physics 70 9 903 910 arXiv quant ph 0205171 2 Bibcode 2002AmJPh 70 903D doi 10 1119 1 1498860 Larsson Jan Ake 2014 Loopholes in Bell inequality tests of local realism Journal of Physics A Mathematical and Theoretical 47 42 424003 arXiv 1407 0363 2 Bibcode 2014JPhA 47P4003L doi 10 1088 1751 8113 47 42 424003 Gerhardt I Liu Q Lamas Linares A Skaar J Scarani V Makarov V Kurtsiefer C 2011 Experimentally faking the violation of Bell s inequalities Physical Review Letters 107 17 170404 arXiv 1106 3224 2 Bibcode 2011PhRvL 107q0404G doi 10 1103 PhysRevLett 107 170404 PMID 22107491 Merali Zeeya 27 Agustos 2015 Quantum spookiness passes toughest test yet Nature News 525 7567 14 15 Bibcode 2015Natur 525 14M doi 10 1038 nature 2015 18255 PMID 26333448 Markoff Jack 21 Ekim 2015 Sorry Einstein Quantum Study Suggests Spooky Action Is Real New York Times 31 Temmuz 2019 tarihinde kaynagindan Erisim tarihi 21 Ekim 2015 Hensen B 21 Ekim 2015 Loophole free Bell inequality violation using electron spins separated by 1 3 kilometres Nature 526 7575 682 686 arXiv 1508 05949 2 Bibcode 2015Natur 526 682H doi 10 1038 nature15759 PMID 26503041 Shalm L K 16 Aralik 2015 Strong Loophole Free Test of Local Realism Physical Review Letters 115 25 250402 arXiv 1511 03189 2 Bibcode 2015PhRvL 115y0402S doi 10 1103 PhysRevLett 115 250402 PMC 5815856 2 PMID 26722906 Giustina M 16 Aralik 2015 Significant Loophole Free Test of Bell s Theorem with Entangled Photons Physical Review Letters 115 25 250401 arXiv 1511 03190 2 Bibcode 2015PhRvL 115y0401G doi 10 1103 PhysRevLett 115 250401 PMID 26722905 Aspect Alain 16 Aralik 2015 Closing the Door on Einstein and Bohr s Quantum Debate 8 123 Bibcode 2015PhyOJ 8 123A doi 10 1103 Physics 8 123 Ahlander Johan Burger Ludwig Pollard Niklas 4 Ekim 2022 Nobel physics prize goes to sleuths of spooky quantum science Reuters Ingilizce 4 Ekim 2022 tarihinde kaynagindan Erisim tarihi 4 Ekim 2022 Schlosshauer Maximilian Kofler Johannes Zeilinger Anton 6 Ocak 2013 A Snapshot of Foundational Attitudes Toward Quantum Mechanics Studies in History and Philosophy of Science Part B Studies in History and Philosophy of Modern Physics 44 3 222 230 arXiv 1301 1069 2 Bibcode 2013SHPMP 44 222S doi 10 1016 j shpsb 2013 04 004 Siddiqui Shabnam Singh Chandralekha 2017 How diverse are physics instructors attitudes and approaches to teaching undergraduate level quantum mechanics European Journal of Physics 38 3 035703 Bibcode 2017EJPh 38c5703S doi 10 1088 1361 6404 aa6131 a b 2019 Copenhagen Interpretation of Quantum Mechanics Zalta Edward N Ed Metaphysics Research Lab Stanford University 29 Nisan 2019 tarihinde kaynagindan Erisim tarihi 16 Eylul 2021 Camilleri K Schlosshauer M 2015 Niels Bohr as Philosopher of Experiment Does Decoherence Theory Challenge Bohr s Doctrine of Classical Concepts 49 73 83 arXiv 1502 06547 2 Bibcode 2015SHPMP 49 73C doi 10 1016 j shpsb 2015 01 005 2002 Popper s experiment and the Copenhagen interpretation 33 23 arXiv quant ph 9910078 2 Bibcode 1999quant ph 10078P doi 10 1016 S1355 2198 01 00034 X Bohr N 13 Ekim 1935 Can Quantum Mechanical Description of Physical Reality be Considered Complete PDF Physical Review 48 8 696 702 Bibcode 1935PhRv 48 696B doi 10 1103 PhysRev 48 696 9 Ocak 2020 tarihinde kaynagindan PDF Erisim tarihi 16 Eylul 2021 Werner Reinhard F 24 Ekim 2014 Comment on What Bell did 47 42 424011 Bibcode 2014JPhA 47P4011W doi 10 1088 1751 8113 47 42 424011 ISSN 1751 8113 Zukowski Marek 2017 Bell s Theorem Tells Us Not What Quantum Mechanics Is but What Quantum Mechanics Is Not Bertlmann Reinhold Zeilinger Anton Ed Quantum Un Speakables II The Frontiers Collection Cham Springer International Publishing ss 175 185 arXiv 1501 05640 2 doi 10 1007 978 3 319 38987 5 10 ISBN 978 3 319 38985 1 1994 The Interpretation of Quantum Mechanics Princeton University Press ISBN 978 0 691 03669 4 OCLC 439453957 5 Ekim 2010 Colloquium An introduction to consistent quantum theory Reviews of Modern Physics Ingilizce 82 4 2835 2844 arXiv 0909 2359 2 Bibcode 2010RvMP 82 2835H doi 10 1103 RevModPhys 82 2835 ISSN 0034 6861 Healey Richard 2016 Quantum Bayesian and Pragmatist Views of Quantum Theory Zalta Edward N Ed Stanford Encyclopedia of Philosophy Metaphysics Research Lab Stanford University 17 Agustos 2021 tarihinde kaynagindan Erisim tarihi 16 Eylul 2021 Deutsch David 2000 Information flow in entangled quantum systems 456 1999 1759 1774 arXiv quant ph 9906007 2 Bibcode 2000RSPSA 456 1759D doi 10 1098 rspa 2000 0585 Timpson Christopher G 2016 Bell on Bell s Theorem The Changing Face of Nonlocality Bell Mary Gao Shan Ed Quantum Nonlocality and Reality 50 years of Bell s theorem Cambridge University Press ss 91 123 arXiv 1501 03521 2 doi 10 1017 CBO9781316219393 008 ISBN 9781316219393 Jaynes E T 1989 Clearing up Mysteries the Original Goal Clearing up Mysteries The Original Goal PDF Maximum Entropy and Bayesian Methods ss 1 27 CiteSeerX 10 1 1 46 1264 2 doi 10 1007 978 94 015 7860 8 1 ISBN 978 90 481 4044 2 28 Ekim 2011 tarihinde kaynagindan PDF Erisim tarihi 18 Ekim 2011 Gill Richard D 2002 Time Finite Statistics and Bell s Fifth Position Proceedings of the Conference Foundations of Probability and Physics 2 Vaxjo Soland Sweden June 2 7 2002 5 Vaxjo University Press ss 179 206 arXiv quant ph 0301059 2 Wood Christopher J 3 Mart 2015 The lesson of causal discovery algorithms for quantum correlations causal explanations of Bell inequality violations require fine tuning 17 3 033002 arXiv 1208 4119 2 Bibcode 2015NJPh 17c3002W doi 10 1088 1367 2630 17 3 033002 ISSN 1367 2630 20 Mart 2023 tarihinde kaynagindan Erisim tarihi 30 Mayis 2023 Groblacher Simon Paterek Tomasz Kaltenbaek Rainer Brukner Caslav Zukowski Marek Aspelmeyer Markus Zeilinger Anton 2007 An experimental test of non local realism Nature 446 7138 871 5 arXiv 0704 2529 2 Bibcode 2007Natur 446 871G doi 10 1038 nature05677 PMID 17443179 Kastner Ruth E May 2010 The quantum liar experiment in Cramer s transactional interpretation Ingilizce 41 2 86 92 arXiv 0906 1626 2 Bibcode 2010SHPMP 41 86K doi 10 1016 j shpsb 2010 01 001 24 Haziran 2018 tarihinde kaynagindan Erisim tarihi 16 Eylul 2021 t Hooft Gerard 2016 The Cellular Automaton Interpretation of Quantum Mechanics Fundamental Theories of Physics 185 Springer doi 10 1007 978 3 319 41285 6 ISBN 978 3 319 41284 9 OCLC 951761277 29 Aralik 2021 tarihinde kaynagindan Erisim tarihi 27 Agustos 2020
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State