Bölme aritmetiğin temelini oluşturan dört ana işlemden biri olarak kabul edilir Diğer üç ana işlem ise toplama

Bölme, aritmetiğin temelini oluşturan dört ana işlemden biri olarak kabul edilir. Diğer üç ana işlem ise toplama, çıkarma ve çarpma olarak sıralanır. İşlem sırasında bölünen miktar bölünen olarak adlandırılırken, bu miktarın bölündüğü sayıya bölen denir ve işlemin sonucunda elde edilen değer bölüm olarak tanımlanır.

20 / 4 = 5 işleminin elmalarla gösterimi. Sözlü şekilde "20 bölü dört eşittir beş." olarak ifade edilir.

Temel düzeyde, iki doğal sayının bölünme işlemi, diğer olası yorumlara ek olarak, bir sayının başka bir sayı içerisinde ne sıklıkla yer aldığının hesaplanmasını içeren bir süreç olarak ele alınabilir.^:7 Örnek vermek gerekirse, 20 elma dört birey arasında eşit biçimde dağıtıldığında, her biri 5'er elma alır (ilgili görsel incelenebilir). Ancak bu durumda, tekrarlanan sayı veya içinde yer alan sayı (bölen), tam sayı olmayabilir.

Kalanlı bölme veya Öklid bölmesi, iki doğal sayı arasında gerçekleştirilen ve birinci sayının içinde ikinci sayının tamamıyla yer aldığı defaların sayısını ifade eden tam sayı bir bölüm ile, bölüm hesaplaması sırasında birinci sayının bir kısmının ikinci sayının büyüklüğü kadar daha fazla tahsis edilemediği için arta kalan kalanı içerir. Mesela, 21 elma dört kişi arasında paylaştırıldığında, her bir birey yine 5 elma alır ve bir elma artar.

Bölme işleminin sürekli olarak bir sayı üretmesi ve bir tam sayı bölümü ile bir kalan vermemesi için, doğal sayıların rasyonel sayılar veya reel sayılar ile genişletilmesi gereklidir. Bu genişletilmiş sayı sistemlerinde, bölme, çarpma işleminin tersi olarak işlev görür; yani $a = c / b$ ifadesi, $a \times b = c$ olarak değerlendirilir ( $b$ değerinin sıfır olmadığı varsayımı altında.) Eğer $b = 0$ ise, bu durum olarak adlandırılır ve tanımı mevcut değildir.^:246 21 elmalı durumda ise, her birey 5 elma ve bir çeyrek elma alır, bu şekilde hiç artan kalmaz.

Matematiksel yapıların tanımlanmasıyla ilgili çeşitli yollar içinde, farklı iki tür bölme işlemine ev sahipliği yapar. Öklid bölmesi (kalanlı bölme) içeren yapılar, olarak adlandırılır ve bu yapılar arasında, tek içeren yer alır; bu halkalar, tek değişkenli formüllerle çarpma ve toplama işlemlerini tanımlar. Sıfır olmayan tüm elemanlarla (tek sonuç veren) bölme işleminin tanımlandığı yapılar, alanlar ve olarak bilinir. Bir halkada ise bölme işlemi her zaman mümkün olan elemanlar olarak adlandırılır (örneğin, tam sayılar halkasındaki 1 ve -1 gibi). Ayrıca, bölme işleminin cebirsel yapılar bağlamında başka bir genelleştirmesi şeklindedir; bu yapıda "bölme" işleminin sonucu bir sayı yerine bir grup olarak karşımıza çıkar.

Giriş

Bölme işlemi, bölme ve bölüntü kavramları çerçevesinde en temel biçimde ele alınabilir: Bölme perspektifinden, $20 / 5$ ifadesi, 20 sayısına erişmek için eklenmesi gereken 5'lerin sayısını temsil eder. Bölüntü perspektifinden ise, $20 / 5$ ifadesi, 20 birimlik bir setin bölündüğü beş parçanın her birinin büyüklüğünü ifade eder. Örneğin, 20 elma, dört elmadan oluşan beş gruba ayrılır; bu durum "yirmi bölü beş dört eder" şeklinde ifade edilir. Bu durum, $20 / 5 = 4$ veya $20 / 5 = 4$ şeklinde gösterilir. Bu örnekte, 20 bölünen olarak, 5 bölen olarak ve 4 bölüm olarak tanımlanır.

Diğer temel matematik işlemlerinden farklı olarak, doğal sayıların bölünmesi esnasında, bölünen sayının tam bölünememesi sonucunda bazen bir kalan meydana gelir; mesela, $10 / 3$ işlemi sonucunda 1 kalan kalır, çünkü 10 sayısı 3'ün bir katı değildir. Bu tür durumlarda kalan, bölümün eklenebilir, bu nedenle $10 / 3$ işlemi $3 1 / 3$ veya $3.33...$ olarak ifade edilebilir. Ancak, tam sayı bölmesi bağlamında, kesirli kısım olmaksızın, kalan genellikle ayrı olarak tutulur (veya nadiren atılır veya yuvarlanır). Kalanın kesir olarak değerlendirildiği durumlar, bir rasyonel sayı oluşumuna neden olur. Tam sayıların bölünme işlemlerinin tüm potansiyel sonuçlarını içerecek şekilde genişletilmesiyle tüm rasyonel sayılar kümesi oluşturulur.

Çarpma ve toplama işlemlerinin tersine, bölme işlemi değişme özelliğine sahip değildir; bu, $a / b$ ifadesinin her durumda $b / a$ ile eşit olmayacağı anlamına gelir. Ayrıca, bölme işlemi genel olarak birleşimsel de değildir, yani birden fazla bölme işlemi gerçekleştirildiğinde, işlemlerin uygulama sırası sonucu etkileyebilir. Örnek vermek gerekirse, $(24 / 6) / 2 = 2$ sonucu elde edilirken, $24 / (6 / 2) = 8$ sonucu elde edilir (parantez kullanımı, parantez içindeki işlemlerin dışındakilerden önce yapıldığını belirtir).

Bölme işlemi, geleneksel olarak sol-birleşimsel niteliktedir. Bu bağlamda, ardışık bölme işlemleri söz konusu olduğunda, hesaplama işleminin sırası soldan sağa doğru yapılır:

a/b/c=(a/b)/c=a/(b\times c)\;\neq \;a/(b/c)=(a\times c)/b.

Ayrıca, bölme işlemi toplama ve çıkarma üzerinde sağ-dağılma özelliği gösterir, bu,

{\frac {a\pm b}{c}}=(a\pm b)/c=(a/c)\pm (b/c)={\frac {a}{c}}\pm {\frac {b}{c}}.

şeklinde ifade edilebilir.

Çarpma işlemi için de benzer bir durum söz konusudur; $(a+b)\times c=a\times c+b\times c$ şeklinde ifade edilir. Buna karşın, bölme işlemi sol-dağılma özelliğine sahip değildir,

{\frac {a}{b+c}}=a/(b+c);\neq ;(a/b)+(a/c)={\frac {ac+ab}{bc}}.

Mesela,

{\frac {12}{2+4}}={\frac {12}{6}}=2

örneğinde olduğu gibi, fakat

{\frac {12}{2}}+{\frac {12}{4}}=6+3=9

durumunda sonuçlar farklıdır.

Çarpma işlemi, hem sol-dağılma hem de sağ-dağılma özelliğine sahiptir ve bu nedenle dağılma özelliği gösterir.

Notasyon

Artı ve eksiler. «Næringsoppgave 1» adlı resmi Norveç ticaret beyanı formundan bir alıntıda eksi işareti alternatifi olarak kullanılan bir .

Matematikte bölme işlemi, bölünen sayının bölen sayının üzerine yazılması ve aralarında, ayrıca olarak da bilinen yatay bir çizgi bulunması şeklinde gösterilir. Örneğin, "a bölü b" ifadesi şu şekilde yazılabilir:

{\frac {a}{b}}

Bu yöntem, bölme işleminin tanımlanmasında, bilgisayar programlama dili çoğunluğunda tercih edilen yaygın bir yöntemdir, zira bu, basit bir ASCII karakter dizisi olarak rahatlıkla yazılabilir. (Ayrıca, bu gösterim soyut cebir alanında bölüm nesneleri için kullanılan tek yöntemdir.) MATLAB ve GNU Octave gibi bazı matematiksel yazılımlar, işlenenlerin sırasını tersine çevirerek, bölme operatörü olarak ters eğik çizgi kullanılmasına olanak tanır:

b\backslash a

Bu iki biçim arasındaki bir tipografik varyasyon olarak, bir eğik çizgi (kesir çizgisi) kullanılır, fakat bu durumda bölünen yukarıya, bölen ise aşağıya yerleştirilir:

{}^{a}\!/{}_{b}

Bu gösterim şekillerinden her biri, bir kesiri ifade etmek için kullanılabilir. Bir kesir, bölünen ve bölenin her ikisi de tam sayı olan ve bölme işleminin daha ileri değerlendirilmeye ihtiyaç duymadığı bir bölme ifadesidir (bunlar genellikle pay ve payda olarak adlandırılır). Bölme işlemini göstermenin başka bir yolu ise, özellikle aritmetikte yaygın olarak kullanılan (÷, olarak da adlandırılır) kullanmaktır:

a\div b

Bu gösterim şekli, genellikle yalnızca ilkokul matematiğinde nadir olarak karşımıza çıkar. -9.6, bu işaretin kullanılmamasını önermektedir. Ayrıca, bu bölme işareti, bölme işleminin kendisini temsil etmek amacıyla da kullanılır; örneğin bir hesap makinesinin tuşu üzerinde bir etiket olarak. Obelus sembolü, İsviçreli matematikçi tarafından 1659 yılında Teutsche Algebra isimli çalışmasında ilk kez tanıtılmıştır.^:211 ÷ simgesi, bazı Avrupa ülkelerinde çıkarma işareti olarak kullanıldığı için, bu kullanım yanılgılara yol açabilir.

Bazı İngilizce konuşulmayan ülkelerde bölme işlemi için iki nokta üst üste işareti kullanılmaktadır:

a:b

Bu gösterim, Gottfried Wilhelm Leibniz tarafından 1684 yılında yayımlanan Acta eruditorum isimli çalışmasında ilk kez kullanılmıştır.^:295 Leibniz, oran ve bölme işlemleri için farklı semboller kullanılmasına karşıydı. Ancak, İngilizce dil kullanımında, iki nokta üst üste işareti yalnızca oran gibi ilişkili bir kavramı ifade etmek amacıyla kullanılmaktadır.

19. yüzyıldan itibaren, ABD'deki ders kitaplarında, özellikle konuları ele alınırken, anın bye bölünmesini belirtmek için $b)a$ veya $b{\overline {)a}}$ biçimleri tercih edilmiştir. Bu notasyonun tarihçesi tam olarak belirgin değildir, zira zaman içinde bir evrim sürecinden geçmiştir.

Hesaplama

Manuel yöntemler

Bölme işlemi, sıklıkla bir nesne grubunun, örneğin bir grup şekerlemenin, eşit kısımlara "bölünmesi" fikri ile öğretilir. Her turda her bir bölüme birden fazla nesne atanması, bölünen miktarın bölenin katları kadar azaltılarak tekrarlanan bir süreç olan '' – yöntemine ilham verir. Bu yöntemde bölünen, bölenin çeşitli katları çıkarılarak azaltılır.

Bu süreç, belirli bir aşamada kısmi kalana göre daha fazla katın çıkarılmasına olanak tanıyarak, çift yönlü parçalama gibi daha esnek yöntemlerin geliştirilmesine de imkan sağlar.

İki tam sayının bölünmesi, eğer bölen küçükse yöntemi, eğer bölen büyükse yöntemi kullanılarak daha sistematik ve verimli bir biçimde gerçekleştirilebilir. Bölünen sayıda bir kesirli kısım mevcut ise (bu, bir olarak tanımlanabilir), bu işlem birler basamağından daha ileriye, istenen kadar devam ettirilebilir. Bölenin kesirli bir kısmı varsa, sorun her iki sayıda da ondalık noktayı sağa taşıyarak yeniden formüle edilebilir, böylece bölenin kesir içermemesi sağlanır; bu da sorunun daha kolay çözülmesine olanak tanır (örn., 10/2.5 = 100/25 = 4).

Bölme işlemi bir abaküs kullanılarak da yapılabilir.

Logaritma tabloları, iki sayının logaritmalarının çıkarılması ve sonucun bulunması süreci ile iki sayının bölünmesi için kullanılabilir.

, bölme işlemi için C ölçeği üzerindeki bölen ile D ölçeği üzerindeki bölüneni hizalayarak kullanılabilir. Bölüm, C ölçeğinin sol başlangıç noktası ile hizalanmış D ölçeği üzerinde yer alır. Ancak, kullanıcının ondalık noktasının konumunu zihinsel olarak izlemesi gerekir.

Bilgisayar yöntemleri

Günümüz hesap makinesileri ve bilgisayarları, uzun bölme işlemine benzer yöntemlerle ya da daha hızlı tekniklerle bölme işlemini gerçekleştirir.

Modüler aritmetikte (bir asal sayıya göre modülo) ve reel sayılar için, sıfır olmayan sayılar bir özelliğine sahiptir. Bu durumlarda, $x$ ile bölme, $x$ 'in çarpmaya göre tersi ile çarpım işlemi şeklinde gerçekleştirilebilir. Bu teknik sıklıkla bilgisayar aritmetiğinde tercih edilen daha hızlı yöntemler arasında yer alır.

Farklı bağlamlarda bölme

Öklid bölmesi

Öklid bölmesi, tam sayıların bölünmesi sürecinin tipik sonuçlarını matematiksel olarak formüle eder. Bu formülasyon, b ≠ 0 olmak üzere, a bölünen ve b bölen iki tam sayı verildiğinde, q bölüm ve r kalan olacak şekilde, eşsiz tam sayıların var olduğunu öne sürer. İşlem sonucunda a = bq + r eşitliği sağlanır ve 0 ≤ r < |b| koşulu yerine getirilir, burada |b| ifadesi b sayısının mutlak değerini gösterir.

Tam sayılarla bölme

Tam sayılar, bölme işlemi altında bir yapı sergilemezler. Sıfıra bölme işlemi tanımsız olduğu gibi, bölüm sadece bölünenin bölenin tam sayı katı olması durumunda tam sayı değerindedir. Örneğin, 26 sayısının 11 ile bölünmesi tam sayı bir sonuç üretmez. Bu tür durumlarda beş farklı yöntemden biri tercih edilebilir:

26'nın 11'e bölünemeyeceğini ifade etmek; bu durumda bölme işlemi bir olarak ele alınır.
Sonucu kayan noktalı sayı formunda yaklaşık bir değer olarak sunmak; bu yöntem genellikle sayısal hesaplama süreçlerinde benimsenir.
Sonucu 26'nın 11'e bölünmesiyle elde edilen ${\tfrac {26}{11}}$ şeklinde bir kesir olarak veya alternatif olarak ${\tfrac {26}{11}}=2{\tfrac {4}{11}}.$ şeklinde bir bileşik sayı olarak vermek. Bu kesirler genellikle sadeleştirilir; örneğin, 52'nin 22'ye bölünmesi sonucu da ${\tfrac {26}{11}}$ şeklindedir. Bu sadeleştirme işlemi, en büyük ortak bölenin çıkarılmasıyla yapılır.
Sonucu bir tam sayı bölüm ve kalan olarak vermek, örneğin ${\tfrac {26}{11}}=2{\mbox{ kalan }}4$ . Bu durum, iki tam sayı sonucu ile gerçekleştirilen bölme, temelinde Öklid algoritması bulunan Öklid bölmesi olarak adlandırılır.
Yalnızca tam sayı bölümü cevap olarak sunmak, yani ${\tfrac {26}{11}}=2$ ; bu durum, 2 veya 3'teki sayıların ile işlenmesidir. Bu yaklaşım bazen tam sayı bölmesi olarak tanımlanır ve "//" işareti ile gösterilir.

Bir bilgisayar programı içerisinde tam sayılar üzerinde bölme işlemi yapılması özel bir hassasiyet gerektirir. Bazı programlama dilleri, yukarıda belirtilen 5. örnekte olduğu gibi, tam sayı bölmesini ele alır ve sonuç olarak bir tam sayı verir. Diğer diller, örneğin MATLAB ve diğer her türlü Bilgisayarlı cebir sistemi, yukarıdaki 3. örnek gibi bir rasyonel sayı olarak cevap döndürür. Bu diller, diğer durumların sonuçlarını elde etmek için fonksiyonlar sunar, bu sonuçlar doğrudan veya 3. durumun sonucundan türetilmiş olabilir.

Tam sayı bölmesi için kullanılan adlar ve semboller arasında div, /, \ ve % yer alır. Bölünen ya da bölenin negatif olduğu durumlarda tam sayı bölmesinin tanımları değişkenlik gösterir: yuvarlama ya sıfıra doğru (genellikle T-bölmesi olarak adlandırılır) ya da 'e doğru (F-bölmesi olarak bilinir) yapılabilir; daha az yaygın olan diğer yöntemler için modulo işlemine bakılabilir.

Bölünebilme kuralları, bir tam sayının başka bir tam sayıya tam olarak bölünüp bölünmediğini belirlemek için bazen hızlı bir şekilde kullanılabilir.

Rasyonel sayılar

İki rasyonel sayı arasında gerçekleştirilen bölme işlemi, bölenin sıfır olmaması durumunda, sonuç olarak başka bir rasyonel sayı üretir. p/q ve r/s şeklinde ifade edilen iki rasyonel sayının bölünmesi, 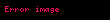${p/q \over r/s}={p \over q}\times {s \over r}={ps \over qr}.$ biçiminde hesaplanabilir.

Bu dört değerden her biri tam sayıdır ve sadece p sıfır olabilir. Bu tanımlama, bölme işleminin çarpma işleminin tersi olmasını sağlar.

Reel sayılar

İki reel sayı arasındaki bölme işlemi, bölen sıfır olmadığında, sonuç olarak başka bir reel sayı elde edilmesini sağlar. Bu, a/b = c ifadesinin, yalnızca a = cb ve b ≠ 0 olduğu durumlarda geçerli olacak şekilde tanımlanmıştır.

Karmaşık sayılar

İki karmaşık sayı arasında gerçekleştirilen bölme işlemi, bölen sıfır olmadığında, paydanın eşleniği kullanılarak hesaplandığında başka bir karmaşık sayı olarak ifade edilir: ${p+iq \over r+is}={(p+iq)(r-is) \over (r+is)(r-is)}={pr+qs+i(qr-ps) \over r^{2}+s^{2}}={pr+qs \over r^{2}+s^{2}}+i{qr-ps \over r^{2}+s^{2}}.$

Bu süreç, $r-is$ ile çarpma ve bölme işlemleri, genellikle 'gerçekleştirme' veya olarak tanımlanır. Bu işlemde p, q, r, s değerleri reel sayılardır ve r ve s değerleri eş zamanlı olarak 0 olamaz.

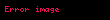
Kutupsal forma sahip karmaşık sayıların bölünmesi, yukarıda tanımlanan yöntemden daha basit bir süreçtir: ${pe^{iq} \over re^{is}}={pe^{iq}e^{-is} \over re^{is}e^{-is}}={p \over r}e^{i(q-s)}.$

Bu durumda da, p, q, r, s değerleri reel sayılardır ve r 0 olamaz. Bu işlemler, karmaşık sayıların bölünmesini matematiksel olarak daha ulaşılabilir kılar.

Polinomlar

Tek değişkenli polinomların bir alan üzerinde bölünmesi işlemi formüle edilebilir. Tam sayılarla yapılan bölme işlemlerinde olduğu gibi, bu durumda da bir kalan elde edilir. Bu konuda daha fazla bilgi için ve el ile yapılan hesaplamalar için polinom uzun bölme veya yöntemlerine başvurulabilir.

Matrisler

Matrisler arasında bir bölme işlemi formüle edilebilir. Bu işlem genellikle A / B = AB⁻¹ şeklinde tanımlanır; burada B⁻¹ B matrisinin tersini temsil eder. Ancak, olası karışıklıkları engellemek adına genellikle AB⁻¹ ifadesi açıkça yazılır. Ayrıca, bağlamında tanımlanan işlemi de uygulanabilir.

Sol ve sağ bölme işlemleri

Matris çarpımının değişmez olması nedeniyle, A matrisinin tersinin varlığı şartıyla, A matrisi ve B matrisi arasında bir veya ters eğik çizgi ile bölme işlemi tanımlanabilir: A \ B = A⁻¹B. Bu tanımın geçerli olması için, B⁻¹'nin varlığı zorunlu değildir. Bununla birlikte, genel olarak kabul gören A / B = AB⁻¹ tanımı bu bağlamda sıklıkla sağ bölme veya eğik çizgi ile bölme olarak ifade edilir, böylece anlam karmaşası önlenir.

Sol ve sağ bölme bu şekilde tanımlandığında, A / (BC) ifadesinin sonucu genelde (A / B) / C ile aynı olmaz, aynı şekilde (AB) \ C ifadesinin sonucu da A \ (B \ C) ile aynı olmaz. Ancak, A / (BC) = (A / C) / B ve (AB) \ C = B \ (A \ C) eşitliklerinin geçerli olduğu durumlar bulunmaktadır.

Sankiters

A⁻¹ ve/veya B⁻¹'nin mevcut olmaması durumlarında karşılaşılabilecek problemleri ortadan kaldırmak için, bölme işlemi kullanılarak çarpma şeklinde de tanımlanabilir. Bu durumda, A / B = AB⁺ ve A \ B = A⁺B, burada A⁺ ve B⁺ sırasıyla A ve B matrislerinin sankiterslerini belirtir.

Soyut cebirde

Soyut cebir alanında, ikili bir işlem olan ∗ (genelde çarpma olarak adlandırılır) ile tanımlanmış bir içinde, a ile b arasındaki sol bölme (a \ b şeklinde gösterilir), a ∗ x = b denklemi için x değeri bulunarak tanımlanır, bu çözüm eğer mevcutsa ve tek ise geçerlidir. Aynı şekilde, b ile a arasındaki sağ bölme (b / a şeklinde gösterilir), y ∗ a = b denklemi için y değeri bulunarak tanımlanır. Bu tanım, ∗ işleminin değişme, birleşme veya birim eleman gibi özel özellikler gerektirmez. Eğer hem a \ b hem de b / a işlemleri tüm a ve b değerleri için var ise ve benzersiz ise, bu yapı bir olarak adlandırılır. Bir quasigroupta, bu tanımlamalar doğrultusunda, bölme işlemi birim eleman veya tersinim olmaksızın dahi mümkündür.

"Sadeleşme" bağlamında "bölme", taşıyan bir eleman aracılığıyla her türlü magmada gerçekleştirilebilir. Bu durum, matris cebirleri, kuaterniyon cebirleri ve kuazigruplar gibi örneklerde görülebilir. Tamlık bölgelerde, her elemanın tersinin bulunması zorunlu olmadığı için, sadeleşme özelliğine sahip bir eleman a ile ab veya ca biçimindeki elemanlar üzerinde, sırasıyla sol veya sağ sadeleştirme yoluyla bölme işlemi uygulanabilir. Eğer bir halka sonlu ise ve her bir sıfır olmayan eleman sadeleştirilebiliyorsa, güvercin deliği ilkesinin uygulanması sonucunda, halkanın sıfır olmayan tüm elemanlarının tersinir olduğu ve sıfır olmayan her elemanla bölme işleminin mümkün olduğu sonucuna varılır. Cebirlerin (teknik anlamıyla) bir bölme işlemine sahip olup olmadığını anlamak için, konusundaki sayfaya yönlendirilirsiniz. Özellikle, herhangi bir gerçek reel sayılar R, karmaşık sayılar C, kuaterniyonlar H veya O ile olduğunu göstermek için kullanılabilir.

Kalkülüs

İki işlevin oranının türevi, bölme kuralına göre belirlenir: ${\left({\frac {f}{g}}\right)}'={\frac {f'g-fg'}{g^{2}}}.$

Sıfıra bölünme

Bir sayının sıfıra bölünmesi, çoğu matematiksel sistemde tanımsız olarak kabul edilir, çünkü sıfır ile çarpılan herhangi bir sonlu sayının çarpımı daima sıfır sonucunu verir. Bu tür bir ifadenin çoğu hesap makinesine girilmesi genellikle bir hata mesajıyla sonuçlanır. Bununla birlikte, ve gibi bazı ileri düzey matematik dallarında sıfıra bölme işlemi mümkündür. Bu tür cebirlerde, bölme işlemi geleneksel tanımlardan farklı bir anlam taşır.

Ayrıca bakınız

Notlar

^ Sıfıra bölme, reel sayıların veya ile genişletilmesi, ya da sıfıra yaklaşan sayılarla gerçekleştirilen bölüm işlemlerinin limitleri gibi bazı özel durumlarda tanımlanabilir. Örnek olarak: $lim x \to0 sin x / x = 1.$

Kaynakça

^ Blake, A. G. (1887). Arithmetic. Dublin, Ireland: .
^ ^a ^b Eric W. Weisstein, Bölme (MathWorld)
^ Eric W. Weisstein, Division by Zero (MathWorld)
^ Derbyshire, John (2004). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin Books. ISBN .
^ Eric W. Weisstein, Tam Sayı Bölmesi (MathWorld)
^ http://www.mathwords.com/c/commutative.htm 28 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde alındı
^ http://www.mathwords.com/a/associative_operation.htm 28 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde alındı
^ George Mark Bergman: Order of arithmetic operations 5 Mart 2017 tarihinde Wayback Machine sitesinde .
^ Education Place: The Order of Operations 8 Haziran 2017 tarihinde Wayback Machine sitesinde .
^ ^a ^b Cajori, Florian (1929). A History of Mathematical Notations. Open Court Pub. Co.
^ "6. Writing Systems and Punctuation" (PDF). The Unicode® Standard: Version 10.0 – Core Specification. Unicode Consortium. June 2017. s. 280, Obelus.
^ Thomas Sonnabend (2010). Mathematics for Teachers: An Interactive Approach for Grades K–8. Brooks/Cole, Cengage Learning (Charles Van Wagner). s. 126. ISBN .
^ Smith, David Eugene (1925). History Of Mathematics Vol II. Ginn And Company.
^ Kojima, Takashi (9 Temmuz 2012). Advanced Abacus: Theory and Practice (İngilizce). Tuttle Publishing. ISBN .
^ http://mathworld.wolfram.com/DivisionbyZero.html 23 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde erişildi
^ Jesper Carlström. "Sıfıra Bölme Üzerine" 17 Ağustos 2019 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde erişildi

[4] Sıfıra bölme, reel sayıların veya ile genişletilmesi, ya da sıfıra yaklaşan sayılarla gerçekleştirilen bölüm işlemlerinin limitleri gibi bazı özel durumlarda tanımlanabilir. Örnek olarak: $lim x \to0 sin x / x = 1.$

[1] Blake, A. G. (1887). Arithmetic. Dublin, Ireland: .

[mwdiv-2] Eric W. Weisstein, Bölme (MathWorld)

[db0-3] Eric W. Weisstein, Division by Zero (MathWorld)

[5] Derbyshire, John (2004). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin Books. ISBN .

[mwintdiv-6] Eric W. Weisstein, Tam Sayı Bölmesi (MathWorld)

[7] ttp://www.mathwords.com/c/commutative.htm 28 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde alındı

[8] ttp://www.mathwords.com/a/associative_operation.htm 28 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde alındı

[Order_of_arithmetic_operations-9] George Mark Bergman: Order of arithmetic operations 5 Mart 2017 tarihinde Wayback Machine sitesinde .

[The_Order_of_Operations-10] Education Place: The Order of Operations 8 Haziran 2017 tarihinde Wayback Machine sitesinde .

[Cajori-11] Cajori, Florian (1929). A History of Mathematical Notations. Open Court Pub. Co.

[12] "6. Writing Systems and Punctuation" (PDF). The Unicode® Standard: Version 10.0 – Core Specification. Unicode Consortium. June 2017. s. 280, Obelus.

[13] Thomas Sonnabend (2010). Mathematics for Teachers: An Interactive Approach for Grades K–8. Brooks/Cole, Cengage Learning (Charles Van Wagner). s. 126. ISBN .

[Smith-14] Smith, David Eugene (1925). History Of Mathematics Vol II. Ginn And Company.

[15] Kojima, Takashi (9 Temmuz 2012). Advanced Abacus: Theory and Practice (İngilizce). Tuttle Publishing. ISBN .

[16] ttp://mathworld.wolfram.com/DivisionbyZero.html 23 Ekim 2018 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde erişildi

[17] Jesper Carlström. "Sıfıra Bölme Üzerine" 17 Ağustos 2019 tarihinde Wayback Machine sitesinde . 23 Ekim 2018 tarihinde erişildi