Fizikte, kurtulma hızı kütleçekim alanındaki (yerçekimi etkisindeki) herhangi bir cismin kinetik enerjisinin söz konusu alana bağıl potansiyel enerjisine eşit olduğu andaki hızıdır. Genellikle üç boyutlu bir uzayda bulunan cismin kendisini etkileyen kurtulabilmesi için ulaşması gereken sürati ifade eder.

Ayrıntılı tanım

Belirli bir kütleçekimsel alan etkisi altında ve pozisyonda, bir cismin kütleçekim kaynağından herhangi bir ek ivme gerektirmeden kaçabilmesi için sahip olması gereken minimum hız o cismin kurtulma hızıdır. Kurtulma hızına sahip cisim, kaçmaya çalıştığı kütleye geri düşmez veya o cisim etrafında herhangi bir yörüngede (orbit) hareket etmez. Kurtulma hızı teoride yönden bağımsızdır; yani bu hıza sahip cisim üç boyutlu bir uzayda hangi yönde hareket ediyor olursa olsun çekim kaynağından kaçmayı başaracaktır. Ancak yön, pratik uzay uygulamalarında önemlidir. Çünkü uzay mühendisliği bilimince de sıkça incelendiği gibi, cismin fırlatılış hızı ile beraber sahip olacağı son yörüngeyi belirler. Dolayısıyla, kutupsal (polar) yörüngeye yerleştirilecek bir uyduyu taşıyan füzeye atmosferdeki yükselişi esnasında verilecek yön ile eliptik bir yörüngeye yerleştirilecek başka bir uyduyu taşıyan füzeye verilecek yön, hemen hemen aynı yükseliş hızına sahip de olsalar, farklıdır. Kurtulma hızına ulaştırılıp, Dünya'nın yerçekim alanını terk ettirilecek (örn. uzay sondaları) gibi cisimler fırlatılışın genellikle tüm aşamalarını atmosfere dik olarak geçtikten sonra uzay ortamında ateşlenen nispeten küçük roket motorlarıyla gidecekleri hedef gezegene doğru yönlendirilirler.
Aynı fiziksel teoremi tersten düşünecek olursak, tek merkezli bir gravitasyonel (kütleçekimsel) alanın etkisi altında ve sonsuz uzaklıktaki bir cisim, söz konusu kütleçekimsel alanı yaratan kütleye yaklaşırken en fazla o cisimden kaçarken erişmesi gereken minimum hız olan kurtulma hızında seyir edecektir. Kurtulma hızı genellikle kütlelerin yüzeyinde ölçülür. Yani, "Dünya'nın kurtulma hızı 11.2 km/sn'dir" dediğimizde aslında Dünya'nın yüzeyinde, deniz seviyesindeki bir konuma relatif kurtulma hızından bahsederiz. Buna nazaran, örneğin 9,000 km yüksekte (uzayda) cismin Dünya'nın yerçekiminden kaçması için sahip olması gereken kurtulma hızı 7.1 km/s'dir. Bir başka deyişle, cisim yerçekim kaynağından uzaklaştıkça, o kaynaktan kaçabilmesi için erişmesi gereken kurtulma hızı azalır.
Terimin yanlış kullanımları
Kurtulma hızı, herhangi bir cismin büyük kütlenin etrafındaki herhangi bir yörüngeden çıkması için sahip olması gereken hızla karıştırılmamalıdır. Belirli bir motor ve hareket kabiliyetine sahip cisim (örneğin bir helikopter), büyük kütlenin kütle merkezinden istediği herhangi bir hızda uzaklaşabilir. Uzaklık arttıkça, cismin büyük kütlenin yerçekiminden ilelebet kurtulabilmesi için çıkması gereken hız azalacaktır. Yani, cismin büyük kütlenin çekim etkisinden kurtulabilmesi için cisme verilmesi gereken ilk hızdır.
Bazı bilinen gök cisimlerinin kurtulma hızları

| Fırlatılış yeri | Kaçılan gökcismi | Ve | Fırlatılış yeri | Kaçılan gökcismi | Ve | |
|---|---|---|---|---|---|---|
| Güneş'in yüzeyi, | Güneş: | 617.5 km/sn | ||||
| Merkür'ün yüzeyi, | Merkür: | 4.4 km/sn | Merkür'ün yüzeyi, | Güneş: | 67.7 km/s | |
| Venüs'ün yüzeyi, | Venüs: | 10.4 km/sn | Venüs'ün yüzeyi, | Güneş: | 49.5 km/s | |
| Dünya'nın yüzeyi, | Dünya: | 11.2 km/sn | Dünya'nın yüzeyi, | Güneş: | 42.1 km/s | |
| Ay'ın yüzeyi, | Ay: | 2.4 km/sn | Ay'ın yüzeyi, | Dünya: | 1.4 km/s | |
| Mars'ın yüzeyi, | Mars: | 5.0 km/sn | Mars'ın yüzeyi: | Güneş: | 34.1 km/s | |
| Jüpiter'in yüzeyi, | Jüpiter: | 59.5 km/sn | Jüpiter'in yüzeyi, | Güneş: | 18.5 km/s | |
| Satürn'ün yüzeyi, | Satürn: | 35.5 km/sn | Satürn'ün yüzeyi, | Güneş: | 13.6 km/s | |
| Uranüs'ün yüzeyi, | Uranüs: | 21.3 km/sn | Uranüs'ün yüzeyi, | Güneş: | 9.6 km/s | |
| Neptün'ün yüzeyi, | Neptün: | 23.5 km/sn | Neptün'ün yüzeyi, | Güneş: | 7.7 km/s | |
| Güneş Sistemi, | Samanyolu galaksisi: | ~1000 km/sn | ||||
| Herhangi bir Karadeliğin yüzeyi, | Karadelik | ≥ 299,792.458 km/sn |
Atmosfer yüzünden Dünya yüzeyine yakın irtifalarda cisme 11.2 km/s'lik hipersonik bir hız kazandırmak, cismin hava molekülleri ile çarpışması sonucu yanarak parçalanmasına sebep olacağından pratikte mümkün değildir. Gerçek uzay uygulamalarında, atmosferin yavaşlatıcı etkisini egale etmek için cisim öncelikle alçak Dünya yörüngesine yerleştirilir, sonra ikinci bir motor ateşlemesiyle kurtulma hızına ulaştırılır.
Kurtulma hızının hesaplanması
Tek merkezli, basit bir çekim alanından kurtulma durumunda kurtulma hızı, cismin sahip olduğu kinetik enerjinin kütleçekimsel potansiyel enerjiye (eksi) eşit olduğu andaki meblâdır.
Burada 
Belirli bir irtifada kurtulma hızı, o irtifada dairesel orbitte hareket eden cismin hızının 

Kurtulma hızını işlemce kullanarak türevleme
Aşağıdaki türevlerde Newton'un evrensel çekim kanunu, Newton'un hareket kanunları ve integral işlemce kullanılmıştır.
g ve r kullanarak türevleme
Dünya'nın kurtulma hızı, yüzeyindeki standart yerçekimine bağıl ivme g kullanılarak elde edilebilir. Bu durumda Dünya'nın toplam kütlesi M veya yerçekimi sabitini G'nin bilinmesine de gerek yoktur. Şimdi,
- r = Dünya'nın yarıçapı
- g = Dünya'nın yüzeyindeki yerçekim ivmesi
olsun. Dünya'nın yüzeyinin üzerindeki irtifalarda, yerçekimi ivmesi Newton'un evrensel çekim kanunu'ndaki ilişkisi ile bulunur. Dünya'nın yüzeyinden s yükseklikteki bir noktada (ve s > r olduğunda) yerçekimi ivmesi 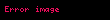
Bu, m kütleli cismin gezegenin yerçekiminden kaçabilmesi için sahip olması gereken kinetik enerjidir. Tabi v hızıyla ilerleyen ve m kütleli cismin toplam kinetik enerjisi Ek = (1/2)mv² formülü ile hesaplandığına göre,
şeklinde bir eşitlik kurabiliriz. Burada m'ler birbirini iptal eder ve eşitliği v için çözersek,
sonucuna ulaşırız. Dünya'nın yarıçapını r = 6400 kilometre, yüzeyindeki yerçekimi ivmesini de g = 9.8 m/s² olarak alırsak,
olacaktır. Bu rakam Isaac Newton'un hesapladığı 11 km/s'lik meblanın biraz üzerindedir.
G ve M kullanarak türevleme
Aşağıdaki eşitlikte G kütleçekim sabiti, M de Dünya'nın veya yerçekiminden kaçılacak başka bir kaynağın kütlesi olsun.
Burada türevin zincir kuralını uygulayabiliriz.
Eğer 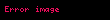
olacaktır. Biz buradan kurtulma hızını (v0) istediğimize göre,
ve
Buna göre v0 kurtulma hızı, r0 de kaçılan gezegenin yarıçapıdır. Bu noktada okuyucuya yukarıdaki türevde ile arasındaki sayısal eşitliğin esas alındığını hatırlatmak yerinde olacaktır.
Türevler tutarlı mıdır?
Yerçekimine bağlı-kütleçekimsel-- ivmeye (g), kütleçekim sabiti G ve gezegenin kütlesi M kullanılarak erişilebilinir:
Burada r gezegenin yarıçapı olduğuna göre,
olur. Dolayısıyla yukarıda verilen iki türev birbiriyle tutarlıdır.
Birden fazla kütleçekim kaynağı ve vektörel etkiler
Birden fazla çekim kaynağının bulunduğu kompleks senaryolarda cismin ortamdan kaçması için ihtiyaç duyduğu net kurtulma hızı, cismin bulunduğu vektörde sahip olduğu her etki kaynağına bağıl potansiyel enerjilerin toplanması ile elde edilir. Dolayısıyla, cisim için tüm sistemden kurtulma hızı, her bir etki kaynağının kurtulma hızlarının karelerinin toplamının kare köküne eşit olacaktır.
Buna bir örnek verecek olursak, Dünya'nın yüzeyinden fırlatılacak bir cisim için hem Dünya'ya hem de Güneş'e bağıl net kurtulma hızı 
Yerçekim drenajı
Kütlesel yoğunluğun gezegen içinde homojen olarak dağılmasi gibi hipotezsel bir varsayımda bulunacak olursak, cismin söz konusu gezegenin yüzeyinden merkezine doğru uzanan silindir şeklindeki uzun bir tünele (sürtünmesiz ortam) bırakıldığında erişeceği en yüksek hız, mevzû bahis gezegenin kurtulma hızının 

Elbette uzay mühendislerince kullanılan daha gerçekçi kurtulma hızı hesaplamaları gezegenlerin yoğunluğunun kütlesi boyunca heterojen ve düzensiz dağıldığı gerçeği göz ardı edilmeden yapılır.
Ayrıca bakınız
- Yerçekimi
- Uzay mekiği
- Karadelik - Çekim etkisinden kaçabilmek için ışık hızına eşit kurtulma hızı gerektiren bir gökcismi!
Kaynakça
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizikte kurtulma hizi kutlecekim alanindaki yercekimi etkisindeki herhangi bir cismin kinetik enerjisinin soz konusu alana bagil potansiyel enerjisine esit oldugu andaki hizidir Genellikle uc boyutlu bir uzayda bulunan cismin kendisini etkileyen kurtulabilmesi icin ulasmasi gereken surati ifade eder Uzay Mekigi Atlantis bir gorev icin UUI ye firlatilirken goruluyor Mekik Dunya nin yercekimsel alanini terk etmeyecegi icin firlatilista kurtulma hizina ulasmasi gerekmez Ayrintili tanimIsaac Newton un kurtulma hizi ile ilgili bu diyagrami dunyanin ayni noktasindan ayni yonde ancak farkli hizlarda firlatilan cisimlerin izleyecekleri yolu yorunge betimlemektedir E yorungesinin kurtulma hizinin uzerinde firlatilan cisme ait oldugu anlasilmaktadir Dolayisiyla bu cisim dunyanin yercekiminden kacabilecektir Belirli bir kutlecekimsel alan etkisi altinda ve pozisyonda bir cismin kutlecekim kaynagindan herhangi bir ek ivme gerektirmeden kacabilmesi icin sahip olmasi gereken minimum hiz o cismin kurtulma hizidir Kurtulma hizina sahip cisim kacmaya calistigi kutleye geri dusmez veya o cisim etrafinda herhangi bir yorungede orbit hareket etmez Kurtulma hizi teoride yonden bagimsizdir yani bu hiza sahip cisim uc boyutlu bir uzayda hangi yonde hareket ediyor olursa olsun cekim kaynagindan kacmayi basaracaktir Ancak yon pratik uzay uygulamalarinda onemlidir Cunku uzay muhendisligi bilimince de sikca incelendigi gibi cismin firlatilis hizi ile beraber sahip olacagi son yorungeyi belirler Dolayisiyla kutupsal polar yorungeye yerlestirilecek bir uyduyu tasiyan fuzeye atmosferdeki yukselisi esnasinda verilecek yon ile eliptik bir yorungeye yerlestirilecek baska bir uyduyu tasiyan fuzeye verilecek yon hemen hemen ayni yukselis hizina sahip de olsalar farklidir Kurtulma hizina ulastirilip Dunya nin yercekim alanini terk ettirilecek orn uzay sondalari gibi cisimler firlatilisin genellikle tum asamalarini atmosfere dik olarak gectikten sonra uzay ortaminda ateslenen nispeten kucuk roket motorlariyla gidecekleri hedef gezegene dogru yonlendirilirler Ayni fiziksel teoremi tersten dusunecek olursak tek merkezli bir gravitasyonel kutlecekimsel alanin etkisi altinda ve sonsuz uzakliktaki bir cisim soz konusu kutlecekimsel alani yaratan kutleye yaklasirken en fazla o cisimden kacarken erismesi gereken minimum hiz olan kurtulma hizinda seyir edecektir Kurtulma hizi genellikle kutlelerin yuzeyinde olculur Yani Dunya nin kurtulma hizi 11 2 km sn dir dedigimizde aslinda Dunya nin yuzeyinde deniz seviyesindeki bir konuma relatif kurtulma hizindan bahsederiz Buna nazaran ornegin 9 000 km yuksekte uzayda cismin Dunya nin yercekiminden kacmasi icin sahip olmasi gereken kurtulma hizi 7 1 km s dir Bir baska deyisle cisim yercekim kaynagindan uzaklastikca o kaynaktan kacabilmesi icin erismesi gereken kurtulma hizi azalir Terimin yanlis kullanimlariKurtulma hizi herhangi bir cismin buyuk kutlenin etrafindaki herhangi bir yorungeden cikmasi icin sahip olmasi gereken hizla karistirilmamalidir Belirli bir motor ve hareket kabiliyetine sahip cisim ornegin bir helikopter buyuk kutlenin kutle merkezinden istedigi herhangi bir hizda uzaklasabilir Uzaklik arttikca cismin buyuk kutlenin yercekiminden ilelebet kurtulabilmesi icin cikmasi gereken hiz azalacaktir Yani cismin buyuk kutlenin cekim etkisinden kurtulabilmesi icin cisme verilmesi gereken ilk hizdir Bazi bilinen gok cisimlerinin kurtulma hizlariGezegenimizin kacabilmesi icin cismin 11 2 km s lik bir kurtulma hizina ulasmasi gerekir Cismin Gunes in kurtulma hizina ulasip Gunes Sistemi ni terk edebilmesi icin ise 42 1 km s lik surate ulasmalidir Firlatilis yeri Kacilan gokcismi Ve Firlatilis yeri Kacilan gokcismi VeGunes in yuzeyi Gunes 617 5 km snMerkur un yuzeyi Merkur 4 4 km sn Merkur un yuzeyi Gunes 67 7 km sVenus un yuzeyi Venus 10 4 km sn Venus un yuzeyi Gunes 49 5 km sDunya nin yuzeyi Dunya 11 2 km sn Dunya nin yuzeyi Gunes 42 1 km sAy in yuzeyi Ay 2 4 km sn Ay in yuzeyi Dunya 1 4 km sMars in yuzeyi Mars 5 0 km sn Mars in yuzeyi Gunes 34 1 km sJupiter in yuzeyi Jupiter 59 5 km sn Jupiter in yuzeyi Gunes 18 5 km sSaturn un yuzeyi Saturn 35 5 km sn Saturn un yuzeyi Gunes 13 6 km sUranus un yuzeyi Uranus 21 3 km sn Uranus un yuzeyi Gunes 9 6 km sNeptun un yuzeyi Neptun 23 5 km sn Neptun un yuzeyi Gunes 7 7 km sGunes Sistemi Samanyolu galaksisi 1000 km snHerhangi bir Karadeligin yuzeyi Karadelik 299 792 458 km sn Atmosfer yuzunden Dunya yuzeyine yakin irtifalarda cisme 11 2 km s lik hipersonik bir hiz kazandirmak cismin hava molekulleri ile carpismasi sonucu yanarak parcalanmasina sebep olacagindan pratikte mumkun degildir Gercek uzay uygulamalarinda atmosferin yavaslatici etkisini egale etmek icin cisim oncelikle alcak Dunya yorungesine yerlestirilir sonra ikinci bir motor ateslemesiyle kurtulma hizina ulastirilir Kurtulma hizinin hesaplanmasiTek merkezli basit bir cekim alanindan kurtulma durumunda kurtulma hizi cismin sahip oldugu kinetik enerjinin kutlecekimsel potansiyel enerjiye eksi esit oldugu andaki mebladir 12mve2 GMmr displaystyle begin matrix frac 1 2 end matrix mv e 2 frac GMm r ve 2GMr 2mr 2gr displaystyle v e sqrt frac 2GM r sqrt frac 2 mu r sqrt 2gr Burada ve displaystyle v e kurtulma hizi G kutlecekim sabiti M kacilan cismin kutlesi m kacan cismin kutlesi g yercekimi ivmesi r cismin merkezi ile kurtulma hizinin hesaplandigi nokta arasindaki mesafe ve m ise standart kutlecekim parametresini sembolize etmektedir Belirli bir irtifada kurtulma hizi o irtifada dairesel orbitte hareket eden cismin hizinin 2 displaystyle sqrt 2 katina esittir Kuresel olarak homojen dagilimli bir kutleye sahip cisim icin yuzeyden kacista ihtiyac duyacagi kurtulma hizi ve displaystyle v e m s cinsinden yaklasik 2 364 10 5 m1 5kg 0 5s 1 carpi yaricap r metre cinsinden carpi averaj yogunlugun r kg m cinsinden karekoku olur ve 2 364 10 5rr displaystyle v e approx 2 364 times 10 5 r sqrt rho Kurtulma hizini islemce kullanarak turevlemeAsagidaki turevlerde Newton un evrensel cekim kanunu Newton un hareket kanunlari ve integral islemce kullanilmistir g ve r kullanarak turevleme Dunya nin kurtulma hizi yuzeyindeki standart yercekimine bagil ivme g kullanilarak elde edilebilir Bu durumda Dunya nin toplam kutlesi M veya yercekimi sabitini G nin bilinmesine de gerek yoktur Simdi r Dunya nin yaricapig Dunya nin yuzeyindeki yercekim ivmesi olsun Dunya nin yuzeyinin uzerindeki irtifalarda yercekimi ivmesi Newton un evrensel cekim kanunu ndaki iliskisi ile bulunur Dunya nin yuzeyinden s yukseklikteki bir noktada ve s gt r oldugunda yercekimi ivmesi g r s 2 displaystyle g r s 2 dir Burada m kutlesine sahip cismin yuzeydeki agirligi gm iken s yuksekligindeki agirligi gm r s olur Dolayisiyla m kutleli ve yuzeyden s yukseklikteki cismi yuzeyden s ds yuksekligine cikartabilmek icin ihtiyac duyulan enerji gm r s ds olacaktir Bu deger s arttikca hizla azalacagindan dolayi cismin sonsuz yukseklige cikartilabilmesi icin ihtiyac duyulan toplam enerji sonsuza ulasmaz ve sonlu bir meblaya yaklasir Bu mebla yukaridaki ifadenin integralidir r gm r s 2ds gmr2 r s 2ds gmr2 s 1 s rs displaystyle int r infty gm r s 2 ds gmr 2 int r infty s 2 ds gmr 2 left s 1 right s r s infty gmr2 0 r 1 gmr displaystyle gmr 2 left 0 r 1 right gmr Bu m kutleli cismin gezegenin yercekiminden kacabilmesi icin sahip olmasi gereken kinetik enerjidir Tabi v hiziyla ilerleyen ve m kutleli cismin toplam kinetik enerjisi Ek 1 2 mv formulu ile hesaplandigina gore 12mv2 gmr displaystyle begin matrix frac 1 2 end matrix mv 2 gmr seklinde bir esitlik kurabiliriz Burada m ler birbirini iptal eder ve esitligi v icin cozersek v 2gr displaystyle v sqrt 2gr sonucuna ulasiriz Dunya nin yaricapini r 6400 kilometre yuzeyindeki yercekimi ivmesini de g 9 8 m s olarak alirsak v 2 9 8 m s2 6 4 106 m 11200 m s displaystyle v cong sqrt 2 left 9 8 mathrm m mathrm s 2 right 6 4 times 10 6 mathrm m 11 200 mathrm m mathrm s olacaktir Bu rakam Isaac Newton un hesapladigi 11 km s lik meblanin biraz uzerindedir G ve M kullanarak turevleme Asagidaki esitlikte G kutlecekim sabiti M de Dunya nin veya yercekiminden kacilacak baska bir kaynagin kutlesi olsun ma mdvdt GMmr2 displaystyle ma m frac dv dt frac GMm r 2 a dvdt GMr2 displaystyle a frac dv dt frac GM r 2 Burada turevin zincir kuralini uygulayabiliriz dvdt dvdr drdt GMr2 displaystyle frac dv dt frac dv dr cdot frac dr dt frac GM r 2 Eger v drdt displaystyle v frac dr dt ise dvdr v GMr2 displaystyle frac dv dr cdot v frac GM r 2 v dv GMr2dr displaystyle v cdot dv frac GM r 2 dr v0v t vdv r0r t GMr2dr displaystyle int v 0 v t v dv int r 0 r t frac GM r 2 dr v t 22 v022 GMr t GMr0 displaystyle frac v t 2 2 frac v 0 2 2 frac GM r t frac GM r 0 olacaktir Biz buradan kurtulma hizini v0 istedigimize gore t r t displaystyle t rightarrow infty r t rightarrow infty ve v t 0 displaystyle v t rightarrow 0 v022 GMr0 displaystyle frac v 0 2 2 frac GM r 0 v0 2GMr0 displaystyle v 0 sqrt frac 2GM r 0 Buna gore v0 kurtulma hizi r0 de kacilan gezegenin yaricapidir Bu noktada okuyucuya yukaridaki turevde ile arasindaki sayisal esitligin esas alindigini hatirlatmak yerinde olacaktir Turevler tutarli midir Yercekimine bagli kutlecekimsel ivmeye g kutlecekim sabiti G ve gezegenin kutlesi M kullanilarak erisilebilinir g PMr2 FUN7 displaystyle g frac PM r 2 FUN 7 Burada r gezegenin yaricapi olduguna gore v 2gr 2GMrr2 2GMr displaystyle v sqrt 2gr sqrt frac 2GMr r 2 sqrt frac 2GM r olur Dolayisiyla yukarida verilen iki turev birbiriyle tutarlidir Birden fazla kutlecekim kaynagi ve vektorel etkilerBirden fazla cekim kaynaginin bulundugu kompleks senaryolarda cismin ortamdan kacmasi icin ihtiyac duydugu net kurtulma hizi cismin bulundugu vektorde sahip oldugu her etki kaynagina bagil potansiyel enerjilerin toplanmasi ile elde edilir Dolayisiyla cisim icin tum sistemden kurtulma hizi her bir etki kaynaginin kurtulma hizlarinin karelerinin toplaminin kare kokune esit olacaktir Buna bir ornek verecek olursak Dunya nin yuzeyinden firlatilacak bir cisim icin hem Dunya ya hem de Gunes e bagil net kurtulma hizi 11 22 42 12 43 56 km s displaystyle scriptstyle sqrt 11 2 2 42 1 2 43 56 mathrm km mathrm s seklinde ifade edilir Buna binayen cisim dunyanin gunes etrafindaki 30 km s lik naturel yorungesel vektore paralel firlatildiginda cismin gunes sistemini terk edebilmesi icin 13 6 km s lik oz kurtulma hizina sahip olmasi yeterlidir Yercekim drenajiKutlesel yogunlugun gezegen icinde homojen olarak dagilmasi gibi hipotezsel bir varsayimda bulunacak olursak cismin soz konusu gezegenin yuzeyinden merkezine dogru uzanan silindir seklindeki uzun bir tunele surtunmesiz ortam birakildiginda erisecegi en yuksek hiz mevzu bahis gezegenin kurtulma hizinin 2 displaystyle scriptstyle sqrt 2 ye bolumune esittir Bu sayi ayni zamanda cismin dusuk irtifada gezegen etrafinda tam dairesel yorungedeki hiziyla da esdegerdir Buna gore cismin gezegenin merkezinden firlatildiginda erismesi gereken kurtulma hizi yuzeyinden firlatildiginda erismesi gereken hizin 1 5 displaystyle scriptstyle sqrt 1 5 kati olacaktir Elbette uzay muhendislerince kullanilan daha gercekci kurtulma hizi hesaplamalari gezegenlerin yogunlugunun kutlesi boyunca heterojen ve duzensiz dagildigi gercegi goz ardi edilmeden yapilir Ayrica bakinizYercekimi Uzay mekigi Karadelik Cekim etkisinden kacabilmek icin isik hizina esit kurtulma hizi gerektiren bir gokcismi Kaynakca Georgia Eyalet Universitesi 7 Kasim 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 22 Mayis 2009 Bate Mueller and White p 35
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans