Büyük sayılar, gündelik yaşamda normalde kullanılmayan büyük sayıları ifade eder. Terim genellikle büyük pozitif tam sayıları veya daha genel anlamda büyük pozitif reel sayıları belirtir. Fakat, diğer anlamlar için de kullanılabilir.
Çok büyük sayılar matematik, kozmoloji, kriptografi ve gibi alanlarda kullanılır. Bazı insanlar sayıları "astronomik olarak büyük" şeklinde söyler. Yine de gökbiliminde kullanılan çok büyük sayıları bile matematiksel olarak tanımlamak kolaydır.
Büyük ve küçük sayıları ifade etmek için bilimsel gösterimi kullanma
Bilimsel gösterim, bilimsel çalışmalarda karşılaşılan birçok değeri ifade etmek için oluşturuldu. Örneğin 1,0 × 109, bir milyar demektir. 1 rakamından sonra 9 tane sıfır kullanılır ve 1 000 000 000 şeklinde yazılır. Benzer şekilde 1,0 × 10−9, milyarda bir demektir ve 0,000 000 001 şeklinde yazılır. Dokuz tane sıfır yerine 109 yazma, hem okuyucular fazla zahmet çekmemiş olur hem de çok fazla sıfırın bulunduğu uzun serilerdeki sayıların karıştırılma ihtimali azalmış olur.
Büyük sayılar her an yanımızda
Her gün gerçek dünyada kullandığımız bazı nesnelerin büyük sayı ile ilişkili örnekleri:
- 500-1000 GB'lık bilgisayar sabit diskinin bit sayısı (normal olarak yaklaşık 1013)
- insan vücudundaki hücrelerin sayısı (1014'den fazla)
- insan beynindeki nöronların sayısı (tahmini 1014)
- Avogadro sayısı, bir moldeki "öz varlıklar"ın (genellikle atom veya molekül) sayısı. 12 gram Karbon-12'deki atom sayısı; (yaklaşık olarak 6,022 × 1023 bölü mol)
Astronomik olarak büyük sayılar
Uzunluk ve zaman bakımından nitelendirilen diğer büyük sayılar, astronomi ve kozmoloji'de bulundu. Örneğin, Büyük Patlamadan bu yana kainatın 13,7 milyar (4,3 × 1017 saniye) yaşında olduğu öne sürülüyor. Gözlemlenebilir evren 93 milyar ışık yılı, (8,8 × 1026 metre) genişliğindedir ve yaklaşık 125 milyar (1,25 × 1011) galaksi içindeki 5 × 1022yıldızdan oluşur. Bunlar Hubble Uzay Teleskobu gözlemine göredir. Gözlemlenebilir evrende kabaca 1080temel parçacık vardır.
Kanada'daki Alberta Üniversitesi fizikçilerinden 'e göre, bir fizikçi tarafından açıkça hesaplanan en uzun zaman, 10101010101.1 yıldır.
Kombinatorik işlemler de hızlıca büyük sayılara doğru gider. Karışık düzendeki nesnelerin permütasyonlarının sayısını açıklayan faktöriyel fonksiyonu, nesne sayısına göre çok hızlı bir şekilde artar. Stirling yaklaşımı, bu şekilde büyümeyi asimtotiktik şekilde ifade ederek bir ipucu verir.
Kombinasyonel işlemler, çok büyük sayıları üretir. Bu sayıların çok büyük olmalarından dolayı, normalde sadece kendi logaritmalarında kullanılırlar.
ve benzer sayılar, algoritmik bilgi teorisinde bit betiklerini ifade etmek için kullanılır.
Bilgisayarlar ve hesapsal karışıklık
Moore Yasası, genel olarak bir mikroişlemcinin her bir transistör sayısının her 18 ayda iki katına çıkacağı tahminine dayanır. Bu, insanlara, bilgisayarların herhangi bir matematik problemini, ne derece karmaşık olursa olsun, çözebileceği fikrini oluşturdu (Turing Testine bakınız).
1980 ile 2000 yılları arasında sabit disk hacimleri 10 megabayttan (1 × 107 bayt) 100 gigabayt (1011 bayt) üzerine çıktı. 100 gigabaytlık bir disk, tüm dünyadaki 6 milyar insanın isimlerini, herhangi bir sıkıştırma programı kullanmaksızın, depolama kapasitesine sahiptir. Fakat 40 karakter uzunluğundaki olası tüm şifrelerin depolanması konusu oldukça zorludur. Her bir karakterin bir bayta eşit olduğunu düşünürsek, yaklaşık olarak 2320 tane şifre üretilir. Bu da yaklaşık 2 × 1096 eder. Evrenin hesaplama kapasitesi, adlı yazısında Seth Lloyd, eğer evrendeki her bir zerre, büyük bir bilgisayarın parçasıymış gibi kullanılabilseydi, sadece yaklaşık 1090 bit depolayabilirdi ki, bu da gerekli sözlük boyutunun milyonda birinden daha azdır. Bununla beraber sabit diske bilgi depolama ile onları hesaplama çok farklı işlevlerdir. Bir yandan şu an için depolamanın sınırları olsa bile, fakat hesaplama hızı ise farklı bir konudur.
Örnekler
Ayrıca aşağıdaki; Sayılara, sıralı örnekler bölümüne bakınız
(10.000.000.000), "10 milyar"dır (veya uzun ölçeklerde bazen 10.000 milyon olarak da adlandırılır).
- googol = 10100=(10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000)
- sentilyon = 10303 veya 10600, sayı adlandırma sistemine bağlı olarak
- googolplex = 10googol=1010100
- Skewes sayıları: İlki yaklaşık olarak
, ikincisi
Dünyada basılan toplam materyallar kabaca 1,6 × 1018 bittir. Bu sayı şöyle ifade edilebilir 
Karşılaştırma:
Birinci sayı, ikincisinden çok daha büyüktür. Çünkü birinci sayının üs kulesi (3 tane kule), her ne kadar tabanı 1,1 gibi çok küçük bir sayı olsa bile, daha fazladır.
Sistematik olarak daha hızlı artış sırası oluşturma



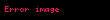
Bu, verilen bir sayıdaki yeni dizilimi oluşturma işlemidir. Bu tekrarlanabilir (örn, (özyinelemeye) uygulayabiliriz) ve tekrar sayı matristeki tek bir diziyi, her birinin 10. elemanını alarak seçebiliriz. Tüm bu işlem aynı şekilde tekrar ve tekrar uygulayabiliriz.



Bu işlemi tekrarlayarak şunu elde ederiz; 
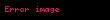
Bunu tüm işleme uygularsak daha fazla seri elde ederiz. n=10 seçersek (10→10), (10→10→10), (10→10→10→10),... dizilerini elde ederiz. Bu, işlemleri serinin başından itibaren tekrar ve tekrar ederek kullanılabilir. Hatta 
Tüm bu işlemdeki her bir seri, kendi sıralama türü tarafından şu şekilde tanımlanabilir:
- (10→n→k), n üslü, k - 1 sıralama türüne sahip seri
- (10→10→n→k), n üslü ω + k - 1 sıralama türüne sahip seri
- (10→10→10→n→k), n üslü 2ω + k - 1 sıralama türüne sahip seri
- (10→10), (10→10→10), (10→10→10→10),... ω² sıralama türüne sahip dizi
n = 1 hariç 
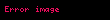
- n = 1, 3, 4, 5, 6,.. için
sağlanırken, n = 2 için sadece "=" (eşitlik) vardır..
- n = 1, 4, 5, 6,.. için
iken n = 2 ve 3 için ">" vardır.
Yukarıdaki açıklama, de benzer şekilde tanımlar.
Çok büyük sayıların yazım sistemini standartlaştırma
Çok büyük sayıların yazımı için standart yol, artış sırasına göre onları kolayca sıralamayı sağlar ve bir sayının diğerinden ne kadar büyük olduğu fikrini verebilir.
Bilimsel gösterimde sayıları karşılaştıralım. Örneklerimiz 5×104 ve 2×105 olsun. önce üsleri karşılaştırın. Burada 5 > 4'tür. Bu yüzden 2×105 > 5×104 olur. Eğer üsler eşitse mantis (veya katsayı) karşılaştırılır. 5 > 2 olduğundan dolayı 5×104 > 2×104
10 tabanlı tetrasyon, 


Bunlar, her ifadenin bir göre genelleştirildiği çok yuvarlak sayılardır. Bir sayının ne kadar büyük olduğunu belirlemenin basit yolu, bu serideki iki sayının ortasındakini belirlemektir.
Daha fazla doğruluk için aradaki sayılar 



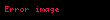
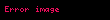
Googolplex sayısı: 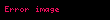
Başka bir örnek:
(
ile
arasında)
Bir sayının "büyüklük sırası", çarpım adedi olan n tarafından belirlenebilir. 1 ile 10 arasındaki bir sayısı belirlemek için 
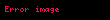

olduğuna dikkat edin.
Örn, 
Eğer kulenin yüksekliği büyükse, büyük sayılar için, bunu yerine çeşitli ifadeler uygulanabilir. Eğer yükseklik yaklaşık olarak verilirse, üsttekine bir değer verme mantıklı değildir. Bu yüzden, çift ok gösterimi kullanabiliriz. Örn, 
Örnekler:
sayısı (
ile
arasındadır)
sayısı (
ile
arasındadır)
Yukarıdakine benzer şekilde, eğer 

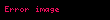

Eğer 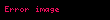
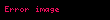

Eğer üç oklu operatörün (işlecin) sağdaki argüman büyükse, yukarıdaki işlemler tekrar edilir. Örn, 


Operatörleri (işleçleri) daha fazla oklarla devam ettirebilir ve şöyle yazabiliriz: 
Bu gösterimi, hiperişlem ve Conway dizisi ok gösterimi ile karşılaştıralım:
= ( a → b → n ) = hiper(a, n + 2, b)
İlkinin avantajı, eğer b bir fonksiyon ise, bu fonksiyonun üsleri için doğal bir gösterim vardır (sadece n tane ok yazıldığında): 
= ( 10 → ( 10 → ( 10 → b → 2 ) → 2 ) → 2 )
ve sadece özel durumlarda uzun iç içe girmiş dizi gösterimi kısaltılır. b = 1 için:
= ( 10 → 3 → 3 ) elde edilir.
b çok büyük sayı olduğunda genellikle, 




Sayıları yaklaşık olarak ifade etmek için, n nin değer azalış sıralarındaki sapmalara gerek yoktur. Örneğin, 
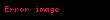
Artan okun üstindisi büyükse, bunun için özel ifadeler uygulanabilir. Eğer bu üstindis tam olarak belli değilse, işleci belli bir üsse yükseltmek veya netür bir değer olduğunu ayarlamak için hiçbir nokta yoktur. Basitçe sağda standart bir değer kullanabiliriz. 10'u 
Yukarıdaki işlem bu n için tekrar ve tekrar uygulanabilir. Böylece ilk okun üstindisinde 
- (10 → 10 → (10 → 10 →
) ) =
Eğer derece, elverişlilik için çok büyük ise, bu derece sayısını yazıldığı yere sayısal bir gösterim kullanılır (birçok ok yazmak yerine ok üstindisi kullanma gibi). 


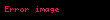
Graham sayısı ile karşılaştırma: 10 yerine 3 sayısını kullanır ve 64 ok derecesine sahiptir. En üstte 4 sayısı vardır. Burada 
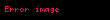
Eğer 
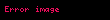





k belirlenemeyecek kadar çok büyükse, ilgili sayı 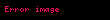


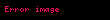

Çok büyük bir sayıyı Conway dizisi ok gösterimine yazmak için, bu dizi uzunluğu için sayının ne kadar büyük olduğunu açıklanmalıdır. Örneğin sadece dizideki 10 elemanını kullanma, başka bir ifadeyle onun 10, 10→10, 10→10→10, .. serisindeki konumunu belirleme. Hatta serideki konumu bile büyük bir sayı ise, bunun için aynı teknikleri uygulayabiliriz.
Sayılara, sıralı örnekler
- (1 → Y) = 1 (Her Y alt dizisi için)
- (2 → 2 → Y) = 4 (Her Y alt dizisi için)
= (2 → 3 → 2) = 16
= (3 → 2 → 2) = 27
- 44 = (4 → 2 → 2) = 256
- 55 = (5 → 2 → 2) = 3125
- 66 = (6 → 2 → 2) = 46.656
= (2 → 3 → 3) = (2 → 4 → 2) = 65.536
- 77 = (7 → 2 → 2) = 823.543
- 88 = (8 → 2 → 2) = 16.777.216
- 99 = (9 → 2 → 2) = 387.420.489
- 1010 = (10 → 2 → 2) = 10.000.000.000
= (3 → 3 → 2) = (3 → 2 → 3) = 7.625.597.484.987
- googol =
= (4 → 3 → 2) =
- Gözlemlenebilir evrenin Planck uzunluğuna göre yaklaşık değeri =
- (2 → 5 → 2) =
, 47nci ve Nisan 2010 itibarıyla bilinen en büyük (sayısı).
= (10 → 3 → 2)
= (3 → 4 → 2) =
- googolplex =
- (2 → 6 → 2) =
= (10 → 4 → 2)
- (2 → 7 → 2) =
= (10 → 5 → 2)
= (10 → 6 → 2)
= (10 → 7 → 2)
= (10 → 8 → 2)
= (10 → 9 → 2)
= (10 → 2 → 3) = (10 → 10 → 2)
- (2 → 3 → 4) = (2 → 4 → 3) = (2 → 65.536 → 2)
= (10 → 3 → 3)
= (10 → 4 → 3)
= (10 → 5 → 3)
= (10 → 6 → 3)
= (10 → 7 → 3)
= (10 → 8 → 3)
= (10 → 9 → 3)
= (10 → 2 → 4) = (10 → 10 → 3)
= (10 → 3 → 4)
= (4 → 4 → 4)
= (10 → 4 → 4)
= (10 → 5 → 4)
= (10 → 6 → 4)
= (10 → 7 → 4)
= (10 → 8 → 4)
= (10 → 9 → 4)
= (10 → 2 → 5) = (10 → 10 → 4)
- (2 → 3 → 2 → 2) = (2 → 3 → 8)
- (3 → 2 → 2 → 2) = (3 → 2 → 9) = (3 → 3 → 8)
- (10 → 10 → 10) = (10 → 2 → 11)
- (10 → 2 → 2 → 2) = (10 → 2 → 100)
- (10 → 10 → 2 → 2) = (10 → 2 →
) =
- (10 → 10 →
)
- (10 → 10 → 3 → 2) = (10 → 10 → (10 → 10 →
)) =
- (10 → 10 → 10 → 2)
- (10 → 10 → 64 → 2)
- Graham sayısı
- (10 → 10 → 65 → 2)
- (10 → 10 → 10 → 3)
- (10 → 10 → 10 → 4)
Temel değerleri karşılaştırma
Aşağıdaki anlatımlar 10'dan başka 100 tabanlı değerleri açıklıyor.



(Burada eğer n büyükse, rahatça
"yaklaşık olarak eşittir"
) diyebiliriz.
(karşılaştırın
; Burada eğer n büyükse,
"yaklaşık olarak eşittir"
) diyebiliriz
(karşılaştırın
)
(compare
)
(compare
; eğer n büyükse bu "yaklaşık olarak" eşittir)
Doğruluk



Çok büyük sayılarda doğruluk
Aşırı büyük sayılarda göreceli hata da büyük olabilirken dikkate almak istediğimiz sayıların "büyüklüğüne yakın" bir hassasiyeti olabilir. Örneğin,
ile
'u göz önüne alalım.
Göreceli hata,
'dır
Bu büyük bir hatadır. Yine de göreceli hatayı logaritmada göz önünde bulundurabiliriz. Bu sebeple 10 tabanındaki logaritmalar 10 ve 9'dur. Böylece logaritmadaki göreceli hata sadece %10 olur.
Eğer a ve b küçük göreceli bir hataya sahipse üstel fonksiyonların göreceli hataları oldukça büyüktür,
ile
'nin
göreceli hataları büyüktür ve
ile
de
daha büyük göreceli hataya sahip olacaktır. Sonraki soru şöyle olacaktır: hangi seviyedeki yinelenen logaritmada iki sayıyı karşılaştırabiliriz? Göz önünde bulunduracağımız bir hassasiyet vardır
ile
"yakın büüklükte" olur. Bu iki sayı arasındaki göreceli hata büyüktür ve onların logaritmaları arasındaki göreceli hata yine büyüktür. Bununla beraber bunların ikinci yineleme logaritmalarındaki hata küçüktür:
ile
Örneğin, yineleme logaritmalarını karşılaştırma bunun gibidir.
Çok büyük sayıların yaklaşık aritmetiği
Çok büyük sayılarında uygulanan olağan aritmetik işlemlere ait birkaç genel kural vardır:
- İki çok büyük sayıyı toplama ve çarpmanın her ikisinin sonucu da "yaklaşık olarak" sayılardan birine eşittir.
Buradan:
- Çok büyük kuvvete yükselen büyük bir sayı "yaklaşık olarak" aşağıdaki iki değerden birine eşittir: İlk değer ve 10, ikincinin kuvvetine. Örneğin, çok büyük n için
((megayı hesaplamaya) bakınız) ve
olur. Burada
, (Knuth tablolarına) bakınız.
Bazı hesaplanamayan serilerdeki büyük sayılar
fonksiyonu Σ, herhangi bir daha hızlı büyüyen bir fonksiyondur. Göreceli girdi değeri küçük olsa bile kendisi kocamandır. n = 1, 2, 3, 4 için Σ(n) fonksiyonu 1, 4, 6, 13'dür. Σ(5) bilinmiyor, fakat ≥ 4098 olarak tanımlanıyor. Σ(6), en az 4,6×101439'dur.
da, herhangi hesaplanabilir fonksiyonlardan daha hızlı büyüyen serilerle ilgili birkaç çalışma yapmıştır.
Sonsuz sayılar
Her ne kadar yukarıdaki tüm sayılar çok büyük olsa bile, yine de tümü . Matematiğin belirli alanları sonsuz ve tanımlar. Örneğin , doğal sayıların sonsuz serisinin ve sonraki en büyük nicel sayıdır. 

Gösterimler
Aşırı büyük sayıların bazı gösterimleri:
- Knuth yukarı ok gösterimi / hiperişlemler / tetrasyon içeren Ackermann işlevi
- Conway dizisi ok gösterimi
- Steinhaus-Moser gösterimi; büyük sayıların yapı yöntemi bir yana bu, çokgenli grafiksel gösterimi de içerir. Geleneksel fonksiyon gösterimleri gibi alternatif gösterimler de aynı fonksiyonlarla kullanılabilirler.
Bu gösterimler aslında, tam sayılarla hızlı bir şekilde artar tam sayı değişkenlerinin fonksiyonlarıdır. Fonksiyonlardaki hızlı artma bile, tekrarlı bir şekilde, bu fonksiyonları argüman olarak büyük tam sayılarla uygulayarak kolayca elde edilebilir.
Ayrıca bakınız
Alıntılar
- ^ Lloyd, Seth (2002). "Computational capacity of the universe" (PDF). Phys. Rev. Lett. 88 (23). s. 237901. doi:10.1103/PhysRevLett.88.237901. (PMID) 12059399. eprint quant-ph/0110141. 3 Eylül 2013 tarihinde kaynağından . Erişim tarihi: 17 Eylül 2007.
- ^ 10'un yerine başka bir sayı da kullanılabilir. O 1'den daha büyük olmalıdır ve eğer
ise, artış dizisi elde etmek için o 2'den daha büyük olmalıdır.
- ^ Önceki değerle karşılaştırma ile ilgili:
. Böylece 4 yerine 1, 10 yerine 3 sayılarını koyarak 64 adım başlama, dengeyi daha fazla sağlanmış olur
- ^ (PDF). 16 Temmuz 2010 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 29 Temmuz 2010.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Buyuk sayilar gundelik yasamda normalde kullanilmayan buyuk sayilari ifade eder Terim genellikle buyuk pozitif tam sayilari veya daha genel anlamda buyuk pozitif reel sayilari belirtir Fakat diger anlamlar icin de kullanilabilir Cok buyuk sayilar matematik kozmoloji kriptografi ve gibi alanlarda kullanilir Bazi insanlar sayilari astronomik olarak buyuk seklinde soyler Yine de gokbiliminde kullanilan cok buyuk sayilari bile matematiksel olarak tanimlamak kolaydir Buyuk ve kucuk sayilari ifade etmek icin bilimsel gosterimi kullanmaBilimsel gosterim bilimsel calismalarda karsilasilan bircok degeri ifade etmek icin olusturuldu Ornegin 1 0 109 bir milyar demektir 1 rakamindan sonra 9 tane sifir kullanilir ve 1 000 000 000 seklinde yazilir Benzer sekilde 1 0 10 9 milyarda bir demektir ve 0 000 000 001 seklinde yazilir Dokuz tane sifir yerine 109 yazma hem okuyucular fazla zahmet cekmemis olur hem de cok fazla sifirin bulundugu uzun serilerdeki sayilarin karistirilma ihtimali azalmis olur Buyuk sayilar her an yanimizdaHer gun gercek dunyada kullandigimiz bazi nesnelerin buyuk sayi ile iliskili ornekleri 500 1000 GB lik bilgisayar sabit diskinin bit sayisi normal olarak yaklasik 1013 insan vucudundaki hucrelerin sayisi 1014 den fazla insan beynindeki noronlarin sayisi tahmini 1014 Avogadro sayisi bir moldeki oz varliklar in genellikle atom veya molekul sayisi 12 gram Karbon 12 deki atom sayisi yaklasik olarak 6 022 1023 bolu mol Astronomik olarak buyuk sayilarUzunluk ve zaman bakimindan nitelendirilen diger buyuk sayilar astronomi ve kozmoloji de bulundu Ornegin Buyuk Patlamadan bu yana kainatin 13 7 milyar 4 3 1017 saniye yasinda oldugu one suruluyor Gozlemlenebilir evren 93 milyar isik yili 8 8 1026 metre genisligindedir ve yaklasik 125 milyar 1 25 1011 galaksi icindeki 5 1022yildizdan olusur Bunlar Hubble Uzay Teleskobu gozlemine goredir Gozlemlenebilir evrende kabaca 1080temel parcacik vardir Kanada daki Alberta Universitesi fizikcilerinden e gore bir fizikci tarafindan acikca hesaplanan en uzun zaman 10101010101 1 yildir Kombinatorik islemler de hizlica buyuk sayilara dogru gider Karisik duzendeki nesnelerin permutasyonlarinin sayisini aciklayan faktoriyel fonksiyonu nesne sayisina gore cok hizli bir sekilde artar Stirling yaklasimi bu sekilde buyumeyi asimtotiktik sekilde ifade ederek bir ipucu verir Kombinasyonel islemler cok buyuk sayilari uretir Bu sayilarin cok buyuk olmalarindan dolayi normalde sadece kendi logaritmalarinda kullanilirlar ve benzer sayilar algoritmik bilgi teorisinde bit betiklerini ifade etmek icin kullanilir Bilgisayarlar ve hesapsal karisiklikMoore Yasasi genel olarak bir mikroislemcinin her bir transistor sayisinin her 18 ayda iki katina cikacagi tahminine dayanir Bu insanlara bilgisayarlarin herhangi bir matematik problemini ne derece karmasik olursa olsun cozebilecegi fikrini olusturdu Turing Testine bakiniz 1980 ile 2000 yillari arasinda sabit disk hacimleri 10 megabayttan 1 107 bayt 100 gigabayt 1011 bayt uzerine cikti 100 gigabaytlik bir disk tum dunyadaki 6 milyar insanin isimlerini herhangi bir sikistirma programi kullanmaksizin depolama kapasitesine sahiptir Fakat 40 karakter uzunlugundaki olasi tum sifrelerin depolanmasi konusu oldukca zorludur Her bir karakterin bir bayta esit oldugunu dusunursek yaklasik olarak 2320 tane sifre uretilir Bu da yaklasik 2 1096 eder Evrenin hesaplama kapasitesi adli yazisinda Seth Lloyd eger evrendeki her bir zerre buyuk bir bilgisayarin parcasiymis gibi kullanilabilseydi sadece yaklasik 1090 bit depolayabilirdi ki bu da gerekli sozluk boyutunun milyonda birinden daha azdir Bununla beraber sabit diske bilgi depolama ile onlari hesaplama cok farkli islevlerdir Bir yandan su an icin depolamanin sinirlari olsa bile fakat hesaplama hizi ise farkli bir konudur OrneklerAyrica asagidaki Sayilara sirali ornekler bolumune bakiniz 1010 displaystyle 10 10 10 000 000 000 10 milyar dir veya uzun olceklerde bazen 10 000 milyon olarak da adlandirilir googol 10100 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 sentilyon 10303 veya 10600 sayi adlandirma sistemine bagli olarak googolplex 10googol 1010100 Skewes sayilari Ilki yaklasik olarak 10101034 displaystyle 10 10 10 34 ikincisi 1010101000 displaystyle 10 10 10 1000 Dunyada basilan toplam materyallar kabaca 1 6 1018 bittir Bu sayi soyle ifade edilebilir 21 6 1018 104 8 1017 displaystyle 2 1 6 times 10 18 approx 10 4 8 times 10 17 Karsilastirma 1 11 11 11000 10101 02 1040 displaystyle 1 1 1 1 1 1 1000 approx 10 10 1 02 times 10 40 100010001000 10103000 48 displaystyle 1000 1000 1000 approx 10 10 3000 48 Birinci sayi ikincisinden cok daha buyuktur Cunku birinci sayinin us kulesi 3 tane kule her ne kadar tabani 1 1 gibi cok kucuk bir sayi olsa bile daha fazladir Sistematik olarak daha hizli artis sirasi olusturmaf0 n displaystyle f 0 n n 1 tam sayi dizisini uygun olacak sekilde bir fonksiyon gibi yazarak f0 1 gt 1 displaystyle f 0 1 gt 1 ile arttiralim Sonraki dizilerden biri fk n fk 1n 1 displaystyle f k n f k 1 n 1 ile bulunabilir Burada f0 10 f1 10 displaystyle f 0 10 f 1 10 capraz dizi secebiliriz Bu verilen bir sayidaki yeni dizilimi olusturma islemidir Bu tekrarlanabilir orn ozyinelemeye uygulayabiliriz ve tekrar sayi matristeki tek bir diziyi her birinin 10 elemanini alarak secebiliriz Tum bu islem ayni sekilde tekrar ve tekrar uygulayabiliriz f0 n 10n 10 n displaystyle f 0 n 10 n 10 to n islemi bir 10 elemanini n degiskeninden onceki seriye eklemeye denk gelir Buradaki n serinin sonundadir Sunu elde ederiz fk n fk 1n 1 10 k 1n 10 n k 1 displaystyle f k n f k 1 n 1 10 uparrow k 1 n 10 to n to k 1 ve matristen secilen yeni dizi k eleman olan fk 1 10 fk10 1 10 k10 10 10 k 10 10 k 1 displaystyle f k 1 10 f k 10 1 10 uparrow k 10 10 to 10 to k 10 to 10 to k to 1 dir Bu islemi tekrarlayarak sunu elde ederiz 10 10 k n displaystyle 10 to 10 to k to n n nin ardisik degerleri icin ve k 10 secerek tek bir dizi elde ederiz soyle ki 10 10 10 n displaystyle 10 to 10 to 10 to n Bunu tum isleme uygularsak daha fazla seri elde ederiz n 10 secersek 10 10 10 10 10 10 10 10 10 dizilerini elde ederiz Bu islemleri serinin basindan itibaren tekrar ve tekrar ederek kullanilabilir Hatta f1 2 displaystyle f 1 2 degeri bu seri icin zaten 10 milyar arti bir uzunlugunda bir Conway dizisi olsa bile Tum bu islemdeki her bir seri kendi siralama turu tarafindan su sekilde tanimlanabilir 10 n k n uslu k 1 siralama turune sahip seri 10 10 n k n uslu w k 1 siralama turune sahip seri 10 10 10 n k n uslu 2w k 1 siralama turune sahip seri 10 10 10 10 10 10 10 10 10 w siralama turune sahip dizi n 1 haric fa n lt fa 1 n displaystyle f a n lt f a 1 n saglanir a lt b icin daima fa n lt fb n displaystyle f a n lt f b n saglanmayabilir Ornegin n 1 3 4 5 6 icin f3 n lt fw n displaystyle f 3 n lt f omega n saglanirken n 2 icin sadece esitlik vardir n 1 4 5 6 icin f4 n lt fw n displaystyle f 4 n lt f omega n iken n 2 ve 3 icin gt vardir Yukaridaki aciklama de benzer sekilde tanimlar Cok buyuk sayilarin yazim sistemini standartlastirmaCok buyuk sayilarin yazimi icin standart yol artis sirasina gore onlari kolayca siralamayi saglar ve bir sayinin digerinden ne kadar buyuk oldugu fikrini verebilir Bilimsel gosterimde sayilari karsilastiralim Orneklerimiz 5 104 ve 2 105 olsun once usleri karsilastirin Burada 5 gt 4 tur Bu yuzden 2 105 gt 5 104 olur Eger usler esitse mantis veya katsayi karsilastirilir 5 gt 2 oldugundan dolayi 5 104 gt 2 104 10 tabanli tetrasyon 10 n 10 n 2 10 n1 displaystyle 10 uparrow uparrow n 10 to n to 2 10 uparrow n 1 serisini verir 10 sayilarinin us kulesi tetrasyonu 10 n displaystyle 10 uparrow n f n 10n displaystyle f n 10 n fonksiyonunun ayrica fonksiyon googolplex de plex oneki ile kisaltilir Googol ailesine bakiniz bir verir Bunlar her ifadenin bir gore genellestirildigi cok yuvarlak sayilardir Bir sayinin ne kadar buyuk oldugunu belirlemenin basit yolu bu serideki iki sayinin ortasindakini belirlemektir Daha fazla dogruluk icin aradaki sayilar 10 na displaystyle 10 uparrow n a formunda ifade edilebilir Orn 10s li bir us kulesi tetrasyon ve onun ustundeki bir sayinin bilimsel gosterim soyledir 10101010104 829 displaystyle 10 10 10 10 10 4 829 sayisi 10 5 displaystyle 10 uparrow uparrow 5 ile 10 6 displaystyle 10 uparrow uparrow 6 arasinda bir sayidir eger 1 lt a lt 10 displaystyle 1 lt a lt 10 ise 10 n lt 10 na lt 10 n 1 displaystyle 10 uparrow uparrow n lt 10 uparrow n a lt 10 uparrow uparrow n 1 olduguna dikkat edin Tetrasyonu gercek yuksekliklere genisletmeye bakiniz Googolplex sayisi 1010100 10 2100 10 32 displaystyle 10 10 100 10 uparrow 2 100 10 uparrow 3 2 Baska bir ornek 2 4 22 2 65 536 tane 2 10 65 531 6 0 1019 728 10 65 5334 3 displaystyle 2 uparrow uparrow uparrow 4 begin matrix underbrace 2 2 2 qquad quad 65 536 mbox tane 2 end matrix approx 10 uparrow 65 531 6 0 times 10 19 728 approx 10 uparrow 65 533 4 3 10 65 533 displaystyle 10 uparrow uparrow 65 533 ile 10 65 534 displaystyle 10 uparrow uparrow 65 534 arasinda Bir sayinin buyukluk sirasi carpim adedi olan n tarafindan belirlenebilir 1 ile 10 arasindaki bir sayisi belirlemek icin log10 displaystyle log 10 kullanilmalidir Sayi 10 n displaystyle 10 uparrow uparrow n ile 10 n 1 displaystyle 10 uparrow uparrow n 1 arasindadir 10 10 nx 10 n10x displaystyle 10 10 uparrow n x 10 uparrow n 10 x olduguna dikkat edin Orn 10 nx displaystyle 10 uparrow n x ifadesindeki x sayisi eger cok buyukse bir tane daha us kule yapabilir ve x yerine log10x koyulur veya alt kuleden tum sayinin log10 ifadesindeki x bulunur Eger us kule tetrasyon 10 dan farkli bir veya daha fazla sayi icerirse farkli sonuca sahip iki yaklasim meydana gelir Alttaki bir tane 10 ile genisleyen kulenin yerine gecen ustteki 10 ile genisleyen ile ayni degildir fakat elbetteki tum us kule 10 dan farkli ve ayni adette sayi icerirse benzer dusunce uygulanir Eger kulenin yuksekligi buyukse buyuk sayilar icin bunu yerine cesitli ifadeler uygulanabilir Eger yukseklik yaklasik olarak verilirse usttekine bir deger verme mantikli degildir Bu yuzden cift ok gosterimi kullanabiliriz Orn 10 7 21 108 displaystyle 10 uparrow uparrow 7 21 times 10 8 Eger cift oktan sonraki degerin kendisi cok buyuk bir sayi ise yukaridaki islemler bu degere tekrarlanarak uygulanabilir Ornekler 10 1010103 81 1017 displaystyle 10 uparrow uparrow 10 10 10 3 81 times 10 17 sayisi 10 2 displaystyle 10 uparrow uparrow uparrow 2 ile 10 3 displaystyle 10 uparrow uparrow uparrow 3 arasindadir 10 10 10 497 9 73 1032 10 2 10 497 9 73 1032 displaystyle 10 uparrow uparrow 10 uparrow uparrow 10 uparrow 497 9 73 times 10 32 10 uparrow uparrow 2 10 uparrow 497 9 73 times 10 32 sayisi 10 4 displaystyle 10 uparrow uparrow uparrow 4 ile 10 5 displaystyle 10 uparrow uparrow uparrow 5 arasindadir Yukaridakine benzer sekilde eger 10 displaystyle 10 uparrow un ussu tam olarak belli degilse saga bir deger vermek mantikli degildir ve 10 displaystyle 10 uparrow us gosterimini kullanma yerine 10 displaystyle 10 uparrow uparrow un ussune 1 ekleyebiliriz Boylece orn 10 3 2 8 1012 displaystyle 10 uparrow uparrow 3 2 8 times 10 12 elde ederiz Eger 10 displaystyle 10 uparrow uparrow un ussu buyukse bu usse cesitli ifadeler uygulanabilir Eger us tam olarak belli degilse ayni sekilde 10 displaystyle 10 uparrow uparrow us gosterimini kullanma yerine uc ok operatorunu kullanilir Orn 10 7 3 106 displaystyle 10 uparrow uparrow uparrow 7 3 times 10 6 olur Eger uc oklu operatorun islecin sagdaki arguman buyukse yukaridaki islemler tekrar edilir Orn 10 10 2 10 497 9 73 1032 displaystyle 10 uparrow uparrow uparrow 10 uparrow uparrow 2 10 uparrow 497 9 73 times 10 32 sayisi 10 10 4 displaystyle 10 uparrow uparrow uparrow 10 uparrow uparrow uparrow 4 ile 10 10 5 displaystyle 10 uparrow uparrow uparrow 10 uparrow uparrow uparrow 5 arasindadir Bu islem tekrarlanabilir Boylece uc oklu islecin gucune sahip olabiliriz Operatorleri islecleri daha fazla oklarla devam ettirebilir ve soyle yazabiliriz n displaystyle uparrow n Bu gosterimi hiperislem ve Conway dizisi ok gosterimi ile karsilastiralim a nb displaystyle a uparrow n b a b n hiper a n 2 b Ilkinin avantaji eger b bir fonksiyon ise bu fonksiyonun usleri icin dogal bir gosterim vardir sadece n tane ok yazildiginda a n kb displaystyle a uparrow n k b Ornegin 10 2 3b displaystyle 10 uparrow 2 3 b 10 10 10 b 2 2 2 ve sadece ozel durumlarda uzun ic ice girmis dizi gosterimi kisaltilir b 1 icin 10 33 10 2 31 displaystyle 10 uparrow 3 3 10 uparrow 2 3 1 10 3 3 elde edilir b cok buyuk sayi oldugunda genellikle 10 n kn displaystyle 10 uparrow n k n seklinde uslu bir seri nnin degeri azaltilarak yazilir kn displaystyle k n tam sayi usleridir Sondaki bir sayi gosterimi belirtir kn displaystyle k n gibi bir sayi cok buyuk oldugunda kn 1 displaystyle k n 1 degeri 1 azaltilir ve n 1 kn 1 displaystyle n 1 k n 1 in sagindaki her sey tekrar yazilir Sayilari yaklasik olarak ifade etmek icin n nin deger azalis siralarindaki sapmalara gerek yoktur Ornegin 10 10 5a 10 6a displaystyle 10 uparrow 10 uparrow uparrow 5 a 10 uparrow uparrow 6 a ve 10 10 3 10 10 10 1 10 3 displaystyle 10 uparrow 10 uparrow uparrow uparrow 3 10 uparrow uparrow 10 uparrow uparrow 10 1 approx 10 uparrow uparrow uparrow 3 Beklenenin aksine elde edilen x sayisi cok buyuktur x ve 10x hemen hemen esittir buyuk sayilarin aritmetigi icin Artan okun ustindisi buyukse bunun icin ozel ifadeler uygulanabilir Eger bu ustindis tam olarak belli degilse isleci belli bir usse yukseltmek veya netur bir deger oldugunu ayarlamak icin hicbir nokta yoktur Basitce sagda standart bir deger kullanabiliriz 10 u 10 n10 10 10 n displaystyle 10 uparrow n 10 10 to 10 to n gibi yaklasik n ile azaltiriz Daha fazla sayi kullanmanin avantaji icin yukari ok gosterimi artik uygulanmaz ve dizi gosterimini kullanabiliriz Yukaridaki islem bu n icin tekrar ve tekrar uygulanabilir Boylece ilk okun ustindisinde n displaystyle uparrow n seklinde bir gosterim elde edilir Yoksa ic ice dizi gosterimi olmus olacak Ornegin 10 10 10 10 3 105 displaystyle 3 times 10 5 10 10 3 1051010 displaystyle 10 uparrow 10 uparrow 3 times 10 5 10 10 Eger derece elverislilik icin cok buyuk ise bu derece sayisini yazildigi yere sayisal bir gosterim kullanilir bircok ok yazmak yerine ok ustindisi kullanma gibi f n 10 n10 displaystyle f n 10 uparrow n 10 10 10 n gibi bir fonksiyonu arttirarak bu derecelerin fnin fonksiyonel kuvveti olmasi saglanir fm n displaystyle f m n formunda bir sayi yazmamiza olanak verir Burada m kesin ifade ve n ise ister kesin olsun ister olmasin tam sayidir ornegin f2 3 105 displaystyle f 2 3 times 10 5 Eger n buyukse onu kisaltmak icin yukaridakilerden birini kullanabiliriz Bu sayilarin en uygunu fm 1 10 10 m 2 formundakilerdir Ornegin 10 10 3 2 10 10 10101010 displaystyle 10 to 10 to 3 to 2 10 uparrow 10 uparrow 10 10 10 10 Graham sayisi ile karsilastirma 10 yerine 3 sayisini kullanir ve 64 ok derecesine sahiptir En ustte 4 sayisi vardir Burada G lt 3 3 65 2 lt 10 10 65 2 f65 1 displaystyle G lt 3 rightarrow 3 rightarrow 65 rightarrow 2 lt 10 to 10 to 65 to 2 f 65 1 dir Ayrica G lt f64 4 lt f65 1 displaystyle G lt f 64 4 lt f 65 1 dir Eger fm n displaystyle f m n deki m bilinemeyecek kadar cok buyukse orn n 1 ve yukari dogru tekrar mye kadar giderse sabit n kullanabiliriz Orn yukari oklarin derece sayisi ustindisli yukari ok gosteriminde kendini ifade eder f nin fonksiyonel us gosterimini kullanma fnin carpim derecesini verir g n fn 1 displaystyle g n f n 1 gibi bir fonksiyonu arttirma bu derecelerin g gibi bir fonksiyonun derecesi olmasini saglar ve gm n displaystyle g m n seklinde yazilir Buradaki m tam bilinen ve n de ister tam bilinsin ister bilinmesin bir tam sayidir 10 10 m 3 gm 1 Eger n buyukse onu kisaltmak icin yukaridakilerden herhangi birini kullanabiliriz Benzer sekilde orn h gibi bir fonksiyonu da arttirabiliriz Eger daha cok fonksiyona ihtiyac duyulursa her seferinde yeni bir harf kullanmak yerine sayi kullanabiliriz Orn bir ustindis gibi Boylece fkm n displaystyle f k m n formunda sayilar elde ederiz Burada k ve m bilinen ifade ve n ister bilinsin ister bilinmesin bir tam sayidir Yukaridaki f icin k 1 g icin k 2 kullanarak 10 10 n k fk n fk 1n 1 displaystyle f k n f k 1 n 1 elde edilir Eger n buyukse fkmk displaystyle f k m k seklinde k nin ice dogru azaldigi ic ice formlar elde edilir 10 n pn displaystyle 10 uparrow n p n nin us serisinin icindeki arguman n nin degerleriyle azalir k belirlenemeyecek kadar cok buyukse ilgili sayi fn 10 displaystyle f n 10 10 10 10 n olarak yaklasik bir n ile kisaltilir 10n displaystyle 10 n 10 n serisinden 10 n10 displaystyle 10 uparrow n 10 10 10 n serisine giden islemin sonraki fn 10 displaystyle f n 10 10 10 10 n dizisine cok benzer sekilde gittigine dikkat edin Bir 10 elemanini dizi gosteriminde diziye eklemek genel bir islemdir Bu islem tekrarlanabilir onceki bolume de bakiniz Bu fonksiyonun sonraki surumlerini numaralandirmak icin fqkmqk displaystyle f qk m qk fonksiyonu kullanilarak bir sayi belirlenebilir Cok buyuk bir sayiyi Conway dizisi ok gosterimine yazmak icin bu dizi uzunlugu icin sayinin ne kadar buyuk oldugunu aciklanmalidir Ornegin sadece dizideki 10 elemanini kullanma baska bir ifadeyle onun 10 10 10 10 10 10 serisindeki konumunu belirleme Hatta serideki konumu bile buyuk bir sayi ise bunun icin ayni teknikleri uygulayabiliriz Sayilara sirali ornekler 1 Y 1 Her Y alt dizisi icin 2 2 Y 4 Her Y alt dizisi icin 222 displaystyle 2 2 2 2 3 2 16 33 displaystyle 3 3 3 2 2 27 44 4 2 2 256 55 5 2 2 3125 66 6 2 2 46 656 2222 displaystyle 2 2 2 2 2 3 3 2 4 2 65 536 77 7 2 2 823 543 88 8 2 2 16 777 216 99 9 2 2 387 420 489 1010 10 2 2 10 000 000 000 333 displaystyle 3 3 3 3 3 2 3 2 3 7 625 597 484 987 googol 10100 displaystyle 10 100 444 displaystyle 4 4 4 4 3 2 1 34078079299 10154 displaystyle 1 34078079299 times 10 154 Gozlemlenebilir evrenin Planck uzunluguna gore yaklasik degeri 8 5 10184 displaystyle 8 5 times 10 184 2 5 2 265536 2 0 1019 729 displaystyle 2 65536 approx 2 0 times 10 19 729 M43 112 609 3 16 1012 978 188 10107 1 displaystyle M 43 112 609 approx 3 16 times 10 12 978 188 approx 10 10 7 1 47nci ve Nisan 2010 itibariyla bilinen en buyuk sayisi 101010 10 3 10 31 displaystyle 10 10 10 10 uparrow uparrow 3 10 uparrow 3 1 10 3 2 3333 displaystyle 3 3 3 3 3 4 2 103 63833464 1012 displaystyle 10 3 63833464 times 10 12 googolplex 1010100 displaystyle 10 10 100 2 6 2 2265536 106 0 1019 728 displaystyle 2 2 65536 approx 10 6 0 times 10 19 728 10101010 10 4 10 41 displaystyle 10 10 10 10 10 uparrow uparrow 4 10 uparrow 4 1 10 4 2 2 7 2 22265536 10106 0 1019 728 displaystyle 2 2 2 65536 approx 10 10 6 0 times 10 19 728 10 5 10 51 displaystyle 10 uparrow uparrow 5 10 uparrow 5 1 10 5 2 10 6 10 61 displaystyle 10 uparrow uparrow 6 10 uparrow 6 1 10 6 2 10 7 10 71 displaystyle 10 uparrow uparrow 7 10 uparrow 7 1 10 7 2 10 8 10 81 displaystyle 10 uparrow uparrow 8 10 uparrow 8 1 10 8 2 10 9 10 91 displaystyle 10 uparrow uparrow 9 10 uparrow 9 1 10 9 2 10 8783 displaystyle 10 uparrow 8 783 10 2 10 10 10 101 displaystyle 10 uparrow uparrow uparrow 2 10 uparrow uparrow 10 10 uparrow 10 1 10 2 3 10 10 2 2 3 4 2 4 3 2 65 536 2 10 65531 6 0 1019 728 displaystyle approx 10 uparrow 65531 6 0 times 10 19 728 3 3 3 3 3 10 7 6 1012 displaystyle 3 uparrow uparrow uparrow 3 3 to 3 to 3 approx 10 uparrow uparrow 7 6 times 10 12 10 1010103 81 1017 10 1010103 81 1017 2 displaystyle 10 uparrow uparrow 10 10 10 3 81 times 10 17 10 to 10 10 10 3 81 times 10 17 to 2 10 3 10 31 displaystyle 10 uparrow uparrow uparrow 3 10 uparrow uparrow 3 1 10 3 3 10 211 displaystyle 10 uparrow uparrow 2 11 10 21010103 81 1017 displaystyle 10 uparrow uparrow 2 10 10 10 3 81 times 10 17 10 4 10 41 displaystyle 10 uparrow uparrow uparrow 4 10 uparrow uparrow 4 1 10 4 3 10 2 10 497 9 73 1032 displaystyle 10 uparrow uparrow 2 10 uparrow 497 9 73 times 10 32 10 5 10 51 displaystyle 10 uparrow uparrow uparrow 5 10 uparrow uparrow 5 1 10 5 3 10 6 10 61 displaystyle 10 uparrow uparrow uparrow 6 10 uparrow uparrow 6 1 10 6 3 10 7 10 71 displaystyle 10 uparrow uparrow uparrow 7 10 uparrow uparrow 7 1 10 7 3 10 8 10 81 displaystyle 10 uparrow uparrow uparrow 8 10 uparrow uparrow 8 1 10 8 3 10 9 10 91 displaystyle 10 uparrow uparrow uparrow 9 10 uparrow uparrow 9 1 10 9 3 10 2 10 10 10 101 displaystyle 10 uparrow uparrow uparrow uparrow 2 10 uparrow uparrow uparrow 10 10 uparrow uparrow 1 01 10 2 4 10 10 3 10 3 10 31 displaystyle 10 uparrow uparrow uparrow uparrow 3 10 uparrow uparrow uparrow 3 1 10 3 4 4 4 displaystyle 4 uparrow uparrow uparrow uparrow 4 4 4 4 10 2 10 3154 displaystyle approx 10 uparrow uparrow uparrow 2 10 uparrow uparrow 3 154 10 4 10 41 displaystyle 10 uparrow uparrow uparrow uparrow 4 10 uparrow uparrow uparrow 4 1 10 4 4 10 5 10 51 displaystyle 10 uparrow uparrow uparrow uparrow 5 10 uparrow uparrow uparrow 5 1 10 5 4 10 6 10 61 displaystyle 10 uparrow uparrow uparrow uparrow 6 10 uparrow uparrow uparrow 6 1 10 6 4 10 7 10 71 displaystyle 10 uparrow uparrow uparrow uparrow 7 10 uparrow uparrow uparrow 7 1 10 7 4 10 8 10 81 displaystyle 10 uparrow uparrow uparrow uparrow 8 10 uparrow uparrow uparrow 8 1 10 8 4 10 9 10 91 displaystyle 10 uparrow uparrow uparrow uparrow 9 10 uparrow uparrow uparrow 9 1 10 9 4 10 2 10 10 10 101 displaystyle 10 uparrow uparrow uparrow uparrow uparrow 2 10 uparrow uparrow uparrow uparrow 10 10 uparrow uparrow uparrow 10 1 10 2 5 10 10 4 2 3 2 2 2 3 8 3 2 2 2 3 2 9 3 3 8 10 10 10 10 2 11 10 2 2 2 10 2 100 10 10 2 2 10 2 1010 displaystyle 10 10 10 101010 displaystyle 10 uparrow 10 10 10 10 10 1010103 81 1017 displaystyle 10 10 10 3 81 times 10 17 10 10 3 2 10 10 10 10 1010 displaystyle 10 10 10 10 10101010 displaystyle 10 uparrow 10 uparrow 10 10 10 10 10 10 10 2 10 10 64 2 Graham sayisi 10 10 65 2 10 10 10 3 10 10 10 4 Temel degerleri karsilastirmaAsagidaki anlatimlar 10 dan baska 100 tabanli degerleri acikliyor 10012 1024 displaystyle 100 12 10 24 10 tabaninin ussu ikiye katlandi 10010012 102 1024 displaystyle 100 100 12 10 2 10 24 yukaridaki gibi 10010010012 10102 1024 0 3 displaystyle 100 100 100 12 10 10 2 10 24 0 3 en yuksekteki us ikiye katlanmaktan cok az fazladir 100 2 10200 displaystyle 100 uparrow uparrow 2 10 200 100 3 102 10200 displaystyle 100 uparrow uparrow 3 10 2 times 10 200 100 4 10 2 2 10200 0 3 10 2 2 10200 10 3200 3 10 42 3 displaystyle 100 uparrow uparrow 4 10 uparrow 2 2 times 10 200 0 3 10 uparrow 2 2 times 10 200 10 uparrow 3 200 3 10 uparrow 4 2 3 100 n 10 n 2 2 10200 10 n 1200 3 10 n2 3 lt 10 n 1 displaystyle 100 uparrow uparrow n 10 uparrow n 2 2 times 10 200 10 uparrow n 1 200 3 10 uparrow n 2 3 lt 10 uparrow uparrow n 1 Burada eger n buyukse rahatca 100 n displaystyle 100 uparrow uparrow n yaklasik olarak esittir 10 n displaystyle 10 uparrow uparrow n diyebiliriz 100 2 10 98 2 10200 10 1002 3 displaystyle 100 uparrow uparrow uparrow 2 10 uparrow 98 2 times 10 200 10 uparrow 100 2 3 100 3 10 10 98 2 10200 10 10 1002 3 displaystyle 100 uparrow uparrow uparrow 3 10 uparrow uparrow 10 uparrow 98 2 times 10 200 10 uparrow uparrow 10 uparrow 100 2 3 100 n 10 n 2 10 98 2 10200 10 n 2 10 1002 3 lt 10 n 1 displaystyle 100 uparrow uparrow uparrow n 10 uparrow uparrow n 2 10 uparrow 98 2 times 10 200 10 uparrow uparrow n 2 10 uparrow 100 2 3 lt 10 uparrow uparrow uparrow n 1 karsilastirin 10 n 10 n 2 10 101 lt 10 n 1 displaystyle 10 uparrow uparrow uparrow n 10 uparrow uparrow n 2 10 uparrow 10 1 lt 10 uparrow uparrow uparrow n 1 Burada eger n buyukse 100 n displaystyle 100 uparrow uparrow uparrow n yaklasik olarak esittir 10 n displaystyle 10 uparrow uparrow uparrow n diyebiliriz 100 2 10 98 10 1002 3 displaystyle 100 uparrow uparrow uparrow uparrow 2 10 uparrow uparrow 98 10 uparrow 100 2 3 karsilastirin 10 2 10 8 10 101 displaystyle 10 uparrow uparrow uparrow uparrow 2 10 uparrow uparrow 8 10 uparrow 10 1 100 3 10 10 98 10 1002 3 displaystyle 100 uparrow uparrow uparrow uparrow 3 10 uparrow uparrow uparrow 10 uparrow uparrow 98 10 uparrow 100 2 3 compare 10 3 10 10 8 10 101 displaystyle 10 uparrow uparrow uparrow uparrow 3 10 uparrow uparrow uparrow 10 uparrow uparrow 8 10 uparrow 10 1 100 n 10 n 2 10 98 10 1002 3 displaystyle 100 uparrow uparrow uparrow uparrow n 10 uparrow uparrow uparrow n 2 10 uparrow uparrow 98 10 uparrow 100 2 3 compare 10 n 10 n 2 10 8 10 101 displaystyle 10 uparrow uparrow uparrow uparrow n 10 uparrow uparrow uparrow n 2 10 uparrow uparrow 8 10 uparrow 10 1 eger n buyukse bu yaklasik olarak esittir Dogruluk10n displaystyle 10 n sayisi icin n deki bir birimlik degismenin sonucu 10 faktor olarak degistirecegine dikkat edin 106 2 103 displaystyle 10 6 2 times 10 3 gibi bir sayida 6 2 de belirli sekilleri kullanarak tam yuvarlama ussun dogruluk degerini 50 daha az veya 50 daha cok yapabilir Benzer sekilde 1050 displaystyle 10 50 faktoru cok buyuk ya da cok kucuk olabilir Cok buyuk sayilarda dogruluk Asiri buyuk sayilarda goreceli hata da buyuk olabilirken dikkate almak istedigimiz sayilarin buyuklugune yakin bir hassasiyeti olabilir Ornegin 1010 displaystyle 10 10 ile 109 displaystyle 10 9 u goz onune alalim Goreceli hata 1 1091010 1 110 90 displaystyle 1 frac 10 9 10 10 1 frac 1 10 90 dir Bu buyuk bir hatadir Yine de goreceli hatayi logaritmada goz onunde bulundurabiliriz Bu sebeple 10 tabanindaki logaritmalar 10 ve 9 dur Boylece logaritmadaki goreceli hata sadece 10 olur Eger a ve b kucuk goreceli bir hataya sahipse ustel fonksiyonlarin goreceli hatalari oldukca buyuktur 10a displaystyle 10 a ile 10b displaystyle 10 b nin goreceli hatalari buyuktur ve 1010a displaystyle 10 10 a ile 1010b displaystyle 10 10 b de daha buyuk goreceli hataya sahip olacaktir Sonraki soru soyle olacaktir hangi seviyedeki yinelenen logaritmada iki sayiyi karsilastirabiliriz Goz onunde bulunduracagimiz bir hassasiyet vardir 101010 displaystyle 10 10 10 ile 10109 displaystyle 10 10 9 yakin buuklukte olur Bu iki sayi arasindaki goreceli hata buyuktur ve onlarin logaritmalari arasindaki goreceli hata yine buyuktur Bununla beraber bunlarin ikinci yineleme logaritmalarindaki hata kucuktur log10 log10 101010 10 displaystyle log 10 log 10 10 10 10 10 ile log10 log10 10109 9 displaystyle log 10 log 10 10 10 9 9 Ornegin yineleme logaritmalarini karsilastirma bunun gibidir Cok buyuk sayilarin yaklasik aritmetigi Cok buyuk sayilarinda uygulanan olagan aritmetik islemlere ait birkac genel kural vardir Iki cok buyuk sayiyi toplama ve carpmanin her ikisinin sonucu da yaklasik olarak sayilardan birine esittir 10a 10b 10a10b 1010b log10 a displaystyle 10 a 10 b 10 a10 b 10 10 b log 10 a Buradan Cok buyuk kuvvete yukselen buyuk bir sayi yaklasik olarak asagidaki iki degerden birine esittir Ilk deger ve 10 ikincinin kuvvetine Ornegin cok buyuk n icin nn 10n displaystyle n n approx 10 n megayi hesaplamaya bakiniz ve 2n 10n displaystyle 2 n approx 10 n olur Burada 2 65536 gt 10 65533 displaystyle 2 uparrow uparrow 65536 gt 10 uparrow uparrow 65533 Knuth tablolarina bakiniz Bazi hesaplanamayan serilerdeki buyuk sayilarfonksiyonu S herhangi bir daha hizli buyuyen bir fonksiyondur Goreceli girdi degeri kucuk olsa bile kendisi kocamandir n 1 2 3 4 icin S n fonksiyonu 1 4 6 13 dur S 5 bilinmiyor fakat 4098 olarak tanimlaniyor S 6 en az 4 6 101439 dur da herhangi hesaplanabilir fonksiyonlardan daha hizli buyuyen serilerle ilgili birkac calisma yapmistir Sonsuz sayilarHer ne kadar yukaridaki tum sayilar cok buyuk olsa bile yine de tumu Matematigin belirli alanlari sonsuz ve tanimlar Ornegin dogal sayilarin sonsuz serisinin ve sonraki en buyuk nicel sayidir c displaystyle mathfrak c c ℵ1 displaystyle mathfrak c aleph 1 onermesi sureklilik hipotezi olarak bilinir GosterimlerAsiri buyuk sayilarin bazi gosterimleri Knuth yukari ok gosterimi hiperislemler tetrasyon iceren Ackermann islevi Conway dizisi ok gosterimi Steinhaus Moser gosterimi buyuk sayilarin yapi yontemi bir yana bu cokgenli grafiksel gosterimi de icerir Geleneksel fonksiyon gosterimleri gibi alternatif gosterimler de ayni fonksiyonlarla kullanilabilirler Bu gosterimler aslinda tam sayilarla hizli bir sekilde artar tam sayi degiskenlerinin fonksiyonlaridir Fonksiyonlardaki hizli artma bile tekrarli bir sekilde bu fonksiyonlari arguman olarak buyuk tam sayilarla uygulayarak kolayca elde edilebilir Ayrica bakinizUstel buyume Graham sayisi Buyuk sayilar yasasi Buyuk sayilarin adlari Rakam TetrasyonAlintilar Lloyd Seth 2002 Computational capacity of the universe PDF Phys Rev Lett 88 23 s 237901 doi 10 1103 PhysRevLett 88 237901 PMID 12059399 eprint quant ph 0110141 3 Eylul 2013 tarihinde kaynagindan Erisim tarihi 17 Eylul 2007 10 un yerine baska bir sayi da kullanilabilir O 1 den daha buyuk olmalidir ve eger f0 1 2 displaystyle f 0 1 2 ise artis dizisi elde etmek icin o 2 den daha buyuk olmalidir Onceki degerle karsilastirma ile ilgili 10 n10 lt 3 n 13 displaystyle 10 uparrow n 10 lt 3 uparrow n 1 3 Boylece 4 yerine 1 10 yerine 3 sayilarini koyarak 64 adim baslama dengeyi daha fazla saglanmis olur PDF 16 Temmuz 2010 tarihinde kaynagindan PDF arsivlendi Erisim tarihi 29 Temmuz 2010
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans