Enerjinin korunumu yasası, yalıtılmış bir sistemdeki toplam enerjinin değişmeyeceğini söyler. Enerji ne yok edilebilir ne de yoktan var edilebilir, ama enerji türü değişebilir; örneğin, dinamitin patlamasıyla kimyasal enerji kinetik enerjiye dönüşebilir.
Enerjinin korunumu yasası gereği birinci tür devridaim makinesinin çalışması imkânsızdır. (Bu türde dışarıdan enerji alınmadan iş yapılacağı iddia edilir.) Başka bir deyişle, dışarıdan enerji almayan bir sistem, çevresine sahip olduğundan daha çok enerji sağlayamaz.
Tarihçe

Antik Yunan filozoflarına değin (Miletli Thales) y. MÖ 550 her şeyin kökeni olan maddenin döngüsüne (korunumuna) dair izler vardı. Ancak, denmek istenenin günümüz "madde-enerji" kavramlarıyla eşleştirmek için yeterince güçlü bir neden yok. (Örneğin, Thales maddenin kökeninin (arkhe, ana madde) su olduğunu söylüyordu). Empedocles (MÖ 490–MÖ 430) ise evrenin dört öğeden (toprak, hava, su ve ateş) oluştuğunu oluştuğunu öne sürüyordu. "Hiçlikten varlık yaratılamaz, varlık hiç olamaz." diyor, bu dört öğenin sürekli olarak birbirine dönüştüğünü söylüyordu.
1638 yılında, Galileo Galilei çeşitli konulardaki çalışmalarını -ünlü 'kesikli sarkacı' (enerji korunumuyla açıklanırsa potansiyel enerjinin ve kinetik enerjinin birbirine dönüşerek hareketi devam ettirdiği bir sistem) da içinde- yayınladı.
Hareketi -kinetik enerjiyi açıklarken- matematiksel dille anlatan ilk kişi Gottfried Wilhelm Leibniz olmuştu (1676-1689). Leibniz pek çok mekanik sistemde dışarıdan bir etki olmadıkça, sistemin kendi davranışını sürdürme eğiliminde olduğunu keşfetti (vi hızıyla hareket halinde olan mi kütlelerinden oluşan sistemler):
Bu niceliğe ya da sistemin yaşam kuvveti adını verdi. Bu ilke dışarıdan bir sürtünme kuvveti olmadıkça enerjinin neredeyse korunduğunu gösteriyordu (bu noktada kinetik enerjinin korunumunu). O zamanlar pek çok fizikçi momentumun korunumu (sürtünme kuvveti varlığında bile işleyen bir ilke) ile ilgileniyordu, momentumun matematiksel gösterilişi:
ve korunan vis vivaya karşılık geliyordu. Daha sonra gösterildiği gibi, esnek çarpışmalar olarak adlandırılan durumlarda kinetik enerji de momentum da aynı anda korunuyordu.
Pek çok mühendis; , , Carl Holtzmann, ve momentumun korunumu ilkesinin uygulamalı kullanımlar için tek başına yetersiz olduğunu düşündüklerinden, Leibniz'in ilkesinden de yararlanmayı gerekli görüyorlardı. Bu ilke aynı zamanda kimi kimyacılar tarafından da desteklenmişti: William Hyde Wollaston. Bazı akademisyenler (ör; John Playfair) kinetik enerjinin bütünüyle korunmadığını göstermişti. Doğal olarak bu termodinamiğin ikinci yasasına dayalı modern hesaplamalara göre barizdi, ancak 18. ve 19. yüzyıllarda kayıp enerji hâlâ bilinmiyordu. Zamanla, sürtünme kuvveti etkisi altında gerçekleşen hareket sonucunda oluşan ısının vis vivanın başka bir biçimi olup olmayacağından kuşkulanıldı. 1783 yılında, Antoine Lavoisier ve Pierre-Simon Laplace birbiriyle çelişen iki kueamı -vis viva ve - gözden geçirdiler.Kont Rumford'un 1798 yılında, top güllelerini oyma sırasında (kalibresini ayarlamak için yapılan işlemler) açığa çıkan ısıyı gözlemlemesi mekanik anlamda hareketin ısıya dönüşmesi yöndeki kanıyı güçlendirdi, daha da önemlisi korunum ölçülebiliyordu ve öngörülebilirdi (kinetik enerji ile ısı enerjisini birbirine bağlayan evrensel korunum sabiti hesaba katıldığında). Sonrasında -1807 yılında, Thomas Young tarafından kullanıldıktan sonra- vis viva, "enerji" (ya da erke) olarak anılmaya başlandı.

Vis viva, sonradan daha yerinde bir formülle şöyle tanımlandı:
Kinetik enerjinin işe dönüşümünü anlatan bu formül, Gaspard-Gustave Coriolis ve Jean-Victor Poncelet'nin 1819-1839 yılları arasındaki çalışmalarının sonucudur. Daha önceleri quantité de travail (iş niceliği), sonraları, travail mécanique (mekanik iş) olarak bilinen bu kavram, mühendislik hesaplamlarında kullanıldı.
1837 yılında Zeitschrift für Physik dergisinde yayınlanan Über die Natur der Wärme başlıklı makalede, Karl Friedrich Mohr enerjinin korunumu ile ilgili ilk genel "öğretiyi" şu tümcelerle anlattı: "kimyada bilinen 54 elemente karşılık fizik dünyasında, Kraf [iş ya da enerji] olarak bilinen, sadece bir etken var. Farklı koşullarda farklı kavramlar olarak görünebilir, hareket, kimyasal benzerlik, kohezyon, elektrik, ışık ve manyetizma; ancak bu biçimlerin herhangi biri diğerine dönüşebilir."
Isının mekanik karşılığı
Modern enerji korunumu prensibinin gelişiminde kilit aşama, nın ispatlanmasıydı. Isının yoktan var edilemeyeceğini ya da yok edilemeyeceğini söyleyen kabul görürken, aksinin olduğunu iddia eden enerji korunumu prensibi ısının ve mekanik işin birbirine dönüşebileceğini söylüyordu.
On sekizinci yüzyılın ortalarında Rus bir bilim adamı, Mikhail Lomonosov, kalori teorisine karşı olan, kan hücresi-ısının kinetik enerjisi adlı postulatını ortaya attı. Deneysel çalışmaları sonucu, Lomonosov, ısının kalorik sıvının parçacıkları vasıtasıyla iletilmediği sonucuna vardı.
1798 yılında Count Rumford (Benjamin Thompson) top güllelerinin kalibrasyonu sırasında sürtünmeden kaynaklanan ısının miktarını ölçtüler ve ısının kinetik enerjinin bir formu olduğu fikrini geliştirdiler; hesaplamalar kalori teorisini çürütmüştü ancak kesinliğini tam anlamıyla ifade etmekten yoksundu.

Mekanik eşitlik prensibi modern haliyle ilk defa Alman cerrah Julius Robert von Mayer tarafından ifade edildi, 1842 yılında. Mayer bu sonuca Endonezya'daki Hollanda kolonilerini ziyareti sırasında varmıştı, buradaki hastaları daha az oksijen tükettiklerinden (ve tabi bundan dolayı daha az enerjiye sahiplerdi-daha sıcak bir iklimde vücut sıcaklıklarını korumak için-) kanları daha koyu kırmızıydı. Isının ve mekanik işin birer enerji formu olduğunu keşfetti ve 1845 yılında, fiziğe dair bilgisini ilerlettikten sonra, iş ve ısı arasında sayısal ilişkiyi anlatan bir monografi yayınladı.

Aynı dönemde,1843 yılında, James Prescott Joule-Mayer'den bağımsız olarak- mekanik eşitliği bir dizi deneyle keşfetti. En önemlisi, şimdi "Joule aparatı" olarak bilinen, ipe bağlı bir ağırlığın aşağıya hareket etmesiyle dönen su içinde bir çıkrık düzeneği. Aşağıya inen ağırlık sebebiyle azalan yer çekimsel potansiyel enerjinin, suyun içinde dönen çıkrıktaki sürtünmeden kaynaklanan iç enerji artışına eşit olduğunu gösterdi.
1840–1843 dönemi sonrası, benzer deneyler isimli, Danimarkalılar dışında fazlaca bilinmeyen, mühendis tarafından tekrar yapıldı.
Joule ve Mayer'in çalışmaları itirazlar ve olumsuz tepkilerle karşılaştı ancak nihayetinde Joule'ün çalışması genel olarak kabul gördü.
{{|Joule ve Mayer'in çalışmalarında kimin öncül olduğuna yönelik ayrıntılı bilgi için bkz.|Mechanical equivalent of heat: Priority}}
1844 yılında, William Robert Grove mekanik, ısı, ışık, elektrik ve manyetizma arasındaki ilişkiyi, hepsini tek bir "kuvvet" olarak betimleyen, anlatan postulatını ortaya attı, (günümüz diliyle enerji ). Grove 1874'te, teorilerini Fiziksel Kuvvetler Arasındaki İlişki isimli bir kitapta yayınladı. 1847 yılında, Joule'ün önceki çalışmalarından yararlanan, Sadi Carnot, ve Hermann von Helmholtz Grove ile benzer sonuçlara ulaştılar ve Über die Erhaltung der Kraft isimli kitapta yayınladılar çalışmalarını (On the Conservation of Force, 1847). Teorinin modern haliyle genel anlamda kabul görmesi bu yayın aracılığıyla olmuştur.
1850 yılında, William Rankine ilk defa enerji korunumu kanunu ibaresini resmen kullanmıştır.
1877 yılında, bu prensibin Sir Isaac Newton'dan köken aldığını iddia etmiştir, Philosophiae Naturalis Principia Mathematicadaki 40 41 nolu önermelere dayanarak.Tait'in çalışmasına günümüz diliyle ilerleyici tarihçilik deniyor(ayrıntılı bilgi için, ).
Kütle–enerji denkliği
Madde proton, elektron nötron gibi parçacıklardan oluşur. Dinlenme ya da esas kütlesi vardır. On dokuzuncu yüzyıldaki bilinen (kısıtlı) çalışmalara göre bu esas kütle korunuyordu. 1905 yılında, Einstein'ın özel görelilik teorisi bu esas kütlenin esas enerjinin belli bir oranına karşılık geldiğini gösterdi. Bunun anlamı, belli bir miktar esas kütle, enerjinin pek çok formuna dönüşebilirdi (kinetik, potansiyel elektromanyetik ışıma enerjisi gibi). Bu olduğunda, yirminci yüzyılda yaşanan tecrübelerimizde olduğu gibi, aksine esas kütle korunmuyordu. Tüm enerji formları toplam kütle ve toplam enerjiyi meydana getiriyordu.
Örneğin; elektron ve pozitronun her biri esas kütleye sahiptir. Esas enerjilerini fotonun elektromanyetik ışıma enerjisine dönüştürerek birlikte yok olabilirler (geride kütle bırakmaksızın). Eğer bu olay fotonun enerjisini aktarabileceği bir çevresi olmayan izole bir sistemde meydana gelirse, sitemin toplam kütlesi de toplam enerjisi de değişmez. Üretilen elektromanyetik ışıma enerjisi, sistemdeki pozitron ve elektronun yok olmadan önce oluşturduğu kadar eylemsizlik (ve ağırlık) meydana getirir. Tersine, maddesiz-enerji yok olarak meydana madde (esas kütlesi olan bir madde) meydana getirir.
Sonuç olarak, enerjinin korunumu (toplam madde veya esas enerji) ve kütlenin korunumu (toplam madde, sadece esas madde değil), kanunlarının ikisinin de birbirini karşıladığı kabul edilir. On dokuzuncu yüzyılda bu denklikler iki ayrı kavram olarak ele alınırdı.
Beta Çözünmesinin Korunumu
1911 yılında beta çözünmesinin parçalı değil de devamlı bir ışıma olduğu keşfedildiğinde, o zamanlar beta ışımasının atom çekirdeğinden bir elektron ışıması olduğu sanılıyordu, enerji korunumuyla çelişen bir fenomen olduğu düşünülmüştü. Bu problem 1933 yılında, elektronun yanı sıra bir nötrinonun da ışıdığını gösteren Enrico Fermi tarafından çözüldü, böylece kayıp olarak görülen enerjinin kaynağı bulunmuş oldu.
Termodinamiğin İlk Kanunu
Termodinamiğin ilk kanunu şöyle anlatılabilir: Kapalı bir sistem için,
, or equivalently,
Denklemdeki 
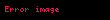
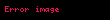
İş ve ısıdan önce kullanılan δ sembolü, iç enerjideki artışı gösteren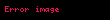


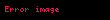
Entropi, ısının işe dönüşme olasılığını açıklayan sisteme dayanan (bu hesaplamalardan türetilen) fonksiyonudur.
Basit sıkıştırılabilir bir sistem için, sistemin yaptığı iş şöyle gösterilebilir:
Bu denklemde;
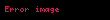
Bu denklemde, 

Basit açık bir sistem için(çevresiyle kütle değişimi yapabilen), tek tip parçacık içeren, ilk kanun şöyle yazılabilir:
Bu denklemde 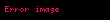

Noether'in Teoremi
Enerji korunumu pek çok fiziksel teoride geçerliliğini korur. Noether teoremine (devamlı bir simetrisi olan her fiziksel teorinin ifade ettiği kavramların korunur olduğunu anlatır) dayanarak, matematiksel bir bakış açısıyla; teorinin simetrisi zamandan bağımsızsa bu durumdaki korunur kavram "enerji"dir (enerjinin zamandan bağımsız olduğunu da söyleyerek). Enerji korunumu kanunu zamanın simetrisinin değişiminin bir sonucudur; enerji korunumu deneysel çalışmalarla gösterilen kanunların zamandan bağımsızlığına dayanır. Felsefi söylemle şöyle de ifade edilebilir; "her şey kendi içinde zamandan bağımsızdır." Başka bir deyişle, eğer fiziksel bir sistem zamanın bağımsız bir şekilde var (kendi fonksiyonlarında devam ediyorsa) ise, o sistemin enerjisi (değişen zaman boyunca enerji ile ilgili ekstra bilgi için, ) korunurdur. Tam tersi, bir sistem zamanın simetrisinin değişimiyle değişiyorsa (örneğin, zamana bağlı potansiyel enerji) enerji korunumu bu sistem için geçerli değildir (tabi bu enerjisi korunmayan sistemi enerjisi korunan bir sistemin alt sistemi olarak ele almazsak). Enerjisi zamanla değişen herhangi bir sistem, enerjisi korunur başka bir sistemin alt sistemi olarak gösterilebileceğinden (evrene kadar genellemek yanlış bir yaklaşım olur),enerjiyi ölçmek için baz aldığımız noktaya göre her sistemin enerjisi korunur olabilir. Tanımlı sistemlerde (sonsuza gitmeyen)enerji korunumu kanunu geçerlidir (özel ve genel göreliliğin, hatta kuantum elektrodinamiğinin, açıklandığı sistemlerde).
Görelilik
Albert Einstein'ın keşfinin ardından, enerji, enerji-momentum 4 vektörünün bir parçası olarak görüldü (ayrıntılı bilgi için bkz. ). Bu vektörün her bir bileşeni, herhangi kapalı bir sistemde (aynı şartlardan bakıldığında, ayrıntılı bilgi için bkz. ), zamandan bağımsızdır (korunur). Parçacıkların esas kütlesi, parçacıklar sisteminin değişmez kütlesi-momentum merkezi de denebilir-(ayrıntılı bilgi için bkz. ) için; vektör uzunluğu da korunurdur (bkz. )
Tek bir "yoğun" parçacığın göreceli enerjisi, hareketinden kaynaklı kinetik enerjisine ek olarak esas kütlesinden de kaynaklı olan enerjiden meydana gelir. Kinetik enerjinin düşük olduğu zamanlarda (tek parçacıklar için) ya da parçacıklar sistemi için kinetik enerji sabit kaldığında, parçacığın ya da parçacıklar sisteminin toplam enerjisi esas kütle veya değişmez kütle cinsinden bu formülle ifade edilir; 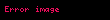
Buna göre, enerji korunumu kanunu zamanın göreceli olduğu durumlarda bile (gözlemcinin şartları enerjisi ölçülen sistemle aynı olmalı) zamandan bağımsız bir şekilde geçerliliğini koruyor. Bu da demektir ki farklı gözlemciler enerji değerleri açısından farklı hesaplamalar yapmış olsa bile toplam enerji korunur, gözlemcilerden bağımsızdır (buna enerji-momentum ilişkisi denir, ayrıntılı bilgi için bkz. ).
Genel görelilikte enerji-momentum korunumu gerilim-enerji-momentum belirsizliği ile ölçülür (ayrıntılı bilgi için bkz. ). Genel görelilik teorisi evrende enerji korunumu olup olmadığı konusunda net bir cevap vermez(olmama ihtimali de çıkarılabilir).
Kuantum teorisi
Kuantum mekaniğinde, bir kuantum sisteminin enerjisi kendinden-eklemli (ya da Hermitian) Hamilton operatörleriyle açıklanır (ayrıntılı bilgi çin bkz. , Hilbert uzayı ). Eğer bir operatör zamandan bağımsızsa, var olma/ortaya çıkma olasılığı sistemin zamanla değişimi sonucunda dahi aynı kalır. Bu sebeple tahmini/beklenen enerjisi de zamandan bağımsızdır. Kuantum alan teorisinde yerel enerji korunumu Noether'in teoreminden gelen enerji-momentum tensör operatörüyle açıklanır. Kuantum teorisindeki evrensel zaman operatörü kaybından dolayı ortaya çıkan pozisyon-momentum belirsizliğinin aksine zaman-enerji belirsizliği sadece özel birkaç durum için söz konusudur (bkz. belirsizlik ilkesi). Belirli zamanlardaki enerji miktarı, zaman-enerji belirsizliği sorununa yakalanılma dan yüksek bir kesinlikle hesaplanabilir. Sonuç olarak, enerjinin korunumu kanunu kuantum mekaniğinde bile baş vurulan temelleri sağlam bir kavramdır.
Ayrıca bakınız
Dipnotlar
- ^ Walter Lewin. Work, Kinetic Energy, and Universal Gravitation. MIT Course 8.01: Classical Mechanics, Lecture 11 (ogg) (videotape). Cambridge, Massachusetts, USA: . Etkinlik zamanı: 45.35-49.11. 28 Ekim 2012 tarihinde kaynağından . Erişim tarihi: 23 Aralık 2010.
150 Joule sizi öldürmeye yeter.
- ^ Planck, M. (1923/1927). termodinamik üstüne inceleme, İngilizce üçüncü baskısı A. Ogg tarafından Almanca yedinci baskısından çevrildi, Longmans, Green & Co., London,sayfa 40.
- ^ Janko, Richard (2004). "Empedocles, "On Nature"" (PDF). Zeitschrift für Papyrologie und Epigraphik. Cilt 150. ss. 1-26. 9 Ağustos 2017 tarihinde kaynağından (PDF). Erişim tarihi: 20 Aralık 2020.
- ^ Lavoisier, A.L. & Laplace, P.S. (1780) "Memoir on Heat", Académie Royale des Sciences pp. 4–355
- ^ von Mayer, J.R. (1842) "Remarks on the forces of inorganic nature" in Annalen der Chemie und Pharmacie, 43, 233
- ^ Mayer, J.R. (1845). Die organische Bewegung in ihrem Zusammenhange mit dem Stoffwechsel. Ein Beitrag zur Naturkunde, Dechsler, Heilbronn.
- ^ {{Kitap kaynağı | yazar=Grove, W. R. | başlık=The Correlation of Physical Forces | url=https://archive.org/details/correlationphys06grovgoog |yer= Londra | yayıncı=Longmans, Green | yıl=1874 |basım=6.6
- ^ . Bartleby. 2 Ekim 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 6 Nisan 2014.
- ^ William John Macquorn Rankine (1853) "On the General Law of the Transformation of Energy," Proceedings of the Philosophical Society of Glasgow, vol. 3, no. 5, pages 276-280; reprinted in: (1) Philosophical Magazine, series 4, vol. 5, no. 30, pages 106-117 15 Nisan 2014 tarihinde Wayback Machine sitesinde . (February 1853); and (2) W. J. Millar, ed., Miscellaneous Scientific Papers: by W. J. Macquorn Rankine, ... (London, England: Charles Griffin and Co., 1881), part II, pages 203-208: "The law of the Conservation of Energy is already known—viz. that the sum of all the energies of the universe, actual and potential, is unchangeable."
- ^ Hadden, Richard W. (1994). On the shoulders of merchants: exchange and the mathematical conception of nature in early modern Europe. SUNY Press. s. 13. ISBN . 27 Haziran 2014 tarihinde kaynağından . Erişim tarihi: 19 Ocak 2015., Chapter 1, p. 13 30 Eylül 2014 tarihinde Wayback Machine sitesinde .
- ^ Smith, D. A. (1980). . Aust. J. Phys. Cilt 33. ss. 95-105. 12 Ekim 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Mart 2013.
Kaynakça
Güncel kaynaklar
- Goldstein, Martin, and Inge F., (1993). The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN .
- Nolan, Peter J. (1996). Fundamentals of College Physics, 2nd ed. William C. Brown Publishers.
- Oxtoby & Nachtrieb (1996). Principles of Modern Chemistry, 3rd ed. Saunders College Publishing.
- Papineau, D. (2002). Thinking about Consciousness. Oxford: Oxford University Press.
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN .
- Stenger, Victor J. (2000). Timeless Reality. Prometheus Books. Especially chpt. 12. Nontechnical.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN .
- , Cornelius (1970). The Variational Principles of Mechanics. Toronto: University of Toronto Press. ISBN .
Fikirlerin tarihçesi
- Brown, T.M. (1965). "Resource letter EEC-1 on the evolution of energy concepts from Galileo to Helmholtz". American Journal of Physics. 33 (10). ss. 759-765. Bibcode:1965AmJPh..33..759B. doi:10.1119/1.1970980.
- Cardwell, D.S.L. (1971). From Watt to Clausius: The Rise of Thermodynamics in the Early Industrial Age. Londra: Heinemann. ISBN .
- Guillen, M. (1999). . New York: Abacus. ISBN .
- Hiebert, E.N. (1981). Historical Roots of the Principle of Conservation of Energy. Madison, Wis.: Ayer Co Pub. ISBN .
- Kuhn, T.S. (1957) "Energy conservation as an example of simultaneous discovery", in M. Clagett (ed.) Critical Problems in the History of Science pp.321–56
- Sarton, G.; Joule, J. P.; Carnot, Sadi (1929). "The discovery of the law of conservation of energy". Isis. Cilt 13. ss. 18-49. doi:10.1086/346430.
- Smith, C. (1998). The Science of Energy: Cultural History of Energy Physics in Victorian Britain. Londra: Heinemann. ISBN .
- Mach, E. (1872). History and Root of the Principles of the Conservation of Energy. Open Court Pub. Co., Illinois.
- Poincaré, H. (1905). Science and Hypothesis. Walter Scott Publishing Co. Ltd; Dover reprint, 1952. ISBN ., Chapter 8, "Energy and Thermo-dynamics"
Dış bağlantılar
- MISN-0-158 The First Law of Thermodynamics 24 Eylül 2015 tarihinde Wayback Machine sitesinde . (PDF file) by Jerzy Borysowicz for Project PHYSNET14 Mayıs 2017 tarihinde Wayback Machine sitesinde ..
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Enerjinin korunumu yasasi yalitilmis bir sistemdeki toplam enerjinin degismeyecegini soyler Enerji ne yok edilebilir ne de yoktan var edilebilir ama enerji turu degisebilir ornegin dinamitin patlamasiyla kimyasal enerji kinetik enerjiye donusebilir source source source source track track track MIT de fizik ogretmeni Walter Lewin bir gulleye salinim hareketi yaptirarak enerjinin korunumunu anlatiyor Enerjinin korunumu yasasi geregi birinci tur devridaim makinesinin calismasi imkansizdir Bu turde disaridan enerji alinmadan is yapilacagi iddia edilir Baska bir deyisle disaridan enerji almayan bir sistem cevresine sahip oldugundan daha cok enerji saglayamaz TarihceAlman hezarfen Gottfried Leibniz 1646 1716 kinetik enerjinin korunumu ilkesini ortaya atan doga bilimciydi Antik Yunan filozoflarina degin Miletli Thales y MO 550 her seyin kokeni olan maddenin dongusune korunumuna dair izler vardi Ancak denmek istenenin gunumuz madde enerji kavramlariyla eslestirmek icin yeterince guclu bir neden yok Ornegin Thales maddenin kokeninin arkhe ana madde su oldugunu soyluyordu Empedocles MO 490 MO 430 ise evrenin dort ogeden toprak hava su ve ates olustugunu olustugunu one suruyordu Hiclikten varlik yaratilamaz varlik hic olamaz diyor bu dort ogenin surekli olarak birbirine donustugunu soyluyordu 1638 yilinda Galileo Galilei cesitli konulardaki calismalarini unlu kesikli sarkaci enerji korunumuyla aciklanirsa potansiyel enerjinin ve kinetik enerjinin birbirine donuserek hareketi devam ettirdigi bir sistem da icinde yayinladi Hareketi kinetik enerjiyi aciklarken matematiksel dille anlatan ilk kisi Gottfried Wilhelm Leibniz olmustu 1676 1689 Leibniz pek cok mekanik sistemde disaridan bir etki olmadikca sistemin kendi davranisini surdurme egiliminde oldugunu kesfetti vi hiziyla hareket halinde olan mi kutlelerinden olusan sistemler imivi2 displaystyle sum i m i v i 2 Bu nicelige ya da sistemin yasam kuvveti adini verdi Bu ilke disaridan bir surtunme kuvveti olmadikca enerjinin neredeyse korundugunu gosteriyordu bu noktada kinetik enerjinin korunumunu O zamanlar pek cok fizikci momentumun korunumu surtunme kuvveti varliginda bile isleyen bir ilke ile ilgileniyordu momentumun matematiksel gosterilisi imivi displaystyle sum i m i v i ve korunan vis vivaya karsilik geliyordu Daha sonra gosterildigi gibi esnek carpismalar olarak adlandirilan durumlarda kinetik enerji de momentum da ayni anda korunuyordu Pek cok muhendis Carl Holtzmann ve momentumun korunumu ilkesinin uygulamali kullanimlar icin tek basina yetersiz oldugunu dusunduklerinden Leibniz in ilkesinden de yararlanmayi gerekli goruyorlardi Bu ilke ayni zamanda kimi kimyacilar tarafindan da desteklenmisti William Hyde Wollaston Bazi akademisyenler or John Playfair kinetik enerjinin butunuyle korunmadigini gostermisti Dogal olarak bu termodinamigin ikinci yasasina dayali modern hesaplamalara gore barizdi ancak 18 ve 19 yuzyillarda kayip enerji hala bilinmiyordu Zamanla surtunme kuvveti etkisi altinda gerceklesen hareket sonucunda olusan isinin vis vivanin baska bir bicimi olup olmayacagindan kuskulanildi 1783 yilinda Antoine Lavoisier ve Pierre Simon Laplace birbiriyle celisen iki kueami vis viva ve gozden gecirdiler Kont Rumford un 1798 yilinda top gullelerini oyma sirasinda kalibresini ayarlamak icin yapilan islemler aciga cikan isiyi gozlemlemesi mekanik anlamda hareketin isiya donusmesi yondeki kaniyi guclendirdi daha da onemlisi korunum olculebiliyordu ve ongorulebilirdi kinetik enerji ile isi enerjisini birbirine baglayan evrensel korunum sabiti hesaba katildiginda Sonrasinda 1807 yilinda Thomas Young tarafindan kullanildiktan sonra vis viva enerji ya da erke olarak anilmaya baslandi Gaspard Gustave Coriolis Vis viva sonradan daha yerinde bir formulle soyle tanimlandi 12 imivi2 displaystyle frac 1 2 sum i m i v i 2 Kinetik enerjinin ise donusumunu anlatan bu formul Gaspard Gustave Coriolis ve Jean Victor Poncelet nin 1819 1839 yillari arasindaki calismalarinin sonucudur Daha onceleri quantite de travail is niceligi sonralari travail mecanique mekanik is olarak bilinen bu kavram muhendislik hesaplamlarinda kullanildi 1837 yilinda Zeitschrift fur Physik dergisinde yayinlanan Uber die Natur der Warme baslikli makalede Karl Friedrich Mohr enerjinin korunumu ile ilgili ilk genel ogretiyi su tumcelerle anlatti kimyada bilinen 54 elemente karsilik fizik dunyasinda Kraf is ya da enerji olarak bilinen sadece bir etken var Farkli kosullarda farkli kavramlar olarak gorunebilir hareket kimyasal benzerlik kohezyon elektrik isik ve manyetizma ancak bu bicimlerin herhangi biri digerine donusebilir Isinin mekanik karsiligi Modern enerji korunumu prensibinin gelisiminde kilit asama nin ispatlanmasiydi Isinin yoktan var edilemeyecegini ya da yok edilemeyecegini soyleyen kabul gorurken aksinin oldugunu iddia eden enerji korunumu prensibi isinin ve mekanik isin birbirine donusebilecegini soyluyordu On sekizinci yuzyilin ortalarinda Rus bir bilim adami Mikhail Lomonosov kalori teorisine karsi olan kan hucresi isinin kinetik enerjisi adli postulatini ortaya atti Deneysel calismalari sonucu Lomonosov isinin kalorik sivinin parcaciklari vasitasiyla iletilmedigi sonucuna vardi 1798 yilinda Count Rumford Benjamin Thompson top gullelerinin kalibrasyonu sirasinda surtunmeden kaynaklanan isinin miktarini olctuler ve isinin kinetik enerjinin bir formu oldugu fikrini gelistirdiler hesaplamalar kalori teorisini curutmustu ancak kesinligini tam anlamiyla ifade etmekten yoksundu James Prescott Joule Mekanik esitlik prensibi modern haliyle ilk defa Alman cerrah Julius Robert von Mayer tarafindan ifade edildi 1842 yilinda Mayer bu sonuca Endonezya daki Hollanda kolonilerini ziyareti sirasinda varmisti buradaki hastalari daha az oksijen tukettiklerinden ve tabi bundan dolayi daha az enerjiye sahiplerdi daha sicak bir iklimde vucut sicakliklarini korumak icin kanlari daha koyu kirmiziydi Isinin ve mekanik isin birer enerji formu oldugunu kesfetti ve 1845 yilinda fizige dair bilgisini ilerlettikten sonra is ve isi arasinda sayisal iliskiyi anlatan bir monografi yayinladi Isinin mekanik denkligini olcmek icin kullanilan Joule aparati Ipin ucuna suya gomulu olan cikrigin donmesini saglamak icin bir cisim asili Ayni donemde 1843 yilinda James Prescott Joule Mayer den bagimsiz olarak mekanik esitligi bir dizi deneyle kesfetti En onemlisi simdi Joule aparati olarak bilinen ipe bagli bir agirligin asagiya hareket etmesiyle donen su icinde bir cikrik duzenegi Asagiya inen agirlik sebebiyle azalan yer cekimsel potansiyel enerjinin suyun icinde donen cikriktaki surtunmeden kaynaklanan ic enerji artisina esit oldugunu gosterdi 1840 1843 donemi sonrasi benzer deneyler isimli Danimarkalilar disinda fazlaca bilinmeyen muhendis tarafindan tekrar yapildi Joule ve Mayer in calismalari itirazlar ve olumsuz tepkilerle karsilasti ancak nihayetinde Joule un calismasi genel olarak kabul gordu Joule ve Mayer in calismalarinda kimin oncul olduguna yonelik ayrintili bilgi icin bkz Mechanical equivalent of heat Priority 1844 yilinda William Robert Grove mekanik isi isik elektrik ve manyetizma arasindaki iliskiyi hepsini tek bir kuvvet olarak betimleyen anlatan postulatini ortaya atti gunumuz diliyle enerji Grove 1874 te teorilerini Fiziksel Kuvvetler Arasindaki Iliski isimli bir kitapta yayinladi 1847 yilinda Joule un onceki calismalarindan yararlanan Sadi Carnot ve Hermann von Helmholtz Grove ile benzer sonuclara ulastilar ve Uber die Erhaltung der Kraft isimli kitapta yayinladilar calismalarini On the Conservation of Force 1847 Teorinin modern haliyle genel anlamda kabul gormesi bu yayin araciligiyla olmustur 1850 yilinda William Rankine ilk defa enerji korunumu kanunu ibaresini resmen kullanmistir 1877 yilinda bu prensibin Sir Isaac Newton dan koken aldigini iddia etmistir Philosophiae Naturalis Principia Mathematicadaki 40 41 nolu onermelere dayanarak Tait in calismasina gunumuz diliyle ilerleyici tarihcilik deniyor ayrintili bilgi icin Kutle enerji denkligi Madde proton elektron notron gibi parcaciklardan olusur Dinlenme ya da esas kutlesi vardir On dokuzuncu yuzyildaki bilinen kisitli calismalara gore bu esas kutle korunuyordu 1905 yilinda Einstein in ozel gorelilik teorisi bu esas kutlenin esas enerjinin belli bir oranina karsilik geldigini gosterdi Bunun anlami belli bir miktar esas kutle enerjinin pek cok formuna donusebilirdi kinetik potansiyel elektromanyetik isima enerjisi gibi Bu oldugunda yirminci yuzyilda yasanan tecrubelerimizde oldugu gibi aksine esas kutle korunmuyordu Tum enerji formlari toplam kutle ve toplam enerjiyi meydana getiriyordu Ornegin elektron ve pozitronun her biri esas kutleye sahiptir Esas enerjilerini fotonun elektromanyetik isima enerjisine donusturerek birlikte yok olabilirler geride kutle birakmaksizin Eger bu olay fotonun enerjisini aktarabilecegi bir cevresi olmayan izole bir sistemde meydana gelirse sitemin toplam kutlesi de toplam enerjisi de degismez Uretilen elektromanyetik isima enerjisi sistemdeki pozitron ve elektronun yok olmadan once olusturdugu kadar eylemsizlik ve agirlik meydana getirir Tersine maddesiz enerji yok olarak meydana madde esas kutlesi olan bir madde meydana getirir Sonuc olarak enerjinin korunumu toplam madde veya esas enerji ve kutlenin korunumu toplammadde sadece esas madde degil kanunlarinin ikisinin de birbirini karsiladigi kabul edilir On dokuzuncu yuzyilda bu denklikler iki ayri kavram olarak ele alinirdi Beta Cozunmesinin Korunumu 1911 yilinda beta cozunmesinin parcali degil de devamli bir isima oldugu kesfedildiginde o zamanlar beta isimasinin atom cekirdeginden bir elektron isimasi oldugu saniliyordu enerji korunumuyla celisen bir fenomen oldugu dusunulmustu Bu problem 1933 yilinda elektronun yani sira bir notrinonun da isidigini gosteren Enrico Fermi tarafindan cozuldu boylece kayip olarak gorulen enerjinin kaynagi bulunmus oldu Termodinamigin Ilk KanunuTermodinamigin ilk kanunu soyle anlatilabilir Kapali bir sistem icin dQ dU dW displaystyle delta Q mathrm d U delta W or equivalently dU dQ dW displaystyle mathrm d U delta Q delta W Denklemdeki dQ displaystyle delta Q isitilmak suretiyle sisteme eklenen enerjiye dW displaystyle delta W sistemin cevresine yaptigi cevresindekilerin ustunde ise ve dU displaystyle mathrm d U ise ic enerjideki degisime karsilik gelir Is ve isidan once kullanilan d sembolu ic enerjideki artisi gosterendU displaystyle mathrm d U sembolunden farkli olarak yorumlanmis enerji artisini gosterir bkz Is ve isi sisteme eklenen ya da sistemden ayrilan enerji miktarlarini gostermek icin uretilmis kavramlardir termodinamik olarak dengede olan bir sistemin ic enerjisini U displaystyle U gosterdiginde Sonuc olarak dQ displaystyle delta Q ile gosterilen isi enerjisinin anlami herhangi bir andaki enerji miktari degil isitilma sonucunda sisteme eklenen enerjidir Ayni sekilde dW displaystyle delta W ile gosterilen is enerjisinin anlami da yapilan is sonucu kaybedilen enerjidir Sonuc olarak o anin kosullari verildiginde termodinamik bir sistemin o anki enerjisi bulunabilir ancak sadece verilen bu kadar bilgiyle sistemin o an oncesinde isitilmasi ya da sogutulmasi sonucu kaybettigi kazandigi ya da is yaparak kaybettigi enerji bilinemez Entropi isinin ise donusme olasiligini aciklayan sisteme dayanan bu hesaplamalardan turetilen fonksiyonudur Basit sikistirilabilir bir sistem icin sistemin yaptigi is soyle gosterilebilir dW PdV displaystyle delta W P mathrm d V Bu denklemde P displaystyle P basinc ve dV displaystyle dV hacimdeki degisikligi ifade eder ikisi de sistemin birer degiskenidir Isi enerjisi de su sekilde gosterilebilir dQ TdS displaystyle delta Q T mathrm d S Bu denklemde T displaystyle T sicaklik ve dS displaystyle mathrm d S ise entropide meydana gelen kucuk degisimi ifade eder sicaklik ve entropi sistemi tarif eden degiskenlerdir Basit acik bir sistem icin cevresiyle kutle degisimi yapabilen tek tip parcacik iceren ilk kanun soyle yazilabilir dU dQ dW u dM displaystyle mathrm d U delta Q delta W u dM Bu denklemde dM displaystyle dM eklenen kutle u displaystyle u eklenen miktardaki parcacik basina dusen ic enerjiyi gosterir Kutle artisi sistem herhangi bir is yapmadan hacim degisikligini de meydana getirebilir Ornegin su su buhari sistemi buhar sisteminin hacmi sivinin kaynamasindan dolayi artabilir Geri donusumlu oldugunda sistemin yaptigi is soyle gosterilebilir dW P dV vdM displaystyle delta W P dV v dM denklemdeki v sisteme eklenen kutleye ait hacimdir Noether in TeoremiEnerji korunumu pek cok fiziksel teoride gecerliligini korur Noether teoremine devamli bir simetrisi olan her fiziksel teorinin ifade ettigi kavramlarin korunur oldugunu anlatir dayanarak matematiksel bir bakis acisiyla teorinin simetrisi zamandan bagimsizsa bu durumdaki korunur kavram enerji dir enerjinin zamandan bagimsiz oldugunu da soyleyerek Enerji korunumu kanunu zamanin simetrisinin degisiminin bir sonucudur enerji korunumu deneysel calismalarla gosterilen kanunlarin zamandan bagimsizligina dayanir Felsefi soylemle soyle de ifade edilebilir her sey kendi icinde zamandan bagimsizdir Baska bir deyisle eger fiziksel bir sistem zamanin bagimsiz bir sekilde var kendi fonksiyonlarinda devam ediyorsa ise o sistemin enerjisi degisen zaman boyunca enerji ile ilgili ekstra bilgi icin korunurdur Tam tersi bir sistem zamanin simetrisinin degisimiyle degisiyorsa ornegin zamana bagli potansiyel enerji enerji korunumu bu sistem icin gecerli degildir tabi bu enerjisi korunmayan sistemi enerjisi korunan bir sistemin alt sistemi olarak ele almazsak Enerjisi zamanla degisen herhangi bir sistem enerjisi korunur baska bir sistemin alt sistemi olarak gosterilebileceginden evrene kadar genellemek yanlis bir yaklasim olur enerjiyi olcmek icin baz aldigimiz noktaya gore her sistemin enerjisi korunur olabilir Tanimli sistemlerde sonsuza gitmeyen enerji korunumu kanunu gecerlidir ozel ve genel goreliligin hatta kuantum elektrodinamiginin aciklandigi sistemlerde GorelilikAlbert Einstein in kesfinin ardindan enerji enerji momentum 4 vektorunun bir parcasi olarak goruldu ayrintili bilgi icin bkz Bu vektorun her bir bileseni herhangi kapali bir sistemde ayni sartlardan bakildiginda ayrintili bilgi icin bkz zamandan bagimsizdir korunur Parcaciklarin esas kutlesi parcaciklar sisteminin degismez kutlesi momentum merkezi de denebilir ayrintili bilgi icin bkz icin vektor uzunlugu da korunurdur bkz Tek bir yogun parcacigin goreceli enerjisi hareketinden kaynakli kinetik enerjisine ek olarak esas kutlesinden de kaynakli olan enerjiden meydana gelir Kinetik enerjinin dusuk oldugu zamanlarda tek parcaciklar icin ya da parcaciklar sistemi icin kinetik enerji sabit kaldiginda parcacigin ya da parcaciklar sisteminin toplam enerjisi esas kutle veya degismez kutle cinsinden bu formulle ifade edilir E mc2 displaystyle E mc 2 Buna gore enerji korunumu kanunu zamanin goreceli oldugu durumlarda bile gozlemcinin sartlari enerjisi olculen sistemle ayni olmali zamandan bagimsiz bir sekilde gecerliligini koruyor Bu da demektir ki farkli gozlemciler enerji degerleri acisindan farkli hesaplamalar yapmis olsa bile toplam enerji korunur gozlemcilerden bagimsizdir buna enerji momentum iliskisi denir ayrintili bilgi icin bkz Genel gorelilikte enerji momentum korunumu gerilim enerji momentum belirsizligi ile olculur ayrintili bilgi icin bkz Genel gorelilik teorisi evrende enerji korunumu olup olmadigi konusunda net bir cevap vermez olmama ihtimali de cikarilabilir Kuantum teorisiKuantum mekaniginde bir kuantum sisteminin enerjisi kendinden eklemli ya da Hermitian Hamilton operatorleriyle aciklanir ayrintili bilgi cin bkz Hilbert uzayi Eger bir operator zamandan bagimsizsa var olma ortaya cikma olasiligi sistemin zamanla degisimi sonucunda dahi ayni kalir Bu sebeple tahmini beklenen enerjisi de zamandan bagimsizdir Kuantum alan teorisinde yerel enerji korunumu Noether in teoreminden gelen enerji momentum tensor operatoruyle aciklanir Kuantum teorisindeki evrensel zaman operatoru kaybindan dolayi ortaya cikan pozisyon momentum belirsizliginin aksine zaman enerji belirsizligi sadece ozel birkac durum icin soz konusudur bkz belirsizlik ilkesi Belirli zamanlardaki enerji miktari zaman enerji belirsizligi sorununa yakalanilma dan yuksek bir kesinlikle hesaplanabilir Sonuc olarak enerjinin korunumu kanunu kuantum mekaniginde bile bas vurulan temelleri saglam bir kavramdir Ayrica bakinizTermodinamik kanunlariDipnotlar Walter Lewin Work Kinetic Energy and Universal Gravitation MIT Course 8 01 Classical Mechanics Lecture 11 ogg videotape Cambridge Massachusetts USA Etkinlik zamani 45 35 49 11 28 Ekim 2012 tarihinde kaynagindan Erisim tarihi 23 Aralik 2010 150 Joule sizi oldurmeye yeter Planck M 1923 1927 termodinamik ustune inceleme Ingilizce ucuncu baskisi A Ogg tarafindan Almanca yedinci baskisindan cevrildi Longmans Green amp Co London sayfa 40 Janko Richard 2004 Empedocles On Nature PDF Zeitschrift fur Papyrologie und Epigraphik Cilt 150 ss 1 26 9 Agustos 2017 tarihinde kaynagindan PDF Erisim tarihi 20 Aralik 2020 Lavoisier A L amp Laplace P S 1780 Memoir on Heat Academie Royale des Sciences pp 4 355 von Mayer J R 1842 Remarks on the forces of inorganic nature in Annalen der Chemie und Pharmacie 43 233 Mayer J R 1845 Die organische Bewegung in ihrem Zusammenhange mit dem Stoffwechsel Ein Beitrag zur Naturkunde Dechsler Heilbronn Kitap kaynagi yazar Grove W R baslik The Correlation of Physical Forces url https archive org details correlationphys06grovgoog yer Londra yayinci Longmans Green yil 1874 basim 6 6 Bartleby 2 Ekim 2015 tarihinde kaynagindan arsivlendi Erisim tarihi 6 Nisan 2014 William John Macquorn Rankine 1853 On the General Law of the Transformation of Energy Proceedings of the Philosophical Society of Glasgow vol 3 no 5 pages 276 280 reprinted in 1 Philosophical Magazine series 4 vol 5 no 30 pages 106 117 15 Nisan 2014 tarihinde Wayback Machine sitesinde February 1853 and 2 W J Millar ed Miscellaneous Scientific Papers by W J Macquorn Rankine London England Charles Griffin and Co 1881 part II pages 203 208 The law of the Conservation of Energy is already known viz that the sum of all the energies of the universe actual and potential is unchangeable Hadden Richard W 1994 On the shoulders of merchants exchange and the mathematical conception of nature in early modern Europe SUNY Press s 13 ISBN 0 7914 2011 6 27 Haziran 2014 tarihinde kaynagindan Erisim tarihi 19 Ocak 2015 Chapter 1 p 13 30 Eylul 2014 tarihinde Wayback Machine sitesinde Smith D A 1980 Aust J Phys Cilt 33 ss 95 105 12 Ekim 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 8 Mart 2013 KaynakcaGuncel kaynaklar Goldstein Martin and Inge F 1993 The Refrigerator and the Universe Harvard Univ Press A gentle introduction Kroemer Herbert Kittel Charles 1980 Thermal Physics 2nd ed W H Freeman Company ISBN 0 7167 1088 9 KB1 bakim Birden fazla ad yazar listesi link Nolan Peter J 1996 Fundamentals of College Physics 2nd ed William C Brown Publishers Oxtoby amp Nachtrieb 1996 Principles of Modern Chemistry 3rd ed Saunders College Publishing Papineau D 2002 Thinking about Consciousness Oxford Oxford University Press Serway Raymond A Jewett John W 2004 Physics for Scientists and Engineers 6th ed Brooks Cole ISBN 0 534 40842 7 KB1 bakim Birden fazla ad yazar listesi link Stenger Victor J 2000 Timeless Reality Prometheus Books Especially chpt 12 Nontechnical Tipler Paul 2004 Physics for Scientists and Engineers Mechanics Oscillations and Waves Thermodynamics 5th ed W H Freeman ISBN 0 7167 0809 4 Cornelius 1970 The Variational Principles of Mechanics Toronto University of Toronto Press ISBN 0 8020 1743 6 Fikirlerin tarihcesi Brown T M 1965 Resource letter EEC 1 on the evolution of energy concepts from Galileo to Helmholtz American Journal of Physics 33 10 ss 759 765 Bibcode 1965AmJPh 33 759B doi 10 1119 1 1970980 Cardwell D S L 1971 From Watt to Clausius The Rise of Thermodynamics in the Early Industrial Age Londra Heinemann ISBN 0 435 54150 1 Guillen M 1999 New York Abacus ISBN 0 349 11064 6 Hiebert E N 1981 Historical Roots of the Principle of Conservation of Energy Madison Wis Ayer Co Pub ISBN 0 405 13880 6 Kuhn T S 1957 Energy conservation as an example of simultaneous discovery in M Clagett ed Critical Problems in the History of Science pp 321 56 Sarton G Joule J P Carnot Sadi 1929 The discovery of the law of conservation of energy Isis Cilt 13 ss 18 49 doi 10 1086 346430 Smith C 1998 The Science of Energy Cultural History of Energy Physics in Victorian Britain Londra Heinemann ISBN 0 485 11431 3 Mach E 1872 History and Root of the Principles of the Conservation of Energy Open Court Pub Co Illinois Poincare H 1905 Science and Hypothesis Walter Scott Publishing Co Ltd Dover reprint 1952 ISBN 0 486 60221 4 Chapter 8 Energy and Thermo dynamics Dis baglantilarMISN 0 158 The First Law of Thermodynamics 24 Eylul 2015 tarihinde Wayback Machine sitesinde PDF file by Jerzy Borysowicz for Project PHYSNET14 Mayis 2017 tarihinde Wayback Machine sitesinde
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans