Zamanda sonlu farklar yöntemi

Zamanda sonlu farklar yöntemi, kısaca FDTD (İngilizce: Finite-difference time-domain) ya da Yee yöntemi, hesaplamalı elektromanyetizmada kullanılan bir sonlu farklar tekniğidir. Zaman düzleminde çalışan bir yöntem olduğundan ötürü, elektromanyetik spektrumun mikrodalga veya görünür ışık gibi farklı bölgelerinde anten veya fotonik aygıt tasarımı gibi çeşitli problemlerin çözümünde kullanılır. Aynı zamanda bu özellik, simülasyonu yapılan sistemin geniş bir frekans yelpazesine tepkisinin gözlenebilmesini sağlamaktadır. Matris tersinmesi gerektirmeyen bu FDTD, en yaygın elektromanyetik simülasyon yöntemlerinden biri olarak kabul edilir.

Bir ışık saçılması probleminin FDTD ile modellenmesi. Sol ve sağdaki resimler 500 nm dalga boyundaki bir ışık hüzmesinin 5 µm çapındaki birer fotoreseptör hücreden saçılmasını göstermektedir. Ortadaki referans resmi ise aynı boyuttaki bir yarıktan ışığın kırınımını temsil eder.

FDTD yönteminin temeli, elektromanyetik teorinin temelini oluşturan Maxwell denklemleri'nin zamanda ve uzayda ayrıklaştırılmasına dayalıdır. Denklemlerdeki zamana ve uzaya bağlı kısmi türevlerinin sonlu farklar cinsinden yazılması ile yaklaşık bir çözüm elde edilebilir. Simülasyon yapılacak alan kare şeklindeki kafeslere bölünür ve elektrik ile manyetik alan değişkenleri bu kafesin kenarlarına yerleştirilir. Ayrıklaştırılmış denklemler kullanılarak her bir kafesteki değişkenler sırası ile uzaya ve zamana bağlı olarak ile güncellenir. Bu şekilde spesifik bir malzeme ya da aygıtta elektromanyetik dalgaların zamana ve uzaya göre değişimi yaklaşık olarak hesaplanabilmektedir. FDTD, problemlere özgün farklı sınır koşullarına uyarlanabilmektedir ve bu şekilde, açık radyasyon problemleri ve periyodik sistemler çözülebilir.

Zamanda sonlu farklar yöntemi, 1966 yılında Kane S. Yee tarafından keşfedilmiştir ve bundan ötürü Yee yöntemi olarak da adlandırılır. Yönteme FDTD ismi, Northwestern Üniversitesi'nde görevli Allen Taflove tarafından 1980 yılında verilmiştir. FDTD, bilgisayarların işlemci gücünün artması ile 1980'li ve 1990'lı yıllarda savunma sanayisinde ve akademide sıklıkla kullanılmaya başlanmıştır. Yöntemi kullanan çok sayıda simülasyon ve CAD yazılımı bulunur.

Yöntem

Yee algoritması

FDTD yöntemindeki ayrıklaştırma şemaları: a) İki boyutlu uzayda TE polarizasyonu için dalga şeması; b) İki boyutlu uzayda TM polarizasyonu için dalga şeması; c) Üç boyutlu uzayda Yee kafesi

FDTD algoritmasında zamana bağlı Maxwell denklemleri merkezî sonlu fark yaklaşımı ile zaman ve uzayda ayrıklaştırılır. Daha sonra ayrıklaştırılan uzayda zamana bağlı olarak sırayla elektrik ve manyetik alan vektörleri iterasyon ile çözülür. FDTD'yi diğer sonlu farklarından ayıran ana özellik, bu yöntemdeki uzay ayrıklaştırmasında "Yee kafesi" ya da "Yee ızgarası" adı verilen spesifik bir şemanın kullanılmasıdır. Bu şemaya göre Kartezyen koordinat sisteminde üç boyutlu uzay, kutu şeklinde kafeslere bölünür. Kenarlarına elektrik alanı vektörleri, yüzey normallerine ise manyetik alan vektörlerinin yerleştirildiği kafesler, yarı boyları kadar uzayda hareket ettirilir. Her harekette rotasyonel operatör kullanılan Maxwell denklemleri çözülür. Simülasyon alanını oluşturan her noktalardaki elektrik alanları her bir koordinat ekseninde kendinden önceki ve sonraki manyetik alan vektörleri ile adım adım güncellenir ve aynısı, her zaman adımı için sırasıyla elektrik ve manyetik alanlar için yapılır. Her zaman iterasyonunda uzaydaki yeni elektrik alan değerleri için (Maxwell-Faraday denklemi), yeni manyetik alanlar için ise Maxwell-Ampère denklemi kullanılır. Bu algoritma, simülasyon alanında simetrinin olduğu durumlarda simülasyonu hızlandırmak için bir ve iki boyutlu uzaya da uygulanabilmektedir.

Kıvrımlı yüzeylerin ve geometrilerin kafeslerle ayrıklaştırılması her türlü nümerik hatalara yol açacağından uzaydaki bilinmeyen sayısını artırmak gerekebilir. Bu durum problemin karmaşıklığını artırabildiğinden, FDTD'nin bu durumlarda performansının artırılabilmesi için uyumlu ayrıklaştırma algoritmaları geliştirilmiştir. Yee algoritması, küp şeklinde olmayan ve silindirik koordinat sistemlerindeki kafeslere de uyarlanabilmektedir. Silindirik koordinat sistemindeki yöntem, BOR/FDTD olarak adlandırılır. Yee algoritması aynı zamanda paralelize edilebilmektedir ve algoritmaya devre modellemesinin uygulanabilmesi mümkündür.

Nümerik stabilite ve dağılma

Tek boyutlu basit bir FDTD simülasyonunda nümerik dağılma. Bu simülasyondaki elektrik alan darbesi bir boşluk ortamında ilerlemesine rağmen hareket ettikçe bozunur.

FDTD simülasyonunun stabil olması ve sonsuz değerler sapmaması için bazı stabilite koşullarına uyması gerekir. Bunlardan biri ayrık noktalarda ilerleyen bir dalganın simülasyonunda kullanılan zaman adımı süresinin dalganın bir yandaki noktaya ilerleme süresinden daha kısa olması gerektiğini belirten Courant-Friedrichs-Lewy koşuludur. Üç boyutlu bir küp şeması için bu koşul şu şekilde ifade edilebilir:

${\displaystyle \Delta t\leq {\frac {1}{c{\sqrt {{\frac {1}{\Delta x^{2}}}+{\frac {1}{\Delta y^{2}}}+{\frac {1}{\Delta z^{2}}}}}}}={\frac {1}{c{\sqrt {\frac {3}{\Delta x^{2}}}}}}={\frac {\Delta x}{c{\sqrt {3}}}}}$

Burada ${\displaystyle c}$ ışık hızı, ${\displaystyle \Delta t}$ birim zaman adımı süresi ve ${\displaystyle \Delta x}$ de birim uzay adımı uzunluğudur. Yee'nin orijinal makalesinde stabilite koşulu hatalı verilmiş ve Allen Taflove ile Morris Brodwin'in 1975 yılındaki makalesinde düzeltilmiştir.Von Neumann stabilite analizi diğer sonlu farklar metotlarında olduğu gibi FDTD için de geçerlidir. 1990'lı yıllardan itibaren koşulsuz stabil olan FDTD yöntemleri de geliştirilmiştir.

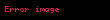
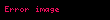
FDTD algoritması, farklı dalga boyları için, nümerik dağılma adı verilen yapay dağılma ve faz hatalarına yol açabilir. Bu durum, dalganın vakuma çok yakın özelliklere sahip ama tam da vakum olmayan bir ortamda ilerlemesine benzetilebilir. Nümerik dağılmada vakumda ilerleyen bir dalga darbesini oluşturan frekans elemanları hareket sırasında hiçbir fiziksel faktör olmamasına rağmen bozunma veya dağılma yaşayabilir. FDTD modellemesinde nümerik dağılmanın ve hata limitlerinin göz önünde bulundurulması gerekir; bu durumu telafi etmek için farklı metot ve algoritmalar mevcuttur. Nümerik dağılmayı azaltmakta kullanılan başlıca metotlardan biri zamanda yarı spektral yöntemdir (PSTD); bu yöntemde uzaydaki türevler ayrık Fourier dönüşümü yardımı ile alınır. Elektrik ve manyetik alanların Laguerre polinomları cinsinden açılımı ile de koşulsuz stabilite elde edilebilir. FDTD'nin zaman bazlı bir algoritma olmasından dolayı da malzemelerin farklı frekans tepkilerini modellemek için konvolüsyon temelli algoritmaların kullanılması gerekebilir; bağıl geçirgenliğin zaman bazlı tepkisi için malzemeye bağlı olarak Lorentz ve Debye modelleri kullanılır.Doğrusal olmayan malzemeler ve kazanç ortamları için benzer modellemeler de mevcuttur.

Sınır ve kaynak koşulları

Bir saçılma problemi için FDTD şeması. Çizgili sınır alanları mükemmel eşlenmiş katmanları (PML) belirtmektedir. Problemde "toplam alan ve saçılan alan" formülasyonu (TFSF) uygulanmaktadır; objeden saçılan alanlar A noktasından verilen düzlem dalga kaynağının B noktasındaki toplam alandan çıkarılması ile elde edilir.

Maxwell denklemlerinin sınırsızve açık uzayda çözümü ilgili sınır koşullarının belirlenmesini gerektirir. FDTD iterasyonları her ne kadar teknik olarak açık uzayda sonsuza kadar devam ettirilebilir olsa da, hiçbir bilgisayarın sınırsız veriyi saklaması etkili ve mümkün olmamasından ötürü, çözümün arandığı alanı izole eden sınır koşulları belirlenmiştir. Bazı elektromanyetik analiz yöntemlerinde kullanılan mükemmel elektrik iletken (PEC) sınır koşulları birçok FDTD uygulamalarında fiziksel olarak anlamlı olmayan sonuçlar vermeyebilir. Bu nedenle yöntem için soğuran sınır koşulları veya yutucu sınır koşulları geliştirilmiştir.

Soğuran sınır koşullarında simülasyon sınırlarının dışına çıkan dalgaların geri yansıma yapmadan soğurulması hedeflenir. Bu sınır koşulları, simülasyon alanlarının kaplayan ve içinde hareket eden dalgaların yansımadan soğurulduğu bir katman olarak düşünülebilir. Yee kafesi için ilk stabil soğuran sınır koşulu modeli 1981'de G. Mur tarafından bulunmuştur. Buna karşın ilk soğuran sınır koşullu modelleri farklı frekanslar için dağılmadan çalışsa da, soğuran yüzeylere dik gelmeyen düzlem dalgalarda yapay yansımalara yol açmaktaydı. 1994'te J. Berenger tarafından icat edilen mükemmel eşlenmiş katman (PML) sınır koşulu yaygın olarak kullanılmaktadır. Bu yöntemde katmana farklı açılardan gelen dalgalar yapay bileşenlerine ayrılır ve bu bileşenlerin yeni ortamda dalga empedansları eşlenir. Bu sırada dalga üstel bir operatör ile soğurulur. Daha sonraki araştırmalarda PML'lerin etkinliği yapay anizotropi ve esnek koordinat dönüşümleri ile geliştirilmiştir. Aslında fiziksel olmayan PML yöntemi az da olsa yapay yansımalara ve negatif indisli metamalzeme gibi ortamlarda stabilite sorunlarına yol açabilir. Standart PML yöntemi aynı zamanda evanesan dalgaların etkili bir biçimde soğurulmasında sorun yaşayabilmekte, PML'in performansı bu durumlarda konvolüsyonel metotlar ile iyileştirilebilmektedir.

Fotonik kristal ve frekans seçici yüzey gibi periyodik yapıların FDTD simülasyonu için ise periyodik sınır koşulları kullanılabilir. Bu sınır koşulları periyodik yapıyı oluşturan tek bir birimin simülasyonu ile tüm yapının tepkisinin ölçülmesini sağlar. Bu şekilde periyodik yapılar için büyük simülasyon problemlerinin hesaplanması basitleştirilebilir. Fotonik kristallerde kullanılan sınır koşulları Bloch ile Floquet teorilerine göre modellenebilir.Anten ve radar problemlerinde ise uzak alan bölgesindeki radyasyonun hesaplanması gerekebilir. Bu tarz problemlerde simülasyon bölgesi genişletilmeden antenin yakın alan bölgesindeki elektrik ve manyetik alanların işlenmesi ile bu veriler elde edilebilir. FDTD teorisinde bu işlem yakın alan-uzak alan dönüşümü olarak ifade edilir.

FDTD simülasyonlarında probleme uygun bir elektromanyetik dalga kaynağının tanımlanması gerekmektedir. Bu kaynak simülasyon bölgesine tek bir noktada ya da birden fazla noktalarda tanımlı bir elektrik/manyetik alan veya elektrik/manyetik akım yoğunluğu değeri şeklinde entegre edilebilir. Biyoelektromanyetizma ve savunma sanayi gibi birçok alanda düzlem dalga kaynakları kullanılır. FDTD simülasyonlarındaki en yaygın düzlem dalga formülasyonlarından biri özellikle saçılma problemlerinde işleyiş gören "toplam alan ve saçılan alan" formülasyonudur. Bu tip dalga kaynaklarında simülasyon bölgesi toplam alanların ve saçılan alanların bulunduğu iki bölgeye ayrılır; toplam alanların bulunduğu bölge saçılmaya yol açan objeyi kapsar ve diğer bölge bu bölge ile sınır koşullarının arasını doldurur. Toplam alanlar bölgesinin bir tarafından gönderilen dalganın öbür tarafından çıkarılması ile süperpozisyon prensibi kullanılarak objenin elektromanyetik alana tepkisi hesaplanabilir. Dalga kılavuzu gibi rezonant modlara sahip yapılar için ise bu modlarda salınım yapan kaynakların kullanılması gerekir.Lazer simülasyonları için gereken Gauss ışını ve ultra kısa darbe kaynakları da "toplam alan ve saçılan alan" formülasyonu ile modellenebilir.

Avantajları ve dezavantajları

FDTD yönteminin avantajları arasında basitliği ve homojen olmayan malzemelerin kolaylıkla modellenebilmesi bulunur. FDTD özellikle dalga boyunun aygıt ya da cisim geometrisi ile kıyaslanabilir boyutlarda olduğu problemlerde verimlidir. Yöntemde matris tersinmesi gibi karmaşıklığı yüksek işlemlerin kullanılmasına ihtiyaç duyulmadığından FDTD, genellikle frekans temelli diğer yöntemlere göre çok büyük sayıda bilinmeyenli problemlerin çözümünde kullanılabilir. Yöntemin zamana bağlı olması tek bir simülasyon ile sistemin geniş bir yelpazedeki frekans tepkisinin ölçülebilmesini mümkün kılar. FDTD, aynı zamanda moment yönteminin (MoM) aksine modellenen yapının Green fonksiyonunun hesaplanmasını gerektirmez.

Yöntemin dezavantajları arasında kübik kafes kullanımı ve malzeme dispersiyonu modellemeleri bulunur. Yee algoritmasında kullanılan ortogonal kafesler eğimli ve kıvrımlı yapıların modellemesinde bazı ayrıklaştırma hatalarına yol açabilir. Ortogonal ve karesel olmayan kafes algoritmaları geliştirilmişse de, bunlar Yee algoritmasına göre basitliğini ve etkinliğini kaybeder. FDTD, aynı zamanda mükemmel ya da iyi iletken malzemelerin modellenmesinde MoM kadar etkili değildir. Bunun başlıca nedeni FDTD'nin aksine MoM'da iletken yapıların sadece yüzeylerinin ayrıklaştırılmasıdır. Simülasyon bölgesinin dalga boylarından çok daha büyük olması durumunda ise faz hataları oluşabilir. Aynı zamanda standart FDTD'de, Courant-Friedrichs-Lewy koşulunun getirdiği birim zaman adım sınırı nedeniyle bazı düşük frekans biyoelektromanyetizma ve çok geniş ölçekli tümleşim (VLSI) problemleri çözülemez ve bu problemler için daha karmaşık koşulsuz stabil FDTD formülasyonları gerekir.

Tarihçe ve uygulamaları

Plazmonik nanopartiküllerin ışıkla (düzlem dalga) etkileşiminin FDTD simülasyonu. Renk skalası elektrik alan genliğini göstermektedir. Bu modelleme, yöntemin fotonikteki kullanımlarına bir örnektir.

FDTD, elektromanyetik problemlerin çözümünde kullanılan en yaygın yöntemlerden birisi olarak kabul edilir. Yöntem, süper bilgisayarların yaygınlaşması ve kişisel bilgisayarların işlem kapasitelerinin büyük ölçüde artması ile 1970'lerden itibaren popülerlik kazanmıştır. Basitliği, matris tersinmesi gerektirmemesi ve işlemsel verimliliği nedeniyle akademide ve endüstride sıklıkla tercih edilir.

Kane S. Yee, Maxwell denklemleri için geliştirdiği kafes algoritması ile ilgili makaleyi 1966 yılında IEEE Transactions on Antennas and Propagation dergisinde yayımladı. Bu makale ilk dönemlerinde mühendislik camiasından ilgi görmemişti. İlk kez Taflove ve Brodwin tarafından 1975'te biyoelektromanyetik modellemelere uygulanan yöntem, daha sonraki yıllarda elektromanyetik darbe ile radar kesiti problemlerine uygulandı. 1970'ler ve 1980'lerde savunma sanayisinde çalışan araştırmacılar, o dönemki frekans bazlı yöntemlerin sınırlamaları nedeniyle FDTD'ye yöneldi. Taflove, 1980'deki dielektrik ve iletken malzemelerdeki sinüzoidal dalgaların Yee algoritması ile modellenmesi ile ilgili çalışmasında yönteme "zamanda sonlu farklar yöntemi" ("finite-difference time-domain") ismini verdi. 1980'ler itibari ile dalga kılavuzu, anten ve mikroşerit gibi elektronik aygıtların FDTD modelleri mühendislik literatüründe yayımlandı. Bu dönemlerde aynı zamanda insan vücudu gibi homojen olmayan malzemelerin elektromanyetik modellenmesine olan ilgi artması, FDTD'nin popülerliğine katkıda bulundu. 1990'larda Berenger tarafından mükemmel eşlenmiş katmanların icat edilmesi ile yöntemin açık problemlere uygulanması kolaylaştı. Bu dönemlerde anten ve optik problemlerinin FDTD çözümü ile ilgili mühendislik literatüründeki yayınlar artış gösterdi. 2000'lerde ise bu algoritmaları kullanan ticari yazılımlar yaygınlaştı. FDTD'nin 2000'li ve 2010'lu yıllarda elektromanyetik modelleme literatürüne temel bir yöntem olarak yerleşmesi ile alandaki teorik araştırmalar daha karmaşık algoritmalara yöneldi.

Anten ve mikrodalga mühendisliği dışında FDTD'nin kullanıldığı alanlar arasında optik, fotonik, nanoteknoloji, dijital elektronik, düşük frekanslı jeofizik, biyoelektromanyetizma ve tıbbi görüntüleme teknolojileri bulunur. Yöntemin zamana bağlı olması lazer ışımaları ve solitonlar gibi doğrusal olmayan süreçlerin doğal bir şekilde simülasyonunu mümkün kılar.Katı hâl yapıları gibi karmaşık ve stokastik sistemlerin simülasyonunda ise sisteme kuantum mekaniği ve moleküler dinamik formülleri Yee algoritması ile entegre edilebilirken benzer şekilde plazmalar ve elektriksel kırılım akışkanlar dinamiği ve benzeri prensipler kullanılarak modellenebilmiştir.

FDTD yöntemini kullanan birçok ticari ve açık kaynak yazılım bulunur. Akademi ve endüstride kullanılan bazı FDTD simülasyon yazılımlarına örnek olarak REMCON XFDTD, Lumerical FDTD, RSoft Full Wave ve Massachusetts Teknoloji Enstitüsü'nün açık kaynak yazılımı MEEP verilebilir. Mikrodalga mühendisliğinde sıklıkla kullanılan CST Microwave Studio yazılımında ise FDTD ile ilişki olan (sonlu integral tekniği) (FIT) kullanılır.

Ayrıca bakınız

• Sonlu elemanlar yöntemi
• Sonlu hacim yöntemi

Kaynakça

Özel

1. ^ Solovei, Irina; Kreysing, Moritz; Lanctôt, Christian; Kösem, Süleyman; Peich, Leo; Cremer, Thomas; Guck, Jochen; Joffe1, Boris (2009). "Nuclear Architecture of Rod Photoreceptor Cells Adapts to Vision in Mammalian Evolution". Cell (İngilizce). 137 (2): 356-368. doi:10.1016/j.cell.2009.01.052. 
2. ^ Taflove & Hagness 2005, ss. 58-79.
3. ^ Taflove & Hagness 2005, s. 610.
4. ^ Yu et al. 2006, s. 33.
5. ^ Yu et al. 2006, ss. 11-13.
6. ^ Yu et al. 2006, ss. 193-194.
7. ^ Yu et al. 2006, s. 145.
8. ^ Thomas, V. A.; Jones, M. E.; Piket-May, M.; Taflove, A.; Harrigan, E. (1994). "The use of SPICE lumped circuits as sub-grid models for FDTD analysis". IEEE Microwave and Guided Wave Letters (İngilizce). 4 (5): 141-143. doi:10.1109/75.289516. 
9. ^ Piket-May, M.; Taflove, A.; Baron, J. (1994). "FD-TD modeling of digital signal propagation in 3-D circuits with passive and active loads". IEEE Transactions on Microwave Theory and Techniques (İngilizce). 42 (8): 1514-1523. doi:10.1109/22.297814. 
10. ^ Taflove & Hagness 2005, ss. 133-135.
11. ^ Taflove, A.; Brodwin, M. E. (1975). "Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell's equations" (PDF). IEEE Transactions on Microwave Theory and Techniques (İngilizce). 23 (8): 623-630. Bibcode:1975ITMTT..23..623T. doi:10.1109/TMTT.1975.1128640. 26 Ocak 2021 tarihinde kaynağından (PDF). Erişim tarihi: 19 Haziran 2020. 
12. ^ Pereda, A.; Vielva, L. A.; Vegas, A.; Prieto, A. (2001). "Analyzing the stability of the FDTD technique by combining the von Neumann method with the Routh-Hurwitz criterion". IEEE Transactions on Microwave Theory and Techniques (İngilizce). 49 (2): 623-630. doi:10.1109/22.903100. 
13. ^ Zhen, Fenghua; Chen, Zhizhang; Zhang, Jiazong (1999). Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method. IEEE Transactions on Microwave Theory and Techniques. 47. ss. 2003-2007. doi:10.1109/22.795075. 
14. ^ Zhen, Fenghua; Chen, Zhizhang; Zhang, Jiazong (2000). Toward the development of a three-dimensional unconditionally stable finite-difference time-domain method. IEEE Transactions on Microwave Theory and Techniques. 48. ss. 1550-1558. doi:10.1109/22.869007. 
15. ^ ^{a b c} Teixeira, F. L. (2010). "A Summary Review on 25 Years of Progress and Future Challenges in FDTD and FETD Techniques". ACES Journal (İngilizce). 25 (1): 1-14. 
16. ^ Taflove & Hagness 2005, s. 107.
17. ^ Taflove & Hagness 2005, ss. 138-153.
18. ^ Liu, Q. H. (1998). "The PSTD algorithm: A time‐domain method requiring only two cells per wavelength". Microwave and Optical Technology Letters (İngilizce). 15 (3): 158-165. doi:10.1002/(SICI)1098-2760(19970620)15:3<158::AID-MOP11>3.0.CO;2-3. 
19. ^ Taflove & Hagness 2005, ss. 156-160.
20. ^ Taflove, Oskooi & Johnson 2013, ss. 21-22.
21. ^ Taflove & Hagness 2005, ss. 353-359.
22. ^ Kelley, D.F.; Luebbers, R.J. (1996). "Piecewise linear recursive convolution for dispersive media using FDTD". IEEE Transactions on Antennas and Propagation (İngilizce). 44 (6): 792-797. doi:10.1109/8.509882. 
23. ^ Taflove & Hagness 2005, ss. 353, 376-403.
24. ^ Akleman, Funda (1998). Zamanda sonlu farklar yöntemi ve yutucu sınır koşulları (Yüksek lisans). İstanbul Teknik Üniversitesi Fen Bilimleri Enstitüsü. 
25. ^ Taflove & Hagness 2005, s. 229.
26. ^ Namiki, T. (1981). "A new FDTD algorithm based on alternating-direction implicit method". IEEE Trans. Electromagn. Compat. (İngilizce). 23 (4): 377-382. doi:10.1109/TEMC.1981.303970. 
27. ^ Taflove & Hagness 2005, ss. 273-274.
28. ^ Berenger, J. (1994). "A perfectly matched layer for the absorption of electromagnetic waves". Journal of Computational Physics (İngilizce). 114 (2): 185-200. Bibcode:1994JCoPh.114..185B. doi:10.1006/jcph.1994.1159. 
29. ^ Sacks, Z. S.; Kingsland, D. M.; Lee, R.; Lee, J. F. (1995). "A perfectly matched anisotropic absorber for use as an absorbing boundary condition". IEEE Transactions on Antennas and Propagation (İngilizce). 43 (12): 1460-1463. Bibcode:1995ITAP...43.1460S. doi:10.1109/8.477075. 
30. ^ Gedney, S. D. (1996). "An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices". IEEE Transactions on Antennas and Propagation (İngilizce). 44 (12): 1630-1639. Bibcode:1996ITAP...44.1630G. doi:10.1109/8.546249. 
31. ^ Chew, W. C.; Weedon, W. H. (1994). "A 3d perfectly matched medium from modified Maxwell's equations with stretched coordinates". Microwave Optical Tech. Letters (İngilizce). 7 (13): 599-604. Bibcode:1994MiOTL...7..599C. doi:10.1002/mop.4650071304. 
32. ^ Teixeira, F. L.; Chew, W. C. (1998). "General closed-form PML constitutive tensors to match arbitrary bianisotropic and dispersive linear media". IEEE Microwave and Guided Wave Letters (İngilizce). 8 (6): 223-225. doi:10.1109/75.678571. 
33. ^ Taflove & Hagness 2005, ss. 293-294.
34. ^ Cummer, Steven A. (2004). "Perfectly matched layer behavior in negative refractive index materials". IEEE Ant. Wireless Prop. Lett (İngilizce). 3 sayfalar =172-175. doi:10.1109/lawp.2004.833710. KB1 bakım: Dikey çizgi eksik ()
35. ^ Dong, X. T.; Rao, X. S.; Gan, Y. B.; Guo, B.; Yin, W. Y. (2004). "Perfectly matched layer-absorbing boundary condition for left-handed materials". IEEE Microwave Wireless Components Lett. (İngilizce). 14: 301-333. doi:10.1109/lmwc.2004.827104. 
36. ^ Loh, Po-Ru; Oskooi, Ardavan F.; Ibanescu, Mihai; Skorobogatiy, Maksim; Johnson, Steven G. (2009). "Fundamental relation between phase and group velocity, and application to the failure of perfectly matched layers in backward-wave structures". Phys. Rev. E (İngilizce). 79 (6): 065601. doi:10.1103/PhysRevE.79.065601. 
37. ^ Berenger, J. (1999). "Evanescent Waves in PML's: Origin of the Numerical Reflection in Wave-Structure Interaction Problems". IEEE Transactions on Antennas and Propagation (İngilizce). 47 (10): 1497-1503. doi:10.1109/8.805891. 
38. ^ Kuzuoğlu, M.; Mittra, R. (1996). "Frequency Dependence of the Constitutive Parameters of Causal Perfectly Matched Anisotropic Absorber". IEEE Microwave and Guided Wave Letters (İngilizce). 6 (12): 447-449. doi:10.1109/75.544545. 
39. ^ Roden, J. Alan; Gedney, Stephen D. (2000). "Convolution PML (CPML): An efficient FDTD implementation of the CFS–PML for arbitrary media". Microwave and Optical Technology Letters (İngilizce). 27 (5): 334-339. doi:10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A. 
40. ^ ^{a b} Taflove & Hagness 2005, ss. 553-555.
41. ^ Harms, P.; Mittra, R.; Ko, Wai (1994). "Implementation of the periodic boundary condition in the finite-difference time-domain algorithm for FSS structures". IEEE Transactions on Antennas and Propagation (İngilizce). 42 (9): 1317-1324. doi:10.1109/8.318653. 
42. ^ Taflove & Hagness 2005, s. 776.
43. ^ Taflove & Hagness 2005, ss. 349-372.
44. ^ Taflove & Hagness 2005, ss. 175-228.
45. ^ Çapoğlu, İlker R.; Taflove, Allen; Backman, Vadim (2013). "Computation of tightly-focused laser beams in the FDTD method". Optics Express (İngilizce). 21 (1): 87-101. doi:10.1364/OE.21.000087. 
46. ^ Çapoğlu, İlker R.; Taflove, Allen; Backman, Vadim (2013). "Generation of an incident focused light pulse in FDTD". Optics Express (İngilizce). 16 (23): 19208-19220. doi:10.1364/OE.16.019208. 
47. ^ ^{a b c d} Taflove & Hagness 2005, ss. 3-4.
48. ^ Bondeson, Rylander & Ingelström 2013, ss. 57-58.
49. ^ ^{a b c d} Davidson 2005, ss. 9-10.
50. ^ ^{a b} Davidson 2005, ss. 11-12.
51. ^ ^{a b c} Davidson 2005, s. 11.
52. ^ ^{a b} Bondeson, Rylander & Ingelström 2013, s. 82.
53. ^ Davidson 2005, s. 119.
54. ^ Taflove & Hagness 2005, ss. 160-161.
55. ^ ^{a b} Shlager, K.L.; Schneider, J.B. (1996). "A selective survey of the finite-difference time-domain literature". IEEE Antennas and Propagation Magazine (İngilizce). 37 (4): 39-57. doi:10.1109/74.414731. 
56. ^ Davidson 2005, ss. 8-9.
57. ^ Taflove & Hagness 2005, ss. 1-4.
58. ^ Yee, Kane (1966). "Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media". IEEE Transactions on Antennas and Propagation (İngilizce). 14 (3): 302-307. Bibcode:1966ITAP...14..302Y. doi:10.1109/TAP.1966.1138693. 
59. ^ Pile, David (2015). "Numerical solution". Nature Photonics (İngilizce). 9: 5-6. doi:10.1038/nphoton.2014.305. 
60. ^ Taflove, A.; Brodwin, M. E. (1975). "Computation of the electromagnetic fields and induced temperatures within a model of the microwave-irradiated human eye" (PDF). IEEE Transactions on Microwave Theory and Techniques (İngilizce). 23 (11): 888-896. Bibcode:1975ITMTT..23..888T. doi:10.1109/TMTT.1975.1128708. 4 Mart 2016 tarihinde kaynağından (PDF). Erişim tarihi: 31 Aralık 2020. 
61. ^ Holland, R. (1977). "Threde: A free-field EMP coupling and scattering code". IEEE Transactions on Nuclear Science. 24 (6): 2416-2421. Bibcode:1977ITNS...24.2416H. doi:10.1109/TNS.1977.4329229. 
62. ^ Taflove, A.; Umashankar, K. R. (1983). "Radar cross section of general three-dimensional scatterers" (PDF). IEEE Transactions on Electromagnetic Compatibility. 25 (4): 433-440. doi:10.1109/TEMC.1983.304133. 4 Mart 2016 tarihinde kaynağından (PDF). Erişim tarihi: 31 Aralık 2020. 
63. ^ Taflove, A. (1980). "Application of the finite-difference time-domain method to sinusoidal steady state electromagnetic penetration problems" (PDF). IEEE Trans. Electromagn. Compat. (İngilizce). 22 (3): 191-202. Bibcode:1980ITElC..22..191T. doi:10.1109/TEMC.1980.303879. 18 Ocak 2021 tarihinde kaynağından (PDF). Erişim tarihi: 19 Haziran 2020. 
64. ^ Choi, D. H.; Hoefer, W. J. (1986). "The finite-difference time-domain method and its application to eigenvalue problems". IEEE Transactions on Microwave Theory and Techniques. 34 (12): 1464-1470. Bibcode:1986ITMTT..34.1464C. doi:10.1109/TMTT.1986.1133564. 
65. ^ Tirkas, P. A.; Balanis, C. A. (1991). Finite-difference time-domain technique for radiation by horn antennas. IEEE Antennas and Propagation Society International Symposium Digest. 3. ss. 1750-1753. doi:10.1109/APS.1991.175196. ISBN . 
66. ^ Kashiwa, T.; Fukai, I. (1990). "A treatment by FDTD method of dispersive characteristics associated with electronic polarization". Microwave and Optical Technology Letters. 3 (6): 203-205. doi:10.1002/mop.4650030606. 
67. ^ Zhang, X.; Fang, J.; Mei, K. K.; Liu, Y. (1988). "Calculation of the dispersive characteristics of microstrips by the time-domain finite-difference method". IEEE Transactions on Microwave Theory and Techniques. 36 (2): 263-267. Bibcode:1988ITMTT..36..263Z. doi:10.1109/22.3514. 
68. ^ Bondeson, Rylander & Ingelström 2013, s. 58.
69. ^ Taflove & Hagness 2005, ss. 19-29.
70. ^ Huang, Yingyan; Ho, Seng-Tiong (1996). "Computational model of solid-state, molecular, or atomic media for FDTD simulation based on a multi-level multi-electron system governed by Pauli exclusion and Fermi-Dirac thermalization with application to semiconductor photonics". Optics Express (İngilizce). 14 (8): 3569-3587. doi:10.1364/OE.14.003569. 
71. ^ Chen, Hanning; McMahon, Jeffrey M.; Ratner, Mark A.; Schatz, George C. (2010). "Classical Electrodynamics Coupled to Quantum Mechanics for Calculation of Molecular Optical Properties: a RT-TDDFT/FDTD Approach". J. Phys. Chem. C (İngilizce). 114 (34): 14384-14392. doi:10.1021/jp1043392. 
72. ^ Willis, K. J.; Ayubi-Moak, J. S.; Hagness, S. C.; Knezevic, I. (2009). "Global modeling of carrier-field dynamics in semiconductors using EMC–FDTD". Journal of Computational Electronics (İngilizce). 8. doi:10.1007/s10825-009-0280-4. 
73. ^ Slavcheva, G. M.; Arnold, J. M.; Ziolkowski, R. W. (2004). "FDTD simulation of the nonlinear gain dynamics in active optical waveguides and semiconductor microcavities". IEEE Journal of Selected Topics in Quantum Electronics (İngilizce). 10 (5): 1052-1062. doi:10.1109/JSTQE.2004.836023. 
74. ^ Ward, J.; Swenson, C.; Furse, C. (2005). "The impedance of a short dipole antenna in a magnetized plasma via a finite difference time domain model". IEEE Transactions on Antennas and Propagation (İngilizce). 53 (8): 2711-2718. doi:10.1109/TAP.2005.851823. 
75. ^ Chaudhury, Bhaskar; Boeuf, Jean-Pierre (2010). "Computational Studies of Filamentary Pattern Formation in a High Power Microwave Breakdown Generated Air Plasma". IEEE Transactions on Plasma Science (İngilizce). 38 (9): 2281-2288. doi:10.1109/TPS.2010.2055893. 
76. ^ Su, Changyi; Ke, Haixin; Hubing, Todd (2009). "Overview of Electromagnetic Modeling Software". 25th Annual Review of Progress in Applied Computational Electromagnetics (İngilizce): 736-741. 
77. ^ Chrostowski & Hochberg 2015, s. 32.
78. ^ F. Oskooi, Ardavan; Roundy, David; Ibanescu, Mihai; Bermel, Peter; Joannopoulos, J. D.; G. Johnson, Steven (2010). "Meep: A flexible free-software package for electromagnetic simulations by the FDTD method". Computer Physics Communications (İngilizce). 181 (3): 687-702. doi:10.1016/j.cpc.2009.11.008. 
79. ^ Davidson 2005, ss. 107-108.
80. ^ Debes, Klaus. . microwaves101.com (İngilizce). 19 Eylül 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Ocak 2021. 

Genel

• Bondeson, Anders; Rylander, Thomas; Ingelström, Pär (2013). Computational Electromagnetics (İngilizce). Springer. ISBN . 
• Chrostowski, Lukas; Hochberg, Michael (2015). Silicon Photonics Design (İngilizce). Cambridge University Press. ISBN . 
• Davidson, David B. (2005). Computational Electromagnetics for RF and Microwave Engineering (İngilizce). Cambridge University Press. ISBN . 
• Kunz, Karl S.; Luebbers, Raymond J. (1993). The Finite Difference Time Domain Method for Electromagnetics (İngilizce). CRC Press. ISBN . 
• Özen, Şükrü; Arı, Niyazi; Çolak, Ömer H.; Teşneli, Ahmet Y. (2008). Elektromanyetikte Sonlu Farklar Metodu (1 bas.). Palme. ISBN . 
• Taflove, Allen; Hagness, Susan C. (2005). Computational Electrodynamics: The Finite-Difference Time-Domain Method (İngilizce) (3 bas.). Artech House Publishers. ISBN . 
• Taflove, Allen; Oskooi, Ardavan; Johnson, Steven G., (Ed.) (2013). Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology (İngilizce). Artech House. ISBN . 
• Yu, Wenhua; Mittra, Raj; Su, Tao; Yang, Xiaoling (2006). Parallel Finite-Difference Time-Domain Method (İngilizce). Artech House Publishers. ISBN . 
• Sevgi, Levent (1999). Elektromagnetik Problemler ve Sayısal Yöntemler (1 bas.). Birsen Yayınevi. ISBN . 
• Sullivan, Dennis M. (2013). Electromagnetic Simulation Using the FDTD Method (İngilizce) (2 bas.). IEEE. ISBN . 

Dış bağlantılar

Wikimedia Commons'ta Zamanda sonlu farklar yöntemi ile ilgili ortam dosyaları bulunmaktadır.

• Nature Photonics dergisinin Allen Taflove ile FDTD'nin tarihi üzerine röportajı (İngilizce)
• EMPossible'ın FDTD ile modelleme dersi 21 Haziran 2020 tarihinde Wayback Machine sitesinde . (İngilizce)
• FDTD yöntemini anlamak 22 Haziran 2020 tarihinde Wayback Machine sitesinde . (İngilizce)
• MIT profesörü S. G. Johnson'ın PML ders notları 1 Ağustos 2020 tarihinde Wayback Machine sitesinde . (İngilizce)
• FDTD temelleri 14 Şubat 2019 tarihinde Wayback Machine sitesinde . (İngilizce)
• (İngilizce)