Bu maddede birçok sorun bulunmaktadır. Lütfen sayfayı geliştirin veya bu sorunlar konusunda bir yorum yapın.
|
Temel grup, Henri Poincaré'in 1895'te yayınladığı "Analysis Situs" adlı makalesinde tanımlanmıştır. Kavram, Bernhard Riemann, Poincaré ve Felix Klein'ın çalışmalarıyla Riemann yüzeyleri teorisinden ortaya çıkmıştır. Karmaşık değerli fonksiyonların monodromik özelliklerini açıkladığı gibi kapalı yüzeylerin tam bir topolojik sınıflandırılmasını sağlar.
Yollar ve Homotopiler
Bu bölümde topolojik uzayları ele alacağız. Yolların tanımında kullanacağımız 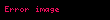

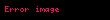

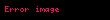

Yol
Bir 




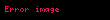

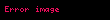


 'in grafiği üzerinde kırmızı ok ile belirtilen oryantasyonu.
'in grafiği üzerinde kırmızı ok ile belirtilen oryantasyonu.Örnekler
İlk örnek olarak, 
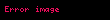


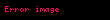




• 
• 
Ayrıca 

Diğer bir örnek olarak da bir 


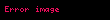
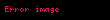









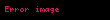 fonksiyonunu ve siyah oklar
fonksiyonunu ve siyah oklar  yolunu temsil etmektedir.
yolunu temsil etmektedir.Şimdi 
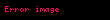

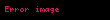

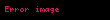

Bunun için, sürekli ve daima artan bir fonksiyon tanımlayalım. 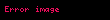
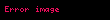
Sonra bileşke fonksiyonu yazalım. 
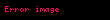

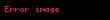


Bu bileşke fonksiyonunun bileşenleri 


Sonuç olarak 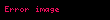


 ve
ve  yolları.
yolları.Ters Yol









Örnek olarak, 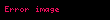








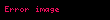
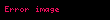

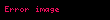

 yolu (kırmızı oklarla gösterilmiştir.)
yolu (kırmızı oklarla gösterilmiştir.)Birim çember üzerinde yol örneğini inceleyelim;
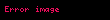



Bu fonksiyon aşağıdaki özellikleri sağlamaktadır:
•
•

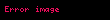

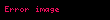
Bu nedenle,
Birim küre üzerinde yol örneğinde ise, 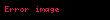





Sonuç olarak, 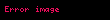



-
![image]() Şekil 5
Şekil 5 -
![image]() Şekil 6
Şekil 6
Diğer yandan, 
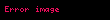
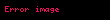



Homeomorfizma
Herhangi 




Tanım



Önermeler
kümesi fonksiyon bileşkesi
altında bir gruptur.
Kanıtı için, önce 


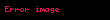


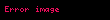
İki sürekli fonksiyonun bileşkesi de sürekli bir fonksiyon olduğundan 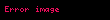
Öte yandan, 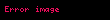



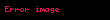
Şimdi (
•Bileşim özelliği: Herhangi 

• 



•Birim eleman: 



Öte yandan 


Sonuç olarak her 

•Terslenebilme: Herhangi bir 


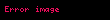

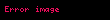
Herhangi 
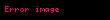
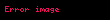










- Eğer
ise
ve
olur.
Kanıtını şöyle açıklayabiliriz; herhangi 








Şimdi 


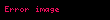

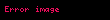





Sonuç olarak, her 


Yollar üzerinde denklik bağıntısı





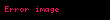
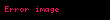
•yansıma: 




•simetri: 










•geçişme: 


Varsayımlara göre, 




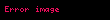
Sonuç olarak 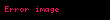
Homotopi
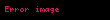
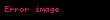



(i) Her 



(ii) 





Önermeler
- Yolların bileşkesi, yolların denklik sınıfları üzerinde iyi tanımlıdır.
Önermenin kanıtını şöyle açıklayabiliriz: 











- Bir uzayda sabit başlangıç ve bitiş noktaları olan yollar üzerindeki homotopi ilişkisi bir denklik bağıntısıdır. Uzaydaki bir
yolunun homotopi sınıfı
ile gösterilir.
İspatını yaparken, Homotopi ilişkisinin yansıma, simetri ve geçişme özelliklerini sağladığı göstermeli.
•yansıma: 





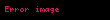
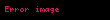






•simetri: 





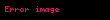






Şimdi 














•geçişme: 












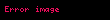





şeklinde tanımlayalım. Açıkça görüyoruz ki;
fonksiyonu
noktası dışında her yerde süreklidir.
Öte yandan 




Dolayısıyla 
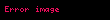




Sonuç olarak 

gruptur.
Kanıtını göstermek için, örnek olarak 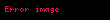


•Birim elemanı 





• 





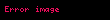
• 
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bu maddede bircok sorun bulunmaktadir Lutfen sayfayi gelistirin veya bu sorunlar konusunda tartisma sayfasinda bir yorum yapin Bu madde Vikipedi bicem el kitabina uygun degildir Maddeyi Vikipedi standartlarina uygun bicimde duzenleyerek Vikipedi ye katkida bulunabilirsiniz Gerekli duzenleme yapilmadan bu sablon kaldirilmamalidir Haziran 2019 Bu maddedeki uslubun ansiklopedik bir yazidan beklenen resmi ve ciddi usluba uygun olmadigi dusunulmektedir Maddeyi gelistirerek ya da konuyla ilgili tartismaya katilarak Vikipedi ye katkida bulunabilirsiniz Bu maddedeki bilgilerin dogrulanabilmesi icin ek kaynaklar gerekli Lutfen guvenilir kaynaklar ekleyerek maddenin gelistirilmesine yardimci olun Kaynaksiz icerik itiraz konusu olabilir ve kaldirilabilir Kaynak ara Temel grup haber gazete kitap akademik JSTOR Mart 2022 Bu sablonun nasil ve ne zaman kaldirilmasi gerektigini ogrenin Temel grup Henri Poincare in 1895 te yayinladigi Analysis Situs adli makalesinde tanimlanmistir Kavram Bernhard Riemann Poincare ve Felix Klein in calismalariyla Riemann yuzeyleri teorisinden ortaya cikmistir Karmasik degerli fonksiyonlarin monodromik ozelliklerini acikladigi gibi kapali yuzeylerin tam bir topolojik siniflandirilmasini saglar Yollar ve HomotopilerBu bolumde topolojik uzaylari ele alacagiz Yollarin taniminda kullanacagimiz I displaystyle I araligi 0 1 displaystyle 0 1 kapali araligi olacaktir Son olarak baslangic noktasi p displaystyle p ve bitis noktasi q displaystyle q olan yollara p displaystyle p den q displaystyle q ya giden yollar diyecegiz Yol Bir X displaystyle X uzayi alalim Bir a 0 1 X displaystyle alpha colon 0 1 to X surekli fonksiyonuna X displaystyle X uzayinda bir yol denir Boyle bir a displaystyle alpha yolu icin a 0 displaystyle alpha 0 noktasi baslangic noktasi ve a 1 displaystyle alpha 1 noktasi bitis noktasi olarak adlandirilir x y X displaystyle x y in X olsun Baslangic ile bitis noktalari sirasiyla x displaystyle x ve y displaystyle y olan ve I 0 1 displaystyle I 0 1 den X displaystyle X uzayina giden butun yollarin kumesi P x y f 0 1 X f 0 x f 1 y displaystyle mathbf P x y f colon 0 1 to X f 0 x f 1 y olarak tanimlanir Sekil 1 f displaystyle f in grafigi uzerinde kirmizi ok ile belirtilen oryantasyonu Ornekler Ilk ornek olarak X 0 1 displaystyle X 0 1 uzayinda bir f 0 1 X displaystyle f colon 0 1 to X fonksiyonunu f x x2 displaystyle f x x 2 olarak tanimlayalim X displaystyle X R2 displaystyle mathbb R 2 uzayindaki yollar genellikle f 0 1 displaystyle varphi colon 0 1 to R2 displaystyle mathbb R 2 t x t y t displaystyle t to x t y t fonksiyonu ile temsil edilir Burada x t displaystyle x t ve y t displaystyle y t surekli fonksiyonlardir Simdi bir f 0 1 displaystyle varphi colon 0 1 to R2 displaystyle mathbb R 2 yolunu f t t t2 displaystyle varphi t t t 2 seklinde tanimlayalim Bu durumda f 0 0 0 displaystyle varphi 0 0 0 noktasi baslangic noktasi ve f 1 1 1 displaystyle varphi 1 1 1 bitis noktasidir Ayrica 0 1 displaystyle 0 1 uzerindeki oryantasyonun f displaystyle varphi fonksiyonunun goruntusunun yonlendirmesini icerdiginin de altini cizelim Diger bir ornek olarak da bir g 1 1 1 1 displaystyle g colon 1 1 to 1 1 fonksiyonunu ele alalim ve g x x3 displaystyle g x x 3 olsun g displaystyle g fonksiyonunun grafigi X displaystyle X uzayi olmak uzere bu uzaydaki yollara bakalim Bir b1 I X displaystyle beta 1 colon I to X fonksiyonunu b1 t t t3 displaystyle beta 1 t t t 3 olarak tanimlayalim b1 0 0 0 b1 1 1 1 displaystyle beta 1 0 0 0 beta 1 1 1 1 oldugunu goruyoruz b1 displaystyle beta 1 in bilesenleri olan t displaystyle t ve t3 displaystyle t 3 I displaystyle I uzerinde surekli birer fonksiyon oldugundan b1 displaystyle beta 1 in y x3 displaystyle y x 3 fonksiyonu icin bir yol oldugunu soyleyebiliriz Sekil 2 Mavi oklar f1 displaystyle varphi 1 fonksiyonunu ve siyah oklar b1 displaystyle beta 1 yolunu temsil etmektedir Simdi f1 1 1 displaystyle varphi 1 colon 1 1 to R2 displaystyle mathbb R 2 fonksiyonunu ele alalim oyle ki f1 t t t3 displaystyle varphi 1 t t t 3 olsun f1 displaystyle varphi 1 bir yol degildir cunku tanim kumesi I 0 1 displaystyle I 0 1 degildir f1 displaystyle varphi 1 fonksiyonunu kullanarak x3 displaystyle x 3 grafiginin uzerinde baska bir yol bulacagiz Bunun icin surekli ve daima artan bir fonksiyon tanimlayalim f I 1 1 displaystyle f colon I to 1 1 fonksiyonu f t 2t 1 displaystyle f t 2t 1 olarak tanimlansin Sonra bileske fonksiyonu yazalim f1 f t I displaystyle varphi 1 circ f t colon I to R2 displaystyle mathbb R 2 oyle ki f1 f t 2t 1 2t 1 3 displaystyle varphi 1 circ f t 2t 1 2t 1 3 olsun f1 f 0 displaystyle varphi 1 circ f 0 1 1 displaystyle 1 1 ve f1 f 1 1 1 displaystyle varphi 1 circ f 1 1 1 olmaktadir Bu bileske fonksiyonunun bilesenleri 2t 1 displaystyle 2t 1 ve 2t 1 3 displaystyle 2t 1 3 I displaystyle I tanim araliginda surekli fonksiyon olduklarindan bu bileske fonksiyonun surekli oldugu sonucuna ulasilir Sonuc olarak f1 f displaystyle varphi 1 circ f X displaystyle X uzayinda bir yol olur Sekil 3 f displaystyle varphi ve f displaystyle bar varphi yollari Ters Yol p displaystyle p den q displaystyle q ya giden bir f I X displaystyle varphi colon I to X yolu icin f displaystyle bar varphi ters yolu f t displaystyle bar varphi t f 1 t displaystyle varphi 1 t olarak tanimlanir Bu durumda f displaystyle bar varphi yolunun baslangic noktasi q displaystyle q ve bitis noktasi p displaystyle p olur Ornek olarak f I 1 1 displaystyle varphi colon I to 1 1 yolunu f t 2t 1 displaystyle varphi t 2t 1 olarak tanimlayalim Bu durumda f 0 1 displaystyle varphi 0 1 ve f 1 0 displaystyle varphi 1 0 olur f displaystyle varphi uzerindeki oryantasyonu ters cevirirsek f I 1 1 displaystyle bar varphi colon I to 1 1 olarak tanimli f t displaystyle bar varphi t f 1 t displaystyle varphi 1 t olan ters yolunu elde ederiz Sekil 3 f 0 displaystyle bar varphi 0 f 1 1 displaystyle varphi 1 1 ve f 1 1 displaystyle bar varphi 1 1 f 0 1 displaystyle varphi 0 1 f 1 1 displaystyle varphi 1 1 oldugunu not edelim Sekil 4 Birim cember ve uzerindeki f displaystyle varphi yolu kirmizi oklarla gosterilmistir Birim cember uzerinde yol ornegini inceleyelim S1 displaystyle S 1 birim cember olmak uzere f I S1 C displaystyle varphi colon I to S 1 subset mathbb C fonksiyonunu f t displaystyle varphi t e2ip cos 2pt isin 2pt displaystyle e 2i pi cos 2 pi t i sin 2 pi t olarak tanimlayalim Bu fonksiyon asagidaki ozellikleri saglamaktadir f displaystyle varphi sureklidir cunku ustel fonksiyonun surekli oldugunu biliyoruz f 0 1 displaystyle varphi 0 1 f 14 i displaystyle varphi bigg frac 1 4 bigg i f 12 1 displaystyle varphi bigg frac 1 2 bigg 1 f 34 i displaystyle varphi bigg frac 3 4 bigg i f 1 1 displaystyle varphi 1 1 Bu nedenle f displaystyle varphi birim cember uzerindeki pozitif yonlu bir yoldur Sekil 4 Birim kure uzerinde yol orneginde ise R3 displaystyle R 3 uzerindeki birim kureyi ele alalim S2 x y z R3 x2 y2 z2 1 displaystyle S 2 left x y z in mathbb R 3 mid x 2 y 2 z 2 1 right f 0 1 S2 R3 displaystyle varphi colon 0 1 to S 2 subset mathbb R 3 fonksiyonunu f t displaystyle varphi t cos pt sin pt 0 displaystyle cos pi t sin pi t 0 seklinde tanimlayalim Bu sekilde tanimli f displaystyle varphi fonksiyonu bariz bir sekilde sureklidir cunku kosinus ve sinus fonksiyonlari sureklidir Sonuc olarak f 0 1 0 0 f 12 0 1 0 displaystyle varphi 0 1 0 0 varphi bigg frac 1 2 bigg 0 1 0 ve f 1 1 0 0 displaystyle varphi 1 1 0 0 olur Bu yuzden f displaystyle varphi fonksiyonu S2 displaystyle S 2 uzerinde bir yoldur ve oryantasyonu Sekil 5 teki gibidir Sekil 5 Sekil 6 Diger yandan b I S2 R3 displaystyle beta colon I to S 2 subset mathbb R 3 b t displaystyle beta t 0 sin p2t cos p2t displaystyle 0 sin pi 2t cos pi 2t biciminde tanimli olan fonksiyon sureklidir ve b 0 0 0 1 b 1 0 1 0 displaystyle beta 0 0 0 1 beta 1 0 1 0 oldugundan b displaystyle beta fonksiyonu S2 displaystyle S 2 uzerinde baska bir yola ornektir Sekil 6 Homeomorfizma Herhangi X displaystyle X ve Y displaystyle Y topolojik uzaylari arasinda bir homeomorfizma f X Y displaystyle f colon X to Y birebir ve orten bir fonksiyon seklinde tanimlanir f displaystyle f ve f 1 Y X displaystyle f 1 colon Y to X surekli fonksiyonlardir Tanim I displaystyle I dan I displaystyle I ya giden daima artan homeomorfizmalarin kumesi su sekilde tanimlanir Homeo I I f I I f daima artan ve homeomorfizma displaystyle operatorname Homeo I I left f colon I to I mid f text daima artan ve homeomorfizma right Onermeler Homeo I I displaystyle operatorname Homeo I I kumesi fonksiyon bileskesi displaystyle circ altinda bir gruptur Kaniti icin once Homeo I I displaystyle operatorname Homeo I I kumesinin displaystyle circ islemi altinda kapali oldugunu gostermek yeterlidir Herhangi f g Homeo I I displaystyle f g in operatorname Homeo I I secelim f g I I Homeo I I displaystyle f circ g colon I to I in operatorname Homeo I I oldugunu gosterecegiz f displaystyle f daima artan ve surekli bir fonksiyon olup tersi de sureklidir Ayni sekilde g displaystyle g icin de ayni ozellikler saglanir Iki artan fonksiyonun bileskesi de artan olacagindan f g displaystyle f circ g fonksiyonu da artan olur Iki surekli fonksiyonun bileskesi de surekli bir fonksiyon oldugundan f g displaystyle f circ g fonksiyonu da surekli olur Ote yandan f 1 displaystyle f 1 ve g 1 displaystyle g 1 fonksiyonlarinin surekli oldugunu biliyoruz O halde f g 1 displaystyle f circ g 1 g 1 f 1 displaystyle g 1 circ f 1 fonksiyonu da surekli olur Sonuc olarak f g I I Homeo I I displaystyle f circ g colon I to I in operatorname Homeo I I elde ederiz Simdi Homeo I I displaystyle operatorname Homeo I I circ kumesinin grup aksiyomlarini bilesim birim eleman terslenebilme sagladigini gosterelim Bilesim ozelligi Herhangi f g h Homeo I I displaystyle f g h in operatorname Homeo I I secelim Rastgele bir x I displaystyle x in I elemani alalim O halde h g f x h g f x h g f x displaystyle h circ g circ f x h g circ f x h g f x ve h g f x h g f x h g f x displaystyle h circ g circ f x h circ g f x h g f x oldugundan her x I displaystyle x in I icin h g f x h g f x displaystyle h circ g circ f x h circ g circ f x olur Birim eleman Id I I displaystyle operatorname Id colon I to I fonksiyonu Id x x displaystyle operatorname Id x x oldugunda Homeo I I displaystyle operatorname Homeo I I circ nun birim elemanidir cunku Id displaystyle operatorname Id birim fonksiyon sureklidir birebir ve ortendir daima artandir Ote yandan Id 1 I I displaystyle operatorname Id 1 colon I to I ters fonksiyonu da sureklidir cunku her x I displaystyle x in I icin Id 1 x Id x Id 1 Id displaystyle operatorname Id 1 x operatorname Id x Leftrightarrow operatorname Id 1 operatorname Id Sonuc olarak her x I displaystyle x in I icin f Id x f Id x f x Id f x Id f x f x displaystyle f circ operatorname Id x f operatorname Id x f x operatorname Id circ f x operatorname Id f x f x olmaktadir Terslenebilme Herhangi bir f Homeo I I displaystyle f in operatorname Homeo I I alalim Homeo I I displaystyle operatorname Homeo I I in tanimindan dolayi f displaystyle f in daima artan birebir orten ve surekli oldugunu ve f 1 displaystyle f 1 in de surekli oldugunu biliyoruz f 1 Homeo I I displaystyle f 1 in operatorname Homeo I I oldugunu gostermek gereklidir Bunun icin f 1 displaystyle f 1 in daima artan oldugunu gostermek yeterlidir Herhangi x y I displaystyle x y in I alalim ve x lt y displaystyle x lt y oldugunu varsayalim f 1 x lt f 1 y displaystyle f 1 x lt f 1 y oldugunu gosterelim f displaystyle f daima artandir ve x lt y displaystyle x lt y oldugu icin f x lt f y displaystyle f x lt f y olur f displaystyle f in birebir ve ortenlik ozelliginden dolayi f a x displaystyle f a x ve f b y displaystyle f b y olan biricik a b I displaystyle a b in I elemanlari vardir f displaystyle f daima artan ve x lt y displaystyle x lt y oldugu icin f a lt f b displaystyle f a lt f b olur Bu yuzden a lt b displaystyle a lt b ve f 1 x lt f 1 y displaystyle f 1 x lt f 1 y olur Sonuc olarak displaystyle circ islemi altinda Homeo I I displaystyle operatorname Homeo I I bir gruptur Eger h Homeo I I displaystyle h in operatorname Homeo I I ise h 0 0 displaystyle h 0 0 ve h 1 1 displaystyle h 1 1 olur Kanitini soyle aciklayabiliriz herhangi h Homeo I I displaystyle h in operatorname Homeo I I alalim yani h I I displaystyle h colon I to I surekli daima artan ve birebir orten bir homeomorfizmadir O halde f 1 displaystyle f 1 fonksiyonu da sureklidir h 0 0 1 displaystyle h 0 neq 0 1 olsun ki bu h 0 x 0 1 displaystyle h 0 x in 0 1 anlamina gelir 0 1 displaystyle 0 1 araliginin baglantili connected oldugunu biliyoruz O zaman h displaystyle h surekli oldugundan h 0 1 displaystyle h 0 1 in de baglantili oldugunu soyleyebiliriz h displaystyle h birebir ve orten oldugundan h 0 1 0 x x 1 displaystyle h 0 1 0 x cup x 1 olur Fakat 0 x x 1 displaystyle 0 x cup x 1 baglantili degildir Bu yuzden h 0 0 1 displaystyle h 0 neq 0 1 varsayimiyla bir celiski elde ederiz Yani h 0 0 1 displaystyle h 0 0 1 olur Simdi h 0 0 displaystyle h 0 0 oldugunu gosterelim h 0 1 displaystyle h 0 1 oldugunu varsayalim h displaystyle h fonksiyonu daima artan ve 0 lt 1 displaystyle 0 lt 1 oldugundan h 0 lt h 1 displaystyle h 0 lt h 1 olur bu da 1 lt h 1 displaystyle 1 lt h 1 demektir h 0 1 0 1 displaystyle h colon 0 1 to 0 1 oldugundan h 1 displaystyle h 1 degeri 1 displaystyle 1 den buyuk olamaz O halde h 0 0 displaystyle h 0 0 olur Ayni muhakeme ile h 1 1 displaystyle h 1 1 sonucu elde edilir Sonuc olarak her h Homeo I I displaystyle h in operatorname Homeo I I icin h 0 0 displaystyle h 0 0 ve h 1 1 displaystyle h 1 1 olur Yollar uzerinde denklik bagintisi X displaystyle X uzayinda f g I X displaystyle f g colon I to X yollarini dusunelim Eger f g h displaystyle f g circ h esitligini saglayan bir h Homeo I I displaystyle h in operatorname Homeo I I varsa o halde f g displaystyle f approx g denilir displaystyle approx bir denklik bagintisidir onermesinin ispatini soyle aciklayabiliriz displaystyle approx bagintisinin yansima simetri ve gecisme ozelliklerini sagladigini gosterecegiz yansima f I X displaystyle f colon I to X herhangi bir yol olsun Eger h displaystyle h fonksiyonunu Id I I displaystyle operatorname Id colon I to I seklinde tanimli birim fonksiyon alirsak f f h displaystyle f f circ h olur Dolayisiyla f f displaystyle f approx f olur simetri f g I X displaystyle f g colon I to X herhangi iki yol olsunlar f g displaystyle f approx g oldugunu varsayalim ve g f displaystyle g approx f oldugunu gosterelim f g displaystyle f approx g ise f g h displaystyle f g circ h olacak sekilde bir h Homeo I I displaystyle h in operatorname Homeo I I vardir h displaystyle h fonksiyonunun birebir ve orten oldugunu biliyoruz bu yuzden soyle yazabiliriz f g h f h 1 g displaystyle f g circ h Leftrightarrow f circ h 1 g Yani oyle bir fonksiyon bulmus olduk ki k h 1 Homeo I I displaystyle k h 1 in operatorname Homeo I I ve g f k displaystyle g f circ k oldu Sonuc olarak g f displaystyle g approx f olur gecisme f g h I X displaystyle f g h colon I to X herhangi uc yol olsunlar f g displaystyle f approx g ve g h displaystyle g approx h olduklarini varsayalim ve f h displaystyle f approx h oldugunu gosterelim Varsayimlara gore f g ff displaystyle f g circ varphi f ve g h fg displaystyle g h circ varphi g esitliklerini saglayan ff fg Homeo I I displaystyle varphi f varphi g in operatorname Homeo I I elemanlari vardir Bu nedenle f g ff f h fg ff displaystyle f g circ varphi f Leftrightarrow f h circ varphi g circ varphi f dir ff fg Homeo I I displaystyle varphi f varphi g in operatorname Homeo I I oldugundan ff fg Homeo I I displaystyle varphi f circ varphi g in operatorname Homeo I I olur Yani k ff fg Homeo I I displaystyle k varphi f circ varphi g in operatorname Homeo I I elemani f h k displaystyle f h circ k esitligini saglar Dolayisiyla f h displaystyle f approx h olur Sonuc olarak displaystyle approx bir denklik bagintisidir Homotopi f1 displaystyle varphi 1 ve f2 displaystyle varphi 2 fonksiyonlari X displaystyle X uzayinda iki yol olsun Bu yollarin bir homotopisi F I I X displaystyle F colon I times I to X a t F a t displaystyle a t mapsto F a t seklinde tanimli ve asagidaki sartlari saglayan surekli bir fonksiyondur i Her a displaystyle a sayisi icin F a t I X displaystyle F a t colon I to X p displaystyle p den q displaystyle q ya giden bir yol belirtir ii p displaystyle p den q displaystyle q ya giden f1 displaystyle varphi 1 f2 displaystyle varphi 2 yollari icin F 0 t displaystyle F 0 t f1 displaystyle varphi 1 ve F 1 t displaystyle F 1 t f2 displaystyle varphi 2 dir f1 displaystyle varphi 1 ve f2 displaystyle varphi 2 yollari bu sekilde bir F displaystyle F homotopisi ile baglanirlarsa f1 displaystyle varphi 1 ve f2 displaystyle varphi 2 homotopiktirler denilir ve f1 f2 displaystyle varphi 1 simeq varphi 2 seklinde gosterilir Onermeler Yollarin bileskesi yollarin denklik siniflari uzerinde iyi tanimlidir Onermenin kanitini soyle aciklayabiliriz f0 displaystyle varphi 0 f1 displaystyle varphi 1 f0 displaystyle varphi 0 ve f1 displaystyle varphi 1 0 1 X displaystyle 0 1 rightarrow X seklinde tanimli yollar olsun Eger f0 f0 displaystyle varphi 0 simeq varphi 0 ve f1 f1 displaystyle varphi 1 simeq varphi 1 oldugunda f0 f1 f0 f1 displaystyle varphi 0 circ varphi 1 simeq varphi 0 circ varphi 1 denkligi saglaniyorsa bu bileske islemi iyi tanimlidir f0 ve f0 displaystyle varphi 0 text ve varphi 0 arasinda F displaystyle F homotopisi ve f1 ve f1 displaystyle varphi 1 text ve varphi 1 arasinda ise G displaystyle G homotopisi tanimli olsun F G displaystyle displaystyle F circ G homotopisini asagidaki sekilde tanimladigimiz zaman yollarin bileskesinin iyi tanimli oldugunu gostermis oluruz F G s t F 2s t 0 s 12G 2s 1 t 12 s 1 displaystyle F circ G s t begin cases F 2s t amp 0 leq s leq frac 1 2 G 2s 1 t amp frac 1 2 leq s leq 1 end cases oldugunda F G s 0 F 2s 0 f0 F G s 1 G 2s 1 1 f1 displaystyle displaystyle F circ G s 0 F 2s 0 varphi 0 text F star G s 1 G 2s 1 1 varphi 1 esitliklerini elde ederiz Bu yuzden f0 f1 f0 f1 displaystyle displaystyle varphi 0 circ varphi 1 simeq varphi 0 circ varphi 1 denkligi saglanir Bu yuzden yollarin bileskesi yollarin denklik siniflari uzerinde iyi tanimlidir Bir uzayda sabit baslangic ve bitis noktalari olan yollar uzerindeki homotopi iliskisi bir denklik bagintisidir Uzaydaki bir f displaystyle varphi yolunun homotopi sinifi f displaystyle varphi ile gosterilir Ispatini yaparken Homotopi iliskisinin yansima simetri ve gecisme ozelliklerini sagladigi gostermeli yansima f1 I X displaystyle varphi 1 colon I to X p displaystyle p den q displaystyle q ya giden bir yol olsun F I I X displaystyle F colon I times I to X F a t f t displaystyle F a t f t seklinde tanimlanmis F displaystyle F fonksiyonu f1 displaystyle varphi 1 ile f1 displaystyle varphi 1 arasinda bir homotopidir cunku her a displaystyle a icin F a t I X displaystyle F a t colon I to X fonksiyonu p displaystyle p den q displaystyle q ya giden bir yoldur ve F 0 t f1 t F 1 t f1 t displaystyle F 0 t varphi 1 t F 1 t varphi 1 t dir Sonuc olarak f1 f1 displaystyle varphi 1 simeq varphi 1 elde edilir simetri f1 f2 I X displaystyle varphi 1 varphi 2 colon I to X p displaystyle p den q displaystyle q ya giden 2 yol olsun f1 f2 displaystyle varphi 1 simeq varphi 2 oldugunu kabul edelim O halde oyle bir F I I X displaystyle F colon I times I to X seklinde tanimli homotopi vardir ki her sabit a displaystyle a icin F a t I X displaystyle F a t colon I to X fonksiyonu p displaystyle p den q displaystyle q ya giden bir yol olur ve F 0 t displaystyle F 0 t f1 t displaystyle varphi 1 t F 1 t displaystyle F 1 t f2 t displaystyle varphi 2 t dir Simdi F I I X displaystyle F colon I times I to X fonksiyonunu F a t displaystyle F a t F 1 a t displaystyle F 1 a t seklinde tanimlayalim O zaman her sabit a displaystyle a icin F a t displaystyle F a t F 1 a t displaystyle F 1 a t fonksiyonu p displaystyle p den q displaystyle q ya giden bir yoldur ve F 0 t displaystyle F 0 t F 1 t displaystyle F 1 t f2 t displaystyle varphi 2 t ve F 1 t displaystyle F 1 t F 0 t displaystyle F 0 t f1 t displaystyle varphi 1 t olur Sonuc olarak g f displaystyle g simeq f elde edilir gecisme f1 f2 f3 I X displaystyle varphi 1 varphi 2 varphi 3 colon I to X seklinde tanimli 3 yol olsun f1 f2 displaystyle varphi 1 simeq varphi 2 ve f2 f3 displaystyle varphi 2 simeq varphi 3 oldugunu kabul edelim Gostermemiz gereken f1 f3 displaystyle varphi 1 simeq varphi 3 dir f1 f2 displaystyle varphi 1 simeq varphi 2 ve f2 f3 displaystyle varphi 2 simeq varphi 3 oldugundan oyle F displaystyle F ve G displaystyle G homotopileri vardir ki F I I X displaystyle F colon I times I to X F 0 t displaystyle F 0 t f1 t displaystyle varphi 1 t ve F 1 t displaystyle F 1 t f2 t displaystyle varphi 2 t G I I X displaystyle G colon I times I to X G 0 t displaystyle G 0 t f2 t displaystyle varphi 2 t ve G 1 t displaystyle G 1 t f3 t displaystyle varphi 3 t dir Simdi bir H I I X displaystyle H colon I times I to X fonksiyonunu H a t F 2a t 0 a 12 G 2a 1 t 12 a 1 displaystyle begin aligned H a t amp begin cases F 2a t amp 0 leq a leq tfrac 1 2 G 2a 1 t amp tfrac 1 2 leq a leq 1 end cases end aligned seklinde tanimlayalim Acikca goruyoruz ki H a t displaystyle H a t fonksiyonu a 1 2 displaystyle a 1 2 noktasi disinda her yerde sureklidir Ote yandan a 1 2 displaystyle a 1 2 icin lima 1 2 H a t G 0 t displaystyle lim a to 1 2 H a t G 0 t f2 t displaystyle varphi 2 t ve lima 1 2 H a t F 1 t displaystyle lim a to 1 2 H a t F 1 t f2 t displaystyle varphi 2 t olmaktadir Dolayisiyla H a t displaystyle H a t fonksiyonu a 1 2 displaystyle a 1 2 noktasinda da sureklidir Ayrica H 0 t F 0 t displaystyle H 0 t F 0 t f1 t displaystyle varphi 1 t ve H 1 t G 1 t displaystyle H 1 t G 1 t f3 t displaystyle varphi 3 t oldugunu goruyoruz Sonuc olarak f1 f3 displaystyle varphi 1 simeq varphi 3 f1 f3 displaystyle varphi 1 simeq varphi 3 elde edilir p1 X x0 displaystyle pi 1 X x 0 gruptur Kanitini gostermek icin ornek olarak x0 X displaystyle x 0 in X ve p1 X x0 displaystyle pi 1 X x 0 x0 displaystyle x 0 a dayali dongulerinin homotopi siniflarinin kumesi olsun Birim elemani ex0 0 1 X displaystyle e x 0 0 1 longrightarrow X ex0 t x0 displaystyle e x 0 t x 0 olan ex0 displaystyle e x 0 dongusunun sinifidir Herhangi bir f displaystyle f dongusu icin ex0 f f displaystyle e x 0 star f f esitligi saglanir ve homotopi su sekilde tanimlanir F s t ex0 0 t 1 s2f 2t s 1 s 1 1 s2 t 1 displaystyle F s t begin cases e x 0 amp 0 leq t leq frac 1 s 2 f frac 2t s 1 s 1 amp frac 1 s 2 leq t leq 1 end cases f displaystyle f p1 X x0 displaystyle pi 1 X x 0 te bulunan herhangi bir dongu olsun f displaystyle f in tersini f s f 1 s displaystyle overline f s f 1 s olarak tanimlayalim f displaystyle f in tersini yonunu degistirerek tanimladik Simdi ise e ve f f displaystyle e text ve f star overline f arasindaki homotopi su sekilde tanimlanir F s t f 2ts 0 t 12f 2s 1 t 12 t 1 displaystyle F s t begin cases f 2ts amp 0 leq t leq frac 1 2 f 2s 1 t amp frac 1 2 leq t leq 1 end cases f g h p1 X x0 displaystyle f g h in pi 1 X x 0 herhangi uc eleman olsun Simdi ise f g h f g h displaystyle f star g star h f star g star h oldugunu gosterelim Bu kosulu saglayan homotopi su sekilde tanimlanir F t s f 4t1 s 0 t s 14g 4t 1 s s 14 t s 24h 1 41 t2 s s 24
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans