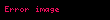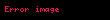Matematikte, çok değişkenli karmaşık analiz ya da çok boyutlu karmaşık analiz, karmaşık koordinat uzayı de ya da bu uzayın altkümeleri üzerinde tanımlı ve karmaşık değer alan fonksiyonların teorisi; yani, birden fazla karmaşık değişkenli fonksiyonların teorisidir.
Karmaşık analiz, değişken sayısından bağımsız olarak bir matematiksel analizin alt disiplini olarak görülse de, karmaşık analiz kavramından ekseriyetle kökleri Euler ve daha öncesine kadar giden ve karmaşık düzlemde yapılan bir değişkenli karmaşık analiz anlaşılır. Birden fazla karmaşık değişkenli fonksiyonlar teorisi, karmaşık analizden önemli noktalarda farklılık gösterir ve bazı matematik cemiyetlerince ayrı araştırma alanı olarak sınıflandırılmıştır. Mesela, bir değişkenli karmaşık analiz, hem Avrupa hem de ABD araştırma cemiyetlerince araştırma alanı olarak 30 rakamıyla, çok değişkenli karmaşık analiz ve analitik uzaylar ise 32 rakamıyla sınıflandırılmıştır.
Tek karmaşık değişkenli fonksiyonların teorisinde olduğu gibi bu alanda da ilk başta incelenen fonksiyonlar genelde holomorf veya başka bir deyişle karmaşık analitiktir. Dolayısıyla, tanımlı oldukları noktalarda yerel olarak zi karmaşık değişkenlerinde kuvvet serileri ile temsilleri vardır. Başka bir denk ifadeyle, çok boyutlu karmaşık uzayda, holomorf fonksiyonlar polinomların yerel olarak düzgün limitleridir veya boyutlu Cauchy-Riemann denklemlerinin yerel olarak kare-integrallenebilir çözümleridir.
Weierstrass çarpım teoremi ve Mittag-Leffler teoremine paralel olarak, meromorf fonksiyonların yerel bilgilerinden (yani sıfırlarından ve kutuplarından) faydalanarak bu kutuplardan oluşan kümeler hariç her yerde meromorf olan fonksiyon oluşturma problemi çok değişkenli karmaşık analizde olarak adlandırılır.
Günümüzde, çok değişkenli karmaşık analizde yapılan araştırma çalışmaları cebirsel geometri, diferansiyel geometri, matematiksel analiz ve kısmî diferansiyel denklemler gibi matematiğin değişik alanlarıyla simbiyotik bir ilişki içerisindedir. Özellikle, bu alanda yapılan çalışmalar, tıkız kompleks manifoldlar ve () alanındaki araştırmalar için önem teşkil etmektedir. Bu çalışmalar, 'de yapılan kompleks analitik geometri veya Stein manifoldu üzerine yapılan çalışmalara değişik bir bakış açısı sağlar.
Alanın adı hakkında
Alanın adı, Türkçedeki ve daha birçok gelişmiş dildeki sayma sistemlerinde birden fazla anlamına gelen bir kelimenin bulunmamasından dolayı ilk okunduğunda garip bir anlaşılmazlık yaratır. Aslında, yazılmak istenen Birden fazla karmaşık değişkenli ve karmaşık değerler alan fonksiyonlar teorisi ifadesidir; ancak, bu ifadenin uzunluğundan dolayı kısa ve tanımlayıcı bir alan adına doğal olarak yönelim olmuştur.
Birden fazla karmaşık değişkenli fonksiyonların teorisine yönelik en erken çalışmalar, çoğunlukla Almanca ve Fransızca yazılmış makalelerde, iki veya hesaplama yapmanın kolay olduğu birkaç karmaşık değişkenli durumda rastlanır. Bu sebeple, bu alanda araştırmalara öncülük yapmış bilim dilleri olan Almanca mehrerer komplexer Veränderlichen ve Fransızca plusieurs variables complexes ifadelerinin kullanımı yayılmış, İngilizce'ye de Several Complex Variables olarak geçmiştir. Bu alandaki öncü makalelerden olan Eugenio Elia Levi'nin İtalyanca makalesi de iki veya daha fazla karmaşık değişkenli fonksiyonlar tabirini kullanmış olsa da, modern İtalyancada kullanılan tabir Funzioni di più variabili complesse ifadesidir ki buradaki più sözü daha çok/fazla anlamı verir. Türkçedeki Çok değişkenli karmaşık analiz kullanımı, Rusçadaki Многомерный комплексный анализ (Çok boyutlu kompleks analiz) kullanımıyla benzerlik göstermektedir.
19. yüzyılın sonlarında ve 20. yüzyılın başlarında çok karmaşık değişkenli fonksiyonlar üzerine yapılan ve hızlanmaya başlayan araştırmalar ve tek değişkenli karmaşık analizden farklılık göstermeye başlayan sonuçlar elde edilmesiyle beraber, bu alanda daha önceden beri çalışılagelen düşük boyutlu karmaşık koordinat uzaylarındaki tanımlı fonksiyonlar yerlerini, 

Tarihi
Birden fazla karmaşık değişkenli fonksiyonların incelenmesi tarihi olarak en azından 19. yüzyılın başlarına kadar götürülse de, 20. yüzyıl başlarında bir değişkenli karmaşık analizden keskin bir şekilde ayrılan sonuçların elde edilmesiyle beraber, teori 


İlk kaynaklar
Çok değişkenli karmaşık analizin Hartogs ve Poincaré ile başlayan çağında altın kaynak vazifesi gören çalışmalar Felix Klein öncülüğünde başlatılan Almanca matematik ansiklopedisi Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen (EMW) bünyesinde bulunmaktadır. EMW'nin Analize ayrılan ikinci cildi beş ayrı kitap olarak yayınlanmıştır.
- Bd.2-2 olarak numaralandırılan ikinci cildin üçüncü kitabının William Osgood tarafından 1901'de yazılan Allgemeine Theorie analytischen Funktionen einer und mehrerer komplexer Variabler başlıklı kısmı ilk derli toplu kaynaktır. Dört alt başlık altında toplanan bu çalışmanın son kısmında ise Birkaç karmaşık değişkenli analitik fonksiyonlar ele alınmıştır.
- Bd. 2-3-1 olarak numaralandırılan ikinci cildin dördüncü kitabının Ludwig Bieberbach tarafından 1920'de yazılan Neuere Untersuchungen über Funktionen von komplexen Variablen başlıklı kısmı William Osgood'un daha önceki ansiklopedi çalışması ve bu ansiklopedi çalışmasından genişletilerek yazılan Lehrbuch der funktionentheorie kitabından sonra yapılmış ikinci ciddi kaynak çalışmadır. Onbir ayrı başlıkta yazılan bu çalışmanın son kısmında Birkaç karmaşık değişkenli analitik fonksiyonlar ve Osgood'un ansiklopedi çalışmasından sonra bu alanda meydana gelen yeni gelişmeler ele alınmıştır.
Osgood'un yazdığı ansiklopedi maddesi daha sonra yine William Osgood tarafından yazılan birinci baskısı 1907'de, ikinci baskısı ise 1912'de yapılan iki ciltlik Lehrbuch Der Funktionentheorie çalışmasına temel oluşturmuştur. Osgood, ayrıca bu alandaki ilk İngilizce eserlerden biri olan Topics in the theory of functions of several complex variables adlı derleme kitabını yazmıştır. Yine, aynı yılda, Andrew Forsyth tarafından 1913'te Kalküta Üniversitesi'nde verdiği derslerden derlenen başka bir İngilizce kitap da yayınlanmıştır; ancak, bu kitap oldukça eleştirilmiştir.
1934'te Heinrich Behnke ve Peter Thullen tarafından yazılan ve 1970'te tekrar baskısı yapılan Theorie der Funktionen mehrerer komplexer Veränderlicher başlıklı kitap uzun yıllar boyunca ana kaynak vazifesi görmüştür. 1948'te Salomon Bochner ve William Ted Martin tarafından yazılan Several Complex Variables adlı kitap ise 1950'den önce yazılmış ve uzun süre kaynak vazifesi görmüş bir başka kitaptır.
Gelişimi
Friedrich Hartogs, Pierre Cousin ve Eugenio Elia Levi'nin öncü çalışmaları ve Kiyoshi Oka'nın 1930'ların ortalarından itibaren seri halinde yayınladığı çalışmalarıyla genel bir teorinin anahatları ortaya çıkmaya başladı. Bu dönemde, bu alanda çalışan diğer matematikçiler arasında öne çıkan isimler Heinrich Behnke, Peter Thullen, Karl Stein, Wilhelm Wirtinger ve Francesco Severi'ydi. Hartogs, 

1945'ten sonra Fransa'da Henri Cartan'ın ve Almanya'da Hans Grauert ve Reinhold Remmert'in seminerlerinde yapılan önemli çalışmalar, teorinin resmini hızla değiştirdi. Özellikle analitik devamlılıkla âlâkalı olmak üzere bir dizi konu açıklığa kavuşturuldu. Özellikle, tek değişkenli teoriden farklılaşan sonuçlar açıkça ortaya konuldu: açık ve bağlantılı her 


Holomorfluk tanımı
Bir değişkenli karmaşık analizdeki her noktada karmaşık türevlenebilme üzerinden yapılan holomorfluk tanımı, çok değişkenli analizde de benzer şekilde geçerlidir. 
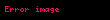

tanımı, 


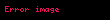

gönderimlerinin her bir koordinatta ayrı ayrı holomorf olması yeterlidir. Bazen, holomorfluk için süreklilik varsayımı da eklenir; ancak, bu varsayım Hartogs teoremi sayesinde gereksizdir.
Denk tanımlar
Karmaşık türevlenebilme
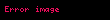



denkliğini sağlayacak karmaşık-doğrusal bir 






Cauchy-Riemann denklemleri
Bir değişkenli karmaşık analizde, 





Çok değişkenli karmaşık analizde, bir 



Wirtinger türevi gösterimi kullanırsak, o zaman 


Kuvvet serisi temsili




O zaman, bu biçimdeki vektör endisler için, 


olarak tanımlanır. O zaman, 



Bir değişkenli karmaşık analizle karşılaştırma
Aynı kalan sonuçlar

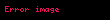
tanımlansın.
- O zaman,
,
cismi üzerinde iyi tanımlı bir cebirdir. Gerçekten de
- İki holomorf fonksiyonun toplamı ve çarpımı yine holomorftur.
tanımlı olduğu her noktada sıfırdan farklı değer alıyorsa, o zaman
de holomorftur.
En büyük mutlak değer teoremi
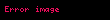
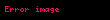







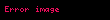
Yerel düzgün yakınsaklık




Özdeşlik teoremi
Holomorf bir fonksiyon açık bir küme üzerinde sıfır değeri alıyorsa, o zaman her yerde tamamen sıfır değeri alır; yani, bu fonksiyon sıfır fonksiyondur.
Açık gönderim teoremi
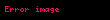

Liouville teoremi
Bir fonksiyon 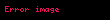
Farklılaşan sonuçlar
Sıfır ve tekilik kümeleri
Bir değişkenli karmaşık analizde holomorf fonksiyonların sıfır değeri aldıkları noktaların bu fonksiyonların tanımlı oldukları kümenin içine limiti olamaz. Yani, karmaşık düzlemdeki açık kümelerde tanımlı holomorf fonksiyonların sıfırları yalıtıktır. Ancak, bu durum yüksek boyutlarda geçerli değildir. Örneğin, 

Çok değişkenli holomorf fonksiyonların tek bir noktada tekilliği olamaz (Hartogs devam teoremi).
Yakınsaklık bölgesi
Bir değişkenli karmaşık analizde holomorf fonksiyonlar tanımlı oldukları her noktada yerel olarak kuvvet serileri olarak temsil edilebilirler. Benzer bir durum, yüksek boyutlar için de geçerlidir. Ancak, bir karmaşık değişkenli karmaşık analizde yakınsaklık bölgesi ya disk olur ya da karmaşık düzlem olur. Bu bakış açısıyla, yüksek boyutlarda yakınsaklık bölgesi sadece ya da çoklu disk (polidisk) veya kompleks koordinat uzayı değildir. Yüksek boyutlarda, kuvvet serilerinin yakınsaklık bölgesi tam Reinhardt bölgesi olmak zorundadır. Ancak, her tam Reinhardt bölgesi aynı zamanda bir kuvvet serisinin yakınsaklık bölgesi olmak zorunda değildir. Bunun için bu bölgelere geometrik özellikler getirmek zorunluluğu vardır. Daha açık bir şekilde yazmak gerekirse, tam Reinhardt ve bir kuvvet serisinin yakınsaklık bölgesidir.
İntegral temsilleri
Bir değişkenli karmaşık analizde holomorf fonksiyonların integral temsili olan Cauchy integral formülünün 

Cauchy integral formülünün yüksek boyutlardaki kolay bir genellemesi karmaşık düzlemdeki açık kümelerin kartezyen çarpımından oluşan bölgeler için çok rahatlıkla gösterilebilir. Buna paralel olarak, analitik çokyüzlüler üzerinde Bergman-Weil formülü de vardır. Ancak, bu haliyle hem kartezyen çarpımı olan bölgeler için geçerli olmasıyla hem de katlı integrallerin topolojik sınır değil de sınırların kartezyen çarpımında olmasıyla yüksek boyutlardaki kullanımı güdük kalmaktadır. Yüksek boyutlarda, bu yönde elde edilmiş Bochner-Martinelli formülü ve gibi değişik temsiller vardır.
Holomorfluk bölgeleri
Karmaşık düzlemdeki her bölge 

Riemann gönderim teoremi
Bir değişkenli karmaşık analizde, karmaşık analizin düzleme eşit olmayan ve basit bağlantılı olan her altkümesi birim diske birebir-örten ve tersi de holomorf olan fonksiyonlar vasıtasıyla denktir. Ancak, benzer bir sonuç yüksek boyutlarda her zaman geçerli değildir. Mesela, Poincaré 
Bu yönde bilinen ayırıcı başka bir özellik Fatou-Bieberbach bölgesidir. 

Notlar
- ^ Alanın İngilizce adının Several Complex Variables olarak yaygınlaşmasında büyük ihtimalle William Osgood'un rolü büyüktür.
- ^ Tr. (yaklaşık çeviri) Uygulamalarıyla beraber matematiksel bilimler ansiklopedisi
- ^ 1898 yılından 1933 yılına kadar devam ettirilen bu ansiklopedi projesinde yaklaşık 20000 sayfayı bulan matematik çalışması 6 cilt (Alm. Bände) altında kümelenmiştir. Her bir cildin içeriği ise kitaplar halinde yayınlanmıştır.
- ^ Çalışmanın birinci kısmında Bir karmaşık değişkenli analitik fonksiyonların genel teorisinin temelleri verilmiştir. İkinci kısımda Geometrik fonksiyon teorisi ele alınmış; üçüncü kısım ise Analitik fonksiyonların sonsuz seriler ve çarpımlarla temsil edilmesi yoluyla incelenmesine ayrılmıştır.
- ^ Bu kitabın ilk baskısı üç kısımdan oluşmuştur: birinci kısım, gerçel değişkenli fonksiyonlar teorisindeki teoremler ve sonuçlara, ikinci kısım analitik fonksiyonlar teorisine, üçüncü kısım ise daha önceki kısımların eliptik fonksiyonlar, seriler ve sonsuz çarpımlar, elamanter fonksiyonlar ve logaritmik potansiyel gibi uygulamalarına ayrılmıştır. 1912'deki ikinci baskıda ise bir önceki baskıdanki üçüncü kısmın son ünitesi ikiye ayrılmış ve ortaya kitabın dördüncü kısmı olarak logaritmik potansiyeller, açıkorur temsiller ve analitik fonksiyonların birbiçimlendirilmesi hakkında yeni malzemeler eklenmiştir.
Kaynakça
- ^ "AMS Mathscinet sınıflandırma sayfası-30". 3 Eylül 2024. 6 Haziran 2023 tarihinde kaynağından arşivlendi. "zbMath Open sınıflandırma sayfası-30". 3 Eylül 2024. 14 Haziran 2020 tarihinde kaynağından arşivlendi.
- ^ "AMS Mathscinet sınıflandırma sayfası-32". 3 Eylül 2024. "zbMath Open sınıflandırma sayfası-32". 3 Eylül 2024. 13 Haziran 2020 tarihinde kaynağından arşivlendi.
- ^ Hörmander, Lars (1965). "L2 estimates and existence theorems for the
operator". Acta Mathematica. Cilt 113. ss. 89-152. doi:10.1007/BF02391775.
- ^ Ohsawa, Takeo (2002). Analysis of Several Complex Variables. ISBN .
- ^ Błocki, Zbigniew (2014). "Cauchy–Riemann meet Monge–Ampère". Bulletin of Mathematical Sciences. 4 (3). ss. 433-480. doi:10.1007/s13373-014-0058-2.
- ^ Levi, Eugenio Elia (1910), "Studii sui punti singolari essenziali delle funzioni analitiche di due o più variabili complesse" [İki veya daha fazla karmaşık değişkenli fonksiyonların esaslı tekillikleri üzerine çalışmalar], , s. III (İtalyanca), XVII (1), ss. 61-87, doi:10.1007/BF02419336, JFM 41.0487.01, 18 Nisan 2021 tarihinde kaynağından arşivlendi, erişim tarihi: 26 Eylül 2024
- ^ Hartogs, Fritz (1906), "Einige Folgerungen aus der Cauchyschen Integralformel bei Funktionen mehrerer Veränderlichen.", Sitzungsberichte der Königlich Bayerischen Akademie der Wissenschaften zu München, Mathematisch-Physikalische Klasse (Almanca), cilt 36, ss. 223-242, JFM 37.0443.01
- ^ Poincare, M. Henri (1907). "Les fonctions analytiques de deux variables et la représentation conforme". Rendiconti del Circolo Matematico di Palermo (Fransızca). 23: 185-220. doi:10.1007/BF03013518. 18 Aralık 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 26 Eylül 2024.
- ^ W. F. Osgood, Allgemeine Theorie der analytischen Funktionen einer oder mehrerer komplexer Grössen. (Bir ve birkaç karmaşık değişkenli analitik fonksiyonlarının genel teorisi), Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. (Almanca)
- ^ L. Bieberbach, Neuere Untersuchungen über Funktionen von komplexen Variablen. (Karmaşık değişkenli fonksiyonların üzerine yapılan son çalışmalar), Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. (Almanca)
- ^ "Lehrbuch der funktionentheorie, von dr. W. F. Osgood." Michigan Üniversitesi Tarihi Matematik Kolleksiyonunda. https://name.umdl.umich.edu/acm2537.0001.001. Michigan Üniversitesi Kütüphanesi Dijital Kolleksiyonlar. Erişim tarihi: 3 Ekim 2024.
- ^ Edward B. Van Vleck (1914). "Osgood's Theory Of Functions-Lehrbuch der Funktionentheorie. Von DR. W. F. OSGOOD. Erster Band mit 158 Figuren. Zweite Auflage. (Bd. XX: 1, B. G. Teubner's Sammlung von Lehrbüchern auf dem Gebiete der mathematischen Wissenschaften.) B. G. Teubner, 1912. 8vo. xii + 766 pp.)" (PDF). Bulletin of the American Mathematical Society. 20 (10): 532–546.
- ^ William Fogg Osgood, Topics in the Theory of Functions of Several Complex Variables (Birkaç karmaşık değişkenli fonksiyonlar teorisinde konular). New York, American Mathematical Society, 1914 (İngilizce).
- ^ Andrew Russell Forsyth (1914). Lectures Introductory to the Theory of Functions of Two Complex Variables. Cambridge University Press.
- ^ Littlewood, John Edensor (1986). A Mathematician's Miscellany. Cambridge University Press. s. 135. ISBN .
A. R. Forsyth, iki değişkenli karmaşık değişkenli fonksiyonlar üzerine Cambridge University Press'ten çıkan bir kitap yayınlamıştır. Baştan aşağıya kötü bir kitap.
- ^ Carmichael, R. D. (1918). "Book Review: Lectures Introductory to the Theory of Functions of Two Complex Variables". Bulletin of the American Mathematical Society. 24 (9): 446-455. doi:10.1090/S0002-9904-1918-03119-4.
- ^ Heinrich Behnke; Peter Thullen (1934). Theorie der Funktionen mehrerer komplexer Veränderlicher. Ergebnisse der Mathematik und ihrer Grenzgebiete (Almanca). Berlin, Heidelberg: Springer Verlag. ISBN .
- ^ Salomon Bochner; William Ted Martin (1948). Several Complex Variables (PDF). Princeton Mathematical Series, vol. 10. Princeton University Press.
- ^ Siu, Yum-Tong (1978). "Pseudoconvexity and the problem of Levi". Bulletin of the American Mathematical Society. 84 (4). ss. 481-513. doi:10.1090/S0002-9904-1978-14483-8. MR 0477104.
- ^ Chen, So-Chin (2000). "Complex analysis in one and several variables". Taiwanese Journal of Mathematics. 4 (4). ss. 531-568. doi:10.11650/twjm/1500407292. JSTOR 43833225. MR 1799753. Zbl 0974.32001.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Matematikte cok degiskenli karmasik analiz ya da cok boyutlu karmasik analiz karmasik koordinat uzayi Cn displaystyle mathbb C n de ya da bu uzayin altkumeleri uzerinde tanimli ve karmasik deger alan fonksiyonlarin teorisi yani birden fazla karmasik degiskenli fonksiyonlarin teorisidir Karmasik analiz degisken sayisindan bagimsiz olarak bir matematiksel analizin alt disiplini olarak gorulse de karmasik analiz kavramindan ekseriyetle kokleri Euler ve daha oncesine kadar giden ve karmasik duzlemde yapilan bir degiskenli karmasik analiz anlasilir Birden fazla karmasik degiskenli fonksiyonlar teorisi karmasik analizden onemli noktalarda farklilik gosterir ve bazi matematik cemiyetlerince ayri arastirma alani olarak siniflandirilmistir Mesela bir degiskenli karmasik analiz hem Avrupa hem de ABD arastirma cemiyetlerince arastirma alani olarak 30 rakamiyla cok degiskenli karmasik analiz ve analitik uzaylar ise 32 rakamiyla siniflandirilmistir Tek karmasik degiskenli fonksiyonlarin teorisinde oldugu gibi bu alanda da ilk basta incelenen fonksiyonlar genelde holomorf veya baska bir deyisle karmasik analitiktir Dolayisiyla tanimli olduklari noktalarda yerel olarak zi karmasik degiskenlerinde kuvvet serileri ile temsilleri vardir Baska bir denk ifadeyle cok boyutlu karmasik uzayda holomorf fonksiyonlar polinomlarin yerel olarak duzgun limitleridir veya n displaystyle n boyutlu Cauchy Riemann denklemlerinin yerel olarak kare integrallenebilir cozumleridir Weierstrass carpim teoremi ve Mittag Leffler teoremine paralel olarak meromorf fonksiyonlarin yerel bilgilerinden yani sifirlarindan ve kutuplarindan faydalanarak bu kutuplardan olusan kumeler haric her yerde meromorf olan fonksiyon olusturma problemi cok degiskenli karmasik analizde olarak adlandirilir Gunumuzde cok degiskenli karmasik analizde yapilan arastirma calismalari cebirsel geometri diferansiyel geometri matematiksel analiz ve kismi diferansiyel denklemler gibi matematigin degisik alanlariyla simbiyotik bir iliski icerisindedir Ozellikle bu alanda yapilan calismalar tikiz kompleks manifoldlar ve CPn displaystyle mathbb CP n alanindaki arastirmalar icin onem teskil etmektedir Bu calismalar Cn displaystyle mathbb C n de yapilan kompleks analitik geometri veya Stein manifoldu uzerine yapilan calismalara degisik bir bakis acisi saglar Alanin adi hakkindaAlanin adi Turkcedeki ve daha bircok gelismis dildeki sayma sistemlerinde birden fazla anlamina gelen bir kelimenin bulunmamasindan dolayi ilk okundugunda garip bir anlasilmazlik yaratir Aslinda yazilmak istenen Birden fazla karmasik degiskenli ve karmasik degerler alan fonksiyonlar teorisi ifadesidir ancak bu ifadenin uzunlugundan dolayi kisa ve tanimlayici bir alan adina dogal olarak yonelim olmustur Birden fazla karmasik degiskenli fonksiyonlarin teorisine yonelik en erken calismalar cogunlukla Almanca ve Fransizca yazilmis makalelerde iki veya hesaplama yapmanin kolay oldugu birkac karmasik degiskenli durumda rastlanir Bu sebeple bu alanda arastirmalara onculuk yapmis bilim dilleri olan Almanca mehrerer komplexer Veranderlichen ve Fransizca plusieurs variables complexes ifadelerinin kullanimi yayilmis Ingilizce ye de Several Complex Variables olarak gecmistir Bu alandaki oncu makalelerden olan Eugenio Elia Levi nin Italyanca makalesi de iki veya daha fazla karmasik degiskenli fonksiyonlar tabirini kullanmis olsa da modern Italyancada kullanilan tabir Funzioni di piu variabili complesse ifadesidir ki buradaki piu sozu daha cok fazla anlami verir Turkcedeki Cok degiskenli karmasik analiz kullanimi Ruscadaki Mnogomernyj kompleksnyj analiz Cok boyutlu kompleks analiz kullanimiyla benzerlik gostermektedir 19 yuzyilin sonlarinda ve 20 yuzyilin baslarinda cok karmasik degiskenli fonksiyonlar uzerine yapilan ve hizlanmaya baslayan arastirmalar ve tek degiskenli karmasik analizden farklilik gostermeye baslayan sonuclar elde edilmesiyle beraber bu alanda daha onceden beri calisilagelen dusuk boyutlu karmasik koordinat uzaylarindaki tanimli fonksiyonlar yerlerini n displaystyle n birden fazla herhangi bir tam sayi olacak sekilde n displaystyle n boyutlu karmasik koordinat uzayinin acik kumelerinde tanimli fonksiyonlara birakmaya baslamistir Aslinda demek istenen ne birkac ne de cok sozudur Sadece birden fazla karmasik degiskenin goz onune alindigi ama bu sayinin genel tutulup asikar edilmedigi ima edilmektedir TarihiBirden fazla karmasik degiskenli fonksiyonlarin incelenmesi tarihi olarak en azindan 19 yuzyilin baslarina kadar goturulse de 20 yuzyil baslarinda bir degiskenli karmasik analizden keskin bir sekilde ayrilan sonuclarin elde edilmesiyle beraber teori n 2 displaystyle n geq 2 icin yeni bir disiplin olarak dogmustur Hartogs un 1906 da C2 displaystyle mathbb C 2 deki bazi bolgelerin holomorfluk bolgesi olamayacagini gostermesi ve Poincare nin karmasik duzlemdeki iki birim diskin kartezyen carpimiyla C2 displaystyle mathbb C 2 deki birim yuvarin birbirine Riemann donusum teoremindeki gibi denk olmayacagini gostermesi cok degiskenli karmasik analizin dogusuna sebep olan oncu iki calismadir Ilk kaynaklar Cok degiskenli karmasik analizin Hartogs ve Poincare ile baslayan caginda altin kaynak vazifesi goren calismalar Felix Klein onculugunde baslatilan Almanca matematik ansiklopedisi Encyklopadie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen EMW bunyesinde bulunmaktadir EMW nin Analize ayrilan ikinci cildi bes ayri kitap olarak yayinlanmistir Bd 2 2 olarak numaralandirilan ikinci cildin ucuncu kitabinin William Osgood tarafindan 1901 de yazilan Allgemeine Theorie analytischen Funktionen einer und mehrerer komplexer Variabler baslikli kismi ilk derli toplu kaynaktir Dort alt baslik altinda toplanan bu calismanin son kisminda ise Birkac karmasik degiskenli analitik fonksiyonlar ele alinmistir Bd 2 3 1 olarak numaralandirilan ikinci cildin dorduncu kitabinin Ludwig Bieberbach tarafindan 1920 de yazilan Neuere Untersuchungen uber Funktionen von komplexen Variablen baslikli kismi William Osgood un daha onceki ansiklopedi calismasi ve bu ansiklopedi calismasindan genisletilerek yazilan Lehrbuch der funktionentheorie kitabindan sonra yapilmis ikinci ciddi kaynak calismadir Onbir ayri baslikta yazilan bu calismanin son kisminda Birkac karmasik degiskenli analitik fonksiyonlar ve Osgood un ansiklopedi calismasindan sonra bu alanda meydana gelen yeni gelismeler ele alinmistir Osgood un yazdigi ansiklopedi maddesi daha sonra yine William Osgood tarafindan yazilan birinci baskisi 1907 de ikinci baskisi ise 1912 de yapilan iki ciltlik Lehrbuch Der Funktionentheorie calismasina temel olusturmustur Osgood ayrica bu alandaki ilk Ingilizce eserlerden biri olan Topics in the theory of functions of several complex variables adli derleme kitabini yazmistir Yine ayni yilda Andrew Forsyth tarafindan 1913 te Kalkuta Universitesi nde verdigi derslerden derlenen baska bir Ingilizce kitap da yayinlanmistir ancak bu kitap oldukca elestirilmistir 1934 te Heinrich Behnke ve Peter Thullen tarafindan yazilan ve 1970 te tekrar baskisi yapilan Theorie der Funktionen mehrerer komplexer Veranderlicher baslikli kitap uzun yillar boyunca ana kaynak vazifesi gormustur 1948 te Salomon Bochner ve William Ted Martin tarafindan yazilan Several Complex Variables adli kitap ise 1950 den once yazilmis ve uzun sure kaynak vazifesi gormus bir baska kitaptir Gelisimi Friedrich Hartogs Pierre Cousin ve Eugenio Elia Levi nin oncu calismalari ve Kiyoshi Oka nin 1930 larin ortalarindan itibaren seri halinde yayinladigi calismalariyla genel bir teorinin anahatlari ortaya cikmaya basladi Bu donemde bu alanda calisan diger matematikciler arasinda one cikan isimler Heinrich Behnke Peter Thullen Karl Stein Wilhelm Wirtinger ve Francesco Severi ydi Hartogs n gt 1 displaystyle n gt 1 iken her analitik fonksiyon f W Cn C displaystyle f Omega subset mathbb C n to mathbb C icin korunmali yalitik her tekilligin aslinda kaldirilabilir tekillik olmasi gerektigi gibi bazi temel sonuclari kanitladi 1945 ten sonra Fransa da Henri Cartan in ve Almanya da Hans Grauert ve Reinhold Remmert in seminerlerinde yapilan onemli calismalar teorinin resmini hizla degistirdi Ozellikle analitik devamlilikla alakali olmak uzere bir dizi konu acikliga kavusturuldu Ozellikle tek degiskenli teoriden farklilasan sonuclar acikca ortaya konuldu acik ve baglantili her D C displaystyle D subset mathbb C kumesi icin bu kumenin siniri uzerinde analitik olarak hicbir yerde devam etmeyecek bir fonksiyon bulabiliriz ama durum n gt 1 displaystyle n gt 1 ikne boyle degildir Aslinda bu turden D displaystyle D ler karmasik koordinat uzayi Cn displaystyle mathbb C n ve ozelinde sozde disbukeylik adi verilen bir sarti saglamaktadir Holomorfluk tanimiBir degiskenli karmasik analizdeki her noktada karmasik turevlenebilme uzerinden yapilan holomorfluk tanimi cok degiskenli analizde de benzer sekilde gecerlidir W displaystyle Omega karmasik duzlemde acik bir kume olmak uzere f W C displaystyle f Omega mapsto mathbb C fonksiyonunun z0 W displaystyle z 0 in Omega noktasinda holomorf olmasi icin verilen f z0 limz z0f z f z0 z z0 displaystyle f z 0 lim z rightarrow z 0 f z f z 0 over z z 0 tanimi n 2 displaystyle n geq 2 iken her bir karmasik degisken icin digerleri sabit tutularak ayri ayri istenir Diger deyisle W displaystyle Omega bu sefer n displaystyle n boyutlu karmasik koordinat uzayi Cn displaystyle mathbb C n de acik bir kume olmak uzere bir g W C displaystyle g Omega mapsto mathbb C fonksiyonunun holomorflugu icin w f z1 zi 1 w zi 1 zn displaystyle omega mapsto f z 1 dots z i 1 omega z i 1 dots z n gonderimlerinin her bir koordinatta ayri ayri holomorf olmasi yeterlidir Bazen holomorfluk icin sureklilik varsayimi da eklenir ancak bu varsayim Hartogs teoremi sayesinde gereksizdir Denk tanimlar Karmasik turevlenebilme W Cn displaystyle Omega subset mathbb C n bolgesinde tanimli ve C displaystyle mathbb C de deger alan bir f displaystyle f fonksiyonunun bir z W displaystyle z in Omega noktasinda holomorflugu icin bu noktada karmasik turevlenebilmesi yeterlidir Diger deyisle f z h f z L h o h displaystyle f z h f z L h o lVert h rVert denkligini saglayacak karmasik dogrusal bir L Cn C displaystyle L mathbb C n to mathbb C gonderimi varsa o zaman f displaystyle f ye z displaystyle z noktasinda holomorftur denilir Eger f displaystyle f fonksiyonu W displaystyle Omega tanim kumesinin tum noktalarinda holomorf ise o zaman f displaystyle f ye W displaystyle Omega uzerinde holomorftur denir Cauchy Riemann denklemleri Bir degiskenli karmasik analizde f W C C displaystyle f Omega subset mathbb C to mathbb C fonksiyonunun bir p W displaystyle p in Omega noktasinda holomorf olmasi icin bu fonksiyonun gercel kismi u displaystyle u ve sanal kismi v displaystyle v nin Cauchy Riemann denklemlerini p displaystyle p noktasi saglamasi gerekli ve yeterlidir u x p v y p ve u y p v x p displaystyle frac partial u partial x p frac partial v partial y p quad text ve quad frac partial u partial y p frac partial v partial x p Cok degiskenli karmasik analizde bir f W Cn C displaystyle f Omega subset mathbb C n to mathbb C fonksiyonunun holomorf olmasi ancak ve ancak her koordinata karsilik gelen degiskende holomorf olmasiyla mumkundur Bu da bir karmasik degiskenli analizdeki sonuclardan yola cikarak fonksiyonun her koordinat degiskenindeki gercel kismi u displaystyle u ve sanal kismi v displaystyle v nin Cauchy Riemann denklemlerini saglamasiyla mumkundur i 1 n u xi v yi ve u yi v xi displaystyle forall i in 1 dots n quad frac partial u partial x i frac partial v partial y i quad text ve quad frac partial u partial y i frac partial v partial x i Wirtinger turevi gosterimi kullanirsak o zaman i 1 n f zi 0 displaystyle forall i in 1 dots n quad frac partial f partial overline z i 0 yazilabilir Fonksiyon 0 0 displaystyle 0 0 dereceli bir hali oldugu icin Cauchy Riemann denklemleri derli toplu bir sekilde f 0 displaystyle bar partial f 0 olarak da yazilabilir Kuvvet serisi temsili N0n a1 a2 an ai N i 1 n displaystyle mathbb N 0 n alpha 1 alpha 2 ldots alpha n alpha i in mathbb N quad forall i 1 ldots n kumesi n textstyle n boyutlu dogal sayilar kumesi olsun a b N0n displaystyle alpha beta in mathbb N 0 n ve X x1 x2 xn Rn displaystyle X x 1 x 2 ldots x n in mathbb R n icin aritmetik siralama mutlak deger faktoriyel ve kuvvet alma islemleri asagidaki gibi tanimlansin a b a1 b1 a2 b2 an bn displaystyle alpha pm beta alpha 1 pm beta 1 alpha 2 pm beta 2 ldots alpha n pm beta n a b ai bi i 1 n displaystyle alpha leq beta quad Leftrightarrow quad alpha i leq beta i quad forall i in 1 ldots n a a1 a2 an displaystyle alpha alpha 1 alpha 2 cdots alpha n a a1 a2 an displaystyle alpha alpha 1 cdot alpha 2 cdots alpha n Xa x1a1 xnan displaystyle X alpha x 1 alpha 1 cdots x n alpha n O zaman bu bicimdeki vektor endisler icin a N0naaXa displaystyle sum alpha in mathbb N 0 n a alpha X alpha bir kuvvet serisi olur ve yakinsakligi mutlak yakinsaklik uzerinden tanimlanir Diger taraftan z displaystyle z merkezli ve r r1 rn R n displaystyle r r 1 cdots r n in mathbb R n yaricapli disk carpimi polidisk P a r w w1 w2 wn Cn ak wk lt rk k 1 n displaystyle P a r w w 1 w 2 dots w n in mathbf C n mid vert a k w k vert lt r k forall k 1 dots n olarak tanimlanir O zaman f P a r C displaystyle f P a r mapsto mathbb C fonksiyonu holomorf ise f z a N0naa z a a displaystyle f z sum alpha in mathbb N 0 n a alpha z a alpha gosterimi vardir Ayrica f a a a f z1a1 znan displaystyle f alpha a frac partial alpha f partial z 1 alpha 1 cdots partial z n alpha n olmak uzere aa f a a a displaystyle a alpha frac f alpha a alpha olur Bir degiskenli karmasik analizle karsilastirmaAyni kalan sonuclar W displaystyle Omega kumesi Cn displaystyle mathbb C n de acik olmak uzere O W f W C f holomorftur displaystyle mathcal O Omega f Omega mapsto mathbb C f text holomorftur tanimlansin O zaman O W displaystyle mathcal O Omega C displaystyle mathbb C cismi uzerinde iyi tanimli bir cebirdir Gercekten de Iki holomorf fonksiyonun toplami ve carpimi yine holomorftur f displaystyle f tanimli oldugu her noktada sifirdan farkli deger aliyorsa o zaman 1f displaystyle frac 1 f de holomorftur En buyuk mutlak deger teoremi W Cn displaystyle Omega subset mathbb C n bir bolge baglantili ve acik olsun f W C displaystyle f Omega mapsto mathbb C fonksiyonu icin f z displaystyle f z nin en buyuk degeri W displaystyle Omega icindeki bir noktada elde ediliyorsa o zaman f displaystyle f sabittir Bu yuzden W displaystyle Omega sinirli bir bolgeyse f W C displaystyle f overline Omega mapsto mathbb C fonksiyonu surekliyse ve sabit degilse f z displaystyle f z en buyuk degerini W displaystyle Omega nin topolojik siniri olan bW displaystyle b Omega uzerinde alir Yerel duzgun yakinsaklik fn W C displaystyle f n Omega mapsto mathbb C yerel duzgun yakinsak bir holomorf fonksiyon dizisi ise yani her z W displaystyle z in Omega icin bir Uz displaystyle U z komsulugu varsa ve fn Uz displaystyle f n U z dizisi duzgun yakinsaksa o zaman limit fonksiyonu da holomorftur Ozdeslik teoremi Holomorf bir fonksiyon acik bir kume uzerinde sifir degeri aliyorsa o zaman her yerde tamamen sifir degeri alir yani bu fonksiyon sifir fonksiyondur Acik gonderim teoremi f W C displaystyle f Omega mapsto mathbb C fonksiyonu sabit degilse f W displaystyle f Omega karmasik duzlemde aciktir Liouville teoremi Bir fonksiyon Cn displaystyle mathbb C n de holomorf ve sinirliysa o zaman sabittir Farklilasan sonuclar Sifir ve tekilik kumeleri Bir degiskenli karmasik analizde holomorf fonksiyonlarin sifir degeri aldiklari noktalarin bu fonksiyonlarin tanimli olduklari kumenin icine limiti olamaz Yani karmasik duzlemdeki acik kumelerde tanimli holomorf fonksiyonlarin sifirlari yalitiktir Ancak bu durum yuksek boyutlarda gecerli degildir Ornegin f z1 z2 z1z2 displaystyle f z 1 z 2 z 1 z 2 olarak tanimli holomorf fonksiyonun sifir kumesi C 0 0 C displaystyle mathbb C times 0 cup 0 times mathbb C kumesidir Cok degiskenli holomorf fonksiyonlarin tek bir noktada tekilligi olamaz Hartogs devam teoremi Yakinsaklik bolgesi Bir degiskenli karmasik analizde holomorf fonksiyonlar tanimli olduklari her noktada yerel olarak kuvvet serileri olarak temsil edilebilirler Benzer bir durum yuksek boyutlar icin de gecerlidir Ancak bir karmasik degiskenli karmasik analizde yakinsaklik bolgesi ya disk olur ya da karmasik duzlem olur Bu bakis acisiyla yuksek boyutlarda yakinsaklik bolgesi sadece ya da coklu disk polidisk veya kompleks koordinat uzayi degildir Yuksek boyutlarda kuvvet serilerinin yakinsaklik bolgesi tam Reinhardt bolgesi olmak zorundadir Ancak her tam Reinhardt bolgesi ayni zamanda bir kuvvet serisinin yakinsaklik bolgesi olmak zorunda degildir Bunun icin bu bolgelere geometrik ozellikler getirmek zorunlulugu vardir Daha acik bir sekilde yazmak gerekirse tam Reinhardt ve bir kuvvet serisinin yakinsaklik bolgesidir Integral temsilleri Bir degiskenli karmasik analizde holomorf fonksiyonlarin integral temsili olan Cauchy integral formulunun n 2 displaystyle n geq 2 icin genellestirmeleri mevcuttur Ancak yuksek boyutlarda n 1 displaystyle n 1 iken oldugu gibi gecerli olan tek bir gosterim mevcut degildir Cauchy integral formulunun yuksek boyutlardaki kolay bir genellemesi karmasik duzlemdeki acik kumelerin kartezyen carpimindan olusan bolgeler icin cok rahatlikla gosterilebilir Buna paralel olarak analitik cokyuzluler uzerinde Bergman Weil formulu de vardir Ancak bu haliyle hem kartezyen carpimi olan bolgeler icin gecerli olmasiyla hem de katli integrallerin topolojik sinir degil de sinirlarin kartezyen carpiminda olmasiyla yuksek boyutlardaki kullanimi guduk kalmaktadir Yuksek boyutlarda bu yonde elde edilmis Bochner Martinelli formulu ve gibi degisik temsiller vardir Holomorfluk bolgeleri Karmasik duzlemdeki her bolge D C displaystyle D subset mathbb C bazi fonksiyonlarin holomorfluk bolgesidir baska bir deyisle her bolgenin uzerinde tanimli ve holomorf olarak devam ettirelemeyen bir holomorf fonksiyon bulunabilir Ancak cok degiskenli karmasik analiz icin durum boyle degildir Diger deyisle Cn n 2 displaystyle mathbb C n n geq 2 deki bazi bolgeler herhangi bir fonksiyonun holomorfluk bolgesi degildir Hartogs onsavi ve Hartogs devam teoremi ile kanitlanan bu ozellik sayesinde holomorfluk bolgesinin karakterizasyonu bu disiplinde onemli bir yer tutar Riemann gonderim teoremi Bir degiskenli karmasik analizde karmasik analizin duzleme esit olmayan ve basit baglantili olan her altkumesi birim diske birebir orten ve tersi de holomorf olan fonksiyonlar vasitasiyla denktir Ancak benzer bir sonuc yuksek boyutlarda her zaman gecerli degildir Mesela Poincare C2 displaystyle mathbb C 2 deki birim polidisk ile birim arasinda boyle bir dunusum olamayacagini gostermistir Bu yonde bilinen ayirici baska bir ozellik Fatou Bieberbach bolgesidir Cn displaystyle mathbb C n nin ozalt kumesi olup da kompleks koordinat uzayi Cn displaystyle mathbb C n ye birebir orten ve tersi de holomorf olan fonksiyonlar vasitasiyla denk olan bu bolgeler karmasik duzlemde yani n 1 displaystyle n 1 iken bulunmaz Notlar Alanin Ingilizce adinin Several Complex Variables olarak yayginlasmasinda buyuk ihtimalle William Osgood un rolu buyuktur Tr yaklasik ceviri Uygulamalariyla beraber matematiksel bilimler ansiklopedisi 1898 yilindan 1933 yilina kadar devam ettirilen bu ansiklopedi projesinde yaklasik 20000 sayfayi bulan matematik calismasi 6 cilt Alm Bande altinda kumelenmistir Her bir cildin icerigi ise kitaplar halinde yayinlanmistir Calismanin birinci kisminda Bir karmasik degiskenli analitik fonksiyonlarin genel teorisinin temelleri verilmistir Ikinci kisimda Geometrik fonksiyon teorisi ele alinmis ucuncu kisim ise Analitik fonksiyonlarin sonsuz seriler ve carpimlarla temsil edilmesi yoluyla incelenmesine ayrilmistir Bu kitabin ilk baskisi uc kisimdan olusmustur birinci kisim gercel degiskenli fonksiyonlar teorisindeki teoremler ve sonuclara ikinci kisim analitik fonksiyonlar teorisine ucuncu kisim ise daha onceki kisimlarin eliptik fonksiyonlar seriler ve sonsuz carpimlar elamanter fonksiyonlar ve logaritmik potansiyel gibi uygulamalarina ayrilmistir 1912 deki ikinci baskida ise bir onceki baskidanki ucuncu kismin son unitesi ikiye ayrilmis ve ortaya kitabin dorduncu kismi olarak logaritmik potansiyeller acikorur temsiller ve analitik fonksiyonlarin birbicimlendirilmesi hakkinda yeni malzemeler eklenmistir Kaynakca AMS Mathscinet siniflandirma sayfasi 30 3 Eylul 2024 6 Haziran 2023 tarihinde kaynagindan arsivlendi zbMath Open siniflandirma sayfasi 30 3 Eylul 2024 14 Haziran 2020 tarihinde kaynagindan arsivlendi AMS Mathscinet siniflandirma sayfasi 32 3 Eylul 2024 zbMath Open siniflandirma sayfasi 32 3 Eylul 2024 13 Haziran 2020 tarihinde kaynagindan arsivlendi Hormander Lars 1965 L2 estimates and existence theorems for the displaystyle bar partial operator Acta Mathematica Cilt 113 ss 89 152 doi 10 1007 BF02391775 Ohsawa Takeo 2002 Analysis of Several Complex Variables ISBN 978 1 4704 4636 9 Blocki Zbigniew 2014 Cauchy Riemann meet Monge Ampere Bulletin of Mathematical Sciences 4 3 ss 433 480 doi 10 1007 s13373 014 0058 2 Levi Eugenio Elia 1910 Studii sui punti singolari essenziali delle funzioni analitiche di due o piu variabili complesse Iki veya daha fazla karmasik degiskenli fonksiyonlarin esasli tekillikleri uzerine calismalar s III Italyanca XVII 1 ss 61 87 doi 10 1007 BF02419336 JFM 41 0487 01 18 Nisan 2021 tarihinde kaynagindan arsivlendi erisim tarihi 26 Eylul 2024 Hartogs Fritz 1906 Einige Folgerungen aus der Cauchyschen Integralformel bei Funktionen mehrerer Veranderlichen Sitzungsberichte der Koniglich Bayerischen Akademie der Wissenschaften zu Munchen Mathematisch Physikalische Klasse Almanca cilt 36 ss 223 242 JFM 37 0443 01 Poincare M Henri 1907 Les fonctions analytiques de deux variables et la representation conforme Rendiconti del Circolo Matematico di Palermo Fransizca 23 185 220 doi 10 1007 BF03013518 18 Aralik 2022 tarihinde kaynagindan arsivlendi Erisim tarihi 26 Eylul 2024 W F Osgood Allgemeine Theorie der analytischen Funktionen einer oder mehrerer komplexer Grossen Bir ve birkac karmasik degiskenli analitik fonksiyonlarinin genel teorisi Encyklopadie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen Almanca L Bieberbach Neuere Untersuchungen uber Funktionen von komplexen Variablen Karmasik degiskenli fonksiyonlarin uzerine yapilan son calismalar Encyklopadie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen Almanca Lehrbuch der funktionentheorie von dr W F Osgood Michigan Universitesi Tarihi Matematik Kolleksiyonunda https name umdl umich edu acm2537 0001 001 Michigan Universitesi Kutuphanesi Dijital Kolleksiyonlar Erisim tarihi 3 Ekim 2024 Edward B Van Vleck 1914 Osgood s Theory Of Functions Lehrbuch der Funktionentheorie Von DR W F OSGOOD Erster Band mit 158 Figuren Zweite Auflage Bd XX 1 B G Teubner s Sammlung von Lehrbuchern auf dem Gebiete der mathematischen Wissenschaften B G Teubner 1912 8vo xii 766 pp PDF Bulletin of the American Mathematical Society 20 10 532 546 William Fogg Osgood Topics in the Theory of Functions of Several Complex Variables Birkac karmasik degiskenli fonksiyonlar teorisinde konular New York American Mathematical Society 1914 Ingilizce Andrew Russell Forsyth 1914 Lectures Introductory to the Theory of Functions of Two Complex Variables Cambridge University Press Littlewood John Edensor 1986 A Mathematician s Miscellany Cambridge University Press s 135 ISBN 9780521337021 A R Forsyth iki degiskenli karmasik degiskenli fonksiyonlar uzerine Cambridge University Press ten cikan bir kitap yayinlamistir Bastan asagiya kotu bir kitap Carmichael R D 1918 Book Review Lectures Introductory to the Theory of Functions of Two Complex Variables Bulletin of the American Mathematical Society 24 9 446 455 doi 10 1090 S0002 9904 1918 03119 4 Heinrich Behnke Peter Thullen 1934 Theorie der Funktionen mehrerer komplexer Veranderlicher Ergebnisse der Mathematik und ihrer Grenzgebiete Almanca Berlin Heidelberg Springer Verlag ISBN 978 3 642 98844 8 Salomon Bochner William Ted Martin 1948 Several Complex Variables PDF Princeton Mathematical Series vol 10 Princeton University Press Siu Yum Tong 1978 Pseudoconvexity and the problem of Levi Bulletin of the American Mathematical Society 84 4 ss 481 513 doi 10 1090 S0002 9904 1978 14483 8 MR 0477104 Chen So Chin 2000 Complex analysis in one and several variables Taiwanese Journal of Mathematics 4 4 ss 531 568 doi 10 11650 twjm 1500407292 JSTOR 43833225 MR 1799753 Zbl 0974 32001
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans