Pi sayısı

Pi sayısı (π), bir dairenin çevresinin çapına bölümü ile elde edilen irrasyonel matematik sabitidir. İsmini, Yunanca περίμετρον (çevre) sözcüğünün ilk harfi olan π harfinden alır. Pi sayısı, Arşimet sabiti ve Ludolph sayısı olarak da bilinir. Aynı zamanda ismini yunancada pie anlamına gelen πίτα' dan alır.

Pi sembolü

π (; "pi" olarak yazılır) sayısı bir matematik sabitidir; çemberin çevresinin çapına oranıdır ve yaklaşık olarak 3,14159'a eşittir. π sayısı matematik ve fizikteki birçok formülde görünür. Bu bir irrasyonel sayıdır yani tam olarak iki tam sayının oranı olarak ifade edilemez ancak ${\displaystyle {\tfrac {22}{7}}}$ gibi kesirler genellikle yaklaşık değer olarak kullanılır. Sonuç olarak, hiçbir zaman bitmez ve girmez. Bu bir aşkın sayıdır yani yalnızca toplamları, çarpımları, üsleri ve tam sayıları içeren bir çözümü olamaz. π'nin aşkınlığı, eski daireyi kareyle çevreleme meydan okumasını bir pergel ve çizgilik (Pergel ve çizgilik çizimleri) ile çözmenin imkansız olduğunu ima eder. π'nin ondalık basamakları rastgele dağıtılmış gibi görünüyor, ancak bu varsayımın kanıtı bulunamadı.

Binlerce yıldır matematikçiler, bazen değerini yüksek bir doğruluk derecesine göre hesaplayarak π hakkındaki anlayışlarını genişletmeye çalıştılar. ve Babilliler de dahil olmak üzere eski uygarlıklar, pratik hesaplamalar için oldukça doğru π yaklaşımları gerektiriyordu. MÖ 250  civarında, Yunan matematikçi Arşimet keyfi doğrulukla π'ye yaklaşmak için bir algoritma yarattı. MS 5. yüzyılda, her ikisi de geometrik teknikler kullanarak, π'yi yedi basamağa yaklaştırırken, beş basamaklı bir tahmin yaptı. π için sonsuz seri'ye dayanan ilk hesaplama formülü, bin yıl sonra keşfedildi. Bir dairenin çevresinin çapına oranını temsil etmek için Yunanca π harfinin bilinen en eski kullanımı 1706'da Galli matematikçi tarafından yapılmıştır.

Kalkülüs'ün icadı kısa sürede π'nin yüzlerce basamağının hesaplanmasına yol açtı, bu tüm pratik bilimsel hesaplamalar için yeterliydi. Bununla birlikte, 20. ve 21. yüzyıllarda matematikçiler ve bilgisayar bilimcileri, artan hesaplama gücüyle birleştiğinde π'nin ondalık gösterimini trilyonlarca basamağa genişleten yeni yaklaşımlar izlediler. Bu hesaplamalar, sayısal serileri hesaplamak için verimli algoritmaların geliştirilmesinin yanı sıra insanın rekor kırma arayışıyla motive edilir. Kapsamlı hesaplamalar, süperbilgisayarları test etmek için de kullanılmıştır.

Tanımı daire ile ilgili olduğu için π, trigonometri ve geometri'deki birçok formülde, özellikle daireler, elipsler ve kürelerle ilgili olanlarda bulunur. Ayrıca kozmoloji, fraktals, termodinamik, mekanik ve elektromanyetizma gibi bilimdeki diğer konulardaki formüllerde de bulunur. Modern matematiksel analizde, bunun yerine genellikle geometriye herhangi bir referans olmaksızın tanımlanır; bu nedenle, sayı teorisi ve istatistik gibi geometri ile çok az ilgisi olan alanlarda da görünür. π'nin her yerde bulunması, onu bilimin içinde ve dışında en çok bilinen matematiksel sabitlerden biri yapar. π'ye adanmış birkaç kitap yayınlandı ve π'nin rakamlarının rekor kıran hesaplamaları genellikle haber manşetleriyle sonuçlanıyor.

Temel bilgiler

İsim

Matematikçiler tarafından bir çemberin çevresinin çapına oranını temsil etmek için kullanılan sembol küçük harf Yunanca harf π'dir ve bazen pi olarak yazılır. İngilizcede π, ( PY). Matematiksel kullanımda, küçük harf π, bir anlamına gelen büyük harfli ve büyütülmüş karşılığı, (Σ gibi toplam anlamına gelen) Π'dan ayırt edilir.

π sembolünün seçimi π sembolünün benimsenmesi bölümünde tartışılmaktadır.

Tanım

Bir dairenin çevresi, çapının üç katından biraz fazladır. Tam orana π denir.

π genellikle bir daire'nin C ile d) arasındaki oran olarak tanımlanır :

$${\displaystyle \pi ={\frac {C}{d}}}$$

Dairenin boyutuna bakılmaksızın C/d oranı sabittir. Örneğin, bir dairenin çapı başka bir dairenin iki katıysa, C/d oranını koruyarak çevresi de iki katına sahip olacaktır. Bu π tanımı dolaylı olarak düz (Öklid) geometrisi kullanır; daire kavramı herhangi bir eğri (Öklid dışı) geometri'ye genişletilebilse de, bu yeni daireler artık π = C/d karşılamayacaktır.

Burada, bir dairenin çevresi, dairenin çevre etrafındaki 'dur; limit(kalkülüste bir kavram) kullanılarak geometriden bağımsız olarak resmi olarak tanımlanabilen bir niceliktir. Örneğin, birim çemberin üst yarısının yay uzunluğu Kartezyen koordinatlar'da x² + y² = 1 denklemiyle doğrudan hesaplanabilir, integral olarak:

$${\displaystyle \pi =\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.}$$

Bunun gibi bir integral, onu 1841'de doğrudan bir integral olarak tanımlayan Karl Weierstrass tarafından π'nin tanımı olarak benimsendi.

Artık integral ilk analitik tanımda yaygın olarak kullanılmaz, çünkü, Remmert 2012'nin açıkladığı gibi, diferansiyel kalkülüs üniversite müfredatında tipik olarak integral hesabından önce gelir, dolayısıyla ikincisine dayanmayan bir π bir tanımının olması arzu edilir. Richard Baltzer'e dayanan ve Edmund Landau tarafından yaygınlaştırılan böyle bir tanım şöyledir: π, kosinüs fonksiyonunun 0'a eşit olduğu en küçük pozitif sayının iki katıdır.π ayrıca sinüs fonksiyonunun sıfıra eşit olduğu en küçük pozitif sayı ve sinüs fonksiyonunun ardışık sıfırları arasındaki farktır. Kosinüs ve sinüs, geometriden bağımsız olarak bir kuvvet serisi veya bir diferansiyel denklem çözümü olarak tanımlanabilir.

Benzer şekilde, π, bir exp z karmaşık değişkeninin, exp z nin özellikleri kullanılarak tanımlanabilir. Kosinüs gibi, karmaşık üstel de birkaç yoldan biriyle tanımlanabilir. exp z'nin bire eşit olduğu karmaşık sayılar kümesi, şu şekilde (hayali) bir aritmetik ilerlemedir:

$${\displaystyle \{\dots ,-2\pi i,0,2\pi i,4\pi i,\dots \}=\{2\pi ki\mid k\in \mathbb {Z} \}}$$

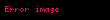
ve bu özelliğe sahip benzersiz bir pozitif gerçek sayı, π vardır.

Topoloji ve cebir gibi karmaşık matematiksel kavramlardan yararlanan aynı fikrin bir varyasyonu aşağıdaki teoremdir: Toplama modulo tam sayıları altındaki reel sayıların R/Z grubundan (çember grubu), mutlak değeri bir olan karmaşık sayıların çarpımsal grubuna, benzersiz (otomorfizma) bir sürekli izomorfizma vardır. π sayısı, bu homomorfizmin türevinin büyüklüğünün yarısı olarak tanımlanır.

İrrasyonellik ve normallik

π bir irrasyonel sayı'dır, yani iki tam sayının oranı olarak yazılamaz. 22/7 ve 355/113 gibi kesirler genellikle π'ye yaklaşmak için kullanılır, ancak hiçbir (tam sayıların oranı) tam değeri olamaz.π irrasyonel olduğundan, içinde sonsuz sayıda basamak vardır ve sonsuz örüntü basamaklara yerleşmez. π}'nin irrasyonel olduğunun birkaç kanıtı vardır; genellikle cebir gerektirirler ve reductio ad absurdum tekniğini kullanılır. π'nin rasyonel sayılar ile yaklaşık olarak hesaplanabileceği derece kesin olarak bilinmiyor; tahminler, irrasyonalite ölçüsünün e veya ln 2 ölçüsünden büyük ama Liouville sayısı ölçüsünden küçük olduğunu ortaya koymuştur.

π rakamlarının görünür bir örüntüsü yoktur ve testleri dahil olmak üzere testlerini geçmiştir; tüm olası basamak dizileri (herhangi bir uzunluktaki) eşit sıklıkta göründüğünde, sonsuz uzunlukta bir sayı normal olarak adlandırılır. π'nin olduğu varsayımı kanıtlanmadı veya çürütülmedi.

Bilgisayarların icadından bu yana, üzerinde istatistiksel analiz yapmak için çok sayıda π basamağı mevcuttu. , π'nin ondalık basamakları üzerinde ayrıntılı istatistiksel analizler yaptı ve bunları normallikle tutarlı buldu; örneğin, 0 ila 9 arasındaki on hanenin ne kadar sıklıkta olduğu istatistiksel anlamlılık testlerine tabi tutuldu ve bir örüntüye dair hiçbir kanıt bulunamadı. Herhangi bir rastgele basamak dizisi, sonsuz maymun teoremi ile rastgele olmayan görünen uzun alt diziler içerir. Bu nedenle, π'nin rakam dizisi rastgelelik için istatistiksel testlerden geçtiğinden, ondalık gösteriminin 762. ondalık basamağından başlayan, altı ardışık 9'lu dizi gibi rastgele görünmeyebilecek bazı rakam dizileri içerir. Bu, 'da Richard Feynman'a atfen "Feynman noktası" olarak da adlandırılır ancak Feynman ile hiçbir bağlantısı bilinmemektedir.

Aşkınlık

π bir aşkın sayı olduğu için, daireyi kareyle çevreleme, klasik pergel ve cetvel kullanılarak sınırlı sayıda adımda mümkün değildir.

π irrasyonel olmasının yanı sıra bir aşkın sayı'dır, bu da x⁵/120 − x³/6 + x = 0 gibi rasyonel katsayılı herhangi bir sabit olmayan 'nin çözümü olamayacağı anlamına gelir.

π aşkınlığının iki önemli sonucu vardır: İlk olarak, π, rasyonel sayılar ve kareköklerin veya n-inci köklerin (^{3 gibi)} √31 veya √10 gibi) herhangi bir sonlu kombinasyonu kullanılarak ifade edilemez. İkincisi, hiçbir aşkın sayı pergel ve cetvel ile oluşturulamadığından, "daireyi kareyle çevreleme" mümkün değildir. Başka bir deyişle, yalnızca pergel ve cetvel kullanarak, alanı belirli bir dairenin alanına tam olarak eşit olan bir kare oluşturmak imkansızdır. Bir daireyi kareyle çevrelemek, önemli geometri problemlerinden biriydi. Modern zamanların amatör matematikçileri, matematiksel olarak imkansız olmasına rağmen, bazen daireyi kareyle çevreleme ve başarı iddiasında bulunmaya çalıştılar.

Sonsuza giden kesirler

İrrasyonel bir sayı olarak π, olarak gösterilemez. Ancak π dahil her sayı, adı verilen, sonsuz bir iç içe geçmiş kesirler serisi ile temsil edilebilir:

$${\displaystyle \pi =3+\textstyle {\cfrac {1}{7+\textstyle {\cfrac {1}{15+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{292+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\textstyle {\cfrac {1}{1+\ddots }}}}}}}}}}}}}}}$$

Sürekli kesrin herhangi bir noktada kesilmesi, π için rasyonel bir yaklaşım verir; bunlardan ilk dördü {3, 22/7, 333/106 ve 355/113 tür. Bu sayılar, sabitin en iyi bilinen ve en çok kullanılan tarihsel yaklaşımları arasındadır. Bu şekilde üretilen her yaklaşım, en iyi rasyonel yaklaşımdır; yani, her biri aynı veya daha küçük paydaya sahip herhangi bir diğer kesirden π'ye daha yakındır.π aşkın olduğundan, tanım gereği cebirsel değildir ve bu nedenle olamaz. Bu nedenle, π bir periyodik sonsuza giden kesir içeremez. π için basit sonsuza giden kesir (yukarıda gösterilmiştir) başka herhangi bir bariz örüntü sergilemese de, birkaç sergiler, örneğin:

$${\displaystyle {\begin{aligned}\pi &=3+\textstyle {\cfrac {1^{2}}{6+\textstyle {\cfrac {3^{2}}{6+\textstyle {\cfrac {5^{2}}{6+\textstyle {\cfrac {7^{2}}{6+\textstyle {\cfrac {9^{2}}{6+\ddots }}}}}}}}}}=\textstyle {\cfrac {4}{1+\textstyle {\cfrac {1^{2}}{2+\textstyle {\cfrac {3^{2}}{2+\textstyle {\cfrac {5^{2}}{2+\textstyle {\cfrac {7^{2}}{2+\ddots }}}}}}}}}}=\textstyle {\cfrac {4}{1+\textstyle {\cfrac {1^{2}}{3+\textstyle {\cfrac {2^{2}}{5+\textstyle {\cfrac {3^{2}}{7+\textstyle {\cfrac {4^{2}}{9+\ddots }}}}}}}}}}\end{aligned}}}$$

Yaklaşık değer ve basamaklar

Bazı pi yaklaşımları şunları içerir:

• Tamsayılar: 3
• Kesirler: Yaklaşık kesirler şunları içerir (artan doğruluk sırasına göre) 22/7, 333/106, 355/113, 52163/16604, 103993/33102, 104348/33215, and 245850922/78256779.

(Liste,  A063674 ve  A063673'den seçilen terimlerdir.)

• Rakamlar: İlk 50 ondalık basamak 3.14159265358979323846264338327950288419716939937510... şeklindedir. (see  A000796)

Diğer sayı sistemlerindeki rakamlar

• İlk 48 2 tabanlı basamak (bit olarak adlandırılır) 11.001001000011111101101010100010001000010110100011... ( A004601'e bakınız) şeklindedir.
• On altılı sayı sistemi içindeki ilk 20 hane (16 tabanlı) 3.243F6A8885A308D31319... ( A062964'e bakınız) şeklindedir.
• İlk beş Altmışlık sayı sistemi (60 tabanlı) basamak 3;8,29,44,0,47 şeklindedir. (see  A060707)
• Üçlü sayı sistemi içindeki ilk 38 basamak 10.0102110122220102110021111102212222201... şeklindedir. ( A004602'ye bakınız)

Karmaşık sayılar ve Euler özdeşliği

e sayısının hayali güçleri ile noktalar arasındaki ilişki, Sıfır noktasında merkezi olan birim çember üzerinde Euler formülü tarafından verilen karmaşık düzlem içinde

Herhangi bir karmaşık sayı, örneğin z, bir çift reel sayı kullanılarak ifade edilebilir. Kutupsal koordinat sisteminde, bir sayı (yarıçap veya r), z'nin karmaşık düzlemin sıfır noktasından olan mesafesini ve diğeri, (açı veya φ) pozitif reel eksenden, saat yönünün tersine dönüşü temsil etmek için kullanılır:

$${\displaystyle z=r\cdot (\cos \varphi +i\sin \varphi ),}$$

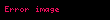
burada i, i² = −1'i sağlayan hayali birimdir. Karmaşık analizde π'nin sık görülmesi, Euler formülüyle tanımlandığı gibi, karmaşık bir değişkenin üstel fonksiyonunun davranışıyla ilgili olabilir:

$${\displaystyle e^{i\varphi }=\cos \varphi +i\sin \varphi ,}$$

burada e sabiti, doğal logaritmanın tabanıdır. Bu formül,e'nin hayali üsleri ile, karmaşık düzlemin sıfır noktası merkezli birim çember üzerindeki noktalar arasında, bir karşılık olma ilişkisi kurar. Euler formülünde φ = π eşitliği, beş önemli matematiksel sabit içerdiği için matematikte önemsenen Euler özdeşliği ile sonuçlanır:

$${\displaystyle e^{i\pi }+1=0.}$$

zⁿ = 1 eşitliğini sağlayan n sayıda farklı karmaşık sayı vardır ve bunlara "birliğin n'inci kökleri" denir ve aşağıdaki formülle verilir:

$${\displaystyle e^{2\pi ik/n}\qquad (k=0,1,2,\dots ,n-1).}$$

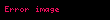
Geçmiş

Antik Çağ

Milattan önceye tarihlenen π için en iyi bilinen yaklaşımlar, iki ondalık basamağa kadar doğruydu; bu, özellikle birinci bin yılın ortalarında, 'nde yedi ondalık basamak doğruluğuna kadar geliştirildi. Bundan sonra, geç Orta Çağ dönemine kadar daha fazla ilerleme kaydedilmedi.

π'nin en eski yazılı tahminleri, Babil ve Mısır'da bulunur, her ikisi de gerçek değerin yüzde biri dahilindedir. Babil'de, MÖ 1900-1600 tarihli bir kil tablet, ima yoluyla π'yi şu şekilde ele alan geometrik bir ifadeye sahiptir: 25/8=3.125. Mısır'da, MÖ 1650 dolaylarına tarihlenen ancak MÖ 1850 tarihli bir belgeden kopyalanan Rhind Papirüsü, π'yi (16/9)² ≈ 3.16. olarak ele alan bir dairenin alanı için bir formüle sahiptir. gibi bazı , Büyük Giza Piramidi'nin π ile ilgili oranlarla inşa edildiğini teorileştirmiş olsalar da, bu teori bilim adamları tarafından geniş çapta kabul görmemektedir. MÖ birinci veya ikinci binyıldan sözlü bir geleneğe tarihlenen 'nin 'nda, yaklaşık 3.08831, 3.08833, 3.004, 3 veya 3.125 olarak çeşitli şekillerde yorumlanan yaklaşık değerler verilmiştir.

Çokgen yaklaşım dönemi

π, çevrelenmiş ve içine çember çizilmiş çokgenlerin çevreleri hesaplanarak tahmin edilebilir.

Archimedes, π'ye yaklaşmak için poligonal yaklaşımı geliştirdi.

π değerini titizlikle hesaplamak için kaydedilen ilk algoritma, Yunan matematikçi Arşimet tarafından MÖ 250 civarında tasarlanan çokgenleri kullanan geometrik bir yaklaşımdı. Bu çokgen algoritma 1.000 yılı aşkın bir süre hakim oldu ve sonuç olarak π bazen Arşimet sabiti olarak anılır. Arşimet, bir dairenin içine ve dışına düzgün bir altıgen çizerek ve 96 kenarlı bir düzgün çokgene ulaşana kadar kenar sayısını art arda ikiye katlayarak π'nin üst ve alt sınırlarını hesapladı. Bu poligonların çevresini hesaplayarak 223/71 < π < 22/7 (yani 3.1408 < π < 3.1429) olduğunu kanıtladı. Arşimet'in 22/7 üst sınırı, π'nin 22/7'ye eşit olduğuna dair yaygın bir popüler inanca yol açmış olabilir. MS 150 civarında, Yunan-Roma bilim adamı Batlamyus, Almagest'inde, Arşimet'ten veya Apollonios'tan almış olabileceği 3.1416'lık bir π değeri verdi. Çokgen algoritmaları kullanan matematikçiler 1630'da π'nin 39 basamağına ulaştılar, bu rekor yalnızca 1699'da sonsuz seriler kullanıldığında 71 basamağa ulaştığı zaman kırıldı.

Eski Çin'de, π değerleri 3,1547 (MS 1 civarında), √10 (MS 100, yaklaşık 3,1623) ve { {sfrac}}'i (3. yüzyıl, yaklaşık 3.1556) içeriyordu. MS 265 civarında, Wei Krallığı matematikçisi Liu Hui, çokgen tabanlı yinelemeli bir algoritma oluşturdu ve bunu 3.1416'lık bir π değeri elde etmek için 3.072 kenarlı bir çokgenle kullandı. MS 265 civarında, matematikçisi Liu Hui bir oluşturdu ve π'nin 3.1416 değerini elde etmek için bunu 3.072-kenarlı bir çokgenle kullandı. Liu daha sonra π'yi hesaplamak için daha hızlı bir yöntem icat etti ve ardışık çokgenlerin alanındaki farklılıkların 4 katsayılı bir geometrik seri oluşturmasından yararlanarak 96 kenarlı bir çokgenle 3.14 değerini elde etti. Çinli matematikçi , MS 480 civarında, 3.1415926 < π < 3.1415927 olduğunu hesapladı ve 12.288 kenarlı bir çokgene uygulanan kullanarak π ≈ 355/113 = 3,14159292035... ve π ≈ 22/7 = 3.142857142857..., yaklaşımlarını önerdi. Bunları sırasıyla Milü (''yakın oran") ve Yuelü ("yaklaşık oran") olarak adlandırdı. İlk yedi ondalık basamağı için doğru bir değerle, bu değer, sonraki 800 yıl boyunca mevcut olan en doğru π yaklaşımı olarak kaldı.

Hintli astronom Aryabhata (MS 499) adlı eserinde 3.1416 değerini kullanmıştır. MÖ 1220'de Fibonacci, Arşimet'ten bağımsız olarak çokgen bir yöntem kullanarak 3.1418'i hesapladı. İtalyan yazar Dante görünüşe göre 3+√2/10 ≈ 3.14142 değerini kullandı.

İranlı astronom Jamshīd al-Kāshī 1424'te 3×2²⁸ kenarlı bir çokgen kullanarak kabaca 16 ondalık basamağa eşdeğer olan 9 basamak üretti ve bu değer yaklaşık 180 yıl dünya rekoru olarak kaldı. 1579'da Fransız matematikçi François Viète, 3×2¹⁷ kenarlı bir çokgenle 9 basamak elde etti. Flaman matematikçi 1593'te 15 ondalık basamağa ulaştı. 1596'da Hollandalı matematikçi 20 haneye ulaştı, daha sonra bu rekoru 35 haneye çıkardı (sonuç olarak π, 20. yüzyılın başlarına kadar Almanya'da "Ludolphian sayısı" olarak adlandırılıyordu). Hollandalı bilim adamı 1621'de 34 haneye ulaştı, ve Avusturyalı gök bilimci , 10⁴⁰ kenar kullanarak 1630'da 38 haneye ulaştı..Christiaan Huygens was able to arrive at 10 decimal places in 1654 using a slightly different method equivalent to .

Sonsuz dizi

π hesaplamasında, 16. ve 17. yüzyıllarda sonsuz seriler tekniklerinin geliştirilmesiyle devrim yaratıldı. Sonsuz bir seri, sonsuz bir dizi terimlerinin toplamıdır. Sonsuz seriler, matematikçilerin π'yi Arşimet ve geometrik teknikler kullanan diğerlerinden çok daha yüksek bir hassasiyetle hesaplamasına izin verdi. Sonsuz seriler π için ve Gottfried Wilhelm Leibniz gibi Avrupalı matematikçiler tarafından kullanılmasına rağmen, yaklaşım 14. veya 15. yüzyılda bir zaman Kerala astronomi ve matematik okulunda ortaya çıktı. MS 1500 civarında, tarafından 'daki Sanskrit ayette π'yi hesaplamak için kullanılabilecek sonsuz bir dizinin yazılı bir açıklaması ortaya kondu. Seriler kanıt olmadan sunulur, ancak kanıtlar MS 1530 civarında daha sonraki bir çalışma olan da sunulur. Sinüs (Nilakantha'nın Madhava'ya atfettiği), kosinüs ve artık bazen olarak anılan arktanjant serileri dahil olmak üzere birkaç sonsuz seri açıklanmıştır. Arktanjant serisine bazen veya Gregory-Leibniz serisi denir. Madhava, π'yi 1400 yılı civarında 11 haneye kadar tahmin etmek için sonsuz seriler kullandı.

1593'te François Viète, şimdi olarak bilinen, olan (daha tipik olarak π hesaplamalarında kullanılan sonsuz bir toplam yerine) aşağıdaki formülü yayınladı:

$${\displaystyle {\frac {2}{\pi }}={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots }$$

1655'te , aynı şekilde sonsuz bir çarpım olan, şimdi olarak bilinen aşağıdaki formülü yayınladı:

$${\displaystyle {\frac {\pi }{2}}={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdots }$$

Isaac Newton π'yi 15 haneye kadar hesaplamak için sonsuz seri kullandı, daha sonra "Bu hesaplamaları kaç rakama kadar yaptığımı size söylemeye utanıyorum" yazdı.

1660'larda İngiliz bilim adamı Isaac Newton ve Alman matematikçi Gottfried Wilhelm Leibniz, π'ye yaklaşmak için birçok sonsuz serinin geliştirilmesine yol açan kalkülüs'ü keşfetti. Newton'un kendisi, 1665 veya 1666'da π'nin 15 basamaklı bir yaklaşımını hesaplamak için bir arksinüs serisi kullandı, daha sonra bununla ilgili olarak "O zamanlar başka bir işim olmadığı için, bu hesaplamaları kaç rakama kadar yaptığımı size söylemeye utanıyorum" yazdı.

1671'de bağımsız olarak, 1673'te Leibniz'te, için Taylor serisi genişletmesini keşfetti:

$${\displaystyle \arctan z=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots }$$

Bazen olarak adlandırılan bu dizi, z = 1 ile değerlendirildiğinde π/4'e eşittir. Ancak z = 1 için pratik olmayacak şekilde yavaş yakınsar (yani, cevaba çok yavaş yaklaşır) ve her ek basamağı hesaplamak için yaklaşık on kat daha fazla terim gerekir.

1699'da İngiliz matematikçi , π'yi 71 haneye kadar hesaplamak için 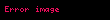${\textstyle z={\frac {1}{\sqrt {3}}}}$ eşitliği ile Gregory–Leibniz serisini kullandı ve çokgen bir algoritma ile belirlenen 39 haneli önceki rekoru kırdı.

1706'da , çok daha hızlı yakınsayan bir algoritma üretmek için Gregory-Leibniz serisini kullandı:

$${\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}.}$$

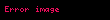
Machin bu formülle π'nin 100 basamağına ulaştı. Diğer matematikçiler, π basamaklarını hesaplamada birkaç ardışık rekor için kullanılan, şimdi olarak bilinen varyantlar yarattı.

Isaac Newton, 1684'te Gregory-Leibniz serisinin yakınsamasını hızlandırdı (yayınlanmamış bir çalışmada; diğerleri sonucu bağımsız olarak keşfetti).

${\displaystyle \arctan x={\frac {x}{1+x^{2}}}+{\frac {2}{3}}{\frac {x^{3}}{(1+x^{2})^{2}}}+{\frac {2\cdot 4}{3\cdot 5}}{\frac {x^{5}}{(1+x^{2})^{3}}}+\cdots }$

Leonhard Euler bu seriyi 1755 diferansiyel hesabı ders kitabında popüler hale getirdi ve daha sonra bunu Machin benzeri formüllerle kullandı, örneğin ${\textstyle {\tfrac {\pi }{4}}=5\arctan {\tfrac {1}{7}}+2\arctan {\tfrac {3}{77}},}$ ile bir saatte π'nin 20 basamağını hesapladı.

Machin benzeri formüller, bilgisayar çağına kadar π'yi hesaplamak için en iyi bilinen yöntem olarak kaldı ve 250 yıl boyunca rekorlar kırmak için kullanıldı ve 1946'da Daniel Ferguson tarafından 620 basamaklı bir yaklaşımla sonuçlandı. (bir hesaplama cihazının yardımı olmadan elde edilen en iyi yaklaşım).

1844'te, Alman matematikçi Carl Friedrich Gauss'un kontrolünde kafasında π'nin 200 ondalığını hesaplamak için bir Machin benzeri formül kullanan tarafından bir rekor kırıldı.

1853'te İngiliz matematikçi , π'yi 607 basamak olarak hesapladı, ancak 528. basamakta bir hata yaparak sonraki tüm basamakların yanlış olmasına yol açtı. 1873'te ek 100 basamak hesaplayarak toplamı 707'ye çıkarsa da, önceki hatası tüm yeni basamakların da yanlış hesaplanmasına yol açtı.

Yakınsama oranı

π için bazı sonsuz seriler diğerlerinden daha hızlı . Given the choice of two infinite series for π, mathematicians will generally use the one that converges more rapidly because faster convergence reduces the amount of computation needed to calculate π to any given accuracy.π için basit bir sonsuz seri :

$${\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}-\cdots }$$

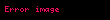
Bu sonsuz dizinin tek tek terimleri toplama eklendikçe, toplam kademeli olarak π'ye yaklaşır ve istenildiği kadar π'ye yaklaşabilir (yeterli sayıda terim ile). Yine de oldukça yavaş yakınsar - 500.000 terimden sonra, π'nin yalnızca beş doğru ondalık basamağını üretir.

π için (15. yüzyılda Nilakantha tarafından yayınlanan) Gregory-Leibniz serisinden daha hızlı yakınsayan sonsuz bir seri:

$${\displaystyle \pi =3+{\frac {4}{2\times 3\times 4}}-{\frac {4}{4\times 5\times 6}}+{\frac {4}{6\times 7\times 8}}-{\frac {4}{8\times 9\times 10}}+\cdots }$$

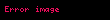
Aşağıdaki tablo, bu iki serinin yakınsama oranlarını karşılaştırmaktadır:

π için sonsuz seriler	1. terimden sonra	2. terimden sonra	3. terimden sonra	4. terimden sonra	5. terimden sonra	yakınsar:
${\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}+{\frac {4}{13}}+\cdots }$	4.0000	2.6666 ...	3.4666 ...	2.8952 ...	3.3396 ...	π = 3.1415 ...
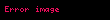${\displaystyle \pi ={3}+{\frac {4}{2\times 3\times 4}}-{\frac {4}{4\times 5\times 6}}+{\frac {4}{6\times 7\times 8}}-\cdots }$	3.0000	3.1666 ...	3.1333 ...	3.1452 ...	3.1396 ...

Beş terimden sonra, Gregory-Leibniz serisinin toplamı, π'nin doğru değerinin 0,2'si içindeyken, Nilakantha'nın serisinin toplamı doğru değerinin 0,002'si içindedir. Nilakantha'nın serisi daha hızlı yakınsar ve π'nin basamaklarını hesaplamak için daha kullanışlıdır. Daha da hızlı yakınsayan seriler arasında ve yer alır, ikincisi terim başına 14 doğru ondalık basamak üretir.

İrrasyonellik ve aşkınlık

π ile ilgili tüm matematiksel gelişmeler, tahminlerin doğruluğunu artırmayı amaçlamadı. Euler 1735'te ters karelerin toplamının tam değerini bularak çözdüğünde, π ile asal sayılar arasında bir bağlantı kurdu ve bu daha sonra Riemann zeta işlevi çalışmasını geliştirmeye katkıda bulundu.

$${\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }$$

İsviçreli bilim adamı Johann Heinrich Lambert 1768'de π'nin irrasyonel olduğunu, yani herhangi iki tam sayının bölümüne eşit olmadığını kanıtladı. Lambert'in ispatı, tanjant fonksiyonunun sürekli kesir temsilinden yararlandı. Fransız matematikçi Adrien-Marie Legendre, 1794'te π²'nin de irrasyonel olduğunu kanıtladı. 1882'de Alman matematikçi Ferdinand von Lindemann, π'nin aşkın olduğunu kanıtladı ve hem Legendre hem de Euler tarafından yapılan bir varsayımı doğruladı. Hardy ve Wright, "kanıtların daha sonra Hilbert, Hurwitz ve diğer yazarlar tarafından değiştirilip basitleştirildiğini" belirtir.

π sembolünün benimsenmesi

Bir çemberin çevresinin çapına oranını temsil etmek için Yunanca π harfinin bilinen en eski kullanımı, 1706'da Galli matematikçi tarafından yapılmıştır.

Leonhard Euler, 1736 ve 1748'de yayınladığı eserlerde Yunanca π harfinin kullanımını yaygınlaştırdı.

İlk kullanımlarda, Yunan harfi π, bir dairenin (Latince'de semiperipheria) ifade etmek için kullanılmıştır. ve daire sabitlerini oluşturmak için δ (çap veya yarı çap için) veya ρ (yarıçap için) ile oranlarda birleştirildi. (O zamandan önce, matematikçiler bunun yerine bazen c veya p gibi harfleri kullanıyorlardı.) Kaydedilen ilk kullanım "${\displaystyle \delta .\pi }$" şeklindedir ve Latince: Clavis Mathematicae'nin 1647 ve sonraki baskılarında çevre ve çap oranını ifade etmek için kullanmıştır.Barrow 3.14... sabitini temsil etmek için aynı şekilde "${\textstyle {\frac {\pi }{\delta }}}$" kullandı. bunun yerine "${\textstyle {\frac {\pi }{\rho }}}$"'yi 6.28...'i temsil etmek için kullandı.

Bir çemberin çevresinin çapına oranını temsil etmek için tek başına Yunanca π harfinin bilinen en eski kullanımı Galli matematikçi 'un 1706 tarihli Latince: Synopsis Palmariorum Matheseos adlı çalışmasında yapılmıştır; veya Matematiğe Yeni Bir Giriş." Yunan harfi s. 243 te, "Çevre (π), yarıçapı 1 olan bir daire için hesaplanmıştır." ifadesinde kullanılmıştır. Ancak Jones, π için denklemlerinin "gerçekten dahiyane Bay 'in hazır kaleminden" olduğunu yazar ve bu da Machin'in Jones'tan önce Yunanca harfi kullanmış olabileceği yönünde spekülasyonlara yol açar. Jones'un gösterimi diğer matematikçiler tarafından hemen benimsenmedi, kesir gösterimi 1767'ye kadar hâlâ kullanılıyordu.

Euler, 1727 tarihli Havanın Özelliklerini Açıklayan Deneme ile başlayarak tek harfli formu kullanmaya başladı, ancak, bu ve sonraki bazı yazılarda çevrenin yarıçapa oranı olan π = 6.28... kullanmıştı. Euler π = 3.14...'ü ilk olarak 1736 tarihli adlı çalışmasında kullandı ve geniş çapta okunan 1748 tarihli Latince:  adlı çalışmasında devam etti (şöyle yazdı: "Kısa olması adına bu sayıyı π olarak yazacağız; böylece π şuna eşittir: yarıçapı 1 olan bir dairenin çevresinin yarısı"). Euler, Avrupa'daki diğer matematikçilerle yoğun bir şekilde yazıştığı için, Yunan harfinin kullanımı hızla yayıldı ve uygulama bundan sonra Batı dünyasında evrensel olarak benimsendi, ancak tanım 1761 gibi geç bir tarihe kadar hâlâ 3.14... ve 6.28... arasında değişiyordu.

Daha fazla basamak için modern arayış

Bilgisayar çağı ve yinelemeli algoritmalar

:
Başlat

$${\displaystyle \textstyle a_{0}=1,\quad b_{0}={\frac {1}{\sqrt {2}}},\quad t_{0}={\frac {1}{4}},\quad p_{0}=1.}$$

Yinele

$${\displaystyle \textstyle a_{n+1}={\frac {a_{n}+b_{n}}{2}},\quad \quad b_{n+1}={\sqrt {a_{n}b_{n}}},}$$

$${\displaystyle \textstyle t_{n+1}=t_{n}-p_{n}(a_{n}-a_{n+1})^{2},\quad \quad p_{n+1}=2p_{n}.}$$

Ardından, π için bir tahmin şu şekilde verilir:

$${\displaystyle \textstyle \pi \approx {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}.}$$

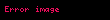
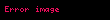
20. yüzyılın ortalarında bilgisayarların gelişimi, π rakamlarının aranmasında yeniden devrim yarattı. Matematikçiler ve Levi Smith, 1949'da bir masa hesap makinesi kullanarak 1.120 haneye ulaştı. George Reitwiesner ve John von Neumann liderliğindeki bir ekip (arctan) sonsuz serisini kullanarak aynı yıl ENIAC bilgisayar üzerinde 70 saatlik bilgisayar çalışması gerektiren bir hesaplamayla 2.037 basamak elde etti. Her zaman bir arctan serisine dayanan rekor, 1973'te 1 milyon haneye ulaşılana kadar art arda kırıldı (1957'de 7.480 hane; 1958'de 10.000 hane; 1961'de 100.000 hane).

1980 civarında iki ek gelişme, π'yi hesaplama yeteneğini bir kez daha hızlandırdı. Birincisi, sonsuz serilerden çok daha hızlı olan π hesaplaması için yeni keşfi; ve ikincisi, büyük sayıları çok hızlı bir şekilde çarpabilen hızlı çarpma algoritmalarının icadı.

Birincisi, π hesaplaması için sonsuz serilerden çok daha hızlı olan yeni keşfi; ve ikincisi, büyük sayıları çok hızlı bir şekilde çarpabilen 'nın icadı. Bu tür algoritmalar modern π hesaplamalarında özellikle önemlidir çünkü bilgisayarın zamanının çoğu çarpmaya ayrılmıştır. Bunlar arasında Karatsuba algoritması, Toom-Cook çarpması ve Fourier dönüşümü tabanlı yöntemler bulunur.

Yinelemeli algoritmalar, 1975-1976'da fizikçi Eugene Salamin ve bilim adamı Richard Brent tarafından bağımsız olarak yayınlandı. Bunlar sonsuz serilere güvenmekten kaçınır. Yinelemeli bir algoritma, her yinelemede önceki adımların çıktılarını girdi olarak kullanarak belirli bir hesaplamayı tekrarlar ve her adımda istenen değere yaklaşan bir sonuç üretir. Yaklaşım aslında 160 yılı aşkın bir süre önce Carl Friedrich Gauss tarafından şu anda (AGM yöntemi) veya olarak adlandırılan yöntemle icat edildi. Salamin ve Brent tarafından değiştirildiği şekliyle, Brent-Salamin algoritması olarak da anılır.

Yinelemeli algoritmalar, sonsuz dizi algoritmalarından daha hızlı oldukları için 1980'den sonra yaygın olarak kullanıldı: sonsuz diziler tipik olarak birbirini izleyen terimlerde doğru basamak sayısını artırırken, yinelemeli algoritmalar genellikle her adımda doğru basamak sayısını "çarpar". Örneğin, Brent-Salamin algoritması, her yinelemede basamak sayısını ikiye katlar.

1984'te ve kardeşler, her adımdaki basamak sayısını dört katına çıkaran yinelemeli bir algoritma ürettiler; ve 1987'de, her adımda basamak sayısını beş kat artıran bir algoritma. Yinelemeli yöntemler, Japon matematikçi tarafından 1995 ve 2002 yılları arasında π hesaplaması için çeşitli rekorlar kırmak için kullanıldı. Bu hızlı yakınsamanın bir bedeli var: yinelemeli algoritmalar, sonsuz serilerden önemli ölçüde daha fazla bellek gerektirir.

π sayısını hesaplama nedenleri

Matematikçiler yeni algoritmalar keşfettikçe ve bilgisayarlar kullanılabilir hale geldikçe, π'nin bilinen ondalık basamaklarının sayısı önemli ölçüde arttı. Dikey ölçek .

π içeren çoğu sayısal hesaplama için, bir avuç rakam yeterli kesinlik sağlar. Jörg Arndt ve Christoph Haenel'e göre, çoğu kozmolojik hesaplamayı yapmak için otuz dokuz basamak yeterlidir, çünkü gözlemlenebilir evrenin çevresini bir atom hassasiyetiyle hesaplamak için gereken doğruluk budur. Hesaplamalı telafi etmek için gereken ek basamakları hesaba katan Arndt, herhangi bir bilimsel uygulama için birkaç yüz basamağın yeterli olacağı sonucuna varır. Buna rağmen, insanlar π'yi binlerce ve milyonlarca basamaklı olarak hesaplamak için yoğun bir şekilde çalıştılar. Bu çaba kısmen insanların rekor kırma dürtüsüne atfedilebilir ve π ile elde edilen bu tür başarılar genellikle dünya çapında manşetlere konu olur.Süper bilgisayarları test etme, sayısal analiz algoritmalarını test etme (yüksek hassasiyetli çarpma algoritmaları dahil); ve saf matematiğin kendisinde, π'nin rakamlarının rastgeleliğini değerlendirmek için veri sağlar.

Hızlı yakınsak seriler

Srinivasa Ramanujan, Hindistan'da izole bir şekilde çalışarak π hesaplaması için pek çok yenilikçi seri üretti.

Modern π hesap makineleri, yalnızca yinelemeli algoritmalar kullanmaz. 1980'lerde ve 1990'larda yinelemeli algoritmalar kadar hızlı ancak daha basit ve daha az bellek kullanan yeni sonsuz seriler keşfedildi. Hızlı yinelemeli algoritmalar, 1914'te Hintli matematikçi Srinivasa Ramanujan π için zarafetleri, matematiksel derinlikleri ve hızlı yakınsamalarıyla dikkat çeken düzinelerce yenilikçi yeni formül yayınladığında öngörülmüştü. dayanan formüllerinden biri,

$${\displaystyle {\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{k!^{4}\left(396^{4k}\right)}}.}$$

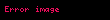
Bu seri, Machin'in formülü de dahil olmak üzere çoğu arctan serisinden çok daha hızlı yakınsar., 1985'te 17 milyon basamaklı bir rekor kırarak π hesaplamasındaki ilerlemeler için bunu ilk kullanan kişiydi. Ramanujan'ın formülleri, Borwein kardeşler ( ve ) ve tarafından geliştirilen modern algoritmaları öngörüyordu. 1987'de geliştirilen ,

$${\displaystyle {\frac {1}{\pi }}={\frac {\sqrt {10005}}{4270934400}}\sum _{k=0}^{\infty }{\frac {(6k)!(13591409+545140134k)}{(3k)!\,k!^{3}(-640320)^{3k}}}.}$$

Terim başına yaklaşık 14 basamak π üretir ve birkaç kayıt ayarı π hesaplaması için kullanılmıştır. Bunlar arasında 1989'da Chudnovsky kardeşler tarafından 1 milyar (10⁹) haneyi aşan ilk rakamlar, 2011'de Alexander Yee ve Shigeru Kondo tarafından 10 trilyon (10¹³) hane ve 2022'de Emma Haruka Iwao tarafından 100 trilyon hane yer alıyor. Benzer formüller için ayrıca bkz.

2006'da matematikçi , aşağıdaki şablona uygun olarak π için birkaç yeni formül oluşturmak için PSLQ'yu kullandı:

$${\displaystyle \pi ^{k}=\sum _{n=1}^{\infty }{\frac {1}{n^{k}}}\left({\frac {a}{q^{n}-1}}+{\frac {b}{q^{2n}-1}}+{\frac {c}{q^{4n}-1}}\right),}$$

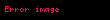
burada q eşittir e^π (Gelfond sabiti), k tek sayıdır ve a, b, c Plouffe'un hesapladığı belirli rasyonel sayılardır.

Monte Carlo yöntemleri

. a ve b iğneleri rastgele bırakılıyor.

Rastgele noktalar, içinde bir daire bulunan bir kareye yerleştirilir.

Birden fazla rastgele denemenin sonuçlarını değerlendiren , π'nin yaklaşık değerlerini oluşturmak için kullanılabilir. Buffon'un iğnesi böyle bir tekniktir: ℓ uzunluğundaki bir iğne, t birim aralıklarla paralel çizgilerin çizildiği bir yüzey üzerine n kez düşürülürse ve bu seferlerin x tanesi bir çizgiyi geçerek durursa (x > 0), o zaman sayımlara göre π yaklaşık olarak hesaplanabilir:

$${\displaystyle \pi \approx {\frac {2n\ell }{xt}}.}$$

π'yi hesaplamak için başka bir Monte Carlo yöntemi, kare içine çizilmiş bir daire çizmek ve kareye rastgele noktalar yerleştirmektir. Daire içindeki noktaların toplam nokta sayısına oranı yaklaşık olarak π/4 olacaktır.

200 adımlı beş rastgele yürüyüş. W₂₀₀ mutlak değeri için örnek ortalama μ = 56/5 ve dolayısıyla 2(200)μ⁻² ≈ 3.19 π'nin 0.05 dahilindedir.

Olasılığı kullanarak π'yi hesaplamanın başka bir yolu, bir dizi (adil) yazı tura atmasıyla oluşturulan rastgele bir yürüyüşle başlamaktır: eşit olasılıklarla X_k ∈ olacak şekilde bağımsız rassal değişkenler X_k. İlişkili rastgele yürüyüş

$${\displaystyle W_{n}=\sum _{k=1}^{n}X_{k}}$$

böylece her n için, W_n, kaydırılmış ve ölçeklendirilmiş bir binom dağılımı'ndan çizilir. n değiştikçe, W_n (ayrık) bir stokastik süreci tanımlar. O zaman π şu şekilde hesaplanabilir:

$${\displaystyle \pi =\lim _{n\to \infty }{\frac {2n}{E[|W_{n}|]^{2}}}.}$$

Bu Monte Carlo yöntemi, çemberlerle herhangi bir ilişkiden bağımsızdır ve aşağıda tartışılan merkezî limit teoremi'nin bir sonucudur.

π'ye yaklaşmak için bu Monte Carlo yöntemleri, diğer yöntemlere kıyasla çok yavaştır ve elde edilen tam basamak sayısı hakkında herhangi bir bilgi sağlamaz. Bu nedenle, hız veya doğruluk istendiğinde asla π'ye yaklaşmak için kullanılmazlar.

Spigot algoritmaları

1995'te π'ye yeni araştırma yolları açan iki algoritma keşfedildi. Musluktan damlayan su gibi, hesaplandıktan sonra tekrar kullanılmayan π'nin tek basamaklarını ürettikleri için olarak adlandırılırlar. Bu, nihai sonuç üretilene kadar tüm ara basamakları tutan ve kullanan sonsuz seri veya yinelemeli algoritmaların tersidir.

Matematikçiler ve Stanley Rabinowitz 1995'te basit bir musluk algoritması ürettiler. Hızı, arctan algoritmalarıyla karşılaştırılabilir, ancak yinelemeli algoritmalar kadar hızlı değildir.

Başka bir musluk algoritması olan rakam çıkarma algoritması, 1995 yılında Simon Plouffe tarafından keşfedildi:

$${\displaystyle \pi =\sum _{k=0}^{\infty }{\frac {1}{16^{k}}}\left({\frac {4}{8k+1}}-{\frac {2}{8k+4}}-{\frac {1}{8k+5}}-{\frac {1}{8k+6}}\right).}$$

Bu formül, kendisinden önceki diğerlerinin aksine, önceki tüm basamakları hesaplamadan π'nin herhangi bir onaltılık basamağını üretebilir. Bireysel ikili basamaklar, bireysel onaltılık basamaklardan çıkarılabilir ve sekizlik basamaklar, bir veya iki onaltılık basamaktan çıkarılabilir. Algoritmanın varyasyonları keşfedildi, ancak ondalık basamakları hızla üreten hiçbir basamak çıkarma algoritması henüz bulunamadı. Rakam çıkarma algoritmalarının önemli bir uygulaması, kayıt π hesaplamalarının yeni iddialarını doğrulamaktır: Yeni bir kayıt talep edildikten sonra, ondalık sonuç onaltılığa dönüştürülür ve ardından sona yakın birkaç rastgele onaltılık basamağı hesaplamak için bir basamak çıkarma algoritması kullanılır; eşleşirlerse, bu, tüm hesaplamanın doğru olduğuna dair bir güven ölçüsü sağlar.

1998 ve 2000 yılları arasında, dağıtılmış bilgi işlem projesi , 0 olduğu ortaya çıkan π'nin katrilyonuncu (10¹⁵th) bitini hesaplamak için (BBP algoritmasının bir modifikasyonu) kullandı. Eylül 2010'da bir Yahoo! çalışanı şirketin uygulamasını 23 günlük bir süre boyunca bin bilgisayarda iki katrilyonuncu (2×10¹⁵th) bitte 256 bit π'yi hesaplamak için kullandı ki bu yine sıfırdır.

Matematikteki rol ve karakterizasyonlar

π daire ile yakından ilişkili olduğu için geometri ve trigonometri alanlarındaki birçok formülde, özellikle daireler, küreler veya elipslerle ilgili olanlarda bulunur. İstatistik, fizik, Fourier analizi ve sayı teorisi gibi diğer bilim dalları da bazı önemli formüllerinde π'yi içerir.

Geometri ve trigonometri

Dairenin alanı gölgeli alanın π katına eşittir. birim çember'in alanı π'dir.

π, elips, küre, koni ve simit (geometri) gibi dairelere dayalı geometrik şekillerin alan ve hacim formüllerinde görünür. π içeren daha yaygın formüllerden bazıları aşağıdadır.

• Yarıçapı r olan bir çemberin çevresi 2πr'dir.
• Yarıçapı r olan dairenin alanı πr²'dir.
• Yarı büyük ekseni a ve yarı küçük ekseni b olan bir elipsin alanı πab'dır.
• Yarıçapı r olan bir kürenin hacmi 4/3πr³'dir.
• Yarıçapı r olan bir kürenin yüzey alanı 4πr²'dir.

Yukarıdaki formüllerden bazıları, aşağıda verilen n-boyutlu topun hacminin ve onun sınırı olan (n-1)-boyutlu kürenin yüzey alanının özel durumlarıdır.

Dairelerin dışında, sabit genişlikte başka eğriler de vardır. Barbier teoremine göre, sabit genişliğe sahip her eğrinin çevresi, genişliğinin π katıdır. Reuleaux üçgeni (üç dairenin yarıçapları olarak bir eşkenar üçgenin kenarlarıyla kesişmesinden oluşur) genişliği için mümkün olan en küçük alana ve daire en büyüğüne sahiptir. Dairesel olmayan pürüzsüz ve hatta sabit genişlikte de vardır.

Daireler tarafından oluşturulan şekillerin çevresini, alanını veya hacmini tanımlayan Belirli integraller, tipik olarak π içeren değerlere sahiptir. Örneğin, 1 yarıçaplı bir çemberin alanının yarısını belirten bir integral şu şekilde verilir:

$${\displaystyle \int _{-1}^{1}{\sqrt {1-x^{2}}}\,dx={\frac {\pi }{2}}.}$$

Bu integralde, √1 − x² işlevi bir yarım dairenin ${\displaystyle x}$ ekseni üzerindeki yüksekliği temsil eder (karekök, Pisagor teoreminin bir sonucudur) ve integral, 'nin altındaki alanı hesaplar.

Açı birimleri

Sinüs ve kosinüs fonksiyonları 2π periyot ile tekrarlanır.

Trigonometrik fonksiyonlar açılara dayanır ve matematikçiler genellikle ölçüm birimi olarak radyan kullanır. π, tam bir daire 2π radyanlık bir açıyı kaplayacak şekilde tanımlanan radyan cinsinden ölçülen açılarda önemli bir rol oynar. 180°'nin açı ölçüsü π radyan ve 1° = π/180 radyan'a eşittir.

Yaygın trigonometrik fonksiyonlar, π'nin katları olan periyotlara sahiptir; örneğin, sinüs ve kosinüsün periyodu 2π'dir, dolayısıyla herhangi bir θ açısı ve herhangi bir k tam sayısı için,

$${\displaystyle \sin \theta =\sin \left(\theta +2\pi k\right){\text{ and }}\cos \theta =\cos \left(\theta +2\pi k\right).}$$

Yaklaşık değeri

Pi sayısının bazı yaklaşık değerleri şu şekildedir:

• Bölümler: 22/7, 333/106, 355/113, 52163/16604, 103993/33102 ve 245850922/78256779.*
• Onlu sayı sistemi : İlk yüz basamak; 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 ....
• İkili sayı sistemi: 11.001001000011111101101010100010001000010110100011 ....
• Üçlü sayı sistemi: 10.010211012222010211002111110221222220111201212121 ....
• On altılı sayı sistemi:3.243F6A8885A308D31319 ....
• : 3;8,29,44,1

Pi (π) formülleri

Pi (π) formüllerinden başlıcaları şunlardır:^[]

:

${\displaystyle \pi ={3}+{\frac {4}{{3^{3}}-3}}-{\frac {4}{{5^{3}}-5}}+{\frac {4}{{7^{3}}-7}}-{\frac {4}{{9^{3}}-9}}+...}$

${\displaystyle \pi ={3}+{\frac {4}{2\times 3\times 4}}-{\frac {4}{4\times 5\times 6}}+{\frac {4}{6\times 7\times 8}}-{\frac {4}{8\times 9\times 10}}+...}$

---

Franciscus Vieta:

${\displaystyle \pi =2\times {\frac {2}{\sqrt {2}}}\times {\frac {2}{\sqrt {2+{\sqrt {2}}}}}\times {\frac {2}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}\times {\frac {2}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}\times \cdots }$

---

:

${\displaystyle \pi =4\sum _{n=0}^{\infty }{\cfrac {(-1)^{n}}{2n+1}}=4\left({\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+-\cdots \right)\!={\cfrac {4}{1+{\cfrac {1^{2}}{2+{\cfrac {3^{2}}{2+{\cfrac {5^{2}}{2+\ddots }}}}}}}}\!}$

---

Isaac Newton:

${\displaystyle \pi =\sum _{n=0}^{\infty }{\cfrac {{2^{n+1}}\cdot {(n!)^{2}}}{(2n+1)!}}}$

---

Leonhard Euler:

${\displaystyle \pi =-i\ln(-1)}$

---

Bailey-:

${\displaystyle \pi =\sum _{n=0}^{\infty }{\biggl (}{\frac {1}{16}}{\biggr )}^{n}\left({\frac {4}{8n+1}}-{\frac {2}{8n+4}}-{\frac {1}{8n+5}}-{\frac {1}{8n+6}}\right)}$

---

Fabrice Bellard:

${\displaystyle \pi =\sum _{n=0}^{\infty }{\frac {1}{2^{6}}}{\biggl (}{\frac {-1}{2^{10}}}{\biggr )}^{n}\left(-{\frac {2^{5}}{4n+1}}-{\frac {1}{4n+3}}+{\frac {2^{8}}{10n+1}}-{\frac {2^{6}}{10n+3}}-{\frac {2^{2}}{10n+5}}-{\frac {2^{2}}{10n+7}}+{\frac {1}{10n+9}}\right)\!}$

---

-:

${\displaystyle \pi =\sum _{n=0}^{\infty }{\biggl (}{\frac {-1}{4}}{\biggr )}^{n}\left({\frac {2}{4n+1}}+{\frac {2}{4n+2}}+{\frac {1}{4n+3}}\right)}$

Ayrıca bakınız

• Geometri
• Pi Günü

Notlar

1. ^ Özellikle, π'nin bir olduğu varsayılıyor, bu da basamaklarında, tüm tabanlarda belirli bir tür istatistiksel rastgelelik anlamına geliyor
2. ^ The precise integral that Weierstrass used was ${\displaystyle \pi =\int _{-\infty }^{\infty }{\frac {dx}{1+x^{2}}}.}$ Remmert 2012, s. 148
3. ^ Gösterilen polinom, sinüs fonksiyonunun Taylor serisi açılımının ilk birkaç terimidir.

Kaynakça

1. ^ . 9 Temmuz 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Temmuz 2015. 
2. ^ Andrews, Askey & Roy 1999, s. 59.
3. ^ Gupta, R. C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. 14 (1–4): 68-71. 
4. ^ ^{a b c} (1706). Synopsis Palmariorum Matheseos. Londra: J. Wale. ss. 243, 263. There are various other ways of finding the Lengths, or Areas of particular Curve Lines or Planes, which may very much facilitate the Practice; as for instance, in the Circle, the Diameter is to Circumference as 1 to
   ${\displaystyle {\overline {{\tfrac {16}{5}}-{\tfrac {4}{239}}}}-{\tfrac {1}{3}}{\overline {{\tfrac {16}{5^{3}}}-{\tfrac {4}{239^{3}}}}}+{\tfrac {1}{5}}{\overline {{\tfrac {16}{5^{5}}}-{\tfrac {4}{239^{5}}}}}-,\,\&c.=}$
   3.14159, &c. = π. This Series (among others for the same purpose, and drawn from the same Principle) I receiv'd from the Excellent Analyst, and my much Esteem'd Friend Mr. ; and by means thereof, 's Number, or that in Art. 64.38. may be Examin'd with all desireable Ease and Dispatch. 

   Reprinted in Smith, David Eugene (1929). "William Jones: The First Use of π for the Circle Ratio". A Source Book in Mathematics. McGraw–Hill. ss. 346-347. 

5. ^ "π^e trillion digits of π". pi2e.ch. 6 Aralık 2016 tarihinde kaynağından . 
6. ^ (14 Mart 2019). "Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes' constant on Google Cloud". Google Cloud Platform. 19 Ekim 2019 tarihinde kaynağından . Erişim tarihi: 12 Nisan 2019. 
7. ^ Arndt & Haenel 2006, s. 17.
8. ^ Bailey, David H.; Plouffe, Simon M.; Borwein, Peter B.; Borwein, Jonathan M. (1997). "The quest for PI". . 19 (1): 50-56. CiteSeerX 10.1.1.138.7085 $2. doi:10.1007/BF03024340. ISSN 0343-6993. 
9. ^ ^{a b} Oughtred, William (1652). Theorematum in libris Archimedis de sphaera et cylindro declarario (Latince). Excudebat L. Lichfield, Veneunt apud T. Robinson. δ.π :: semidiameter. semiperipheria 
10. ^ "pi". Dictionary.reference.com. 2 Mart 1993. 28 Temmuz 2014 tarihinde kaynağından . Erişim tarihi: 18 Haziran 2012. 
11. ^ ^{a b c} Arndt & Haenel 2006, s. 8.
12. ^ . Calculus. 1 (2.2yıl=1967 bas.). Wiley. s. 102. From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length 
13. ^ ^{a b c} Remmert 2012, s. 129.
14. ^ Baltzer, Richard (1870). Die Elemente der Mathematik [The Elements of Mathematics] (Almanca). Hirzel. s. 195. 14 Eylül 2016 tarihinde kaynağından . 
15. ^ Landau, Edmund (1934). Einführung in die Differentialrechnung und Integralrechnung (Almanca). Noordoff. s. 193. 
16. ^ ^{a b} Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. s. 183. ISBN . 
17. ^ Rudin, Walter (1986). Real and complex analysis. McGraw-Hill. s. 2. 
18. ^ Ahlfors, Lars (1966). Complex analysis. McGraw-Hill. s. 46. 
19. ^ Bourbaki, Nicolas (1981). Topologie generale. §VIII.2: Springer. 
20. ^ Bourbaki, Nicolas (1979). Fonctions d'une variable réelle (Fransızca). §II.3: Springer. 
21. ^ ^{a b} Arndt & Haenel 2006, s. 5.
22. ^ Salikhov, V. (2008). "On the Irrationality Measure of pi". Russian Mathematical Surveys. 53 (3): 570-572. Bibcode:2008RuMaS..63..570S. doi:10.1070/RM2008v063n03ABEH004543. 
23. ^ Arndt & Haenel 2006, ss. 22–23.
24. ^ Arndt & Haenel 2006, ss. 22, 28–30.
25. ^ Arndt & Haenel 2006, s. 3.
26. ^ Arndt & Haenel 2006, s. 6.
27. ^ Posamentier & Lehmann 2004, s. 25
28. ^ Eymard & Lafon 2004, s. 129
29. ^ Beckmann, Peter (1989) [1974]. History of Pi. St. Martin's Press. s. 37. ISBN . 
30. ^ Schlager, Neil; Lauer, Josh (2001). Science and Its Times: Understanding the Social Significance of Scientific Discovery. Gale Group. ISBN . 13 Aralık 2019 tarihinde kaynağından . Erişim tarihi: 19 Aralık 2019. , p. 185.
31. ^ ^{a b} Eymard & Lafon 2004, s. 78
32. ^ Arndt & Haenel 2006, s. 33.
33. ^ ^{a b} Mollin, R. A. (1999). "Continued fraction gems". Nieuw Archief voor Wiskunde. 17 (3): 383-405. MR 1743850. 
34. ^ Lange, L.J. (May 1999). "An Elegant Continued Fraction for π". . 106 (5): 456-458. doi:10.2307/2589152. JSTOR 2589152. 
35. ^ Arndt & Haenel 2006, s. 240.
36. ^ Arndt & Haenel 2006, s. 242.
37. ^ Kennedy, E.S. (1978). "Abu-r-Raihan al-Biruni, 973–1048". Journal for the History of Astronomy. 9: 65. Bibcode:1978JHA.....9...65K. doi:10.1177/002182867800900106.  Ptolemy used a three-sexagesimal-digit approximation, and Jamshīd al-Kāshī expanded this to nine digits; see Aaboe, Asger (1964). Episodes from the Early History of Mathematics. New Mathematical Library. 13. New York: Random House. s. 125. ISBN . 29 Kasım 2016 tarihinde kaynağından . 
38. ^ Abramson 2014, Section 8.5: Polar form of complex numbers.
39. ^ ^{a b} Bronshteĭn & Semendiaev 1971, s. 592
40. ^ Maor, Eli (2009). E: The Story of a Number. Princeton University Press. s. 160. ISBN . 
41. ^ Andrews, Askey & Roy 1999, s. 14.
42. ^ ^{a b} Arndt & Haenel 2006, s. 167.
43. ^ Herz-Fischler, Roger (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. ss. 67-77, 165-166. ISBN . 29 Kasım 2016 tarihinde kaynağından . Erişim tarihi: 5 Haziran 2013. 
44. ^ Plofker, Kim (2009). Mathematics in India. Princeton University Press. s. 27. ISBN . 
45. ^ Arndt & Haenel 2006, s. 170.
46. ^ Arndt & Haenel 2006, ss. 175, 205.
47. ^ (2014). "The life of π: from Archimedes to ENIAC and beyond". Sidoli, Nathan; Van Brummelen, Glen (Ed.). From Alexandria, through Baghdad: Surveys and studies in the ancient Greek and medieval Islamic mathematical sciences in honor of J. L. Berggren. Heidelberg: Springer. ss. 531-561. doi:10.1007/978-3-642-36736-6_24. MR 3203895. 
48. ^ Arndt & Haenel 2006, s. 171.
49. ^ Arndt & Haenel 2006, s. 176.
50. ^ Boyer & Merzbach 1991, s. 168.
51. ^ Arndt & Haenel 2006, ss. 15–16, 175, 184–186, 205. Grienberger achieved 39 digits in 1630; Sharp 71 digits in 1699.
52. ^ Arndt & Haenel 2006, ss. 176–177.
53. ^ ^{a b} Boyer & Merzbach 1991, s. 202
54. ^ Arndt & Haenel 2006, s. 177.
55. ^ Arndt & Haenel 2006, s. 178.
56. ^ Arndt & Haenel 2006, s. 179.
57. ^ ^{a b} Arndt & Haenel 2006, s. 180.
58. ^ Azarian, Mohammad K. (2010). "al-Risāla al-muhītīyya: A Summary". Missouri Journal of Mathematical Sciences. 22 (2): 64-85. doi:10.35834/mjms/1312233136 . 
59. ^ O'Connor, John J.; Robertson, Edmund F. (1999). "Ghiyath al-Din Jamshid Mas'ud al-Kashi". MacTutor History of Mathematics archive. 12 Nisan 2011 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2012. 
60. ^ ^{a b c} Arndt & Haenel 2006, s. 182.
61. ^ Arndt & Haenel 2006, ss. 182–183.
62. ^ Arndt & Haenel 2006, s. 183.
63. ^ (1630). (PDF) (Latince). 1 Şubat 2014 tarihinde kaynağından (PDF) arşivlendi.  His evaluation was 3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199.
64. ^ Brezinski, C. (2009). "Some pioneers of extrapolation methods". ; Cools, Ronald (Ed.). The Birth of Numerical Analysis. World Scientific. ss. 1-22. doi:10.1142/9789812836267_0001. ISBN . 25 Mart 2023 tarihinde kaynağından . Erişim tarihi: 15 Nisan 2023. 
65. ^ Yoder, Joella G. (1996). "Following in the footsteps of geometry: The mathematical world of Christiaan Huygens". De Zeventiende Eeuw. 12: 83-93. 12 Mayıs 2021 tarihinde kaynağından . Erişim tarihi: 15 Nisan 2023 – vasıtasıyla. 
66. ^ Arndt & Haenel 2006, ss. 185–191
67. ^ ^{a b c} Roy, Ranjan (1990). "The Discovery of the Series Formula for π by Leibniz, Gregory and Nilakantha" (PDF). Mathematics Magazine. 63 (5): 291-306. doi:10.1080/0025570X.1990.11977541. 14 Mart 2023 tarihinde kaynağından (PDF). Erişim tarihi: 15 Nisan 2023. 
68. ^ Arndt & Haenel 2006, ss. 185–186.
69. ^ Joseph, George Gheverghese (1991). The Crest of the Peacock: Non-European Roots of Mathematics. Princeton University Press. s. 264. ISBN . 
70. ^ Arndt & Haenel 2006, s. 187.
71. ^  A060294
72. ^ Vieta, Franciscus (1593). Variorum de rebus mathematicis responsorum. VIII. 
73. ^ ^{a b} Arndt & Haenel 2006, s. 188. Newton quoted by Arndt.
74. ^ Eymard & Lafon 2004, ss. 53–54
75. ^ Cooker, M.J. (2011). (PDF). Mathematical Gazette. 95 (533): 218-226. doi:10.1017/S0025557200002928. 4 Mayıs 2019 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 15 Nisan 2023. 
76. ^ Arndt & Haenel 2006, s. 189.
77. ^ Tweddle, Ian (1991). "John Machin and Robert Simson on Inverse-tangent Series for π". Archive for History of Exact Sciences. 42 (1): 1-14. doi:10.1007/BF00384331. JSTOR 41133896. 
78. ^ Arndt & Haenel 2006, ss. 192–193.
79. ^ ^{a b} Arndt & Haenel 2006, ss. 72–74
80. ^ (1938). "On Arccotangent Relations for π" (PDF). American Mathematical Monthly. 45 (10): 657-664 Published by: Mathematical Association of America. doi:10.1080/00029890.1938.11990873. JSTOR 2302434. 7 Mart 2023 tarihinde kaynağından (PDF). Erişim tarihi: 15 Nisan 2023. 
81. ^ Roy, Ranjan (2021) [1st ed. 2011]. Series and Products in the Development of Mathematics. 1 (2 bas.). Cambridge University Press. ss. 215-216, 219-220. 

    Newton, Isaac (1971). (Ed.). The Mathematical Papers of Isaac Newton. 4, 1674–1684. Cambridge University Press. ss. 526-653. 

82. ^ Sandifer, Ed (2009). (PDF). How Euler Did It. 19 Mart 2014 tarihinde kaynağından (PDF) arşivlendi.  Reprinted in Sandifer, Ed (2014). How Euler Did Even More. Mathematical Association of America. ss. 109-118. 

    Euler, Leonhard (1755). "§2.2.30". (Latince). Academiae Imperialis Scientiarium Petropolitanae. s. 318. E 212. 

    Euler, Leonhard (1798) [written 1779]. "Investigatio quarundam serierum, quae ad rationem peripheriae circuli ad diametrum vero proxime definiendam maxime sunt accommodatae". Nova acta academiae scientiarum Petropolitinae. 11: 133-149, 167-168. E 705. 

    Chien-Lih, Hwang (2004). "88.38 Some Observations on the Method of Arctangents for the Calculation of π". Mathematical Gazette. 88 (512): 270-278. doi:10.1017/S0025557200175060. 

    Chien-Lih, Hwang (2005). "89.67 An elementary derivation of Euler's series for the arctangent function". Mathematical Gazette. 89 (516): 469-470. doi:10.1017/S0025557200178404. 

83. ^ Arndt & Haenel 2006, ss. 192–196, 205.
84. ^ Arndt & Haenel 2006, ss. 194–196
85. ^ Hayes, Brian (September 2014). "Pencil, Paper, and Pi". American Scientist. 102 (5). s. 342. doi:10.1511/2014.110.342. 22 Ocak 2022 tarihinde kaynağından . Erişim tarihi: 22 Ocak 2022. 
86. ^ Borwein, J.M.; Borwein, P.B. (1988). "Ramanujan and Pi". Scientific American. 256 (2): 112-117. Bibcode:1988SciAm.258b.112B. doi:10.1038/scientificamerican0288-112. 
    Arndt & Haenel 2006, ss. 15–17, 70–72, 104, 156, 192–197, 201–202
87. ^ Arndt & Haenel 2006, ss. 69–72.
88. ^ Borwein, J.M.; Borwein, P.B.; Dilcher, K. (1989). "Pi, Euler Numbers, and Asymptotic Expansions". American Mathematical Monthly. 96 (8): 681-687. doi:10.2307/2324715. hdl:1959.13/1043679 . JSTOR 2324715. 
89. ^ Arndt & Haenel 2006, Formula 16.10, p. 223.
90. ^ Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised bas.). Penguin. s. 35. ISBN . 
91. ^ Posamentier & Lehmann 2004, s. 284
92. ^ Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", reprinted in Berggren, Borwein & Borwein 1997, ss. 129–140
93. ^ (1882). "Über die Ludolph'sche Zahl". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin. 2: 679-682. 
94. ^ Arndt & Haenel 2006, s. 196.
95. ^ Hardy and Wright 1938 and 2000: 177 footnote § 11.13–14 references Lindemann's proof as appearing at Math. Ann. 20 (1882), 213–225.
96. ^ cf Hardy and Wright 1938 and 2000:177 footnote § 11.13–14. The proofs that e and π are transcendental can be found on pp. 170–176. They cite two sources of the proofs at Landau 1927 or Perron 1910; see the "List of Books" at pp. 417–419 for full citations.
97. ^ ^{a b} Cajori, Florian (2007). A History of Mathematical Notations: Vol. II (İngilizce). Cosimo, Inc. ss. 8-13. ISBN . the ratio of the length of a circle to its diameter was represented in the fractional form by the use of two letters ... J.A. Segner ... in 1767, he represented 3.14159... by δ:π, as did Oughtred more than a century earlier 
98. ^ {{{Kaynakça}}}
    See p. 220: used the letter π to represent the periphery (that is, the circumference) of a circle.
99. ^ ^{a b} Smith, David E. (1958). History of Mathematics (İngilizce). Courier Corporation. s. 312. ISBN . 
100. ^ Archibald, R.C. (1921). "Historical Notes on the Relation e^−(π/2) = iⁱ". The American Mathematical Monthly. 28 (3): 116-121. doi:10.2307/2972388. JSTOR 2972388. It is noticeable that these letters are never used separately, that is, π is not used for 'Semiperipheria' 
101. ^ ^{a b c} Arndt & Haenel 2006, s. 166.
102. ^ See, for example, Oughtred, William (1648). Clavis Mathematicæ [The key to mathematics] (Latince). Londra: Thomas Harper. s. 69.  (English translation: Oughtred, William (1694). Key of the Mathematics (İngilizce). J. Salusbury. )
103. ^ Barrow, Isaac (1860). "Lecture XXIV". Whewell, William (Ed.). The mathematical works of Isaac Barrow (Latince). Harvard University. Cambridge University press. s. 381. 
104. ^ Gregorius, David (1695). "Ad Reverendum Virum D. Henricum Aldrich S.T.T. Decanum Aedis Christi Oxoniae". Philosophical Transactions (Latince). 19 (231): 637-652. Bibcode:1695RSPT...19..637G. doi:10.1098/rstl.1695.0114 . JSTOR 102382. 
105. ^ Arndt & Haenel 2006, s. 165: A facsimile of Jones' text is in Berggren, Borwein & Borwein 1997, ss. 108–109.
106. ^ Segner, Joannes Andreas (1756). Cursus Mathematicus (Latince). Halae Magdeburgicae. s. 282. 15 Ekim 2017 tarihinde kaynağından . Erişim tarihi: 15 Ekim 2017. 
107. ^ Euler, Leonhard (1727). "Tentamen explicationis phaenomenorum aeris" (PDF). Commentarii Academiae Scientiarum Imperialis Petropolitana (Latince). 2: 351. E007. 1 Nisan 2016 tarihinde kaynağından (PDF). Erişim tarihi: 15 Ekim 2017. Sumatur pro ratione radii ad peripheriem, I : π  English translation by Ian Bruce 10 Haziran 2016 tarihinde Wayback Machine sitesinde .: "π is taken for the ratio of the radius to the periphery [note that in this work, Euler's π is double our π.]"
108. ^ Euler, Leonhard (1747). Henry, Charles (Ed.). Lettres inédites d'Euler à d'Alembert. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche (Fransızca). 19 (1886 tarihinde yayınlandı). s. 139. E858. Car, soit π la circonference d'un cercle, dout le rayon est = 1  English translation in Cajori, Florian (1913). "History of the Exponential and Logarithmic Concepts". The American Mathematical Monthly. 20 (3): 75-84. doi:10.2307/2973441. JSTOR 2973441. Letting π be the circumference (!) of a circle of unit radius 
109. ^ Euler, Leonhard (1736). "Ch. 3 Prop. 34 Cor. 1". Mechanica sive motus scientia analytice exposita. (cum tabulis) (Latince). 1. Academiae scientiarum Petropoli. s. 113. E015. Denotet 1 : π rationem diametri ad peripheriam  English translation by Ian Bruce 10 Haziran 2016 tarihinde Wayback Machine sitesinde . : "Let 1 : π denote the ratio of the diameter to the circumference"
110. ^ Euler, Leonhard (1707–1783) (1922). Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio (Latince). Lipsae: B.G. Teubneri. ss. 133-134. E101. 16 Ekim 2017 tarihinde kaynağından . Erişim tarihi: 15 Ekim 2017. 
111. ^ Segner, Johann Andreas von (1761). Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm (Latince). Renger. s. 374. Si autem π notet peripheriam circuli, cuius diameter eſt 2 
112. ^ Arndt & Haenel 2006, s. 205.
113. ^ ^{a b} Arndt & Haenel 2006, s. 197.
114. ^ Reitwiesner, George (1950). "An ENIAC Determination of pi and e to 2000 Decimal Places". Mathematical Tables and Other Aids to Computation. 4 (29): 11-15. doi:10.2307/2002695. JSTOR 2002695. 
115. ^ Arndt & Haenel 2006, ss. 15–17.
116. ^ Arndt & Haenel 2006, s. 131.
117. ^ Arndt & Haenel 2006, ss. 132, 140.
118. ^ ^{a b} Arndt & Haenel 2006, s. 87.
119. ^ Arndt & Haenel 2006, ss. 111 (5 times); pp. 113–114 (4 times). For details of algorithms, see Borwein, Jonathan; Borwein, Peter (1987). Pi and the AGM: a Study in Analytic Number Theory and Computational Complexity. Wiley. ISBN . 
120. ^ ^{a b c} Bailey, David H. (16 Mayıs 2003). "Some Background on Kanada's Recent Pi Calculation" (PDF). 15 Nisan 2012 tarihinde kaynağından (PDF). Erişim tarihi: 12 Nisan 2012. 
121. ^ Arndt & Haenel 2006, ss. 17–19
122. ^ Schudel, Matt (25 Mart 2009). "John W. Wrench, Jr.: Mathematician Had a Taste for Pi". The Washington Post. s. B5. 
123. ^ Connor, Steve (8 Ocak 2010). "The Big Question: How close have we come to knowing the precise value of pi?". The Independent. Londra. 2 Nisan 2012 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2012. 
124. ^ Arndt & Haenel 2006, s. 18.
125. ^ Arndt & Haenel 2006, ss. 103–104
126. ^ Arndt & Haenel 2006, s. 104
127. ^ Arndt & Haenel 2006, ss. 104, 206
128. ^ Arndt & Haenel 2006, ss. 110–111
129. ^ Eymard & Lafon 2004, s. 254
130. ^ ^{a b} ; (2016). "15.2 Computational records". Pi: The Next Generation, A Sourcebook on the Recent History of Pi and Its Computation. Springer International Publishing. s. 469. doi:10.1007/978-3-319-32377-0. ISBN . 
131. ^ Cassel, David (11 Haziran 2022). "How Google's Emma Haruka Iwao Helped Set a New Record for Pi". The New Stack. 11 Haziran 2022 tarihinde kaynağından . Erişim tarihi: 15 Nisan 2023. 
132. ^ (April 2006). "Identities inspired by Ramanujan's Notebooks (part 2)" (PDF). 14 Ocak 2012 tarihinde kaynağından (PDF). Erişim tarihi: 10 Nisan 2009. 
133. ^ Arndt & Haenel 2006, s. 39
134. ^ Arndt & Haenel 2006, ss. 39–40
     Posamentier & Lehmann 2004, s. 105
135. ^ (1960). "Projection Constants". . 95 (3): 451-465. doi:10.1090/s0002-9947-1960-0114110-9 . 
136. ^ Arndt & Haenel 2006, ss. 43
     Posamentier & Lehmann 2004, ss. 105–108
137. ^ ^{a b} Arndt & Haenel 2006, ss. 77–84.
138. ^ ^{a b} (2006). "Unbounded spigot algorithms for the digits of pi" (PDF). . 113 (4): 318-328. doi:10.2307/27641917. JSTOR 27641917. MR 2211758. 23 Mart 2023 tarihinde kaynağından (PDF). Erişim tarihi: 15 Nisan 2023. 
139. ^ ^{a b} Arndt & Haenel 2006, s. 77.
140. ^ Rabinowitz, Stanley; Wagon, Stan (March 1995). "A spigot algorithm for the digits of Pi". American Mathematical Monthly. 102 (3): 195-203. doi:10.2307/2975006. JSTOR 2975006. 
141. ^ Arndt & Haenel 2006, ss. 117, 126–128.
142. ^ Arndt & Haenel 2006, s. 128. Plouffe did create a decimal digit extraction algorithm, but it is slower than full, direct computation of all preceding digits.
143. ^ Arndt & Haenel 2006, s. 20
     Bellards formula in: Bellard, Fabrice. . 12 Eylül 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Ekim 2007. 
144. ^ Palmer, Jason (16 Eylül 2010). "Pi record smashed as team finds two-quadrillionth digit". BBC News. 17 Mart 2011 tarihinde kaynağından . Erişim tarihi: 26 Mart 2011. 
145. ^ Bronshteĭn & Semendiaev 1971, ss. 200, 209
146. ^ Martini, Horst; Montejano, Luis; (2019). Bodies of Constant Width: An Introduction to Convex Geometry with Applications. Birkhäuser. doi:10.1007/978-3-030-03868-7. ISBN . MR 3930585. 

     See Barbier's theorem, Corollary 5.1.1, p. 98; Reuleaux triangles, pp. 3, 10; smooth curves such as an analytic curve due to Rabinowitz, § 5.3.3, pp. 111–112.

147. ^ Herman, Edwin; (2016). "Section 5.5, Exercise 316". Calculus. 1. . s. 594. 
148. ^ Abramson 2014, Section 5.1: Angles.
149. ^ Eymard, Pierre; Lafon, Jean Pierre (1999). The Number Pi. American Mathematical Society. ISBN . 
150. ^ Arndt & Haenel 2006, s. 240
151. ^ Arndt & Haenel 2006, s. 242
152. ^ . www.pi314.net. 13 Temmuz 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Mart 2022. 
153. ^ . www.pi314.net. 2 Temmuz 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Mart 2022. 

Dış bağlantılar

• Pi Çılgınlığı 18 Mayıs 2012 tarihinde Wayback Machine sitesinde . (Türkçe)
• (İngilizce)
• Project Gutenberg'de π'nin detaylı değeri 1 Temmuz 2004 tarihinde Wayback Machine sitesinde . (İngilizce)
• Pi formülleri ve online pi hesabı 26 Mayıs 2011 tarihinde Wayback Machine sitesinde . (İngilizce)