Tam sayılar,sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar (1, 2, 3, …) ve bunların negatif değerlerinden oluşan negatif sayılardan (−1, −2, −3, …) oluşan sayı kümesidir.

Tüm tam sayıların oluşturduğu küme, çoğunlukla kalın harf biçimindeki Z veya kullanılarak şeklinde ifade edilir. Z harfi Almanca Zahlen (sayılar) sözcüğünden gelir.
Doğal sayılar kümesi , tam sayılar kümesinin bir alt kümesi olarak tanımlanır. Bu tam sayılar kümesi, ardından tüm rasyonel sayılar kümesi ’nun ve bu küme de reel sayılar kümesi ’nin bir alt kümesi olarak sıralanır. Doğal sayılar kümesine benzer biçimde, tam sayılar kümesi de özelliği gösterir. Tam sayı kavramı, kesirli bir kısmı bulunmayan ve böylelikle doğrudan reel sayı olarak ifade edilebilen sayılar için kullanılır. Mesela, 21, 4, 0 ve -2048 tam sayılardır; buna karşın 9.75, 512 ve √2 tam sayı olarak değerlendirilmez.
Doğal sayı kümelerini kapsayan yapılar içerisinde, tam sayılar hem en minimal grup hem de en minimal halka yapısını teşkil ederler. Cebirsel sayı teorisi alanında, tam sayılar zaman zaman, onları daha geniş bir kapsamda ele alınan ile karıştırmamak adına rasyonel tam sayılar olarak özel bir şekilde tanımlanır. Gerçekte, rasyonel olarak ifade edilen tam sayılar, hem cebirsel tam sayı özelliklerini taşır hem de rasyonel sayılar kategorisinde değerlendirilirler.
Tarihçe
İlk Türkçe tam sayı teriminin kullanımlarından biri 1955'e dayanır.
Tarih boyunca tam sayı terimi, 1'in katları olan sayılar için veya (tam sayılı kesirlerin) tam kısımlarını ifade etmek için kullanılmıştır. Başlangıçta yalnızca pozitif tam sayılar ele alınmış ve bu durum, terimin doğal sayılarla eşanlamlı hale gelmesine yol açmıştır. Tam sayı kavramının tanımı, negatif sayıların faydasının zamanla kabul edilmesiyle genişletilmiş ve bu sayılar da tanımın içine dahil edilmiştir. Örneğin, Leonhard Euler, 1765 tarihli Cebirin Unsurları adlı çalışmasında tam sayıları, hem pozitif hem de negatif sayıları içerecek biçimde tanımlamıştır. Bununla birlikte, Avrupalı matematikçilerin büyük bir kısmı 19. yüzyılın ortalarına kadar negatif sayılar konseptine karşı direnç göstermiştir.
Tam sayılar kümesini temsil etmek üzere 'Z' harfinin tercih edilmesi, Almanca'da "sayılar" anlamına gelen Zahlen kelimesinden kaynaklanmaktadır ve bu bağlamda David Hilbert ile ilişkilendirilir. Bu notasyonun ders kitaplarında ilk defa kullanıldığı bilinen örnek, 1947 yılında Nicolas Bourbaki grubu tarafından kaleme alınan isimli eserde yer almaktadır. Notasyonun benimsenmesi hemen gerçekleşmemiştir; mesela, bir başka ders kitabında 'J' harfi kullanılmış ve 1960 yılında yayımlanan bir makalede 'Z', yalnızca sıfır ve pozitif tam sayıları ifade etmek amacıyla tercih edilmiştir. Ancak 1961 itibarıyla, modern cebir metinleri genel olarak 'Z' harfini, hem pozitif hem de negatif tam sayıları kapsayacak şekilde kullanmaya başlamışlardır.
sembolü, çeşitli kümeleri tanımlamak amacıyla farklı yazarların tercihlerine göre değişken notasyonlar ile sıklıkla sembolize edilir: Pozitif tam sayılar için , veya kullanılırken, sıfır ve pozitif tam sayılar için veya ve sıfır olmayan tam sayılar için tercih edilir. Bazı yazarlar, sıfır olmayan tam sayılar için kullanırken, diğerleri bu notasyonu sıfır ve pozitif tam sayılar için veya 'nin birimler grubunu (İng. unit (ring theory)) ifade eden {–1, 1} için kullanmaktadır. Ek olarak, notasyonu, ya modüler p tam sayılarını (yani, tam sayıların denklik sınıflarını) ya da p-adik tam sayılarını tanımlamak için kullanılır.
1950'lerin başlarına dek, bütün sayılar ile tam sayılar arasında bir eşanlamlılık söz konusuydu. 1950'lerin sonlarına doğru, hareketinin bir unsuru olarak, Amerikan ilkokul öğretmenleri "bütün sayılar" (İng. whole numbers) teriminin, negatif sayıları dışlayarak yalnızca doğal sayıları kapsadığını, "tam sayı" teriminin ise negatif sayıları da içerecek şekilde genişletildiğini derslerinde işlemeye başladılar. "Bütün sayı" kavramı (İng. whole numbers), günümüzde hala belirsizliğini sürdürmektedir.
Cebirsel özellikler

Doğal sayılar kümesi gibi, kümesi de toplama ve çarpma gibi ikili işlemler bakımından bir yapıya sahiptir; bu, herhangi iki tam sayının toplamının ve çarpımının yine bir tam sayı olacağı anlamına gelir. Bununla birlikte, negatif doğal sayıların ve özellikle 0'ın dahil edilmesi ile , doğal sayılar kümesinden farklı olarak, çıkarma işlemine yönelik de kapalı bir karakter gösterir.
Tam sayılar kümesi, her bir birimli halka yapısı için, bu yapılara doğru tam sayılardan tekil bir (İng. ring homomorphism) tesis edilebildiği, temel bir olarak işlev görür. Bu (İng. universal property), özgül olarak içerisinde bir (İng. initial object) olarak tanımlanabilirlik, halkasının ayırt edici niteliğini belirler.
kümesi, iki tam sayının birbirine bölünmesi işlemi (örnek olarak, 1 sayısının 2 sayısına bölünmesi durumu gösterilebilir) neticesinde her defasında tam sayı elde edilmeyebileceğinden, bölme işlemi açısından kapalı bir yapı sergilemez. Doğal sayılar kümesi, üs alma işlemine göre kapalılık özelliğine sahipken, tam sayılar kümesi bu özelliği taşımamaktadır; zira üssün negatif değer alması halinde, sonuç kesirli bir sayıya dönüşebilir.
Aşağıdaki tablo, herhangi bir a, b ve c tam sayısı için toplama ve çarpma işlemlerinin bazı temel özelliklerini listelemektedir:
| Toplama | Çarpma | |
|---|---|---|
| : | a + b bir tam sayıdır | a × b bir tam sayıdır |
| Birleşme: | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| Değişme: | a + b = b + a | a × b = b × a |
| Etkisiz elemanın varlığı: | a + 0 = a | a × 1 = a |
| varlığı: | a + (−a) = 0 | Tersinir tam sayılar (−1 ve 1 olarak adlandırılan ) dışında tersi olan tam sayı yoktur. |
| Dağılma: | a × (b + c) = (a × b) + (a × c) ve (a + b) × c = (a × c) + (b × c) | |
| Sıfır : | Eğer a × b = 0, o zaman a = 0 veya b = 0 (veya her ikisi) | |
Toplama işlemi çerçevesinde, kümesine ilişkin olarak sıralanan başlıca beş özelliğin tanımladığı yapı, bu kümenin bir abelyen grup olduğunu ifade eder. Bu küme, her biri sıfırdan farklı olan tam sayıların, sonlu bir 1 + 1 + ... + 1 veya (−1) + (−1) + ... + (−1) şeklindeki toplamları ile ifade edilebilirliği dolayısıyla, aynı zamanda bir özelliği taşır (İng. cyclic group). Gerçekte, toplama işlemi altında , herhangi bir sonsuz devirli grubun, ile olduğu bağlamda, tek sonsuz devirli gruptur.
Çarpma işlemine ilişkin olarak sıralanan ilk dört özelliğin tanımı, kümesinin çarpma altında bir değişmeli monoid yapısına sahip olduğunu gösterir. Ancak, 2 sayısının örneğinde olduğu gibi, her tam sayının çarpmaya ilişkin bir çarpımsal tersi bulunmamaktadır, bu durum kümesinin çarpma işlemi bağlamında bir grup oluşturmadığını ifade eder.
Yukarıda sunulan özellikler cetvelinden (en sonuncu dışında) elde edilen kuralların tümü, toplama ve çarpma işlemleriyle bir arada kümesinin, birimli değişmeli halka olarak tanımlandığını ortaya koyar. Bu yapı, benzer ait nesnelerin ilk örneğidir. içerisinde, değişkenlerin her bir değeri için gerçek olan, yalnızca herhangi bir birimli değişmeli halkada doğru kabul edilen eşitlikler ve ifadeler geçerlidir. Bazı sıfır olmayan tam sayılar, çeşitli halkalarda değerine karşılık gelir.
Tam sayılar kümesinde bulunmaması (özellikler tablosundaki son özellik), değişmeli halka 'nin, bir tamlık bölgesi olarak nitelendirilebileceğini gösterir.
Çarpmaya ilişkin ters elemanların eksikliği, bu durumun kümesinin bölme işlemine kapalı olmadığı gerçeği ile eşdeğer olduğundan, 'nin bir alan olarak tanımlanamayacağı anlamına gelir. Tam sayıları bir olarak barındıran en küçük alan yapı, rasyonel sayılar alanıdır. Tam sayılar kümesinden rasyonel sayılar kümesinin türetilmesi süreci, herhangi bir tamlık bölgesi için (İng. field of fractions) oluşturulması amacıyla modellenebilir. Ayrıca, bir cebirsel sayı alanından (rasyonel sayılara bir uzantı olarak) başlanarak, içerisinde kümesini de barındıran (İng. ring of integers) elde edilebilir.
Her ne kadar üzerinde geleneksel bölme işlemi tanımlanmamış olsa da, "kalan ile bölme" işlemi bu küme üzerinde tanımlanabilir. Bu işleme, Öklid bölmesi adı verilir ve şu kritik özelliği taşır: b ≠ 0 koşulunu sağlayan herhangi a ve b tam sayı çifti için, a = q × b + r ve 0 ≤ r < |b| ilişkilerini sağlayan benzersiz q ve r tams ayıları mevcuttur; burada |b|, b sayısının mutlak değerini ifade eder. Bu bağlamda, q tam sayısı bölüm, r ise a ile b'nin bölünmesi sonucu elde edilen kalan olarak isimlendirilir. En büyük ortak bölenlerin belirlenmesi sürecinde kullanılan Öklid algoritması, ardışık Öklid bölme işlemlerine dayanır.
İlgili metin, kümesinin bir (İng. Euclidean domain) olarak tanımlandığını belirtmektedir. Bu durum, aynı zamanda 'nin bir (İng. principal ideal domain) olduğunu gösterir ve her pozitif tam sayının, asal sayıların çarpımı şeklinde (İng. essentially unique) bir biçimde ifade edilebileceğini ima eder. Bu durum, aritmetiğin temel teoremi olarak bilinir.
Sıralama teorisine ilişkin özellikler
, herhangi bir özelliği gösteren, fakat ne üst ne de alt sınır içeren bir kümedir. kümesinin sıralama ilişkisi aşağıdaki gibi ifade edilir: :... −3 < −2 < −1 < 0 < 1 < 2 < 3 < ... Bir tam sayının sıfır değerinden büyük olması durumunda pozitif, sıfırdan küçük olması durumunda ise negatif olarak nitelendirilir. Sıfır değeri, ne negatif ne de pozitif olarak nitelendirilebilir.
Tam sayılar arasındaki sıralama ilişkisi, cebirsel işlemlerle aşağıdaki biçimde uyum içindedir:
a < b ve c < d olduğunda, a + c < b + d sonucu elde edilir. a < b ve 0 < c olduğunda, ac < bc eşitsizliği geçerlidir.
Bunun sonucu olarak, üzerinde tanımlanan bu sıralama ile birlikte, bir yapısını oluşturur.
Tam sayılar, pozitif elemanları iyi sıralı olan tek ciddi Abel grubudur. Bu, herhangi bir (İng. valuation ring) ya bir cisim—ya da (İng. discrete valuation ring) olduğu ifadesine eşdeğerdir.
Tanımlama
Geleneksel tanımlama
Temel eğitim süreçlerinde, tam sayı kavramı, genellikle pozitif doğal sayılar kümesi, sıfır ve doğal sayıların negatif karşılıklarının birleşimi olarak sezgisel bir yaklaşımla tanımlanmaktadır. Bu tanım, formal bir yapıya kavuşturulabilir: başlangıçta, Peano aksiyomları temel alınarak doğal sayılar kümesi inşa edilir. Ardından, kümesi ile her elemanı arasında birebir eşleme bulunan ve kümesinden ayrık bir kümesi tanımlanır. Bu bağlamda, kümesi için, örneğin, eşlemesi olacak şekilde formundaki sıralı çiftler seçilebilir. Son adımda, 0 elemanı, ne kümesinde ne de kümesinde yer almayacak şekilde, örneğin sıralı çifti olarak belirlenir. Böylelikle, tam sayılar kümesi, birleşimi ile tanımlanmış olur.
Geleneksel aritmetik işlemleri, tam sayılar kümesi üzerinde, pozitif sayılar, negatif sayılar ve sıfır olmak üzere, parçalı fonksiyonlar yardımıyla tanımlanabilir. Mesela, negasyon işlemi şu şekilde ifade edilir:
Geleneksel tanımlama yöntemi, çeşitlilik arz eden durumların ortaya çıkmasına neden olur (her aritmetik işlemin, tam sayı türlerinin her birinin kombinasyonları üzerine tanımlanması gereklidir) ve tam sayıların aritmetik yasalarına olan uyumunun ispatı sürecini oldukça yorucu bir hale getirir.
Sıralı ikili dizilerin eşdeğerlilik sınıfları

Çağdaş küme teorisine dayalı matematikte, aritmetik işlemilerin herhangi bir özgül durum ayrımına gerek kalmadan tanımlanabilmesine imkan veren daha soyut bir yapı tercih edilmektedir. Bu bağlamda, tam sayılar, doğal sayılardan oluşturulan çiftlerin denklik sınıfları olarak formel bir biçimde kurulabilir (a,b).
Sezgisel olarak, (a,b) ifadesi, b'nin a'dan çıkarılması sonucunu temsil eder.1 − 2 ile 4 − 5 gösterimlerinin aynı sayısal değeri temsil ettiği öngörümüzü teyit etmek amacıyla, bu ikili diziler üzerinde belirli bir kural çerçevesinde bir denklik ilişkisi ~ tanımlamaktayız:
yalnızca ve yalnızca
Tam sayılar üzerinde gerçekleştirilen toplama ve çarpım işlemleri, doğal sayılara uygulanan benzer işlemler temel alınarak tanımlanabilir;[(a,b)] gösterimi, içerisinde (a,b) ögesini barındıran denklik sınıfını ifade etmek için kullanılır ve bu durumda işlemler şu şekilde ifade edilir:
Bir tam sayının negatif değeri (veya toplamsal ters öge), ilgili ikilinin elemanlarının yer değiştirilmesiyle elde edilir:
Dolayısıyla, çıkartma işlemi, toplamsal ters ögenin eklenmesi şeklinde tanımlanabilir:
Tam sayılara ilişkin standart sıralama kuralı aşağıdaki gibi ifade edilir:
Bu tanımlamaların, denklik sınıflarının temsilcilerinin seçimiyle ilgisiz olduğu kolaylıkla ispatlanabilir.
Her bir denklik sınıfı, (n,0) veya (0,n) (veya her iki durum için de) formunda özgün bir elemana sahiptir. Doğal sayı n, [(n,0)] sınıfıyla özdeşleştirilmekte (yani doğal sayılar, n'yi [(n,0)]'ye eşleyen bir fonksiyon aracılığıyla tam sayılara ) ve [(0,n)] sınıfı −n olarak ifade edilir (bu durum, kalan tüm sınıfları kapsar ve [(0,0)] sınıfını −0 = 0 olduğundan yeniden tanımlar).
Dolayısıyla, [(a,b)] gösterimi aşağıdaki gibi ifade edilir:
Doğal sayıların, karşılık gelen tam sayılarla özdeşleştirilmesi durumunda (önceden bahsi geçen gömme metodu kullanılarak), bu gösterim yöntemi herhangi bir karmaşıklığa yol açmaz.
Bu gösterim yöntemi, tam sayıların {..., −2, −1, 0, 1, 2, ...} şeklindeki alışılagelmiş temsiline geri dönüş sağlar.
Örneklerden bazıları şu şekildedir:
Diğer yaklaşımlar
Teorik bilgisayar biliminde, tam sayıların inşası için otomatik teorem kanıtlama ve terim yeniden yazım motorları tarafından kullanılan diğer yaklaşımlar mevcuttur. Tam sayılar, birkaç temel işlem (örneğin, sıfır, bir sonraki, bir önceki) kullanılarak ve muhtemelen, zaten inşa edilmiş olduğu varsayılan doğal sayılar kullanılarak oluşturulan (İng. term algebra) olarak temsil edilir (örneğin, Peano yaklaşımı kullanılarak).
İşaretli tam sayıların oluşturulması amacıyla, en azından on farklı yöntem mevcuttur. Bu yapılar, çeşitli parametrelere göre ayrışır: Yapıyı gerçekleştirmek amacıyla başvurulan temel işlemlerin adedi, bu işlemlerin kabul ettiği argümanların sayısı ve nitelikleri (çoğunlukla 0 ile 2 arasında değişir); belirli işlemler için doğal sayıların argüman olarak kullanılıp kullanılmadığı ve işlemlerin serbest yapılandırıcı olup olmadığı, yani bir tam sayının tek veya birden çok cebirsel ifadeyle ifade edilebilirliği.
Bir önceki bölümde tanıtılan tam sayıların inşası yöntemi, iki doğal sayıyı argüman olarak alan ve sonucunda bir tam sayı (bu durumda x-y'ye eşit) veren tekil bir temel işlem olan çift işlemine dayanır. Bu işlem serbest nitelikte değildir; zira sıfır tam sayısı, çift(0,0), çift(1,1), çift(2,2) gibi çeşitli şekillerde ifade edilebilir. Bu inşa metodolojisi, yazılımı tarafından benimsenmiş olup; ancak, serbest yapılandırıcıları temel alan ve bilgisayar ortamlarında daha etkin bir şekilde implemente edilebilecek daha sade alternatif inşa teknikleri de mevcuttur.
Bilgisayar bilimi
Tam sayı, sıkça bilgisayar dililerindeki primitif bir veri tipidir. Ancak, tam sayı veri tipleri, pratik bilgisayarların sonlu kapasitesi nedeniyle tüm tam sayıların bir alt kümesini temsil edebilirler. Ayrıca, yaygın ikinin tümleyeni gösteriminde, işaretin içsel tanımı "negatif" ve "negatif olmayan" arasında ayrım yapar, "negatif, pozitif ve 0" değil. (Bununla birlikte, bir bilgisayarın bir tam sayı değerinin gerçekten pozitif olup olmadığını belirlemesi kesinlikle mümkündür.) Sabit uzunluklu tam sayı yaklaşım veri tipleri (veya alt kümeleri), birkaç programlama dilinde int veya Integer olarak adlandırılır (ALGOL 68, C, Java, Delphi, vb.).
Tam sayıların değişken uzunluklu temsilleri, bilgisayarın belleğine sığan herhangi bir tam sayıyı depolayabilir. Diğer tam sayı veri tipleri ise genellikle 2'nin bir kuvveti olan bir bit sayısı (4, 8, 16, vb.) veya akılda kalıcı bir ondalık basamak sayısı (örneğin, 9 veya 10) ile sabit bir boyutta uygulanır.
Sayallık (Kardinalite)
Tam sayılar kümesi sayılabilir sonsuzdur, bu da her tam sayının benzersiz bir doğal sayı ile eşleştirilebileceği anlamına gelir. Böyle bir eşleştirmenin bir örneği şöyledir:
- (0, 1), (1, 2), (−1, 3), (2, 4), (−2, 5), (3, 6), . . . , (1 − k, 2k − 1), (k, 2k ), . . .
Daha teknik bir ifadeyle, kardinalitesinin ℵ0 (alef-sıfır) ile eşit olduğu söylenir. ve elemanları arasındaki bu eşleştirme, bir bijection olarak adlandırılır.
Notlar
Ayrıca bakınız
|
Kaynakça
- ^ . www.dildernegi.org.tr. 26 Nisan 2014 tarihinde kaynağından arşivlendi. Erişim tarihi: 22 Ekim 2023.
- ^ Science and Technology Encyclopedia (İngilizce). University of Chicago Press. September 2000. s. 280. ISBN . 30 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 22 Şubat 2024.
- ^ a b c Miller, Jeff (29 Ağustos 2010). . 31 Ocak 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Eylül 2010.
- ^ a b Peter Jephson Cameron (1998). Introduction to Algebra. Oxford University Press. s. 4. ISBN . 8 Aralık 2016 tarihinde kaynağından . Erişim tarihi: 15 Şubat 2016.
- ^ Prep, Kaplan Test (4 Haziran 2019). GMAT Complete 2020: The Ultimate in Comprehensive Self-Study for GMAT (İngilizce). Simon and Schuster. ISBN . 30 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
- ^ . Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics. Ankara Üniversitesi. 24 Şubat 2024 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Şubat 2024.
pozitif tam sayı, ile gösterilen iç açıları
33. harf sırasında bulunan|alıntı=parametresi line feed character içeriyor () - ^ Smedley, Edward; Rose, Hugh James; Rose, Henry John (1845). Encyclopædia Metropolitana (İngilizce). B. Fellowes. s. 537. 8 Mayıs 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
An integer is a multiple of unity
- ^ Encyclopaedia Britannica 1771, s. 367
- ^ Pisano, Leonardo; Boncompagni, Baldassarre (transliteration) (1202). Incipit liber Abbaci compositus to Lionardo filio Bonaccii Pisano in year Mccij [The Book of Calculation] (Latince). Sigler, Laurence E. tarafından çevrildi. Museo Galileo. s. 30. 8 Aralık 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
Nam rupti uel fracti semper ponendi sunt post integra, quamuis prius integra quam rupti pronuntiari debeant.
- ^ Encyclopaedia Britannica 1771, s. 83
- ^ a b Martinez, Alberto (2014). Negative Math. Princeton University Press. ss. 80-109.
- ^ Euler, Leonhard (1771). Vollstandige Anleitung Zur Algebra [Complete Introduction to Algebra] (Almanca). 1. s. 10.
Alle diese Zahlen, so wohl positive als negative, führen den bekannten Nahmen der gantzen Zahlen, welche also entweder größer oder kleiner sind als nichts. Man nennt dieselbe gantze Zahlen, um sie von den gebrochenen, und noch vielerley andern Zahlen, wovon unten gehandelt werden wird, zu unterscheiden.
- ^ The University of Leeds Review (İngilizce). 31-32. University of Leeds. 1989. s. 46. 13 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
Incidentally, Z comes from "Zahl": the notation was created by Hilbert.
- ^ Bourbaki, Nicolas (1951). Algèbre, Chapter 1. 2nd (Fransızca). Paris: Hermann. s. 27.
Le symétrisé de N se note Z; ses éléments sont appelés entiers rationnels.
- ^ Birkhoff, Garrett (1948). Lattice Theory. Revised. American Mathematical Society. s. 63.
the set J of all integers
- ^ Society, Canadian Mathematical (1960). Canadian Journal of Mathematics (İngilizce). Canadian Mathematical Society. s. 374.
Consider the set Z of non-negative integers
- ^ Bezuszka, Stanley (1961). Contemporary Progress in Mathematics: Teacher Supplement [to] Part 1 and Part 2 (İngilizce). Boston College. s. 69. 3 Mayıs 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
Modern Algebra texts generally designate the set of integers by the capital letter Z.
- ^ Keith Pledger and Dave Wilkins, "Edexcel AS and A Level Modular Mathematics: Core Mathematics 1" Pearson 2008
- ^ LK Turner, FJ BUdden, D Knighton, "Advanced Mathematics", Book 2, Longman 1975.
- ^ Mathews, George Ballard (1892). Theory of Numbers (İngilizce). Deighton, Bell and Company. s. 2. 26 Haziran 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
- ^ Betz, William (1934). Junior Mathematics for Today (İngilizce). Ginn. 27 Haziran 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
The whole numbers, or integers, when arranged in their natural order, such as 1, 2, 3, are called consecutive integers.
- ^ Peck, Lyman C. (1950). Elements of Algebra (İngilizce). McGraw-Hill. s. 3. 13 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
The numbers which so arise are called positive whole numbers, or positive integers.
- ^ Hayden, Robert (1981). A history of the "new math" movement in the United States (PhD). Iowa State University. s. 145. doi:10.31274/rtd-180813-5631. 8 Aralık 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
A much more influential force in bringing news of the "new math" to high school teachers and administrators was the National Council of Teachers of Mathematics (NCTM).
- ^ The Growth of Mathematical Ideas, Grades K-12: 24th Yearbook (İngilizce). National Council of Teachers of Mathematics. 1959. s. 14. ISBN . 13 Nisan 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
- ^ Deans, Edwina (1963). Elementary School Mathematics: New Directions (İngilizce). U.S. Department of Health, Education, and Welfare, Office of Education. s. 42. 8 Mayıs 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
- ^ "entry: whole number". The American Heritage Dictionary. HarperCollins. 30 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 24 Şubat 2024.
- ^ "Integer mathematics". Encyclopedia Britannica (İngilizce). 31 Ocak 2018 tarihinde kaynağından . Erişim tarihi: 11 Ağustos 2020.
- ^ (1993). Algebra (3.3yayıncı=Addison-Wesley bas.). ss. 86-87. ISBN .
- ^ Warner, Seth (2012). Modern Algebra. Dover Books on Mathematics. Theorem 20.14, p. 185: Courier Corporation. ISBN . 6 Eylül 2015 tarihinde kaynağından . Erişim tarihi: 29 Nisan 2015.
- ^ Mendelson, Elliott (1985). Number systems and the foundations of analysis. Malabar, Fla. : R.E. Krieger Pub. Co. s. 153. ISBN .
- ^ Mendelson, Elliott (2008). Number Systems and the Foundations of Analysis. Dover Books on Mathematics. Courier Dover Publications. s. 86. ISBN . 8 Aralık 2016 tarihinde kaynağından . Erişim tarihi: 15 Şubat 2016.
- ^ Ivorra Castillo: Álgebra
- ^ Kramer, Jürg; von Pippich, Anna-Maria (2017). From Natural Numbers to Quaternions (İngilizce) (1.1yer=Switzerland bas.). Springer Cham. ss. 78-81. doi:10.1007/978-3-319-69429-0. ISBN .
- ^ Frobisher, Len (1999). Learning to Teach Number: A Handbook for Students and Teachers in the Primary School. The Stanley Thornes Teaching Primary Maths Series. Nelson Thornes. s. 126. ISBN . 8 Aralık 2016 tarihinde kaynağından . Erişim tarihi: 15 Şubat 2016.
- ^ a b c Campbell, Howard E. (1970). The structure of arithmetic. Appleton-Century-Crofts. s. 83. ISBN .
- ^ Garavel, Hubert (2017). On the Most Suitable Axiomatization of Signed Integers. Post-proceedings of the 23rd International Workshop on Algebraic Development Techniques (WADT'2016). Lecture Notes in Computer Science. 10644. Springer. ss. 120-134. doi:10.1007/978-3-319-72044-9_9. ISBN . 26 Ocak 2018 tarihinde kaynağından . Erişim tarihi: 25 Ocak 2018.
= Bibliografya
- Bell, E.T. (1986). . New York: Simon & Schuster. ISBN .)
- Herstein, I.N. Topics in Algebra (2.2tarih=1975 bas.). Wiley. ISBN .
- ; Birkhoff, Garrett. Algebra (3.3tarih=1999 bas.). American Mathematical Society. ISBN .
- A Society of Gentlemen in Scotland (1771). Encyclopaedia Britannica (İngilizce). Edinburgh.
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Tam sayilar sayilar kumesinde yer alan sifir 0 pozitif yonde yer alan dogal sayilar 1 2 3 ve bunlarin negatif degerlerinden olusan negatif sayilardan 1 2 3 olusan sayi kumesidir Karatahtaya yazi tipindeki kalin Z harfi siklikla tum tam sayilar kumesini temsil etmek amaciyla tercih edilir Tum tam sayilarin olusturdugu kume cogunlukla kalin harf bicimindeki Z veya kullanilarak Z displaystyle mathbb Z seklinde ifade edilir Z harfi Almanca Zahlen sayilar sozcugunden gelir Dogal sayilar kumesi N displaystyle mathbb N Z displaystyle mathbb Z tam sayilar kumesinin bir alt kumesi olarak tanimlanir Bu tam sayilar kumesi ardindan tum rasyonel sayilar kumesi Q displaystyle mathbb Q nun ve bu kume de reel sayilar kumesi R displaystyle mathbb R nin bir alt kumesi olarak siralanir Dogal sayilar kumesine benzer bicimde Z displaystyle mathbb Z tam sayilar kumesi de ozelligi gosterir Tam sayi kavrami kesirli bir kismi bulunmayan ve boylelikle dogrudan reel sayi olarak ifade edilebilen sayilar icin kullanilir Mesela 21 4 0 ve 2048 tam sayilardir buna karsin 9 75 5 1 2 ve 2 tam sayi olarak degerlendirilmez Dogal sayi kumelerini kapsayan yapilar icerisinde tam sayilar hem en minimal grup hem de en minimal halka yapisini teskil ederler Cebirsel sayi teorisi alaninda tam sayilar zaman zaman onlari daha genis bir kapsamda ele alinan ile karistirmamak adina rasyonel tam sayilar olarak ozel bir sekilde tanimlanir Gercekte rasyonel olarak ifade edilen tam sayilar hem cebirsel tam sayi ozelliklerini tasir hem de rasyonel sayilar kategorisinde degerlendirilirler Tarihce Ilk Turkce tam sayi teriminin kullanimlarindan biri 1955 e dayanir Tarih boyunca tam sayi terimi 1 in katlari olan sayilar icin veya tam sayili kesirlerin tam kisimlarini ifade etmek icin kullanilmistir Baslangicta yalnizca pozitif tam sayilar ele alinmis ve bu durum terimin dogal sayilarla esanlamli hale gelmesine yol acmistir Tam sayi kavraminin tanimi negatif sayilarin faydasinin zamanla kabul edilmesiyle genisletilmis ve bu sayilar da tanimin icine dahil edilmistir Ornegin Leonhard Euler 1765 tarihli Cebirin Unsurlari adli calismasinda tam sayilari hem pozitif hem de negatif sayilari icerecek bicimde tanimlamistir Bununla birlikte Avrupali matematikcilerin buyuk bir kismi 19 yuzyilin ortalarina kadar negatif sayilar konseptine karsi direnc gostermistir Tam sayilar kumesini temsil etmek uzere Z harfinin tercih edilmesi Almanca da sayilar anlamina gelen Zahlen kelimesinden kaynaklanmaktadir ve bu baglamda David Hilbert ile iliskilendirilir Bu notasyonun ders kitaplarinda ilk defa kullanildigi bilinen ornek 1947 yilinda Nicolas Bourbaki grubu tarafindan kaleme alinan isimli eserde yer almaktadir Notasyonun benimsenmesi hemen gerceklesmemistir mesela bir baska ders kitabinda J harfi kullanilmis ve 1960 yilinda yayimlanan bir makalede Z yalnizca sifir ve pozitif tam sayilari ifade etmek amaciyla tercih edilmistir Ancak 1961 itibariyla modern cebir metinleri genel olarak Z harfini hem pozitif hem de negatif tam sayilari kapsayacak sekilde kullanmaya baslamislardir Z displaystyle mathbb Z sembolu cesitli kumeleri tanimlamak amaciyla farkli yazarlarin tercihlerine gore degisken notasyonlar ile siklikla sembolize edilir Pozitif tam sayilar icin Z displaystyle mathbb Z Z displaystyle mathbb Z veya Z gt displaystyle mathbb Z gt kullanilirken sifir ve pozitif tam sayilar icin Z0 displaystyle mathbb Z 0 veya Z displaystyle mathbb Z geq ve sifir olmayan tam sayilar icin Z displaystyle mathbb Z neq tercih edilir Bazi yazarlar sifir olmayan tam sayilar icin Z displaystyle mathbb Z kullanirken digerleri bu notasyonu sifir ve pozitif tam sayilar icin veya Z displaystyle mathbb Z nin birimler grubunu Ing unit ring theory ifade eden 1 1 icin kullanmaktadir Ek olarak Zp displaystyle mathbb Z p notasyonu ya moduler p tam sayilarini yani tam sayilarin denklik siniflarini ya da p adik tam sayilarini tanimlamak icin kullanilir 1950 lerin baslarina dek butun sayilar ile tam sayilar arasinda bir esanlamlilik soz konusuydu 1950 lerin sonlarina dogru hareketinin bir unsuru olarak Amerikan ilkokul ogretmenleri butun sayilar Ing whole numbers teriminin negatif sayilari dislayarak yalnizca dogal sayilari kapsadigini tam sayi teriminin ise negatif sayilari da icerecek sekilde genisletildigini derslerinde islemeye basladilar Butun sayi kavrami Ing whole numbers gunumuzde hala belirsizligini surdurmektedir Cebirsel ozellikler Tam sayilar teorik olarak sonsuz bir uzunluga sahip olan sayi dogrusu uzerinde birbirinden esit mesafelerle ayrilmis ayrik noktalar seklinde tasavvur edilebilirler Ilgili gosterimde negatif olmayan tam sayi kumeleri mavi renkle temsil edilmis olup negatif degerli tam sayilar ise kirmizi renk ile ifade edilmistir Dogal sayilar kumesi gibi Z displaystyle mathbb Z kumesi de toplama ve carpma gibi ikili islemler bakimindan bir yapiya sahiptir bu herhangi iki tam sayinin toplaminin ve carpiminin yine bir tam sayi olacagi anlamina gelir Bununla birlikte negatif dogal sayilarin ve ozellikle 0 in dahil edilmesi ile Z displaystyle mathbb Z dogal sayilar kumesinden farkli olarak cikarma islemine yonelik de kapali bir karakter gosterir Tam sayilar kumesi her bir birimli halka yapisi icin bu yapilara dogru tam sayilardan tekil bir Ing ring homomorphism tesis edilebildigi temel bir olarak islev gorur Bu Ing universal property ozgul olarak icerisinde bir Ing initial object olarak tanimlanabilirlik Z displaystyle mathbb Z halkasinin ayirt edici niteligini belirler Z displaystyle mathbb Z kumesi iki tam sayinin birbirine bolunmesi islemi ornek olarak 1 sayisinin 2 sayisina bolunmesi durumu gosterilebilir neticesinde her defasinda tam sayi elde edilmeyebileceginden bolme islemi acisindan kapali bir yapi sergilemez Dogal sayilar kumesi us alma islemine gore kapalilik ozelligine sahipken tam sayilar kumesi bu ozelligi tasimamaktadir zira ussun negatif deger almasi halinde sonuc kesirli bir sayiya donusebilir Asagidaki tablo herhangi bir a b ve c tam sayisi icin toplama ve carpma islemlerinin bazi temel ozelliklerini listelemektedir Tam sayilarda toplama ve carpma islemlerinin ozellikleri Toplama Carpma a b bir tam sayidir a b bir tam sayidirBirlesme a b c a b c a b c a b cDegisme a b b a a b b aEtkisiz elemanin varligi a 0 a a 1 avarligi a a 0 Tersinir tam sayilar 1 ve 1 olarak adlandirilan disinda tersi olan tam sayi yoktur Dagilma a b c a b a c ve a b c a c b c Sifir Eger a b 0 o zaman a 0 veya b 0 veya her ikisi Toplama islemi cercevesinde Z displaystyle mathbb Z kumesine iliskin olarak siralanan baslica bes ozelligin tanimladigi yapi bu kumenin bir abelyen grup oldugunu ifade eder Bu kume her biri sifirdan farkli olan tam sayilarin sonlu bir 1 1 1 veya 1 1 1 seklindeki toplamlari ile ifade edilebilirligi dolayisiyla ayni zamanda bir ozelligi tasir Ing cyclic group Gercekte toplama islemi altinda Z displaystyle mathbb Z herhangi bir sonsuz devirli grubun Z displaystyle mathbb Z ile oldugu baglamda tek sonsuz devirli gruptur Carpma islemine iliskin olarak siralanan ilk dort ozelligin tanimi Z displaystyle mathbb Z kumesinin carpma altinda bir degismeli monoid yapisina sahip oldugunu gosterir Ancak 2 sayisinin orneginde oldugu gibi her tam sayinin carpmaya iliskin bir carpimsal tersi bulunmamaktadir bu durum Z displaystyle mathbb Z kumesinin carpma islemi baglaminda bir grup olusturmadigini ifade eder Yukarida sunulan ozellikler cetvelinden en sonuncu disinda elde edilen kurallarin tumu toplama ve carpma islemleriyle bir arada Z displaystyle mathbb Z kumesinin birimli degismeli halka olarak tanimlandigini ortaya koyar Bu yapi benzer ait nesnelerin ilk ornegidir Z displaystyle mathbb Z icerisinde degiskenlerin her bir degeri icin gercek olan yalnizca herhangi bir birimli degismeli halkada dogru kabul edilen esitlikler ve ifadeler gecerlidir Bazi sifir olmayan tam sayilar cesitli halkalarda degerine karsilik gelir Tam sayilar kumesinde bulunmamasi ozellikler tablosundaki son ozellik degismeli halka Z displaystyle mathbb Z nin bir tamlik bolgesi olarak nitelendirilebilecegini gosterir Carpmaya iliskin ters elemanlarin eksikligi bu durumun Z displaystyle mathbb Z kumesinin bolme islemine kapali olmadigi gercegi ile esdeger oldugundan Z displaystyle mathbb Z nin bir alan olarak tanimlanamayacagi anlamina gelir Tam sayilari bir olarak barindiran en kucuk alan yapi rasyonel sayilar alanidir Tam sayilar kumesinden rasyonel sayilar kumesinin turetilmesi sureci herhangi bir tamlik bolgesi icin Ing field of fractions olusturulmasi amaciyla modellenebilir Ayrica bir cebirsel sayi alanindan rasyonel sayilara bir uzanti olarak baslanarak icerisinde Z displaystyle mathbb Z kumesini de barindiran Ing ring of integers elde edilebilir Her ne kadar Z displaystyle mathbb Z uzerinde geleneksel bolme islemi tanimlanmamis olsa da kalan ile bolme islemi bu kume uzerinde tanimlanabilir Bu isleme Oklid bolmesi adi verilir ve su kritik ozelligi tasir b 0 kosulunu saglayan herhangi a ve b tam sayi cifti icin a q b r ve 0 r lt b iliskilerini saglayan benzersiz q ve r tams ayilari mevcuttur burada b b sayisinin mutlak degerini ifade eder Bu baglamda q tam sayisi bolum r ise a ile b nin bolunmesi sonucu elde edilen kalan olarak isimlendirilir En buyuk ortak bolenlerin belirlenmesi surecinde kullanilan Oklid algoritmasi ardisik Oklid bolme islemlerine dayanir Ilgili metin Z displaystyle mathbb Z kumesinin bir Ing Euclidean domain olarak tanimlandigini belirtmektedir Bu durum ayni zamanda Z displaystyle mathbb Z nin bir Ing principal ideal domain oldugunu gosterir ve her pozitif tam sayinin asal sayilarin carpimi seklinde Ing essentially unique bir bicimde ifade edilebilecegini ima eder Bu durum aritmetigin temel teoremi olarak bilinir Siralama teorisine iliskin ozellikler Z displaystyle mathbb Z herhangi bir ozelligi gosteren fakat ne ust ne de alt sinir iceren bir kumedir Z displaystyle mathbb Z kumesinin siralama iliskisi asagidaki gibi ifade edilir 3 lt 2 lt 1 lt 0 lt 1 lt 2 lt 3 lt Bir tam sayinin sifir degerinden buyuk olmasi durumunda pozitif sifirdan kucuk olmasi durumunda ise negatif olarak nitelendirilir Sifir degeri ne negatif ne de pozitif olarak nitelendirilebilir Tam sayilar arasindaki siralama iliskisi cebirsel islemlerle asagidaki bicimde uyum icindedir a lt b ve c lt d oldugunda a c lt b d sonucu elde edilir a lt b ve 0 lt c oldugunda ac lt bc esitsizligi gecerlidir Bunun sonucu olarak Z displaystyle mathbb Z uzerinde tanimlanan bu siralama ile birlikte bir yapisini olusturur Tam sayilar pozitif elemanlari iyi sirali olan tek ciddi Abel grubudur Bu herhangi bir Ing valuation ring ya bir cisim ya da Ing discrete valuation ring oldugu ifadesine esdegerdir Tanimlama Geleneksel tanimlama Temel egitim sureclerinde tam sayi kavrami genellikle pozitif dogal sayilar kumesi sifir ve dogal sayilarin negatif karsiliklarinin birlesimi olarak sezgisel bir yaklasimla tanimlanmaktadir Bu tanim formal bir yapiya kavusturulabilir baslangicta Peano aksiyomlari temel alinarak N displaystyle N dogal sayilar kumesi insa edilir Ardindan N displaystyle N kumesi ile her elemani arasinda birebir esleme bulunan ve N displaystyle N kumesinden ayrik bir N displaystyle N kumesi tanimlanir Bu baglamda N displaystyle N kumesi icin ornegin ps displaystyle psi eslemesi n 1 n displaystyle n mapsto 1 n olacak sekilde 1 n displaystyle 1 n formundaki sirali ciftler secilebilir Son adimda 0 elemani ne N displaystyle N kumesinde ne de N displaystyle N kumesinde yer almayacak sekilde ornegin 0 0 displaystyle 0 0 sirali cifti olarak belirlenir Boylelikle tam sayilar kumesi N N 0 displaystyle N cup N cup 0 birlesimi ile tanimlanmis olur Geleneksel aritmetik islemleri tam sayilar kumesi uzerinde pozitif sayilar negatif sayilar ve sifir olmak uzere parcali fonksiyonlar yardimiyla tanimlanabilir Mesela negasyon islemi su sekilde ifade edilir x ps x eger x Pps 1 x eger x P 0 eger x 0 displaystyle x begin cases psi x amp text eger x in P psi 1 x amp text eger x in P 0 amp text eger x 0 end cases Geleneksel tanimlama yontemi cesitlilik arz eden durumlarin ortaya cikmasina neden olur her aritmetik islemin tam sayi turlerinin her birinin kombinasyonlari uzerine tanimlanmasi gereklidir ve tam sayilarin aritmetik yasalarina olan uyumunun ispati surecini oldukca yorucu bir hale getirir Sirali ikili dizilerin esdegerlilik siniflari Kirmizi isaretler dogal sayilar kumesine ait sirali ikili dizileri ifade etmektedir Birbirine bagli olan kirmizi isaretler cizginin uc kismindaki mavi tam sayi degerlerini temsil eden esdegerlilik siniflarini gosterir Cagdas kume teorisine dayali matematikte aritmetik islemilerin herhangi bir ozgul durum ayrimina gerek kalmadan tanimlanabilmesine imkan veren daha soyut bir yapi tercih edilmektedir Bu baglamda tam sayilar dogal sayilardan olusturulan ciftlerin denklik siniflari olarak formel bir bicimde kurulabilir a b Sezgisel olarak a b ifadesi b nin a dan cikarilmasi sonucunu temsil eder 1 2 ile 4 5 gosterimlerinin ayni sayisal degeri temsil ettigi ongorumuzu teyit etmek amaciyla bu ikili diziler uzerinde belirli bir kural cercevesinde bir denklik iliskisi tanimlamaktayiz a b c d displaystyle a b sim c d yalnizca ve yalnizca a d b c displaystyle a d b c Tam sayilar uzerinde gerceklestirilen toplama ve carpim islemleri dogal sayilara uygulanan benzer islemler temel alinarak tanimlanabilir a b gosterimi icerisinde a b ogesini barindiran denklik sinifini ifade etmek icin kullanilir ve bu durumda islemler su sekilde ifade edilir a b c d a c b d displaystyle a b c d a c b d a b c d ac bd ad bc displaystyle a b cdot c d ac bd ad bc Bir tam sayinin negatif degeri veya toplamsal ters oge ilgili ikilinin elemanlarinin yer degistirilmesiyle elde edilir a b b a displaystyle a b b a Dolayisiyla cikartma islemi toplamsal ters ogenin eklenmesi seklinde tanimlanabilir a b c d a d b c displaystyle a b c d a d b c Tam sayilara iliskin standart siralama kurali asagidaki gibi ifade edilir a b lt c d displaystyle a b lt c d ancak ve ancak a d lt b c displaystyle a d lt b c Bu tanimlamalarin denklik siniflarinin temsilcilerinin secimiyle ilgisiz oldugu kolaylikla ispatlanabilir Her bir denklik sinifi n 0 veya 0 n veya her iki durum icin de formunda ozgun bir elemana sahiptir Dogal sayi n n 0 sinifiyla ozdeslestirilmekte yani dogal sayilar n yi n 0 ye esleyen bir fonksiyon araciligiyla tam sayilara ve 0 n sinifi n olarak ifade edilir bu durum kalan tum siniflari kapsar ve 0 0 sinifini 0 0 oldugundan yeniden tanimlar Dolayisiyla a b gosterimi asagidaki gibi ifade edilir a b eger a b b a eger a lt b displaystyle begin cases a b amp mbox eger a geq b b a amp mbox eger a lt b end cases Dogal sayilarin karsilik gelen tam sayilarla ozdeslestirilmesi durumunda onceden bahsi gecen gomme metodu kullanilarak bu gosterim yontemi herhangi bir karmasikliga yol acmaz Bu gosterim yontemi tam sayilarin 2 1 0 1 2 seklindeki alisilagelmis temsiline geri donus saglar Orneklerden bazilari su sekildedir 0 0 0 1 1 k k 1 1 0 2 1 k 1 k 1 0 1 1 2 k k 1 2 2 0 3 1 k 2 k 2 0 2 1 3 k k 2 displaystyle begin aligned 0 amp 0 0 amp 1 1 amp cdots amp amp k k 1 amp 1 0 amp 2 1 amp cdots amp amp k 1 k 1 amp 0 1 amp 1 2 amp cdots amp amp k k 1 2 amp 2 0 amp 3 1 amp cdots amp amp k 2 k 2 amp 0 2 amp 1 3 amp cdots amp amp k k 2 end aligned Diger yaklasimlar Teorik bilgisayar biliminde tam sayilarin insasi icin otomatik teorem kanitlama ve terim yeniden yazim motorlari tarafindan kullanilan diger yaklasimlar mevcuttur Tam sayilar birkac temel islem ornegin sifir bir sonraki bir onceki kullanilarak ve muhtemelen zaten insa edilmis oldugu varsayilan dogal sayilar kullanilarak olusturulan Ing term algebra olarak temsil edilir ornegin Peano yaklasimi kullanilarak Isaretli tam sayilarin olusturulmasi amaciyla en azindan on farkli yontem mevcuttur Bu yapilar cesitli parametrelere gore ayrisir Yapiyi gerceklestirmek amaciyla basvurulan temel islemlerin adedi bu islemlerin kabul ettigi argumanlarin sayisi ve nitelikleri cogunlukla 0 ile 2 arasinda degisir belirli islemler icin dogal sayilarin arguman olarak kullanilip kullanilmadigi ve islemlerin serbest yapilandirici olup olmadigi yani bir tam sayinin tek veya birden cok cebirsel ifadeyle ifade edilebilirligi Bir onceki bolumde tanitilan tam sayilarin insasi yontemi iki dogal sayiyi arguman olarak alan ve sonucunda bir tam sayi bu durumda x y ye esit veren tekil bir temel islem olan cift x y displaystyle x y islemine dayanir Bu islem serbest nitelikte degildir zira sifir tam sayisi cift 0 0 cift 1 1 cift 2 2 gibi cesitli sekillerde ifade edilebilir Bu insa metodolojisi yazilimi tarafindan benimsenmis olup ancak serbest yapilandiricilari temel alan ve bilgisayar ortamlarinda daha etkin bir sekilde implemente edilebilecek daha sade alternatif insa teknikleri de mevcuttur Bilgisayar bilimi Tam sayi sikca bilgisayar dililerindeki primitif bir veri tipidir Ancak tam sayi veri tipleri pratik bilgisayarlarin sonlu kapasitesi nedeniyle tum tam sayilarin bir alt kumesini temsil edebilirler Ayrica yaygin ikinin tumleyeni gosteriminde isaretin icsel tanimi negatif ve negatif olmayan arasinda ayrim yapar negatif pozitif ve 0 degil Bununla birlikte bir bilgisayarin bir tam sayi degerinin gercekten pozitif olup olmadigini belirlemesi kesinlikle mumkundur Sabit uzunluklu tam sayi yaklasim veri tipleri veya alt kumeleri birkac programlama dilinde int veya Integer olarak adlandirilir ALGOL 68 C Java Delphi vb Tam sayilarin degisken uzunluklu temsilleri bilgisayarin bellegine sigan herhangi bir tam sayiyi depolayabilir Diger tam sayi veri tipleri ise genellikle 2 nin bir kuvveti olan bir bit sayisi 4 8 16 vb veya akilda kalici bir ondalik basamak sayisi ornegin 9 veya 10 ile sabit bir boyutta uygulanir Sayallik Kardinalite Tam sayilar kumesi sayilabilir sonsuzdur bu da her tam sayinin benzersiz bir dogal sayi ile eslestirilebilecegi anlamina gelir Boyle bir eslestirmenin bir ornegi soyledir 0 1 1 2 1 3 2 4 2 5 3 6 1 k 2k 1 k 2k Daha teknik bir ifadeyle Z displaystyle mathbb Z kardinalitesinin ℵ0 alef sifir ile esit oldugu soylenir Z displaystyle mathbb Z ve N displaystyle mathbb N elemanlari arasindaki bu eslestirme bir bijection olarak adlandirilir Notlar Her bir sayi sistemi bir sonraki sayi sistemine izomorfik bir sekilde eslenerek ve bu sistem icerisinde gomulu bir alt kume olusturarak daha kesin bir yapilandirma sunar Kesirsiz ve ondaliksiz sayilarin tamami tam sayilardir Ayrica bakiniz Sayi sistemleri Karmasik C displaystyle mathbb C Reel R displaystyle mathbb R Rasyonel Q displaystyle mathbb Q Tam sayi Z displaystyle mathbb Z Dogal N displaystyle mathbb N Sifir 0Bir 1Asal sayilarBilesik sayilarNegatif tam sayilarKesir Devirli ondalik sayiIrrasyonel Cebirsel irrasyonelAskinSanalKaynakca www dildernegi org tr 26 Nisan 2014 tarihinde kaynagindan arsivlendi Erisim tarihi 22 Ekim 2023 Science and Technology Encyclopedia Ingilizce University of Chicago Press September 2000 s 280 ISBN 978 0 226 74267 0 30 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 22 Subat 2024 a b c Miller Jeff 29 Agustos 2010 31 Ocak 2010 tarihinde kaynagindan arsivlendi Erisim tarihi 20 Eylul 2010 a b Peter Jephson Cameron 1998 Introduction to Algebra Oxford University Press s 4 ISBN 978 0 19 850195 4 8 Aralik 2016 tarihinde kaynagindan Erisim tarihi 15 Subat 2016 Prep Kaplan Test 4 Haziran 2019 GMAT Complete 2020 The Ultimate in Comprehensive Self Study for GMAT Ingilizce Simon and Schuster ISBN 978 1 5062 4844 8 30 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Communications Faculty of Sciences University of Ankara Series A1 Mathematics and Statistics Ankara Universitesi 24 Subat 2024 tarihinde kaynagindan arsivlendi Erisim tarihi 24 Subat 2024 pozitif tam sayi ile gosterilen ic acilari 33 harf sirasinda bulunan alinti parametresi line feed character iceriyor yardim Smedley Edward Rose Hugh James Rose Henry John 1845 Encyclopaedia Metropolitana Ingilizce B Fellowes s 537 8 Mayis 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 An integer is a multiple of unity Encyclopaedia Britannica 1771 s 367 Pisano Leonardo Boncompagni Baldassarre transliteration 1202 Incipit liber Abbaci compositus to Lionardo filio Bonaccii Pisano in year Mccij The Book of Calculation Latince Sigler Laurence E tarafindan cevrildi Museo Galileo s 30 8 Aralik 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Nam rupti uel fracti semper ponendi sunt post integra quamuis prius integra quam rupti pronuntiari debeant Encyclopaedia Britannica 1771 s 83 a b Martinez Alberto 2014 Negative Math Princeton University Press ss 80 109 Euler Leonhard 1771 Vollstandige Anleitung Zur Algebra Complete Introduction to Algebra Almanca 1 s 10 Alle diese Zahlen so wohl positive als negative fuhren den bekannten Nahmen der gantzen Zahlen welche also entweder grosser oder kleiner sind als nichts Man nennt dieselbe gantze Zahlen um sie von den gebrochenen und noch vielerley andern Zahlen wovon unten gehandelt werden wird zu unterscheiden The University of Leeds Review Ingilizce 31 32 University of Leeds 1989 s 46 13 Nisan 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Incidentally Z comes from Zahl the notation was created by Hilbert Bourbaki Nicolas 1951 Algebre Chapter 1 2nd Fransizca Paris Hermann s 27 Le symetrise de N se note Z ses elements sont appeles entiers rationnels Birkhoff Garrett 1948 Lattice Theory Revised American Mathematical Society s 63 the set J of all integers Society Canadian Mathematical 1960 Canadian Journal of Mathematics Ingilizce Canadian Mathematical Society s 374 Consider the set Z of non negative integers Bezuszka Stanley 1961 Contemporary Progress in Mathematics Teacher Supplement to Part 1 and Part 2 Ingilizce Boston College s 69 3 Mayis 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Modern Algebra texts generally designate the set of integers by the capital letter Z Keith Pledger and Dave Wilkins Edexcel AS and A Level Modular Mathematics Core Mathematics 1 Pearson 2008 LK Turner FJ BUdden D Knighton Advanced Mathematics Book 2 Longman 1975 Mathews George Ballard 1892 Theory of Numbers Ingilizce Deighton Bell and Company s 2 26 Haziran 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Betz William 1934 Junior Mathematics for Today Ingilizce Ginn 27 Haziran 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 The whole numbers or integers when arranged in their natural order such as 1 2 3 are called consecutive integers Peck Lyman C 1950 Elements of Algebra Ingilizce McGraw Hill s 3 13 Nisan 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 The numbers which so arise are called positive whole numbers or positive integers Hayden Robert 1981 A history of the new math movement in the United States PhD Iowa State University s 145 doi 10 31274 rtd 180813 5631 8 Aralik 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 A much more influential force in bringing news of the new math to high school teachers and administrators was the National Council of Teachers of Mathematics NCTM The Growth of Mathematical Ideas Grades K 12 24th Yearbook Ingilizce National Council of Teachers of Mathematics 1959 s 14 ISBN 9780608166186 13 Nisan 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Deans Edwina 1963 Elementary School Mathematics New Directions Ingilizce U S Department of Health Education and Welfare Office of Education s 42 8 Mayis 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 entry whole number The American Heritage Dictionary HarperCollins 30 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 24 Subat 2024 Integer mathematics Encyclopedia Britannica Ingilizce 31 Ocak 2018 tarihinde kaynagindan Erisim tarihi 11 Agustos 2020 1993 Algebra 3 3yayinci Addison Wesley bas ss 86 87 ISBN 978 0 201 55540 0 Warner Seth 2012 Modern Algebra Dover Books on Mathematics Theorem 20 14 p 185 Courier Corporation ISBN 978 0 486 13709 4 6 Eylul 2015 tarihinde kaynagindan Erisim tarihi 29 Nisan 2015 Mendelson Elliott 1985 Number systems and the foundations of analysis Malabar Fla R E Krieger Pub Co s 153 ISBN 978 0 89874 818 5 Mendelson Elliott 2008 Number Systems and the Foundations of Analysis Dover Books on Mathematics Courier Dover Publications s 86 ISBN 978 0 486 45792 5 8 Aralik 2016 tarihinde kaynagindan Erisim tarihi 15 Subat 2016 Ivorra Castillo Algebra Kramer Jurg von Pippich Anna Maria 2017 From Natural Numbers to Quaternions Ingilizce 1 1yer Switzerland bas Springer Cham ss 78 81 doi 10 1007 978 3 319 69429 0 ISBN 978 3 319 69427 6 Frobisher Len 1999 Learning to Teach Number A Handbook for Students and Teachers in the Primary School The Stanley Thornes Teaching Primary Maths Series Nelson Thornes s 126 ISBN 978 0 7487 3515 0 8 Aralik 2016 tarihinde kaynagindan Erisim tarihi 15 Subat 2016 a b c Campbell Howard E 1970 The structure of arithmetic Appleton Century Crofts s 83 ISBN 978 0 390 16895 5 Garavel Hubert 2017 On the Most Suitable Axiomatization of Signed Integers Post proceedings of the 23rd International Workshop on Algebraic Development Techniques WADT 2016 Lecture Notes in Computer Science 10644 Springer ss 120 134 doi 10 1007 978 3 319 72044 9 9 ISBN 978 3 319 72043 2 26 Ocak 2018 tarihinde kaynagindan Erisim tarihi 25 Ocak 2018 BibliografyaBell E T 1986 New York Simon amp Schuster ISBN 0 671 46400 0 Herstein I N Topics in Algebra 2 2tarih 1975 bas Wiley ISBN 0 471 01090 1 Birkhoff Garrett Algebra 3 3tarih 1999 bas American Mathematical Society ISBN 0 8218 1646 2 A Society of Gentlemen in Scotland 1771 Encyclopaedia Britannica Ingilizce Edinburgh
 Azərbaycanca
Azərbaycanca Deutsch
Deutsch 日本語
日本語 Lietuvos
Lietuvos සිංහල
සිංහල Türkçe
Türkçe Українська
Українська United State
United State

















![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5aFpHRTJNMlJsTlRVek56UmhZVEE1TURFelltVTJOV05oWVRGak16TmhZVEF4TmpSbFkySXouc3Zn.svg)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4MlpXRTRZelV4WVdRMVpqSTVOamhtWTJZMU56ZzRaV0l5TWpCa05HWTBORFl6WWpJNE5UZzQuc3Zn.svg)
![{\displaystyle -[(a,b)]:=[(b,a)].}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4NU5URmtNREUzTVdWa01XVmtaamN3TldVM01ETTVNak0xTW1ZelpEQTNZamswWldRMFl6YzAuc3Zn.svg)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5bFpqaGhaalE0T1dNM1kyWm1OREJtWlRSalptVTJObVExWVRjd05qZ3pOMlpqTUdFMlpHWTIuc3Zn.svg)
![{\displaystyle [(a,b)]<[(c,d)]}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk5a05XWTFaRGxrTTJZeVpXWXpPV1U0WTJZNU1EWTVNalU0T1dZd1lqazNPVFExTkRVME5UTTIuc3Zn.svg)

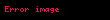
![{\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}}](https://www.wikipedia.tr-tr.nina.az/image/aHR0cHM6Ly93d3cud2lraXBlZGlhLnRyLXRyLm5pbmEuYXovaW1hZ2UvYUhSMGNITTZMeTkzYVd0cGJXVmthV0V1YjNKbkwyRndhUzl5WlhOMFgzWXhMMjFsWkdsaEwyMWhkR2d2Y21WdVpHVnlMM04yWnk4ek1qVmpObUU0TTJFNE5HVTBabVV3T0dKaFl6QXpaVFExTTJZMk56UmlNV1ptT0RObFlXTXguc3Zn.svg)