Orbit

Gök mekaniğinde yörünge veya yörünge hareketi, bir gezegenin yıldız etrafındaki veya bir doğal uydunun gezegen etrafındaki veya bir gezegen, doğal uydu, asteroit veya lagrange noktası gibi uzaydaki bir nesne veya konum etrafındaki yapay uydunun izlediği kavisli bir yoldur. Yörünge, düzenli olarak tekrar eden bir yolu tanımlamakla birlikte, tekrar etmeyen bir yolu da ifade edebilir. Gezegenler ve uydular Kepler'in gezegensel hareket yasalarında tanımlandığı gibi, kütle merkezi elips biçiminde izledikleri yolun odak noktasında olacak şekilde yaklaşık olarak eliptik yörüngeleri takip ederler.

Düşük dışmerkezli bir yörüngeyi (daireye yakın, kırmızı) ve yüksek dışmerkezli bir yörüngeyi (elips, mor) gösteren animasyon.

Çoğu durum için yörünge hareketi, kütleçekimini ters-kare yasasına uyan bir kuvvet olarak açıklayan Newton mekaniği tarafından yeterince tahmin edilebilir. Bununla birlikte, Albert Einstein'ın kütleçekimini uzay zamanın bükülmesi olarak açıkladığı ve yörüngelerin jeodezikleri takip ettiği genel görelilik teorisi, yörünge hareketinin tam mekaniğinin daha doğru bir şekilde hesaplanmasını ve anlaşılmasını sağlar.

Tarihi

Tarihsel olarak, gezegenlerin görünür hareketleri Avrupalı ve Arap filozoflar ve astronomlar tarafından göksel küreler yaklaşımı kullanılarak tanımlanmıştır. Bu model yıldızların ve gezegenlerin bağlı olduğu hareket eden kusursuz kürelerin veya halkaların varlığını öne sürüyordu. Bu bakış açısı göklerin kürenin hareketinden ayrı olarak sabit bir biçimde kaldığını varsayıyor ve herhangi bir kütleçekim anlayışı geliştirmiyordu. Gezegenlerin hareketlerinin daha doğru bir şekilde hesaplanabilmesiyle gibi teorik mekanizmalar bu anlayışa eklenmiştir. Gökyüzündeki gezegen konumlarının doğru bir şekilde tahmin edilebilmesine imkan verse de bu model hesaplamaların tutarlılığı açısından çok daha fazla sayıda episikllere ihtiyaç duymaktaydı. Bu nedenle model zamanla geçerliliğini ve kullanışlılığını geniş oranda yitirmeye başladı. Başlangıçta yermerkezli yani jeosentrik olan bu model, modeli basitleştirmeye yardımcı olmak amacıyla Kopernik tarafından Güneş'i merkeze yerleştirecek şekilde değiştirildi. 16. yüzyılda gökküreden geçmekte olan kuyruklu yıldızların gözlemlenmesiyle birlikte modelin tutarlılığı daha da tartışmalı hale geldi.

Modern yörünge anlayışının temelleri gezegen hareketlerini üç adet yasa ile özetleyen Johannes Kepler tarafından oluşturulmuştur. Bunlardan ilkinde, Kepler daha önceki dönemlerde varsayılandan farklı olarak Güneş'in gezegen yörüngelerinin tam merkezinde olmadığını fakat olduğunu, bu nedenle Güneş Sistemi'ndeki gezegen yörüngelerinin dairesel veya episikl değil eliptik olduğunu bulmuştur. İkincisinde, Kepler her gezegenin yörünge hızının önceden düşünüldüğü gibi sabit olmadığını, hızın gezegenin Güneş'e olan uzaklığına bağlı olduğunu keşfetmiştir. Üçüncüsünde ise, Kepler Güneş'in etrafında dönen tüm gezegenlerin yörünge özellikleri arasında evrensel bir ilişkiyi formüle etmiştir. Buna göre, gezegenlerin Güneş'e olan uzaklıklarının karesi yörünge periyotlarının karesi ile orantılıdır. Örneğin, Jüpiter ve Venüs sırasıyla Güneş'ten yaklaşık olarak 5,2 ve 0,723 AU uzaklıkta bulunmaktadırlar. Bu gezegenlerin yörünge periyotları ise yine sırasıyla yaklaşık 11,86 ve 0,615 yıldır. Jüpiter'in 5,2³/11,86² oranı ile Venüs'ün 0,723³/0,615² oranı pratikte birbirine eşit olup, Kepler'in ortaya attığı yasa ile uyumludur. Bu kuralları karşılayan idealleştirilmiş yörüngeler Kepler yörüngeleri olarak bilinir.

Isaac Newton, Kepler'in yasalarının yerçekimi teorisinden türetilebileceğini ve genel olarak yerçekimine maruz kalan cisimlerin yörüngelerinin birer konik kesit olduğunu göstermiştir (burada yerçekimi kuvvetinin anlık olarak yayıldığı varsayılmaktadır). Newton, bir çift cisim için yörüngelerin boyutlarının kütleleriyle ters orantılı olduğunu ve bu cisimlerin ortak kütle merkezlerinin etrafında döndüklerini kanıtlamıştır. Cisimlerden birinin diğerinden çok daha kütleli olduğu durumlarda (bir gezegenin etrafında dönen yapay bir uydu örneğinde olduğu gibi), kütle merkezini daha kütleli olan cismin merkeziyle çakışıyor kabul etmek uygun bir yaklaşımdır.

Newton mekaniğindeki ilerlemeler Kepler yörüngelerinin arkasındaki basit varsayımları, örneğin diğer cisimlerden kaynaklanan pertürbasyonları ya da küresel cisimlerden ziyade küre benzeri cisimlerin etkisini keşfetmek için kullanıldı. Joseph-Louis Lagrange, Newton mekaniğine kuvvetten çok enerjiyi vurgulayan yeni bir yaklaşım geliştirdi ve Lagrange noktalarını keşfederek üç cisim probleminde ilerleme kaydetti. Urbain Le Verrier, 1846'da klasik mekaniğin dramatik bir şekilde doğrulanmasıyla, Uranüs'ün yörüngesindeki açıklanamayan bozulmalara dayanarak Neptün'ün konumunu tahmin edebildi.

Albert Einstein 1916 tarihli Genel Görelilik Teorisinin Temeli adlı makalesinde yerçekiminin uzay-zamanın eğriliğinden kaynaklandığını açıklamış ve Newton'un değişimlerin anlık olarak yayıldığı varsayımını ortadan kaldırmıştır. Bu durum astronomların Newton mekaniğinin yörüngeleri anlamada en yüksek doğruluğu sağlamadığını fark etmelerine yol açmıştır. Görelilik teorisinde yörüngeler jeodezik yörüngeleri takip eder ve bu yörüngeler genellikle Newton tahminlerine oldukça iyi oranda yaklaşır (çok güçlü yerçekimi alanlarının ve çok yüksek hızların olduğu durumlar hariç) ancak aradaki farklar ölçülebilirdir. Esasen, teoriler arasında ayrım yapabilen tüm deneysel kanıtlar, deneysel ölçüm doğruluğu dahilinde görelilik teorisini kabul etmektedir. Genel göreliliğin asıl haklılığı, ilk olarak Le Verrier tarafından kaydedilen Merkür'ün günberi presesyonundaki açıklanamayan miktarı açıklayabilmesidir. Bununla birlikte, Newton'un çözümü, kullanımı önemli ölçüde daha kolay ve yeterince doğru olduğu için çoğu kısa vadeli amaç için hala kullanılmaktadır.

Gezegen yörüngeleri

İçerisinde gezegenler, cüce gezegenler, asteroitler ve diğer küçük gezegenler, kuyruklu yıldızlar ile uzay enkazlarını barındırmakta olan bir gezegen sisteminin elemanları, sistemin merkezinde bulunan bir yıldız etrafında eliptik yörüngeler üzerinde hareket etmektedir. Ancak bu cisimler, sistemin merkezinde yer alan yıldızın tam orta noktası merkezli olarak çizilen elipsler üzerinde değil, iki cisim probleminde de anlatıldığı üzere kütlelerine göre yıldız bünyesinde veya yıldızın dış noktalarından birinde bulunan bir çift merkezi çevresinde dönmektedir. Yörüngesi boyunca herhangi bir noktada, herhangi bir gezegen, çift merkezine göre belirli bir kinetik ve potansiyel enerji değerine sahip olacaktır ve bu iki enerjinin toplamı, yörüngesi boyunca her noktada sabit bir değerdir. Sonuç olarak, bir gezegen enberi konumuna yaklaşırken, potansiyel enerjisi azaldıkça gezegenin hızı artacaktır; tersi durumda enöte konumuna yaklaşıldığında ise potansiyel enerjisi arttıkça hızı azalacaktır.

Karşılıklı kütleçekimsel tedirginlikler dolayısıyla, gezegensel yörüngelerin dışmerkezlikleri zamanla değişmektedir. Güneş Sisteminin en küçük gezegeni olan Merkür en yüksek dışmerkezlikli yörüngeye sahiptir. Halihazırdaki devirde, Mars, Merkür'ün ardından dışmerkezlik büyüklüğünde ikinci sırada yer almakta olup, Venüs ve Neptün sistem içindeki en düşük dışmerkezliğe sahip gezegenlerdir.

Kanunlar

Yörüngelerin anlaşılabilmesi için birkaç temel kural bulunmaktadır:

• Yerçekimi gibi bir kuvvet düz bir çizgide uçmaya çalışan bir nesneyi kavisli bir yola çeker.
• Nesne esas cisme doğru çekildiğinde cismin içine düşer. Ancak yeterli teğetsel hıza sahipse bu cisim cisme çarpmak yerine daimi olarak kavisli bir yol izler. Bu kapsamdaki cisimler için yörüngedeki cisim tabiri kullanılabilir.

Hareket eden iki cismin kütleleriyle birlikte var olan bir hız ilişkisi pratikte dört adet alt türe ayrılabilir. Bunlar:

Yörüngesiz rotalar

Bozulmuş eliptik rota aralığı veya tam bir tur yörüngede bulunamama durumu

Yörüngesel gezengeler (veya basitçe yörüngeler)

• En yakın noktası başlangıç noktasının tam karşısında olan eliptik rota aralığı
• Dairesel yol
• En yakın noktası başlangıç noktasında bulunan olan eliptik rota aralığı

Açık veya kaçış rotası

• Parabolik rota
• Hiperbolik rota

Yörünge roketlerinin, roketi atmosferin üzerine çıkarmak için önce dikey olarak fırlatıldığını (bu da sürtünme direncine neden olur) ve daha sonra yavaşça eğildiğini ve yörünge hızına ulaşmak için roket motorunu atmosfere paralel olarak ateşlemeyi bitirdiğini belirtmek gerekir.

Yörüngeye girdikten sonra hızları onları atmosferin üzerinde yörüngede tutar. Örneğin, eliptik bir yörünge yoğun havaya dalarsa, nesne hızını kaybedecek ve yeniden atmosfere girecektir (yani düşecektir). Bazen bir uzay aracı, genellikle aerobraking manevrası olarak adlandırılan bir hareketle atmosferi kasıtlı olarak keser.

Örnekleme

Newton'un top güllesi modeli fırlatılan bir cismin ne şekilde tekrar düşeceğini öngörmektedir.

Bir gezegen çevresindeki yörüngenin çiziminde gösterildiği üzere, Newton'un top güllesi modeli bu duruma uygun bir örnek teşkil etmektedir. Bu örnek, top üzerindeki hava sürtünmesi etkisi göz ardı edilmesi veya atmosfer etkisini aşacak oranda yüksek bir dağın varlığı kabul edildiğinde bu dağın tepesindeki bir topun, seçilen herhangi bir namlu çıkış hızında bir gülleyi yatay olarak ateşleyebildiği bir 'düşünce deneyidir'.

Eğer top düşük bir başlangıç hızıyla ateşlenirse, topun aldığı yol aşağıya doğru kıvrılır ve yere çarpar (A). Ateşleme hızı arttıkça, gülle toptan daha uzaktaki bir noktada (B) yere çarpar, çünkü top hala yere doğru düşerken, yer giderek ondan uzaklaşmaktadır. Tüm bu hareketler aslında teknik anlamda "yörüngelerdir" - ağırlık merkezi etrafındaki eliptik bir yolun bir kısmını tanımlarlar - ancak bu iki durumda yörünge Dünya'ya çarparak kesintiye uğrar.

Eğer gülle yeterli bir hızla ateşlenirse, yer de en az güllenin düştüğü mesefe kadar eğilerek gülleden uzaklaşır, yani gülle asla yere çarpmaz. Artık kesintisiz ya da dairesel yörünge olarak adlandırılabilecek bir yörünge oluşmuş olur. Gezegenin ağırlık merkezi ve kütlesinin üzerindeki herhangi bir yükseklik kombinasyonu için, (C)'de gösterildiği gibi dairesel bir yörünge üreten ve Dünyanın kütlesine göre çok küçük olduğu varsayılan topun kütlesinden etkilenmeyen belirli bir ateşleme hızı vardır.

Ateşleme hızı arttırıldıkça kesintisiz eliptik yörüngeler oluşur; bunlardan biri (D)'de gösterilmiştir. İlk ateşleme şekildeki gibi Dünya yüzeyinin üzerindeyse, daha yavaş ateşleme hızında da kesintiye uğramayan eliptik yörüngeler oluşacaktır; bunlar Dünya'ya en çok yarım yörünge ötesinde ve ateşleme noktasının tam karşısında, dairesel yörüngenin altındaki noktada yaklaşacaktır.

Kaçış hızı adı verilen ve gezegenin kütlesine ve cismin sınır merkezinden uzaklığına bağlı olan belirli bir yatay ateşleme hızında, parabolik bir yola sahip açık bir yörünge (E) elde edilir. Daha da yüksek hızlarda nesne bir dizi hiperbolik yörünge izleyecektir. Pratik anlamda, bu yörünge türlerinin her ikisi de nesnenin gezegenin çekiminden "kurtulduğu" ve bir daha geri dönmemek üzere "uzaya gittiği" anlamına gelir.

Newton hareket yasaları

Newton kütleçekim kanunu ve iki cisim problemi için hareket yasaları

Çoğu durumda rölativistik etkiler ihmal edilebilir ve Newton yasaları hareketin yeterince doğru bir tanımını verir. Bir cismin ivmesi, üzerine etki eden kuvvetlerin toplamının kütlesine bölünmesine eşittir ve bir cisme etki eden yerçekimi kuvveti, çeken iki cismin kütlelerinin çarpımıyla orantılıdır ve aralarındaki mesafenin karesiyle ters orantılı olarak azalır. Bu Newtoncu yaklaşıma göre, iki noktalı kütlelerden ya da küresel cisimlerden oluşan bir sistem için, sadece karşılıklı kütle çekiminden etkilenen yörüngeleri tam olarak hesaplanabilir. Eğer ağır cisim küçük cisimden çok daha büyükse, bir gezegenin yörüngesinde dönen bir uydu ya da küçük bir ay ya da Güneş'in yörüngesinde dönen Dünya örneğinde olduğu gibi, hareketi ağır cismi merkez alan bir koordinat sistemi cinsinden tanımlamak yeterince doğru ve uygundur. İki cismin kütlelerinin karşılaştırılabilir olduğu durumda da tam bir Newton çözümü hala yeterlidir ve koordinat sistemini sistemin kütlesinin merkezine yerleştirerek elde edilebilir.

Kütleçekimsel potansiyel enerji tanımı

Enerji yerçekimi alanları ile ilişkilidir. Diğer bir cisimden uzaktaki sabit bir cisim, kendisine doğru çekilirse harici bir etki yapabilir ve bu nedenle yerçekimsel potansiyel enerjiye sahiptir. İki cismi yerçekiminin çekimine karşı ayırmak için güç gerektiğinden, cisimler ayrıldıkça yerçekimi potansiyel enerjileri artar ve birbirlerine yaklaştıkça azalır. Noktasal kütleler için, ayrılma sıfıra yaklaştıkça çekim enerjisi sıfıra düşer. Birbirlerinden sonsuz uzaklıkta olduklarında potansiyel enerjinin sıfır değerine sahip olduğunu ve dolayısıyla daha küçük sonlu mesafeler için negatif bir değere (sıfırdan azaldığı için) sahip olduğunu varsaymak uygun ve gelenekseldir.

Yörüngesel enerjiler ve yörünge şekilleri

Sadece iki yerçekimsel cisim etkileşime girdiğinde, yörüngeleri konik bir kesiti takip eder. Yörünge açık (cismin asla geri dönmeyeceği anlamına gelir) ya da kapalı (geri dönen) olabilir. Hangisi olduğu sistemin toplam enerjisine (kinetik + potansiyel enerji) bağlıdır. Açık bir yörünge durumunda, yörüngenin herhangi bir konumundaki hız en azından o konum için kaçış hızıdır, kapalı bir yörünge durumunda ise hız her zaman kaçış hızından azdır. Kinetik enerji hiçbir zaman negatif olmadığından, sonsuz ayrılıkta potansiyel enerjiyi sıfır olarak kabul eden genel kural benimsenirse, bağlı yörüngeler negatif toplam enerjiye, parabolik yörüngeler sıfır toplam enerjiye ve hiperbolik yörüngeler pozitif toplam enerjiye sahip olacaktır.

Açık bir yörünge, yörüngesinin o noktasında tam olarak kaçış hızına sahipse parabolik bir şekle sahip olacak ve hızı kaçış hızından büyük olduğunda bir hiperbol şekline sahip olacaktır. Kaçış hızı ya da daha büyük olan cisimler birbirlerine yaklaştıklarında, en yakın oldukları anda birbirlerinin etrafında kısa bir süre dönerler ve sonra sonsuza kadar ayrılırlar.

Tüm kapalı yörüngeler bir elips şeklindedir. Dairesel yörünge, elipsin odaklarının çakıştığı özel bir durumdur. Yörüngedeki cismin Dünya'ya en yakın olduğu noktaya yerberi denir ve yörünge Dünya'dan başka bir cisimle ilgili olduğunda enberi (daha nadir olarak " perifokus" ya da " perisentron") olarak adlandırılır. Uydunun Dünya'dan en uzak olduğu noktaya yeröte, enöte ya da bazen apifokus veya aposantron denir. Enberiden enöteye çizilen bir çizgi apsis çizgisidir. Bu, elipsin ana eksenidir ve iki nokta arasındaki en uzun kısmından geçen çizgidir.

Kepler kanunları

Kapalı yörüngeleri izleyen cisimler yollarını periyot adı verilen belirli bir sürede tekrarlarlar. Bu hareket, Newton'un yasalarından matematiksel olarak türetilebilen Kepler'in deneysel yasaları ile tanımlanır. Bunlar aşağıdaki gibi formüle edilebilir:

1. Bir gezegenin Güneş etrafındaki yörüngesi bir elipstir ve Güneş bu elipsin odak noktalarından birinde yer alır. (Bu odak noktası aslında Güneş-gezegen sisteminin çift merkezidir; basitlik açısından bu açıklamada Güneş'in kütlesinin gezegenin kütlesinden sonsuz derecede büyük olduğu varsayılmaktadır). Gezegenin yörüngesi yörünge düzlemi adı verilen bir düzlemde uzanır. Yörünge üzerinde kendisini çeken cisme en yakın nokta enberi olarak adlandırılır. Kendisini çeken cisimden en uzak noktaya ise enöte denir. Belirli cisimlerin yörüngeleri için özel terimler de kullanılmaktadır; Güneş'in etrafında dönen cisimlerin günberi ve günöte, Dünya'nın etrafında dönen cisimlerin yerberi ve yeröte, Ay'ın etrafında dönen cisimlerin ise ayberi ve ayöte (ya da sırasıyla periselene ve aposelene) yörüngeleri vardır. Sadece Güneş'in değil, herhangi bir yıldızın etrafındaki yörüngenin de bir periastronu ve bir apastronu vardır.
2. Gezegen yörüngesinde hareket ederken, Güneş'ten gezegene uzanan çizgi, gezegenin bu süre zarfında yörüngesinin hangi kısmını izlediğine bakılmaksızın, belirli bir süre boyunca yörünge düzleminin sabit bir alanını tarar. Bu, gezegenin günberi yakınında günöte yakınından daha hızlı hareket ettiği anlamına gelir, çünkü daha küçük mesafede aynı alanı kaplamak için daha büyük bir yay izlemesi gerekir. Bu yasa genellikle "eşit zamanda eşit alan" olarak ifade edilir.
3. Belirli bir yörünge için, yörünge yarı-büyük ekseninin küpü ile yörünge periyodunun karesinin oranı eşittir.

Newton kütleçekim yasasının sınırları

Noktasal bir kütlenin ya da Newtoncu çekim alanına sahip küresel bir cismin bağlı yörüngeleri kapalı elipsler olup, aynı yolu tam olarak ve sonsuza kadar tekrarlarken, küresel olmayan ya da Newton'vari olmayan herhangi bir etki (örneğin ya da rölativistik etkiler, dolayısıyla çekim alanının davranışının mesafeyle değişmesi) yörüngenin şeklinin kapalı elipslerin karakteristik Newton iki cisim hareketinden sapmasına neden olacaktır. İki cisim çözümleri Newton tarafından 1687 yılında Principia'da yayınlanmıştır. 1912'de üç cisim problemini çözebilecek yakınsak bir sonsuz seri geliştirmiştir; ancak bu seri çok yavaş yakınsamakta ve pek kullanışlı bulunmamaktadır. Lagrange noktaları gibi özel durumlar dışında, dört ya da daha fazla cisim içeren bir sistemin hareket denklemlerini çözecek bir yöntem henüz bilinmemektedir.

Çoklu cisim problemleri yaklaşımları

Kesin bir kapalı form çözümü yerine, çok sayıda cisim içeren yörüngeler keyfi olarak yüksek doğrulukla tahmin edilebilir. Bu yaklaşımlar iki şekilde olabilir:

Bunlardan biri saf eliptik hareketi temel alır ve birden fazla cismin yerçekimsel etkisini hesaba katmak için pertürbasyon terimleri kullanır. Bu, astronomik cisimlerin konumlarını hesaplamak için uygundur. Uyduların, gezegenlerin ve diğer cisimlerin hareket denklemleri büyük bir doğrulukla bilinir ve göksel navigasyon için tablolar oluşturmak için kullanılır. Yine de, Newton sonrası yöntemlerle ele alınması gereken seküler olgular da bulunmaktadır.

Diferansiyel denklem formu bilimsel veya görev planlama amaçları için kullanılır. Newton yasalarına göre, bir cisme etki eden tüm kuvvetlerin toplamı, o cismin kütlesi ile ivmesinin çarpımına eşittir (F = ma). Bu nedenle ivmeler konumlar cinsinden ifade edilebilir. Pertürbasyon terimlerini bu şekilde tanımlamak çok daha basittir. Konum ve hızın başlangıç değerlerinden sonraki konum ve hızları tahmin etmek bir başlangıç değer problemini çözmeye tekabül eder. Sayısal yöntemler nesnelerin konumlarını ve hızlarını kısa bir süre sonra hesaplar, ardından da bu hesaplamayı durmadan tekrarlar. Ancak, bir bilgisayarın matematiğinin sınırlı doğruluğundan kaynaklanan küçük aritmetik hatalar kümülatiftir ve bu da bu yaklaşımın doğruluğunu sınırlar.

Çok sayıda nesne içeren diferansiyel simülasyonlar, kütle merkezleri arasında hiyerarşik çiftler halinde hesaplamalar yapar. Bu şema kullanılarak galaksiler, yıldız kümeleri ve diğer büyük nesne toplulukları simüle edilebilmiştir.

Newtoncu yörüngesel hareket analizi

Aşağıdaki formül bu tür bir eliptik yörünge için geçerlidir. Sadece merkezi cisme doğru olan yerçekimi ivmesinin aralarındaki mesafenin karesinin tersi ile ilişkili olduğunu belirten Newton yerçekimi yasası ile başlanırsa:

${\displaystyle F_{2}=-{\frac {Gm_{1}m_{2}}{r^{2}}}}$

Burada F₂, m₁ kütlesinin m₂ kütlesine uyguladığı çekim kuvvetinin m2 kütlesine uyguladığı kuvvet, G evrensel çekim sabiti ve r iki kütle merkezi arasındaki mesafedir.

Newton'un İkinci Yasası'na göre, m₂'ye etki eden kuvvetlerin toplamı o cismin ivmesiyle ilişkilidir:

${\displaystyle F_{2}=m_{2}A_{2}}$

Burada A₂, m₂'ye etki eden m₁'in çekim kuvveti F₂'nin neden olduğu m₂'nin ivmesidir.

where is the acceleration of caused by the force of gravitational attraction F₂ of m₁ acting on m₂.

1. ve 2. denklemlerin birleştirilmesi:

${\displaystyle -{\frac {Gm_{1}m_{2}}{r^{2}}}=m_{2}A_{2}}$

İvme için çözüm, A₂:

${\displaystyle A_{2}={\frac {F_{2}}{m_{2}}}=-{\frac {1}{m_{2}}}{\frac {Gm_{1}m_{2}}{r^{2}}}=-{\frac {\mu }{r^{2}}}}$

burada ${\displaystyle \mu \,}$ standart yerçekimi parametresidir, ki bu durumda ${\displaystyle Gm_{1}}$ olarak gösterilir. Tanımlanan sistemin m₂ olduğu anlaşılmaktadır, bu nedenle alt simgeler atılabilir.

Merkezi cismin durağan olarak kabul edilebilecek kadar büyük olduğu varsayılmakta ve genel göreliliğin daha ince etkileri göz ardı edilmektedir.

Bir sarkaç veya yaya bağlı bir cisim elips içinde sallanırken, ${\displaystyle A=F/m=-kr.}$ formülünde gösterildiği gibi içe doğru ivme/kuvvet mesafesi ile orantılıdır. Vektörlerin toplanma şekli nedeniyle, kuvvetin ${\displaystyle {\hat {\mathbf {x} }}}$ veya ${\displaystyle {\hat {\mathbf {y} }}}$ yönlerindeki bileşenleri de mesafelerin ilgili bileşenleriyle orantılıdır, ${\displaystyle r''_{x}=A_{x}=-kr_{x}}$. Dolayısıyla, tüm analiz bu boyutlarda ayrı ayrı yapılabilir. Bu, elipsin ${\displaystyle x=A\cos(t)}$ ve ${\displaystyle y=B\sin(t)}$ harmonik parabolik denklemleri ile sonuçlanır.

Yörüngedeki nesnenin 𝑡 anındaki konumu, kutupsal koordinatlarda vektör hesabı kullanılarak hem standart Öklid temelinde hem de orijini kuvvet merkeziyle çakışan (kutupsal temelde) düzlem üzerinde bulunur. ${\displaystyle r}$ cisim ile merkez arasındaki mesafe ve ${\displaystyle \theta }$ cismin döndüğü açı olsun. ${\displaystyle {\hat {\mathbf {x} }}}$ ve ${\displaystyle {\hat {\mathbf {y} }}}$ standart Öklid tabanları olsun ve ${\displaystyle {\hat {\mathbf {r} }}=\cos(\theta ){\hat {\mathbf {x} }}+\sin(\theta ){\hat {\mathbf {y} }}}$ ve ${\displaystyle {\hat {\boldsymbol {\theta }}}=-\sin(\theta ){\hat {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}}$ radyal ve enine kutupsal taban olsun; bu durumda ilki merkezi cisimden yörüngedeki nesnenin mevcut konumuna işaret eden birim vektör ve ikincisi yörüngedeki nesnenin saat yönünün tersine bir daire çizmesi halinde gideceği yöne işaret eden ortogonal birim vektördür. O zaman yörüngedeki nesneye giden vektör:

${\displaystyle {\hat {\mathbf {O} }}=r\cos(\theta ){\hat {\mathbf {x} }}+r\sin(\theta ){\hat {\mathbf {y} }}=r{\hat {\mathbf {r} }}}$

Bu mesafe ve açının zaman içinde nasıl değiştiğinin standart türevlerini belirtmek için ${\displaystyle {\dot {r}}}$ ve ${\displaystyle {\dot {\theta }}}$ kullanılır. Bir vektörün zaman içinde nasıl değiştiğini görmek için ${\displaystyle t}$ zamanındaki konumunu ${\displaystyle t+\delta t}$ zamanındakinden çıkarıp ${\displaystyle \delta t}$'ye bölerek türevi alınır. Elde edilen sonuç da bir vektör olacaktır. Temel vektör ${\displaystyle {\hat {\mathbf {r} }}}$ nesne yörüngede döndükçe hareket ettiğinden, onu farklılaştırarak başlanır. ${\displaystyle t}$ zamanından ${\displaystyle t+\delta t}$, ${\displaystyle {\hat {\mathbf {r} }}}$ vektörü başlangıcını orijinde tutar ve ${\displaystyle \theta +{\dot {\theta }}\ \delta t}$ açısıyla dönerek başını ${\displaystyle {\dot {\theta }}\ \delta t}$ dik yönünde ${\displaystyle \theta }$ mesafesi kadar hareket ettirir ve ${\displaystyle {\dot {\theta }}{\hat {\boldsymbol {\theta }}}}$, ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ 'nin bir türevini verir.

${\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\cos(\theta ){\hat {\mathbf {x} }}+\sin(\theta ){\hat {\mathbf {y} }}\\{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {\mathbf {r} }}&=-\sin(\theta ){\dot {\theta }}{\hat {\mathbf {x} }}+\cos(\theta ){\dot {\theta }}{\hat {\mathbf {y} }}={\dot {\theta }}{\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\theta }}}&=-\sin(\theta ){\hat {\mathbf {x} }}+\cos(\theta ){\hat {\mathbf {y} }}\\{\frac {\delta {\hat {\boldsymbol {\theta }}}}{\delta t}}={\dot {\boldsymbol {\theta }}}&=-\cos(\theta ){\dot {\theta }}{\hat {\mathbf {x} }}-\sin(\theta ){\dot {\theta }}{\hat {\mathbf {y} }}=-{\dot {\theta }}{\hat {\mathbf {r} }}\end{aligned}}}$

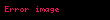
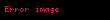
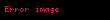
Artık yörüngede dönen cismin hızı ve ivmesi bulunabilir.

${\displaystyle {\begin{aligned}{\hat {\mathbf {O} }}&=r{\hat {\mathbf {r} }}\\{\dot {\mathbf {O} }}&={\frac {\delta r}{\delta t}}{\hat {\mathbf {r} }}+r{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {r}}{\hat {\mathbf {r} }}+r\left[{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]\\{\ddot {\mathbf {O} }}&=\left[{\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]+\left[{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}-r{\dot {\theta }}^{2}{\hat {\mathbf {r} }}\right]\\&=\left[{\ddot {r}}-r{\dot {\theta }}^{2}\right]{\hat {\mathbf {r} }}+\left[r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}\right]{\hat {\boldsymbol {\theta }}}\end{aligned}}}$

${\displaystyle {\hat {\mathbf {r} }}}$ ve ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ katsayıları radyal ve enine yönlerdeki ivmeleri verir. Belirtildiği gibi, yerçekimi nedeniyle bu ilkini Newton ${\displaystyle -\mu /r^{2}}$ olarak verir ikincisi ise sıfırdır.

   

${\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=-{\frac {\mu }{r^{2}}}}$

(1)

   

   

${\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}=0}$

(2)

   Denklem (2), parçalara göre entegrasyon kullanılarak yeniden düzenlenebilir.

${\displaystyle r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}={\frac {1}{r}}{\frac {d}{dt}}\left(r^{2}{\dot {\theta }}\right)=0}$

Yörüngedeki nesne çakılmadığı sürece sıfır olmadığı için bu değer ${\displaystyle r}$ ile çarpılabilir. Bu durumda türevin sıfır olması fonksiyonun sabit olduğunu gösterir.

   

${\displaystyle r^{2}{\dot {\theta }}=h}$

(3)

   Bu aslında Kepler'in ikinci yasasının teorik kanıtıdır (Bir gezegen ile Güneş'i birleştiren bir çizgi, eşit zaman aralıklarında eşit alanları süpürür). Bütünleşme sabiti olan "h", birim kütle başına düşen açısal momentumdur.

Denklem (1)'den bir yörünge denklemi elde edilebilmesi için zamanın elimine edilmesi gerekmektedir. (Ayrıca bakınız.) Kutupsal koordinatlarda bu, yörüngedeki nesnenin merkeze olan uzaklığını ${\displaystyle r}$ açısının bir fonksiyonu olarak ifade edecektir ${\displaystyle \theta }$ . Ancak, ${\displaystyle u=1/r}$ yardımcı değişkenini tanıtmak ve ${\displaystyle u}$'yi ${\displaystyle \theta }$'nın bir fonksiyonu olarak ifade etmek daha kolaydır. ${\displaystyle r}$'nin zamana göre türevleri, ${\displaystyle u}$'nin açıya göre türevleri olarak yeniden yazılabilir.

${\displaystyle u={1 \over r}}$

${\displaystyle {\dot {\theta }}={\frac {h}{r^{2}}}=hu^{2}}$ (türev (3))

${\displaystyle {\begin{aligned}{\frac {\delta u}{\delta \theta }}&={\frac {\delta }{\delta t}}\left({\frac {1}{r}}\right){\frac {\delta t}{\delta \theta }}=-{\frac {\dot {r}}{r^{2}{\dot {\theta }}}}=-{\frac {\dot {r}}{h}}\\{\frac {\delta ^{2}u}{\delta \theta ^{2}}}&=-{\frac {1}{h}}{\frac {\delta {\dot {r}}}{\delta t}}{\frac {\delta t}{\delta \theta }}=-{\frac {\ddot {r}}{h{\dot {\theta }}}}=-{\frac {\ddot {r}}{h^{2}u^{2}}}\ \ \ {\text{ or }}\ \ \ {\ddot {r}}=-h^{2}u^{2}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}\end{aligned}}}$

Bunları (1)'e eklemek şunu sağlar:

${\displaystyle {\begin{aligned}{\ddot {r}}-r{\dot {\theta }}^{2}&=-{\frac {\mu }{r^{2}}}\\-h^{2}u^{2}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}-{\frac {1}{u}}\left(hu^{2}\right)^{2}&=-\mu u^{2}\end{aligned}}}$

   

${\displaystyle {\frac {\delta ^{2}u}{\delta \theta ^{2}}}+u={\frac {\mu }{h^{2}}}}$

(4)

   Dolayısıyla, yerçekimi kuvveti için - ya da daha genel olarak, "herhangi bir" ters kare kuvvet yasası için - denklemin sağ tarafı bir sabit haline gelir ve denklemin harmonik denklem olduğu görülür (bağımlı değişkenin orijininin kaymasına kadar). Çözüm şudur:

${\displaystyle u(\theta )={\frac {\mu }{h^{2}}}+A\cos(\theta -\theta _{0})}$

Burada A ve θ₀ rassal sabitlerdir. Cismin yörüngesinin bu sonuç denklemi, odak noktalarından birine göre Kutupsal formdaki bir elipsin denklemidir. Bu,${\displaystyle e\equiv h^{2}A/\mu }$ dış merkezlik, ${\displaystyle a\equiv h^{2}/\mu \left(1-e^{2}\right)}$ yarı büyük eksen olmak üzere daha standart bir forma sokulur. Son olarak ${\displaystyle \theta _{0}\equiv 0}$ olarak alındığında elipsin uzun ekseni pozitif x koordinatı boyunca uzanır.

${\displaystyle r(\theta )={\frac {a\left(1-e^{2}\right)}{1+e\cos \theta }}}$

İki cisimli sistem torkun etkisi altında olduğunda, açısal momentum h sabit değildir. Aşağıdaki hesaplamadan sonra:

${\displaystyle {\begin{aligned}{\frac {\delta r}{\delta \theta }}&=-{\frac {1}{u^{2}}}{\frac {\delta u}{\delta \theta }}=-{\frac {h}{m}}{\frac {\delta u}{\delta \theta }}\\{\frac {\delta ^{2}r}{\delta \theta ^{2}}}&=-{\frac {h^{2}u^{2}}{m^{2}}}{\frac {\delta ^{2}u}{\delta \theta ^{2}}}-{\frac {hu^{2}}{m^{2}}}{\frac {\delta h}{\delta \theta }}{\frac {\delta u}{\delta \theta }}\\\left({\frac {\delta \theta }{\delta t}}\right)^{2}r&={\frac {h^{2}u^{3}}{m^{2}}}\end{aligned}}}$

iki cisimli sistemin elde edilir.

   

${\displaystyle {\frac {\delta }{\delta \theta }}\left(h{\frac {\delta u}{\delta \theta }}\right)+hu={\frac {\mu }{h}}}$

(5)

   

Göreli yörüngesel hareket

Yörünge mekaniğinin yukarıdaki klasik (Newtoncu) analizi, genel göreliliğin çerçeve sürüklenmesi ve yerçekimsel zaman genişlemesi gibi daha ince etkilerinin ihmal edilebilir olduğunu varsayar. Çok büyük kütleli cisimlerin yakınında (Merkür'ün Güneş etrafındaki yörüngesinin presesyonunda olduğu gibi) veya aşırı hassasiyet gerektiğinde (GPS uyduları için yörünge elemanlarının ve zaman sinyali referanslarının hesaplanmasında olduğu gibi) göreceli etkiler ihmal edilebilir olmaktan çıkar.

Yörünge düzlemleri

Buraya kadar yapılan analiz iki boyutludur; uzayda sabitlenmiş bir düzlemde bozulmamış bir yörüngenin iki boyutlu olduğu ortaya çıkmıştır ve bu nedenle üç boyuta genişletme, iki boyutlu düzlemin ilgili gezegensel cismin kutuplarına göre gerekli açıya döndürülmesini gerektirir.

Bunu üç boyutta yapmak için rotasyon, benzersiz bir şekilde belirlemek için üç sayı gerektirir; geleneksel olarak bunlar üç açı olarak ifade edilir.

Yörünge periyodu

Yörünge periyodu, yörüngedeki bir cismin bir yörüngeyi tamamlamak için ne kadar zaman harcadığıdır.

Yörüngeleri tespit etmek

Bir cisim etrafındaki Kepler yörüngesini belirlemek için altı parametre gerekir. Örneğin, cismin başlangıç konumunu belirleyen üç sayı ile hızını belirleyen üç değer, zaman içinde ileriye (veya geriye) doğru hesaplanabilen benzersiz bir yörünge tanımlayacaktır. Ancak, geleneksel olarak kullanılan parametreler biraz farklıdır.

Geleneksel olarak kullanılan yörünge elemanları kümesi, Johannes Kepler ve yasalarından sonra Kepleryan elemanlar kümesi olarak adlandırılır. Kepleryan elemanlar altı tanedir:

• Eğim (i)
• Çıkış düğümü boylamı (Ω)
• Periapsis argümanı (ω)
• Eksantriklik (e)
• Yarı büyük eksen (a)
• Devirdeki ortalama anomali (M₀).

Temelde, bir cismin yörünge elemanları bilindiğinde, konumu zaman içinde sonsuza kadar ileriye ve geriye doğru hesaplanabilir. Ancak pratikte, yörüngeler varsayılan bir noktasal kaynaktan gelen basit yerçekiminden başka kuvvetler tarafından etkilenir veya tedirgin edilir (bir sonraki bölüme bakınız) ve dolayısıyla yörünge elemanları zamanla değişir.

Tedirginlik

Yörünge tedirginliği, ana kütle çekim cisminin genel kuvvetinden veya ortalama itkisinden çok daha küçük olan ve yörüngedeki iki cismin dışında bulunan bir kuvvet veya itkinin, yörüngenin parametrelerini zaman içinde değiştiren bir ivmeye neden olmasıdır.

Radyal, ters yönlü veya enine tedirginlikler

Yörüngedeki bir cisme verilen küçük bir radyal itki eksantrikliği değiştirir, ancak yörünge periyodunu değiştirmez (birinci dereceden). İleriye veya geriye doğru bir itme (yani yörünge hareketi boyunca uygulanan bir itme) hem eksantrikliği hem de yörünge periyodunu değiştirir. Özellikle, enberideki ters yönlü bir itki enötedeki irtifayı yükseltirken, ters yönlü bir itki bunun tam tersini yapar. Enine bir itme (yörünge düzleminin dışında) periyodu veya dış merkezliği değiştirmeden yörünge düzleminin dönmesine neden olur. Her durumda, kapalı bir yörünge yine de tedirginlik noktasıyla kesişecektir.

Yörünge bozunumu

Eğer bir yörünge belirgin bir atmosfere sahip bir gezegensel cisim etrafında ise, sürüklenme nedeniyle bozulabilir. Özellikle her enberi noktasında, cisim atmosferik sürüklenmeye maruz kalır ve enerji kaybeder. Her seferinde yörünge daha az eksantrik (daha dairesel) hale gelir çünkü cisim tam da enerjinin maksimum olduğu anda kinetik enerji kaybeder. Bu, bir sarkacın en düşük noktasında yavaşlatılmasının etkisine benzer; sarkacın salınımının en yüksek noktası daha alçak olur. Birbirini izleyen her yavaşlama ile yörünge yolunun daha büyük bir kısmı atmosferden etkilenir ve etki daha belirgin hale gelir. Sonunda etki o kadar büyük hale gelir ki, maksimum kinetik enerji yörüngeyi atmosferik sürükleme etkisinin sınırlarının üzerine çıkarmaya yetmez. Bu gerçekleştiğinde cisim hızla aşağıya doğru spiral çizecek ve merkezi cisimle kesişecektir.

Bir atmosferin sınırları oldukça değişkendir. Maksimum güneş enerjisi sırasında Dünya'nın atmosferi minimum güneş enerjisi sırasında olduğundan yüz kilometre daha fazla sürüklenmeye neden olur.

Uzun iletken bağlara sahip bazı uydular da Dünya'nın manyetik alanından kaynaklanan elektromanyetik sürüklenme nedeniyle yörünge bozulması yaşayabilir. Tel manyetik alanı kestiğinde bir jeneratör gibi davranarak elektronları bir uçtan diğerine taşır. Yörünge enerjisi telin içinde ısıya dönüştürülür.

Yörüngeler, yolunun bir noktasında cismin kinetik enerjisini değiştiren roket motorları kullanılarak yapay olarak etkilenebilir. Bu, kimyasal ya da elektrik enerjisinin kinetik enerjiye dönüştürülmesidir. Bu şekilde yörünge şekli ya da yönündeki değişiklikler kolaylaştırılabilir.

Bir yörüngeyi yapay olarak etkilemenin bir başka yöntemi de güneş yelkenleri ya da manyetik yelkenler kullanmaktır. Bu itici güç biçimleri Güneş'ten başka hiçbir itici yakıt ya da enerji girdisi gerektirmez ve bu nedenle süresiz olarak kullanılabilir.

Yörünge bozulması, yörüngesinde döndükleri cismin eşzamanlı yörüngesinin altındaki cisimler için gelgit kuvvetleri sonucunda oluşabilir. Yörüngedeki cismin yerçekimi ana cisimde gelgit şişkinlikleri yaratır ve eşzamanlı yörüngenin altında kalan yörüngedeki nesne ana cismin yüzeyinden daha hızlı hareket ettiğinden şişkinlikler kısa bir açıyla ana cismin gerisinde kalır. Çıkıntıların yerçekimi ana-uydu ekseninin biraz dışındadır ve dolayısıyla uydunun hareketiyle birlikte bir bileşene sahiptir. Yakın şişkinlik cismi, uzak şişkinliğin hızlandırdığından daha fazla yavaşlatır ve sonuç olarak yörünge bozulur. Tersine, uydunun çıkıntılar üzerindeki yerçekimi ana cisme tork uygular ve dönüşünü hızlandırır. Yapay uydular yörüngelerinde döndükleri gezegenler üzerinde kayda değer bir gelgit etkisi yaratamayacak kadar küçüktür, ancak Güneş Sistemi'ndeki birkaç uydu bu mekanizma ile yörünge bozunumuna uğramaktadır. Mars'ın en içteki uydusu Phobos bunun en iyi örneğidir ve 50 milyon yıl içinde ya Mars'ın yüzeyine çarpması ya da bir halka şeklinde parçalanması beklenmektedir.

Yörüngeler kütleçekim dalgalarının yayılması yoluyla bozulabilir. Bu mekanizma çoğu yıldız nesnesi için son derece zayıftır, yalnızca birbirlerinin etrafında dönen kara delikler veya nötron yıldızları gibi aşırı kütle ve aşırı ivmenin bir arada olduğu durumlarda önemli hale gelir.

Basıklık

Yörüngede dönen cisimlerin standart analizi, tüm cisimlerin tekdüze kürelerden ya da daha genel olarak her biri tekdüze yoğunlukta eş merkezli kabuklardan oluştuğunu varsayar. Bu tür cisimlerin kütleçekimsel olarak noktasal kaynaklara eşdeğer olduğu gösterilebilir.

Ancak gerçek hayatta birçok cisim kendi etrafında dönmekte ve bu da kütleçekim alanını basıklaştırarak bozmakta ve kütleçekim alanına, cismin yarıçapı ile kıyaslanabilecek mesafelerde önemli olan bir dört kutuplu momenti kazandırmaktadır. Genel durumda, örneğin bir gezegen gibi dönen bir cismin yerçekimi potansiyeli genellikle küresel simetriden sapmaları hesaba katan çok kutuplu olarak genişletilir. Uydu dinamiği açısından, yörünge periyodundan daha uzun zaman aralıklarında kümülatif olan seküler yörünge tedirginlikleri yarattıklarından, çift bölgeli harmonik katsayılar veya çift bölgeli katsayılar özel bir öneme sahiptir. Bunlar cismin uzaydaki simetri ekseninin yönelimine bağlıdır ve yarı büyük eksen haricinde genel olarak tüm yörüngeyi etkiler.

Çoklu kütleçekimsel nesneler

Diğer yerçekimi cisimlerinin etkileri de önemli olabilir. Örneğin, (Ay'ın yörüngesi), Dünya'nın yanı sıra Güneş'in yerçekiminin etkisine imkan vermeden doğru bir şekilde tanımlanamaz. Yaklaşık bir sonuç, cisimlerin daha ağır bir gezegen ya da ayın etrafında, bu tedirginliklere rağmen, daha ağır cismin Hill küresi içinde dengeli bir yörüngede dönüyor olmaları koşuluyla, genellikle makul ölçüde istikrarlı yörüngelere sahip olacaklarıdır.

İkiden fazla kütleçekimi etkisine sahip cisimler söz konusu olduğunda bu durum olarak adlandırılır. Bazı özel durumlar formüle edilmiş olsa da çoğu n-cisim probleminin kapalı formda çözümü yoktur.

Işık radyasyonu ve yıldızlararası rüzgar

Özellikle küçük cisimler için, ışık ve yıldız rüzgarı cismin duruşunda ve hareket yönünde önemli bozulmalara neden olabilir ve zaman içinde kayda değer olabilir. Gezegensel cisimler arasında asteroitlerin hareketi özellikle asteroitler Güneş'e bağlı olarak dönerken büyük zaman aralıklarında etkilenir.

Olağandışı yörüngeler

Matematikçiler periyodik olarak tekrar eden eliptik olmayan yörüngelerde birden fazla cismin bulunmasının prensipte mümkün olduğunu keşfetmişlerdir, ancak bu tür yörüngelerin çoğu kütle, konum veya hızdaki küçük tedirginlikler açısından kararlı değildir. Bununla birlikte, üç hareketli cisim tarafından doldurulan düzlemsel bir sekiz rakamı yörüngesi de dahil olmak üzere bazı özel kararlı durumlar tanımlanmıştır. Daha ileri çalışmalar, düzlemsel olmayan yörüngelerin de mümkün olduğunu keşfetmiştir; bunlardan biri, topolojik olarak bir kenarlarına eşdeğer 4 kabaca dairesel, birbirine kenetlenmiş yörüngede hareket eden 12 kütleyi içermektedir.

Bu tür yörüngelerin evrende doğal olarak bulunmasının, gerekli koşulların tesadüfen oluşma ihtimalinin düşük olması nedeniyle son derece düşük bir olasılık olduğu düşünülmektedir.

Astrodinamik

Yörünge mekaniği veya astrodinamik, balistik ve gök mekaniğinin roketlerin ve diğer uzay araçlarının hareketiyle ilgili pratik sorunlara uygulanmasıdır. Bu nesnelerin hareketi genellikle Newton'un hareket yasalarından ve Newton'un evrensel çekim yasasından hesaplanır. Uzay görevi tasarımı ve kontrolünde temel bir disiplindir. Gök mekaniği, uzay araçları ve yıldız sistemleri, gezegenler, uydular ve kuyruklu yıldızlar gibi doğal astronomik cisimler de dahil olmak üzere yerçekimi etkisi altındaki sistemlerin yörünge dinamiklerini daha geniş bir şekilde ele alır. Yörünge mekaniği, , yörünge düzlemi değişiklikleri ve gezegenler arası transferler dahil olmak üzere uzay aracı yörüngelerine odaklanır ve görev planlayıcıları tarafından itici manevraların sonuçlarını tahmin etmek için kullanılır. Genel görelilik, yörüngeleri hesaplamak için Newton yasalarından daha kesin bir teoridir ve bazen daha fazla doğruluk için veya yüksek yerçekimi durumlarında (Güneş'e yakın yörüngeler gibi) gereklidir.

Dünya yörüngeleri

• Alçak Dünya yörüngesi (LEO): Yüksekliği 2.000 km'ye (0-1.240 mil) kadar olan yer merkezli yörüngeler.
• Orta Dünya yörüngesi (MEO): Yüksekliği 2.000 km'den (1.240 mil) 35.786 kilometre (22.236 mil) ile yer eşzamanlı yörüngenin hemen altına kadar değişen yörüngeler. Ara dairesel yörünge olarak da bilinir. Bunlar "en yaygın olarak 20.200 kilometre (12.600 mil) ya da 20.650 kilometre (12.830 mil) yükseklikte ve 12 saatlik bir yörünge periyoduna sahiptir."
• Hem yer eşzamanlı yörünge (GSO) hem de yer sabit yörünge (GEO) Dünya'nın etrafında Dünya'nın yanal dönüş periyoduna uyan yörüngelerdir. Tüm jeosenkron ve jeostatik yörüngelerin yarı büyük ekseni 42.164 km'dir (26.199 mil). Tüm yer sabit yörüngeler aynı zamanda yer eşzamanlıdır, ancak tüm yer eşzamanlı yörüngeler yer sabit değildir. Bir yer sabit yörünge tam olarak ekvatorun üzerinde kalırken, bir jeosenkron yörünge Dünya yüzeyinin daha fazlasını kapsayacak şekilde kuzeye ve güneye salınabilir. Her ikisi de her bir sidereal günde (Güneş'e göre değil yıldızlara göre) Dünya'nın bir tam turunu tamamlar.
• Yüksek Dünya yörüngesi: Yer eşzamanlı yörüngenin 35.786 km (22.240 mil) yüksekliğinin üzerindeki yörüngeler.

Kütleçekim ölçeği

Yerçekimi sabiti G şu şekilde hesaplanmıştır:

• (6.6742 ± 0.001) × 10⁻¹¹ (kg/m³)⁻¹s⁻².

Böylece sabit, yoğunluk⁻¹ zaman⁻² boyutuna sahiptir. Bu, aşağıdaki özelliklere karşılık gelir.

Mesafelerin (yoğunlukları aynı tutarken cisimlerin boyutları da dahil olmak üzere) zamanı ölçeklendirmeye gerek kalmadan benzer yörüngeler verir: örneğin mesafeler yarıya indirilirse, kütleler 8'e, yerçekimi kuvvetleri 16'ya ve yerçekimi ivmeleri 2'ye bölünür. Dolayısıyla hızlar yarıya iner ve yörünge süreleri ve yerçekimiyle ilgili diğer seyahat süreleri aynı kalır. Örneğin, bir nesne bir kuleden bırakıldığında, yere düşmesi için geçen süre, Dünya'nın ölçekli bir modeli üzerinde kulenin ölçekli bir modeli ile aynı kalır.

Kütleleri aynı tutarak mesafeleri ölçeklendirmek (noktasal kütleler söz konusu olduğunda veya yoğunlukları ayarlayarak) benzer yörüngeler verir; mesafeler 4 ile çarpılırsa, çekim kuvvetleri ve ivmeler 16'ya bölünür, hızlar yarıya iner ve yörünge periyotları 8 ile çarpılır.

Tüm yoğunluklar 4 ile çarpıldığında, yörüngeler aynıdır; yerçekimi kuvvetleri 16 ile ve ivmeler 4 ile çarpılır, hızlar iki katına çıkar ve yörünge periyotları yarıya iner.

Tüm yoğunluklar 4 ile çarpıldığında ve tüm boyutlar yarıya indirildiğinde, yörüngeler benzerdir; kütleler 2'ye bölünür, yerçekimi kuvvetleri aynıdır, yerçekimi ivmeleri iki katına çıkar. Dolayısıyla hızlar aynıdır ve yörünge periyotları yarıya iner.

Tüm bu ölçeklendirme durumlarında, yoğunluklar 4 ile çarpılırsa, süreler yarıya iner; hızlar iki katına çıkarılırsa, kuvvetler 16 ile çarpılır.

Bu özellikler aşağıdaki formülde gösterilmiştir ((yörünge periyodu formülünden türetilmiştir))

${\displaystyle GT^{2}\rho =3\pi \left({\frac {a}{r}}\right)^{3},}$

Yarıçapı r ve ortalama yoğunluğu ρ olan küresel bir cismin etrafındaki küçük bir cismin yarı büyük ekseni a olan eliptik bir yörüngesi için, burada T yörünge periyodudur.

Patentler

Belirli yörüngelerin veya yörünge manevralarının belirli faydalı amaçlara uygulanması patentlere konu olmuştur.

Kütleçekim kilidi

Bazı cisimler diğer cisimlerle gelgitsel olarak kilitlenmiştir, yani gök cisminin bir tarafı sürekli olarak ev sahibi cisme dönüktür. Dünya-Ay ve Pluto-Charon sistemi için durum böyledir.

Ayrıca bakınız

• Gök günlüğü, doğal olarak oluşan astronomik nesnelerin yanı sıra yapay uyduların belirli bir zaman veya zamanlarda gökyüzündeki konumlarının bir derlemesidir.
• Yörüngeler listesi
• Molniya yörünge
• Yörüngesel uzay uçuşu
• Kutupsal yörünge
• , açısal momentumu sıfır olan bir Kepler yörüngesidir. Radyal yörüngedeki iki nesne düz bir çizgi üzerinde doğrudan birbirlerine doğru veya birbirlerinden uzaklaşarak hareket ederler.

Kaynakça

1. ^ "orbit (astronomy)". Encyclopædia Britannica (Online bas.). 5 Mayıs 2015 tarihinde kaynağından . Erişim tarihi: 28 Temmuz 2008. 
2. ^ ^{a b} "The Space Place :: What's a Barycenter". NASA. 8 Ocak 2013 tarihinde kaynağından . Erişim tarihi: 26 Kasım 2012. 
3. ^ Kuhn, The Copernican Revolution, pp. 238, 246–252
4. ^ Encyclopædia Britannica, 1968, vol. 2, p. 645
5. ^ M Caspar, Kepler (1959, Abelard-Schuman), at pp.131–140; A Koyré, The Astronomical Revolution: Copernicus, Kepler, Borelli (1973, Methuen), pp. 277–279
6. ^ "Kepler's laws of planetary motion | Definition, Diagrams, & Facts | Britannica". www.britannica.com (İngilizce). 7 Kasım 2023. 3 Ekim 2023 tarihinde kaynağından . Erişim tarihi: 14 Kasım 2023. 
7. ^ Murray, Carl D.; Dermott, Stanley F. (2010). Solar system dynamics. Transferred to digital print., [Nachdr.] Cambridge: Cambridge Univ. Press. ISBN . 
8. ^ "Planetary Orbits - NASA Science". science.nasa.gov (İngilizce). 13 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 15 Kasım 2023. 
9. ^ "Gravitational potential energy". farside.ph.utexas.edu. 24 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 15 Kasım 2023. 
10. ^ "Planet Tables". www.astronomynotes.com. 16 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 16 Kasım 2023. 
11. ^ Newton, Isaac (1728). A Treatise of the System of the World (İngilizce). F. Fayram. 
12. ^ ^{a b c d} Smith, George, "Newton's Philosophiae Naturalis Principia Mathematica", The Stanford Encyclopedia of Philosophy (Winter 2008 Edition), Edward N. Zalta (ed.), URL = <https://plato.stanford.edu/archives/win2008/entries/newton-principia/>.
13. ^ Carleton, Timothy; Guo, Yicheng; Munshi, Ferah; Tremmel, Michael; Wright, Anna (2021). "An excess of globular clusters in Ultra-Diffuse Galaxies formed through tidal heating". Monthly Notices of the Royal Astronomical Society. 502: 398-406. arXiv:2008.11205 $2. doi:10.1093/mnras/stab031. 
14. ^ Fitzpatrick, Richard (2 Şubat 2006). "Planetary orbits". Classical Mechanics – an introductory course. The University of Texas at Austin. 3 Mart 2001 tarihinde kaynağından . 
15. ^ Luo, Siwei (22 Haziran 2020). "The Sturm-Liouville problem of two-body system". Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30. 
16. ^ "GPS and Relativity". www.astronomy.ohio-state.edu. 10 Kasım 2023 tarihinde kaynağından . Erişim tarihi: 14 Kasım 2023. 
17. ^ Iorio, L. (2011). "Perturbed stellar motions around the rotating black hole in Sgr A* for a generic orientation of its spin axis". Physical Review D. 84 (12): 124001. arXiv:1107.2916 $2. Bibcode:2011PhRvD..84l4001I. doi:10.1103/PhysRevD.84.124001. 
18. ^ Renzetti, G. (2013). "Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Non-Spherical Body Arbitrarily Oriented in Space". Journal of Astrophysics and Astronomy. 34 (4): 341-348. Bibcode:2013JApA...34..341R. doi:10.1007/s12036-013-9186-4. 
19. ^ Renzetti, G. (2014). "Satellite orbital precessions caused by the first odd zonal J3 multipole of a non-spherical body arbitrarily oriented in space". . 352 (2): 493-496. Bibcode:2014Ap&SS.352..493R. doi:10.1007/s10509-014-1915-x. 
20. ^ Chenciner, Alain; Montgomery, Richard (31 Ekim 2000). "A remarkable periodic solution of the three-body problem in the case of equal masses". arXiv:math/0011268 $2. 
21. ^ ^{a b} Peterson, Ivars (23 Eylül 2013). "Strange Orbits". Science News (İngilizce). 22 Kasım 2015 tarihinde kaynağından . Erişim tarihi: 21 Temmuz 2017. 
22. ^ (PDF). Office of Safety and Mission Assurance. 1 Ağustos 1995. 15 Şubat 2013 tarihinde kaynağından (PDF) arşivlendi. , pages 37-38 (6-1,6-2); figure 6-1.
23. ^ ^{a b} . Ancillary Description Writer's Guide, 2013. National Aeronautics and Space Administration (NASA) Global Change Master Directory. 11 Mayıs 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 29 Nisan 2013. 
24. ^ Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications. Hawthorne, CA: Microcosm Press. s. 31. 
25. ^ Ferreira, Becky (19 Şubat 2015). "How Satellite Companies Patent Their Orbits". Motherboard. Vice News. 18 Ocak 2017 tarihinde kaynağından . Erişim tarihi: 20 Eylül 2018.