Bir asal sayı, yalnızca 1'den büyük olup kendisinden küçük iki doğal sayının çarpımı olarak ifade edilemeyen bir doğal sayıdır. 1'den büyük ve asal olmayan doğal sayılara bileşik sayı adı verilir. Örneğin, 5 bir asal sayıdır çünkü onu bir çarpım olarak ifade etmenin mümkün olan yolları, 1 × 5 veya 5 × 1, yalnızca 5 sayısını içermektedir. Ancak, 4 bir bileşik sayıdır çünkü bu, her iki sayının da 4'ten küçük olduğu bir çarpım (2 × 2) şeklindedir. Asal sayılar, aritmetiğin temel teoreminden ötürü sayı teorisi alanında merkezi öneme sahiptir: 1'den büyük her doğal sayı, ya bir asal sayıdır ya da asal sayıların çarpımı olarak, sıralamalarından bağımsız bir şekilde, benzersiz olarak çarpanlarına ayrılabilir.

Bir sayının asal oluş özelliği, asallık olarak tanımlanır. Verilen bir sayısının asallığını denetlemek için kullanılan basit fakat zaman alıcı bir yöntem olan , sayısının 2 ile arasındaki herhangi bir tam sayıya katı olup olmadığını sınar. Daha hızlı algoritmalar arasında, hızlı olmasına karşın küçük bir hata payı barındıran ve her zaman doğru sonucu veren fakat pratikte uygulanabilirliği sınırlı olan yer alır. gibi özel biçimlere sahip sayılar için özellikle hızlı yöntemler mevcuttur. (Aralık 2018 itibarıyla), , 24,862,048 ondalık basamağa sahip bir Mersenne asalıdır.
M.Ö. 300 civarında Öklid tarafından ispatlandığı gibi, asal sayılar . Asal sayılar ile bileşik sayıları birbirinden ayıran kesin ve basit bir formül bulunmamaktadır. Bununla birlikte, doğal sayılar arasındaki asal sayıların dağılımı, genel olarak istatistiksel yöntemlerle modellenebilir. Bu bağlamda elde edilen ilk önemli sonuç, 19. yüzyılın sonlarında ispatlanan asal sayı teoremidir; bu teori, büyük bir sayının rastgele seçilmesi durumunda asal olma olasılığının, sayının basamak sayısına, yani logaritmasına ters oranlı olduğunu ifade eder.
Asal sayılara ilişkin tarihsel bazı sorular henüz çözüme kavuşturulmamıştır. Bu sorular içerisinde her 2'den (En küçük asal sayı 2'dir.) büyük çift tam sayının iki asal sayının toplamı olarak yazılabileceğini ileri süren ve ikişer rakam aralıkla sınırsız sayıda ikiz asal sayı çiftinin var olduğunu iddia eden hipotezi yer almaktadır. Bu tür sorular, sayıların analitik ve cebirsel boyutları üzerine yoğunlaşan sayı teorisi alanlarının gelişimini hızlandırmıştır. Asal sayılar, bilgi teknolojisi alanında, özellikle de büyük sayıların asal çarpanlara güçlüğüne dayanan gibi çeşitli işlemlerde kullanılmaktadır. Soyut cebirde, asal sayılara genelleştirilmiş bir biçimde benzeyen yapılar arasında ve sayılabilir.
Tanım ve örnekler
Bir doğal sayı (1, 2, 3, 4, 5, 6, vb.), 1'den büyük olması ve kendisinden küçük iki doğal sayının çarpımı olarak ifade edilememesi durumunda asal sayı olarak nitelendirilir. 1'den büyük olup asal olmayan sayılara bileşik sayılar adı verilir. Diğer bir ifadeyle, eğer 


Örneğin, 1 ile 6 arasındaki sayılar içinde, 2, 3 ve 5 sayıları asal sayılardır, zira bu sayıları kendinden başka tam bölebilen (kalan bırakmaksızın) başka bir sayı yoktur. 1 sayısı, tanım gereği asal olarak kabul edilmez. 4 = 2 × 2 ve 6 = 2 × 3 her ikisi de bileşik sayı kategorisindedir.

Bir doğal sayı 




İlk 25 asal sayı (100'den küçük tüm asal sayılar) şunlardır:
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 (OEIS'de A000040 dizisi).
2'den büyük hiçbir çift sayı 

Tüm asalların kümesi bazen 

Tarihçe

M.Ö. 1550 civarından kalan Rhind Papirüsü, asal ve bileşik sayılar için farklı formdaki genişlemelerini içerir. Ancak, asal sayıların incelenmesine dair en eski kayıtlar antik Yunan matematikçilerinden gelmektedir, onlar bu sayılara prōtos arithmòs (Grekçe: πρῶτος ἀριθμὸς) demektedirler. Öklid'in Elementleri (M.Ö. 300 civarı) asal sayıların sonsuzluğunu ve aritmetiğin temel teoremini kanıtlar ve bir Mersenne sayısından nasıl bir mükemmel sayı oluşturulacağını gösterir. Başka bir Yunan icadı olan Eratosten kalburu, asal sayı listeleri oluşturmak için hala kullanılmaktadır.
Miladi 1000 yıllarında, İslam dönemi matematikçisi İbnü'l-Heysem, asal sayıları, 

1640 senesinde, Pierre de Fermat tarafından ispatı yapılmamış olmasına rağmen ortaya atılan Fermat'nın küçük teoremi, sonradan Leibniz ve Euler tarafından ispatlanmıştır. Fermat, 







Deneme bölmesinin pratikte uygulanabilir olduğu sayılardan daha büyük sayılar için birçok matematikçi üzerinde çalışmıştır. Belirli sayı formlarına sınırlı yöntemler arasında Fermat sayıları için (1877), (yaklaşık 1878), (1856'da ortaya çıktı) ve genelleştirilmiş bulunmaktadır.
1951 yılından itibaren, en büyük bilinen asal sayıların tümü, bilgisayarlarda gerçekleştirilen bu testlerle keşfedilmiştir. Büyük asal sayıları arama çabası, ve benzeri dağıtık hesaplama projeleri vasıtasıyla matematiksel olmayan topluluklarda da büyük bir ilgi uyandırmıştır. Asal sayıların soyut matematik dışında önemli uygulamalara sahip olmadığına dair görüş, 1970'lerde, asal sayıları temel alan ve RSA kriptosisteminin geliştirilmesi ile çürütülmüştür.
Bilgisayarla yapılan asallık testlerinin ve çarpanlara ayırma işleminin artan pratik önemi, kısıtlama olmaksızın büyük sayılarla başa çıkabilen gelişmiş yöntemlerin geliştirilmesine yol açtı. Asal sayılar teorisinin matematiksel gelişimi, asal sayıların keyfi olarak uzun aritmetik dizilerinin olduğunu belirten (2004) ve 'ın 2013'te sınırlı büyüklükte sonsuz çoklukta olduğunun kanıtı ile de ileriye taşındı.
1 sayısının asallığı
Antik Yunanlıların çoğu, başlangıçta 1'i bir sayı olarak bile kabul etmemiştir, dolayısıyla asallığını tartışmaları mümkün değildi. Nicomachus, Iamblichus, Boethius ve Cassiodorus gibi birkaç Yunan ve sonraki Roma geleneği alimi, asal sayıları tek sayıların bir alt bölümü olarak kabul ettiği için, 2'yi de asal olarak kabul etmemişlerdir. Ancak, Öklid ve diğer birçok Yunan matematikçisi 2'yi asal olarak kabul etmiştir. Orta Çağ İslam matematikçileri genellikle Yunanlıların görüşlerini takip ederek 1'i bir sayı olarak görmemişlerdir. Orta Çağ ve Rönesans boyunca matematikçiler 1'i bir sayı olarak kabul etmeye başlamış ve bazıları onu ilk asal sayı olarak dahil etmiştir. 18. yüzyılın ortalarında Christian Goldbach, Leonhard Euler ile olan yazışmalarında 1'i asal olarak listelemiştir; ancak, Euler kendisi 1'i asal olarak kabul etmemiştir. 19. yüzyılda birçok matematikçi hala 1'i asal olarak kabul etmiş, ve 1'i içeren asal sayı listeleri en son 1956 yılında yayımlanmıştır.
1 sayısı günümüzde ne asal ne de bileşik kabul edilir ve özel bir durumu vardır. Geçmişte pek çok matematikçi 1'i asal sayı olarak kabul ediyordu. 1'in asal olarak kabul edilmesine dayanarak yapılan birçok çalışma geçerliliğini hâlâ sürdürmektedir: ve 'in çalışmaları gibi. Henri Lebesgue, çalışmalarında 1'i asal olarak ele alan son profesyonel matematikçi olarak bilinir. 1 asal olarak ele alındığında bâzı teoremlerde değişikliğe gidilmesi gerekir. Örneğin tüm pozitif tam sayıların "yalnız bir şekilde" asal sayıların çarpımları şeklinde yazılabileceğini söyleyen aritmetiğin temel teoremi, geçmişteki asal sayı tanımına göre geçerli değildir.

Bir sayının asal olarak tanımlanması değiştirilip 1 asal olarak kabul edilseydi, asal sayılarla ilgili birçok ifade daha zor bir şekilde yeniden formüle edilmek zorunda kalırdı. Örneğin, aritmetiğin temel teoremi, her sayının 1'in istenilen sayıda kopyasıyla çeşitli faktörizasyonları olacağı için, 1'den büyük asallara göre faktörizasyonlar açısından yeniden ifade edilmek zorunda kalırdı. Benzer şekilde, Eratosthenes kalburu 1'i bir asal olarak ele alırsa doğru çalışmazdı çünkü 1'in tüm katlarını (yani, tüm diğer sayıları) elemek ve sadece 1 sayısını çıkarmak zorunda kalırdı. Asal sayıların bazı diğer daha teknik özellikleri de 1 numarası için geçerli değildir: örneğin, Euler'in totient fonksiyonu veya için formüller asal sayılar için 1 ile farklıdır. 20. yüzyılın başlarında, matematikçiler 1'in asal olarak listelenmemesi, ancak daha çok "" olarak kendi özel kategorisinde yer alması gerektiği konusunda anlaşmaya başladılar.
Temel özellikler
Çarpanlama
Bir sayının asal sayıların çarpımı olarak yazılması, o sayının asal çarpanlara ayrılması olarak adlandırılır. Örneğin:
Bu çarpımdaki terimlere asal çarpanlar denir. Aynı asal çarpan birden fazla bulunabilir; bu örnekte asal çarpan 

Asal sayıların sayılar teorisi ve genel olarak matematiğe merkezi önemi, aritmetiğin temel teoreminden kaynaklanmaktadır. Bu teorem, 1'den büyük her tam sayının bir veya daha fazla asal sayının çarpımı olarak yazılabileceğini belirtir. Daha da önemlisi, bu çarpım özeldir; yani, aynı sayının her iki asal çarpanlarının çarpımı, çarpanların sıralaması farklı olsa bile, aynı asal sayıların aynı sayıda kopyasını içerecektir. Dolayısıyla, bir asal çarpanlarına ayırma algoritması kullanılarak çarpanlara ayırma işlemi yapmanın birçok farklı yolu olmasına rağmen, hepsi aynı sonucu üretmek zorundadır. Bu nedenle, asal sayılar doğal sayıların "temel yapı taşları" olarak kabul edilebilir.
Asal çarpanlara ayrılmanın benzersizliğinin kanıtlarından bazıları, dayanır: Eğer 








Sonsuzluk
Asal sayıların sayısı sonsuzdur. Diğer bir deyişle, asal sayı dizisi:
- 2, 3, 5, 7, 11, 13, ...
asla son bulmaz. Bu tez, antik Yunan matematikçisi Öklid onuruna, "Öklid Teoremi" olarak isimlendirilmiştir çünkü bu tezin bilinen ilk ispatı onun adıyla ilişkilendirilir. Asal sayıların sonsuzluğunu kanıtlayan birçok metod mevcuttur; bunlar arasında, Euler tarafından gerçekleştirilen analitik ispat, Goldbach'ın Fermat sayıları üzerine kurulu , genel topoloji kullanarak sunduğu , ve ispatı sayılabilir.
Öklid'in ispatı, herhangi bir eksik olduğunu gösterir. Ana fikir, verilen listedeki asal sayıların hepsini çarparak 

sayısını verir.
Temel teorem gereğince, 
şeklinde bir veya daha fazla asal çarpan içeren bir asal çarpanlara ayırımına sahiptir. 

En küçük asal sayıların çarpımlarına bir eklenerek oluşturulan sayılara adı verilir. Bunlardan ilk beşi asal olmakla birlikte, altıncısı,
şeklindedir.
Asal sayı denklemleri
Asal sayıları tespit etmek için bilinen etkin bir yöntem mevcut değildir. Öyle ki, yalnızca asal sayı değerleri üreten, sabit olmayan çok değişkenli bir polinom dahi bulunamamıştır. Bununla birlikte, yalnızca asal sayıları veya tüm asal sayıları temsil edebilen çeşitli ifadeler mevcuttur. Bu ifadelerden biri, 'ne dayalı olup, 2 sayısının defalarca ve diğer tüm asal sayıların ise sadece bir kez elde edilmesini sağlayan bir formüldür. Dokuz değişken ve bir parametreye sahip Diyofantus denklemlerinden oluşan bir küme de mevcuttur; bu kümenin belirgin bir özelliği şöyledir: Eğer ve ancak eğer bu denklem sistemi doğal sayılar kümesi üzerinde bir çözüme sahipse, ilgili parametre bir asal sayıdır. Bu özellik, tüm pozitif değerleri asal sayı olan bir formülün elde edilmesi amacıyla kullanılabilir.
ve tarafından öne sürülen bir teoremle ilgili olarak, asal sayılar üreten diğer formüller de mevcuttur. Bu teoremler, 

İlk formülde, herhangi bir doğal 

Çözüm bekleyen sorular
Matematik alanında, asal sayılarla ilgili bir dizi varsayım ileri sürülmüştür. Çoğunlukla temel bir ifade şekliyle ortaya konan bu varsayımlar, onlarca yıl süresince ispatlanamamıştır: 1912 yılında ortaya atılan başlığı altındaki dört soru günümüze dek çözülememiştir. Bu varsayımlardan bir tanesi, 2'den büyük olan her çift tam sayı 
Ardışık asal sayılar arasındaki farkları ifade eden ile ilgili bir başka problem türü bulunmaktadır. Herhangi bir doğal 



,, ve ,

Analitik özellikler
Analitik sayı teorisi, sayı teorisini, sürekli fonksiyonlar, limitler, sonsuz seriler ve bunların yanı sıra sonsuzluk ve sonsuz küçük kavramlarıyla ilişkili matematiksel yapılar üzerinden detaylı bir şekilde araştırır.
Bu araştırma alanının kökenleri, Leonhard Euler'in Basel problemini çözümüyle ilişkilendirilen ilk önemli çalışmasına dayanır. İlgili sorun, 

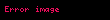
Büyük ölçekte asal sayıların dağılımı, örneğin belirli bir büyük eşik değerinden daha küçük olan asal sayıların sayısı gibi sorular, asal sayı teoremi tarafından açıklanmaktadır; fakat 


biçimindeki doğrusal polinomların sonsuz sayıda asal değere ulaştığını öne sürer. Teoremin ileri versiyonları, bu asal değerlerin terslerinin toplamının ıraksadığını ve aynı 
Öklid teoreminin analitik ispatı
, asal sayıların toplamlarını incelemektedir,
Euler, herhangi bir reel sayı 


Bu durum, asal sayıların sonsuz sayıda olduğunun bir göstergesidir; zira sonlu sayıda asal sayı var olsaydı, bu toplam, her bir 
toplamı, 
, ikiz asalların terslerinin toplamının,
sonlu bir değere sahip olduğunu ifade etmektedir. Brun teoremi nedeniyle, Euler metodunun, sonsuz sayıda ikiz asalın var olduğu iddiasını ele alan çözümlemek amacıyla kullanılabilmesi mümkün değildir.
Belirli bir üst sınıra kadar olan asal sayıların miktarı

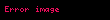 ve logaritmik integral
ve logaritmik integral 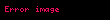 , ile olan yakınsaklığına dair incelemesi.
, ile olan yakınsaklığına dair incelemesi.  değerinin artışı ile her iki göreceli hata oranı da azalarak sıfıra ulaşmaktadır; ancak, logaritmik integralin sıfıra yakınsama hızı, öteki yaklaşıma göre çok daha fazladır.
değerinin artışı ile her iki göreceli hata oranı da azalarak sıfıra ulaşmaktadır; ancak, logaritmik integralin sıfıra yakınsama hızı, öteki yaklaşıma göre çok daha fazladır. olarak adlandırılan 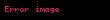

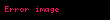

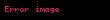
Asal sayı teoremine göre, 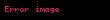
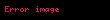
şeklinde gösterilir.
Bu durum, 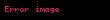



Bu durum, aynı zamanda, 
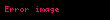
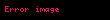
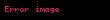
Aritmetik diziler
Aritmetik dizi, dizide yer alan ardışık sayıların her biri arasında sabit bir fark bulunan, sonlu veya sonsuz bir sayılar dizisini ifade eder. Bu farka, dizinin modülü denir. Örneğin,
- 3, 12, 21, 30, 39, ...,
9 modül değerine sahip bir sonsuz aritmetik diziyi temsil eder. Aritmetik bir dizideki sayılar, modül değerine bölündüklerinde aynı kalanı alır; bu durumun bir örneği olarak, kalanın 3 olduğu görülür. Modülün 9 ve kalanın 3 olması, her iki değerin de 3'ün katları olması anlamına gelir, bu yüzden dizideki her bir eleman da 3'ün katıdır. Bu sebeple, bu dizi sadece bir tek asal sayı içermektedir, ki o da 3'tür. Genel anlamda, sonsuz dizi
ancak kalan 



, yalnızca asal sayılardan müteşekkil ve herhangi bir uzunlukta olabilen sonlu aritmetik dizilerin mevcudiyetini ispatlamaktadır.
Kuadratik polinomlar tarafından üretilen asal sayı değerleri

 biçiminde ifade edilen kuadratik polinomdan elde edilen asal sayı değerleri mavi renkle işaretlenmiştir.
biçiminde ifade edilen kuadratik polinomdan elde edilen asal sayı değerleri mavi renkle işaretlenmiştir. Euler, 
Ulam spirali, doğal sayıları, orijini çevreleyen konsantrik kareler halinde spiral bir düzende iki boyutlu bir ızgara üzerine yerleştirir ve asal sayıları belirginleştirir. Görsel bir inceleme sonucunda, asal sayıların belirli diyagonaller üzerinde, diğerlerine kıyasla daha yoğun bir şekilde gruplandığı görülmekte, bu durum bazı ikinci dereceden polinomların, diğerlerine nazaran daha sıklıkla asal değerler ürettiği yönünde bir izlenim uyandırmaktadır.
Zeta fonksiyonu ve Riemann hipotezi

1859 yılından itibaren matematik alanında aydınlatılamamış en meşhur meselelerden biri, aynı zamanda Milenyum Problemleri arasında yer alan Riemann hipotezi, Riemann zeta fonksiyonu 

Euler tarafından ortaya konulan bu toplam ile çarpım arasındaki denklik, olarak isimlendirilmiştir. Euler çarpımı, aritmetiğin temel teoremi sayesinde elde edilmiş olup, zeta fonksiyonunun asal sayılarla derinlemesine ilişkisini açığa çıkarır. Sonsuz sayıda asal sayı bulunması gerektiğini kanıtlama yolunda bu durum, eğer sadece sınırlı sayıda asal sayı varsa, toplam-çarpım eşitliğinin 
Riemann hipotezi, zeta fonksiyonunun sıfırlarının tamamının ya negatif çift sayılardan ya da reel kısımları 1/2'ye eşit olan karmaşık sayılardan oluştuğunu öne sürer.Asal sayı teoreminin ilk kanıtı, bu hipotezin bir versiyonuna, yani reel kısmı 1 olan sıfırların var olmadığı varsayımına dayanmaktaydı, fakat daha basit kanıtlar da ortaya konmuştur. Asal sayı sayım fonksiyonu, aracılığıyla, zeta fonksiyonunun sıfırlarının her birinden bir terimin katkısıyla oluşan bir toplam şeklinde ifade edilebilir; bu toplamın temel bileşeni logaritmik integral olup, geri kalan terimler ana terimin üzerinde ve altında dalgalanmalara yol açar. Bu bağlamda, sıfırların, asal sayıların dağılım düzenini belirlediği söylenebilir. Riemann hipotezi eğer doğruysa, bu dalgalanmalar minimale indirgenecek ve , asal sayı teoreminin öngördüğü gibi, 

Soyut cebir
Modüler aritmetik ve sonlu alanlar
Modüler aritmetik, modül olarak isimlendirilen bir doğal sayı 

Modüler toplama, çıkarma ve çarpma işlemleri, tam sayıların geleneksel toplama, çıkarma veya çarpma işlemlerinin sonucuna, bu sonucun modülünün alınarak yerine konulması yöntemiyle gerçekleştirilir.
Tam sayılar arasındaki eşitlik kavramı, modüler aritmetikte denklik olarak ifade edilir: 



Bu numaralandırma sisteminde, modül bir asal sayı olduğunda ve yalnızca o zaman, sıfır olmayan tüm sayılara bölme işlemi gerçekleştirilebilir. Mesela, modül olarak 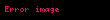

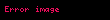

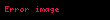




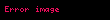


Asal sayılarla ilgili birçok teorem, modüler aritmetik kullanılarak ifade edilebilir. Mesela, Fermat'nın küçük teoremi, eğer bir 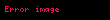

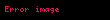

Tüm 
bu denklem, 

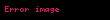
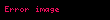

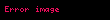
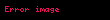
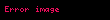

p-sel sayılar
Bir tam sayının 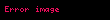



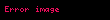









Bu düzen, mutlak değer ve bu kavramlardan türetilmiş tam alan kavramı, ve bu alanların (alanın tamamen sıralı bir toplamsal gruba, düzen olarak da adlandırılan, özel eşlemeler), (alanı gerçek sayılara çarpan olarak eşleyen, norm olarak da bilinen, özel çarpan eşlemeler) ve yerler (verilen alanın yoğun bir küme olarak yer aldığı, tamamlamalar olarak adlandırılan, yapılan genişletmeler) kavramlarına genelleştirilebilir.
Örneğin, rasyonel sayılardan reel sayılara yapılan genişleme, sayılar arasındaki uzaklığın, onların farklarının alışılagelen mutlak değerine dayandığı bir yer olarak tanımlanabilir. Bu bağlamda, bir toplamsal gruba yapılan karşılık gelen eşleme, mutlak değerin olurdu, fakat bu, bir değerlendirme için gerekli olan tüm özellikleri sağlamaz. göre, doğal bir denklik anlayışına kadar, gerçek sayılar ve 
Halkalarda asal elemanlar

Toplama, çıkarma ve çarpma işlemlerinin belirlendiği bir cebirsel yapı olan değişmeli halka, matematiksel yapıların bir çeşididir. Tam sayılar, bu yapıların bir örneği olup, tam sayılar içerisinde yer alan asal sayılar, asal elemanlar ve indirgenemez elemanlar şeklinde iki farklı yöntemle genellenmiştir. 






Herhangi bir halkada, bütün asal elemanlar indirgenemez niteliktedir. Bu durumun tersi genellikle doğru olmamakla birlikte, benzersiz çarpanlara ayırma alanları için geçerlidir.
Aritmetiğin temel teoremi, tanımı gereği, benzersiz çarpanlara ayırma alanları çerçevesinde geçerliliğini korur. Bu tür alanların bir örneği olarak 





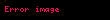

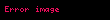
Asal idealler
Bütün halkaların benzersiz çarpanlara ayrılabilen bölgeler olduğu genellenemez. Örnek olarak, tam sayılar 

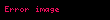
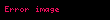

Bir halkanın spektrumu, söz konusu halkanın asal ideallerini içeren noktalarla tanımlanan bir geometrik alandır. Aritmetik geometri alanı, bu kavramdan önemli ölçüde yararlanmakta ve sayı teorisi ile geometri disiplinleri arasında çeşitli kavramsal paralellikler bulunmaktadır. Mesela, bir alana genişletme işlemi sonucu asal ideallerin faktörizasyonu veya dalgalanması gibi cebirsel sayı teorisinin temel problemleri, geometride dalgalanma fenomeni ile benzer özellikler gösterir. Tam sayılar üzerine kurulu sayı teorisi problemlerinin çözümünde bu kavramlar etkili olabilir. Kuadratik sayı alanlarının tam sayılar halkasındaki asal idealler, tam sayı asal sayıları üzerinde kare köklerin varlığını ifade eden kuadratik karşılıklılık teoreminin ispatlanmasında kullanılabilmektedir. Fermat'nın Son Teoremi'ni ispatlama çabalarının ilk aşamaları, siklotomik tam sayılarda benzersiz çarpanlara ayrılmanın başarısız olması ile ilişkilendirilen tam sayı asal sayıları olan düzenli asalların, Kummer tarafından literatüre kazandırılmasına yol açmıştır.
Cebirsel bir sayı alanında, kaç adet tam sayı asal sayısının, birden fazla asal idealin ürünü şeklinde faktörize olduğu meselesi, ile çalışılmıştır. Bu teorem, siklotomik tam sayılar bağlamında uygulandığında, aritmetik ilerlemelerde yer alan asal sayılar hakkındaki Dirichlet teoremini özel bir örnek olarak içermektedir.
Grup kuramı
Sonlu gruplar kuramında, bir asal sayının 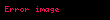
Hesaplamalı yöntemler

Genel anlamda sayı teorisi ve özellikle asal sayılar üzerine yapılan çalışmalar, uzun bir süre boyunca, saf matematiğin matematik dışında herhangi bir uygulaması olmayan kanonik bir örneği olarak kabul edilmiştir. Bunun istisnası, dişli çarkların aşınmasını eşit bir şekilde dağıtabilmek amacıyla dişli dişlerinin asal sayılarla belirlenmesi uygulamasıdır. Bu bağlamda, Britanya'dan matematikçi G. H. Hardy gibi sayı teorisyenleri, çalışmalarının açık bir şekilde herhangi bir askeri amaç taşımadığından dolayı övünç duymuştur.
1970'li yıllarda, asal sayıların açık anahtarlı şifreleme algoritmaları geliştirmek için bir temel olarak kullanılabileceğinin kamuoyuna duyurulmasıyla, sayı teorisinin saflık vizyonu ciddi bir şekilde sarsılmıştır. Bu uygulamalar, asal sayılarla hesaplama yapabilen algoritmaların ve özellikle de bir sayının asal olup olmadığını belirlemeye yönelik yöntemlerin, yani , kapsamlı bir şekilde incelenmesini teşvik etmiştir. Büyük sayılar için kullanışlı olmaktan uzak, en temel asallık testi yöntemi olan deneme bölme yöntemi, yavaşlığı sebebiyle eleştirilmiştir. Modern asallık testlerinin bir kısmı herhangi bir sayıya uygulanabilirken, özel türdeki sayılar için daha verimli testler geliştirilmiştir. Çoğunlukla, asallık testleri sadece argümanın asal olup olmadığını belirlemekle sınırlıdır. Bileşik argümanların bir asal çarpanını (veya tüm asal çarpanlarını) belirleyebilen rutinler, çarpanlara ayırma algoritmaları olarak tanımlanır. Ayrıca, asal sayılar bilgisayar bilimlerinde , anahtarlı tablolarda ve sanki rastgele sayı üreteçlerinde kullanım alanı bulmaktadır.
Deneme bölme yöntemi
Bir tam sayının asallık durumunun belirlenmesinde kullanılan en temel yöntem, olarak isimlendirilir. Bu metod, ilgili tam sayı 




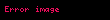



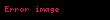
Bu metodun tanımı basit olmakla birlikte, büyük tam sayıların asallık testi için uygulanabilirliği sınırlıdır; zira, bu tam sayıların basamak sayısına bağlı olarak yürütülen testlerin sayısı, üstel bir artış göstermektedir. Bununla birlikte, bölücü büyüklüğü üzerinde karekökten daha az bir sınır belirlenerek kullanılan deneme bölme yöntemi, daha karmaşık yöntemlere başvurulmadan önce, küçük çarpanlara sahip bileşik sayıları hızla belirlemek amacıyla bu süzgeçten geçen sayılar üzerinde hâlâ tercih edilmektedir.
Kalbur yöntemleri

Bilgisayarların var olmadığı dönemlerde, verilen bir sınır değere kadar tüm asalların ya da asal çarpanlaştırmaların listelendiği matematiksel tablolar yaygın biçimde basılmaktaydı. Asal sayıların listesinin elde edilmesinde kullanılan en kadim yöntem, Eratosten kalburu olarak isimlendirilir. Bu yöntemin optimize edilmiş bir çeşidini gösteren animasyon, metodun uygulanışını görselleştirir.
Aynı problem için daha asimptotik açıdan daha verimli bir başka kalbur yöntemi olarak belirlenmiştir. İleri düzey matematikte, elek teorisi benzeri metodlar diğer problemlerin çözümünde de kullanılmaktadır.
Asallık testi ile asallığın kanıtlanması
Bir 





Bu deneyin aynı sayı üzerinde 
Diğer taraftan, bazı algoritmaların sonuçlarının daima doğru olacağına dair bir garanti bulunmaktadır. Bu durumun bir örneği deneme bölme yöntemidir. Kesin doğru çıktı sağlayan algoritmalar, gibi deterministik (rasgele olmayan) algoritmaları, ve algoritmanın nihai yanıtını etkilemeyen rastgele seçimler yapan, örneğin bazı çeşitlerindeki gibi kapsar.
Elips eğri metodu, bir sayının asallığı konusunda bir karara vardığında, kolaylıkla doğrulanabilir bir temin eder. Pratik uygulamalarda, garantili doğruluk sağlayan asallık testleri içinde, elips eğri asallık testi en hızlı olanıdır; ancak, bu testin çalışma zamanı analizi, katı ispatlara değil, dayanır. Matematiksel olarak zaman karmaşıklığı ispatlanmış mevcut olmakla birlikte, uygulamada elips eğri asallığını kanıtlamadan daha yavaş işler. Bu metodlar, rastgele sayılar üretilip test edilerek ve asal olan bir sayı bulunana dek büyük rastgele asal sayılar üretmek için kullanılabilir; bu süreçte, bir hızlı olasılıksal test, garantili doğruluk sağlayan bir algoritma ile kalan sayıların asallığının doğrulanmasından önce, çoğu bileşik sayıyı çabucak elemine etme işlevi görür.
Aşağıda sunulan tablo, mevcut testlerden seçilmiş olanları sıralamaktadır. Bu testlerin çalışma zamanları, incelenmek üzere olan sayıyı temsil eden 




| Test | Geliştirildiği yıl | Tip | Çalışma süresi | Notlar | Kaynaklar |
|---|---|---|---|---|---|
| 2002 | deterministik | 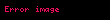 | |||
| 1986 | Las Vegas | 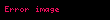 sezgisel olarak sezgisel olarak | |||
| 1980 | Monte Carlo | 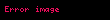 | |||
| 1980 | Monte Carlo | 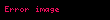 | hata olasılığı 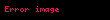 | ||
| 1977 | Monte Carlo | 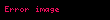 | hata olasılığı  |
Özel amaçlı algoritmalar ve en büyük bilinen asal sayı
Bahse konu testlerin yanı sıra, özgün biçimdeki bazı sayıların asallık durumu, daha hızlı bir metodoloji kullanılarak test edilebilir. Örnek olarak, , bir Mersenne sayısının (iki'nin bir kuvvetinden bir az olan) asal olup olmadığını, deterministik bir yaklaşımla, Miller–Rabin testinin tek bir yinelemesi kadar sürede tespit edebilmektedir. Bu sebepten ötürü, 1992 yılından itibaren ((Aralık 2018 itibarıyla)) sayı, sürekli olarak bir Mersenne asalı olagelmiştir. Mersenne asallarının sonsuz olduğu varsayılmaktadır.
Aşağıdaki tablo, çeşitli kategorilerde tespit edilmiş en büyük asal sayıları içermektedir. Bu asal sayıların bir kısmı, dağıtık hesaplama yöntemiyle keşfedilmiştir. 2009 senesinde, en az on milyon rakam içeren bir asal sayıyı ilk defa bulma başarısı gösteren projesi, yüz bin Amerikan doları mükafatına layık görülmüştür.Electronic Frontier Foundation, yüz milyon ve bir milyar rakam barındıran asal sayılar için sırasıyla yüz elli bin ve iki yüz elli bin dolar ödül sunmaktadır.
| Tip | Asal sayı | Basamak sayısı | Tarih | Kaşif |
|---|---|---|---|---|
| 282,589,933 − 1 | 24,862,048 | Aralık 7, 2018 | Patrick Laroche, | |
| 10,223 × 231,172,165 + 1 | 9,383,761 | Ekim 31, 2016 | Péter Szabolcs, | |
| 208,003! − 1 | 1,015,843 | Temmuz 2016 | Sou Fukui | |
| 1,098,133# − 1 | 476,311 | Mart 2012 | James P. Burt, | |
| İkiz asallar | 2,996,863,034,895 × 21,290,000 ± 1 | 388,342 | Eylül 2016 | Tom Greer, |
Asal çarpanlara ayırma
Bir bileşik tam sayı olan 



Shor algoritması, herhangi bir tam sayının çarpanlarına ayrıştırılmasını bir kuantum bilgisayar üzerinde polinomik sayıda işlem adımı ile gerçekleştirebilir. Bununla birlikte, günümüz teknolojisi, söz konusu algoritmayı sadece minimal büyüklükteki sayılar üzerinde uygulayabilmektedir. (Ekim 2012 itibarıyla), bir kuantum bilgisayarında Shor algoritmasını kullanarak çarpanlarına ayrılan en büyük sayı 21 olarak kaydedilmiştir.
Diğer bilgisayımsal uygulamalar
Çok sayıda açık anahtarlı şifreleme algoritması, örneğin RSA ve Diffie-Hellman anahtar değişimi gibi, büyük asal sayılar üzerine kuruludur (2048-bit asal sayılar yaygın kullanımdadır). RSA algoritması, iki (büyük) sayının çarpımı olan 





Asal sayılar, hash tablolarında yaygın olarak tercih edilmektedir. Carter ve Wegman tarafından geliştirilen orijinal metodolojisi, büyük asal sayılar cinsinden mod alınarak seçilen rastgele doğrusal fonksiyonlar aracılığıyla hash fonksiyonuların hesaplanmasına dayanır. Carter ve Wegman, bu metodu, yine büyük asal sayılar cinsinden mod alınarak daha yüksek dereceden polinomlar kullanılarak genelleştirerek iyileştirmiştir. Asal sayılar, hash fonksiyonlarının yanı sıra, yöntemine dayalı hash tablolarında, sorgulama dizilerinin tablonun tamamını kapsayacak şekilde tasarlanmasını sağlamak amacıyla hash tablo boyutlarının belirlenmesinde de kullanılmaktadır.
Çeşitli yöntemleri, asal sayıların matematiğine dayalıdır. Mesela, Uluslararası Standart Kitap Numarası için kullanılan sağlama toplamları, asal bir sayı olan 11'e göre sayının mod alınarak hesaplanması yoluyla tanımlanmaktadır. 11 sayısının asal bir değere sahip olması, bu metodun hem tek basamaklı hataları hem de yan yana bulunan rakamların yer değiştirme hatalarını tespit edebilmesine olanak tanır. gibi başka bir kontrol toplamı yöntemi, 
Diğer uygulamalar
Asal sayılar, sayılar teorisinin yanı sıra, soyut cebir ve temel geometri gibi matematiğin diğer disiplinlerinde de geniş uygulama alanlarına sahiptir. Mesela, asal sayılar kadar noktanın iki boyutlu bir düzlem üzerine öyle bir yerleştirilmesi mümkündür ki, bu noktalardan herhangi üçü düz bir çizgi üzerinde konumlanmaz, (İng. No-three-in-line problem) ya da bu noktalar arasından seçilen her üçlü tarafından oluşturulan üçgenlerin sahip olması sağlanabilir. Ayrıca, bir polinomun indirgenemezliğinin, polinomun katsayılarının bir asal sayı ve bu asal sayının karesi ile bölünebilirliğine dayanarak tespit edilmesini sağlayan , indirgenemez polinomlar üzerine bir test olarak öne çıkmaktadır.

Asal sayı kavramı, matematiğin çeşitli dallarında farklı şekillerde genelleştirilmiş kadar önemlidir. Genellikle, "asal" kelimesi, uygun bir anlamda, minimaliteyi veya ayrıştırılamazlığı belirtir. Örneğin, verilen bir alanın , hem 0 hem de 1'i içeren en küçük alt alandır. Bu, rasyonel sayılar alanı veya asal sayıda elemana sahip bir sonlu alandır, isminin kaynağı budur. Sıklıkla, "asal" kelimesi kullanılarak bir nesnenin, esasen benzersiz bir şekilde, asal bileşenlerine ayrıştırılabileceği anlamı da amaçlanır. Örneğin, düğüm teorisinde, bir iki önemsiz düğümün olarak yazılamayacak şekilde ayrıştırılamaz bir düğümdür. Herhangi bir düğüm, asal düğümlerin bağlı toplamı olarak benzersiz bir şekilde ifade edilebilir. bu türe başka bir örnektir.
Matematik ve bilgisayar bilimlerinin ötesinde, asal sayıların kuantum mekaniğine potansiyel ilişkileri mevcut olup, kültür ve edebiyat alanlarında metaforik öğeler olarak değerlendirilmişlerdir. Bunun yanı sıra, evrimsel biyoloji alanında, ağustos böceğilerinin yaşam evrelerinin izah edilmesinde asal sayılar başvurulan bir araç olmuştur.
Yapılandırılabilir çokgenler ve çokgen bölümlendirmeleri

şeklinde tanımlanan ve 





Herhangi bir dışbükey çokgenin, 


Kuantum mekaniği
ve Freeman Dyson'ın 1970'lerde gerçekleştirdikleri çalışmaların öncülüğünde, matematik ve fizik alanında uzmanlar, Riemann zeta fonksiyonunun kökleri ile kuantum sistemlerinin enerji düzeyleri arasında bir bağlantı olabileceğini öne sürmüşlerdir. Aynı zamanda, asal sayılar, ve gibi matematiksel yapılar vasıtasıyla alanında da kritik bir öneme sahiptir.
Biyoloji
cinsi ağustos böceğilerinin uyguladığı evrimsel strateji, asal sayılardan faydalanmaktadır. Bu böcek türleri, ömürlerinin büyük bir kısmını yer altında larva formunda geçirmekte, yalnızca 7, 13 veya 17 yıl gibi asal sayıları temsil eden süreler sonunda erginleşip yeryüzüne çıkarlar, çiftleşirler ve birkaç hafta içinde yaşam döngülerini tamamlayarak ölürler. Bu asal sayılara dayanan üreme döngüsü sürelerinin, avcıların bu döngülere uyum sağlamasını engellemek amacıyla evrildiği biyologlar tarafından öne sürülmektedir. Öte yandan, bambu bitkilerinde görülen çiçeklenme periyotlarının, çarpanlarında yalnızca küçük asal sayılar içeren olduğu varsayılmaktadır. Bu durum, bambunun çiçeklenme zamanlamalarının küçük asal sayılara dayalı bir düzenlilik gösterdiğini işaret etmektedir.
Sanat ve edebiyat
Asal sayılar, pek çok sanatçı ve yazar üzerinde derin bir etkiye sahip olmuştur. Fransız besteci Olivier Messiaen, "doğal olaylar"ı referans alarak ametrik müzik üretmede asal sayıları kullanmıştır. (1935) ve (1949–50) eserlerinde, birbirinden farklı asal sayılara dayanan motif uzunluklarını simultane kullanımıyla öngörülemez ritimler oluşturmuştur: "Neumes rythmiques" adlı üçüncü etütte 41, 43, 47 ve 53 gibi asal sayılar yer almaktadır. Messiaen, bu kompozisyon tekniğini "doğanın hareketlerinden, serbest ve eşitsiz süreçlerde meydana gelen hareketlerden ilham alarak" geliştirdiğini belirtmiştir.
Bilim kurgu eseri Contact'ta, Carl Sagan, uzaylılarla iletişim kurma sürecinde iki boyutlu görüntü düzlemlerinin oluşturulmasında asal sayıların çarpanlarına ayrılmasının potansiyel bir yöntem olarak kullanılabileceğini ileri sürmüştür. Bu düşünceyi ilk defa 1975 yılında Amerikan astronom Frank Drake ile informal bir şekilde ortaya koymuştur. adlı eserde, yazar Mark Haddon, ana karakterin, Asperger sendromuna sahip matematiksel yeteneği yüksek bir genç, zihinsel durumunu yansıtmak amacıyla hikayenin bölümlerini ardışık asal sayılar kullanarak düzenlemiştir.'nun adlı romanında asal sayılar, yalnızlık ve tecrit duygularını sembolize etmek için kullanılmış, asal sayılar tam sayılar içerisinde "yabancı" olarak tasvir edilmiştir.
Asal oturanlar
Aritmetiğin temel teoremi 1'den büyük tüm tam sayıların asal sayıların çarpımları şeklinde yazılabileceğini, üstelik yazımın da (asal çarpanların değişik sıralanması hariç) yalnız bir şekilde (teklik) olacağını söyler. Bir sayının asal çarpanlara ayrılmasında bir asal sayı birden fazla tekrar edebilir. Dolayısıyla asal sayılar, doğal sayıların "temel inşa taşları" olarak düşünülebilir.
Örneğin, 23244'ü şu şekilde asal çarpanlarına ayırabiliriz:
23244 = 22 × 3 × 13 × 149
ve 23244'ün diğer asal çarpanlara ayırış şekilleri yukarıdaki ile aynıdır, fakat asal sayıların sıralaması değişik olabilir. Büyük sayılar için değişik asal çarpanlara ayırma algoritmaları vardır.
İkiz asallar
Aralarındaki fark iki olan asal sayılar hakkındaki ikiz asallar konjektürü.
- Örneğin:
- (3, 5)
- (5, 7)
- (11, 13)
- (17, 19)
- (29, 31)
- (41, 43)
- (59, 61)
- (71, 73)
- (101, 103)
- (107, 109)
Chen asalları
Bir a asal sayısı (a+2) biçiminde yazıldığında asal ya da yarı asal oluyorsa a değeri, Chen asalı olarak adlandırılmaktadır. İkiz asallarda, küçük sayı aynı zamanda Chen asalıdır.
Asal örnekler:
- a = 5
5 + 2 = 7
- a = 11
11 + 2 = 13
Yarı asal örnekler:
- a = 2
2 + 2 = 4
2 × 2 = 4
- a = 7
7 + 2 = 9
3 × 3 = 9
Mersenne asalları
Bir a doğal sayısı (2a – 1) biçiminde yazıldığında hesaplanan değer Mersenne sayısı, asal oluyorsa aynı zamanda Mersenne asalı olarak adlandırılmaktadır. Mersenne asalları hesaplanırken, a sayısı da asal olarak alınmaktadır. Ancak a sayısının asal olarak alındığı bazı durumlarda, bileşik Mersenne sayıları hesaplanabilmektedir. Bilinen en büyük asal sayı olan 282,589,933 − 1, Mersenne asalıdır.
Mersenne asalları:
- 22 – 1 = 3
- 25 – 1 = 31
Bileşik Mersenne sayıları:
- 211 – 1 = 2047
Goldbach hipotezi
Asal sayılarla ilgili Goldbach hipotezi, doğru gözükmesine rağmen halen ispatlanamamıştır. "Her çift (2 hariç) sayı iki asal sayının toplamı mıdır?"
Örneğin:
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7
- 12 = 5 + 7
- 14 = 3 + 11
- 16 = 3 + 13
- 18 = 5 + 13
- 20 = 3 + 17
- 22 = 3 + 19
- 24 = 5 + 19
- 26 = 7 + 19
- 28 = 5 + 23
- 30 = 7 + 23
- 32 = 3 + 29
- 34 = 5 + 29
- 36 = 7 + 29
Ayrıca bakınız
- Asal sayıların listesi
- Eratosten kalburu
- (Mersenne asallları)
- Fermat'nın küçük teoremi
- Öklid teoremi
- Goldbach hipotezi
- İkiz asallar
- Yarı asal
- Lasa sayı
|
Not listesi
- ^ Aimé Ferrier'in 1951'de bir mekanik hesap makinesi ile keşfettiği 44 basamaklı asal sayı, elektronik bilgisayarların yardımı olmadan keşfedilen en büyük asal sayı olma özelliğini korumaktadır.
- ^ a b Beiler'e göre, sayı teorisi uzmanı , asal sayılarla sıkı bir ilişki içinde bulunan , "herhangi bir pratik uygulama ile kendilerini kirletmedikleri için" özellikle benimsemiştir, Katz ise, asal sayıların dağılımı konusundaki çalışmalarıyla tanınan Edmund Landau'nun, matematiğin pratik uygulamalarına derin bir antipati duyduğunu ve bu sebeple, pratik faydaları önceden kanıtlanmış olan geometri gibi alanlardan uzak durduğunu ifade etmektedir.
- ^ Bu testte,
terimi,
sayısının varsayılan asal
sayısına modulo bir kare olması durumunda negatif, aksi halde pozitiftir. Genel olarak,
asal olmayan değerler için,
terimi negatifleştirilmiş Jacobi sembolü olarak tanımlanır ve bu kullanılarak hesaplanabilir.
- ^ Aslında, elips eğri asallığını kanıtlama analizlerinin büyük bir kısmı, algoritmaya giriş olarak sunulan sayının önceden bir olasılıksal testten geçtiği varsayımına dayanmaktadır.
- ^
parametresine bağlı olarak tanımlanan fonksiyonu,
# şeklinde ifade edilir ve bu fonksiyon,
değerine kadar olan tüm asal sayıların çarpımını hesaplar. terimi ise,
biçimlerinden herhangi birine uygun olan asal sayıları ifade etmek için kullanılır.
Kaynakça
- ^ a b "GIMPS Project Discovers Largest Known Prime Number: 282,589,933-1". Mersenne Research, Inc. 21 Aralık 2018. 8 Eylül 2023 tarihinde kaynağından . Erişim tarihi: 21 Aralık 2018.
- ^ "Arşivlenmiş kopya". 12 Nisan 2020 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2020.
- ^ (1997). The Mathematical Olympiad Handbook: An Introduction to Problem Solving Based on the First 32 British Mathematical Olympiads 1965–1996
![image]() . Oxford University Press. s. 26. ISBN .
. Oxford University Press. s. 26. ISBN . - ^ Henderson, Anne (2014). Dyslexia, Dyscalculia and Mathematics: A practical guide (2. bas.). Routledge. s. 62. ISBN .
- ^ (1960). The Giant Golden Book of Mathematics: Exploring the World of Numbers and Space
![image]() . Golden Press. s. 16. OCLC 6975809.
. Golden Press. s. 16. OCLC 6975809. - ^ Leff, Lawrence S. (2000). Math Workbook for the SAT I
![image]() . Barron's Educational Series. s. 360. ISBN .
. Barron's Educational Series. s. 360. ISBN . - ^ (1978). "Section 2: Unique factorization". Elementary number theory (2. bas.). W.H. Freeman and Co. s. 10. ISBN .
- ^ Sierpiński, Wacław (1988). Elementary Theory of Numbers. North-Holland Mathematical Library. 31 (2. bas.). Elsevier. s. 113. ISBN .
- ^ a b (2004). "The great prime number record races". . 51 (4): 414-416. MR 2039814.
- ^ (1997). Numbers and Geometry. Undergraduate Texts in Mathematics. Springer. s. 9. ISBN .
- ^ Sierpiński, Wacław (1964). A Selection of Problems in the Theory of Numbers
![image]() . New York: Macmillan. s. 40. MR 0170843.
. New York: Macmillan. s. 40. MR 0170843. - ^ (2000). "Notations and Conventions". Elementary Methods in Number Theory. Graduate Texts in Mathematics. 195. Springer. ISBN . MR 1732941.
- ^ Faticoni, Theodore G. (2012). The Mathematics of Infinity: A Guide to Great Ideas. Pure and Applied Mathematics: A Wiley Series of Texts, Monographs and Tracts. 111 (2.2yayıncı=John Wiley & Sons bas.). s. 44. ISBN .
- ^ Bruins, Evert Marie, review in Mathematical Reviews of Gillings, R.J. (1974). "The recto of the Rhind Mathematical Papyrus. How did the ancient Egyptian scribe prepare it?". Archive for History of Exact Sciences. 12 (4). ss. 291-298. doi:10.1007/BF01307175. MR 0497458.
- ^ (2010). Mathematics and Its History. Undergraduate Texts in Mathematics (3. bas.). Springer. s. 40. ISBN .
- ^ a b (Aralık 1982). "The Search for Prime Numbers". Scientific American. 247 (6). ss. 136-147. Bibcode:1982SciAm.247f.136P. doi:10.1038/scientificamerican1282-136. JSTOR 24966751.
- ^ a b c d Mollin, Richard A. (2002). "A brief history of factoring and primality testing B. C. (before computers)". Mathematics Magazine. 75 (1). ss. 18-29. doi:10.2307/3219180. JSTOR 3219180. MR 2107288.
- ^ O'Connor, John J.; Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor Matematik Tarihi arşivi
- ^ Sandifer 2007, 8. Fermat's Little Theorem (November 2003), p. 45
- ^ Sandifer, C. Edward (2014). How Euler Did Even More. Mathematical Association of America. s. 42. ISBN .
- ^ Koshy, Thomas (2002). Elementary Number Theory with Applications. Academic Press. s. 369. ISBN .
- ^ Yuan, Wang (2002). Goldbach Conjecture. Series In Pure Mathematics (2.2cilt=4 bas.). World Scientific. s. 21. ISBN .
- ^ Narkiewicz, Wladyslaw (2000). "1.2 Sum of Reciprocals of Primes". The Development of Prime Number Theory: From Euclid to Hardy and Littlewood. Springer Monographs in Mathematics. Springer. s. 11. ISBN .
- ^ Tchebychev, P. (1852). "Asal Sayılar Üzerine Bir Bellek" (PDF). Journal de mathématiques pures et appliquées. Série 1 (Fransızca): 366-390. 6 Kasım 2022 tarihinde kaynağından (PDF). Erişim tarihi: 8 Mart 2024.. (Postulatın kanıtı: 371–382). Ayrıca bkz. Mémoires de l'Académie Impériale des Sciences de St. Pétersbourg, cilt 7, sayfa 15–33, 1854
- ^ (2000). "Asal sayı teoreminin yüzyıllık tarihi". Bambah, R.P.; Dumir, V.C.; Hans-Gill, R.J. (Ed.). Sayı Teorisi. Matematikte Eğilimler. Basel: Birkhäuser. ss. 1-14. MR 1764793.
- ^ (1976). "7. Aritmetik Dizilerdeki Asallar Üzerine Dirichlet Teoremi". Analitik Sayı Teorisi'ne Giriş. New York; Heidelberg: Springer-Verlag. ss. 146-156. MR 0434929.
- ^ Chabert, Jean-Luc (2012). A History of Algorithms: From the Pebble to the Microchip. Springer. s. 261. ISBN .
- ^ Rosen, Kenneth H. (2000). "Theorem 9.20. Proth's Primality Test". Elementary Number Theory and Its Applications (4.4yayıncı=Addison-Wesley bas.). s. 342. ISBN .
- ^ Cooper, S. Barry; Hodges, Andrew (2016). The Once and Future Turing. Cambridge University Press. ss. 37-38. ISBN .
- ^ Rosen 2000, s. 245.
- ^ Beiler, Albert H. (1999) [1966]. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. Dover. s. 2. ISBN . OCLC 444171535.
- ^ Katz, Shaul (2004). "Berlin roots – Zionist incarnation: the ethos of pure mathematics and the beginnings of the Einstein Institute of Mathematics at the Hebrew University of Jerusalem". Science in Context. 17 (1–2). ss. 199-234. doi:10.1017/S0269889704000092. MR 2089305.
- ^ a b c Kraft, James S.; Washington, Lawrence C. (2014). Elementary Number Theory. Textbooks in mathematics. CRC Press. s. 7. ISBN .
- ^ Bauer, Craig P. (2013). Secret History: The Story of Cryptology. Discrete Mathematics and Its Applications. CRC Press. s. 468. ISBN .
- ^ ; (1991). Old and New Unsolved Problems in Plane Geometry and Number Theory. Dolciani mathematical expositions. 11. Cambridge University Press. s. 224. ISBN .
- ^ a b Neale 2017, ss. 18, 47.
- ^ a b Caldwell, Chris K.; Reddick, Angela; Xiong, Yeng; Keller, Wilfrid (2012). "The history of the primality of one: a selection of sources". . 15 (9): Article 12.9.8. MR 3005523. 12 Nisan 2018 tarihinde kaynağından . Erişim tarihi: 8 Mart 2024. For a selection of quotes from and about the ancient Greek positions on the status of 1 and 2, see in particular pp. 3–4. For the Islamic mathematicians, see p. 6.
- ^ Tarán, Leonardo (1981). Speusippus of Athens: A Critical Study With a Collection of the Related Texts and Commentary. Philosophia Antiqua : A Series of Monographs on Ancient Philosophy. 39. Brill. ss. 35-38. ISBN .
- ^ Caldwell et al. 2012, pp. 7–13. See in particular the entries for Stevin, Brancker, Wallis, and Prestet.
- ^ Caldwell et al. 2012, s. 15.
- ^ a b c Caldwell, Chris K.; Xiong, Yeng (2012). "What is the smallest prime?" (PDF).
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Bir asal sayi yalnizca 1 den buyuk olup kendisinden kucuk iki dogal sayinin carpimi olarak ifade edilemeyen bir dogal sayidir 1 den buyuk ve asal olmayan dogal sayilara bilesik sayi adi verilir Ornegin 5 bir asal sayidir cunku onu bir carpim olarak ifade etmenin mumkun olan yollari 1 5 veya 5 1 yalnizca 5 sayisini icermektedir Ancak 4 bir bilesik sayidir cunku bu her iki sayinin da 4 ten kucuk oldugu bir carpim 2 2 seklindedir Asal sayilar aritmetigin temel teoreminden oturu sayi teorisi alaninda merkezi oneme sahiptir 1 den buyuk her dogal sayi ya bir asal sayidir ya da asal sayilarin carpimi olarak siralamalarindan bagimsiz bir sekilde benzersiz olarak carpanlarina ayrilabilir Bilesik sayilar dikdortgen bicimlerine duzenlenebilirken asal sayilarin bu bicimde duzenlenmesi mumkun degildir Bir sayinin asal olus ozelligi asallik olarak tanimlanir Verilen bir n displaystyle n sayisinin asalligini denetlemek icin kullanilan basit fakat zaman alici bir yontem olan n displaystyle n sayisinin 2 ile n displaystyle sqrt n arasindaki herhangi bir tam sayiya kati olup olmadigini sinar Daha hizli algoritmalar arasinda hizli olmasina karsin kucuk bir hata payi barindiran ve her zaman dogru sonucu veren fakat pratikte uygulanabilirligi sinirli olan yer alir gibi ozel bicimlere sahip sayilar icin ozellikle hizli yontemler mevcuttur Aralik 2018 2018 12 itibariyla 24 862 048 ondalik basamaga sahip bir Mersenne asalidir M O 300 civarinda Oklid tarafindan ispatlandigi gibi asal sayilar Asal sayilar ile bilesik sayilari birbirinden ayiran kesin ve basit bir formul bulunmamaktadir Bununla birlikte dogal sayilar arasindaki asal sayilarin dagilimi genel olarak istatistiksel yontemlerle modellenebilir Bu baglamda elde edilen ilk onemli sonuc 19 yuzyilin sonlarinda ispatlanan asal sayi teoremidir bu teori buyuk bir sayinin rastgele secilmesi durumunda asal olma olasiliginin sayinin basamak sayisina yani logaritmasina ters oranli oldugunu ifade eder Asal sayilara iliskin tarihsel bazi sorular henuz cozume kavusturulmamistir Bu sorular icerisinde her 2 den En kucuk asal sayi 2 dir buyuk cift tam sayinin iki asal sayinin toplami olarak yazilabilecegini ileri suren ve ikiser rakam aralikla sinirsiz sayida ikiz asal sayi ciftinin var oldugunu iddia eden hipotezi yer almaktadir Bu tur sorular sayilarin analitik ve cebirsel boyutlari uzerine yogunlasan sayi teorisi alanlarinin gelisimini hizlandirmistir Asal sayilar bilgi teknolojisi alaninda ozellikle de buyuk sayilarin asal carpanlara guclugune dayanan gibi cesitli islemlerde kullanilmaktadir Soyut cebirde asal sayilara genellestirilmis bir bicimde benzeyen yapilar arasinda ve sayilabilir Tanim ve orneklerBir dogal sayi 1 2 3 4 5 6 vb 1 den buyuk olmasi ve kendisinden kucuk iki dogal sayinin carpimi olarak ifade edilememesi durumunda asal sayi olarak nitelendirilir 1 den buyuk olup asal olmayan sayilara bilesik sayilar adi verilir Diger bir ifadeyle eger n displaystyle n sayisi kendinden kucuk birden fazla esit parcaya bolunemez ise ya da n displaystyle n kadar nokta tam bir dikdortgen olarak sekillendirilemez ise n displaystyle n bir asal sayidir Ornegin 1 ile 6 arasindaki sayilar icinde 2 3 ve 5 sayilari asal sayilardir zira bu sayilari kendinden baska tam bolebilen kalan birakmaksizin baska bir sayi yoktur 1 sayisi tanim geregi asal olarak kabul edilmez 4 2 2 ve 6 2 3 her ikisi de bilesik sayi kategorisindedir kullanilarak yapilan gosterim 7 sayisinin asal oldugunu cunku 2 3 4 5 veya 6 sayilariyla tam olarak bolunemedigini ortaya koyuyor Bir dogal sayi n displaystyle n in bolenleri n displaystyle n sayisini esit olarak bolebilen dogal sayilardir Her dogal sayi kendisi ve 1 olmak uzere iki temel bolene sahiptir Eger bir sayinin bu ikisinden baska bir boleni varsa asal sayi olamaz Bu durum asal sayilarin alternatif bir tanimini sunar Yalnizca iki pozitif bolene sahip olan sayilar asal sayilardir Bu iki bolen 1 ve sayinin kendisidir Tek bir bolene sahip olan 1 sayisi bu tanim cercevesinde asal kabul edilmez Ayni kavrami baska bir sekilde ifade etmek gerekirse bir sayi n displaystyle n 1 den buyukse ve 2 3 n 1 displaystyle 2 3 dots n 1 sayilarindan hicbiri n displaystyle n sayisini esit bolmezse o sayi asaldir Ilk 25 asal sayi 100 den kucuk tum asal sayilar sunlardir 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 OEIS de A000040 dizisi 2 den buyuk hicbir cift sayi n displaystyle n asal olamaz cunku herhangi bir boyle sayi 2 n 2 displaystyle 2 times n 2 olarak ifade edilebilir Bu nedenle 2 disindaki her asal sayi bir tek sayidir ve tek asal olarak adlandirilir Benzer sekilde alisilagelmis ondalik sistemde yazildiginda 5 ten buyuk tum asal sayilar 1 3 7 veya 9 ile biter Diger rakamlarla biten sayilar hep bilesiktir 0 2 4 6 veya 8 ile biten ondalik sayilar cifttir ve 0 veya 5 ile biten ondalik sayilar 5 e bolunebilir Tum asallarin kumesi bazen P displaystyle mathbf P kalin harflerle buyuk bir P veya P displaystyle mathbb P tahtaya yazi tipiyle buyuk bir P ile gosterilir TarihceRhind Papirusu M O 1550 civarindan kalan Rhind Papirusu asal ve bilesik sayilar icin farkli formdaki genislemelerini icerir Ancak asal sayilarin incelenmesine dair en eski kayitlar antik Yunan matematikcilerinden gelmektedir onlar bu sayilara prōtos arithmos Grekce prῶtos ἀri8mὸs demektedirler Oklid in Elementleri M O 300 civari asal sayilarin sonsuzlugunu ve aritmetigin temel teoremini kanitlar ve bir Mersenne sayisindan nasil bir mukemmel sayi olusturulacagini gosterir Baska bir Yunan icadi olan Eratosten kalburu asal sayi listeleri olusturmak icin hala kullanilmaktadir Miladi 1000 yillarinda Islam donemi matematikcisi Ibnu l Heysem asal sayilari n 1 1 displaystyle n 1 1 ifadesini tam bolunebilen n displaystyle n sayilari olarak tanimlayan ni buldu Ayrica tum cift mukemmel sayilarin Oklid in Mersenne asallarini kullanarak yapilan insasindan geldigini one surdu ancak bunu kanitlayamadi Bir diger Islam donemi matematikcisi Eratosten kalburunun ust sinirin karekokune kadar olan asal bolenleri dikkate alarak hizlandirilabilecegini gozlemledi Fibonacci Islami matematikten gelen yenilikleri Avrupa ya tasidi Onun kitabi 1202 asalligi test etmek icin tanimlayan ilk eser oldu ve yine karekokune kadar olan bolenleri kullanmayi onerdi 1640 senesinde Pierre de Fermat tarafindan ispati yapilmamis olmasina ragmen ortaya atilan Fermat nin kucuk teoremi sonradan Leibniz ve Euler tarafindan ispatlanmistir Fermat 22n 1 displaystyle 2 2 n 1 formuluyle ifade edilen Fermat sayilarinin asallik ozelliklerini arastirmis Marin Mersenne ise p displaystyle p nin asal oldugu durumlarda 2p 1 displaystyle 2 p 1 formunda tanimlanan Mersenne asallarini incelemistir Goldbach Euler e yazdigi 1742 tarihli mektupta her cift sayinin iki asal sayinin toplami olarak ifade edilebilecegini oneren Goldbach hipotezini dile getirmistir Euler tum cift mukemmel sayilarin Mersenne asallari kullanilarak olusturulabilecegini gosteren Heysem varsayimini gunumuzde olarak adlandirilir kanitlamistir Euler ayrica asal sayilarin sonsuz oldugunu ve asal sayilarin terslerinin toplaminin diverjansini 12 13 15 17 111 displaystyle tfrac 1 2 tfrac 1 3 tfrac 1 5 tfrac 1 7 tfrac 1 11 cdots matematiksel analiz metodolojilerini bu alana tasiyarak kanitlamistir 19 yuzyilin baslarinda Legendre ve Gauss x displaystyle x sonsuza yaklastikca x displaystyle x e kadar olan asal sayilarin sayisinin x log x displaystyle x log x ile oldugunu tahmin etmislerdir burada log x displaystyle log x x displaystyle x in Asal sayilarin bu yuksek yogunlugunun bir zayif sonucu idir bu postulat her n gt 1 displaystyle n gt 1 icin n displaystyle n ile 2n displaystyle 2n arasinda bir asal sayi oldugunu one surer ve 1852 de Pafnuty Chebyshev tarafindan kanitlanmistir Bernhard Riemann in fikirleri Legendre ve Gauss un tahminini kanitlamak icin bir cerceve cizdi Yakindan ilgili olan Riemann hipotezi hala kanitlanmamis olmasina ragmen Riemann in cizdigi cerceve 1896 da Hadamard ve tarafindan tamamlandi ve sonuc simdi asal sayilar teoremi olarak bilinmektedir 19 yuzyilin baska bir onemli sonucu idi belirli aritmetik dizilerin sonsuz coklukta asal sayi icerdigini belirtir Deneme bolmesinin pratikte uygulanabilir oldugu sayilardan daha buyuk sayilar icin bircok matematikci uzerinde calismistir Belirli sayi formlarina sinirli yontemler arasinda Fermat sayilari icin 1877 yaklasik 1878 1856 da ortaya cikti ve genellestirilmis bulunmaktadir 1951 yilindan itibaren en buyuk bilinen asal sayilarin tumu bilgisayarlarda gerceklestirilen bu testlerle kesfedilmistir Buyuk asal sayilari arama cabasi ve benzeri dagitik hesaplama projeleri vasitasiyla matematiksel olmayan topluluklarda da buyuk bir ilgi uyandirmistir Asal sayilarin soyut matematik disinda onemli uygulamalara sahip olmadigina dair gorus 1970 lerde asal sayilari temel alan ve RSA kriptosisteminin gelistirilmesi ile curutulmustur Bilgisayarla yapilan asallik testlerinin ve carpanlara ayirma isleminin artan pratik onemi kisitlama olmaksizin buyuk sayilarla basa cikabilen gelismis yontemlerin gelistirilmesine yol acti Asal sayilar teorisinin matematiksel gelisimi asal sayilarin keyfi olarak uzun aritmetik dizilerinin oldugunu belirten 2004 ve in 2013 te sinirli buyuklukte sonsuz coklukta oldugunun kaniti ile de ileriye tasindi 1 sayisinin asalligi Antik Yunanlilarin cogu baslangicta 1 i bir sayi olarak bile kabul etmemistir dolayisiyla asalligini tartismalari mumkun degildi Nicomachus Iamblichus Boethius ve Cassiodorus gibi birkac Yunan ve sonraki Roma gelenegi alimi asal sayilari tek sayilarin bir alt bolumu olarak kabul ettigi icin 2 yi de asal olarak kabul etmemislerdir Ancak Oklid ve diger bircok Yunan matematikcisi 2 yi asal olarak kabul etmistir Orta Cag Islam matematikcileri genellikle Yunanlilarin goruslerini takip ederek 1 i bir sayi olarak gormemislerdir Orta Cag ve Ronesans boyunca matematikciler 1 i bir sayi olarak kabul etmeye baslamis ve bazilari onu ilk asal sayi olarak dahil etmistir 18 yuzyilin ortalarinda Christian Goldbach Leonhard Euler ile olan yazismalarinda 1 i asal olarak listelemistir ancak Euler kendisi 1 i asal olarak kabul etmemistir 19 yuzyilda bircok matematikci hala 1 i asal olarak kabul etmis ve 1 i iceren asal sayi listeleri en son 1956 yilinda yayimlanmistir 1 sayisi gunumuzde ne asal ne de bilesik kabul edilir ve ozel bir durumu vardir Gecmiste pek cok matematikci 1 i asal sayi olarak kabul ediyordu 1 in asal olarak kabul edilmesine dayanarak yapilan bircok calisma gecerliligini hala surdurmektedir ve in calismalari gibi Henri Lebesgue calismalarinda 1 i asal olarak ele alan son profesyonel matematikci olarak bilinir 1 asal olarak ele alindiginda bazi teoremlerde degisiklige gidilmesi gerekir Ornegin tum pozitif tam sayilarin yalniz bir sekilde asal sayilarin carpimlari seklinde yazilabilecegini soyleyen aritmetigin temel teoremi gecmisteki asal sayi tanimina gore gecerli degildir Resimdeki ornek 11 in asal olup 12 nin asal olmadigini gosteriyor Bir sayinin asal olarak tanimlanmasi degistirilip 1 asal olarak kabul edilseydi asal sayilarla ilgili bircok ifade daha zor bir sekilde yeniden formule edilmek zorunda kalirdi Ornegin aritmetigin temel teoremi her sayinin 1 in istenilen sayida kopyasiyla cesitli faktorizasyonlari olacagi icin 1 den buyuk asallara gore faktorizasyonlar acisindan yeniden ifade edilmek zorunda kalirdi Benzer sekilde Eratosthenes kalburu 1 i bir asal olarak ele alirsa dogru calismazdi cunku 1 in tum katlarini yani tum diger sayilari elemek ve sadece 1 sayisini cikarmak zorunda kalirdi Asal sayilarin bazi diger daha teknik ozellikleri de 1 numarasi icin gecerli degildir ornegin Euler in totient fonksiyonu veya icin formuller asal sayilar icin 1 ile farklidir 20 yuzyilin baslarinda matematikciler 1 in asal olarak listelenmemesi ancak daha cok olarak kendi ozel kategorisinde yer almasi gerektigi konusunda anlasmaya basladilar Temel ozelliklerCarpanlama Bir sayinin asal sayilarin carpimi olarak yazilmasi o sayinin asal carpanlara ayrilmasi olarak adlandirilir Ornegin 34866 2 3 3 13 149 2 32 13 149 displaystyle begin aligned 34866 amp 2 times 3 times 3 times 13 times 149 amp 2 times 3 2 times 13 times 149 end aligned Bu carpimdaki terimlere asal carpanlar denir Ayni asal carpan birden fazla bulunabilir bu ornekte asal carpan 3 displaystyle 3 iki defa gorulmektedir Bir asal sayi birden fazla kez bulundugunda ussel sayilar kullanilarak ayni asal sayi gruplandirilabilir ornegin yukaridaki sonucun ikinci yazim seklinde 32 displaystyle 3 2 3 displaystyle 3 sayisinin karesini veya ikinci kuvvetini gosterir Asal sayilarin sayilar teorisi ve genel olarak matematige merkezi onemi aritmetigin temel teoreminden kaynaklanmaktadir Bu teorem 1 den buyuk her tam sayinin bir veya daha fazla asal sayinin carpimi olarak yazilabilecegini belirtir Daha da onemlisi bu carpim ozeldir yani ayni sayinin her iki asal carpanlarinin carpimi carpanlarin siralamasi farkli olsa bile ayni asal sayilarin ayni sayida kopyasini icerecektir Dolayisiyla bir asal carpanlarina ayirma algoritmasi kullanilarak carpanlara ayirma islemi yapmanin bircok farkli yolu olmasina ragmen hepsi ayni sonucu uretmek zorundadir Bu nedenle asal sayilar dogal sayilarin temel yapi taslari olarak kabul edilebilir Asal carpanlara ayrilmanin benzersizliginin kanitlarindan bazilari dayanir Eger p displaystyle p bir asal sayiysa ve p displaystyle p a displaystyle a ve b displaystyle b tam sayilarinin carpimi olan ab displaystyle ab yi bolerse o zaman p displaystyle p ya a displaystyle a yi ya da b displaystyle b yi veya her ikisini de boler Aksine bir sayi p displaystyle p bir carpimi boldugunde daima carpimin en az bir faktorunu bolerse o zaman p displaystyle p asal olmalidir Sonsuzluk Asal sayilarin sayisi sonsuzdur Diger bir deyisle asal sayi dizisi 2 3 5 7 11 13 asla son bulmaz Bu tez antik Yunan matematikcisi Oklid onuruna Oklid Teoremi olarak isimlendirilmistir cunku bu tezin bilinen ilk ispati onun adiyla iliskilendirilir Asal sayilarin sonsuzlugunu kanitlayan bircok metod mevcuttur bunlar arasinda Euler tarafindan gerceklestirilen analitik ispat Goldbach in Fermat sayilari uzerine kurulu genel topoloji kullanarak sundugu ve ispati sayilabilir Oklid in ispati herhangi bir eksik oldugunu gosterir Ana fikir verilen listedeki asal sayilarin hepsini carparak 1 displaystyle 1 eklemektir Eger liste p1 p2 pn displaystyle p 1 p 2 ldots p n asal sayilarindan olusuyorsa bu N 1 p1 p2 pn displaystyle N 1 p 1 cdot p 2 cdots p n sayisini verir Temel teorem geregince N displaystyle N sayisi N p1 p2 pm displaystyle N p 1 cdot p 2 cdots p m seklinde bir veya daha fazla asal carpan iceren bir asal carpanlara ayirimina sahiptir N displaystyle N sayisi bu carpanlarca tam bolunebilirken verilen asal sayi listesindeki herhangi bir sayi ile bolundugunde 1 kalanini verir bu durum N displaystyle N sayisinin asal carpanlarinin verilen liste icinde yer alamayacagini gosterir Asal sayilarin sonlu bir listesinin olmamasi gercegi asal sayilarin sonsuz oldugunu zorunlu kilar En kucuk asal sayilarin carpimlarina bir eklenerek olusturulan sayilara adi verilir Bunlardan ilk besi asal olmakla birlikte altincisi 1 2 3 5 7 11 13 30031 59 509 displaystyle 1 2 cdot 3 cdot 5 cdot 7 cdot 11 cdot 13 30031 59 cdot 509 seklindedir Asal sayi denklemleri Asal sayilari tespit etmek icin bilinen etkin bir yontem mevcut degildir Oyle ki yalnizca asal sayi degerleri ureten sabit olmayan cok degiskenli bir polinom dahi bulunamamistir Bununla birlikte yalnizca asal sayilari veya tum asal sayilari temsil edebilen cesitli ifadeler mevcuttur Bu ifadelerden biri ne dayali olup 2 sayisinin defalarca ve diger tum asal sayilarin ise sadece bir kez elde edilmesini saglayan bir formuldur Dokuz degisken ve bir parametreye sahip Diyofantus denklemlerinden olusan bir kume de mevcuttur bu kumenin belirgin bir ozelligi soyledir Eger ve ancak eger bu denklem sistemi dogal sayilar kumesi uzerinde bir cozume sahipse ilgili parametre bir asal sayidir Bu ozellik tum pozitif degerleri asal sayi olan bir formulun elde edilmesi amaciyla kullanilabilir ve tarafindan one surulen bir teoremle ilgili olarak asal sayilar ureten diger formuller de mevcuttur Bu teoremler A gt 1 displaystyle A gt 1 ve m displaystyle mu seklinde ifade edilen gercek sabitlerin varligini one surer A3n ve 2 22m displaystyle left lfloor A 3 n right rfloor text ve left lfloor 2 cdots 2 2 mu right rfloor Ilk formulde herhangi bir dogal n displaystyle n sayisi icin belirtilen sayilar asal niteliktedir ikinci formulde ise uslerin herhangi bir sayida olusu durumunda da sayilar asal ozellik gosterirler Bu baglamda displaystyle lfloor cdot rfloor sembolu incelenen sayiya esit veya bu sayidan daha az olan en yuksek tam sayiyi ifade eden belirtmektedir Fakat A displaystyle A veya m displaystyle mu degerlerinin hesaplanabilmesi icin asal sayilarin ilk etapta elde edilmis olmasi gerekliligi goz onunde bulunduruldugunda bu formullerin asal sayi uretimi acisindan pratikte bir yarari bulunmamaktadir Cozum bekleyen sorular Matematik alaninda asal sayilarla ilgili bir dizi varsayim ileri surulmustur Cogunlukla temel bir ifade sekliyle ortaya konan bu varsayimlar onlarca yil suresince ispatlanamamistir 1912 yilinda ortaya atilan basligi altindaki dort soru gunumuze dek cozulememistir Bu varsayimlardan bir tanesi 2 den buyuk olan her cift tam sayi n displaystyle n nin iki asal sayinin toplami seklinde ifade edilebilecegini one suren Goldbach hipotezi ile iliskilendirilmistir 2014 itibariyla soz konusu varsayim n 4 1018 displaystyle n 4 cdot 10 18 degerine ulasan tum sayilar icin teyit edilmistir Bu iddiadan daha zayif onermeler ispatlanmistir mesela yeterli buyuklukteki her tek tam sayinin uc asal sayinin toplami seklinde ifade edilebilecegini belirtmektedir yeterli buyuklukteki herhangi bir cift sayinin bir asal sayi ile bir yari asal iki asal sayinin carpimi toplami seklinde gosterilebilecegini one surmektedir Bunun yani sira 10 degerinden buyuk olan her cift tam sayi alti asal sayinin toplami seklinde ifade edilebilir Bu tur sorularin incelendigi sayi teorisi dali olarak adlandirilmaktadir Ardisik asal sayilar arasindaki farklari ifade eden ile ilgili bir baska problem turu bulunmaktadir Herhangi bir dogal n displaystyle n sayisi icin n 2 n 3 n n displaystyle n 2 n 3 dots n n dizisinin n 1 displaystyle n 1 adet bilesik sayi icerdigi goz onune alindiginda istenilen buyuklukte asal bosluklarin mevcudiyeti tespit edilebilir Bununla birlikte buyuk asal araliklarin olusumu bu argumanin isaret ettiginden cok daha once gerceklesmektedir Mesela 8 birimlik ilk asal sayi farki 89 ile 97 arasindaki asal sayilar arasinda gozlemlenir bu 8 40320 displaystyle 8 40320 degerinden onemli olcude daha dusuktur Iki asal sayi arasindaki farkin 2 olmasi durumunda ikiz asal ciftlerinin sonsuz sayida var oldugu one surulmektedir bu onerme ikiz asal hipotezi olarak bilinir ise daha genis bir perspektiften her pozitif k displaystyle k tam sayi degeri icin ardisik asal sayi ciftlerinin 2k displaystyle 2k farkla ayrildigi durumlarin sonsuz sayida oldugunu ifade etmektedir ve 1 displaystyle 1 ile n displaystyle n arasindaki asal sayilar arasindaki maksimum bosluklarin yaklasik olarak en fazla n displaystyle sqrt n olmasi gerektigini ileri surmektedir bu cikarim Riemann hipotezi cercevesinde elde edilen bilinen bir sonuctur Ancak daha iddiali olan en buyuk bosluk boyutunu O log n 2 displaystyle O log n 2 olarak tahmin etmektedir Iki asal sayi arasindaki bosluklar asal sayilarin arasindaki farklarin desenlerini ifade eden seklinde genellestirilebilir Bu desenlerin sonsuz sayida varligi ve yogunlugu asal sayilarin asal sayi teoremi ile belirlenen yogunluga sahip rastgele bir sayi dizisi gibi davrandigini oneren sezgisel temellere dayanan inceleme konusudur Analitik ozelliklerAnalitik sayi teorisi sayi teorisini surekli fonksiyonlar limitler sonsuz seriler ve bunlarin yani sira sonsuzluk ve sonsuz kucuk kavramlariyla iliskili matematiksel yapilar uzerinden detayli bir sekilde arastirir Bu arastirma alaninin kokenleri Leonhard Euler in Basel problemini cozumuyle iliskilendirilen ilk onemli calismasina dayanir Ilgili sorun 1 14 19 116 displaystyle 1 tfrac 1 4 tfrac 1 9 tfrac 1 16 dots seklinde ifade edilen sonsuz serinin degerinin ne oldugunu sorgulamaktadir bu deger gunumuzde Riemann zeta fonksiyonu nun z 2 displaystyle zeta 2 degeri olarak kabul edilmektedir Soz konusu fonksiyon asal sayilarla ve matematigin en onemli cozulememis problemlerinden biri olan Riemann hipotezi ile siki bir sekilde iliskilidir Euler in bu konudaki katkisi z 2 p2 6 displaystyle zeta 2 pi 2 6 esitligini ispatlamasiyla one cikmaktadir Bu sayinin ters degeri olan 6 p2 displaystyle 6 pi 2 genis bir deger araligindan uniform dagilimla secilen iki rastgele sayinin birbirleriyle aralarinda asal yani ortak hicbir carpana sahip olmayan olma ihtimalinin sinir degerini temsil etmektedir Buyuk olcekte asal sayilarin dagilimi ornegin belirli bir buyuk esik degerinden daha kucuk olan asal sayilarin sayisi gibi sorular asal sayi teoremi tarafindan aciklanmaktadir fakat n displaystyle n inci asal sayiyi belirleyen etkin bir formul mevcut degildir temel versiyonu aralarinda asal olan a displaystyle a ve b displaystyle b tam sayilari icin p n a bn displaystyle p n a bn bicimindeki dogrusal polinomlarin sonsuz sayida asal degere ulastigini one surer Teoremin ileri versiyonlari bu asal degerlerin terslerinin toplaminin iraksadigini ve ayni b displaystyle b degerine sahip farkli dogrusal polinomlarin asal sayilar bakimindan yaklasik olarak ayni oranlara sahip oldugunu ifade eder Daha yuksek dereceli polinomlarda asal sayi oranlarina iliskin varsayimlar ortaya konmus olmakla birlikte bu varsayimlar henuz kanitlanmamistir ve tam sayi girdileri icin sonsuz kez asal olan bir kuadratik polinomun varligi bilinmemektedir Oklid teoreminin analitik ispati asal sayilarin toplamlarini incelemektedir 12 13 15 17 1p displaystyle frac 1 2 frac 1 3 frac 1 5 frac 1 7 cdots frac 1 p Euler herhangi bir reel sayi x displaystyle x icin bu toplamin x displaystyle x degerinden daha buyuk olacagi bir asal p displaystyle p sayisinin mevcut oldugunu kanitlamistir Bu durum asal sayilarin sonsuz sayida oldugunun bir gostergesidir zira sonlu sayida asal sayi var olsaydi bu toplam her bir x displaystyle x degerini asmak yerine en buyuk asal sayida en yuksek degerine erisirdi Bu serinin buyume orani ile daha detayli bir bicimde tanimlanmistir Karsilastirma amaciyla 112 122 132 1n2 displaystyle frac 1 1 2 frac 1 2 2 frac 1 3 2 cdots frac 1 n 2 toplami n displaystyle n sonsuza yaklastikca sonsuzluga yonelmez bkz Basel problemi Bu cercevede her iki kume de sonsuz sayida olmasina ragmen asal sayilarin dogal sayi karelerine gore daha siklikla ortaya ciktigi gorulmektedir ikiz asallarin terslerinin toplaminin 13 15 15 17 111 113 displaystyle left frac 1 3 frac 1 5 right left frac 1 5 frac 1 7 right left frac 1 11 frac 1 13 right cdots sonlu bir degere sahip oldugunu ifade etmektedir Brun teoremi nedeniyle Euler metodunun sonsuz sayida ikiz asalin var oldugu iddiasini ele alan cozumlemek amaciyla kullanilabilmesi mumkun degildir Belirli bir ust sinira kadar olan asal sayilarin miktari nlog n displaystyle tfrac n log n ve logaritmik integral Li n displaystyle operatorname Li n ile olan yakinsakligina dair incelemesi n displaystyle n degerinin artisi ile her iki goreceli hata orani da azalarak sifira ulasmaktadir ancak logaritmik integralin sifira yakinsama hizi oteki yaklasima gore cok daha fazladir olarak adlandirilan p n displaystyle pi n n displaystyle n degerine esit veya ondan kucuk olan asal sayilarin toplam sayisini ifade etmek icin kullanilan bir fonksiyondur Ornek olarak p 11 5 displaystyle pi 11 5 olarak ifade edilir zira 11 sayisina esit veya bu sayidan daha kucuk olan bes adet asal sayi mevcuttur gibi metodlar n displaystyle n ye kadar olan asal sayilarin her birini tek tek siralamaktan cok daha hizli bir sekilde p n displaystyle pi n degerinin dogru hesaplamasini gerceklestirebilir Asal sayi teoremine gore p n displaystyle pi n degeri n log n displaystyle n log n ifadesine asimptotiktir yani p n nlog n displaystyle pi n sim frac n log n seklinde gosterilir Bu durum p n displaystyle pi n ile sag taraftaki ifadenin oraninin n displaystyle n degeri sonsuzluga ulastikca 1 degerine yakinsadigini ifade eder Bu durum n displaystyle n degerinden daha kucuk rastgele bir sayinin asal sayi olma ihtimalinin yaklasik olarak n displaystyle n sayisinin basamak sayisina ters orantili oldugunu gostermektedir Bu durum ayni zamanda n displaystyle n siradaki asal sayinin buyuklugunun nlog n displaystyle n log n ile orantili oldugunu ve bunun sonucu olarak asal sayilar arasindaki ortalama bosluk buyuklugunun log n displaystyle log n ile orantili oldugunu gostermektedir p n displaystyle pi n degerinin daha dogru bir tahmini kullanilarak saglanmaktadir p n Li n 2ndtlog t displaystyle pi n sim operatorname Li n int 2 n frac dt log t Aritmetik diziler Aritmetik dizi dizide yer alan ardisik sayilarin her biri arasinda sabit bir fark bulunan sonlu veya sonsuz bir sayilar dizisini ifade eder Bu farka dizinin modulu denir Ornegin 3 12 21 30 39 9 modul degerine sahip bir sonsuz aritmetik diziyi temsil eder Aritmetik bir dizideki sayilar modul degerine bolunduklerinde ayni kalani alir bu durumun bir ornegi olarak kalanin 3 oldugu gorulur Modulun 9 ve kalanin 3 olmasi her iki degerin de 3 un katlari olmasi anlamina gelir bu yuzden dizideki her bir eleman da 3 un katidir Bu sebeple bu dizi sadece bir tek asal sayi icermektedir ki o da 3 tur Genel anlamda sonsuz dizi a a q a 2q a 3q displaystyle a a q a 2q a 3q dots ancak kalan a displaystyle a ve modul q displaystyle q birbirine gore asal oldugunda birden fazla asal sayi icerebilir Eger bu iki deger birbirine gore asal ise ilerlemenin sonsuz sayida asal sayi icerdigini one surer Incelemis oldugumuz yatay seridin her bir sirasi modul 9 a gore mumkun olan dokuz farkli dizi ilerlemesinden bir tanesini temsil etmekte olup asal sayilar kirmizi renkle vurgulanmistir Mod 9 degerleri 0 3 veya 6 olan sayi dizileri en fazla bir adet asal sayiyi bu sayi 3 tur barindirabilirken mod 9 degerleri 2 4 5 7 ve 8 olan sayi dizileri her bir dizi icinde benzer asal sayi miktarlariyla birlikte sonsuz sayida asal sayi icermektedir yalnizca asal sayilardan mutesekkil ve herhangi bir uzunlukta olabilen sonlu aritmetik dizilerin mevcudiyetini ispatlamaktadir Kuadratik polinomlar tarafindan uretilen asal sayi degerleri Ulam spirali Asal sayilar kirmizi olarak belirtilmistir belirli diyagonaller uzerinde yogun bir dagilim gosterirken bazi diyagonallerde bu yogunluk gozlemlenmemektedir 4n2 2n 41 displaystyle 4n 2 2n 41 biciminde ifade edilen kuadratik polinomdan elde edilen asal sayi degerleri mavi renkle isaretlenmistir Euler n2 n 41 displaystyle n 2 n 41 biciminde ifade edilen fonksiyonun 1 n 40 displaystyle 1 leq n leq 40 araligindaki n degerleri icin asal sayi degerleri urettigine dikkat cekmistir bununla birlikte bu fonksiyonun ileri degerleri arasinda bilesik sayilarin da yer aldigi gozlemlenmistir Bu fenomen icin bir aciklama arayisi ve ile ilgili olarak cebirsel sayi teorisinin derinliklerine dalmayi gerektirmistir tam sayili katsayilara sahip degerleri icerisindeki asal sayilarin yogunlugunun logaritmik integral ve polinom katsayilarinin fonksiyonu olarak ongorulmesine yoneliktir Su ana kadar herhangi bir ikinci dereceden polinomun sonsuz sayida asal sayi degeri urettigi ispatlanamamistir Ulam spirali dogal sayilari orijini cevreleyen konsantrik kareler halinde spiral bir duzende iki boyutlu bir izgara uzerine yerlestirir ve asal sayilari belirginlestirir Gorsel bir inceleme sonucunda asal sayilarin belirli diyagonaller uzerinde digerlerine kiyasla daha yogun bir sekilde gruplandigi gorulmekte bu durum bazi ikinci dereceden polinomlarin digerlerine nazaran daha siklikla asal degerler urettigi yonunde bir izlenim uyandirmaktadir Zeta fonksiyonu ve Riemann hipotezi Zeta fonksiyonunun mutlak degerlerine iliskin cizim fonksiyonun belirli ozelliklerini sergilemektedir 1859 yilindan itibaren matematik alaninda aydinlatilamamis en meshur meselelerden biri ayni zamanda Milenyum Problemleri arasinda yer alan Riemann hipotezi Riemann zeta fonksiyonu z s displaystyle zeta s nun sifir noktalarinin konumlarini sorgular Bu fonksiyon karmasik sayilar uzerinde tanimli bir analitik fonksiyon niteligindedir Reel kismi bir degerinden buyuk s displaystyle s karmasik sayilari icin fonksiyon hem tum tam sayilar uzerinden hesaplanan bir sonsuz seri hem de asal sayilar uzerinden tanimlanan bir ile ifade edilir z s n 1 1ns p asal11 p s displaystyle zeta s sum n 1 infty frac 1 n s prod p text asal frac 1 1 p s Euler tarafindan ortaya konulan bu toplam ile carpim arasindaki denklik olarak isimlendirilmistir Euler carpimi aritmetigin temel teoremi sayesinde elde edilmis olup zeta fonksiyonunun asal sayilarla derinlemesine iliskisini aciga cikarir Sonsuz sayida asal sayi bulunmasi gerektigini kanitlama yolunda bu durum eger sadece sinirli sayida asal sayi varsa toplam carpim esitliginin s 1 displaystyle s 1 noktasinda da gecerli olmasi gerekirken toplamin diverjans gosterdigi harmonik seri 1 12 13 displaystyle 1 tfrac 1 2 tfrac 1 3 dots gibi carpimin ise sonlu bir deger almasi gerektigiyle sonuclanan bir celiski ile karsi karsiya kalinir Riemann hipotezi zeta fonksiyonunun sifirlarinin tamaminin ya negatif cift sayilardan ya da reel kisimlari 1 2 ye esit olan karmasik sayilardan olustugunu one surer Asal sayi teoreminin ilk kaniti bu hipotezin bir versiyonuna yani reel kismi 1 olan sifirlarin var olmadigi varsayimina dayanmaktaydi fakat daha basit kanitlar da ortaya konmustur Asal sayi sayim fonksiyonu araciligiyla zeta fonksiyonunun sifirlarinin her birinden bir terimin katkisiyla olusan bir toplam seklinde ifade edilebilir bu toplamin temel bileseni logaritmik integral olup geri kalan terimler ana terimin uzerinde ve altinda dalgalanmalara yol acar Bu baglamda sifirlarin asal sayilarin dagilim duzenini belirledigi soylenebilir Riemann hipotezi eger dogruysa bu dalgalanmalar minimale indirgenecek ve asal sayi teoreminin ongordugu gibi x displaystyle x sayisina yakin araliklarda yaklasik olarak x displaystyle x sayisinin karekoku buyuklugundeki araliklar icin da gecerli olacaktir Soyut cebirModuler aritmetik ve sonlu alanlar Moduler aritmetik modul olarak isimlendirilen bir dogal sayi n displaystyle n icin yalnizca 0 1 2 n 1 displaystyle 0 1 2 dots n 1 sayilarinin kullanildigi geleneksel aritmetik islemlerin modifiye edilmis bir seklidir Diger tum dogal sayilar n displaystyle n ile bolme islemi sonrasinda elde edilen kalan deger ile bu sisteme dahil edilerek karsiliklari bulunur Moduler toplama cikarma ve carpma islemleri tam sayilarin geleneksel toplama cikarma veya carpma islemlerinin sonucuna bu sonucun modulunun alinarak yerine konulmasi yontemiyle gerceklestirilir Tam sayilar arasindaki esitlik kavrami moduler aritmetikte denklik olarak ifade edilir x displaystyle x ile y displaystyle y n displaystyle n ile bolunduklerinde ayni kalan degerine sahip olduklarinda denk olmalari durumu x y displaystyle x equiv y mod n displaystyle n seklinde belirtilir Bu numaralandirma sisteminde modul bir asal sayi oldugunda ve yalnizca o zaman sifir olmayan tum sayilara bolme islemi gerceklestirilebilir Mesela modul olarak 7 displaystyle 7 asal sayisinin secilmesi durumunda 3 displaystyle 3 sayisi ile bolme islemi gerceklestirilebilir 2 3 3mod7 displaystyle 2 3 equiv 3 bmod 7 zira her iki tarafin da 3 displaystyle 3 ile carpilmasi paydalardaki terimlerin sadelestirilmesi sonucunda 2 9mod7 displaystyle 2 equiv 9 bmod 7 gecerli denklemini ortaya cikarir Ancak bilesik bir modul olan 6 displaystyle 6 icin 3 displaystyle 3 ile bolme islemi gerceklestirilemez 2 3 xmod6 displaystyle 2 3 equiv x bmod 6 denkleminin gecerli bir cozumu bulunmamaktadir payda terimlerinin 3 displaystyle 3 ile carpilmasi denklemin sol tarafini 2 displaystyle 2 yaparken sag tarafini 0 displaystyle 0 ya da 3 displaystyle 3 olarak degistirir Soyut cebir terminolojisinde bolme isleminin yapilabilir olmasi bir asal sayinin modulu altinda moduler aritmetigin bir alan daha ozgul bir ifadeyle bir sonlu alan olusturdugu ancak diger modullerin yalnizca bir halka sagladigi fakat bir alan olusturmadigi anlamina gelir Asal sayilarla ilgili bircok teorem moduler aritmetik kullanilarak ifade edilebilir Mesela Fermat nin kucuk teoremi eger bir a 0 displaystyle a not equiv 0 mod p displaystyle p ise o zaman ap 1 1 displaystyle a p 1 equiv 1 mod p displaystyle p olacagini one surer Tum a displaystyle a degerleri icin bu toplamin gerceklestirilmesi su denklemi ortaya cikarir a 1p 1ap 1 p 1 1 1 modp displaystyle sum a 1 p 1 a p 1 equiv p 1 cdot 1 equiv 1 pmod p bu denklem p displaystyle p asal sayi oldugu durumlarda gecerlidir bu denklemin p displaystyle p sayisinin asal olmasi icin yeterli bir kosul oldugunu ileri surer gore p gt 1 displaystyle p gt 1 olan bir tam sayinin asal oldugu yalniz ve yalniz p 1 displaystyle p 1 faktoriyelinin p displaystyle p modunda 1 displaystyle 1 ile denk olmasi durumunda gecerlidir Bilesik bir sayi n r s displaystyle n r cdot s icin bu durum soz konusu olamaz zira bu sayinin carpanlarindan birisi hem n hem de n 1 displaystyle n 1 i bolebilecek ve bu nedenle n 1 1 modn displaystyle n 1 equiv 1 pmod n esitligi mumkun olmayacaktir p sel sayilar Bir tam sayinin np n displaystyle nu p n n displaystyle n sayisinin asal carpan ayristirmasinda p displaystyle p asalinin kac defa yer aldiginin gostergesidir Bu kavram tam sayilar icin gecerli oldugu gibi rasyonel sayilar icin de bir kesirin p displaystyle p sel duzeninin np m np n displaystyle nu p m nu p n olarak tanimlanmasiyla genisletilebilir Herhangi bir rasyonel sayi icin p displaystyle p sel mutlak deger q p displaystyle q p q p p np q displaystyle q p p nu p q seklinde ifade edilir Bir tam sayinin p displaystyle p sel mutlak degeri ile carpilmasi onun carpan ayristirmasindaki p displaystyle p asal carpanlarini ortadan kaldirir sadece diger asal sayilari birakir Tipki iki gercek sayi arasindaki uzakligin onlarin farklarinin mutlak degeri ile olculebilmesi gibi iki rasyonel sayi arasindaki uzaklik da onlarin p displaystyle p sel uzakligi yani farklarinin p displaystyle p sel mutlak degeri ile olculebilir Bu uzaklik tanimina gore iki sayi birbirine yakin kabul edilir kucuk bir uzakliga sahiptirler eger farklari p displaystyle p nin yuksek bir derecesi ile bolunebiliyorsa Rasyonel sayilarin ve onlarin uzakliklarinin ek sinirlayici degerler eklenerek gercek sayilar gibi bir olusturuldugu sekilde p displaystyle p sel uzaklik ile rasyonel sayilar farkli bir tam alan olan p displaystyle p sel sayilar olarak genisletilebilir Bu duzen mutlak deger ve bu kavramlardan turetilmis tam alan kavrami ve bu alanlarin alanin tamamen sirali bir toplamsal gruba duzen olarak da adlandirilan ozel eslemeler alani gercek sayilara carpan olarak esleyen norm olarak da bilinen ozel carpan eslemeler ve yerler verilen alanin yogun bir kume olarak yer aldigi tamamlamalar olarak adlandirilan yapilan genisletmeler kavramlarina genellestirilebilir Ornegin rasyonel sayilardan reel sayilara yapilan genisleme sayilar arasindaki uzakligin onlarin farklarinin alisilagelen mutlak degerine dayandigi bir yer olarak tanimlanabilir Bu baglamda bir toplamsal gruba yapilan karsilik gelen esleme mutlak degerin olurdu fakat bu bir degerlendirme icin gerekli olan tum ozellikleri saglamaz gore dogal bir denklik anlayisina kadar gercek sayilar ve p displaystyle p sel sayilar onlarin duzen ve mutlak degerleri ile rasyonel sayilar uzerinde tanimlanmis tek degerlendirmeler mutlak degerler ve yerlerdir rasyonel sayilar uzerindeki belirli sorunlarin onlarin her bir yerinden elde edilen cozumlerin birlestirilmesi yoluyla cozulebilmesini saglar bu durum asal sayilarin sayi teorisindeki kritik onemini bir kez daha altini cizer Halkalarda asal elemanlar Norm degeri 500 u asmayan Gauss asallari kompleks sayilar icerisinde ozellikle Gauss tam sayilari kapsaminda asallik ozelligi tasiyan ozel bir sayi alt kumesini ifade eder Bu baglamda norm vektor uzayindaki sifir vektoru haric her bir vektore kati bir sekilde pozitif bir uzunluk veya boyut atayan matematiksel bir fonksiyonu belirtir Toplama cikarma ve carpma islemlerinin belirlendigi bir cebirsel yapi olan degismeli halka matematiksel yapilarin bir cesididir Tam sayilar bu yapilarin bir ornegi olup tam sayilar icerisinde yer alan asal sayilar asal elemanlar ve indirgenemez elemanlar seklinde iki farkli yontemle genellenmistir R displaystyle R halkasindaki sifirdan farkli p displaystyle p elemani carpmaya gore tersi olmadiginda yani bir birim olmadiginda ve p displaystyle p elemani R displaystyle R nin iki elemaninin carpimi xy displaystyle xy i boldugunde x displaystyle x veya y displaystyle y elemanlarindan en az birini bolebilme ozelligini gosterdiginde asal olarak nitelendirilir Bir elemanin ne bir birim ne de iki birim olmayan elemanlarin carpimi olmamasi durumunda ise indirgenemez olarak tanimlanir Tam sayilar halkasinda asal ve indirgenemez elemanlar ayni kume icinde bulunur 11 7 5 3 2 2 3 5 7 11 displaystyle dots 11 7 5 3 2 2 3 5 7 11 dots Herhangi bir halkada butun asal elemanlar indirgenemez niteliktedir Bu durumun tersi genellikle dogru olmamakla birlikte benzersiz carpanlara ayirma alanlari icin gecerlidir Aritmetigin temel teoremi tanimi geregi benzersiz carpanlara ayirma alanlari cercevesinde gecerliligini korur Bu tur alanlarin bir ornegi olarak Z i displaystyle mathbb Z i uzerinden tanimlanan Gauss tam sayilari gosterilebilir Bu alan a displaystyle a ve b displaystyle b herhangi tam sayilar olmak uzere a bi displaystyle a bi formundaki karmasik sayilardan olusan bir halkayi ifade eder ve bu baglamda i displaystyle i hayali birimi temsil eder Bu yapidaki asal elemanlara Gauss asal sayilari adi verilir Tam sayilar arasinda asal kabul edilen her sayinin Gauss tam sayilari icinde asal olarak kabul edilmemesi mumkundur mesela 2 sayisi 1 i displaystyle 1 i ve 1 i displaystyle 1 i olmak uzere iki Gauss asalinin carpimi olarak ifade edilebilir 3 mod 4 ile kongruent olan rasyonel asallar Gauss tam sayilarinda asal olarak kabul edilirken 1 mod 4 ile kongruent olan rasyonel asallar asal olarak kabul edilmez Bu durum kaynaklanir bu teorem tek bir asal sayi p displaystyle p nin p x2 y2 displaystyle p x 2 y 2 formunda iki karenin toplami olarak ifade edilebilecegini ve bu sayede p displaystyle p 1 mod 4 iken p x iy x iy displaystyle p x iy x iy seklinde carpanlara ayrilabilecegini ongorur Asal idealler Butun halkalarin benzersiz carpanlara ayrilabilen bolgeler oldugu genellenemez Ornek olarak tam sayilar a displaystyle a ve b displaystyle b icin tanimlanan a b 5 displaystyle a b sqrt 5 sayilar halkasinda 21 displaystyle 21 sayisi 21 3 7 1 2 5 1 2 5 displaystyle 21 3 cdot 7 1 2 sqrt 5 1 2 sqrt 5 seklinde iki farkli carpanlara ayrilabilir ancak bu carpanlarin hicbiri daha ileri indirgenebilir durumda degildir bu da benzersiz carpanlara ayrim ozelliginin bulunmadigini gosterir Benzersiz carpanlara ayrim ozelliginin genis bir halkalar sinifina uygulanabilmesi icin sayi kavrami bir halkanin ogeleri alt kumesi olan ve bu ogelerin ciftlerinin tum toplamlari ile halka ogeleri ile olan tum carpimlarini barindiran bir ile yer degistirebilir Asal idealler bir asal ogenin urettigi bir asal ideal olmasi anlaminda asal ogeleri genellestiren ve degismeli cebir cebirsel sayilar teorisi ile cebirsel geometri alanlarinda onemli bir arac ve arastirma nesnesidir Tam sayilar halkasinin asal idealleri ise 0 2 3 5 7 11 seklinde siralanabilir Aritmetigin temel teoremi bir degismeli halka icerisindeki her idealin bir kesisimi olarak tanimlanabilecegini belirten ile genellestirilmistir bu ideal turleri asal kuvvetlerin uygun bir sekilde genellenmis halidir Bir halkanin spektrumu soz konusu halkanin asal ideallerini iceren noktalarla tanimlanan bir geometrik alandir Aritmetik geometri alani bu kavramdan onemli olcude yararlanmakta ve sayi teorisi ile geometri disiplinleri arasinda cesitli kavramsal paralellikler bulunmaktadir Mesela bir alana genisletme islemi sonucu asal ideallerin faktorizasyonu veya dalgalanmasi gibi cebirsel sayi teorisinin temel problemleri geometride dalgalanma fenomeni ile benzer ozellikler gosterir Tam sayilar uzerine kurulu sayi teorisi problemlerinin cozumunde bu kavramlar etkili olabilir Kuadratik sayi alanlarinin tam sayilar halkasindaki asal idealler tam sayi asal sayilari uzerinde kare koklerin varligini ifade eden kuadratik karsiliklilik teoreminin ispatlanmasinda kullanilabilmektedir Fermat nin Son Teoremi ni ispatlama cabalarinin ilk asamalari siklotomik tam sayilarda benzersiz carpanlara ayrilmanin basarisiz olmasi ile iliskilendirilen tam sayi asal sayilari olan duzenli asallarin Kummer tarafindan literature kazandirilmasina yol acmistir Cebirsel bir sayi alaninda kac adet tam sayi asal sayisinin birden fazla asal idealin urunu seklinde faktorize oldugu meselesi ile calisilmistir Bu teorem siklotomik tam sayilar baglaminda uygulandiginda aritmetik ilerlemelerde yer alan asal sayilar hakkindaki Dirichlet teoremini ozel bir ornek olarak icermektedir Grup kurami Sonlu gruplar kuraminda bir asal sayinin pn displaystyle p n kuvvetinin bir grubun bolunebilmesi durumunda ilgili grubun pn displaystyle p n mertebesinde en az bir altgruba sahip oldugunu belirtir Lagrange teoremi uyarinca asal sayida bir mertebe ile tanimlanan her grup bir niteligindedir ve tarafindan mertebesi yalnizca iki farkli asal sayi ile bolunebilen her grup ozellik gosterir Hesaplamali yontemlerBu tarim aletinin icerisinde yer alan kucuk disli 13 dise sahiptir ki bu bir asal sayidir ortada yer alan disli ise 21 dise sahiptir ve bu 13 ile goreceli olarak asaldir Genel anlamda sayi teorisi ve ozellikle asal sayilar uzerine yapilan calismalar uzun bir sure boyunca saf matematigin matematik disinda herhangi bir uygulamasi olmayan kanonik bir ornegi olarak kabul edilmistir Bunun istisnasi disli carklarin asinmasini esit bir sekilde dagitabilmek amaciyla disli dislerinin asal sayilarla belirlenmesi uygulamasidir Bu baglamda Britanya dan matematikci G H Hardy gibi sayi teorisyenleri calismalarinin acik bir sekilde herhangi bir askeri amac tasimadigindan dolayi ovunc duymustur 1970 li yillarda asal sayilarin acik anahtarli sifreleme algoritmalari gelistirmek icin bir temel olarak kullanilabileceginin kamuoyuna duyurulmasiyla sayi teorisinin saflik vizyonu ciddi bir sekilde sarsilmistir Bu uygulamalar asal sayilarla hesaplama yapabilen algoritmalarin ve ozellikle de bir sayinin asal olup olmadigini belirlemeye yonelik yontemlerin yani kapsamli bir sekilde incelenmesini tesvik etmistir Buyuk sayilar icin kullanisli olmaktan uzak en temel asallik testi yontemi olan deneme bolme yontemi yavasligi sebebiyle elestirilmistir Modern asallik testlerinin bir kismi herhangi bir sayiya uygulanabilirken ozel turdeki sayilar icin daha verimli testler gelistirilmistir Cogunlukla asallik testleri sadece argumanin asal olup olmadigini belirlemekle sinirlidir Bilesik argumanlarin bir asal carpanini veya tum asal carpanlarini belirleyebilen rutinler carpanlara ayirma algoritmalari olarak tanimlanir Ayrica asal sayilar bilgisayar bilimlerinde anahtarli tablolarda ve sanki rastgele sayi ureteclerinde kullanim alani bulmaktadir Deneme bolme yontemi Bir tam sayinin asallik durumunun belirlenmesinde kullanilan en temel yontem olarak isimlendirilir Bu metod ilgili tam sayi n displaystyle n i 2 den baslayarak n displaystyle n in karekokune kadar olan her tam sayiya bolme islemi uygular Bu sayilardan herhangi biri tarafindan n displaystyle n duzgun bir sekilde bolunebilirse n displaystyle n bilesik olarak tanimlanir aksi halde asal olarak kabul edilir n displaystyle n in karekokunden buyuk tam sayilarin kontrol edilmesine gerek yoktur cunku n a b displaystyle n a cdot b oldugu durumda a displaystyle a ve b displaystyle b carpanlarindan biri her zaman n displaystyle n in karekokune esit veya ondan kucuktur Bu yontemin bir diger iyilestirmesi bu aralikta yalnizca asal sayilarin carpan olarak kontrol edilmesidir Ornek olarak 37 sayisinin asal olup olmadiginin belirlenmesi surecinde bu metod 2 den 37 displaystyle sqrt 37 degerine kadar olan asal sayilar yani 2 3 ve 5 sayilari ile bolme islemi gerceklestirir Yapilan her bolme islemi sifirdan farkli bir kalan ile sonuclandigi icin 37 sayisi asal olarak tanimlanir Bu metodun tanimi basit olmakla birlikte buyuk tam sayilarin asallik testi icin uygulanabilirligi sinirlidir zira bu tam sayilarin basamak sayisina bagli olarak yurutulen testlerin sayisi ustel bir artis gostermektedir Bununla birlikte bolucu buyuklugu uzerinde karekokten daha az bir sinir belirlenerek kullanilan deneme bolme yontemi daha karmasik yontemlere basvurulmadan once kucuk carpanlara sahip bilesik sayilari hizla belirlemek amaciyla bu suzgecten gecen sayilar uzerinde hala tercih edilmektedir Kalbur yontemleri Eratosten kalburu baslangicta tum sayilarin isaretsiz gri oldugu bir durumla ise koyulur Ardindan tekrarlanan islemlerle ilk isaretsiz sayiyi tespit eder bu sayiyi asal olarak isaretler koyu renkler ve bu sayinin karesi ile bu sayidan sonra gelen tum katlarini bilesik olarak isaretler daha soluk renkler 2 kirmizi 3 yesil 5 mavi ve 7 sari sayilarinin katlarinin isaretlenmesinin ardindan tablonun karekokune kadar olan tum asallar ele alinmis ve isaretlenmemis kalan sayilar 11 13 vb asal olarak nitelendirilir magenta Bilgisayarlarin var olmadigi donemlerde verilen bir sinir degere kadar tum asallarin ya da asal carpanlastirmalarin listelendigi matematiksel tablolar yaygin bicimde basilmaktaydi Asal sayilarin listesinin elde edilmesinde kullanilan en kadim yontem Eratosten kalburu olarak isimlendirilir Bu yontemin optimize edilmis bir cesidini gosteren animasyon metodun uygulanisini gorsellestirir Ayni problem icin daha asimptotik acidan daha verimli bir baska kalbur yontemi olarak belirlenmistir Ileri duzey matematikte elek teorisi benzeri metodlar diger problemlerin cozumunde de kullanilmaktadir Asallik testi ile asalligin kanitlanmasi Bir n displaystyle n sayisinin asal olup olmadigini belirlemek amaciyla kullanilan en gelismis modern testlerden bazilari yanlis bir sonuc uretme ihtimali olan olasiliksal veya Monte Carlo algoritmalaridir Ornegin bir p displaystyle p sayisi icin uygulamasinda 2 displaystyle 2 ile p 2 displaystyle p 2 arasindan rastgele secilen bir a displaystyle a sayisi uzerinden a p 1 2 1 displaystyle a p 1 2 pm 1 ifadesinin p displaystyle p tarafindan bolunebilirligi araciligiyla denetlenir Bu durumda algoritma pozitif yanit verir aksi takdirde negatif yanit verir p displaystyle p sayisi gercekten asal ise algoritma her zaman pozitif yanit verir fakat p displaystyle p bilesik bir sayi ise pozitif yanit verme olasiligi en fazla 1 2 negatif yanit verme olasiligi ise en az 1 2 dir Bu deneyin ayni sayi uzerinde n displaystyle n defa yinelenmesi halinde bir bilesik sayinin her seferinde bu deneyden basariyla gecme ihtimali en cok 1 2n displaystyle 1 2 n olarak belirlenir Deneylerin sayisi arttikca bu ihtimal ussel olarak azaldigindan yinelenen deneyi gecen bir sayinin asal olduguna iliskin yuksek bir guven seviyesi fakat kesin bir kanit degil elde edilir Diger taraftan eger deney en az bir kere dahi basarisizlikla sonuclanirsa bu durumda soz konusu sayinin mutlaka bilesik oldugu kesinlesir Bu sekilde bir testi gecmeyi basaran bilesik sayilara Ing pseudoprime adi verilir Diger taraftan bazi algoritmalarin sonuclarinin daima dogru olacagina dair bir garanti bulunmaktadir Bu durumun bir ornegi deneme bolme yontemidir Kesin dogru cikti saglayan algoritmalar gibi deterministik rasgele olmayan algoritmalari ve algoritmanin nihai yanitini etkilemeyen rastgele secimler yapan ornegin bazi cesitlerindeki gibi kapsar Elips egri metodu bir sayinin asalligi konusunda bir karara vardiginda kolaylikla dogrulanabilir bir temin eder Pratik uygulamalarda garantili dogruluk saglayan asallik testleri icinde elips egri asallik testi en hizli olanidir ancak bu testin calisma zamani analizi kati ispatlara degil dayanir Matematiksel olarak zaman karmasikligi ispatlanmis mevcut olmakla birlikte uygulamada elips egri asalligini kanitlamadan daha yavas isler Bu metodlar rastgele sayilar uretilip test edilerek ve asal olan bir sayi bulunana dek buyuk rastgele asal sayilar uretmek icin kullanilabilir bu surecte bir hizli olasiliksal test garantili dogruluk saglayan bir algoritma ile kalan sayilarin asalliginin dogrulanmasindan once cogu bilesik sayiyi cabucak elemine etme islevi gorur Asagida sunulan tablo mevcut testlerden secilmis olanlari siralamaktadir Bu testlerin calisma zamanlari incelenmek uzere olan sayiyi temsil eden n displaystyle n ve olasiliksal algoritmalar icin gerceklestirilen testlerin sayisini ifade eden k displaystyle k ile iliskilendirilmistir Ek olarak e displaystyle varepsilon keyfi olarak belirlenebilen kucuk bir pozitif degeri simgeler ve log belirli bir tabana atifta bulunmaksizin logaritmayi isaret eder Buyuk O gosterimi her bir zaman kisitinin boyutsuz birimlerden zaman birimlerine cevrilebilmesi icin bir sabit faktor ile carpilmasi gerektigini belirtir bu faktor algoritmanin uygulandigi bilgisayarin turu gibi uygulama ayrintilarina baglidir fakat n displaystyle n ve k displaystyle k girdi parametrelerine bagli olmaz Test Gelistirildigi yil Tip Calisma suresi Notlar Kaynaklar2002 deterministik O log n 6 e displaystyle O log n 6 varepsilon 1986 Las Vegas O log n 4 e displaystyle O log n 4 varepsilon sezgisel olarak1980 Monte Carlo O log n 2 e displaystyle O log n 2 varepsilon 1980 Monte Carlo O k log n 2 e displaystyle O k log n 2 varepsilon hata olasiligi 4 k displaystyle 4 k 1977 Monte Carlo O k log n 2 e displaystyle O k log n 2 varepsilon hata olasiligi 2 k displaystyle 2 k Ozel amacli algoritmalar ve en buyuk bilinen asal sayi Bahse konu testlerin yani sira ozgun bicimdeki bazi sayilarin asallik durumu daha hizli bir metodoloji kullanilarak test edilebilir Ornek olarak bir Mersenne sayisinin iki nin bir kuvvetinden bir az olan asal olup olmadigini deterministik bir yaklasimla Miller Rabin testinin tek bir yinelemesi kadar surede tespit edebilmektedir Bu sebepten oturu 1992 yilindan itibaren Aralik 2018 2018 12 itibariyla sayi surekli olarak bir Mersenne asali olagelmistir Mersenne asallarinin sonsuz oldugu varsayilmaktadir Asagidaki tablo cesitli kategorilerde tespit edilmis en buyuk asal sayilari icermektedir Bu asal sayilarin bir kismi dagitik hesaplama yontemiyle kesfedilmistir 2009 senesinde en az on milyon rakam iceren bir asal sayiyi ilk defa bulma basarisi gosteren projesi yuz bin Amerikan dolari mukafatina layik gorulmustur Electronic Frontier Foundation yuz milyon ve bir milyar rakam barindiran asal sayilar icin sirasiyla yuz elli bin ve iki yuz elli bin dolar odul sunmaktadir Tip Asal sayi Basamak sayisi Tarih Kasif282 589 933 1 24 862 048 Aralik 7 2018 Patrick Laroche 10 223 231 172 165 1 9 383 761 Ekim 31 2016 Peter Szabolcs 208 003 1 1 015 843 Temmuz 2016 Sou Fukui1 098 133 1 476 311 Mart 2012 James P Burt Ikiz asallar 2 996 863 034 895 21 290 000 1 388 342 Eylul 2016 Tom Greer Asal carpanlara ayirma Bir bilesik tam sayi olan n displaystyle n icin onun bir veya tum asal carpanlarini tespit etme islemi n displaystyle n sayisinin carpanlara ayrilmasi olarak isimlendirilir Bu surec asalligin sinanmasindan bariz bir sekilde daha zor bir hal almaktadir ve bircok carpanlara ayrilma algoritmasi tanimlanmis olmasina ragmen bunlar en hizli asallik testi metodlarina kiyasla daha yavas calismaktadirlar Deneme bolunmesi ve gibi yontemler n displaystyle n sayisinin oldukca kucuk carpanlarini kesfetmek amaciyla kullanilabilir ve n displaystyle n sayisinin az buyuklukte carpanlari varsa yontemi etkili olabilmektedir Carpanlarinin buyuklugunden bagimsiz olarak herhangi bir buyuklukteki sayilar icin uygulanabilir yontemler arasinda ve metodlari yer almaktadir Asallik testlerinde oldugu gibi girdinin ozgul bir yapida olmasini zorunlu kilan carpanlara ayrilma algoritmalari da mevcuttur bunlar arasinda bulunmaktadir Aralik 2019 itibariyla genel amacli bir algoritmayla carpanlarina ayrilmis en buyuk sayi 240 ondalik basamaga 795 bit sahip dir ve bu iki buyuk asal sayinin carpimindan meydana gelmektedir Shor algoritmasi herhangi bir tam sayinin carpanlarina ayristirilmasini bir kuantum bilgisayar uzerinde polinomik sayida islem adimi ile gerceklestirebilir Bununla birlikte gunumuz teknolojisi soz konusu algoritmayi sadece minimal buyuklukteki sayilar uzerinde uygulayabilmektedir Ekim 2012 2012 10 itibariyla bir kuantum bilgisayarinda Shor algoritmasini kullanarak carpanlarina ayrilan en buyuk sayi 21 olarak kaydedilmistir Diger bilgisayimsal uygulamalar Cok sayida acik anahtarli sifreleme algoritmasi ornegin RSA ve Diffie Hellman anahtar degisimi gibi buyuk asal sayilar uzerine kuruludur 2048 bit asal sayilar yaygin kullanimdadir RSA algoritmasi iki buyuk sayinin carpimi olan x displaystyle x ve y displaystyle y sayilarinin carpimini yapmanin bu carpim xy displaystyle xy sonucu bilindiginde x displaystyle x ve y displaystyle y aralarinda aralarinda asal kabul edilen sayilarini bulmaktan cok daha kolay yani daha etkili oldugu onermesine dayalidir Diffie Hellman anahtar degisim mekanizmasi abmodc displaystyle a b bmod c seklinde ifade edilen isleminin etkili algoritmalarla gerceklestirilebilmesi gercegine bagliyken bu islemin tersi olan ayrik logaritma probleminin zor oldugu kabul edilmektedir Asal sayilar hash tablolarinda yaygin olarak tercih edilmektedir Carter ve Wegman tarafindan gelistirilen orijinal metodolojisi buyuk asal sayilar cinsinden mod alinarak secilen rastgele dogrusal fonksiyonlar araciligiyla hash fonksiyonularin hesaplanmasina dayanir Carter ve Wegman bu metodu yine buyuk asal sayilar cinsinden mod alinarak daha yuksek dereceden polinomlar kullanilarak genellestirerek iyilestirmistir Asal sayilar hash fonksiyonlarinin yani sira yontemine dayali hash tablolarinda sorgulama dizilerinin tablonun tamamini kapsayacak sekilde tasarlanmasini saglamak amaciyla hash tablo boyutlarinin belirlenmesinde de kullanilmaktadir Cesitli yontemleri asal sayilarin matematigine dayalidir Mesela Uluslararasi Standart Kitap Numarasi icin kullanilan saglama toplamlari asal bir sayi olan 11 e gore sayinin mod alinarak hesaplanmasi yoluyla tanimlanmaktadir 11 sayisinin asal bir degere sahip olmasi bu metodun hem tek basamakli hatalari hem de yan yana bulunan rakamlarin yer degistirme hatalarini tespit edebilmesine olanak tanir gibi baska bir kontrol toplami yontemi 216 displaystyle 2 16 degerinden kucuk olan en buyuk asal sayi 65521 e gore moduler aritmetik kullanmaktadir Asal sayilar ayrica ve gibi cesitli rastgele sayi ureteci modellerinde temel birer bilesen olarak kullanilmaktadir Diger uygulamalarAsal sayilar sayilar teorisinin yani sira soyut cebir ve temel geometri gibi matematigin diger disiplinlerinde de genis uygulama alanlarina sahiptir Mesela asal sayilar kadar noktanin iki boyutlu bir duzlem uzerine oyle bir yerlestirilmesi mumkundur ki bu noktalardan herhangi ucu duz bir cizgi uzerinde konumlanmaz Ing No three in line problem ya da bu noktalar arasindan secilen her uclu tarafindan olusturulan ucgenlerin sahip olmasi saglanabilir Ayrica bir polinomun indirgenemezliginin polinomun katsayilarinin bir asal sayi ve bu asal sayinin karesi ile bolunebilirligine dayanarak tespit edilmesini saglayan indirgenemez polinomlar uzerine bir test olarak one cikmaktadir Baglanmis iki asal dugumun toplami Asal sayi kavrami matematigin cesitli dallarinda farkli sekillerde genellestirilmis kadar onemlidir Genellikle asal kelimesi uygun bir anlamda minimaliteyi veya ayristirilamazligi belirtir Ornegin verilen bir alanin hem 0 hem de 1 i iceren en kucuk alt alandir Bu rasyonel sayilar alani veya asal sayida elemana sahip bir sonlu alandir isminin kaynagi budur Siklikla asal kelimesi kullanilarak bir nesnenin esasen benzersiz bir sekilde asal bilesenlerine ayristirilabilecegi anlami da amaclanir Ornegin dugum teorisinde bir iki onemsiz dugumun olarak yazilamayacak sekilde ayristirilamaz bir dugumdur Herhangi bir dugum asal dugumlerin bagli toplami olarak benzersiz bir sekilde ifade edilebilir bu ture baska bir ornektir Matematik ve bilgisayar bilimlerinin otesinde asal sayilarin kuantum mekanigine potansiyel iliskileri mevcut olup kultur ve edebiyat alanlarinda metaforik ogeler olarak degerlendirilmislerdir Bunun yani sira evrimsel biyoloji alaninda agustos bocegilerinin yasam evrelerinin izah edilmesinde asal sayilar basvurulan bir arac olmustur Yapilandirilabilir cokgenler ve cokgen bolumlendirmeleri Cetvel ve pergel yardimiyla duzenli bir besgenin olusturulmasi Bu islem yalnizca 5 sayisinin bir Fermat asali olmasi sayesinde gerceklestirilebilmektedir Fermat asalilari Fk 22k 1 displaystyle F k 2 2 k 1 seklinde tanimlanan ve k displaystyle k negatif olmayan bir tam sayi oldugunda gecerli olan asal sayilar olarak bilinir Bu terim her biri bu formdaki sayilarin asal oldugunu varsayan Pierre de Fermat ya atfen kullanilir Ilk bes Fermat sayisi 3 5 17 257 ve 65 537 asal niteliktedir fakat F5 displaystyle F 5 ve 2017 yili itibariyla incelenmis diger tum Fermat sayilari bilesik olarak siniflandirilmistir Bir duzenli n displaystyle n genin cetvel ve pergel kullanilarak cizilebilir olmasi ancak ve ancak n displaystyle n in tek asal faktorleri var ise birbirinden farkli Fermat asallari oldugunda mumkundur Benzer sekilde bir duzenli n displaystyle n genin cizimi n displaystyle n sayisinin asal carpanlarinin 2 veya 3 un herhangi bir sayida tekrari ile birlikte farkli iceren potansiyel olarak bos bir kume olmasi durumunda cetvel pergel ve bir kullanilarak gerceklestirilebilir Herhangi bir disbukey cokgenin n displaystyle n sayisi bir asal sayinin kuvveti oldugunda esit alan ve esit cevreye sahip n displaystyle n adet daha kucuk disbukey cokgenlere ayrilmasi mumkundur fakat n displaystyle n degerinin asal sayinin kuvveti disindaki diger degerleri icin bu durumun gecerli olup olmadigi bilinmemektedir Kuantum mekanigi ve Freeman Dyson in 1970 lerde gerceklestirdikleri calismalarin onculugunde matematik ve fizik alaninda uzmanlar Riemann zeta fonksiyonunun kokleri ile kuantum sistemlerinin enerji duzeyleri arasinda bir baglanti olabilecegini one surmuslerdir Ayni zamanda asal sayilar ve gibi matematiksel yapilar vasitasiyla alaninda da kritik bir oneme sahiptir Biyoloji cinsi agustos bocegilerinin uyguladigi evrimsel strateji asal sayilardan faydalanmaktadir Bu bocek turleri omurlerinin buyuk bir kismini yer altinda larva formunda gecirmekte yalnizca 7 13 veya 17 yil gibi asal sayilari temsil eden sureler sonunda erginlesip yeryuzune cikarlar ciftlesirler ve birkac hafta icinde yasam dongulerini tamamlayarak olurler Bu asal sayilara dayanan ureme dongusu surelerinin avcilarin bu dongulere uyum saglamasini engellemek amaciyla evrildigi biyologlar tarafindan one surulmektedir Ote yandan bambu bitkilerinde gorulen ciceklenme periyotlarinin carpanlarinda yalnizca kucuk asal sayilar iceren oldugu varsayilmaktadir Bu durum bambunun ciceklenme zamanlamalarinin kucuk asal sayilara dayali bir duzenlilik gosterdigini isaret etmektedir Sanat ve edebiyat Asal sayilar pek cok sanatci ve yazar uzerinde derin bir etkiye sahip olmustur Fransiz besteci Olivier Messiaen dogal olaylar i referans alarak ametrik muzik uretmede asal sayilari kullanmistir 1935 ve 1949 50 eserlerinde birbirinden farkli asal sayilara dayanan motif uzunluklarini simultane kullanimiyla ongorulemez ritimler olusturmustur Neumes rythmiques adli ucuncu etutte 41 43 47 ve 53 gibi asal sayilar yer almaktadir Messiaen bu kompozisyon teknigini doganin hareketlerinden serbest ve esitsiz sureclerde meydana gelen hareketlerden ilham alarak gelistirdigini belirtmistir Bilim kurgu eseri Contact ta Carl Sagan uzaylilarla iletisim kurma surecinde iki boyutlu goruntu duzlemlerinin olusturulmasinda asal sayilarin carpanlarina ayrilmasinin potansiyel bir yontem olarak kullanilabilecegini ileri surmustur Bu dusunceyi ilk defa 1975 yilinda Amerikan astronom Frank Drake ile informal bir sekilde ortaya koymustur adli eserde yazar Mark Haddon ana karakterin Asperger sendromuna sahip matematiksel yetenegi yuksek bir genc zihinsel durumunu yansitmak amaciyla hikayenin bolumlerini ardisik asal sayilar kullanarak duzenlemistir nun adli romaninda asal sayilar yalnizlik ve tecrit duygularini sembolize etmek icin kullanilmis asal sayilar tam sayilar icerisinde yabanci olarak tasvir edilmistir Asal oturanlarAritmetigin temel teoremi 1 den buyuk tum tam sayilarin asal sayilarin carpimlari seklinde yazilabilecegini ustelik yazimin da asal carpanlarin degisik siralanmasi haric yalniz bir sekilde teklik olacagini soyler Bir sayinin asal carpanlara ayrilmasinda bir asal sayi birden fazla tekrar edebilir Dolayisiyla asal sayilar dogal sayilarin temel insa taslari olarak dusunulebilir Ornegin 23244 u su sekilde asal carpanlarina ayirabiliriz 23244 22 3 13 149 ve 23244 un diger asal carpanlara ayiris sekilleri yukaridaki ile aynidir fakat asal sayilarin siralamasi degisik olabilir Buyuk sayilar icin degisik asal carpanlara ayirma algoritmalari vardir Ikiz asallar Aralarindaki fark iki olan asal sayilar hakkindaki ikiz asallar konjekturu Ornegin 3 5 5 7 11 13 17 19 29 31 41 43 59 61 71 73 101 103 107 109 Chen asallari Bir a asal sayisi a 2 biciminde yazildiginda asal ya da yari asal oluyorsa a degeri Chen asali olarak adlandirilmaktadir Ikiz asallarda kucuk sayi ayni zamanda Chen asalidir Asal ornekler a 5 displaystyle Rightarrow 5 2 7 a 11 displaystyle Rightarrow 11 2 13 Yari asal ornekler a 2 displaystyle Rightarrow 2 2 4 displaystyle land 2 2 4 a 7 displaystyle Rightarrow 7 2 9 displaystyle land 3 3 9Mersenne asallari Bir a dogal sayisi 2a 1 biciminde yazildiginda hesaplanan deger Mersenne sayisi asal oluyorsa ayni zamanda Mersenne asali olarak adlandirilmaktadir Mersenne asallari hesaplanirken a sayisi da asal olarak alinmaktadir Ancak a sayisinin asal olarak alindigi bazi durumlarda bilesik Mersenne sayilari hesaplanabilmektedir Bilinen en buyuk asal sayi olan 282 589 933 1 Mersenne asalidir Mersenne asallari 22 1 3 25 1 31 Bilesik Mersenne sayilari 211 1 2047Goldbach hipotezi Asal sayilarla ilgili Goldbach hipotezi dogru gozukmesine ragmen halen ispatlanamamistir Her cift 2 haric sayi iki asal sayinin toplami midir Ornegin 4 2 2 6 3 3 8 3 5 10 3 7 12 5 7 14 3 11 16 3 13 18 5 13 20 3 17 22 3 19 24 5 19 26 7 19 28 5 23 30 7 23 32 3 29 34 5 29 36 7 29Ayrica bakinizAsal sayilarin listesi Eratosten kalburu Mersenne asalllari Fermat nin kucuk teoremi Oklid teoremi Goldbach hipotezi Ikiz asallar Yari asal Lasa sayiSayi sistemleri Karmasik C displaystyle mathbb C Reel R displaystyle mathbb R Rasyonel Q displaystyle mathbb Q Tam sayi Z displaystyle mathbb Z Dogal N displaystyle mathbb N Sifir 0Bir 1Asal sayilarBilesik sayilarNegatif tam sayilarKesir Devirli ondalik sayiIrrasyonel Cebirsel irrasyonelAskinSanalNot listesi Aime Ferrier in 1951 de bir mekanik hesap makinesi ile kesfettigi 44 basamakli asal sayi elektronik bilgisayarlarin yardimi olmadan kesfedilen en buyuk asal sayi olma ozelligini korumaktadir a b Beiler e gore sayi teorisi uzmani asal sayilarla siki bir iliski icinde bulunan herhangi bir pratik uygulama ile kendilerini kirletmedikleri icin ozellikle benimsemistir Katz ise asal sayilarin dagilimi konusundaki calismalariyla taninan Edmund Landau nun matematigin pratik uygulamalarina derin bir antipati duydugunu ve bu sebeple pratik faydalari onceden kanitlanmis olan geometri gibi alanlardan uzak durdugunu ifade etmektedir Bu testte 1 displaystyle pm 1 terimi a displaystyle a sayisinin varsayilan asal p displaystyle p sayisina modulo bir kare olmasi durumunda negatif aksi halde pozitiftir Genel olarak p displaystyle p asal olmayan degerler icin 1 displaystyle pm 1 terimi negatiflestirilmis Jacobi sembolu olarak tanimlanir ve bu kullanilarak hesaplanabilir Aslinda elips egri asalligini kanitlama analizlerinin buyuk bir kismi algoritmaya giris olarak sunulan sayinin onceden bir olasiliksal testten gectigi varsayimina dayanmaktadir n displaystyle n parametresine bagli olarak tanimlanan fonksiyonu n displaystyle n seklinde ifade edilir ve bu fonksiyon n displaystyle n degerine kadar olan tum asal sayilarin carpimini hesaplar terimi ise n 1 displaystyle n pm 1 bicimlerinden herhangi birine uygun olan asal sayilari ifade etmek icin kullanilir Kaynakca a b GIMPS Project Discovers Largest Known Prime Number 282 589 933 1 Mersenne Research Inc 21 Aralik 2018 8 Eylul 2023 tarihinde kaynagindan Erisim tarihi 21 Aralik 2018 Arsivlenmis kopya 12 Nisan 2020 tarihinde kaynagindan Erisim tarihi 7 Nisan 2020 1997 The Mathematical Olympiad Handbook An Introduction to Problem Solving Based on the First 32 British Mathematical Olympiads 1965 1996 Oxford University Press s 26 ISBN 978 0 19 850105 3 Henderson Anne 2014 Dyslexia Dyscalculia and Mathematics A practical guide 2 bas Routledge s 62 ISBN 978 1 136 63662 2 1960 The Giant Golden Book of Mathematics Exploring the World of Numbers and Space Golden Press s 16 OCLC 6975809 Leff Lawrence S 2000 Math Workbook for the SAT I Barron s Educational Series s 360 ISBN 978 0 7641 0768 9 1978 Section 2 Unique factorization Elementary number theory 2 bas W H Freeman and Co s 10 ISBN 978 0 7167 0076 0 Sierpinski Waclaw 1988 Elementary Theory of Numbers North Holland Mathematical Library 31 2 bas Elsevier s 113 ISBN 978 0 08 096019 7 a b 2004 The great prime number record races 51 4 414 416 MR 2039814 1997 Numbers and Geometry Undergraduate Texts in Mathematics Springer s 9 ISBN 978 0 387 98289 2 Sierpinski Waclaw 1964 A Selection of Problems in the Theory of Numbers New York Macmillan s 40 MR 0170843 2000 Notations and Conventions Elementary Methods in Number Theory Graduate Texts in Mathematics 195 Springer ISBN 978 0 387 22738 2 MR 1732941 Faticoni Theodore G 2012 The Mathematics of Infinity A Guide to Great Ideas Pure and Applied Mathematics A Wiley Series of Texts Monographs and Tracts 111 2 2yayinci John Wiley amp Sons bas s 44 ISBN 978 1 118 24382 4 Bruins Evert Marie review in Mathematical Reviews of Gillings R J 1974 The recto of the Rhind Mathematical Papyrus How did the ancient Egyptian scribe prepare it Archive for History of Exact Sciences 12 4 ss 291 298 doi 10 1007 BF01307175 MR 0497458 2010 Mathematics and Its History Undergraduate Texts in Mathematics 3 bas Springer s 40 ISBN 978 1 4419 6052 8 a b Aralik 1982 The Search for Prime Numbers Scientific American 247 6 ss 136 147 Bibcode 1982SciAm 247f 136P doi 10 1038 scientificamerican1282 136 JSTOR 24966751 a b c d Mollin Richard A 2002 A brief history of factoring and primality testing B C before computers Mathematics Magazine 75 1 ss 18 29 doi 10 2307 3219180 JSTOR 3219180 MR 2107288 O Connor John J Robertson Edmund F Abu Ali al Hasan ibn al Haytham MacTutor Matematik Tarihi arsivi Sandifer 2007 8 Fermat s Little Theorem November 2003 p 45 Sandifer C Edward 2014 How Euler Did Even More Mathematical Association of America s 42 ISBN 978 0 88385 584 3 Koshy Thomas 2002 Elementary Number Theory with Applications Academic Press s 369 ISBN 978 0 12 421171 1 Yuan Wang 2002 Goldbach Conjecture Series In Pure Mathematics 2 2cilt 4 bas World Scientific s 21 ISBN 978 981 4487 52 8 Narkiewicz Wladyslaw 2000 1 2 Sum of Reciprocals of Primes The Development of Prime Number Theory From Euclid to Hardy and Littlewood Springer Monographs in Mathematics Springer s 11 ISBN 978 3 540 66289 1 Tchebychev P 1852 Asal Sayilar Uzerine Bir Bellek PDF Journal de mathematiques pures et appliquees Serie 1 Fransizca 366 390 6 Kasim 2022 tarihinde kaynagindan PDF Erisim tarihi 8 Mart 2024 Postulatin kaniti 371 382 Ayrica bkz Memoires de l Academie Imperiale des Sciences de St Petersbourg cilt 7 sayfa 15 33 1854 2000 Asal sayi teoreminin yuzyillik tarihi Bambah R P Dumir V C Hans Gill R J Ed Sayi Teorisi Matematikte Egilimler Basel Birkhauser ss 1 14 MR 1764793 1976 7 Aritmetik Dizilerdeki Asallar Uzerine Dirichlet Teoremi Analitik Sayi Teorisi ne Giris New York Heidelberg Springer Verlag ss 146 156 MR 0434929 Chabert Jean Luc 2012 A History of Algorithms From the Pebble to the Microchip Springer s 261 ISBN 978 3 642 18192 4 Rosen Kenneth H 2000 Theorem 9 20 Proth s Primality Test Elementary Number Theory and Its Applications 4 4yayinci Addison Wesley bas s 342 ISBN 978 0 201 87073 2 Cooper S Barry Hodges Andrew 2016 The Once and Future Turing Cambridge University Press ss 37 38 ISBN 978 1 107 01083 3 Rosen 2000 s 245 Beiler Albert H 1999 1966 Recreations in the Theory of Numbers The Queen of Mathematics Entertains Dover s 2 ISBN 978 0 486 21096 4 OCLC 444171535 Katz Shaul 2004 Berlin roots Zionist incarnation the ethos of pure mathematics and the beginnings of the Einstein Institute of Mathematics at the Hebrew University of Jerusalem Science in Context 17 1 2 ss 199 234 doi 10 1017 S0269889704000092 MR 2089305 a b c Kraft James S Washington Lawrence C 2014 Elementary Number Theory Textbooks in mathematics CRC Press s 7 ISBN 978 1 4987 0269 0 Bauer Craig P 2013 Secret History The Story of Cryptology Discrete Mathematics and Its Applications CRC Press s 468 ISBN 978 1 4665 6186 1 1991 Old and New Unsolved Problems in Plane Geometry and Number Theory Dolciani mathematical expositions 11 Cambridge University Press s 224 ISBN 978 0 88385 315 3 a b Neale 2017 ss 18 47 a b Caldwell Chris K Reddick Angela Xiong Yeng Keller Wilfrid 2012 The history of the primality of one a selection of sources 15 9 Article 12 9 8 MR 3005523 12 Nisan 2018 tarihinde kaynagindan Erisim tarihi 8 Mart 2024 For a selection of quotes from and about the ancient Greek positions on the status of 1 and 2 see in particular pp 3 4 For the Islamic mathematicians see p 6 Taran Leonardo 1981 Speusippus of Athens A Critical Study With a Collection of the Related Texts and Commentary Philosophia Antiqua A Series of Monographs on Ancient Philosophy 39 Brill ss 35 38 ISBN 978 90 04 06505 5 Caldwell et al 2012 pp 7 13 See in particular the entries for Stevin Brancker Wallis and Prestet Caldwell et al 2012 s 15 a b c Caldwell Chris K Xiong Yeng 2012 What is the smallest prime PDF
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans