Fizik disiplininde, kuvvet bir cismin hızını değiştirmeye zorlayabilen, yani ivmelenmeye sebebiyet verebilen - hızında veya yönünde bir değişiklik oluşturabilen - bir etki olarak tanımlanır, bu etki diğer kuvvetlerle dengelenmediği müddetçe geçerlidir. Itme ya da çekme gibi günlük kullanımda yer alan eylemler, kuvvet konsepti ile matematiksel bir netliğe ulaşır. Kuvvetin hem hem de yönü önemli olduğundan, kuvvet bir vektör olarak ifade edilir. Kuvvet için SI birimi, newton (N)'dur ve genellikle F simgesi ile gösterilir.
Kuvvet | |
 | |
Kuvvetler, bir nesneye uygulanan itme veya çekme olarak tanımlanabilir. Bu kuvvetler, yerçekimi, manyetizma veya bir kütlenin ivmelenmesine neden olabilecek herhangi bir fenomen kaynaklı olabilir. | |
| Yaygın sembol(ler): | , F, F |
| temel SI birimlerinden türetimi: | kg·m·s−2 |
| SI nicelik boyutu: | wikidata |
| SI birimi: | newton (N) |
| Diğer niceliklerden türetimi: | F = ma |

Klasik mekanikte, kuvvet merkezî bir öneme sahiptir. Kuvvet, sabit bir kütleye sahip bir cisme etki eden kuvvetin, cismin kütlesi ile bu cismin maruz kaldığı ivmenin çarpımına eşit olduğunu ifade eden Newton'un hareket yasaları dahilinde ele alınır. Klasik mekanikte yaygın olarak rastlanan kuvvet çeşitleri elastiklik, sürtünme kuvveti, temas ya da "normal" kuvvetler ve kütleçekim kuvvetleridir. Kuvvetin dönüsel karşılığı olan tork, bir cismin dönüş hızındaki değişimleri meydana getirir. Genişlemiş bir cismin her bir parçası genellikle yanındaki parçalara kuvvet uygular; bu kuvvetlerin cisim içindeki dağılımı içsel mekanik gerilimi oluşturur. Denge halinde, bu gerilimler cismin herhangi bir ivmelenme göstermemesi için kuvvetlerin birbirini dengelemesiyle sonuçlanır. Bunlar dengede olmadığında, katı materyallerde veya sıvılarda akışa yol açabilirler.
Modern fizik alanında, görelilik ve kuantum mekaniği dahil olmak üzere, hareket yasaları, kuvvetin temel kaynağı olarak temel etkileşimlere dayanarak yeniden düzenlenmiştir. Ancak, klasik mekaniğin sunduğu kuvvet anlayışı, pratik amaçlar için faydalıdır.
Kavram gelişimi
Antik dönemdeki filozoflar, hareketsiz ve hareket halindeki cisimler ile basit makinelerin analizinde kuvvet konseptini temel almışlar, fakat Aristo ve Arşimet gibi düşünürler, kuvvetin doğru anlaşılması noktasında hatalar yapmışlardır. Bu durum, kısmen, sürtünme kuvvetinin zaman zaman açık olmayan niteliğinin ve doğal hareketin içeriğine dair yetersiz görüşlerin eksik kavranmasından kaynaklanmaktadır. Temel yanılgılardan biri, sabit bir hızla hareketin devam etmesi için kuvvetin zorunlu olduğu inancıdır. Hareket ve kuvvet üzerine önceki yanlış kavrayışlar, Galileo Galilei ve Isaac Newton tarafından zamanla düzeltilmiştir. Matematiksel derinliği ile Newton, iki yüz yıl boyunca daha da geliştirilmeyecek olan hareket yasalarını ortaya koymuştur.
19. yüzyılın başlarında, Einstein ışık hızına yaklaşan hızlara sahip nesneler üzerindeki kuvvetlerin davranışını doğru bir şekilde tahmin eden ve yerçekimi ile eylemsizlik kuvvetleri hakkında bilgiler sunan bir görelilik kuramı ortaya koymuştur. Kuantum mekaniğine ilişkin çağdaş anlayışlar ve ışık hızına yakın hızlara parçacıkları ivmelendirebilen teknolojik gelişmeler ışığında, parçacık fiziği alanı, atomlardan daha küçük parçacıklar arasındaki kuvvetleri açıklamak amacıyla bir Standart Model tasarlamıştır. Standart Model, kuvvetlerin yayılımı ve emilimi süreçlerinde temel bir rol oynayan ayar bozonları adı verilen değişim parçacıklarının varlığını öngörmektedir. Bilinen yalnızca dört ana etkileşim vardır: Güç sıralamasına göre azalan şekilde bunlar; güçlü, elektromanyetik, zayıf ve kütleçekimsel kuvvetlerdir.:((2–10)):79 1970'ler ve 1980'lerde gerçekleştirilen Yüksek enerji parçacık fiziği gözlemleri, zayıf ve elektromanyetik kuvvetlerin, daha temel bir elektrozayıf etkileşimin tezahürleri olduğunu onaylamıştır.
Newton öncesi kavramlar

Antik dönemden itibaren, kuvvet kavramı, basit makinelerin her birinin işleyişi için temel bir unsur olarak tanınmıştır. Basit bir makine tarafından sağlanan , daha az kuvvet kullanılmasını sağlarken, bu kuvvetin aynı miktar iş için daha büyük bir mesafe boyunca etki etmesine olanak tanımıştır. Kuvvetlerin karakteristiklerinin detaylı incelenmesi, özellikle sıvılar içerisinde bulunan yüzdürme kuvvetinin formülasyonunu yapmasıyla tanınan Arşimet'in eserlerinde zirveye ulaşmıştır.
Aristo, Aristo kozmolojisinde kuvvet kavramına dair felsefi bir muhakeme sunmuştur. Onun perspektifine göre, yer küresi, içerisindeki farklı "doğal konumlar"da istirahat eden dört temel elementten oluşmaktadır. Aristo, öncelikle toprak ve su elementlerinden meydana gelen, Dünya üzerinde hareketsiz durumda bulunan cisimlerin, yer yüzeyinde kendi doğal konumlarında olduklarını ve müdahale edilmezlerse bu durumun devam edeceğini savunmuştur. Cisimlerin kendi "doğal konumlarını" bulma yönündeki doğuştan gelen eğilimi (örn., ağır cisimlerin düşme eğilimi) ile doğal olmayan veya zoraki hareketi; yani, bir kuvvetin devamlı olarak uygulanmasını gerektiren hareketi ayırt etmiştir. Bu kuram, nesnelerin hareket şekillerine dair günlük gözlemlere dayanarak, bir arabanın hareket etmekte kalması için gerekli olan sürekli kuvvet uygulaması gibi, atkı (İng. projectile) örneğinde okların uçuşu gibi davranışları açıklama noktasında kavramsal zorluklarla karşılaşmıştır. Bir okçu, uçuşun başlangıcında oku harekete geçirir ve daha sonra, üzerinde algılanabilir bir etkin nedenin bulunmadığı halde, ok hava boyunca ilerler. Aristo bu problemi teşhis etmiş ve atkının yolu boyunca itilen havanın, atımı hedefine taşıdığını önermiştir. Bu açıklama, hareketin devamını sağlayabilmek için hava gibi kesintisiz bir ortamın varlığını gerektirmektedir.
Aristo fiziği, 6. yüzyıl itibarıyla eleştirilere maruz kalmıştır, ancak bu eksiklikler, Galileo Galilei’nin 17. yüzyılda gerçekleştirdiği çalışmalara değin giderilememiştir. Galileo, Aristoteles'in hareket teorisine meydan okuyan bir deney gerçekleştirmiştir. Bu deneyde, bir eğim boyunca yuvarlanan taş ve top mermilerinin, bu cisimlerin kütlesinden bağımsız olarak yer çekimi ile hızlandığını ve bir kuvvet, örneğin sürtünme, uygulanmadıkça hızlarını muhafaza ettiklerini ortaya koymuştur. Galileo’nun, hareketi sürdürmek yerine değiştirmek için kuvvet gerektiği tezi, , René Descartes ve Pierre Gassendi tarafından ileriye taşınmış ve Newton fiziğinin temel prensiplerinden biri haline gelmiştir.
17. yüzyılın başlarında, Newton'un Principia eserinden önce, "kuvvet" (Latince vis) terimi, bir noktanın ivmelenmesi gibi, çok sayıda fiziksel ve fiziksel olmayan fenomene uygulanagelmiştir. Bir nokta kütlesinin ve onun hızının karesinin çarpımı, Leibniz tarafından "canlı kuvvet" (Latince vis viva) olarak isimlendirilmiştir. Günümüz kuvvet kavramı, Newton'ın tanımladığı "ivmelenme kuvveti" (Latince vis motrix) ile örtüşmektedir.
Newton mekaniği
Isaac Newton, atalet ve kuvvet gibi kavramlar yardımıyla tüm cisimlerin hareketlerini tanımlamıştır. Newton, 1687 yılında, kendi alanındaki en önemli eseri Philosophiæ Naturalis Principia Mathematica'ı yayımlar. Bu çalışmasında Newton, günümüz fizik biliminin kuvvetlerin açıklanmasına yön veren üç temel hareket yasasını belirlemiştir. Newton'un yasalarının matematiksel ifadeleri, yeni matematiksel metodolojilerle birlikte zaman içinde gelişim göstermiştir.
Birinci yasa
Newton'un ilk hareket yasasına göre, hareketsizlik halinde bulunan bir cismin doğal eğilimi hareketsizliğe devam etmek, sabit hız ile doğrusal bir trajektorya üzerinde hareket eden bir cismin ise bu sabit hızda ve doğrultuda hareketine devam etme eğilimindedir. Bu sonuç, fizik kanunlarının tüm eylemsiz gözlemciler açısından değişmez olduğunu belirten ilkeye dayanarak, ilk durumdan türetilmiştir; i.e., hareket halinde olduklarını hissetmeyen tüm gözlemciler. Bir cisimle eş zamanlı hareket eden bir gözlemci, bu cismin hareketsizlik halinde olduğunu algılayacaktır. Bu bağlamda, cismin doğal eğilimi, bu gözlemciye göre hareketsizlik durumunu korumaktır, bu da sabit hızla ve doğrusal bir yolda hareket ettiğini gözlemleyen birisinin, cismin bu hareket tarzını sürdüreceğini görmesini sağlar.:1–7

İkinci yasa
İlk yasaya göre, düz bir çizgi boyunca sabit bir hızla gerçekleşen hareket için herhangi bir sebep zorunlu değildir. Asıl olarak, hareketin değişimi bir sebebi gerektirmekte olup, Newton'un ikinci yasası kuvvet ile hareketin değişim süreci arasındaki nicel ilişkiyi açıklamaktadır. (Newton'un ikinci yasasına) göre, bir cisim üzerine etki eden net kuvvet, cismin zaman içindeki momentum değişiminin eşdeğerdir. Cismin kütlesi sabit kaldığında, bu yasa, cismin ivmesinin, üzerine etki eden net kuvvete doğrudan orantılı olduğunu, bu kuvvetin yönünde olduğunu ve cismin kütlesi ile ters orantılı olduğunu öngörmektedir.(ss204–207)
Newton'un ikinci yasasının çağdaş bir ifadesi, bir vektör denklemi şeklindedir:
bu denklemede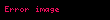 , sistemin momentumunu ve
, sistemin momentumunu ve  , net ((vektörlerin toplamı)) kuvveti temsil eder.(s399) Bir cisim dengede ise, tanımsal olarak net kuvvet sıfırdır (bununla birlikte, dengelenmiş kuvvetler mevcut olabilir). İkinci yasa, bir nesne üzerinde dengelenmemiş bir kuvvetin varlığında, nesnenin momentumunun zaman içinde değişeceğini öne sürer.
, net ((vektörlerin toplamı)) kuvveti temsil eder.(s399) Bir cisim dengede ise, tanımsal olarak net kuvvet sıfırdır (bununla birlikte, dengelenmiş kuvvetler mevcut olabilir). İkinci yasa, bir nesne üzerinde dengelenmemiş bir kuvvetin varlığında, nesnenin momentumunun zaman içinde değişeceğini öne sürer.Mühendislikte sık karşılaşılan durumlarda, bir sistemin kütlesi değişmez kabul edilir ve bu, ikinci yasayı basit bir cebirsel forma indirger. Momentumun tanımı gereğince,

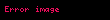 , hızı ifade eder.:((9-1,9-2)) Newton'un ikinci yasası, (sabit kütleli) bir sistemde uygulandığında, m sabit kabul edilerek türev işlemcinin dışına çıkarılabilir. Böylece denklem şu şekle dönüşür:
, hızı ifade eder.:((9-1,9-2)) Newton'un ikinci yasası, (sabit kütleli) bir sistemde uygulandığında, m sabit kabul edilerek türev işlemcinin dışına çıkarılabilir. Böylece denklem şu şekle dönüşür: 
Üçüncü yasa
Bir cismin başka bir cisme kuvvet uygulaması durumunda, ikinci cisim de derhal ilk cisme karşılık olarak eşit büyüklükte ve ters yönde bir kuvvet uygular. Vektörel ifadeyle, eğer 

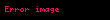
 etki ve
etki ve  olarak adlandırılır.
olarak adlandırılır. Newton'un üçüncü yasası, farklı cisimlerin varlığının sonucunda ortaya çıkan kuvvetlerin analizinde simetri prensibinin uygulanmasının bir ürünüdür. Bu yasa, tüm kuvvetlerin, çeşitli cisimler arasındaki karşılıklı etkileşimler olduğunu belirtir; dolayısıyla tek yönlü bir kuvvet veya yalnız bir cisim üzerine etki eden bir kuvvetin mümkün olmadığını ifade eder.
Cisim-1 ve cisim-2'den meydana gelen bir sistemde, bu nesneler arasındaki karşılıklı etkileşimler sonucu meydana gelen sistem üzerindeki net kuvvetin sıfır olduğu görülür:
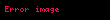
Newton'un ikinci ve üçüncü yasalarının bir araya getirilmesi ile, bir sistem içerisindeki doğrusal momentumun, herhangi bir kapalı sistem içinde korunduğu ispatlanabilir. İki parçacıklı bir sistemde, 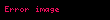


"Kuvvet" tanımlaması
Birtakım ders kitapları, Newton'un ikinci yasasını kuvvetin tanımı olarak benimser. Bununla birlikte, sabit bir kütle 
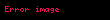
Kuvvetlerin birleştirilmesi

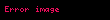 ile
ile  'nin aritmetik toplamı,
'nin aritmetik toplamı,  vektörünü oluşturur.
vektörünü oluşturur.Kuvvetler, belirlenen bir yön içerisinde etki ederler ve uygulanan itme veya çekmenin şiddetine bağlı olarak değişen sahiptirler. Bu karakteristikler sayesinde kuvvetler, "" olarak tanımlanır. Bu durum, yön içermeyen fiziksel niceliklerden (skaler nicelikler olarak ifade edilir) farklı matematiksel prensiplerin kuvvetler için geçerli olduğunu gösterir. İki kuvvetin aynı cisim üzerine etkisini değerlendirirken, sonuçları hesaplayabilmek adına her iki kuvvetin de büyüklüğünü ve yönünü bilmenin zorunlu olduğu örnekler mevcuttur. Eğer her bir kuvvet için bu bilgilerin her ikisi de sağlanmamışsa, durum muğlaktır.:197
Tarih boyunca, kuvvetlerin nicel incelemesi ilk kez, birbiriyle zıt yönde etki ederek birbirlerini iptal eden birkaç kuvvetin var olduğu durumlarında gerçekleştirilmiştir. Bu deneyler, kuvvetlerin toplanabilir vektörel nicelikler olduğunu; ayrıca büyüklük ve yön gibi özelliklere sahip olduklarını vurgulayan temel özellikleri sergilemektedir. Bir nokta parçacık üzerinde iki farklı kuvvetin etki etmesi durumunda, bileşke (İng. resultant) olarak ifade edilen sonuç kuvvet (bu aynı zamanda net kuvvet olarak da bilinir), paralelkenar yasasına dayanan vektör toplama yöntemiyle hesaplanabilir: bir paralelkenarın iki kenarı ile temsil edilen vektörlerin toplanması, paralelkenarın çaprazı ile eş büyüklük ve yön özelliklerine sahip eşdeğer bir sonuç vektörü üretir. Bu bileşke vektörünün büyüklüğü, ilgili iki kuvvetin büyüklüklerinin farkı ile toplamı arasında değişiklik gösterir, bu değişim onların etki hatları arasındaki açı ile doğrudan ilişkilidir.(ch.12)

Serbest cisim diyagramları, bir sisteme etki eden kuvvetlerin izlenmesinde kullanışlı bir araç olarak değerlendirilebilir. İdeal bir durumda, bu diyagramlar net kuvvetin grafik vektör toplamı yoluyla tespit edilebilmesi için, kuvvet vektörlerinin açılarını ve görelili büyüklüklerini muhafaza edecek şekilde çizilir.
Kuvvetler, toplama işlemine ek olarak, birbirine dik açılar oluşturacak şekilde bağımsız bileşenlere de çözümlenebilirler. Bu bağlamda, kuzeydoğu yönünde etki eden bir yatay kuvvet, kuzeye ve doğuya doğru etki eden iki farklı kuvvete ayrıştırılabilir. Bu bileşenlerin vektörel toplamı, ilk kuvvetin elde edilmesini sağlar. Kuvvet vektörlerinin bir dizi taban vektör bileşenlerine çözümlenmesi, büyüklük ve yön kullanarak yapılandan daha matematiksel olarak düzenli bir metod sunar.Dik bileşenler söz konusu olduğunda, vektörlerin toplamının bileşenleri, vektörlerin bileşenlerinin skaler toplamları ile tayin edilir. Dik bileşenler, birbirlerine dik açıda etki eden kuvvetlerin birbirlerinin büyüklüğü veya yönü üzerinde etkisi olmadığından birbirlerinden bağımsızdır. En uygun matematiksel çözümü sağlayacak taban vektörler setini seçme işlemi, hangi taban vektörlerinin matematiği en kolaylaştıracağını düşünülerek gerçekleştirilir. Bir kuvvetle aynı yönde olan bir taban vektörü seçmek tercih edilir, çünkü bu durumda söz konusu kuvvet yalnızca tek bir sıfır olmayan bileşene sahip olacaktır. Dik kuvvet vektörleri, diğer iki bileşene dik açıda olan üçüncü bir bileşeni içerebilir şekilde üç boyutlu olabilir.(ch.12)
Denge
Bir nesne üzerine etki eden bütün kuvvetlerin dengelenmesi durumunda, bu nesnenin denge durumunda olduğu ifade edilir.:566 Bu bağlamda, denge; bir nokta parçacığa etki eden toplam kuvvetin sıfıra eşit olduğu (yani, tüm kuvvetlerin vektör toplamının sıfır olması durumu) zaman gerçekleşir. Genişletilmiş bir nesne durumunda ise, net torkun da sıfır olması şarttır. Bir cisim, belirli bir referans çerçevesi bağlamında statik denge içinde ise eğer, o cisim dinlenme durumundadır ve ivmelenmemektedir; öte yandan, dinamik denge içindeki bir cisim, sürekli bir hızla ve düz bir hat üzerinde hareket etmektedir, yani, hareket halindedir ancak ivmelenmemektedir. Bir gözlemci tarafından statik denge olarak algılanan durum, başka bir gözlemci tarafından dinamik denge olarak değerlendirilebilir ve bunun tersi de mümkündür.:566
Statik Denge
Klasik mekanik biliminin ortaya çıkışının çok öncesinde, statik denge kavramı iyi bir şekilde kavranmıştır. Dinlenme halindeki cisimlerin üzerine etki eden net kuvvetin sıfır olduğu bilinmektedir.
Statik denge durumunun en temel örneği, iki kuvvetin büyüklük açısından birbirine eşit olması ancak yön bakımından birbirine zıt olması halidir. Bir örnek olarak, düz bir yüzeyde bulunan bir cisim, yerçekimi kuvveti nedeniyle Dünya'nın merkezine doğru aşağı yönde çekilir. Bu süreçte, yüzeyden cisime, aşağı yönde uygulanan kuvvete eş değerde bir yukarı yönlü kuvvet (bu kuvvete normal kuvvet adı verilir) uygulanır. Bu senaryo, net bir kuvvetin oluşmamasını ve sonuç olarak herhangi bir ivmelenmenin meydana gelmemesini sağlar.
Sürtünme özelliği gösteren bir yüzey üzerinde konumlanmış bir cisme karşı itme kuvveti uygulanması, uygulanan kuvvetin cisim ile masa yüzeyi arasında oluşan kuvveti tarafından nötralize edilmesi nedeniyle cismin pozisyon değiştirmemesi sonucunu doğurabilir. Hareketin olmadığı bir senaryoda, statik sürtünme kuvveti uygulanan kuvvetle kesin bir denge oluşturur ve bu durum herhangi bir ivmelenme meydana gelmemesini sağlar. Statik sürtünme kuvveti, yüzey ile cisim arasındaki temasın karakteristiklerine bağlı olarak tanımlanan bir üst sınır değerine kadar, uygulanan kuvvete bağlı olarak artış veya azalış gösterir.
İki kuvvet arasındaki statik dengenin sağlanması, terazi ve gibi basit ölçüm araçları aracılığıyla kuvvetlerin ölçümünde en sık başvurulan yöntemdir. Bir örnek olarak, dikey bir el kantarı üzerine asılan bir nesne, nesne üzerine etki eden yerçekimi kuvveti ile bu kuvvete karşı gelen ve nesnenin ağırlığına denk gelen "yayın tepki kuvveti" arasında bir denge durumu yaşar. Bu tip araçların kullanımı ile, sabit yoğunluk değerine sahip nesneler için yerçekimi kuvvetinin hacme doğru orantılı olduğu gibi bazı niceliksel kuvvet yasaları keşfedilmiştir (bu durum, standart ağırlık tanımlarının binlerce yıl boyunca geniş çapta kullanılmasına olanak sağlamıştır); kaldırma kuvveti için Arşimet prensibi, kaldıraç üzerine Arşimet'in analizi; gaz basıncı için Boyle yasası ve yaylar için Hooke yasası gibi. Bu teoriler, Isaac Newton'ın hareket yasalarını ortaya koymasından önce formüle edilmiş ve deneysel olarak teyit edilmiştir.(ch.12)
Dinamik Denge

Dinamik denge, Aristotelesçi fizikteki bazı ön kabullerin gözlem ve mantıksal çerçevede tutarsızlıklar içerdiğini tespit eden Galileo tarafından ilk defa ortaya konulmuştur. Galileo, basit hız ekleme işleminin, "mutlak " anlayışının geçersiz olduğunu gösterdiğini fark etmiştir. Galileo'ya göre, sabit bir hızda hareket, dinlenme hali ile birebir eşdeğerdir. Bu durum, cisimlerin kütleye sahip olmaları nedeniyle doğal olarak bir "doğal dinlenme hali"ne yönlendirdiği Aristoteles'in düşüncesinin aksini işaret eder. Basit deneyler, Galileo'nun sabit hız ve dinlenme halinin eşdeğerliği üzerine kurulu anlayışının doğruluğunu kanıtlamıştır. Mesela, sabit bir hızla ilerleyen bir geminin karga yuvasından bırakılan bir top mermisinin, Aristoteles fizik anlayışına göre, gemi hareket ederken doğrudan aşağı düşmesi beklenirken, deneyin gerçekleştirilmesi sonucunda top mermisi her zaman, sanki gemi ile birlikte seyahat etmesi gerektiğini bilircesine, direğin dibine düşer. Düşerken top mermisi üzerine herhangi bir ileri yatay kuvvet uygulanmadığından, elde kalan tek sonuç, top mermisinin düşerken gemi ile aynı hızda hareket etmeye devam ettiğidir. Dolayısıyla, top mermisinin sabit ileri hızda hareketini devam ettirmek için herhangi bir ek kuvvete ihtiyaç duyulmamaktadır.
Ayrıca, sabit bir hızda ilerleyen her cismin, net kuvvetin sıfır olduğu bir durumda olduğu kabul edilmelidir. Dinamik denge, bir cisim üzerindeki tüm kuvvetlerin birbirini dengelemesine rağmen cismin hala sabit bir hızda hareket ettiği durumdur. Dinamik dengenin basit bir örneği, kinetik sürtünmenin olduğu bir yüzey üzerinde sabit hızla ilerleme durumunda görülür. Bu tür bir senaryoda, hareket yönünde bir kuvvet uygulanırken, kinetik sürtünme kuvveti uygulanan kuvvete tam bir karşıtlık gösterir. Bu, net kuvvetin sıfır olmasına neden olur; ancak, cisim sıfır olmayan bir hızla harekete başladığı için, sıfır olmayan bir hızla hareket etmeye devam eder. Aristoteles, bu hareketi uygulanan kuvvet tarafından meydana getirildiği şeklinde yanlış bir yorumda bulunmuştur. Kinetik sürtünme dikkate alındığında, sabit hız hareketini tetikleyen herhangi bir net kuvvetin olmadığı açıkça görülmektedir.(ch.12)
Klasik mekanikte kuvvet örnekleri
Bazı kuvvetler, temel kuvvetlerin doğrudan sonucu olarak ortaya çıkar. Bu gibi durumlar kapsamında, fiziksel kavrayışı derinleştirmek amacıyla idealize edilmiş modellerden yararlanılabilir. Örnek olarak, her katı nesne, katı cisim modeli çerçevesinde ele alınır.
Yerçekimi

Isaac Newton’un çalışmalarıyla birlikte evrensel bir etki olarak kabul gören yer çekimi kavramı günümüzde anlaşılmıştır. Newton öncesinde, cisimlerin Dünya yönünde düşme eğilimleri, gök cisimlerinin hareketleriyle ilişkilendirilmemişti. Galileo, serbest düşüş halindeki cisimlerin ivmelenmelerinin sabit olduğunu ve cismin kütlesinden bağımsız bulunduğunu tespit ederek, düşen cisimlerin karakteristiklerini açıklamada kritik bir rol üstlenmiştir. Günümüzde, Dünya'nın yüzeyine doğru olan yer çekimi kaynaklı ivme, genellikle 


Serbest düşüş halindeki bir cisim için, karşıt bir kuvvet olmadığından, cismin üzerindeki net kuvvet onun ağırlığına eşittir. Serbest düşüşte olmayan cisimlerde ise yerçekimi kuvveti, bu cisimlerin desteklerince uygulanan tepki kuvvetleri ile dengelenir. Örneğin, yere basan bir birey, yere temas eden kısmı üzerine uygulanan normal kuvvet (tepki kuvveti) nedeniyle, aşağı yönlü ağırlığının tam olarak dengelediği bir durumda, net kuvvet sıfırdır.(ch.12)
Newton'un yerçekimi kuramına yaptığı katkı, Aristoteles tarafından sürekli hareket halinde olan doğal durumda bulunduğu düşünülen gök cisimlerinin hareketlerini, Dünya üzerinde gözlemlenen düşme hareketleriyle entegre etmekti. Newton, daha önceden Kepler'in gezegensel hareket yasaları ile açıklanmış olan gök cisimlerinin hareketlerini açıklayabilen bir yerçekimi yasası önerdi.
Newton, yerçekiminin etkilerinin uzak mesafelerde farklı biçimlerde gözlenebileceğini keşfetmiştir. Bu bağlamda, Newton, Ay'ın Dünya çevresindeki ivmesinin, yerçekiminin azalan bir ters kare kanununa bağlı olarak aynı yerçekimi kuvveti ile açıklanabileceğini tespit etmiştir. Bununla birlikte, bir cismin yerçekimiyle ivmelenmesinin, onu çeken diğer cismin kütlesi ile doğru orantılı olduğu sonucuna varmıştır. Bu düşüncelerin bütünleştirilmesiyle, Dünya'nın kütlesi (
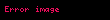
 , Dünya'nın merkezinden dışa doğru yönlendirilen birim vektör olarak tanımlanmaktadır.
, Dünya'nın merkezinden dışa doğru yönlendirilen birim vektör olarak tanımlanmaktadır.Bu denklemde, yerçekiminin göreli şiddetini açıklamak amacıyla, boyutsal bir sabit olan 


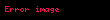
 iki cismin kütle merkezleri arasındaki uzaklığı ifade eder,
iki cismin kütle merkezleri arasındaki uzaklığı ifade eder,  ise birinci cismin merkezinden ikinci cismin merkezine doğru yönlendirilmiş birim vektördür.
ise birinci cismin merkezinden ikinci cismin merkezine doğru yönlendirilmiş birim vektördür.Bu denklem, 20. yüzyıl başlarına dek güneş sistemi içerisindeki hareketlerin açıklanmasında temel bir referans noktası olarak kabul edilmiştir. Bu dönem boyunca, bir gezegen, ay, kuyruklu yıldız veya asteroitin yörüngesinde birden çok gök cisminin etkileri sonucunda meydana gelen sapmaları hesaplamak üzere ileri düzey pertürbasyon teorisi teknikleri ortaya konmuştur. Bu formalizm, matematikçilere, henüz gözlemlenmemiş olan gezegen Neptün'ün varlığını öngörebilmeleri için gereken yeterli doğruluğu sağlamıştır.
Elektromanyetik
Elektrostatik kuvvet, 1784 yılında Coulomb tarafından, iki yük arasında özgün bir şekilde mevcut olan bir kuvvet olarak açıklanmıştır.:519 Elektrostatik kuvvetin karakteristikleri, ters kare kanunu ile orantılı değişim göstermesi, radial yön ile belirlenmesi, hem çekici hem de itici etkileşim sunması (doğuştan özelliği taşıması), yüklü nesnelerin kütlesinden bağımsız olması ve süperpozisyon ilkesine uygun davranması şeklindedir. Coulomb yasası, bu gözlemlerin tümünü bütünleştiren kesin ve net bir ifadedir.
Günümüz matematikçileri ve fizikçileri, uzaydaki herhangi bir noktada bir elektrik yüküne etki eden elektrostatik kuvveti saptamak amacıyla elektrik alanı kavramını yararlı bulmuşlardır. Elektrik alanı, uzayın herhangi bir noktasında varsayımsal bir "" yerleştirilerek ve Coulomb yasası kullanılarak elektrostatik kuvvetin hesaplanması esasına dayanır.:((4-6–4-8)) Elektrik alanı, şu formülle ifade edilir:

 , hipotetik test yükünün büyüklüğünü temsil eder. Aynı bağlamda, manyetik alan kavramı, mıknatısların uzaktan birbirlerini nasıl etkileyebileceğini açıklamak üzere geliştirilmiştir. Lorentz kuvvet yasası, elektrik ve manyetik alanların bir yüklü cisme uyguladığı kuvveti şu şekilde formüle eder: burada
, hipotetik test yükünün büyüklüğünü temsil eder. Aynı bağlamda, manyetik alan kavramı, mıknatısların uzaktan birbirlerini nasıl etkileyebileceğini açıklamak üzere geliştirilmiştir. Lorentz kuvvet yasası, elektrik ve manyetik alanların bir yüklü cisme uyguladığı kuvveti şu şekilde formüle eder: burada  , elektromanyetik kuvvet;
, elektromanyetik kuvvet;  , cismin bulunduğu yerdeki elektrik alanı;
, cismin bulunduğu yerdeki elektrik alanı;  , manyetik alan; ve
, manyetik alan; ve 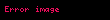 , parçacığın hızını gösterir. Lorentz kuvvetine manyetik katkı, hız vektörünün manyetik alan ile çapraz çarpımı şeklinde gerçekleşir.:482
, parçacığın hızını gösterir. Lorentz kuvvetine manyetik katkı, hız vektörünün manyetik alan ile çapraz çarpımı şeklinde gerçekleşir.:482Elektrik ve manyetik alanların kökenleri, James Clerk Maxwell'ın 1864 yılında önceki teorileri bir araya getirerek 20 adet skaler denklem şeklinde ifade etmesi ve bu denklemlerin daha sonra Oliver Heaviside ve Josiah Willard Gibbs tarafından dört vektör denklemine dönüştürülmesi ile tam anlamıyla açıklığa kavuşturulmuştur. "Maxwell denklemleri", bu alanların kaynaklarını duran ve hareket eden yükler olarak ve aynı zamanda alanların birbirleriyle olan etkileşimlerini kapsamlı bir şekilde tanımlar. Maxwell'in bu çalışmaları, elektrik ve manyetik alanların ışık hızında seyahat eden bir dalga ile "kendi kendine oluşabilen" yapılar olduğunu ortaya çıkarmıştır. Bu bulgu, elektromanyetik teori ve optik alanlarını bütünleştirmiş ve elektromanyetik spektrumun eksiksiz bir açıklamasına doğrudan katkıda bulunmuştur.
Normal

Temas halindeki nesneler arasındaki doğrudan etki eden kuvvete normal kuvvet adı verilir. Bu kuvvet, nesneler arasındaki ara yüzeye dik olarak sistemin toplam kuvvetinin bir bileşenini oluşturur.:264 Normal kuvvet, Newton'un üçüncü kanunu ile sıkı bir bağlantı içindedir. Örneğin, normal kuvvet masaların ve yer döşemelerinin yapısal dayanıklılığından sorumlu olup, aynı zamanda harici bir kuvvet katı bir cisim üzerine uygulandığında bu kuvvete tepki olarak ortaya çıkar. Normal kuvvetin uygulamada görülen bir örneği, sabit bir yüzeye çarpan bir cismin aldığı darbe kuvvetidir.(ch.12)
Sürtünme
Sürtünme, iki cismin birbirine göre hareketini engelleyen bir kuvvettir. Makroskobik düzeyde, sürtünme kuvveti, temas noktasında etki eden normal kuvvet ile doğrudan bir ilişkiye sahiptir. Sürtünme kuvvetleri, temel olarak iki farklı kategori altında incelenir: ve .:267
Statik sürtünme kuvveti (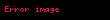
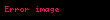
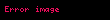
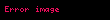
Kinetik sürtünme kuvveti (
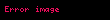
burada 
Gerilim
Gerilim kuvvetleri, modellemelerde kütle barındırmayan, sürtünmesiz, kopmaz ve esnemez özellikler gösteren ideal ipler kullanılarak tasarlanabilir. Bu tür ipler, ideal kasnaklar ile entegre edilebilir; bu kasnaklar, iplerin fiziksel yönelimlerini değiştirmelerine olanak tanır. İdeal ipler, gerilim kuvvetlerini eylem-tepki çifti olarak anında iletebilirler, böylece eğer iki obje ideal bir ip ile birbirine bağlanmışsa, birinci obje tarafından ip boyunca uygulanan herhangi bir kuvvet, otomatik olarak ikinci obje tarafından ip boyunca zıt yönde bir kuvvetle karşılanır.
Hareketli kasnakların kullanımıyla, aynı ipin aynı nesneye defalarca bağlanması yoluyla, yük üzerindeki gerilim kuvveti artırılabilir. Yüke etki eden her bir ip, ipteki gerilim kuvvetinin bir katını daha yüke uygular. Bu tür düzenekler, yükü hareket ettirmek için gereken ipin yer değiştiren uzunluğunda bir artışla orantılı olarak, önemli bir elde etmeyi mümkün kılar. Bu tandem etkiler, makinenin karmaşıklığına rağmen, yüke uygulanan işin değişmemesi nedeniyle mekanik enerjinin korunumu ile sonuçlanır.(ch.12)
Yay

Temel bir elastik kuvvet, bir yayın kendi doğal boyuna geri dönmesini sağlamaya yöneliktir. İdeal yay, kütle içermeyen, sürtünmesiz, kopmayan ve sınırsız esneyebilir olarak tanımlanır. Bu tür yaylar, yayın denge durumundan olan yer değiştirmeye bağlı olarak, daraldığında itme veya genişlediğinde çekme kuvveti uygular. Bu lineer ilişki, 1676'da Robert Hooke tarafından tanımlanmış ve Hooke yasası adıyla bilinir hale gelmiştir. Eğer 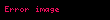
 , ilgili yayın özelliklerine göre belirlenen yay sabiti (veya kuvvet sabiti)dir. Eksi işaret, kuvvetin uygulanan yüke zıt yönde etki gösterme eğilimini temsil eder.(ch.12)
, ilgili yayın özelliklerine göre belirlenen yay sabiti (veya kuvvet sabiti)dir. Eksi işaret, kuvvetin uygulanan yüke zıt yönde etki gösterme eğilimini temsil eder.(ch.12)Merkezcil
Düzgün dairesel hareket gerçekleştiren bir cisim için, cisim üzerinde etki eden net kuvvet aşağıdaki gibi ifade edilir:
burada cismin kütlesi,
cismin kütlesi,  cismin hızı,
cismin hızı,  ise cismin dairesel yoldaki merkeze olan uzaklığı ve
ise cismin dairesel yoldaki merkeze olan uzaklığı ve  merkezden dışarıya radial yönde gösteren birim vektör olarak tanımlanmıştır. Bu durum, cismin hissettiği net kuvvetin sürekli olarak eğri yolun merkezine doğru yönlendirildiğini gösterir. Bu tür kuvvetler, cismin hareketiyle ilişkili hız vektörüne dik olarak etkiler ve bu nedenle cismin hızının büyüklüğünü (hızın değeri) değiştirmez, yalnızca hız vektörünün yönünü değiştirir. Daha genel bir ifadeyle, bir cismi ivmelendiren net kuvvet, yola dik ve yola teğet olacak şekilde iki bileşene ayrılabilir. Bu, cismin hızını azaltarak veya artırarak ivmelenmesini sağlayan teğetsel kuvvetle birlikte, yön değişikliğini sağlayan radial (merkezcil) kuvveti içerir.(ch.12)
merkezden dışarıya radial yönde gösteren birim vektör olarak tanımlanmıştır. Bu durum, cismin hissettiği net kuvvetin sürekli olarak eğri yolun merkezine doğru yönlendirildiğini gösterir. Bu tür kuvvetler, cismin hareketiyle ilişkili hız vektörüne dik olarak etkiler ve bu nedenle cismin hızının büyüklüğünü (hızın değeri) değiştirmez, yalnızca hız vektörünün yönünü değiştirir. Daha genel bir ifadeyle, bir cismi ivmelendiren net kuvvet, yola dik ve yola teğet olacak şekilde iki bileşene ayrılabilir. Bu, cismin hızını azaltarak veya artırarak ivmelenmesini sağlayan teğetsel kuvvetle birlikte, yön değişikliğini sağlayan radial (merkezcil) kuvveti içerir.(ch.12)Süreklilik mekaniği

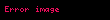 ), yerçekimi kuvveti (
), yerçekimi kuvveti ( ) ile büyüklük açısından eşitlendiğinde, cisim dinamik denge haline ulaşarak terminal hızına erişir.
) ile büyüklük açısından eşitlendiğinde, cisim dinamik denge haline ulaşarak terminal hızına erişir.Newton yasaları ve genel Newton mekaniği başlangıçta, idealize edilmiş nokta parçacıklar üzerindeki kuvvet etkileşimlerini açıklamak amacıyla ortaya konulmuştur, ancak bu durum üç boyutlu nesneleri doğrudan kapsamamaktadır. Gerçekte, maddenin genişlemiş bir yapısal formu vardır ve bir nesnenin belirli bir bölümüne etki eden kuvvetler, nesnenin diğer bölümlerini de etkileyebilir. Nesnelerdeki atomları bir arada tutan yapıların akışkanlık, büzülme, genişleme veya şekil değiştirme yeteneği olduğu durumlar için süreklilik mekaniği teorileri, kuvvetlerin malzemeler üzerindeki etkilerini tanımlar. Örneğin, genişlemiş akışkanlarda, basınç farkları, basınç gradyanları boyunca kuvvetlerin yönlendirilmesine yol açar:

 akışkan içindeki objenin hacmini ve
akışkan içindeki objenin hacmini ve  uzaydaki tüm noktalardaki basıncı tanımlayan skaler fonksiyonu ifade eder. Basınç gradyanları ve farklılıkları, yerçekimi alanlarında askıda kalan akışkanlar için yüzdürme kuvveti, atmosfer biliminde rüzgarlar ve aerodinamik ve uçuş ile ilişkili kaldırma kuvvetini tetikler.(ch.12)
uzaydaki tüm noktalardaki basıncı tanımlayan skaler fonksiyonu ifade eder. Basınç gradyanları ve farklılıkları, yerçekimi alanlarında askıda kalan akışkanlar için yüzdürme kuvveti, atmosfer biliminde rüzgarlar ve aerodinamik ve uçuş ile ilişkili kaldırma kuvvetini tetikler.(ch.12)ile bağlantılı olarak tanımlanan özgül bir kuvvet, akışkan direncidir: Bu, bir cismin viskozite nedeniyle akışkan bir ortamda hareket etmesine karşı koyan bir cisim kuvvetidir. Özellikle "Stokes sürüklemesi" durumunda, bu kuvvet hızın büyüklüğü ile yaklaşık olarak doğru orantılıdır ancak yön olarak tersine işler:
şu şekilde tanımlanır:, akışkanın fiziksel özellikleri ile nesnenin boyutlarına (genellikle kesit alanı) dayalı bir sabit değerdir ve
, nesnenin hız vektörünü ifade eder.(ch.12)
Süreklilik mekaniği çerçevesinde kuvvetler, belirli bir gerilim tensörü aracılığıyla ifade edilir. Bu tensör, genelde
formülü ile gösterilir, burada , gerilim tensörunun değerlendirildiği hacimdeki alakalı kesit alanını temsil eder. Bu kuramsal yapı, kesit alanına dik kuvvetlerle ilişkili basınç bileşenlerini (tensörün matris diyagonalleri) ve kesit alanına paralel kuvvetlerle ilişkili kayma bileşenlerini (off-diagonal elemanlar) kapsar. Gerilim tensörü, tüm deformasyon türlerini (gerilmeler) içeren kuvvetleri, çekme gerilimleri ve sıkıştırmaları da dahil olmak üzere, hesaplar.:133–134:((38-1–38-11))
, gerilim tensörunun değerlendirildiği hacimdeki alakalı kesit alanını temsil eder. Bu kuramsal yapı, kesit alanına dik kuvvetlerle ilişkili basınç bileşenlerini (tensörün matris diyagonalleri) ve kesit alanına paralel kuvvetlerle ilişkili kayma bileşenlerini (off-diagonal elemanlar) kapsar. Gerilim tensörü, tüm deformasyon türlerini (gerilmeler) içeren kuvvetleri, çekme gerilimleri ve sıkıştırmaları da dahil olmak üzere, hesaplar.:133–134:((38-1–38-11))Kurgusal kuvvetler
Belirli kuvvetler, çerçeve bağımlı olarak nitelendirilir; bu, Newton dışı (yani eylemsiz olmayan) referans çerçevelerinin benimsenmesi sonucu ortaya çıktıklarını ifade eder. Bu tür kuvvetlere örnek olarak merkezkaç kuvveti ve Coriolis kuvveti verilebilir. Bu kuvvetler, hızlanmayan referans çerçevelerinde mevcut olmadıkları için kurgusal olarak tanımlanır.(ch.12) Ayrıca, bu kuvvetlerin gerçek olmaması nedeniyle "sanki kuvvetler" (İng. pseudo forces) olarak da isimlendirilirler.:((12-11))
Genel görelilik kapsamında, yerçekimi kuvveti, uzayzamanın düz geometriden sapması durumlarında ortaya çıkan kurgusal bir kuvvet olarak değerlendirilir. Bu bağlamda, yerçekimi, klasik mekanikte ele alınan bir kuvvet olmaktan ziyade, görelilik teorisinde farklı bir yorumlama alanına girer ve uzayzamanın geometrisiyle ilişkili bir fenomen olarak incelenir.
Kuvvet temelli kavramlar
Döndürme ve Tork

Genişletilmiş cisimlerin dönüşünü tetikleyen kuvvetler, torklar ile bağlantılıdır. Matematiksel ifadeyle, bir kuvvetin 
 , kuvvetin uygulandığı noktanın referans noktasına göre pozisyon vektörünü temsil eder. Bu tanım, torkun büyüklüğünün ve yönünün, uygulama noktasının konumuna göre nasıl değişebileceğini matematiksel olarak açıklar.:497
, kuvvetin uygulandığı noktanın referans noktasına göre pozisyon vektörünü temsil eder. Bu tanım, torkun büyüklüğünün ve yönünün, uygulama noktasının konumuna göre nasıl değişebileceğini matematiksel olarak açıklar.:497Tork, kuvvetin dönüşsel karşılığıdır; benzer biçimde, açı , açısal hız hızın ve açısal momentum ise momentumun dönüşsel eşdeğerleridir. Newton'un birinci hareket yasası uyarınca, tüm cisimlerin dengesiz bir tork uygulanmadığı sürece açısal momentumlarını korumasını sağlayan dönüşsel atalet mevcuttur. Aynı şekilde, Newton'un ikinci hareket yasası, rijit bir cismin anlık açısal ivmesinin hesaplanması için benzer bir formülasyon sağlar:

, cismin eylemsizlik momentini,
, cismin açısal ivmesini temsil eder.:502
Bu, kütlenin dönüşsel karşılığı olan eylemsizlik momentinin tanımını oluşturur. Mekaniğin daha gelişmiş teorilerinde, belirli bir zaman dilimi boyunca gerçekleşen dönüşlerin açıklandığı durumlarda, eylemsizlik momenti, ile ikame edilmelidir. Bu tensör, uygun biçimde analiz edildiğinde, devinme ve üğrüm gibi dönüşlerin karakteristiklerini eksiksiz olarak belirler.(ss96–113)
Alternatif olarak, Newton'un ikinci yasasının diferansiyel formülasyonu, torkun başka bir tanımını sunar:

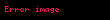 , parçacığın açısal momentumunu ifade eder. Bu ifade, açısal momentumun zamanla nasıl değiştiğini gösterir ve bu değişim miktarı, torkun büyüklüğünü belirler.
, parçacığın açısal momentumunu ifade eder. Bu ifade, açısal momentumun zamanla nasıl değiştiğini gösterir ve bu değişim miktarı, torkun büyüklüğünü belirler. Newton'un üçüncü yasasının, tork uygulayan her cismin, kendisine eşit büyüklükte fakat zıt yönde bir tork deneyimlemesini zorunlu kılar, ve dolayısıyla, içsel torklar vasıtasıyla dönmeler ve devinmeler gerçekleştiren kapalı sistemlerde açısal momentumun korunumunun sağlandığını ifade eder. Bu prensip, sistemin iç dinamikleri arasındaki etkileşimlerin dengede olduğunu ve sistemdeki toplam açısal momentumun zamanla değişmediğini gösterir.
Çekiş
Çekiş, kuvvetin zamanla nasıl değiştiğinin hızını ifade eder ve matematiksel olarak şu şekilde tanımlanır:
Bu tanım, bir kuvvetin belirli bir zaman aralığındaki değişim oranını ölçer ve bu oran, çeşitli dinamik sistemlerde önemli bir biomekanik değişken olarak kabul edilir.
Diğer terimler olan çeki (

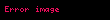
Kinematik integraller
Kuvvetler, kinematik değişkenlere göre integrasyon yaparak çeşitli fiziksel kavramların tanımlanmasında kullanılabilir. Örnek olarak, zaman parametresine göre yapılan entegrasyon, impuls kavramını ortaya koymaktadır:

Pozisyon değişkenine göre yapılan integrasyon, bir kuvvetin gerçekleştirdiği işin tanımını sağlar::((13-3))
bu işlem, kinetik enerjideki değişimlerle eşdeğerdir ve (iş-enerji ilkesine) yol açar.:((13-3))Güç P, iş W değerinin zamanla değişim oranıdır, dW/dt ve belirli bir zaman dilimi dt süresince meydana gelen pozisyon değişimi 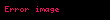

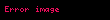
Potansiyel enerji
Genellikle, bir kuvvet yerine, onunla matematiksel olarak ilişkili olan potansiyel enerji alanı kavramından yararlanılır. Mesela, bir cisme etki eden yerçekimi kuvveti, cismin bulunduğu noktada var olan yerçekimi alanının etkisi olarak değerlendirilebilir. Enerji tanımını (iş tanımı üzerinden) matematiksel olarak yeniden formüle ederek, bir potansiyel skaler alan 

Kuvvetler, enerji korunumunu sağlayan konservatif ve sağlamayan konservatif olmayan olarak iki ana kategoriye ayrılabilir. Konservatif kuvvetler bir gradyanına denk gelirken, konservatif olmayan kuvvetler bu özelliği taşımaz.(ch.12)
Korunum
Bir kapalı sisteme etki eden bir korunumlu (konservatif) kuvvet, enerjinin kinetik ve potansiyel enerji türleri arasında dönüşüm yapmasını sağlayan ilişkili mekanik işle karakterize edilir. Kapalı bir sistemde, korunumlu bir kuvvetin etkisi altında sistemdeki net mekanik enerji korunur. Bu kuvvet, uzaydaki iki farklı nokta arasındaki potansiyel enerji farkıyla doğrudan ilişkilendirilebilir, ve bu bağlamda, suyun bir kot haritası tarafından belirlenen yükseklik farklarına göre akış yönü ve şiddeti gibi, potansiyel alanın bir sonucu olarak değerlendirilebilir.(ch.12)
Korunumlu kuvvetler içerisinde yerçekimi, elektromanyetik kuvvet ve yay kuvveti yer almaktadır. Bu kuvvetlerin her biri için modeller, çoğunlukla potansiyellerden kaynaklanan ve belirli bir radial vektör 
Yerçekimi durumunda:
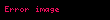
 yerçekimi sabiti'ni ve
yerçekimi sabiti'ni ve  ise n numaralı cismin kütlesini ifade eder. Bu ifade, iki kütle arasındaki çekim kuvvetinin, kütleler arası mesafenin karesi ile ters orantılı olduğunu ve kuvvetin yönünün birleştirici doğrultuda olduğunu gösterir.
ise n numaralı cismin kütlesini ifade eder. Bu ifade, iki kütle arasındaki çekim kuvvetinin, kütleler arası mesafenin karesi ile ters orantılı olduğunu ve kuvvetin yönünün birleştirici doğrultuda olduğunu gösterir. Elektrostatik kuvvetler bağlamında:
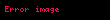
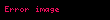 , boş uzayın elektriksel geçirgenliği olarak tanımlanır ve
, boş uzayın elektriksel geçirgenliği olarak tanımlanır ve 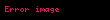 n numaralı cismin elektrik yükünü temsil eder.
n numaralı cismin elektrik yükünü temsil eder. Yay kuvvetleri durumunda:

 , ilgili yayın yay sabiti olarak bilinir ve bu sabit, yayın esneklik özelliğini gösterir.(ch.12)
, ilgili yayın yay sabiti olarak bilinir ve bu sabit, yayın esneklik özelliğini gösterir.(ch.12)Belirli fiziksel durumlar kapsamında, kuvvetlerin yalnızca potansiyel gradyanlarına bağlı olarak modellenmesi yetersiz kalabilir. Bu durum, çoğunlukla üzerinden yapılan makroskopik istatistiksel ortalamanın bir sonucudur. Örnek olarak, statik sürtünme, atomlar arası çok sayıda elektrostatik potansiyel gradyanlarından kaynaklansa da, makro ölçekli herhangi bir konum vektöründen bağımsız olarak kendini bir kuvvet modeli olarak gösterir. Sürtünme dışında korunumlu olmayan diğer kuvvetler arasında çeşitli , gerilim, basınç ve sürükleme yer alır. Detaylı bir açıklama ile, bu makroskopik kuvvetlerin her biri, mikroskopik potansiyel gradyanlarının toplam sonuçları olarak konservatif kuvvetlerin bir neticesidir.(ch.12)
Makroskopik düzeyde korunumlu olmayan kuvvetler ile mikroskopik düzeyde korunumlu kuvvetler arasındaki ilişki, istatistiksel mekanik kullanılarak detaylı bir şekilde incelenir. Makroskopik kapalı sistemlerde, korunumlu olmayan kuvvetler, sistemlerin iç enerjilerinde değişikliklere yol açar ve sıklıkla ısı transferi ile ilişkilendirilirler. Termodinamiğin ikinci yasası gereğince, korunumlu olmayan kuvvetler, kapalı sistemler içerisinde enerjinin daha düzenli halden daha rastgele koşullara doğru dönüşümüne neden olurken, entropinin artmasına yol açar.(ch.12)
Birimler
SI sisteminde kuvvetin birimi newton (sembolü N) olarak tanımlanır. Newton, bir kilogram kütleyi saniye karede bir metre ivmelendirebilmek için gereken kuvvet miktarını ifade eder ve bu birim kg·m·s−2 olarak formüle edilir. Karşılık gelen CGS birimi ise dyndir, bu birim bir gram kütleyi saniye karede bir santimetre ivmelendirmek için gerekli olan kuvveti ifade eder, yani g·cm·s−2. Dolayısıyla, bir newton yaklaşık 100,000 dyn değerine eşdeğerdir.
Yerçekimi kuvvetlerini ölçmek için kullanılan sistemindeki , pound-kuvvet (lbf) olarak tanımlanmıştır. Bu birim, bir üzerine standart yerçekimi alanında, yani 9.80665 m·s−2 ivme ile etki eden kuvvet olarak ifade edilir. Pound-kuvvet, alternatif bir kütle birimi olarak kullanılabilir: bir slug, bir pound-kuvvetin etkisi altında saniyede bir feet kare ivme kazandığında bu kütleye eşittir. Ayrıca, mutlak fps sistemi olarak adlandırılan farklı bir foot-pound-second sistemine özgü başka bir kuvvet birimi olan poundal, bir pound kütleyi saniyede bir feet kare hızlandırmak için gereken kuvvet olarak tanımlanır.
Pound-kuvvet'in metrik sistemdeki karşılığı olan kilogram-kuvvet (kgf) (bazı durumlarda kilopond olarak da bilinir), newton kadar yaygın olmamakla birlikte, bir kilogramlık bir kütleye standart yerçekimi tarafından uygulanan kuvveti ifade eder. Kilogram-kuvvet, çok nadir kullanılan bir kütle birimi olan 'ı (bazen mug veya hyl olarak da adlandırılır) tanımlar; bu kütle, 1 kgf'lik bir kuvvete maruz kaldığında 1 m·s−2 hızlanır. Kilogram-kuvvet, günümüzün modern SI sisteminin bir parçası değildir ve genel olarak kullanımı önerilmemektedir; ancak bazı özel durumlar için, örneğin uçak ağırlıklarının, jet motorlarının itme kuvvetlerinin, bisiklet jant tellerinin gerilimlerinin, tork anahtarlarının ayarlarının ve motorların çıkış torklarının belirtilmesinde kullanılmaktadır.
| Newton (SI birimi) | Dyn | Kilogram-kuvvet, kilopond (kp) | Pound-kuvvet | Poundal | |
|---|---|---|---|---|---|
| 1 N | ≡ 1 kg·m/s2 | = 105 dyn | ≈ 0,10197 kg-f | ≈ 0,22481 lb-f | ≈ 7,2330 pdl |
| 1 dyn | = 10−5 N | ≡ 1 g·cm/s2 | ≈ 1,0197×10−6 kg-f | ≈ 2,2481×10−6 lb-f | ≈ 7,2330×10−5 pdl |
| 1 kg-f veya 1 kp | = 9,80665 N | = 980665 dyn | ≡ gn × 1 kg | ≈ 2,2046 lb-f | ≈ 70,932 pdl |
| 1 lb-f | ≈ 4,448222 N | ≈ 444822 dyn | ≈ 0,45359 kg-f | ≡ gn × 1 lb | ≈ 32,174 pdl |
| 1 pdl | ≈ 0,138255 N | ≈ 13825 dyn | ≈ 0,014098 kg-f | ≈ 0,031081 lb-f | ≡ 1 lb·ft/s2 |
| Burada tüm yerçekimi birimleri için kilogram-kuvvetin (kg-f) resmi tanımında kullanılan değeri (9,80665 m/s2) olarak alınmıştır. | |||||
- İlgili diğer bir birim için maddesine bakınız.
Kuvvet kavramının güncellenmesi
20. yüzyılın başlarında, gözlemlenen astronomik ve mikroskop-altı düzeydeki deneysel sonuçlarını açıklamaya yönelik yeni fiziksel teoriler geliştirilmiştir. Aşağıda daha detaylı bir şekilde ele alınacağı üzere, görelilik teorisi momentin tanımını modifiye etmiş, kuantum mekaniği ise Newton yasalarının doğrudan geçerli olmadığı mikroskopik düzeylerde "kuvvet" kavramını yeniden formüle etmiştir.
Özel görelilik kuramı
Özel görelilik kuramı kapsamında, kütle ve enerji arasındaki eşdeğerlik, bir cismin hızlandırılması için gerekli işin hesaplanmasıyla anlaşılabilir. Bir cismin hızı arttıkça, bu durum enerjisi ve dolayısıyla kütle eşdeğeri (eylemsizliği) artışına yol açar. Bu nedenle, cismin daha önceki daha düşük hızına kıyasla aynı oranda hızlandırılması için daha fazla kuvvet gerekir. Newton'un ikinci yasası,
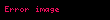
 değerleri için momentumun korunumu sağlanabilmesi adına, momentum şu şekilde yeniden tanımlanmalıdır:
değerleri için momentumun korunumu sağlanabilmesi adına, momentum şu şekilde yeniden tanımlanmalıdır: 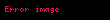
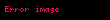 durgun kütleyi ve
durgun kütleyi ve  ışık hızını ifade eder. Bu yeni tanım, yüksek hızlarda momentumun korunumunu anlamak için esastır.
ışık hızını ifade eder. Bu yeni tanım, yüksek hızlarda momentumun korunumunu anlamak için esastır. Sabit ve sıfırdan farklı durgun kütlesi 



 değerine ulaşması mümkün değildir.(§15–8):26 Eğer
değerine ulaşması mümkün değildir.(§15–8):26 Eğer  ,
,  değerine kıyasla önemli derecede düşükse,
değerine kıyasla önemli derecede düşükse,  değeri yaklaşık olarak 1 olur ve
değeri yaklaşık olarak 1 olur ve 

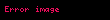 dört-vektör,
dört-vektör,  değişmez kütle ve
değişmez kütle ve  olduğunda görelilik açısından geçerlidir.
olduğunda görelilik açısından geçerlidir.Kuantum mekaniği
Kuantum mekaniği, moleküler, atomik veya atom altı boyutlardaki fenomenleri açıklamak amacıyla ortaya konmuş bir fizik teorisidir. Genel bir yaklaşımla, bir sistemin boyutları ne kadar küçükse, bu sistemi açıklamak için gerekli matematiksel modelin kuantum etkilerini dikkate alması o derece önem kazanır. Kuantum fiziğinin temel prensipleri, klasik fiziğinkinden ayrılır. Nesnelerin pozisyon, momentum ve enerji gibi özelliklere sahip olduğu fikri yerine, belirli bir yapıldığında ne tür sonuçlar elde edilebileceği üzerine odaklanılır. Kuantum mekaniği, fizikçilerin seçilen ölçümün belirli bir sonucu elde etme olasılığını hesaplamalarına imkan verir. Her ölçüm için beklenen değer, mümkün sonuçların olasılıkları ile ağırlıklandırılarak hesaplanan ortalamadır.
Kuantum mekaniğinde, etkileşimler çoğunlukla kuvvetten ziyade, enerji kavramları aracılığıyla tanımlanır. , kuantum beklenti değerleri ile klasik kuvvet kavramı arasında bir ilişki kurar; bu ilişki, kuantum fiziğinin klasik fizikten köklü bir şekilde ayrılması nedeniyle doğası gereği tam olarak kesin olmayan bir yapıya sahiptir. Kuantum fizik alanında, bir konum veya momentum ölçümünün beklenti değerlerini hesaplamak için temel araç olarak kullanılır. Bu beklenti değerleri genelde zaman içinde değişim gösterir; yani, örneğin bir pozisyon ölçümü yapıldığında, muhtemel farklı sonuçlar için olasılıklar değişebilir. Ehrenfest teoremi, genel olarak, bu beklenti değerlerinin zaman içindeki değişimini açıklayan denklemlerin, Newton'un ikinci kanununu hatırlatan bir biçimde, potansiyel enerjinin negatif türevi olarak tanımlanmış bir kuvvetle formüle edildiğini öne sürer. Ancak, bir durumda kuantum etkileri ne kadar belirginse, bu benzerlikten yola çıkarak anlamlı sonuçlar elde etmek o ölçüde güçleşir.
Kuantum mekaniği, mikroskop-altı düzeydeki kuvvetlerle etkileşimde bulunan, özellikle atomlar için hayati önem taşıyan iki yeni kısıtlayıcı unsur sunar. Çekirdeğin yoğun çekim gücüne karşın, belirsizlik ilkesi bir elektronun olasılık dağılımının minimum sınırlarını belirler ve Pauli dışarlama ilkesi elektronların aynı olasılık dağılımını paylaşmasını önler. Bu durum, dejenerasyon basıncı olarak adlandırılan bir basınç yaratır. Atomlar, moleküller, sıvılar ve katılar üzerinde dejenerasyon basıncı ve çekici elektromanyetik kuvvet arasındaki dinamik denge, bu yapıların sağlar.
Kuantum alan teorisi

Çağdaş parçacık fiziği alanında, kuvvetler ve parçacıkların ivmelenmeleri, momentum taşıyıcı ayar bozonlarının alışverişinin matematiksel bir türevi olarak izah edilmektedir. Kuantum alan teorisi ve genel görelilik kuramlarının ilerlemesiyle, kuvvet kavramının aslında gereksiz olduğu ve bu kavramın, (momentum korunumundan) ( ve kuantum elektrodinamiğinde sanal parçacıklarının momentumları dahil) kaynaklandığı kavranmıştır. Momentum korunumu, uzayın homojenliği veya simetrisi üzerinden doğrudan çıkarımlanabilir ve bu nedenle, kuvvet kavramından daha temel bir öneme sahiptir. Bu bağlamda, günümüzde tanımlanan temel kuvvetler, daha isabetli bir deyişle "temel etkileşimler" olarak nitelendirilmektedir.:199–128
Bu tür etkileşimlerin ayrıntılı sonuçlarını öngörebilmek için ileri düzey matematiksel tanımlar gereklidir; ancak, Feynman diyagramı kullanımı yoluyla bu etkileşimlerin kavramsal olarak basit bir biçimde ifade edilmesi mümkündür. Feynman diyagramında her madde parçacığı, zaman boyunca ilerleyen ve genellikle diyagramda yukarı veya sağa doğru artış gösteren düz bir çizgi ile temsil edilir (bkz. Hayat Çizgisi). Madde ve antimadde parçacıkları, Feynman diyagramı üzerindeki yayılım yönleri hariç, birbirleriyle özdeştir. Parçacıkların hayat çizgileri etkileşim düğümlerinde kesişmekte ve Feynman diyagramı, bir etkileşimden doğan kuvveti, parçacık hayat çizgilerinin yön değişikliği ile ilişkilendirilmiş şekilde düğüm noktasında oluşmuş olarak gösterir. Ayar bozonları, dalgalı çizgiler halinde düğümden yayılır ve sanal parçacıkların değiş-tokuşu halinde, yanındaki bir düğümde emilir. Feynman diyagramlarının avantajı, kuvvetlerden kavram olarak ayrı olmakla birlikte, genel temel etkileşim resminin bir parçası olan diğer fiziksel olayların da aynı ilkelerle açıklanabilmesidir. Örneğin, bir Feynman diyagramı, zayıf nükleer kuvvetten sorumlu olan aynı ayar bozonu aracılığıyla gerçekleşen bir nötronun bozunmasını, elektron, proton ve antineutrino üretimiyle detaylı bir şekilde tasvir edebilir.
Temel etkileşimler
Evrendeki tüm tanımlanmış kuvvetler, dört temel etkileşim kategorisine ayrılmaktadır. Güçlü ve zayıf kuvvetler yalnızca çok kısa mesafelerde etkili olup atomaltı parçacıklar arasında, özellikle nükleonlar ve bileşik çekirdekler arasındaki etkileşimlerden sorumludur. Elektromanyetik kuvvet, elektrik yükleri arasındaki etkileşimlerde; yerçekimi kuvveti ise kütleler arasındaki etkileşimlerde görev alır. Doğadaki diğer tüm kuvvetler, bu dört temel etkileşimin, kuantum mekaniği çerçevesinde işlemesi ve Schrödinger denklemi ile Pauli dışlama ilkesinden kaynaklanan kısıtlamalar ile ilişkilidir. Mesela, sürtünme kuvveti, iki yüzey arasındaki atomlar arasında etki eden elektromanyetik kuvvetin bir gösterimidir. Yaylardaki kuvvetler, Hooke yasası tarafından modellenmekte olup, bu kuvvetler elektromanyetik kuvvetlerin bir sonucudur. Merkezkaç kuvvetleri, dönen referans çerçevelerindeki ivmelenmeden doğrudan kaynaklanan ivme kuvvetleridir.:((12-11)):359
Farklı kavramların neticesinde kuvvetler üzerine temel teoriler ortaya konmuştur. Mesela, Newton'un evrensel yerçekimi teorisine göre, Dünya'nın yüzeyine yakın bir yerde düşen cisimler için etkin olan kuvvet, Ay'ın ve Güneş çevresindeki gezegenlerin hareketlerinden de sorumlu olan kuvvettir. Michael Faraday ve James Clerk Maxwell, elektriksel ve manyetik kuvvetlerin, elektromanyetizma teorisinde birleştiğini göstermişlerdir. Yirminci yüzyılda, kuantum mekaniğinin ilerlemesi, yerçekimi dışındaki ilk üç temel kuvvetin, maddenin (fermionların) ayar bozonu adı verilen sanal parçacıklar aracılığıyla etkileşiminin bir sonucu olduğunu ortaya koymuştur.Standart Model çerçevesinde, parçacık fiziğindeki bu kuvvetler arasındaki benzerlikler, bilim insanlarına elektrozayıf teoride zayıf ve elektromanyetik kuvvetlerin birleştirilmesini öngörmelerini sağlamış ve bu teori sonraki gözlemlerle doğrulanmıştır.
| Etkileşim/Özellik | Yerçekimi | Zayıf | Elektromanyetik | Güçlü | |
|---|---|---|---|---|---|
| (Elektrozayıf) | Temel | Kalıntı | |||
| Uygulama Alanları: | Kütle - Enerji | Tat | Elektrik yükü | Renk yükü | Atom çekirdekleri |
| Etkilenen parçacık tipleri: | Genel | Kuarklar, Leptonlar | Elektriksel yüklü | Kuarklar, Gluonlar | Hadronlar |
| Taşıyıcı parçacıklar: | Graviton (henüz tespit edilmedi) | W+ W− Z0 | γ | Gluonlar | Mezonlar |
| Kuarklar için güç değerlendirmesi: | 10-41 | 10-4 | 1 | 60 | Kuarklara uygulanamaz |
| Proton/nötron güç mertebesi | 10-36 | 10-7 | 1 | Hadronlara uygulanamaz | 20 |
Yerçekimsel

Newton'ın yerçekimi yasası, uzaktan etkileşim olarak tanımlanabilir: Örneğin, Güneş gibi bir nesne, Dünya gibi başka bir nesneyi, aralarındaki uzaklığa bakılmaksızın etkileyebilir. Bu etkileşim, anlık bir nitelik taşır. Newton'un teorisine göre, herhangi bir cismin konumu değiştiğinde, diğer tüm cisimler tarafından hissedilen yerçekimi çekimleri aynı anda değişir. Albert Einstein, bu durumun özel görelilikle çeliştiğini ve etkilerin ışık hızından daha hızlı yayılamayacağı öngörüsüyle uyumsuz olduğunu belirtmiştir. Einstein, bu nedenle, göreliliğe uygun yeni bir yerçekimi teorisi geliştirilmesinin gerekliliğini vurgulamıştır.
Merkür'ün yörüngesi, Newton'ın yerçekimi yasalarıyla öngörülenin dışında bir seyir izlemekteydi. Bazı astrofizikçiler, bu anormalliği açıklayabilecek keşfedilmemiş bir gezegen (Vulcan) hipotezini ileri sürmüşlerdir. Einstein, genel görelilik teorisini geliştirirken Merkür'ün bu problemli yörüngesine yoğunlaşmış ve teorisinin, söz konusu farklılıkları açıklayabilecek bir düzeltme sağladığını tespit etmiştir. Bu bulgu, Newton'ın yerçekimi teorisinin kusurlu olduğunun ilk kez kanıtlandığı bir an olmuştur.
Genel görelilik, günümüze kadar yerçekimini en iyi açıklayan teori olarak kabul görmüştür. Bu teoriye göre, yerçekimi bir kuvvet olarak değerlendirilmez; aksine, yerçekimi alanlarında serbestçe hareket eden nesneler, kendi ataletleri doğrultusunda düz hatlar boyunca içerisinde yol alırlar – bu, iki uzay-zaman olayı arasındaki en kısa uzay-zaman yolculuğu olarak tanımlanır. Nesnenin bakış açısından bakıldığında, tüm hareketler, yerçekiminin hiçbir etkisi olmadığı gibi gerçekleşir. Ancak hareket geniş bir çerçeveden incelendiğinde, uzay-zamanın eğriliği gözlemlenebilir ve kuvvet, nesnenin eğimli yörüngesi üzerinden tespit edilir. Bu bağlamda, uzay-zamandaki düz çizgi yolu, uzayda eğri bir hat olarak algılanır ve bu, nesnenin balistik yörünge olarak adlandırılır. Örneğin, düzgün bir yerçekimi alanında yerden atılan bir basketbol topu, parabolik bir yörüngede hareket eder. Uzay-zaman yörüngesi neredeyse düz bir çizgidir ve az bir eğrilik gösterir (eğrilik yarıçapı birkaç ışık yılı seviyesindedir). Nesnenin ivme değişikliğinin zaman türevi, "yerçekimi kuvveti" olarak ifade edilir.
Elektromanyetizma
Maxwell denklemleri ve bu denklemlere dayalı olarak geliştirilen teknikler, elektrik ve manyetizma alanlarında kuvvetle ilgili geniş bir fiziksel fenomenler dizisini etkili bir şekilde açıklamaktadır. Bu klasik teori, zaten görelilik etkilerini barındırmaktadır. Temel parçacıklar arasında gerçekleşen kuantize elektromanyetik etkileşimlerin anlaşılması, kuantum elektrodinamiği (QED) ile mümkündür. QED içerisinde, fotonlar tüm elektromanyetik etkileşimleri, elektromanyetik kuvvet de dahil olmak üzere tanımlayan temel değişim parçacıkları olarak işlev görür.
Güçlü nükleer
Çağdaş fizikte, genellikle parçacık fiziğinin kuantum teorileri çerçevesinde meydana gelen etkileşimler olarak nitelendirilen iki tür "nükleer kuvvet" tanımlanmaktadır. Güçlü nükleer kuvvet, atom çekirdeklerinin yapısal bütünlüğünü sağlamakla yükümlüdür ve protonlar arası elektromanyetik itme kuvvetini etkisiz hale getirebilme kapasitesi nedeniyle bu ismi kazanmıştır.:940
Güçlü kuvvet, günümüzde kuarklar ve gluonlar arasındaki etkileşimleri, kuantum kromodinamiği (QCD) teorisinin detaylı bir biçimde açıkladığı bir fenomen olarak kabul edilmektedir. Bu temel kuvvet, gluonlar vasıtasıyla kuarklar, antikuarklar ve gluonların kendileri üzerinde etkili olup, yalnızca temel parçacıklar üzerinde doğrudan bir etkiye sahiptir. Hadronlar arasında, özellikle atom çekirdeklerinde yer alan nükleonlar arasında gözlemlenen kalıntı etki, nükleer kuvvet olarak adlandırılır. Bu durumda güçlü kuvvet, nükleer kuvvetin klasik taşıyıcıları olan sanal pi ve ro mezonlarını oluşturan gluonlar aracılığıyla dolaylı bir etkileşim sergiler. için yapılan pek çok araştırmanın başarısızlıkla sonuçlanması, etkilenen temel parçacıkların doğrudan gözlemlenemeyeceğini ortaya koymuştur. Bu fenomen, renk hapsi olarak tanımlanmaktadır.(s232)
Zayıf nükleer
Temel etkileşimler içerisinde eşsiz bir niteliğe sahip olan zayıf nükleer kuvvet, bağlı durumlar oluşturmaz. Bu kuvvet, ağır W ve Z bozonları arasındaki değişimden kaynaklanır ve iki çeşit bozonun aracılık ettiği iki tür etkileşime, yani elektrik yükü taşıyan W+ ve W− bozonlarını içeren yüklü akım ve elektriksel olarak nötr Z0 bozonlarını içeren nötr akıma ayrılır. Zayıf etkileşimin en bilinen örneği, atom çekirdeklerindeki nötronların beta bozunumu ve bunun sonucu ortaya çıkan radyoaktivitedir.:951 Bu, yüklü akım türünden bir etkileşimdir. "Zayıf" terimi, bu kuvvetin güçlü kuvvete kıyasla yaklaşık 1013 kat daha düşük alan şiddetine sahip olmasından gelmektedir. Ancak, kısa mesafelerde yerçekiminden daha güçlüdür. Elektromanyetik kuvvetler ile zayıf kuvvetin 1015 K sıcaklığında ayırt edilemez olduğunu ortaya koyan tutarlı bir elektrozayıf teori de geliştirilmiştir. Bu sıcaklıklar, Büyük Patlamanın başlangıç anlarında plazma çarpışmaları sırasında gerçekleşmiştir.:201
Ayrıca bakınız
Kaynakça
- ^ a b c d e f g h ; ; University Physics (6.6yıl=1982 bas.). Addison-Wesley. ss. 18-38. ISBN .
- ^ Cohen, Michael. "Classical Mechanics: a Critical Introduction" (PDF). University of Pennsylvania. 3 Temmuz 2022 tarihinde kaynağından (PDF). Erişim tarihi: 9 Ocak 2024.
- ^ a b (1897). The Works of Archimedes. Erişim tarihi: 14 Ekim 2007 – Internet Archive vasıtasıyla.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab Feynman, Richard P.; ; (2010). The Feynman lectures on physics. Vol. I: Mainly mechanics, radiation and heat (New millennium bas.). New York: Basic Books. ISBN .
- ^ a b c d e f g h i j k l m n o p q r s t u v w x Kleppner, Daniel; Kolenkow, Robert J. (2014). https://archive.org/details/KleppnerD.KolenkowR.J.IntroductionToMechanics2014/page/n102
|bölümurl=eksik başlık (). An Introduction to Mechanics (2.2bölüm=Chapter 3: Forces and equations of motion bas.). Cambridge: Cambridge University Press. ISBN . - ^ a b Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books. ISBN .
- ^ Lang, Helen S. (1998). The order of nature in Aristotle's physics : place and the elements. Cambridge: Cambridge Univ. Press. ISBN .
- ^ Hetherington, Norriss S. (1993). Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives. Garland Reference Library of the Humanities. s. 100. ISBN .
- ^ Sorabji, Richard (2010). "John Philoponus". Philoponus and the Rejection of Aristotelian Science (2.2yayıncı=Institute of Classical Studies, University of London bas.). s. 47. ISBN . JSTOR 44216227. OCLC 878730683.
- ^ Maier, Anneliese (1982). Sargent, Steven D. (Ed.). On the Threshold of Exact Science. University of Pennsylvania Press. s. 79. ISBN . OCLC 495305340.
- ^ a b Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN .
- ^ LoLordo, Antonia (2007). Pierre Gassendi and the Birth of Early Modern Philosophy. New York: Cambridge University Press. ss. 175-180. ISBN . OCLC 182818133. 20 Nisan 2022 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2024.
- ^ Arnold, V. I.; Kozlov, V. V.; Neĩshtadt, A. I. (1988). "Mathematical aspects of classical and celestial mechanics". Encyclopaedia of Mathematical Sciences, Dynamical Systems III. 3. Anosov, D. V. Berlin: Springer-Verlag. ISBN . OCLC 16404140. 9 Aralık 2022 tarihinde kaynağından . Erişim tarihi: 7 Nisan 2024.
- ^ a b c d e f Newton, Isaac (1999). The Principia Mathematical Principles of Natural Philosophy. Berkeley: University of California Press. ISBN . Bu eser, ve Anne Whitman tarafından, Julia Budenz'in katkılarıyla İngilizce'ye son dönemde çevrilmiştir.
- ^ Howland, R. A. (2006). Intermediate dynamics a linear algebraic approach (Online-Ausg. bas.). New York: Springer. ss. 255-256. ISBN .
- ^ (2005). It's About Time: Understanding Einstein's Relativity. Princeton University Press. ISBN .
- ^ a b c d e f g h i Ling, Samuel J.; Sanny, Jeff; Moebs, William; ve diğerleri. (2021). University Physics, Volume 1. . ISBN . 16 Aralık 2021 tarihinde kaynağından . Erişim tarihi: 11 Nisan 2024.
- ^ Hellingman, C. (1992). "Newton's third law revisited". Phys. Educ. 27 (2): 112-115. Bibcode:1992PhyEd..27..112H. doi:10.1088/0031-9120/27/2/011.
Quoting Newton in the Principia: It is not one action by which the Sun attracts Jupiter, and another by which Jupiter attracts the Sun; but it is one action by which the Sun and Jupiter mutually endeavour to come nearer together.
- ^ Resnick, Robert; Halliday, David; Krane, Kenneth S. (2002). Physics. 1 (5 bas.). ISBN .
Any single force is only one aspect of a mutual interaction between two bodies.
- ^ Landau, L. D.; ; (1967). General Physics; mechanics and molecular physics. Oxford: Pergamon Press. ISBN . Translated by: J. B. Sykes, A. D. Petford, and C. L. Petford. LCCN-67-30260-{{{3}}}. In section 7, pp. 12–14, this book defines force as dp/dt.
- ^ Kibble, Tom W. B.; Berkshire, Frank H. (2004). Classical Mechanics (5.5isbn=1860944248 bas.). Londra: Imperial College Press. According to page 12, "[Force] can of course be introduced, by defining it through Newton's second law".
- ^ de Lange, O. L.; Pierrus, J. (2010). Solved Problems in Classical Mechanics. Oxford: Oxford University Press. ISBN . According to page 3, "[Newton's second law of motion] can be regarded as defining force".
- ^ ; Saletan, Eugene J. (1998). Classical dynamics: A Contemporary Approach. Cambridge [England]: Cambridge University Press. s. 9. ISBN . OCLC 857769535.
- ^ ; Olenick, Richard P.; ; (2007). The Mechanical Universe: Mechanics and Heat (Advanced bas.). Cambridge [Cambridgeshire]: Cambridge University Press. s. 134. ISBN . OCLC 227002144.
- ^ a b Thornton, Stephen T.; Marion, Jerry B. (2004). Classical Dynamics of Particles and Systems (5.5yayıncı=Thomson Brooks/Cole bas.). ss. 49-50. ISBN .
- ^ a b Landau, Lev D.; (1969). Mechanics. 1. Sykes, J. B.; Bell, J. S. tarafından çevrildi (2.2seri= bas.). Pergamon Press. ISBN .
- ^ (1999). Concepts of Force: A study in the foundations of dynamics (Facsim. bas.). Mineola, NY: Dover Publications. ss. 220-222. ISBN .
- ^ Noll, Walter (April 2007). "On the Concept of Force" (PDF). Carnegie Mellon University. 17 Aralık 2013 tarihinde kaynağından (PDF). Erişim tarihi: 28 Ekim 2013.
- ^ . Physics Tutorial Menu. . 16 Ocak 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Ocak 2008.
- ^ Henderson, Tom (2004). . The Physics Classroom and Mathsoft Engineering & Education, Inc. 1 Ocak 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Ocak 2008.
- ^ . Physics Static Equilibrium (forces and torques). . 19 Ekim 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 2 Ocak 2008.
- ^ Cook, A. H. (1965). "A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory". Nature. 208 (5007): 279. Bibcode:1965Natur.208..279C. doi:10.1038/208279a0.
- ^ a b Young, Hugh; Freedman, Roger; Sears, Francis; ve Zemansky, Mark (1949) . Pearson Education. s. 59–82.
- ^ Watkins, Thayer. . Department of Economics. San José State University. 10 Şubat 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Ocak 2008.
- ^ Kollerstrom, Nick (2001). . University College London. 11 Kasım 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 19 Mart 2007.
- ^ a b c d e Cutnell, John D.; Johnson, Kenneth W. (2004). Physics (6.6yer=Hoboken, NJ bas.). Wiley. ISBN .
- ^ Coulomb, Charles (1784). "Recherches théoriques et expérimentales sur la force de torsion et sur l'élasticité des fils de metal". Histoire de l'Académie Royale des Sciences: 229-269.
- ^ a b Feynman, Richard P.; ; (2010). The Feynman lectures on physics. Vol. II: Mainly electromagnetism and matter (New millennium bas.). New York: Basic Books. ISBN .
- ^ (1966). The principles of electromagnetic theory and of relativity. Dordrecht: D. Reidel. s. 85. ISBN . OCLC 844001.
- ^ Ling, Samuel J.; Sanny, Jeff; Moebs, William (2021). University Physics, Volume 2. . ISBN . 3 Nisan 2024 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ Scharf, Toralf (2007). "Chapter 2". Polarized light in liquid crystals and polymers. John Wiley and Sons. s. 19. ISBN .
- ^ Duffin, William (1980). Electricity and Magnetism (3.3isbn=978-0-07-084111-6 bas.). McGraw-Hill. ss. 364-383.
- ^ . Non-Calculus Based Physics I. 27 Aralık 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ocak 2008.
- ^ Fitzpatrick, Richard (2 Şubat 2006). "Strings, pulleys, and inclines". 18 Aralık 2007 tarihinde kaynağından . Erişim tarihi: 4 Ocak 2008.
- ^ Nave, Carl Rod. "Elasticity". HyperPhysics. University of Guelph. 1 Haziran 2023 tarihinde kaynağından . Erişim tarihi: 28 Ekim 2013.
- ^ Nave, Carl Rod. "Centripetal Force". HyperPhysics. University of Guelph. 1 Aralık 2013 tarihinde kaynağından . Erişim tarihi: 28 Ekim 2013.
- ^ Mallette, Vincent (1982–2008). . Publications in Science and Mathematics, Computing and the Humanities. Inwit Publishing, Inc. 29 Şubat 2000 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ocak 2008.
- ^ (2009). General Relativity and the Einstein Equations. Oxford: Oxford University Press. s. 39. ISBN . OCLC 317496332.
- ^ Nave, Carl Rod. "Newton's 2nd Law: Rotation". HyperPhysics. University of Guelph. 21 Şubat 2014 tarihinde kaynağından . Erişim tarihi: 28 Ekim 2013.
- ^ Fitzpatrick, Richard (7 Ocak 2007). "Newton's third law of motion". 5 Aralık 2007 tarihinde kaynağından . Erişim tarihi: 4 Ocak 2008.
- ^ "Yank: the time derivative of force is an important biomechanical variable in sensorimotor systems". 9 Nisan 2024 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ "Tremor-related feature engineering for machine learning based Parkinson's disease diagnostics". 7 Ekim 2022 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ "Comparison of methods of derivation of the yank-time signal from the vertical ground reaction force–time signal for identification of movement-related events". 17 Aralık 2020 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ "The use of yank-time signal as an alternative to identify kinematic events and define phases in human countermovement jumping".
- ^ Harry, John R.; Barker, Leland A.; Tinsley, Grant M.; Krzyszkowski, John; Chowning, Luke D.; McMahon, John J.; Lake, Jason (5 Mayıs 2021). "Relationships among countermovement vertical jump performance metrics, strategy variables, and inter-limb asymmetry in females". Sports Biomechanics (İngilizce): 1-19. doi:10.1080/14763141.2021.1908412. ISSN 1476-3141. 10 Nisan 2024 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ Rosendo, Andre; Tanaka, Takayuki; Kaneko, Shun’ichi (20 Nisan 2012). "A Yank-Based Variable Coefficient Method for a Low-Powered Semi-Active Power Assist System". Journal of Robotics and Mechatronics. 24 (2): 291-297. doi:10.20965/jrm.2012.p0291. 10 Nisan 2024 tarihinde kaynağından . Erişim tarihi: 14 Nisan 2024.
- ^ Hibbeler, Russell C. (2010). Engineering Mechanics (12.12isbn=978-0-13-607791-6 bas.). Pearson Prentice Hall. s. 222.
- ^ Singh, Sunil Kumar (25 Ağustos 2007). "Conservative force". Connexions. 16 Kasım 2012 tarihinde kaynağından . Erişim tarihi: 4 Ocak 2008.
- ^ Davis, Doug. "Conservation of Energy". General physics. 1 Haziran 2023 tarihinde kaynağından . Erişim tarihi: 4 Ocak 2008.
- ^ a b c d e Wandmacher, Cornelius; Johnson, Arnold (1995). Metric Units in Engineering. ASCE Publications. s. 15. ISBN .
- ^ a b French, A. P. (1972). Special Relativity. The MIT introductory physics series (reprint bas.). Londra: Chapman & Hall. ISBN .
- ^ Wilson, John B. . The Science Realm: John's Virtual Sci-Tech Universe. 26 Haziran 2009 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ocak 2008.
- ^ (1993). "Hidden variables and the two theorems of John Bell". Reviews of Modern Physics. 65 (3): 803-815. arXiv:1802.10119 $2. Bibcode:1993RvMP...65..803M. doi:10.1103/RevModPhys.65.803.
It is a fundamental quantum doctrine that a measurement does not, in general, reveal a pre-existing value of the measured property.
- ^ Schaffer, Kathryn; Barreto Lemos, Gabriela (24 Mayıs 2019). "Obliterating Thingness: An Introduction to the "What" and the "So What" of Quantum Physics". (İngilizce). 26: 7-26. arXiv:1908.07936 $2. doi:10.1007/s10699-019-09608-5. ISSN 1233-1821.
- ^ Marshman, Emily; (1 Mart 2017). "Investigating and improving student understanding of the probability distributions for measuring physical observables in quantum mechanics". European Journal of Physics. 38 (2): 025705. Bibcode:2017EJPh...38b5705M. doi:10.1088/1361-6404/aa57d1. ISSN 0143-0807.
- ^ Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2005). Quantum Mechanics. Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan tarafından çevrildi. John Wiley & Sons. s. 242. ISBN .
- ^ (1993). Quantum Theory: Concepts and Methods. . s. 302. ISBN . OCLC 28854083.
- ^ Lieb, Elliott H. (1 Ekim 1976). "The stability of matter". Reviews of Modern Physics (İngilizce). 48 (4): 553-569. doi:10.1103/RevModPhys.48.553. ISSN 0034-6861.
the fact that if one tries to compress a wave function anywhere then the kinetic energy will increase. This principle was provided by Sobolev (1938)...
- ^ a b Lieb, Elliott H. (1990). "The stability of matter: from atoms to stars". Bulletin of the American Mathematical Society (İngilizce). 22 (1): 1-49. doi:10.1090/S0273-0979-1990-15831-8. ISSN 0273-0979.
bulk matter is stable, and has a volume proportional to the number of particles, because of the Pauli exclusion principle for fermions (Le., the electrons). Effectively the electrons behave like a fluid with energy density
, and this limits the compression caused by the attractive electrostatic forces.
- ^ Griffiths (2005). Introduction to Quantum Mechanics, Second Edition. London, UK: Prentice Hall. ss. 221-223. ISBN .
- ^ a b Shifman, Mikhail (1999). ITEP lectures on particle physics and field theory. World Scientific. ISBN .
- ^ . The Particle Adventure. 18 Aralık 2007 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ocak 2008.
- ^ (12 Ekim 1999). "Additional background material on the Nobel Prize in Physics 1999". Nobel Prize. 26 Temmuz 2023 tarihinde kaynağından . Erişim tarihi: 26 Temmuz 2023.
- ^ "Powerful New Black Hole Probe Arrives at Paranal". 24 Eylül 2015 tarihinde kaynağından . Erişim tarihi: 13 Ağustos 2015.
- ^ Siegel, Ethan (20 Mayıs 2016). "When Did Isaac Newton Finally Fail?". Forbes. 3 Ocak 2017 tarihinde kaynağından . Erişim tarihi: 3 Ocak 2017.
- ^ Panofsky, Wolfgang K.; Phillips, Melba (2005). Classical electricity and magnetism (2 bas.). Mineola, NY: Dover Publ. ISBN .
- ^ (2010). Quantum Field Theory in a Nutshell (2.2isbn=978-0-691-14034-6 bas.). Princeton University Press. s. 29.
- ^ "strong, 7.g physics". Oxford English Dictionary (Çevrimiçi bas.). Oxford University Press. (Abonelik veya katılımcı kurum üyeliği gerekli.)
- ^ Stevens, Tab (10 Temmuz 2003). . 16 Ekim 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 4 Ocak 2008.
- ^ Goldberg, Dave (2017). The Standard Model in a Nutshell. Princeton University Press. ISBN .
- ^ a b Greiner, Walter; Müller, Berndt; Greiner, Walter (2009). Gauge theory of weak interactions: with 75 worked examples and exercises (4 bas.). Heidelberg: Springer. ISBN .
- ^ (2008). The Cosmic Microwave Background. Cambridge University Press. ss. 41-42. ISBN .
wikipedia, wiki, viki, vikipedia, oku, kitap, kütüphane, kütübhane, ara, ara bul, bul, herşey, ne arasanız burada,hikayeler, makale, kitaplar, öğren, wiki, bilgi, tarih, yukle, izle, telefon için, turk, türk, türkçe, turkce, nasıl yapılır, ne demek, nasıl, yapmak, yapılır, indir, ücretsiz, ücretsiz indir, bedava, bedava indir, mp3, video, mp4, 3gp, jpg, jpeg, gif, png, resim, müzik, şarkı, film, film, oyun, oyunlar, mobil, cep telefonu, telefon, android, ios, apple, samsung, iphone, xiomi, xiaomi, redmi, honor, oppo, nokia, sonya, mi, pc, web, computer, bilgisayar
Fizik disiplininde kuvvet bir cismin hizini degistirmeye zorlayabilen yani ivmelenmeye sebebiyet verebilen hizinda veya yonunde bir degisiklik olusturabilen bir etki olarak tanimlanir bu etki diger kuvvetlerle dengelenmedigi muddetce gecerlidir Itme ya da cekme gibi gunluk kullanimda yer alan eylemler kuvvet konsepti ile matematiksel bir netlige ulasir Kuvvetin hem hem de yonu onemli oldugundan kuvvet bir vektor olarak ifade edilir Kuvvet icin SI birimi newton N dur ve genellikle F simgesi ile gosterilir KuvvetKuvvetler bir nesneye uygulanan itme veya cekme olarak tanimlanabilir Bu kuvvetler yercekimi manyetizma veya bir kutlenin ivmelenmesine neden olabilecek herhangi bir fenomen kaynakli olabilir Yaygin sembol ler F displaystyle vec F F Ftemel SI birimlerinden turetimi kg m s 2SI nicelik boyutu wikidataSI birimi newton N Diger niceliklerden turetimi F maKuvvetler siklikla itme ya da cekme olarak tanimlanir Kutlecekim manyetizma veya kutlenin ivmelenmesine sebep olan herhangi bir sey kuvvetin nedeni olabilir Klasik mekanikte kuvvet merkezi bir oneme sahiptir Kuvvet sabit bir kutleye sahip bir cisme etki eden kuvvetin cismin kutlesi ile bu cismin maruz kaldigi ivmenin carpimina esit oldugunu ifade eden Newton un hareket yasalari dahilinde ele alinir Klasik mekanikte yaygin olarak rastlanan kuvvet cesitleri elastiklik surtunme kuvveti temas ya da normal kuvvetler ve kutlecekim kuvvetleridir Kuvvetin donusel karsiligi olan tork bir cismin donus hizindaki degisimleri meydana getirir Genislemis bir cismin her bir parcasi genellikle yanindaki parcalara kuvvet uygular bu kuvvetlerin cisim icindeki dagilimi icsel mekanik gerilimi olusturur Denge halinde bu gerilimler cismin herhangi bir ivmelenme gostermemesi icin kuvvetlerin birbirini dengelemesiyle sonuclanir Bunlar dengede olmadiginda kati materyallerde veya sivilarda akisa yol acabilirler Modern fizik alaninda gorelilik ve kuantum mekanigi dahil olmak uzere hareket yasalari kuvvetin temel kaynagi olarak temel etkilesimlere dayanarak yeniden duzenlenmistir Ancak klasik mekanigin sundugu kuvvet anlayisi pratik amaclar icin faydalidir Kavram gelisimiAntik donemdeki filozoflar hareketsiz ve hareket halindeki cisimler ile basit makinelerin analizinde kuvvet konseptini temel almislar fakat Aristo ve Arsimet gibi dusunurler kuvvetin dogru anlasilmasi noktasinda hatalar yapmislardir Bu durum kismen surtunme kuvvetinin zaman zaman acik olmayan niteliginin ve dogal hareketin icerigine dair yetersiz goruslerin eksik kavranmasindan kaynaklanmaktadir Temel yanilgilardan biri sabit bir hizla hareketin devam etmesi icin kuvvetin zorunlu oldugu inancidir Hareket ve kuvvet uzerine onceki yanlis kavrayislar Galileo Galilei ve Isaac Newton tarafindan zamanla duzeltilmistir Matematiksel derinligi ile Newton iki yuz yil boyunca daha da gelistirilmeyecek olan hareket yasalarini ortaya koymustur 19 yuzyilin baslarinda Einstein isik hizina yaklasan hizlara sahip nesneler uzerindeki kuvvetlerin davranisini dogru bir sekilde tahmin eden ve yercekimi ile eylemsizlik kuvvetleri hakkinda bilgiler sunan bir gorelilik kurami ortaya koymustur Kuantum mekanigine iliskin cagdas anlayislar ve isik hizina yakin hizlara parcaciklari ivmelendirebilen teknolojik gelismeler isiginda parcacik fizigi alani atomlardan daha kucuk parcaciklar arasindaki kuvvetleri aciklamak amaciyla bir Standart Model tasarlamistir Standart Model kuvvetlerin yayilimi ve emilimi sureclerinde temel bir rol oynayan ayar bozonlari adi verilen degisim parcaciklarinin varligini ongormektedir Bilinen yalnizca dort ana etkilesim vardir Guc siralamasina gore azalan sekilde bunlar guclu elektromanyetik zayif ve kutlecekimsel kuvvetlerdir 2 10 79 1970 ler ve 1980 lerde gerceklestirilen Yuksek enerji parcacik fizigi gozlemleri zayif ve elektromanyetik kuvvetlerin daha temel bir elektrozayif etkilesimin tezahurleri oldugunu onaylamistir Newton oncesi kavramlarAristo bir cismin dogal olmayan hareket gerceklestirmesine sebep olan her turlu etkeni kuvvet olarak tanimlamistir Antik donemden itibaren kuvvet kavrami basit makinelerin her birinin isleyisi icin temel bir unsur olarak taninmistir Basit bir makine tarafindan saglanan daha az kuvvet kullanilmasini saglarken bu kuvvetin ayni miktar is icin daha buyuk bir mesafe boyunca etki etmesine olanak tanimistir Kuvvetlerin karakteristiklerinin detayli incelenmesi ozellikle sivilar icerisinde bulunan yuzdurme kuvvetinin formulasyonunu yapmasiyla taninan Arsimet in eserlerinde zirveye ulasmistir Aristo Aristo kozmolojisinde kuvvet kavramina dair felsefi bir muhakeme sunmustur Onun perspektifine gore yer kuresi icerisindeki farkli dogal konumlar da istirahat eden dort temel elementten olusmaktadir Aristo oncelikle toprak ve su elementlerinden meydana gelen Dunya uzerinde hareketsiz durumda bulunan cisimlerin yer yuzeyinde kendi dogal konumlarinda olduklarini ve mudahale edilmezlerse bu durumun devam edecegini savunmustur Cisimlerin kendi dogal konumlarini bulma yonundeki dogustan gelen egilimi orn agir cisimlerin dusme egilimi ile dogal olmayan veya zoraki hareketi yani bir kuvvetin devamli olarak uygulanmasini gerektiren hareketi ayirt etmistir Bu kuram nesnelerin hareket sekillerine dair gunluk gozlemlere dayanarak bir arabanin hareket etmekte kalmasi icin gerekli olan surekli kuvvet uygulamasi gibi atki Ing projectile orneginde oklarin ucusu gibi davranislari aciklama noktasinda kavramsal zorluklarla karsilasmistir Bir okcu ucusun baslangicinda oku harekete gecirir ve daha sonra uzerinde algilanabilir bir etkin nedenin bulunmadigi halde ok hava boyunca ilerler Aristo bu problemi teshis etmis ve atkinin yolu boyunca itilen havanin atimi hedefine tasidigini onermistir Bu aciklama hareketin devamini saglayabilmek icin hava gibi kesintisiz bir ortamin varligini gerektirmektedir Aristo fizigi 6 yuzyil itibariyla elestirilere maruz kalmistir ancak bu eksiklikler Galileo Galilei nin 17 yuzyilda gerceklestirdigi calismalara degin giderilememistir Galileo Aristoteles in hareket teorisine meydan okuyan bir deney gerceklestirmistir Bu deneyde bir egim boyunca yuvarlanan tas ve top mermilerinin bu cisimlerin kutlesinden bagimsiz olarak yer cekimi ile hizlandigini ve bir kuvvet ornegin surtunme uygulanmadikca hizlarini muhafaza ettiklerini ortaya koymustur Galileo nun hareketi surdurmek yerine degistirmek icin kuvvet gerektigi tezi Rene Descartes ve Pierre Gassendi tarafindan ileriye tasinmis ve Newton fiziginin temel prensiplerinden biri haline gelmistir 17 yuzyilin baslarinda Newton un Principia eserinden once kuvvet Latince vis terimi bir noktanin ivmelenmesi gibi cok sayida fiziksel ve fiziksel olmayan fenomene uygulanagelmistir Bir nokta kutlesinin ve onun hizinin karesinin carpimi Leibniz tarafindan canli kuvvet Latince vis viva olarak isimlendirilmistir Gunumuz kuvvet kavrami Newton in tanimladigi ivmelenme kuvveti Latince vis motrix ile ortusmektedir Newton mekanigiIsaac Newton atalet ve kuvvet gibi kavramlar yardimiyla tum cisimlerin hareketlerini tanimlamistir Newton 1687 yilinda kendi alanindaki en onemli eseri Philosophiae Naturalis Principia Mathematica i yayimlar Bu calismasinda Newton gunumuz fizik biliminin kuvvetlerin aciklanmasina yon veren uc temel hareket yasasini belirlemistir Newton un yasalarinin matematiksel ifadeleri yeni matematiksel metodolojilerle birlikte zaman icinde gelisim gostermistir Birinci yasa Newton un ilk hareket yasasina gore hareketsizlik halinde bulunan bir cismin dogal egilimi hareketsizlige devam etmek sabit hiz ile dogrusal bir trajektorya uzerinde hareket eden bir cismin ise bu sabit hizda ve dogrultuda hareketine devam etme egilimindedir Bu sonuc fizik kanunlarinin tum eylemsiz gozlemciler acisindan degismez oldugunu belirten ilkeye dayanarak ilk durumdan turetilmistir i e hareket halinde olduklarini hissetmeyen tum gozlemciler Bir cisimle es zamanli hareket eden bir gozlemci bu cismin hareketsizlik halinde oldugunu algilayacaktir Bu baglamda cismin dogal egilimi bu gozlemciye gore hareketsizlik durumunu korumaktir bu da sabit hizla ve dogrusal bir yolda hareket ettigini gozlemleyen birisinin cismin bu hareket tarzini surdurecegini gormesini saglar 1 7 1689 itibariyla Isaac Newton Newton kaleme aldigi Principia eserinde uc hareket yasasini geometrik terminoloji ile ifade etmistir Gunumuzde ise fizik bilimi diferansiyel kalkulus ve vektor analizini temel almaktadir Ikinci yasa Ilk yasaya gore duz bir cizgi boyunca sabit bir hizla gerceklesen hareket icin herhangi bir sebep zorunlu degildir Asil olarak hareketin degisimi bir sebebi gerektirmekte olup Newton un ikinci yasasi kuvvet ile hareketin degisim sureci arasindaki nicel iliskiyi aciklamaktadir Newton un ikinci yasasina gore bir cisim uzerine etki eden net kuvvet cismin zaman icindeki momentum degisiminin esdegerdir Cismin kutlesi sabit kaldiginda bu yasa cismin ivmesinin uzerine etki eden net kuvvete dogrudan orantili oldugunu bu kuvvetin yonunde oldugunu ve cismin kutlesi ile ters orantili oldugunu ongormektedir ss204 207 Newton un ikinci yasasinin cagdas bir ifadesi bir vektor denklemi seklindedir bu denklemede p displaystyle vec p sistemin momentumunu ve F displaystyle vec F net vektorlerin toplami kuvveti temsil eder s399 Bir cisim dengede ise tanimsal olarak net kuvvet sifirdir bununla birlikte dengelenmis kuvvetler mevcut olabilir Ikinci yasa bir nesne uzerinde dengelenmemis bir kuvvetin varliginda nesnenin momentumunun zaman icinde degisecegini one surer Muhendislikte sik karsilasilan durumlarda bir sistemin kutlesi degismez kabul edilir ve bu ikinci yasayi basit bir cebirsel forma indirger Momentumun tanimi geregince F dp dt d mv dt displaystyle vec F frac mathrm d vec p mathrm d t frac mathrm d left m vec v right mathrm d t m kutleyi ve v displaystyle vec v hizi ifade eder 9 1 9 2 Newton un ikinci yasasi sabit kutleli bir sistemde uygulandiginda m sabit kabul edilerek turev islemcinin disina cikarilabilir Boylece denklem su sekle donusur F mdv dt displaystyle vec F m frac mathrm d vec v mathrm d t Ivmenin taniminin yerine konulmasiyla Newton un ikinci yasasinin cebirsel formulasyonu elde edilir Ucuncu yasa Bir cismin baska bir cisme kuvvet uygulamasi durumunda ikinci cisim de derhal ilk cisme karsilik olarak esit buyuklukte ve ters yonde bir kuvvet uygular Vektorel ifadeyle eger F 1 2 displaystyle vec F 1 2 birinci cismin ikinci cisim uzerine uyguladigi kuvvetse ve F 2 1 displaystyle vec F 2 1 ikinci cismin birinci cisim uzerine uyguladigi kuvvetse o zamanF 1 2 F 2 1 displaystyle vec F 1 2 vec F 2 1 Bu ilke siklikla etki tepki yasasi olarak tanimlanir burada F 1 2 displaystyle vec F 1 2 etki ve F 2 1 displaystyle vec F 2 1 olarak adlandirilir Newton un ucuncu yasasi farkli cisimlerin varliginin sonucunda ortaya cikan kuvvetlerin analizinde simetri prensibinin uygulanmasinin bir urunudur Bu yasa tum kuvvetlerin cesitli cisimler arasindaki karsilikli etkilesimler oldugunu belirtir dolayisiyla tek yonlu bir kuvvet veya yalniz bir cisim uzerine etki eden bir kuvvetin mumkun olmadigini ifade eder Cisim 1 ve cisim 2 den meydana gelen bir sistemde bu nesneler arasindaki karsilikli etkilesimler sonucu meydana gelen sistem uzerindeki net kuvvetin sifir oldugu gorulur F 1 2 F 2 1 0 displaystyle vec F 1 2 vec F 2 1 0 Daha kapsamli bir acidan bir parcacik toplulugunun olusturdugu kapali sistemde tum icsel kuvvetler dengelenmis durumdadir Parcaciklar birbirlerine nazaran ivmelenme gosterebilir fakat sistemin kutle merkezi herhangi bir ivmelenme gostermez Sisteme disaridan bir kuvvet uygulandiginda kutle merkezinin ivmelenmesi uygulanan dis kuvvetin buyuklugunun sistem kutlesine oraniyla dogru orantili olacaktir 19 1 Newton un ikinci ve ucuncu yasalarinin bir araya getirilmesi ile bir sistem icerisindeki dogrusal momentumun herhangi bir kapali sistem icinde korundugu ispatlanabilir Iki parcacikli bir sistemde p 1 displaystyle vec p 1 birinci cismin momentumunu ve p 2 displaystyle vec p 2 ikinci cismin momentumunu temsil ederse su esitlik gecerlidir dp 1dt dp 2dt F 1 2 F 2 1 0 displaystyle frac mathrm d vec p 1 mathrm d t frac mathrm d vec p 2 mathrm d t vec F 1 2 vec F 2 1 0 Bu argumanlar rastgele bir parcacik sayisina sahip sistemler icin genellestirilebilir Temelde eger tum kuvvetler kutlesi olan cisimlerin etkilesimlerinden kaynaklaniyorsa net momentumun hicbir zaman kaybolmadigi ya da kazanilmadigi bir sistem tanimi mumkundur ch 12 Kuvvet tanimlamasi Birtakim ders kitaplari Newton un ikinci yasasini kuvvetin tanimi olarak benimser Bununla birlikte sabit bir kutle m displaystyle m icin F ma displaystyle vec F m vec a denkleminin herhangi bir tahminsel icerik sunabilmesi ilave bilgilerle desteklenmelidir 12 1 Ayrica bir cismin ivmelenmesi sonucu bir kuvvetin varligi sonucuna varilmasi yalnizca bir atalet referans cercevesi icinde mumkundur 59 Newton yasalarinin hangi unsurlarinin tanim olarak alinacagi ve hangilerinin fiziksel icerik tasidigina dair sorular cesitli yollarla yanitlanmistir ssvii bu kuramin pratikteki kullanimini etkilemez Kuvvet kavramina dair daha acik bir tanim arayan saygin fizikciler filozoflar ve matematikciler arasinda Ernst Mach ve yer almaktadir Kuvvetlerin birlestirilmesiVektorler v1 displaystyle v 1 ile v2 displaystyle v 2 nin aritmetik toplami v displaystyle v vektorunu olusturur Kuvvetler belirlenen bir yon icerisinde etki ederler ve uygulanan itme veya cekmenin siddetine bagli olarak degisen sahiptirler Bu karakteristikler sayesinde kuvvetler olarak tanimlanir Bu durum yon icermeyen fiziksel niceliklerden skaler nicelikler olarak ifade edilir farkli matematiksel prensiplerin kuvvetler icin gecerli oldugunu gosterir Iki kuvvetin ayni cisim uzerine etkisini degerlendirirken sonuclari hesaplayabilmek adina her iki kuvvetin de buyuklugunu ve yonunu bilmenin zorunlu oldugu ornekler mevcuttur Eger her bir kuvvet icin bu bilgilerin her ikisi de saglanmamissa durum muglaktir 197 Tarih boyunca kuvvetlerin nicel incelemesi ilk kez birbiriyle zit yonde etki ederek birbirlerini iptal eden birkac kuvvetin var oldugu durumlarinda gerceklestirilmistir Bu deneyler kuvvetlerin toplanabilir vektorel nicelikler oldugunu ayrica buyukluk ve yon gibi ozelliklere sahip olduklarini vurgulayan temel ozellikleri sergilemektedir Bir nokta parcacik uzerinde iki farkli kuvvetin etki etmesi durumunda bileske Ing resultant olarak ifade edilen sonuc kuvvet bu ayni zamanda net kuvvet olarak da bilinir paralelkenar yasasina dayanan vektor toplama yontemiyle hesaplanabilir bir paralelkenarin iki kenari ile temsil edilen vektorlerin toplanmasi paralelkenarin caprazi ile es buyukluk ve yon ozelliklerine sahip esdeger bir sonuc vektoru uretir Bu bileske vektorunun buyuklugu ilgili iki kuvvetin buyukluklerinin farki ile toplami arasinda degisiklik gosterir bu degisim onlarin etki hatlari arasindaki aci ile dogrudan iliskilidir ch 12 Bir blokun duz bir yuzey ve bir egik duzlem uzerindeki serbest cisim diyagramlari Kuvvetler onlarin buyukluklerinin ve toplam net kuvvetin hesaplanabilmesi icin ayristirilarak toplanir Serbest cisim diyagramlari bir sisteme etki eden kuvvetlerin izlenmesinde kullanisli bir arac olarak degerlendirilebilir Ideal bir durumda bu diyagramlar net kuvvetin grafik vektor toplami yoluyla tespit edilebilmesi icin kuvvet vektorlerinin acilarini ve gorelili buyukluklerini muhafaza edecek sekilde cizilir Kuvvetler toplama islemine ek olarak birbirine dik acilar olusturacak sekilde bagimsiz bilesenlere de cozumlenebilirler Bu baglamda kuzeydogu yonunde etki eden bir yatay kuvvet kuzeye ve doguya dogru etki eden iki farkli kuvvete ayristirilabilir Bu bilesenlerin vektorel toplami ilk kuvvetin elde edilmesini saglar Kuvvet vektorlerinin bir dizi taban vektor bilesenlerine cozumlenmesi buyukluk ve yon kullanarak yapilandan daha matematiksel olarak duzenli bir metod sunar Dik bilesenler soz konusu oldugunda vektorlerin toplaminin bilesenleri vektorlerin bilesenlerinin skaler toplamlari ile tayin edilir Dik bilesenler birbirlerine dik acida etki eden kuvvetlerin birbirlerinin buyuklugu veya yonu uzerinde etkisi olmadigindan birbirlerinden bagimsizdir En uygun matematiksel cozumu saglayacak taban vektorler setini secme islemi hangi taban vektorlerinin matematigi en kolaylastiracagini dusunulerek gerceklestirilir Bir kuvvetle ayni yonde olan bir taban vektoru secmek tercih edilir cunku bu durumda soz konusu kuvvet yalnizca tek bir sifir olmayan bilesene sahip olacaktir Dik kuvvet vektorleri diger iki bilesene dik acida olan ucuncu bir bileseni icerebilir sekilde uc boyutlu olabilir ch 12 Denge Bir nesne uzerine etki eden butun kuvvetlerin dengelenmesi durumunda bu nesnenin denge durumunda oldugu ifade edilir 566 Bu baglamda denge bir nokta parcaciga etki eden toplam kuvvetin sifira esit oldugu yani tum kuvvetlerin vektor toplaminin sifir olmasi durumu zaman gerceklesir Genisletilmis bir nesne durumunda ise net torkun da sifir olmasi sarttir Bir cisim belirli bir referans cercevesi baglaminda statik denge icinde ise eger o cisim dinlenme durumundadir ve ivmelenmemektedir ote yandan dinamik denge icindeki bir cisim surekli bir hizla ve duz bir hat uzerinde hareket etmektedir yani hareket halindedir ancak ivmelenmemektedir Bir gozlemci tarafindan statik denge olarak algilanan durum baska bir gozlemci tarafindan dinamik denge olarak degerlendirilebilir ve bunun tersi de mumkundur 566 Statik Denge Klasik mekanik biliminin ortaya cikisinin cok oncesinde statik denge kavrami iyi bir sekilde kavranmistir Dinlenme halindeki cisimlerin uzerine etki eden net kuvvetin sifir oldugu bilinmektedir Statik denge durumunun en temel ornegi iki kuvvetin buyukluk acisindan birbirine esit olmasi ancak yon bakimindan birbirine zit olmasi halidir Bir ornek olarak duz bir yuzeyde bulunan bir cisim yercekimi kuvveti nedeniyle Dunya nin merkezine dogru asagi yonde cekilir Bu surecte yuzeyden cisime asagi yonde uygulanan kuvvete es degerde bir yukari yonlu kuvvet bu kuvvete normal kuvvet adi verilir uygulanir Bu senaryo net bir kuvvetin olusmamasini ve sonuc olarak herhangi bir ivmelenmenin meydana gelmemesini saglar Surtunme ozelligi gosteren bir yuzey uzerinde konumlanmis bir cisme karsi itme kuvveti uygulanmasi uygulanan kuvvetin cisim ile masa yuzeyi arasinda olusan kuvveti tarafindan notralize edilmesi nedeniyle cismin pozisyon degistirmemesi sonucunu dogurabilir Hareketin olmadigi bir senaryoda statik surtunme kuvveti uygulanan kuvvetle kesin bir denge olusturur ve bu durum herhangi bir ivmelenme meydana gelmemesini saglar Statik surtunme kuvveti yuzey ile cisim arasindaki temasin karakteristiklerine bagli olarak tanimlanan bir ust sinir degerine kadar uygulanan kuvvete bagli olarak artis veya azalis gosterir Iki kuvvet arasindaki statik dengenin saglanmasi terazi ve gibi basit olcum araclari araciligiyla kuvvetlerin olcumunde en sik basvurulan yontemdir Bir ornek olarak dikey bir el kantari uzerine asilan bir nesne nesne uzerine etki eden yercekimi kuvveti ile bu kuvvete karsi gelen ve nesnenin agirligina denk gelen yayin tepki kuvveti arasinda bir denge durumu yasar Bu tip araclarin kullanimi ile sabit yogunluk degerine sahip nesneler icin yercekimi kuvvetinin hacme dogru orantili oldugu gibi bazi niceliksel kuvvet yasalari kesfedilmistir bu durum standart agirlik tanimlarinin binlerce yil boyunca genis capta kullanilmasina olanak saglamistir kaldirma kuvveti icin Arsimet prensibi kaldirac uzerine Arsimet in analizi gaz basinci icin Boyle yasasi ve yaylar icin Hooke yasasi gibi Bu teoriler Isaac Newton in hareket yasalarini ortaya koymasindan once formule edilmis ve deneysel olarak teyit edilmistir ch 12 Dinamik Denge Galileo Galilei Aristo nun kuvvetlerle ilgili aciklamalarinda yer alan temel tutarsizliklari ortaya cikaran ilk bilim insanidir Dinamik denge Aristotelesci fizikteki bazi on kabullerin gozlem ve mantiksal cercevede tutarsizliklar icerdigini tespit eden Galileo tarafindan ilk defa ortaya konulmustur Galileo basit hiz ekleme isleminin mutlak anlayisinin gecersiz oldugunu gosterdigini fark etmistir Galileo ya gore sabit bir hizda hareket dinlenme hali ile birebir esdegerdir Bu durum cisimlerin kutleye sahip olmalari nedeniyle dogal olarak bir dogal dinlenme hali ne yonlendirdigi Aristoteles in dusuncesinin aksini isaret eder Basit deneyler Galileo nun sabit hiz ve dinlenme halinin esdegerligi uzerine kurulu anlayisinin dogrulugunu kanitlamistir Mesela sabit bir hizla ilerleyen bir geminin karga yuvasindan birakilan bir top mermisinin Aristoteles fizik anlayisina gore gemi hareket ederken dogrudan asagi dusmesi beklenirken deneyin gerceklestirilmesi sonucunda top mermisi her zaman sanki gemi ile birlikte seyahat etmesi gerektigini bilircesine diregin dibine duser Duserken top mermisi uzerine herhangi bir ileri yatay kuvvet uygulanmadigindan elde kalan tek sonuc top mermisinin duserken gemi ile ayni hizda hareket etmeye devam ettigidir Dolayisiyla top mermisinin sabit ileri hizda hareketini devam ettirmek icin herhangi bir ek kuvvete ihtiyac duyulmamaktadir Ayrica sabit bir hizda ilerleyen her cismin net kuvvetin sifir oldugu bir durumda oldugu kabul edilmelidir Dinamik denge bir cisim uzerindeki tum kuvvetlerin birbirini dengelemesine ragmen cismin hala sabit bir hizda hareket ettigi durumdur Dinamik dengenin basit bir ornegi kinetik surtunmenin oldugu bir yuzey uzerinde sabit hizla ilerleme durumunda gorulur Bu tur bir senaryoda hareket yonunde bir kuvvet uygulanirken kinetik surtunme kuvveti uygulanan kuvvete tam bir karsitlik gosterir Bu net kuvvetin sifir olmasina neden olur ancak cisim sifir olmayan bir hizla harekete basladigi icin sifir olmayan bir hizla hareket etmeye devam eder Aristoteles bu hareketi uygulanan kuvvet tarafindan meydana getirildigi seklinde yanlis bir yorumda bulunmustur Kinetik surtunme dikkate alindiginda sabit hiz hareketini tetikleyen herhangi bir net kuvvetin olmadigi acikca gorulmektedir ch 12 Klasik mekanikte kuvvet ornekleriBazi kuvvetler temel kuvvetlerin dogrudan sonucu olarak ortaya cikar Bu gibi durumlar kapsaminda fiziksel kavrayisi derinlestirmek amaciyla idealize edilmis modellerden yararlanilabilir Ornek olarak her kati nesne kati cisim modeli cercevesinde ele alinir Yercekimi Bir kullanilarak saniyede 20 kez flas patlatilarak elde edilen serbestce dusen bir basketbol topunun goruntuleri Sagdaki olcum birimleri yaklasik olarak 12 milimetrenin katlari seklindedir Basketbol topu baslangicta hareketsizdir Ilk flasin mesafe sifir gerceklestigi andaki serbest birakilma anindan itibaren dusulen birimlerin sayisi flas sayisinin karesiyle dogru orantilidir Isaac Newton un calismalariyla birlikte evrensel bir etki olarak kabul goren yer cekimi kavrami gunumuzde anlasilmistir Newton oncesinde cisimlerin Dunya yonunde dusme egilimleri gok cisimlerinin hareketleriyle iliskilendirilmemisti Galileo serbest dusus halindeki cisimlerin ivmelenmelerinin sabit oldugunu ve cismin kutlesinden bagimsiz bulundugunu tespit ederek dusen cisimlerin karakteristiklerini aciklamada kritik bir rol ustlenmistir Gunumuzde Dunya nin yuzeyine dogru olan yer cekimi kaynakli ivme genellikle g displaystyle vec g ile ifade edilir ve bu ivmenin buyuklugu saniyede yaklasik 9 81 metre kare olarak belirlenmistir bu deger deniz seviyesinden alinmis olup cografi konuma gore degisiklik gosterebilir bu ivme Dunya nin merkezine dogru yonelir Bu gozlem Dunya nin yuzeyindeki bir nesnenin uzerine etki eden yer cekimi kuvvetinin nesnenin kutlesiyle dogrudan orantili oldugunu gostermektedir Dolayisiyla kutlesi m displaystyle m olan bir nesne su kuvveti hisseder F mg displaystyle vec F m vec g Serbest dusus halindeki bir cisim icin karsit bir kuvvet olmadigindan cismin uzerindeki net kuvvet onun agirligina esittir Serbest dususte olmayan cisimlerde ise yercekimi kuvveti bu cisimlerin desteklerince uygulanan tepki kuvvetleri ile dengelenir Ornegin yere basan bir birey yere temas eden kismi uzerine uygulanan normal kuvvet tepki kuvveti nedeniyle asagi yonlu agirliginin tam olarak dengeledigi bir durumda net kuvvet sifirdir ch 12 Newton un yercekimi kuramina yaptigi katki Aristoteles tarafindan surekli hareket halinde olan dogal durumda bulundugu dusunulen gok cisimlerinin hareketlerini Dunya uzerinde gozlemlenen dusme hareketleriyle entegre etmekti Newton daha onceden Kepler in gezegensel hareket yasalari ile aciklanmis olan gok cisimlerinin hareketlerini aciklayabilen bir yercekimi yasasi onerdi Newton yercekiminin etkilerinin uzak mesafelerde farkli bicimlerde gozlenebilecegini kesfetmistir Bu baglamda Newton Ay in Dunya cevresindeki ivmesinin yercekiminin azalan bir ters kare kanununa bagli olarak ayni yercekimi kuvveti ile aciklanabilecegini tespit etmistir Bununla birlikte bir cismin yercekimiyle ivmelenmesinin onu ceken diger cismin kutlesi ile dogru orantili oldugu sonucuna varmistir Bu dusuncelerin butunlestirilmesiyle Dunya nin kutlesi m displaystyle m oplus ve yaricapi R displaystyle R oplus ile yercekimsel ivme arasindaki iliskiyi ifade eden bir formul elde edilmistir burada r displaystyle hat r Dunya nin merkezinden disa dogru yonlendirilen birim vektor olarak tanimlanmaktadir Bu denklemde yercekiminin goreli siddetini aciklamak amaciyla boyutsal bir sabit olan G displaystyle G kullanilmaktadir Bu sabit Newton un yercekimi sabiti olarak adlandirilmis olup Newton in yasami boyunca degeri bilinmemistir G displaystyle G sabitinin ilk kez olcumu 1798 yilinda Henry Cavendish tarafindan bir ile gerceklestirilmistir bu olcum verilen denklem yardimiyla Dunya nin kutlesinin hesaplanabilmesi acisindan basinda genis bir sekilde Dunya nin kutlesinin olcumu olarak rapor edilmistir Newton gok cisimlerinin hepsinin ayni hareket yasalarini takip ettigini gozlemlemis ve yercekimi yasasinin evrensel olmasi gerektigini anlamistir Temel olarak Newton un evrensel kutlecekim yasasi su sekilde ifade edilir Kutlesi m1 displaystyle m 1 olan bir kuresel cisim uzerine kutlesi m2 displaystyle m 2 olan bir cismin yercekimsel cekiminden kaynaklanan kuvvet seklinde belirlenir burada r displaystyle r iki cismin kutle merkezleri arasindaki uzakligi ifade eder r displaystyle hat r ise birinci cismin merkezinden ikinci cismin merkezine dogru yonlendirilmis birim vektordur Bu denklem 20 yuzyil baslarina dek gunes sistemi icerisindeki hareketlerin aciklanmasinda temel bir referans noktasi olarak kabul edilmistir Bu donem boyunca bir gezegen ay kuyruklu yildiz veya asteroitin yorungesinde birden cok gok cisminin etkileri sonucunda meydana gelen sapmalari hesaplamak uzere ileri duzey perturbasyon teorisi teknikleri ortaya konmustur Bu formalizm matematikcilere henuz gozlemlenmemis olan gezegen Neptun un varligini ongorebilmeleri icin gereken yeterli dogrulugu saglamistir Elektromanyetik Elektrostatik kuvvet 1784 yilinda Coulomb tarafindan iki yuk arasinda ozgun bir sekilde mevcut olan bir kuvvet olarak aciklanmistir 519 Elektrostatik kuvvetin karakteristikleri ters kare kanunu ile orantili degisim gostermesi radial yon ile belirlenmesi hem cekici hem de itici etkilesim sunmasi dogustan ozelligi tasimasi yuklu nesnelerin kutlesinden bagimsiz olmasi ve superpozisyon ilkesine uygun davranmasi seklindedir Coulomb yasasi bu gozlemlerin tumunu butunlestiren kesin ve net bir ifadedir Gunumuz matematikcileri ve fizikcileri uzaydaki herhangi bir noktada bir elektrik yukune etki eden elektrostatik kuvveti saptamak amaciyla elektrik alani kavramini yararli bulmuslardir Elektrik alani uzayin herhangi bir noktasinda varsayimsal bir yerlestirilerek ve Coulomb yasasi kullanilarak elektrostatik kuvvetin hesaplanmasi esasina dayanir 4 6 4 8 Elektrik alani su formulle ifade edilir E F q displaystyle vec E vec F over q burada q displaystyle q hipotetik test yukunun buyuklugunu temsil eder Ayni baglamda manyetik alan kavrami miknatislarin uzaktan birbirlerini nasil etkileyebilecegini aciklamak uzere gelistirilmistir Lorentz kuvvet yasasi elektrik ve manyetik alanlarin bir yuklu cisme uyguladigi kuvveti su sekilde formule eder burada F displaystyle vec F elektromanyetik kuvvet E displaystyle vec E cismin bulundugu yerdeki elektrik alani B displaystyle vec B manyetik alan ve v displaystyle vec v parcacigin hizini gosterir Lorentz kuvvetine manyetik katki hiz vektorunun manyetik alan ile capraz carpimi seklinde gerceklesir 482 Elektrik ve manyetik alanlarin kokenleri James Clerk Maxwell in 1864 yilinda onceki teorileri bir araya getirerek 20 adet skaler denklem seklinde ifade etmesi ve bu denklemlerin daha sonra Oliver Heaviside ve Josiah Willard Gibbs tarafindan dort vektor denklemine donusturulmesi ile tam anlamiyla acikliga kavusturulmustur Maxwell denklemleri bu alanlarin kaynaklarini duran ve hareket eden yukler olarak ve ayni zamanda alanlarin birbirleriyle olan etkilesimlerini kapsamli bir sekilde tanimlar Maxwell in bu calismalari elektrik ve manyetik alanlarin isik hizinda seyahat eden bir dalga ile kendi kendine olusabilen yapilar oldugunu ortaya cikarmistir Bu bulgu elektromanyetik teori ve optik alanlarini butunlestirmis ve elektromanyetik spektrumun eksiksiz bir aciklamasina dogrudan katkida bulunmustur Normal FN nesneye etki eden normal kuvveti ifade eder Temas halindeki nesneler arasindaki dogrudan etki eden kuvvete normal kuvvet adi verilir Bu kuvvet nesneler arasindaki ara yuzeye dik olarak sistemin toplam kuvvetinin bir bilesenini olusturur 264 Normal kuvvet Newton un ucuncu kanunu ile siki bir baglanti icindedir Ornegin normal kuvvet masalarin ve yer dosemelerinin yapisal dayanikliligindan sorumlu olup ayni zamanda harici bir kuvvet kati bir cisim uzerine uygulandiginda bu kuvvete tepki olarak ortaya cikar Normal kuvvetin uygulamada gorulen bir ornegi sabit bir yuzeye carpan bir cismin aldigi darbe kuvvetidir ch 12 Surtunme Surtunme iki cismin birbirine gore hareketini engelleyen bir kuvvettir Makroskobik duzeyde surtunme kuvveti temas noktasinda etki eden normal kuvvet ile dogrudan bir iliskiye sahiptir Surtunme kuvvetleri temel olarak iki farkli kategori altinda incelenir ve 267 Statik surtunme kuvveti Fsf displaystyle F mathrm sf bir cismin bir yuzeye paralel olarak maruz kaldigi kuvvetlere msf displaystyle mu mathrm sf ile normal kuvvetin FN displaystyle F text N carpimi kadar olan sinir degere ulasana dek direnc gosterir Yani statik surtunme kuvvetinin buyuklugu asagidaki esitsizligi tatmin eder 0 Fsf msfFN displaystyle 0 leq F mathrm sf leq mu mathrm sf F mathrm N Kinetik surtunme kuvveti Fkf displaystyle F mathrm kf uygulanan kuvvetlerden ve cismin hareketinden bagimsiz olarak belirlenir Bu durumda kuvvetin buyuklugu su formulle ifade edilir Fkf mkfFN displaystyle F mathrm kf mu mathrm kf F mathrm N burada mkf displaystyle mu mathrm kf ifade eder Genellikle kinetik surtunme katsayisi statik surtunme katsayisindan daha azdir 267 271 Gerilim Gerilim kuvvetleri modellemelerde kutle barindirmayan surtunmesiz kopmaz ve esnemez ozellikler gosteren ideal ipler kullanilarak tasarlanabilir Bu tur ipler ideal kasnaklar ile entegre edilebilir bu kasnaklar iplerin fiziksel yonelimlerini degistirmelerine olanak tanir Ideal ipler gerilim kuvvetlerini eylem tepki cifti olarak aninda iletebilirler boylece eger iki obje ideal bir ip ile birbirine baglanmissa birinci obje tarafindan ip boyunca uygulanan herhangi bir kuvvet otomatik olarak ikinci obje tarafindan ip boyunca zit yonde bir kuvvetle karsilanir Hareketli kasnaklarin kullanimiyla ayni ipin ayni nesneye defalarca baglanmasi yoluyla yuk uzerindeki gerilim kuvveti artirilabilir Yuke etki eden her bir ip ipteki gerilim kuvvetinin bir katini daha yuke uygular Bu tur duzenekler yuku hareket ettirmek icin gereken ipin yer degistiren uzunlugunda bir artisla orantili olarak onemli bir elde etmeyi mumkun kilar Bu tandem etkiler makinenin karmasikligina ragmen yuke uygulanan isin degismemesi nedeniyle mekanik enerjinin korunumu ile sonuclanir ch 12 Yay Fk yay uzerindeki yuke tepki olarak olusan kuvveti gosterir Temel bir elastik kuvvet bir yayin kendi dogal boyuna geri donmesini saglamaya yoneliktir Ideal yay kutle icermeyen surtunmesiz kopmayan ve sinirsiz esneyebilir olarak tanimlanir Bu tur yaylar yayin denge durumundan olan yer degistirmeye bagli olarak daraldiginda itme veya genislediginde cekme kuvveti uygular Bu lineer iliski 1676 da Robert Hooke tarafindan tanimlanmis ve Hooke yasasi adiyla bilinir hale gelmistir Eger Dx displaystyle Delta x yer degistirme miktarini belirtirse ideal bir yayin uyguladigi kuvvet asagidaki formulle ifade edilir burada k displaystyle k ilgili yayin ozelliklerine gore belirlenen yay sabiti veya kuvvet sabiti dir Eksi isaret kuvvetin uygulanan yuke zit yonde etki gosterme egilimini temsil eder ch 12 Merkezcil Duzgun dairesel hareket gerceklestiren bir cisim icin cisim uzerinde etki eden net kuvvet asagidaki gibi ifade edilir burada m displaystyle m cismin kutlesi v displaystyle v cismin hizi r displaystyle r ise cismin dairesel yoldaki merkeze olan uzakligi ve r displaystyle hat r merkezden disariya radial yonde gosteren birim vektor olarak tanimlanmistir Bu durum cismin hissettigi net kuvvetin surekli olarak egri yolun merkezine dogru yonlendirildigini gosterir Bu tur kuvvetler cismin hareketiyle iliskili hiz vektorune dik olarak etkiler ve bu nedenle cismin hizinin buyuklugunu hizin degeri degistirmez yalnizca hiz vektorunun yonunu degistirir Daha genel bir ifadeyle bir cismi ivmelendiren net kuvvet yola dik ve yola teget olacak sekilde iki bilesene ayrilabilir Bu cismin hizini azaltarak veya artirarak ivmelenmesini saglayan tegetsel kuvvetle birlikte yon degisikligini saglayan radial merkezcil kuvveti icerir ch 12 Sureklilik mekanigi Bir dusen cisim uzerindeki hava direncinden kaynaklanan surukleme kuvveti Fd displaystyle F text d yercekimi kuvveti Fg displaystyle F text g ile buyukluk acisindan esitlendiginde cisim dinamik denge haline ulasarak terminal hizina erisir Newton yasalari ve genel Newton mekanigi baslangicta idealize edilmis nokta parcaciklar uzerindeki kuvvet etkilesimlerini aciklamak amaciyla ortaya konulmustur ancak bu durum uc boyutlu nesneleri dogrudan kapsamamaktadir Gercekte maddenin genislemis bir yapisal formu vardir ve bir nesnenin belirli bir bolumune etki eden kuvvetler nesnenin diger bolumlerini de etkileyebilir Nesnelerdeki atomlari bir arada tutan yapilarin akiskanlik buzulme genisleme veya sekil degistirme yetenegi oldugu durumlar icin sureklilik mekanigi teorileri kuvvetlerin malzemeler uzerindeki etkilerini tanimlar Ornegin genislemis akiskanlarda basinc farklari basinc gradyanlari boyunca kuvvetlerin yonlendirilmesine yol acar F V P displaystyle frac vec F V vec nabla P burada V displaystyle V akiskan icindeki objenin hacmini ve P displaystyle P uzaydaki tum noktalardaki basinci tanimlayan skaler fonksiyonu ifade eder Basinc gradyanlari ve farkliliklari yercekimi alanlarinda askida kalan akiskanlar icin yuzdurme kuvveti atmosfer biliminde ruzgarlar ve aerodinamik ve ucus ile iliskili kaldirma kuvvetini tetikler ch 12 ile baglantili olarak tanimlanan ozgul bir kuvvet akiskan direncidir Bu bir cismin viskozite nedeniyle akiskan bir ortamda hareket etmesine karsi koyan bir cisim kuvvetidir Ozellikle Stokes suruklemesi durumunda bu kuvvet hizin buyuklugu ile yaklasik olarak dogru orantilidir ancak yon olarak tersine isler su sekilde tanimlanir b displaystyle b akiskanin fiziksel ozellikleri ile nesnenin boyutlarina genellikle kesit alani dayali bir sabit degerdir ve v displaystyle vec v nesnenin hiz vektorunu ifade eder ch 12 Sureklilik mekanigi cercevesinde kuvvetler belirli bir gerilim tensoru araciligiyla ifade edilir Bu tensor genelde formulu ile gosterilir burada A displaystyle A gerilim tensorunun degerlendirildigi hacimdeki alakali kesit alanini temsil eder Bu kuramsal yapi kesit alanina dik kuvvetlerle iliskili basinc bilesenlerini tensorun matris diyagonalleri ve kesit alanina paralel kuvvetlerle iliskili kayma bilesenlerini off diagonal elemanlar kapsar Gerilim tensoru tum deformasyon turlerini gerilmeler iceren kuvvetleri cekme gerilimleri ve sikistirmalari da dahil olmak uzere hesaplar 133 134 38 1 38 11 Kurgusal kuvvetler Belirli kuvvetler cerceve bagimli olarak nitelendirilir bu Newton disi yani eylemsiz olmayan referans cercevelerinin benimsenmesi sonucu ortaya ciktiklarini ifade eder Bu tur kuvvetlere ornek olarak merkezkac kuvveti ve Coriolis kuvveti verilebilir Bu kuvvetler hizlanmayan referans cercevelerinde mevcut olmadiklari icin kurgusal olarak tanimlanir ch 12 Ayrica bu kuvvetlerin gercek olmamasi nedeniyle sanki kuvvetler Ing pseudo forces olarak da isimlendirilirler 12 11 Genel gorelilik kapsaminda yercekimi kuvveti uzayzamanin duz geometriden sapmasi durumlarinda ortaya cikan kurgusal bir kuvvet olarak degerlendirilir Bu baglamda yercekimi klasik mekanikte ele alinan bir kuvvet olmaktan ziyade gorelilik teorisinde farkli bir yorumlama alanina girer ve uzayzamanin geometrisiyle iliskili bir fenomen olarak incelenir Kuvvet temelli kavramlarDondurme ve Tork Kuvvet F tork t ve momentum vektorleri p ve L arasindaki iliskinin bir doner sistemdeki gosterimi Genisletilmis cisimlerin donusunu tetikleyen kuvvetler torklar ile baglantilidir Matematiksel ifadeyle bir kuvvetin F displaystyle vec F torku herhangi bir referans noktasina gore capraz carpim kullanilarak tanimlanmaktadir burada r displaystyle vec r kuvvetin uygulandigi noktanin referans noktasina gore pozisyon vektorunu temsil eder Bu tanim torkun buyuklugunun ve yonunun uygulama noktasinin konumuna gore nasil degisebilecegini matematiksel olarak aciklar 497 Tork kuvvetin donussel karsiligidir benzer bicimde aci acisal hiz hizin ve acisal momentum ise momentumun donussel esdegerleridir Newton un birinci hareket yasasi uyarinca tum cisimlerin dengesiz bir tork uygulanmadigi surece acisal momentumlarini korumasini saglayan donussel atalet mevcuttur Ayni sekilde Newton un ikinci hareket yasasi rijit bir cismin anlik acisal ivmesinin hesaplanmasi icin benzer bir formulasyon saglar t Ia displaystyle vec tau I vec alpha su sekilde ifade edilir I displaystyle I cismin eylemsizlik momentini a displaystyle vec alpha cismin acisal ivmesini temsil eder 502 Bu kutlenin donussel karsiligi olan eylemsizlik momentinin tanimini olusturur Mekanigin daha gelismis teorilerinde belirli bir zaman dilimi boyunca gerceklesen donuslerin aciklandigi durumlarda eylemsizlik momenti ile ikame edilmelidir Bu tensor uygun bicimde analiz edildiginde devinme ve ugrum gibi donuslerin karakteristiklerini eksiksiz olarak belirler ss96 113 Alternatif olarak Newton un ikinci yasasinin diferansiyel formulasyonu torkun baska bir tanimini sunar t dL dt displaystyle vec tau frac mathrm d vec L mathrm dt bu formulde L displaystyle vec L parcacigin acisal momentumunu ifade eder Bu ifade acisal momentumun zamanla nasil degistigini gosterir ve bu degisim miktari torkun buyuklugunu belirler Newton un ucuncu yasasinin tork uygulayan her cismin kendisine esit buyuklukte fakat zit yonde bir tork deneyimlemesini zorunlu kilar ve dolayisiyla icsel torklar vasitasiyla donmeler ve devinmeler gerceklestiren kapali sistemlerde acisal momentumun korunumunun saglandigini ifade eder Bu prensip sistemin ic dinamikleri arasindaki etkilesimlerin dengede oldugunu ve sistemdeki toplam acisal momentumun zamanla degismedigini gosterir Cekis Cekis kuvvetin zamanla nasil degistiginin hizini ifade eder ve matematiksel olarak su sekilde tanimlanir Y dF dt displaystyle vec Y frac d vec F dt Bu tanim bir kuvvetin belirli bir zaman araligindaki degisim oranini olcer ve bu oran cesitli dinamik sistemlerde onemli bir biomekanik degisken olarak kabul edilir Diger terimler olan ceki T displaystyle vec T kapma S displaystyle vec S ve sallama S displaystyle vec mathcal S gibi ifadeler dogrusal momentumun zamanla iliskili dorduncu besinci ve altinci turevleri icin kullanilmistir Bununla birlikte cekisin ardisik turevlerini ifade etmek icin evrensel olarak kabul gormus bir terminoloji henuz mevcut degildir Bu tur olcumler ozellikle biyomekanik calismalar sporcu performans degerlendirmeleri ve robotik kontrol sistemlerinde onemli olcutler olarak kullanilmaktadir Kinematik integraller Kuvvetler kinematik degiskenlere gore integrasyon yaparak cesitli fiziksel kavramlarin tanimlanmasinda kullanilabilir Ornek olarak zaman parametresine gore yapilan entegrasyon impuls kavramini ortaya koymaktadir J t1t2F dt displaystyle vec J int t 1 t 2 vec F mathrm d t bu islem Newton un ikinci yasasina gore momentumdaki degisime denk gelmekte ve bu baglamda impuls momentum teoremine yol acmaktadir Pozisyon degiskenine gore yapilan integrasyon bir kuvvetin gerceklestirdigi isin tanimini saglar 13 3 bu islem kinetik enerjideki degisimlerle esdegerdir ve is enerji ilkesine yol acar 13 3 Guc P is W degerinin zamanla degisim oranidir dW dt ve belirli bir zaman dilimi dt suresince meydana gelen pozisyon degisimi dx displaystyle d vec x ile yorungenin genislemesi sonucunda hesaplanir 13 2 dW dWdx dx F dx displaystyle mathrm d W frac mathrm d W mathrm d vec x cdot mathrm d vec x vec F cdot mathrm d vec x bu durumda P dWdt dWdx dx dt F v displaystyle P frac mathrm d W mathrm d t frac mathrm d W mathrm d vec x cdot frac mathrm d vec x mathrm d t vec F cdot vec v ile bir cismin hizini ifade eder Potansiyel enerji Genellikle bir kuvvet yerine onunla matematiksel olarak iliskili olan potansiyel enerji alani kavramindan yararlanilir Mesela bir cisme etki eden yercekimi kuvveti cismin bulundugu noktada var olan yercekimi alaninin etkisi olarak degerlendirilebilir Enerji tanimini is tanimi uzerinden matematiksel olarak yeniden formule ederek bir potansiyel skaler alan U r displaystyle U vec r her bir noktadaki kuvvete esit ve ters yonde olan gradiyent ile tanimlanir F U displaystyle vec F vec nabla U Kuvvetler enerji korunumunu saglayan konservatif ve saglamayan konservatif olmayan olarak iki ana kategoriye ayrilabilir Konservatif kuvvetler bir gradyanina denk gelirken konservatif olmayan kuvvetler bu ozelligi tasimaz ch 12 Korunum Bir kapali sisteme etki eden bir korunumlu konservatif kuvvet enerjinin kinetik ve potansiyel enerji turleri arasinda donusum yapmasini saglayan iliskili mekanik isle karakterize edilir Kapali bir sistemde korunumlu bir kuvvetin etkisi altinda sistemdeki net mekanik enerji korunur Bu kuvvet uzaydaki iki farkli nokta arasindaki potansiyel enerji farkiyla dogrudan iliskilendirilebilir ve bu baglamda suyun bir kot haritasi tarafindan belirlenen yukseklik farklarina gore akis yonu ve siddeti gibi potansiyel alanin bir sonucu olarak degerlendirilebilir ch 12 Korunumlu kuvvetler icerisinde yercekimi elektromanyetik kuvvet ve yay kuvveti yer almaktadir Bu kuvvetlerin her biri icin modeller cogunlukla potansiyellerden kaynaklanan ve belirli bir radial vektor r displaystyle vec r ile ifade edilen konum bagimliligi gosterir Bu durumun ornekleri su sekilde siralanabilir Yercekimi durumunda F g Gm1m2r2r displaystyle vec F text g frac Gm 1 m 2 r 2 hat r burada G displaystyle G yercekimi sabiti ni ve mn displaystyle m n ise n numarali cismin kutlesini ifade eder Bu ifade iki kutle arasindaki cekim kuvvetinin kutleler arasi mesafenin karesi ile ters orantili oldugunu ve kuvvetin yonunun birlestirici dogrultuda oldugunu gosterir Elektrostatik kuvvetler baglaminda F e q1q24pe0r2r displaystyle vec F text e frac q 1 q 2 4 pi varepsilon 0 r 2 hat r burada e0 displaystyle varepsilon 0 bos uzayin elektriksel gecirgenligi olarak tanimlanir ve qn displaystyle q n n numarali cismin elektrik yukunu temsil eder Yay kuvvetleri durumunda F s krr displaystyle vec F text s kr hat r burada k displaystyle k ilgili yayin yay sabiti olarak bilinir ve bu sabit yayin esneklik ozelligini gosterir ch 12 Belirli fiziksel durumlar kapsaminda kuvvetlerin yalnizca potansiyel gradyanlarina bagli olarak modellenmesi yetersiz kalabilir Bu durum cogunlukla uzerinden yapilan makroskopik istatistiksel ortalamanin bir sonucudur Ornek olarak statik surtunme atomlar arasi cok sayida elektrostatik potansiyel gradyanlarindan kaynaklansa da makro olcekli herhangi bir konum vektorunden bagimsiz olarak kendini bir kuvvet modeli olarak gosterir Surtunme disinda korunumlu olmayan diger kuvvetler arasinda cesitli gerilim basinc ve surukleme yer alir Detayli bir aciklama ile bu makroskopik kuvvetlerin her biri mikroskopik potansiyel gradyanlarinin toplam sonuclari olarak konservatif kuvvetlerin bir neticesidir ch 12 Makroskopik duzeyde korunumlu olmayan kuvvetler ile mikroskopik duzeyde korunumlu kuvvetler arasindaki iliski istatistiksel mekanik kullanilarak detayli bir sekilde incelenir Makroskopik kapali sistemlerde korunumlu olmayan kuvvetler sistemlerin ic enerjilerinde degisikliklere yol acar ve siklikla isi transferi ile iliskilendirilirler Termodinamigin ikinci yasasi geregince korunumlu olmayan kuvvetler kapali sistemler icerisinde enerjinin daha duzenli halden daha rastgele kosullara dogru donusumune neden olurken entropinin artmasina yol acar ch 12 BirimlerSI sisteminde kuvvetin birimi newton sembolu N olarak tanimlanir Newton bir kilogram kutleyi saniye karede bir metre ivmelendirebilmek icin gereken kuvvet miktarini ifade eder ve bu birim kg m s 2 olarak formule edilir Karsilik gelen CGS birimi ise dyndir bu birim bir gram kutleyi saniye karede bir santimetre ivmelendirmek icin gerekli olan kuvveti ifade eder yani g cm s 2 Dolayisiyla bir newton yaklasik 100 000 dyn degerine esdegerdir Yercekimi kuvvetlerini olcmek icin kullanilan sistemindeki pound kuvvet lbf olarak tanimlanmistir Bu birim bir uzerine standart yercekimi alaninda yani 9 80665 m s 2 ivme ile etki eden kuvvet olarak ifade edilir Pound kuvvet alternatif bir kutle birimi olarak kullanilabilir bir slug bir pound kuvvetin etkisi altinda saniyede bir feet kare ivme kazandiginda bu kutleye esittir Ayrica mutlak fps sistemi olarak adlandirilan farkli bir foot pound second sistemine ozgu baska bir kuvvet birimi olan poundal bir pound kutleyi saniyede bir feet kare hizlandirmak icin gereken kuvvet olarak tanimlanir Pound kuvvet in metrik sistemdeki karsiligi olan kilogram kuvvet kgf bazi durumlarda kilopond olarak da bilinir newton kadar yaygin olmamakla birlikte bir kilogramlik bir kutleye standart yercekimi tarafindan uygulanan kuvveti ifade eder Kilogram kuvvet cok nadir kullanilan bir kutle birimi olan i bazen mug veya hyl olarak da adlandirilir tanimlar bu kutle 1 kgf lik bir kuvvete maruz kaldiginda 1 m s 2 hizlanir Kilogram kuvvet gunumuzun modern SI sisteminin bir parcasi degildir ve genel olarak kullanimi onerilmemektedir ancak bazi ozel durumlar icin ornegin ucak agirliklarinin jet motorlarinin itme kuvvetlerinin bisiklet jant tellerinin gerilimlerinin tork anahtarlarinin ayarlarinin ve motorlarin cikis torklarinin belirtilmesinde kullanilmaktadir Kuvvet birimleri donusum tablosu gtd Newton SI birimi Dyn Kilogram kuvvet kilopond kp Pound kuvvet Poundal1 N 1 kg m s2 105 dyn 0 10197 kg f 0 22481 lb f 7 2330 pdl1 dyn 10 5 N 1 g cm s2 1 0197 10 6 kg f 2 2481 10 6 lb f 7 2330 10 5 pdl1 kg f veya 1 kp 9 80665 N 980665 dyn gn 1 kg 2 2046 lb f 70 932 pdl1 lb f 4 448222 N 444822 dyn 0 45359 kg f gn 1 lb 32 174 pdl1 pdl 0 138255 N 13825 dyn 0 014098 kg f 0 031081 lb f 1 lb ft s2Burada tum yercekimi birimleri icin kilogram kuvvetin kg f resmi taniminda kullanilan degeri 9 80665 m s2 olarak alinmistir Ilgili diger bir birim icin maddesine bakiniz Kuvvet kavraminin guncellenmesi20 yuzyilin baslarinda gozlemlenen astronomik ve mikroskop alti duzeydeki deneysel sonuclarini aciklamaya yonelik yeni fiziksel teoriler gelistirilmistir Asagida daha detayli bir sekilde ele alinacagi uzere gorelilik teorisi momentin tanimini modifiye etmis kuantum mekanigi ise Newton yasalarinin dogrudan gecerli olmadigi mikroskopik duzeylerde kuvvet kavramini yeniden formule etmistir Ozel gorelilik kurami Ozel gorelilik kurami kapsaminda kutle ve enerji arasindaki esdegerlik bir cismin hizlandirilmasi icin gerekli isin hesaplanmasiyla anlasilabilir Bir cismin hizi arttikca bu durum enerjisi ve dolayisiyla kutle esdegeri eylemsizligi artisina yol acar Bu nedenle cismin daha onceki daha dusuk hizina kiyasla ayni oranda hizlandirilmasi icin daha fazla kuvvet gerekir Newton un ikinci yasasi F dp dt displaystyle vec F frac mathrm d vec p mathrm d t bir matematiksel tanim oldugundan dolayi gecerliligini korur 855 876 Ancak gorelilik kuramina gore goreceli hiz v displaystyle v degerleri icin momentumun korunumu saglanabilmesi adina momentum su sekilde yeniden tanimlanmalidir p m0v 1 v2 c2 displaystyle vec p frac m 0 vec v sqrt 1 v 2 c 2 burada m0 displaystyle m 0 durgun kutleyi ve c displaystyle c isik hizini ifade eder Bu yeni tanim yuksek hizlarda momentumun korunumunu anlamak icin esastir Sabit ve sifirdan farkli durgun kutlesi m displaystyle m ile karakterize edilen bir parcacigin x displaystyle x yonunde v displaystyle v hiziyla hareket ettigi durumda kuvvet ve ivme arasindaki matematiksel iliski asagidaki gibidir 216F g3max gmay gmaz displaystyle vec F left gamma 3 ma x gamma ma y gamma ma z right burada Lorentz faktoru olarak bilinen bu terim goreceli hizin isik hizina yaklasmasi durumunda onemli olcude artis gosterir Bu nedenle asiri hizlarda ayni ivmeyi saglamak icin artan kuvvetlerin uygulanmasi gerekmektedir Goreceli hizin c displaystyle c degerine ulasmasi mumkun degildir 15 8 26 Eger v displaystyle v c displaystyle c degerine kiyasla onemli derecede dusukse g displaystyle gamma degeri yaklasik olarak 1 olur ve F ma displaystyle F ma ifadesi yuksek bir yakinsaklik gosterir Gorelilik baglaminda dahi Fm mAm displaystyle F mu mA mu ifadesi kullanilarak baslangic formuna geri donusturulebilir Bu iliski Fm displaystyle F mu dort vektor m displaystyle m degismez kutle ve Am displaystyle A mu oldugunda gorelilik acisindan gecerlidir Kuantum mekanigi Kuantum mekanigi molekuler atomik veya atom alti boyutlardaki fenomenleri aciklamak amaciyla ortaya konmus bir fizik teorisidir Genel bir yaklasimla bir sistemin boyutlari ne kadar kucukse bu sistemi aciklamak icin gerekli matematiksel modelin kuantum etkilerini dikkate almasi o derece onem kazanir Kuantum fiziginin temel prensipleri klasik fiziginkinden ayrilir Nesnelerin pozisyon momentum ve enerji gibi ozelliklere sahip oldugu fikri yerine belirli bir yapildiginda ne tur sonuclar elde edilebilecegi uzerine odaklanilir Kuantum mekanigi fizikcilerin secilen olcumun belirli bir sonucu elde etme olasiligini hesaplamalarina imkan verir Her olcum icin beklenen deger mumkun sonuclarin olasiliklari ile agirliklandirilarak hesaplanan ortalamadir Kuantum mekaniginde etkilesimler cogunlukla kuvvetten ziyade enerji kavramlari araciligiyla tanimlanir kuantum beklenti degerleri ile klasik kuvvet kavrami arasinda bir iliski kurar bu iliski kuantum fiziginin klasik fizikten koklu bir sekilde ayrilmasi nedeniyle dogasi geregi tam olarak kesin olmayan bir yapiya sahiptir Kuantum fizik alaninda bir konum veya momentum olcumunun beklenti degerlerini hesaplamak icin temel arac olarak kullanilir Bu beklenti degerleri genelde zaman icinde degisim gosterir yani ornegin bir pozisyon olcumu yapildiginda muhtemel farkli sonuclar icin olasiliklar degisebilir Ehrenfest teoremi genel olarak bu beklenti degerlerinin zaman icindeki degisimini aciklayan denklemlerin Newton un ikinci kanununu hatirlatan bir bicimde potansiyel enerjinin negatif turevi olarak tanimlanmis bir kuvvetle formule edildigini one surer Ancak bir durumda kuantum etkileri ne kadar belirginse bu benzerlikten yola cikarak anlamli sonuclar elde etmek o olcude guclesir Kuantum mekanigi mikroskop alti duzeydeki kuvvetlerle etkilesimde bulunan ozellikle atomlar icin hayati onem tasiyan iki yeni kisitlayici unsur sunar Cekirdegin yogun cekim gucune karsin belirsizlik ilkesi bir elektronun olasilik dagiliminin minimum sinirlarini belirler ve Pauli disarlama ilkesi elektronlarin ayni olasilik dagilimini paylasmasini onler Bu durum dejenerasyon basinci olarak adlandirilan bir basinc yaratir Atomlar molekuller sivilar ve katilar uzerinde dejenerasyon basinci ve cekici elektromanyetik kuvvet arasindaki dinamik denge bu yapilarin saglar Kuantum alan teorisi Bir notronun protona donusum surecini gosteren Feynman diyagrami W bozonu iki tepe noktasi arasinda itici bir rol ustlenmektedir Cagdas parcacik fizigi alaninda kuvvetler ve parcaciklarin ivmelenmeleri momentum tasiyici ayar bozonlarinin alisverisinin matematiksel bir turevi olarak izah edilmektedir Kuantum alan teorisi ve genel gorelilik kuramlarinin ilerlemesiyle kuvvet kavraminin aslinda gereksiz oldugu ve bu kavramin momentum korunumundan ve kuantum elektrodinamiginde sanal parcaciklarinin momentumlari dahil kaynaklandigi kavranmistir Momentum korunumu uzayin homojenligi veya simetrisi uzerinden dogrudan cikarimlanabilir ve bu nedenle kuvvet kavramindan daha temel bir oneme sahiptir Bu baglamda gunumuzde tanimlanan temel kuvvetler daha isabetli bir deyisle temel etkilesimler olarak nitelendirilmektedir 199 128 Bu tur etkilesimlerin ayrintili sonuclarini ongorebilmek icin ileri duzey matematiksel tanimlar gereklidir ancak Feynman diyagrami kullanimi yoluyla bu etkilesimlerin kavramsal olarak basit bir bicimde ifade edilmesi mumkundur Feynman diyagraminda her madde parcacigi zaman boyunca ilerleyen ve genellikle diyagramda yukari veya saga dogru artis gosteren duz bir cizgi ile temsil edilir bkz Hayat Cizgisi Madde ve antimadde parcaciklari Feynman diyagrami uzerindeki yayilim yonleri haric birbirleriyle ozdestir Parcaciklarin hayat cizgileri etkilesim dugumlerinde kesismekte ve Feynman diyagrami bir etkilesimden dogan kuvveti parcacik hayat cizgilerinin yon degisikligi ile iliskilendirilmis sekilde dugum noktasinda olusmus olarak gosterir Ayar bozonlari dalgali cizgiler halinde dugumden yayilir ve sanal parcaciklarin degis tokusu halinde yanindaki bir dugumde emilir Feynman diyagramlarinin avantaji kuvvetlerden kavram olarak ayri olmakla birlikte genel temel etkilesim resminin bir parcasi olan diger fiziksel olaylarin da ayni ilkelerle aciklanabilmesidir Ornegin bir Feynman diyagrami zayif nukleer kuvvetten sorumlu olan ayni ayar bozonu araciligiyla gerceklesen bir notronun bozunmasini elektron proton ve antineutrino uretimiyle detayli bir sekilde tasvir edebilir Temel etkilesimlerEvrendeki tum tanimlanmis kuvvetler dort temel etkilesim kategorisine ayrilmaktadir Guclu ve zayif kuvvetler yalnizca cok kisa mesafelerde etkili olup atomalti parcaciklar arasinda ozellikle nukleonlar ve bilesik cekirdekler arasindaki etkilesimlerden sorumludur Elektromanyetik kuvvet elektrik yukleri arasindaki etkilesimlerde yercekimi kuvveti ise kutleler arasindaki etkilesimlerde gorev alir Dogadaki diger tum kuvvetler bu dort temel etkilesimin kuantum mekanigi cercevesinde islemesi ve Schrodinger denklemi ile Pauli dislama ilkesinden kaynaklanan kisitlamalar ile iliskilidir Mesela surtunme kuvveti iki yuzey arasindaki atomlar arasinda etki eden elektromanyetik kuvvetin bir gosterimidir Yaylardaki kuvvetler Hooke yasasi tarafindan modellenmekte olup bu kuvvetler elektromanyetik kuvvetlerin bir sonucudur Merkezkac kuvvetleri donen referans cercevelerindeki ivmelenmeden dogrudan kaynaklanan ivme kuvvetleridir 12 11 359 Farkli kavramlarin neticesinde kuvvetler uzerine temel teoriler ortaya konmustur Mesela Newton un evrensel yercekimi teorisine gore Dunya nin yuzeyine yakin bir yerde dusen cisimler icin etkin olan kuvvet Ay in ve Gunes cevresindeki gezegenlerin hareketlerinden de sorumlu olan kuvvettir Michael Faraday ve James Clerk Maxwell elektriksel ve manyetik kuvvetlerin elektromanyetizma teorisinde birlestigini gostermislerdir Yirminci yuzyilda kuantum mekaniginin ilerlemesi yercekimi disindaki ilk uc temel kuvvetin maddenin fermionlarin ayar bozonu adi verilen sanal parcaciklar araciligiyla etkilesiminin bir sonucu oldugunu ortaya koymustur Standart Model cercevesinde parcacik fizigindeki bu kuvvetler arasindaki benzerlikler bilim insanlarina elektrozayif teoride zayif ve elektromanyetik kuvvetlerin birlestirilmesini ongormelerini saglamis ve bu teori sonraki gozlemlerle dogrulanmistir Doganin Temel Kuvvetleri Etkilesim Ozellik Yercekimi Zayif Elektromanyetik Guclu Elektrozayif Temel KalintiUygulama Alanlari Kutle Enerji Tat Elektrik yuku Renk yuku Atom cekirdekleriEtkilenen parcacik tipleri Genel Kuarklar Leptonlar Elektriksel yuklu Kuarklar Gluonlar HadronlarTasiyici parcaciklar Graviton henuz tespit edilmedi W W Z0 g Gluonlar MezonlarKuarklar icin guc degerlendirmesi 10 41 10 4 1 60 Kuarklara uygulanamazProton notron guc mertebesi 10 36 10 7 1 Hadronlara uygulanamaz 20Yercekimsel GRAVITY gibi cihazlar yercekimi kuvveti algilama konusunda guclu bir arac sunmaktadir Newton in yercekimi yasasi uzaktan etkilesim olarak tanimlanabilir Ornegin Gunes gibi bir nesne Dunya gibi baska bir nesneyi aralarindaki uzakliga bakilmaksizin etkileyebilir Bu etkilesim anlik bir nitelik tasir Newton un teorisine gore herhangi bir cismin konumu degistiginde diger tum cisimler tarafindan hissedilen yercekimi cekimleri ayni anda degisir Albert Einstein bu durumun ozel gorelilikle celistigini ve etkilerin isik hizindan daha hizli yayilamayacagi ongorusuyle uyumsuz oldugunu belirtmistir Einstein bu nedenle gorelilige uygun yeni bir yercekimi teorisi gelistirilmesinin gerekliligini vurgulamistir Merkur un yorungesi Newton in yercekimi yasalariyla ongorulenin disinda bir seyir izlemekteydi Bazi astrofizikciler bu anormalligi aciklayabilecek kesfedilmemis bir gezegen Vulcan hipotezini ileri surmuslerdir Einstein genel gorelilik teorisini gelistirirken Merkur un bu problemli yorungesine yogunlasmis ve teorisinin soz konusu farkliliklari aciklayabilecek bir duzeltme sagladigini tespit etmistir Bu bulgu Newton in yercekimi teorisinin kusurlu oldugunun ilk kez kanitlandigi bir an olmustur Genel gorelilik gunumuze kadar yercekimini en iyi aciklayan teori olarak kabul gormustur Bu teoriye gore yercekimi bir kuvvet olarak degerlendirilmez aksine yercekimi alanlarinda serbestce hareket eden nesneler kendi ataletleri dogrultusunda duz hatlar boyunca icerisinde yol alirlar bu iki uzay zaman olayi arasindaki en kisa uzay zaman yolculugu olarak tanimlanir Nesnenin bakis acisindan bakildiginda tum hareketler yercekiminin hicbir etkisi olmadigi gibi gerceklesir Ancak hareket genis bir cerceveden incelendiginde uzay zamanin egriligi gozlemlenebilir ve kuvvet nesnenin egimli yorungesi uzerinden tespit edilir Bu baglamda uzay zamandaki duz cizgi yolu uzayda egri bir hat olarak algilanir ve bu nesnenin balistik yorunge olarak adlandirilir Ornegin duzgun bir yercekimi alaninda yerden atilan bir basketbol topu parabolik bir yorungede hareket eder Uzay zaman yorungesi neredeyse duz bir cizgidir ve az bir egrilik gosterir egrilik yaricapi birkac isik yili seviyesindedir Nesnenin ivme degisikliginin zaman turevi yercekimi kuvveti olarak ifade edilir Elektromanyetizma Maxwell denklemleri ve bu denklemlere dayali olarak gelistirilen teknikler elektrik ve manyetizma alanlarinda kuvvetle ilgili genis bir fiziksel fenomenler dizisini etkili bir sekilde aciklamaktadir Bu klasik teori zaten gorelilik etkilerini barindirmaktadir Temel parcaciklar arasinda gerceklesen kuantize elektromanyetik etkilesimlerin anlasilmasi kuantum elektrodinamigi QED ile mumkundur QED icerisinde fotonlar tum elektromanyetik etkilesimleri elektromanyetik kuvvet de dahil olmak uzere tanimlayan temel degisim parcaciklari olarak islev gorur Guclu nukleer Cagdas fizikte genellikle parcacik fiziginin kuantum teorileri cercevesinde meydana gelen etkilesimler olarak nitelendirilen iki tur nukleer kuvvet tanimlanmaktadir Guclu nukleer kuvvet atom cekirdeklerinin yapisal butunlugunu saglamakla yukumludur ve protonlar arasi elektromanyetik itme kuvvetini etkisiz hale getirebilme kapasitesi nedeniyle bu ismi kazanmistir 940 Guclu kuvvet gunumuzde kuarklar ve gluonlar arasindaki etkilesimleri kuantum kromodinamigi QCD teorisinin detayli bir bicimde acikladigi bir fenomen olarak kabul edilmektedir Bu temel kuvvet gluonlar vasitasiyla kuarklar antikuarklar ve gluonlarin kendileri uzerinde etkili olup yalnizca temel parcaciklar uzerinde dogrudan bir etkiye sahiptir Hadronlar arasinda ozellikle atom cekirdeklerinde yer alan nukleonlar arasinda gozlemlenen kalinti etki nukleer kuvvet olarak adlandirilir Bu durumda guclu kuvvet nukleer kuvvetin klasik tasiyicilari olan sanal pi ve ro mezonlarini olusturan gluonlar araciligiyla dolayli bir etkilesim sergiler icin yapilan pek cok arastirmanin basarisizlikla sonuclanmasi etkilenen temel parcaciklarin dogrudan gozlemlenemeyecegini ortaya koymustur Bu fenomen renk hapsi olarak tanimlanmaktadir s232 Zayif nukleer Temel etkilesimler icerisinde essiz bir nitelige sahip olan zayif nukleer kuvvet bagli durumlar olusturmaz Bu kuvvet agir W ve Z bozonlari arasindaki degisimden kaynaklanir ve iki cesit bozonun aracilik ettigi iki tur etkilesime yani elektrik yuku tasiyan W ve W bozonlarini iceren yuklu akim ve elektriksel olarak notr Z0 bozonlarini iceren notr akima ayrilir Zayif etkilesimin en bilinen ornegi atom cekirdeklerindeki notronlarin beta bozunumu ve bunun sonucu ortaya cikan radyoaktivitedir 951 Bu yuklu akim turunden bir etkilesimdir Zayif terimi bu kuvvetin guclu kuvvete kiyasla yaklasik 1013 kat daha dusuk alan siddetine sahip olmasindan gelmektedir Ancak kisa mesafelerde yercekiminden daha gucludur Elektromanyetik kuvvetler ile zayif kuvvetin 1015 K sicakliginda ayirt edilemez oldugunu ortaya koyan tutarli bir elektrozayif teori de gelistirilmistir Bu sicakliklar Buyuk Patlamanin baslangic anlarinda plazma carpismalari sirasinda gerceklesmistir 201Ayrica bakinizKati cisim dinamigiKaynakca a b c d e f g h University Physics 6 6yil 1982 bas Addison Wesley ss 18 38 ISBN 0 201 07199 1 Cohen Michael Classical Mechanics a Critical Introduction PDF University of Pennsylvania 3 Temmuz 2022 tarihinde kaynagindan PDF Erisim tarihi 9 Ocak 2024 a b 1897 The Works of Archimedes Erisim tarihi 14 Ekim 2007 Internet Archive vasitasiyla a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab Feynman Richard P 2010 The Feynman lectures on physics Vol I Mainly mechanics radiation and heat New millennium bas New York Basic Books ISBN 978 0465024933 a b c d e f g h i j k l m n o p q r s t u v w x Kleppner Daniel Kolenkow Robert J 2014 https archive org details KleppnerD KolenkowR J IntroductionToMechanics2014 page n102 bolumurl eksik baslik yardim An Introduction to Mechanics 2 2bolum Chapter 3 Forces and equations of motion bas Cambridge Cambridge University Press ISBN 978 0521198110 a b Weinberg S 1994 Dreams of a Final Theory Vintage Books ISBN 978 0 679 74408 5 Lang Helen S 1998 The order of nature in Aristotle s physics place and the elements Cambridge Cambridge Univ Press ISBN 978 0521624534 Hetherington Norriss S 1993 Cosmology Historical Literary Philosophical Religious and Scientific Perspectives Garland Reference Library of the Humanities s 100 ISBN 978 0 8153 1085 3 Sorabji Richard 2010 John Philoponus Philoponus and the Rejection of Aristotelian Science 2 2yayinci Institute of Classical Studies University of London bas s 47 ISBN 978 1 905 67018 5 JSTOR 44216227 OCLC 878730683 Maier Anneliese 1982 Sargent Steven D Ed On the Threshold of Exact Science University of Pennsylvania Press s 79 ISBN 978 0 812 27831 6 OCLC 495305340 a b Drake Stillman 1978 Galileo At Work Chicago University of Chicago Press ISBN 0 226 16226 5 LoLordo Antonia 2007 Pierre Gassendi and the Birth of Early Modern Philosophy New York Cambridge University Press ss 175 180 ISBN 978 0 511 34982 9 OCLC 182818133 20 Nisan 2022 tarihinde kaynagindan Erisim tarihi 7 Nisan 2024 Arnold V I Kozlov V V Neĩshtadt A I 1988 Mathematical aspects of classical and celestial mechanics Encyclopaedia of Mathematical Sciences Dynamical Systems III 3 Anosov D V Berlin Springer Verlag ISBN 0 387 17002 2 OCLC 16404140 9 Aralik 2022 tarihinde kaynagindan Erisim tarihi 7 Nisan 2024 a b c d e f Newton Isaac 1999 The Principia Mathematical Principles of Natural Philosophy Berkeley University of California Press ISBN 978 0 520 08817 7 Bu eser ve Anne Whitman tarafindan Julia Budenz in katkilariyla Ingilizce ye son donemde cevrilmistir Howland R A 2006 Intermediate dynamics a linear algebraic approach Online Ausg bas New York Springer ss 255 256 ISBN 978 0387280592 2005 It s About Time Understanding Einstein s Relativity Princeton University Press ISBN 978 0 691 21877 9 a b c d e f g h i Ling Samuel J Sanny Jeff Moebs William ve digerleri 2021 University Physics Volume 1 ISBN 978 1 947 17220 3 16 Aralik 2021 tarihinde kaynagindan Erisim tarihi 11 Nisan 2024 Hellingman C 1992 Newton s third law revisited Phys Educ 27 2 112 115 Bibcode 1992PhyEd 27 112H doi 10 1088 0031 9120 27 2 011 Quoting Newton in the Principia It is not one action by which the Sun attracts Jupiter and another by which Jupiter attracts the Sun but it is one action by which the Sun and Jupiter mutually endeavour to come nearer together Resnick Robert Halliday David Krane Kenneth S 2002 Physics 1 5 bas ISBN 978 0 471 32057 9 Any single force is only one aspect of a mutual interaction between two bodies Landau L D 1967 General Physics mechanics and molecular physics Oxford Pergamon Press ISBN 978 0 08 003304 4 Translated by J B Sykes A D Petford and C L Petford LCCN 67 30260 3 In section 7 pp 12 14 this book defines force as dp dt Kibble Tom W B Berkshire Frank H 2004 Classical Mechanics 5 5isbn 1860944248 bas Londra Imperial College Press According to page 12 Force can of course be introduced by defining it through Newton s second law de Lange O L Pierrus J 2010 Solved Problems in Classical Mechanics Oxford Oxford University Press ISBN 978 0 19 958252 5 According to page 3 Newton s second law of motion can be regarded as defining force Saletan Eugene J 1998 Classical dynamics A Contemporary Approach Cambridge England Cambridge University Press s 9 ISBN 978 1 139 64890 5 OCLC 857769535 Olenick Richard P 2007 The Mechanical Universe Mechanics and Heat Advanced bas Cambridge Cambridgeshire Cambridge University Press s 134 ISBN 978 0 521 71590 4 OCLC 227002144 a b Thornton Stephen T Marion Jerry B 2004 Classical Dynamics of Particles and Systems 5 5yayinci Thomson Brooks Cole bas ss 49 50 ISBN 0 534 40896 6 a b Landau Lev D 1969 Mechanics 1 Sykes J B Bell J S tarafindan cevrildi 2 2seri bas Pergamon Press ISBN 978 0 080 06466 6 1999 Concepts of Force A study in the foundations of dynamics Facsim bas Mineola NY Dover Publications ss 220 222 ISBN 978 0486406893 Noll Walter April 2007 On the Concept of Force PDF Carnegie Mellon University 17 Aralik 2013 tarihinde kaynagindan PDF Erisim tarihi 28 Ekim 2013 Physics Tutorial Menu 16 Ocak 2008 tarihinde kaynagindan arsivlendi Erisim tarihi 2 Ocak 2008 Henderson Tom 2004 The Physics Classroom and Mathsoft Engineering amp Education Inc 1 Ocak 2008 tarihinde kaynagindan arsivlendi Erisim tarihi 2 Ocak 2008 Physics Static Equilibrium forces and torques 19 Ekim 2007 tarihinde kaynagindan arsivlendi Erisim tarihi 2 Ocak 2008 Cook A H 1965 A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory Nature 208 5007 279 Bibcode 1965Natur 208 279C doi 10 1038 208279a0 a b Young Hugh Freedman Roger Sears Francis ve Zemansky Mark 1949 Pearson Education s 59 82 Watkins Thayer Department of Economics San Jose State University 10 Subat 2011 tarihinde kaynagindan arsivlendi Erisim tarihi 5 Ocak 2008 Kollerstrom Nick 2001 University College London 11 Kasim 2005 tarihinde kaynagindan arsivlendi Erisim tarihi 19 Mart 2007 a b c d e Cutnell John D Johnson Kenneth W 2004 Physics 6 6yer Hoboken NJ bas Wiley ISBN 978 0 471 44895 2 Coulomb Charles 1784 Recherches theoriques et experimentales sur la force de torsion et sur l elasticite des fils de metal Histoire de l Academie Royale des Sciences 229 269 a b Feynman Richard P 2010 The Feynman lectures on physics Vol II Mainly electromagnetism and matter New millennium bas New York Basic Books ISBN 978 0465024940 1966 The principles of electromagnetic theory and of relativity Dordrecht D Reidel s 85 ISBN 90 277 0107 5 OCLC 844001 Ling Samuel J Sanny Jeff Moebs William 2021 University Physics Volume 2 ISBN 978 1 947 17221 0 3 Nisan 2024 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 Scharf Toralf 2007 Chapter 2 Polarized light in liquid crystals and polymers John Wiley and Sons s 19 ISBN 978 0 471 74064 3 Duffin William 1980 Electricity and Magnetism 3 3isbn 978 0 07 084111 6 bas McGraw Hill ss 364 383 Non Calculus Based Physics I 27 Aralik 2007 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Ocak 2008 Fitzpatrick Richard 2 Subat 2006 Strings pulleys and inclines 18 Aralik 2007 tarihinde kaynagindan Erisim tarihi 4 Ocak 2008 Nave Carl Rod Elasticity HyperPhysics University of Guelph 1 Haziran 2023 tarihinde kaynagindan Erisim tarihi 28 Ekim 2013 Nave Carl Rod Centripetal Force HyperPhysics University of Guelph 1 Aralik 2013 tarihinde kaynagindan Erisim tarihi 28 Ekim 2013 Mallette Vincent 1982 2008 Publications in Science and Mathematics Computing and the Humanities Inwit Publishing Inc 29 Subat 2000 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Ocak 2008 2009 General Relativity and the Einstein Equations Oxford Oxford University Press s 39 ISBN 978 0 19 155226 7 OCLC 317496332 Nave Carl Rod Newton s 2nd Law Rotation HyperPhysics University of Guelph 21 Subat 2014 tarihinde kaynagindan Erisim tarihi 28 Ekim 2013 Fitzpatrick Richard 7 Ocak 2007 Newton s third law of motion 5 Aralik 2007 tarihinde kaynagindan Erisim tarihi 4 Ocak 2008 Yank the time derivative of force is an important biomechanical variable in sensorimotor systems 9 Nisan 2024 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 Tremor related feature engineering for machine learning based Parkinson s disease diagnostics 7 Ekim 2022 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 Comparison of methods of derivation of the yank time signal from the vertical ground reaction force time signal for identification of movement related events 17 Aralik 2020 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 The use of yank time signal as an alternative to identify kinematic events and define phases in human countermovement jumping Harry John R Barker Leland A Tinsley Grant M Krzyszkowski John Chowning Luke D McMahon John J Lake Jason 5 Mayis 2021 Relationships among countermovement vertical jump performance metrics strategy variables and inter limb asymmetry in females Sports Biomechanics Ingilizce 1 19 doi 10 1080 14763141 2021 1908412 ISSN 1476 3141 10 Nisan 2024 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 Rosendo Andre Tanaka Takayuki Kaneko Shun ichi 20 Nisan 2012 A Yank Based Variable Coefficient Method for a Low Powered Semi Active Power Assist System Journal of Robotics and Mechatronics 24 2 291 297 doi 10 20965 jrm 2012 p0291 10 Nisan 2024 tarihinde kaynagindan Erisim tarihi 14 Nisan 2024 Hibbeler Russell C 2010 Engineering Mechanics 12 12isbn 978 0 13 607791 6 bas Pearson Prentice Hall s 222 Singh Sunil Kumar 25 Agustos 2007 Conservative force Connexions 16 Kasim 2012 tarihinde kaynagindan Erisim tarihi 4 Ocak 2008 Davis Doug Conservation of Energy General physics 1 Haziran 2023 tarihinde kaynagindan Erisim tarihi 4 Ocak 2008 a b c d e Wandmacher Cornelius Johnson Arnold 1995 Metric Units in Engineering ASCE Publications s 15 ISBN 978 0 7844 0070 8 a b French A P 1972 Special Relativity The MIT introductory physics series reprint bas Londra Chapman amp Hall ISBN 978 0 17 771075 9 Wilson John B The Science Realm John s Virtual Sci Tech Universe 26 Haziran 2009 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Ocak 2008 1993 Hidden variables and the two theorems of John Bell Reviews of Modern Physics 65 3 803 815 arXiv 1802 10119 2 Bibcode 1993RvMP 65 803M doi 10 1103 RevModPhys 65 803 It is a fundamental quantum doctrine that a measurement does not in general reveal a pre existing value of the measured property Schaffer Kathryn Barreto Lemos Gabriela 24 Mayis 2019 Obliterating Thingness An Introduction to the What and the So What of Quantum Physics Ingilizce 26 7 26 arXiv 1908 07936 2 doi 10 1007 s10699 019 09608 5 ISSN 1233 1821 Marshman Emily 1 Mart 2017 Investigating and improving student understanding of the probability distributions for measuring physical observables in quantum mechanics European Journal of Physics 38 2 025705 Bibcode 2017EJPh 38b5705M doi 10 1088 1361 6404 aa57d1 ISSN 0143 0807 Cohen Tannoudji Claude Diu Bernard Laloe Franck 2005 Quantum Mechanics Hemley Susan Reid Ostrowsky Nicole Ostrowsky Dan tarafindan cevrildi John Wiley amp Sons s 242 ISBN 0 471 16433 X 1993 Quantum Theory Concepts and Methods s 302 ISBN 0 7923 2549 4 OCLC 28854083 Lieb Elliott H 1 Ekim 1976 The stability of matter Reviews of Modern Physics Ingilizce 48 4 553 569 doi 10 1103 RevModPhys 48 553 ISSN 0034 6861 the fact that if one tries to compress a wave function anywhere then the kinetic energy will increase This principle was provided by Sobolev 1938 a b Lieb Elliott H 1990 The stability of matter from atoms to stars Bulletin of the American Mathematical Society Ingilizce 22 1 1 49 doi 10 1090 S0273 0979 1990 15831 8 ISSN 0273 0979 bulk matter is stable and has a volume proportional to the number of particles because of the Pauli exclusion principle for fermions Le the electrons Effectively the electrons behave like a fluid with energy density r5 3 displaystyle rho 5 3 and this limits the compression caused by the attractive electrostatic forces Griffiths 2005 Introduction to Quantum Mechanics Second Edition London UK Prentice Hall ss 221 223 ISBN 0131244051 a b Shifman Mikhail 1999 ITEP lectures on particle physics and field theory World Scientific ISBN 978 981 02 2639 8 The Particle Adventure 18 Aralik 2007 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Ocak 2008 12 Ekim 1999 Additional background material on the Nobel Prize in Physics 1999 Nobel Prize 26 Temmuz 2023 tarihinde kaynagindan Erisim tarihi 26 Temmuz 2023 Powerful New Black Hole Probe Arrives at Paranal 24 Eylul 2015 tarihinde kaynagindan Erisim tarihi 13 Agustos 2015 Siegel Ethan 20 Mayis 2016 When Did Isaac Newton Finally Fail Forbes 3 Ocak 2017 tarihinde kaynagindan Erisim tarihi 3 Ocak 2017 Panofsky Wolfgang K Phillips Melba 2005 Classical electricity and magnetism 2 bas Mineola NY Dover Publ ISBN 978 0 486 43924 2 2010 Quantum Field Theory in a Nutshell 2 2isbn 978 0 691 14034 6 bas Princeton University Press s 29 strong 7 g physics Oxford English Dictionary Cevrimici bas Oxford University Press Abonelik veya katilimci kurum uyeligi gerekli Stevens Tab 10 Temmuz 2003 16 Ekim 2011 tarihinde kaynagindan arsivlendi Erisim tarihi 4 Ocak 2008 Goldberg Dave 2017 The Standard Model in a Nutshell Princeton University Press ISBN 978 0 691 16759 6 a b Greiner Walter Muller Berndt Greiner Walter 2009 Gauge theory of weak interactions with 75 worked examples and exercises 4 bas Heidelberg Springer ISBN 978 3 540 87842 1 2008 The Cosmic Microwave Background Cambridge University Press ss 41 42 ISBN 978 0 521 84704 9
 Azərbaycanca
Azərbaycanca Беларускі
Беларускі Dansk
Dansk Deutsch
Deutsch Española
Española Français
Français Indonesia
Indonesia Italiana
Italiana 日本語
日本語 Қазақ
Қазақ Lietuvos
Lietuvos Nederlands
Nederlands Português
Português Русский
Русский සිංහල
සිංහල แบบไทย
แบบไทย Türkçe
Türkçe Українська
Українська 中國人
中國人 United State
United State Afrikaans
Afrikaans